Problem Solving
The branch of mathematics labeled algebra includes many different skills: evaluating expressions, factoring, operating with polynomials or rational expressions, solving various types of equations, and more. Those skills are ultimately tools to solve problems, and yet sometimes the appearance of a “word problem” or “story problem” feels like a new challenge. In this chapter, you’ll find some general suggestions for problem solving as well as a look at some of the categories of problems you’ll encounter most often.
General strategies
If you were asked to solve the equation 3x − 7 = 14, you probably wouldn’t have any hesitation. You have the skills necessary to do that. You may not jump into solving the problem below as quickly, but in fact, it’s the same task.
Keisha made and sold 3 bracelets at a craft fair. After she paid $7 for her materials, she had a profit of $14. How much did she charge for 1 bracelet?
The first thing to remember when you face a problem is that you have the skills. The problem is not a new adventure. It’s just a different way of asking you to do things you know how to do.
The second point seems obvious but it’s often forgotten. Look at this problem.
Now, that probably seems silly, but too often that’s how a problem looks to people. They grab the numbers—1, 3, 7, and 14—and then try to figure out what to do with them. It’s not usually a successful strategy. There’s a lot of information going to waste. So the second thing to remember is to take the time to read the problem. You’re not expected to magically know what to do with the numbers. Read the problem to find that out.
Your job is to translate the problem into an equation, so think about what you need for an equation. There wouldn’t be a need to solve unless there’s a variable, some unknown. Locate that first. (Hint: It’s often in the last sentence.) Choose a variable and write down what it stands for.
Keisha made and sold 3 bracelets at a craft fair. After she paid $7 for her materials, she had a profit of $14. How much did she charge for 1 bracelet?
Let x = the cost of 1 bracelet
Pause for a moment to think about units. This one is not too difficult. The cost of a bracelet is probably in dollars (or dollars and cents). Measurements could be in feet or inches or meters or centimeters or something else. What units are you asked to use? Is all the information in compatible units? If you have to convert some quantity to different units, make a choice of what you’ll convert. Don’t convert several if you can make do with converting one. If you have a choice, think about which conversion is easiest.
Just as it doesn’t make sense to skip over all the words, it’s also unwise to get lost in too many words. Focus on what you really need to know.
Keisha made and sold 3 bracelets at a craft fair. After she paid $7 for her materials, she had a profit of $14. How much did she charge for 1 bracelet?
Try to create one sentence that sums up the important information.
3 bracelets at $x each minus $7 leaves $14
Translate that into algebraic symbols.
(3 bracelets at $x each) minus ($7) leaves ($14)
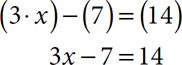
Once you’ve gotten to this point, you’re in familiar territory. You know how to solve this equation. You have the skills.
But it’s not always that easy, you say? There are some types of problems that will require more preparation before you can write the equation and those will be covered later in this chapter. Some will require that you know a common formula, like the area of a triangle or the Pythagorean theorem, but many problems include the needed formula, especially if it is one not used regularly.
The complication you may face is that you know how to solve several different types of equations. In the example above, the equation was a first degree or linear equation. The problem didn’t lead to a quadratic equation because there was nothing that referred to squaring, nor any situation in which two variable quantities are multiplied together. That might come up in a problem about area, or one which specifically talks about squaring. The point is that your job is just to translate what it says. You don’t have to worry about absolute value, or square roots, or rational expressions, or quadratics, unless the problem talks about them.
Like any translation exercise, you need to know your vocabulary and your grammar. Review Chapter 1, Section 1.5 if you need a refresher. Practice with this exercise before looking at the specific types of problems.
For each problem, define a variable and write an equation, but do not solve.
1. If 9 is subtracted from a number, the result is 75. What is the number?
2. If 3 times a certain number is decreased by 17, the result is 43. What is the number?
3. Five times a certain number equals 28 more than that number. What is the number?
4. If 8 times a certain number is decreased by 40, the result is 5 less than the original number. What is the number?
5. A tennis player played 30 games, winning 6 more than she lost. How many games did she win?
6. A father is 5 times as old as his son. The difference between their ages is 44 years. How old is the son?
7. A pen costs 89 cents more than a pencil. Together they cost $1.25. Find the cost of the pen.
8. Carlos and Jaden run on the high school track every evening after work. Combined, they run 6.25 miles but Carlos runs 3 more laps than Jaden. If each lap is 
mile, how many laps does Jaden run?
9. Isaac bought 2 movie tickets and a large bucket of popcorn for $35. A ticket costs twice as much as a large bucket of popcorn. How much does the large bucket of popcorn cost?
10. Kate spends $5.50 a day to ride the bus to and from work, and once a week she spends $8 to have lunch with a friend. When she got paid, Kate set aside $110 for those expenses. Assuming Kate works 5 days a week, how many weeks will that $110 last?
Problems solved with linear equations
Many problems can be solved by linear equations, but there are certain types of problems that follow a clear pattern. Knowing that routine setup for each type of problem makes it easier to translate the problem into an equation. Here are a few of the common types.
Percentage problems
Problems that involve adding tax or a tip to a bill, or applying a discount to a purchase often require you to use percentages. Remember that a percent is just another way of expressing a part or a fraction of a whole. The whole is 100%. A percent greater than 100% indicates more than the whole.
When you calculate, you convert percents to decimals (or fractions): 100% = 1.00, 40% = 0.40, and 3% = 0.03. If you add a tax of 6% to a bill, you’ll have 100% of the bill plus another 6% of the bill, or 106% of the bill. If you receive a 15% discount on your bill, you pay 100% of the bill minus 15% of the bill, or 85% of the bill.
Jeff sees an advertisement for a television at an attractive price. Because Jeff has a loyalty card for the vendor, he receives a 10% discount. When he purchases the TV, the discount is applied, but after that, a 7% tax is added. If Jeff pays $383.27, what was the advertised price to the nearest dollar?
The advertised price of the television, rounded to the nearest dollar, is $398.
Mixture problems
In Chapter 2, you spent some time looking at the general category of mixture problems. Whether they mix coins of different denominators or different types of nuts, candies, teas, or coffees, or even vehicles traveling at different speeds, they can all be made more manageable by organizing the given information into a chart.
The chart should have a row for each individual item and one for the mixture. The columns may show how much (or how many) of the item, the value of one unit of that item, and the total value. In problems about traveling, the columns are the rate of speed, the time traveled, and the total distance. In each case, adding down the last column produces the equation.
Mixing chemicals instead of coffee? The approach is the same, but the column headings change. Your equation still comes from adding down the last column.
A chemist has a 30% solution of a certain chemical, and a pure version of the chemical, but she needs 100 grams of a 65% solution. How many grams of the 30% solution and how many grams of the pure chemical should she mix to produce 100 grams of a 65% solution?
The chemist should use 50 grams of the 30% solution and 50 grams of the pure chemical.
Perimeter problems
Perimeter is the word used to mean the distance around the outside edges of a closed figure. The perimeter of a triangle is the sum of the lengths of its three sides. For some figures, it’s possible to give a formula for the perimeter. The perimeter of a rectangle is P = 2l + 2w, the total of two lengths and two widths. For a square, the perimeter is P = 4s because all sides are the same length. When no particular formula exists, you simply add the lengths of the sides. Perimeter problems will usually tell you how the lengths of sides compare to one another so that you can write an equation that doesn’t involve many different variables.
Each of the two equal sides of an isosceles triangle is 4 centimeters less than twice the third side. The perimeter is 52 centimeters. Find the length of each side.
Let x = the length of the non-equal side
Let 2x − 4 = the length of each of the equal sides
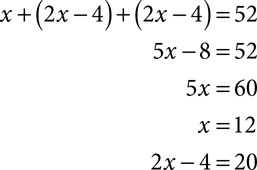
The two equal sides are each 20 centimeters and the third side is 12 centimeters.
Consecutive integer problems
Integers are positive or negative whole numbers and zero. Consecutive integers are integers that follow one another in counting order. The integers 7, 8, and 9 are consecutive integers. If you need to find consecutive integers, you can let x = the smallest integer, like the 7 in the example. Then the second integer can be x + 1, and the third can be x + 2.
Consecutive even integers, like 14, 16, and 18, can be represented as x, x + 2, and x + 4, because you’re counting by 2, not by 1. Consecutive even integers are every other number. Many people are surprised to learn that consecutive odd integers, like 11, 13, and 15, are also represented as x, x + 2, and x + 4. You’re still taking every other number. The difference is just that you’re starting with an odd number instead of an even number.
There are five consecutive integers. If the sum of the last four is decreased by the first, the result is 100. Find the five integers.
The sum of the last four integers decreased by the first integer is 100.
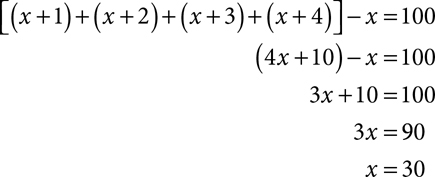
The five consecutive integers are 30, 31, 32, 33, and 34.
Direct variation problems
The ideas of direct variation and combined variation have been covered in Chapter 10. If y varies directly with x, y goes up when x goes up, y goes down when x goes down, and there is a constant of variation, k, that connects x and y. The direct variation equation always has the form y = kx. The constant of variation is the slope of the linear equation, and in direct variation, the y-intercept is always zero.
Word problems about direct variation don’t sound very different than the exercises you’ve seen. Instead of “y varies directly with x,” the problem will use the names of the quantities x and y represent. Use information given in the problem to find k, and then use the specific equation for the problem to find the value the problem asks for.
Water pressure, P, varies directly with the height, h, of the water. When the height is 16 feet, the pressure is 1,000 pounds per square foot. Find the pressure for a height of 10 feet.
Let P = the water pressure in pounds per square foot
Let h = the height in feet
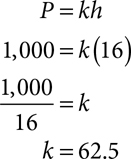
The specific equation for this situation is P = 62.5h.
P = 62.5(10) = 625
For a height of 10 feet, the pressure is 625 pounds per square foot.
1. How many ounces of chocolate that is 60% cocoa should be mixed with 4 ounces of chocolate that is 80% cocoa to produce a mixture that is 75% cocoa?
2. The length of a rectangle is 8 feet less than 3 times the width. The perimeter of the rectangle is 100 feet. Find the length and the width.
3. The area of a rectangle varies directly with its length. When the length is 15 inches, the area is 127.5 square inches. What length will produce an area of 229.5 square inches?
4. If 35% of a certain number is increased by 27, the result will be 80% of the original number. Find the original number.
5. Find 3 consecutive integers whose sum is 96.
6. A vaccine is available in full strength (100%) and 50% solutions, but latest research shows that the safe and effective concentration for children is 65%. How much full-strength vaccine and how much 50% solution should be mixed to produce 100 mg of a 65% solution?
7. The five sides of a pentagon, measured in inches, are consecutive integers. Find the length of each side if the perimeter is 450 inches.
8. Find 4 consecutive even integers whose sum is 124.
9. If your salary is reduced by 10%, by what percent must your new salary be increased to restore your original salary? [Hint: You can make up your own salary, if it helps.]
10. The area of a triangle varies directly with its height. A height of 12.3 cm results in an area of 110.7 cm2. What height will produce an area of 108 cm2?
Problems solved with quadratic equations
Many problems can be solved by using a linear equation, but some problems require other types of equations. Quadratic equations come up frequently and easily. A direct variation equation is usually solved with a linear equation of the form y = kx but if the problem were to say “y varies directly with the square of x” the equation becomes y = kx2. That’s a simple quadratic equation.
When solving these problems, remember to simplify each side of the equation, and then move all terms to one side, so that you have an equation of the form ax2 + bx + c = 0. Solve by factoring, if possible, or use the quadratic formula.
There are many problems in which that change of language, talking about the square of some variable, leads to a quadratic equation. In other problems, the squaring is not mentioned directly, but arises from a formula or because quantities in the problem need to be multiplied.
Pythagorean theorem problems
One rule you’ve probably used many times that leads to equations with squares is the Pythagorean theorem. This right triangle relationship that says that if a and b are the lengths of the legs of a right triangle, the length of the hypotenuse, c, can be found using the rule c2 = a2 + b2.
The longer leg of a right triangle is 14 inches longer than the shorter leg, and 2 inches shorter than the hypotenuse. Find the lengths of the three sides.
It is not reasonable to have a negative side length, so the shorter leg is 10 inches, the longer leg is 10 + 14 = 24 inches, and the hypotenuse is 24 + 2 = 26 inches.
Area problems
Area problems often give rise to quadratic equations because they require that you multiply length times width or base times height. If both quantities involve the variable, the multiplication results in a variable squared.
If one side of a square is increased by 3 feet and the adjacent side is decreased by 2 feet, a rectangle is created that has an area of 36 square feet. Find the area of the original square.
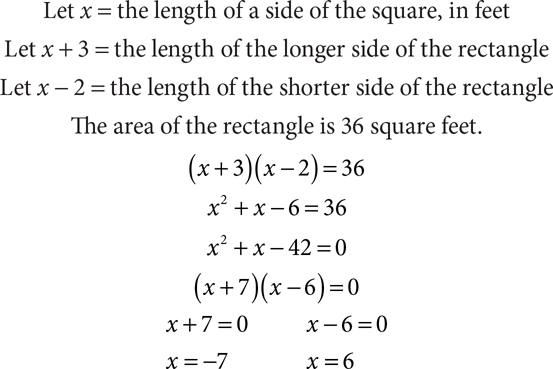
A square cannot have a side with a negative length, so the side of the square is 6 feet, and the area of the square is 36 square feet.
Vertical motion problems
When an object is dropped from a height or thrown upward and allowed to fall back to Earth, its height at any time after it is released depends on three factors: the height from which it was released, the force with which it is thrown, and the force of gravity pulling it back to Earth. This relationship is summarized by the function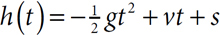 
. In this equation h(t) is the height of the object at time t, g is the acceleration due to gravity (32 feet per second per second in customary units, or 9.8 meters per second per second in metric), and s is the starting height of the object. The v in the middle term refers to the initial velocity of the object. If the object is thrown upward, v is a positive number. If the object is thrown down from a height, v is negative, but if the object is simply released and allowed to fall, v = 0. Be sure to check that units of measurement are consistent.
The chart below summarizes the different forms of the function for different circumstances.
Problems about dropped objects can usually be solved by the square root method, but problems about objects thrown will often require the quadratic formula. Most will have two solutions but only one will make sense in the context of the problem. A negative number for time would refer to before it was thrown, which is not reasonable, so the positive solution would be the one you want. If there are two positive values for time, one indicates the time at which the object reaches that height on the way up, and the other on the way down.
Mr. Patel and his daughter, Deva, like to play catch after dinner. Mr. Patel throws the ball to Deva with an initial velocity of 20 meters per second. When it leaves his hand it is 2 meters above the ground. Deva is most successful in catching the ball when it is 1 meter above the ground. How long after her father throws the ball to Deva will it be 1 meter off the ground?
Let t = the time, in seconds, at which the ball is one meter off the ground
Let v = 20 meters per second
Let s = 2 meters
The particular equation is h(t) = -4.9t2 + 20t + 2.
Find t when h(t) = 1.
Solve 1 = -4.9t2 + 20t + 2 with quadratic formula.
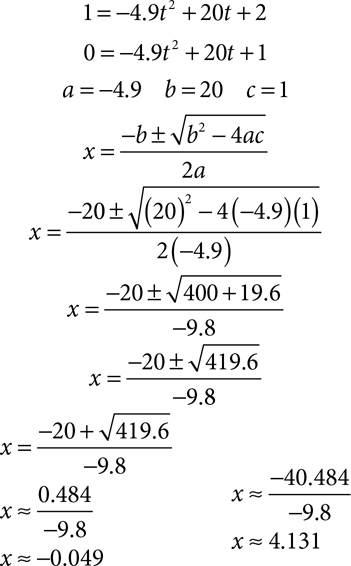
Deva can’t catch the ball before her father throws it, so ignore the negative solution. The ball will be 1 meter off the ground approximately 4.131 seconds after Mr. Patel throws it.
1. The square of a number is 85 less than 22 times the number. What is the number?
2. You have a ladder 20 feet long, and want to lean it against a wall so that the top of the ladder reaches a point 17 feet above the floor. How far from the base of the wall should the foot of the ladder be? [Round to the nearest tenth.]
3. Find three consecutive odd integers such that the square of the first is 3 less than the sum of the other two.
4. A triangle has an area of 45 square meters. The height of the triangle is 3 meters more than twice its base. How long is the base of the triangle?
5. The 86th floor observation deck of the Empire State Building is 320 meters above street level. If an object were dropped from the deck, how long would it take to hit the ground?
6. The perimeter of a rectangle is 28 inches. If the diagonal is 10 inches long, find the dimensions of the rectangle.
7. Before a football game, the referee tosses a coin upward with an initial velocity of 7 meters per second. One team captain must call heads or tails before the coin hits the ground. If the referee’s hand is 1.8 meters above the ground when he tosses the coin, how long does the team captain have to make a call before the coin hits the ground? [Round to the nearest tenth.]
8. A rectangle is 3 times as long as it is wide. If the width is increased by 6 feet, and the length is decreased by 3 feet, the area is doubled. Find the dimensions of the original rectangle.
9. The sum of two numbers is 5. The sum of the squares of the numbers is 53. Find the numbers.
10. Sanjai walked down the stairs from his apartment to the street and then discovered he had forgotten his wallet. His wife came to the window and offered to toss it out so he didn’t have to walk back up. She threw it downward with an initial velocity of 5 meters per second from a height of 13.7 meters. How long did it take to hit the ground? [Round to the nearest tenth.]
Problems solved with rational equations
Rational equations always present a challenge, if only because they can become large and unwieldy. Remember that multiplying through the equation by the simplest common denominator for all rational expressions will clear all the denominators. That may leave a linear equation or a quadratic equation, but solving always seems easier when the denominators are gone.
Extraneous solutions are common in rational equations. Whether you find yourself with one solution or two, remember to check each solution in the original equation. Don’t rely on the version after you clear denominators, because you could have had an earlier error.
The types of problems that most often lead to rational equations are problems about shared work and inverse variation problems.
Work problems
Problems that deal with how long it takes two people (or two machines) to do a job while working together can be organized much the same way as all the mixture problems you saw earlier, if you know one little trick. As soon as you are told how long it takes someone to do the job, express the part of the job they can do in one unit of time—one minute, one hour, one day, whatever.
Suppose George can do a job in two hours and Harry can do it in three hours. How long will it take them to do it working together? You want to set up a table similar to the ones for mixture problems.
The part of the job done in one hour, times the number of hours, will always equal one. Your equation comes not from adding the hours, but from adding the part of the job done in an hour.
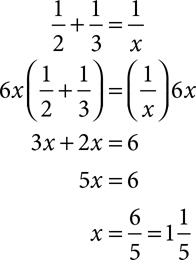
It will take 
hours or 1 hour and 12 minutes for them to do the job together.
Inverse variation problems
Like direct variation problems, inverse variation problems are not very different from the basic statement of the problem. Instead of y and x, you’ll find the names of the quantities that vary inversely. Unlike direct variation, inverse variation problems will have variables in the denominator of a rational expression, so the solution will require solving simple rational equations.
At a fixed temperature, the volume of a certain quantity of gas varies inversely with the pressure. If the volume is 16 in3 when the pressure is 18 psi, find the pressure that produces a volume of 20 in3.
Let V = the volume in cubic inches
Let P = the pressure in psi (pounds per square inch)
Write the general form of the inverse variation equation. Substitute known values to find the constant of variation.
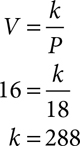
Write the specific equation for this situation. Substitute and solve.
A pressure of 14.4 psi will produce a volume of 20 in3.
1. Two machines in the school office can print final exams. The larger machine can print all the necessary exams in 12 hours, but the smaller one would need 36 hours to do the same job. How long will it take to print all the necessary exams if both machines were used?
2. Elena can complete a quilt in six months, but if she and her mother work on it together, they can complete it in two months. How long would it take Elena’s mom to complete the quilt by herself?
3. Every year, Mr. Song has to produce an annual report that fills many, many pages. If he types it himself, it takes him a week. If he gives it to his administrative assistant to type, she can do it in three days. How long will it take to get the annual report typed if both of them work on it?
4. If the drain pipe in the pool is opened, the pool will drain in eight hours. If, in addition to opening the drain, a pump is set up to pump water out, the pool will be emptied in 5 hours. How long would it take the pump, working alone, to empty the pool?
5. Alicia takes six hours longer than David to complete a project. Working together, they can complete the project in 7.2 hours. How long would it take Alicia to complete the project alone?
6. It takes Ron twice as long to mow his lawn with a push mower as it takes him to mow it with a power mower. He starts working with the power mower but after 45 minutes, he runs out of gas and has to finish the job with the push mower. It takes him an additional 45 minutes to finish the job with the push mower. How long would it have taken Ron to mow the entire lawn with the power mower?
7. For a fixed area, the length and width of a rectangle are inversely related. When the length is 12 cm, the width is 9 cm. Find the width when the length is 27 cm.
8. The time required to drive a fixed distance varies inversely with speed. If a trip takes 6.5 hours at 55 mph, how long will it take if driven at 65 mph?
9. The force of gravity on an object varies inversely with its distance from the center of the Earth. The radius of the Earth is 6378 km. The International Space Station orbits approximately 350 km above the Earth, and the force of gravity acting on it is approximately 2.7 × 1012 Newtons. What would the force of gravity be if the International Space Station were 500 km above the surface of the Earth?
10. The illumination on a surface varies inversely with the square of its distance from a light source. At a distance of 5 ft from the light source, the illumination is 270 foot-candles. At what distance from the same light source will the illumination be 750 foot-candles?
Problems solved with systems
Many of the problems you solved with linear equations could also be solved by means of a system of equations. If a mixture problem talks about making 10 pounds of a tea blend, you could let x represent the amount of one tea and 10 − x represent the amount of the other tea. But you could also let x represent the amount of one tea and y represent the amount of the other, and include the equation x + y = 10 as one equation in your system.
In theory, you could do that with any problem with two unknowns with one variable if you know how the unknowns are related, but that’s easy when you know they add to 10. It’s not so easy when you know that 17 of these and 32 of those cost $107.32. There are times when it’s just easier to use two variables.
Suppose a group of friends go out to get some fast food, and split into two groups in two different lines while waiting to order. The first group bought 8 slices of pizza and 6 soft drinks for $41.14. The second group bought 5 slices of pizza and 6 soft drinks for $30.10. How much does one slice of pizza cost?
Let x = the price of a slice of pizza
Let y = the price of a soft drink
8 slices of pizza and 6 soft drinks cost $41.14
8x + 6y = $41.14
5 slices of pizza and 6 soft drinks for $30.10
5x + 6y = $30.10
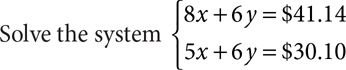
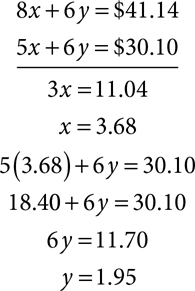
A slice of pizza costs $3.68 and a soft drink costs $1.95.
1. A collection of dimes and nickels is made up of 16 coins and is worth $1.25. How many nickels are in the collection?
2. Adam made a trip to a town 138 miles away. He needed to walk to a bus stop and then ride the bus to the town. The total trip took 6 hours. If Adam walks at 4 miles per hour and the bus has an average speed of 28 mph, how long did Adam walk?
3. Mrs. Connolly invested a total of $6,000 in two investments. One portion was invested at 4% and the remainder at 7%. If her total earnings were $342, find the amount invested at each rate.
4. Chrissy and her younger sister, Claire, play a game to help Claire learn her math facts. Chrissy gives Claire 30 math problems. For each problem Claire gets correct, Chrissy gives her 7 cents, but each time Claire is wrong, she has to give Chrissy back 4 cents. If Claire ends the game with 12 cents, how many problems did she get correct?
5. If the first of two numbers is increased by 10% of the second, the result is 17. If the second number is increased by 25% of the first, the result is 14. Find the numbers.
6. How many pounds of a tea that sells for $1.60 per pound and a tea that sells for $3.20 per pound should be mixed to create 40 pounds of a blend that can be sold for $2.00 per pound?
7. Laura Anne works as a web designer and as an editor. She earns $250 for each web page she creates, and $50 for each page she edits. Last week she worked on a total of 28 pages between these two jobs. If she earned $3,200 last week, how many web pages did Laura Anne produce?
8. A farmer kept pigs and chickens. He has 234 animals, and the animals have a total of 560 legs. How many chickens does he have?
9. Whenever there is a bake sale, Pat makes brownies and cupcakes, 48 pieces total, and they always sell out. Brownies are sold for $1.50 each, and cupcakes for $2.25. At the January sale, Pat’s baked goods sold for a total of $81.00. How many brownies did Pat make?
10. A collection of nickels and dimes is worth $1.35. If the number of nickels and the number of dimes are interchanged, the value would be $1.65. What is the total number of coins?