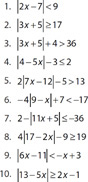Linear inequalities
From the beginning of your training in arithmetic, you used an equal sign (=) to signify several different things: “when you perform this operation you get this result” or “these two expressions have the same value” and others. You may well have taken for granted the equal sign could be read both ways. You saw 5 + 3 = 8 as identical to 8 = 5 + 3. Mathematicians say the relation of equality is symmetric, and not every relationship is. When you meet inequalities, the relationships of “is greater than” or “is less than” in particular, you have relationships that are not symmetric. For example, 7 < 12 is certainly not the same as 12 < 7. One is true; one is not. These not-symmetric relationships bring some new rules.
When you solve an equation, you find the value of the variable that makes the two sides of the equation identical. We think of equations as having one solution, although there are exceptions to that rule. Inequalities, or sentences that involve a variable and say that two expressions are not equal, ask you to find the values that make one side larger than the other. The solution will be a set of numbers, rather than the single value that solves a linear equation. If you think of even the simplest inequality, like x > 4, there are infinitely many numbers that could replace x and make a true statement.
Simple inequalities
Linear inequalities can be solved in much the same way as linear equations with one important exception. When you multiply or divide both sides of an inequality by a negative number, the direction of the inequality sign reverses. Imagine a number line for a moment, and suppose you don’t know the value of x but you do know that the opposite of x is greater than 5. It could be 6, or 10, or 152, or any number to the right of 5 on the number line. If the opposite of x, or −x, were 6, x itself would be −6. If −x were 10, x would be −10. If −x were 152, x would be −152, and so on. Now think about where those values of x lie on the number line. If −x is any number to the right of 5, x is a number to the left of −5. If −x > 5, then x < −5. Remember that the positive and negative sides of the number line are mirror images of one another. When you multiply or divide both sides of an inequality by a negative number, you go through the looking glass and the larger-smaller relationship flips.
Follow the same plan for solving a simple inequality as you would for a simple equation. Simplify the left side, then the right side, until you have no more than one variable term and one constant term on a side. Eliminate one variable term and one constant term by adding or subtracting on both sides. Remember you want the variable on one side and the constant on the other.
It’s only at the last step that you have to think about it a little differently. Your last step is to divide both sides by the coefficient of the variable. If that coefficient is a negative number, you’ll also reverse the direction of the inequality sign: > will become <, and < will become >. If there’s an “or equal to,” it will stay there but the direction of the < or > will change. Here’s an example.
The solution set of an inequality can be graphed on the number line by shading the appropriate portion of the line as shown in Figure 3.1. Use an open circle to mark the boundary of the solution set if the inequality sign is < or >, and a solid dot for inequalities containing ≤ or ≥.
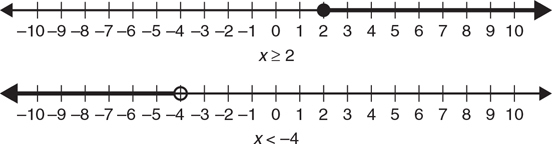
Figure 3.1 Solutions of inequalities graphed on the number line.
Solve each inequality and graph the solution set on a number line.
1. 3x – 5 ≥ 22
2. 2x − 5 > 13 − 4x
3. 3x + 2 ≤ 8x + 22
4. 12x + 3 < x + 36
5. t − 9 ≥ 24 − 10t
6. 2y − 13 > 4(2 − y)
7. 5x + 10(x − 1) ≥ 95
8. 5x − 4 ≤ 13x + 28
9. 3x − 2 < 2x − 3
10. -x + 5 ≥ − 2 + x
Compound inequalities
A compound inequality can be written as two linear inequalities joined by the conjunction and or the conjunction or. The sentence “3x − 7 ≤ 4x + 2 or x − 3 > 9” is an example of a compound inequality using “or.” The sentence “2(3x + 5) ≥ 3x − 19 and x + 11 ≤ 2x − 9” is a compound inequality using “and.” Some and inequalities can be written in a condensed form; for example, the compound inequality 7 > 5x + 2 and 5x + 2 > -13 can be written as 7 > 5x + 2 > -13. One key to using this condensed form is the repetition of the same expression (in this case, 5x + 2) in each inequality as a link between them. You also need to have the inequality signs pointing in the same direction. The condensed form 7 > 5x + 2 > -13 works, and -13 < 5x + 2 < 7 would as well, but 7 > 5x + 2 < -13 does not. To solve compound inequalities, rewrite them as two inequalities, solve each inequality separately, and join the two solutions with the same conjunction.
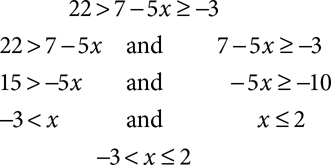
To graph the solution set of a compound inequality, graph the solution sets of the two component inequalities, shading lightly. If the inequalities are connected with the conjunction and, the solution set is the intersection or overlap of the two graphs. You want the numbers that make both the first inequality AND the second inequality true. For compound inequalities that are connected by or, you want to keep both areas of shading. The solution set includes the numbers that solve one inequality OR the other OR both. If the two shaded areas for an or inequality overlap, you may find that you have only one shaded area (see Figure 3.2).
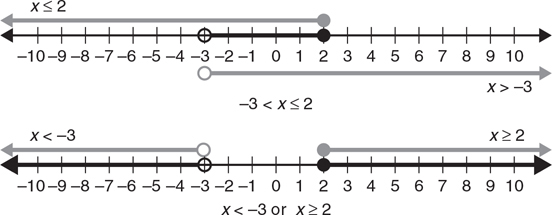
Figure 3.2 Graphing the solution set of a compound inequality
Solve each inequality and graph the solution set on a number line.
1. x − 10 > 30 or x − 4 < − 10
2. 6 < y − 9 < 15
3. −3 ≤ 4x + 5 < 2
4. 6x − 4 ≥ 26 or 3x + 8 < 14
5. −43 < 11x + 1 ≤ 12
6. 8 + 3x > 4 − 3 x or 9x + 12 < − 87 − 2x
7. −10 ≤ 15y + 5 ≤ 6
8. −13 < 47 − 3x < − 2
9. 3x + 4 < 6x + 7 or 5x − 2 > 3x + 18
10. −4y + 31 < y + 16 ≤ 3y + 2
Absolute value inequalities
When you first learn about the idea of absolute value, you describe it in different ways: the number without its sign or a distance without regard to direction. You learn that |7| = 7 but |−7| = 7 as well. Every number has an absolute value, but no absolute value is ever negative. Every absolute value (except 0) may trace back to either a positive or a negative number. That’s important when you start to introduce variables. It’s easy to see the value of x if you’re thinking about |−12| = x, but if you’re trying to determine x in |x| = 5, you need to realize that x could be 5 or −5.
In an absolute value equation, you look for two solutions, unless the absolute value is equal to zero. You consider the possibility that the expression within the absolute value signs is equal to the number on the other side of the equation and the possibility that the expression is equal to the opposite of that number. If you need to solve |3x − 8| = 7, you actually have to solve two equations.
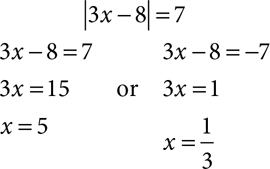
In an absolute value inequality, you also have two cases to consider. If you know, for example, that |x + 1| > 3, you have to consider that x + 1 might be a number greater than 3, like 4 or 12 or 107, so you’d solve x + 1 > 3. But you also have to consider the possibility x + 1 represents a negative number whose absolute value is greater than 3. That could be a number like −4, whose absolute value is 4, or −12, whose absolute value is 12. The absolute value of x + 1 will be greater than 3 when x + 1 is less than −3. The two possibilities you have to examine to solve |x + 1| > 3 are x + 1 > 3 and x + 1 < −3. But only one of those can be true at any time, so |x + 1| > 3 translates to the compound inequality x + 1 < −3 or x + 1 > 3. If your inequality says |x − 2| < 7, x − 2 might be a positive number less than 7, like 3, or a negative number greater than − 7, like −1 (or zero). But if you try some other numbers, like −10, because it’s less than 7, or 12, because it’s greater than −7, you find those don’t work. Only numbers that are both less than 7 and greater than −7 will work. The inequality |x − 2| < 7 is equivalent to − 7 < x − 2 < 7.
To solve an inequality that involves an absolute value, first isolate the absolute value. Simplify the inequality until one side is only an absolute value expression, and the other is as simple as possible. Ideally, it will be just a constant, but if there is a variable term as well, simplify as much as you can.
Rewrite the absolute value inequality as a compound inequality. If the absolute value is greater than the expression on the other side, it will become an or inequality. Absolute values less than an expression translate to an and inequality. The mnemonic “GreatOR, Less ThAND” will help you remember. Translate using the format:
Here are a couple of examples.
|3 + 7x | ≤ 10 becomes −10 ≤ 3 − 7x AND 3 − 7x ≤ 10, or, if you prefer, −10 ≤ 3 − 7x ≤ 10.
Solve each inequality and graph the solution set on a number line.
