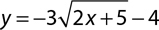Radicals
Once you learn to perform a mathematical operation, it is common to think about how to reverse it. You undo addition with subtraction. You reverse multiplication by division. So once you learn about exponents, or raising a number to a power, it is natural to consider how to reverse that process. If you know the result of exponentiation, of raising a number to a power, how do you find your way back to the number that was the base of the power?
Powers and Roots
For every exponent, every power to which you can raise a base, there is a corresponding root to take you back to the original base. If, for some numbers a and b, a2 = b, then a is the square root of b. Seven is the square root of 49 because 72 = 49. The square root is the root you encounter most often, just as the second power, or square, is the exponent you see most often, but there is a third, or cube root, a fourth root, and a root to “undo” every power. Square roots are written using a radical sign: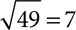 
or, in general, 
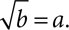The expression under the radical sign is called the radicand. The word “radical” comes from the Latin word radix, meaning root.
You can write other roots in a similar fashion using other powers. Roots other than the square root are indicated by placing a small number, called the index, in the crook of the radical sign. For example, because 23 is equal to 8, two is the cube root of eight, written: 
When no index is shown, the square root is assumed.
When the index of the radical is even, as in square roots, there are both positive and negative roots. Seven is the square root of 49 because 72 = 49, but (−7)2 = 49 as well, so 49 has two square roots, 7 and −7. The positive square root is considered the principal square root, and we agree that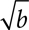 
will denote the principal root of b. We‘ll write 
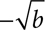if we want the negative square root or 
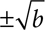if we want both.
There is one only real root when the index is odd. The third, or cube, root of 64 is 4, because 43 = 64 but (−4)3 = −64 not 64. The cube root of −64 is −4.
Notice that, although you‘ve probably learned there is no real square root of a negative number (and that‘s true for all even roots), there is a real cube root of a negative number (and that extends to all odd roots). Because (−4)3 = −64, the cube root of −64 is −4.
Find each of the following roots, if possible. (Try not to use a calculator.)
1. 
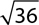
2. 
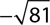
3. 
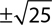
4. 
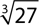
5. 
6. 
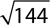
7. 
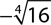
8. 
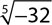
9. 
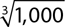
10. 
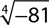
Estimating roots
In the previous exercise, all of the radicands, the numbers under the radical sign, were chosen because they were perfect squares, or perfect cubes, or perfect whatever-power-matched-the-index. There are many, many numbers that don‘t fit that description. The numbers 81 and 100 are both perfect squares, 92 and 102, respectively, but that means that all the numbers between them are not. That means that many numbers will not have tidy integer square roots. (Although we‘re looking at square roots right now, the same can be said for other roots.)
Calculators are a tremendous help when working with roots, because they will give you an estimate of the root accurate to 7 or 8 decimal places. (Before calculators, you had to go look them up in a book of tables, and only get 3 or 4 decimal places.) But for some work, you don‘t need that much information.
Suppose you are working with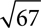 
. You know that 82 = 64 and 92 = 81, and you know 67 is between 64 and 81, closer to 64. That means 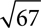is between 8 and 9, closer to 8, and that may be enough to let you estimate your answer. You can do the same with other roots. If you know 33 = 27 and 43 = 64, then 
You can estimate that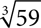 
is between 3 and 4, and closer to 4.
Rational or irrational?
The Real Numbers is the name we give to the set of all numbers used in arithmetic. The Real Numbers include integers, fractions, and decimals, and you‘ve probably seen that those subsets overlap. Integers can be written as fractions by giving them a denominator of 1, and fractions can be written as decimals. Integers, fractions, and decimals are subsets of the Real Numbers that overlap or intersect. The Real Numbers can be divided into two disjoint, or non-overlapping subsets, called the Rational Numbers and the Irrational Numbers.
The Rational Numbers are all numbers that can be written as a ratio of two integers. In simple language, they‘re numbers that can be written as fractions. The Irrational Numbers are the numbers that can‘t be written that way. Rational numbers are easy to think of : ½, −7, and 1.7 are examples. The number ½ is already a fraction, −7 can be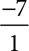 
and 1.7 can be 
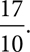Not all decimals are rational, however. Decimals that terminate, like 0.5 or 1.7, can be written as fractions, and repeating decimals, like 0.3333…, which is equal to ⅓, are rational, but decimals that do not terminate and do not repeat cannot be expressed as the ratio of two integers and so are irrational.
Irrational numbers probably don‘t come to mind as quickly, so you may be surprised to know that there are more irrational numbers than rational numbers. Once you find one irrational number, that number times any rational number gives you another irrational number. So if you found 2 irrational numbers, you actually would have twice as many irrationals as rationals, and there are many more than 2 irrational numbers. Many roots are irrational, and therefore are decimals that don‘t terminate and don‘t repeat. For example,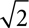 
≈ 1.414213562 … . That decimal goes on forever, and no matter how many digits of it you write, when you square that number, it won‘t give you exactly 2. It will come extremely close, but not exactly equal.
Exact or approximate?
Because you can‘t write all the digits of a decimal that doesn‘t end and doesn‘t repeat, when a root is an irrational number and you try to write it as a decimal, you only get an approximate answer. There are times when an approximate answer is good enough, but at other times, you‘ll want to express the exact value of the root. In those cases, you‘ll have to leave the number in radical form, but you‘ll want to try to rewrite it as a rational number times a simpler radical.
Place each of the following roots between two consecutive integers. Then make your best guess at the approximate value of the root, to the nearest tenth. (Don‘t use your calculator to find the root. Make an educated guess. If you must, you can use your calculator to check.)
1. 
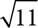
2. 
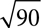
3. 
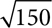
4. 
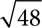
5. 
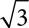
6. 
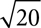
7. 
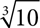
8. 
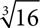
9. 
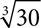
10. 
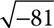
Simplifying radical expressions
To make radicals easier to work with, you‘ll want to put them in simplest radical form. Simplest radical form means the expression contains only one radical, the radicand is as small as possible, and there is no radical in the denominator (or divisor) of a quotient. If there is any arithmetic to be done, do it, so that only one radical remains. The radical 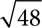is a single radical, but 48 = 16 × 3, and 16 is a perfect square, so it‘s possible to write 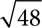as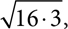 
which is equivalent to 
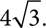Always try to have the smallest possible radicand.
Simplest radical form
The principal rule for simplifying radicals tells us that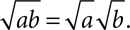 
This rule lets you turn the product of two radicals into a single radical, and it lets you rewrite a radical as a multiple of a smaller radical. You can rewrite 
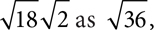or simply 6, and you can take 
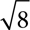and realize that it‘s equivalent to 
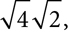which is equal to 2 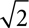because the square root of 4 is 2. By looking for perfect square factors of the radicand and applying this rule, you can rewrite radical expressions with smaller radicands.
When variables appear under radicals, it‘s still possible to simplify if you work carefully: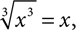 
and 
For even roots, like square roots, you need a bit more care. It‘s easy to think that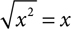 
and you‘ll often see that written, but it‘s not technically correct. If we write 
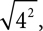that‘s 
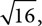which is 4. We said that 
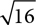would mean the principal square root, so we only need 4, not −4. If we write 
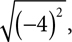however, that‘s also 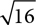, or 4. Notice the original had −4, but we ended with 4. When you write 
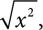you don‘t know if x is a positive number or a negative number, but you want a positive result. To be sure we get that, we say 
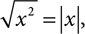the absolute value of x.
Put each expression in simplest radical form.
1. 
2. 
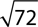
3. 
4. 
5. 
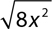
6. 
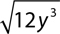
7. 
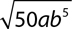
8. 
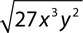
9. 
10. 
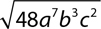
Rationalizing denominators
Because radicals are often irrational, having a radical in the denominator of a fraction can make it hard to estimate the quotient. If you have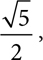 
you can think 
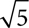is a little more than 2, so if you divide it by 2, you get a little more than 1. When you look at 
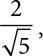on the other hand, it‘s harder to do that kind of approximation. That‘s one reason you don‘t want radicals in the denominator.
If the denominator of an expression is a radical or a multiple of a radical, you can remove the radical, or rationalize the denominator, by multiplying the numerator and denominator of the fraction by the radical in the denominator. This is the same method you use to express fractions with a common denominator. Multiplying both numerator and denominator by the same number is equivalent to multiplying by 1, so it changes the appearance of the fraction but not the value.
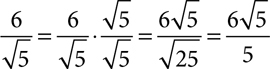
If the denominator is a sum or difference that includes a radical, you will still want to multiply the numerator and denominator by the same number, but multiplying by just the radical will not be effective. You will need to multiply by the conjugate of the denominator, the same two terms connected by the opposite sign. The conjugate of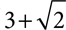 
is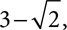 
and the conjugate of 
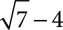is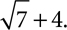 
Multiplying by the conjugate eliminates the radical because when you multiply the sum and difference of the same two terms using the FOIL rule, the middle terms, where the radicals would have been, add to 0.
Rationalize the denominators and put each expression in simplest radical form.
1. 
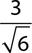
2. 
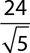
3. 
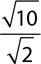
4. 
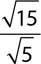
5. 
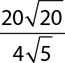
6. 
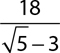
7. 
8. 
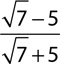
9. 
10. 
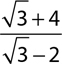
Adding and subtracting radicals
Only like radicals can be combined by addition or subtraction, and they combine like variable terms, by adding or subtracting the coefficients, the numbers in front.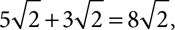 
but 
cannot be combined.
Problems that look like unlike radicals at first glance may simplify down to like radicals. When you need to combine radicals by addition or subtraction, first put each term in simplest radical form and then combine like radicals.
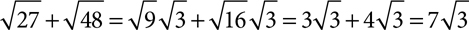
Simplify each expression as completely as possible.
1. 
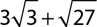
2. 
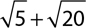
3. 
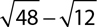
4. 
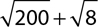
5. 
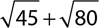
6. 
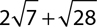
7. 
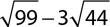
8. 
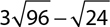
9. 
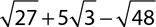
10. 
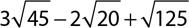
Solving radical equations
Radical equations are equations that contain one or more radicals with the variable in the radicand. The key to solving radical equations is isolating the radical and then raising both sides of the equation to a power so that the radical sign is lifted.
One radical
To solve an equation containing one radical, isolate the radical by moving all terms that do not involve the radical to the other side. Square both sides of the equation, and solve the resulting equation. Be sure to check solutions in the original equation to eliminate any extraneous solutions. Extraneous solutions are values that do not satisfy the equation, even though you‘ve done nothing wrong. They often turn up when solving radical equations.
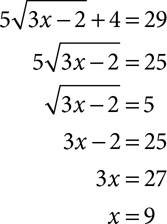
Solve each equation. Check your answers in the original equations. If the equation cannot be solved, write No solution.
1. 
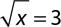
2. 
3. 
4. 
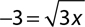
5. 
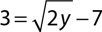
6. 
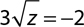
7. 
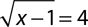
8. 
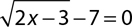
9. 
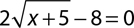
10. 
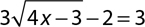
Two radicals
When an equation contains two radicals, choose one to eliminate first. Isolate that radical, and square both sides. This may mean that you need to FOIL one side, and you‘ll probably find that while squaring the isolated radical eliminates that radical, FOIL multiplication on the other side will lift one radical sign but introduce another. Just isolate the remaining radical, square both sides again, and solve the resulting equation. Be sure to check solutions in the original equation. Extraneous solutions are common.
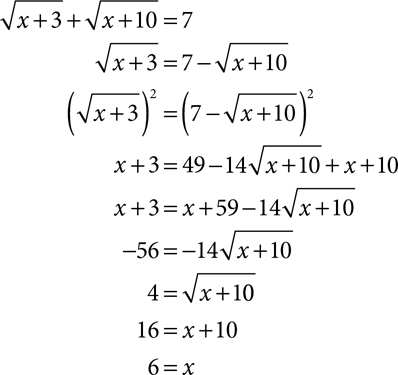
Solve each equation. Check for extraneous solutions.
1. 
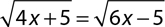
2. 
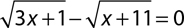
3. 
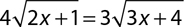
4. 
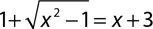
5. 
6. 
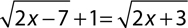
7. 
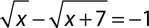
8. 
9. 
10. 
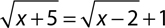
Graphing square root equations
The graph of a square root equation looks like half of a parabola lying on its side. The graph of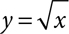 
begins at the origin and forms a slowly rising curve in the first quadrant as shown in Figure 8.1. A negative multiplier in front of the radical will flip the graph over the x-axis.
Figure 8.1 The top half of a parabola on its side is the graph of the square root function.
Because negative numbers have no square roots in the real numbers, the graph only exists for values of x that make the radicand positive. The graph of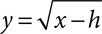 
begins at (h, 0), and the graph of 
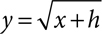begins at (−h, 0). A constant added on the end of the equation moves the graph up or down. Consider where the graph begins before choosing x-values for your table of values.
Graph each function by making a table of values and plotting points.
1. 
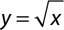
2. 
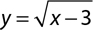
3. 
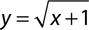
4. 
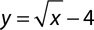
5. 
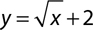
6. 
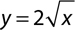
7. 
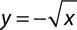
8. 
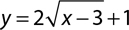
9. 
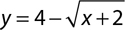
10. 