The Invention of Science

10 Hypotheses/Theories

… an accompt of a Philosophicall discovery … being in my Judgment the oddest if not the most considerable detection i i which hath hitherto beene made in the operations of Nature.

– Isaac Newton to Henry Oldenburg, 18 January 1672

§ 1

‘In the beginning of the Year 1666’ Isaac Newton had just turned twenty-three (his birthday was Christmas Day). The year before, he had obtained his BA degree; a year or so later he began to develop his theory of gravity; less than four years later, in October 1669, he became Lucasian professor of mathematics (at the time the only chair in mathematics at Cambridge), and exactly four years later, in the beginning of 1670, he gave his first university lectures, on the subject of optics. In the beginning of 1666, he tells his readers, he acquired a prism. Plenty of people before Newton had used a prism to split light into the colours of the spectrum; as it happens, all of them had projected the light from the prism on to a nearby surface. Newton set up his prism in his rooms at Trinity: he made a hole in the shutter of his window to let in a thin beam of light and placed his prism near the hole so that the light from it was projected on to a wall that was 22 feet away. The sun is circular; the hole in Newton’s shutter was circular, and so the patch of colours on the wall should also have been circular; but it was not, it was about five times longer than it was wide.¹

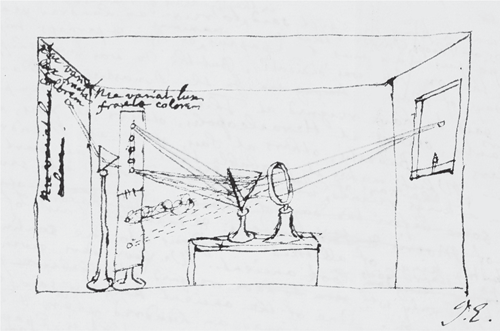
This sketch of the experimentum crucis was produced by Newton to provide a guide for an illustration to accompany the French translation of the Opticks (1720). A ray of light enters the darkened room through a hole in the shutter at the right; it passes through a lens to narrow the beam, and then through a prism, which splits it into the colours of the rainbow, which are projected in an oblong shape on to a screen. One colour passes through a hole in the screen and encounters a second prism. This colour is refracted a second time, but it remains a fine beam of light and its hue is unchanged.

Newton considered various possibilities. He established there was nothing wrong with the prism, and that the light travelled in a straight line from the prism to the wall, that it wasn’t curving in some sort of odd fashion, like a tennis ball with spin on it. So he made the light pass through a smaller hole before the prism, and then passed fractions of the light that emerged through another small hole in a board, on the other side of which he placed a second prism. White light entering the first prism was split into a spectrum of colours, but each colour remained the same as it passed through the second prism, and each colour was refracted by the second prism to the same degree that it had been refracted by the first: this he calls the experimentum crucis. Newton had discovered that white light is not homogeneous but is made out of all the colours of the spectrum, and that each colour is refracted by a different amount as it passes through a prism. He went on to conclude that a reflecting telescope would be far superior to the standard refracting telescope because the image would not be marred by a halo of the different colours of the spectrum (although it was another two years before he had the chance to pursue this idea properly).ii ii In 1670 he lectured on his new theory of light and colours, and in 1672 this became his first publication, ‘A Letter of Mr Isaac Newton, Professor of the Mathematicks in the University of Cambridge; Containing His New Theory about Light and Colors’.

The story as Newton tells it will not do. The experiment he describes cannot be performed in Cambridge at the beginning of the year: it requires the sun to reach an elevation of 40 degrees above the horizon. In any event, Newton was not in Cambridge at the beginning of 1666. In a conversation towards the end of his life he said he had bought the prism in August 1665 (corrected in the manuscript to 1663) at Sturbridge fair, but there was no fair in 1666, and he was not in Cambridge for the fair of 1665. The best we can do is say that the first experiments with a prism probably took place shortly before June 1666 (when Newton left Cambridge to escape the plague), that the prism was purchased at some other fair and that Newton then conducted further experiments, including the crucial experiment, in the summer of 1668.

The exact date hardly matters. More important is the evidence of Newton’s notebooks, which suggests that he knew about the differential refraction of colours in 1664, at which date he already had a prism (perhaps purchased at Sturbridge fair in August 1663). Newton looked through his prism at a card, half of which was white, and half painted black; and at a thread, half of the length of which was red and the other half blue: in both cases the prism appeared to split the object in two, failing to line up one colour with the other. When Newton performed his experiment in 1666 it was probably deliberately designed to produce the elongated spectrum, an effect he describes as if were a complete surprise. Newton’s modern biographer, Richard Westfall, concludes that we should regard Newton’s claim to have been surprised by the oblong image cast by the prism ‘as a rhetorical device which is not to be understood literally’.² Thomas Kuhn maintained that ‘[t]he implication of Newton’s account of 1672 is wrong in that Newton did not proceed so directly or so immediately from the first prism experiment to the final version of the theory as the first paper would imply.’³ Peter Dear goes further (too far, perhaps): Newton’s account is ‘spurious’ for ‘the event described did not actually take place’.⁴

Why would Newton redescribe what had actually happened in this way? One answer is that he wanted to pretend that he had worked from the phenomena to a theory, and not the other way round: the Royal Society admired Bacon, and this would have been the Baconian way to proceed.⁵ Another is that his reference to an experimentum crucis is an implicit nod to Pascal’s Puy-de-Dôme experiment: Pascal’s experiment had been preceded by earlier experiments and earlier theorizing, but in a way that was irrelevant. Why not just cut to the chase? (Boyle would have been horrified, since he had always insisted that experimental reports must be a faithful record of what had actually happened, but in a passage cut from the published version of his paper Newton expressed impatience with lengthy historical narrations.)iii iii

We can debate when Newton conducted his prism experiments, and we can argue about the order in which he performed them and exactly when he formulated his first theory, but there is no scope for debate as to whether Newton conducted the experiments he describes – the events certainly took place, even if the when and why are now hard to establish. Conventional history of science tends to stop at this point. But I want to focus on something else: Newton says in his first publication that he is presenting a new ‘doctrine’; the text is headed by the editor, Oldenburg, ‘A Letter of Mr Isaac Newton … containing his New Theory about Light and Colors’ – this is the first article in the Philosophical Transactions to have the word ‘theory’ in its title, and it is only in subsequent correspondence that Newton himself adopts the word.⁶ A critic, Ignatius Pardies, called Newton’s paper ‘a most ingenious hypothesis’, ‘an extraordinary hypothesis’ which, if true, would overturn the foundations of optics.⁷ Newton, replying in Latin, explained that he had decided not to consider this an insult:

I do not take it amiss that the Rev. Father calls my theory an hypothesis, insomuch as he was not acquainted with it. But my design was quite different, for it seems to contain only certain properties of light, which, now discovered, I think easy to be proved, and which if I had not considered them as true, I would rather have them rejected as vain and empty speculation, than acknowledged even as an hypothesis.⁸

Pardies replied, insisting he had not used the word ‘out of any disrespect’.⁹ Newton responded that he thought of his own work as establishing the properties of light; one might, if one wanted, then hypothesize about the possible cause of those properties, but hypotheses should be subservient to the properties of things, and the only useful ones were the ones that led one to devise new experiments. He went on to complain that, in this case at least, there was no difficulty in constructing hypotheses that appeared to fit the facts: ‘[I]t is an easy matter to accommodate hypotheses to this doctrine. For if any one wish to defend the Cartesian hypothesis, he need only say that the globulesiv iv are unequal, or that the pressures of some of the globules are stronger than others, and that hence they become differently refrangible, and proper to excite the sensation of different colours.’¹⁰ (We know from Newton’s notebooks that he had started his work on refraction with the idea that ‘slowly moved rays are refracted more than swift ones’, precisely the sort of hypothesis he was now rejecting as pointless.)¹¹ He ended his letter by returning to the subject and saying that he was sure Pardies meant no harm, ‘as a practice has arisen of calling by the name hypothesis whatever is explained in philosophy’, but that he felt that this practice could prove ‘prejudicial to true philosophy’.¹²

He had in fact used the word ‘hypothesis’ himself in his original publication, but only to refer to an inaccurate mathematical rule of thumb;¹³ more to the point, Oldenburg had removed a passage in which he insisted that what he was proposing was not an hypothesis, for he had proved his conclusions beyond any doubt.v v Pardies had thus touched on a fundamental difference between Newton and the Royal Society of the 1660s and early 1670s: unlike Newton, the Royal Society favoured tentative expressions of opinion. My first goal in this chapter, then, is to establish why Newton was hostile to the word ‘hypothesis’ and felt that its use in the context of his own work amounted to an insult.

§ 2

The fashion for the word ‘hypothesis’ was new; it began with the publication of Descartes’ Principles in 1644. There, in the third part, Descartes turned from the various ‘hypotheses’ that had been propounded to explain the movements of the planets (those of Ptolemy, Tycho and Copernicus), to discuss the task of explaining movement and change on the earth. Three crucial paragraphs (43–45) carry the following marginal glosses:

43: If a cause allows all the phenomena to be clearly deduced from it, then it is virtually impossible that it should not be true.

44: Nevertheless, I want the causes that I shall set out here to be regarded simply as hypotheses.

45. I shall even make some assumptions which are agreed to be false.¹⁴

It is not surprising that Descartes’ formulations provoked confusion and controversy. First, he seemed to say that a hypothetical cause could give one true knowledge; then to backtrack and say that his arguments were only hypothetical; and finally to acknowledge that some of his arguments must be false. Where did this leave the new philosophy? Was it producing indisputable knowledge that could not be contested? Knowledge that might or might not be true? Or knowledge that was obviously false? From 1644 on, the use and status of hypotheses became a central issue.

In order to understand what is going on here it helps to know that ‘hypothesis’ had three distinct technical meanings in the Middle Ages.¹⁵ In logic an hypothesis was something that came under the thesis (‘hypo-’ means ‘under’ in Greek, as in ‘hypodermic’, a needle which goes under the skin). So one might say that human beings are mortal (the thesis); Socrates is a human being; so Socrates is mortal. Here the statement that Socrates is a human being is an ‘hypothesis’ which follows after the thesis and generates the claim that Socrates is mortal; it can be stated in the hypothetical form ‘If Socrates is a human being, then he is mortal.’ That example is straightforward, but consider this one: the apostle Peter had authority over the Church; the pope is Peter’s successor; therefore the pope has authority over the Church. A Catholic would regard this as a valid syllogism, while a Protestant would maintain that the hypothesis is false; the pope may be Peter’s successor as bishop of Rome, but he is not Peter’s successor in the required sense.

In mathematics the word ‘hypothesis’ was also used to mean a supposition or postulate upon which an argument was based; in geometry, for example, one might propose to argue on the assumption that two angles were equal, even though they had not been proved to be so. But in mathematics the word ‘hypothesis’ also had a quite different technical meaning.¹⁶ An hypothesis was the theoretical model which generated predictions of the future locations of the planets in the heavens. Different hypotheses might produce the same result: for example an eccentric circle will generate exactly the same movement as an epicycle upon a deferent. There might be philosophical reasons for preferring one to the other, but an astronomer could happily use either to perform calculations. Thus what mattered about an hypothesis was not that it be true, but that it produce accurate results (and what we consider to be mistaken hypotheses were quite capable of generating accurate results). Henry Savile, when invited to state a preference between Ptolemy and Copernicus, replied: ‘hee cared not which were true, so the Apparences were solved, and the accompt exact: sith each way either the old of Ptolomy, or the new of Copernicus, would indifferently serve an Astronomer.’¹⁷ In this sense, of an account that saves the phenomena, but may or may not be true, we find Hobbes using the word ‘hypothesis’ (in Latin) before 1640, and this is the sense in which Descartes uses the word ‘hypothesis’ in his discussion of cosmology.vi vi ¹⁸

Those who held that Copernicanism was literally true, however, insisted that in this case the truth of the hypothesis mattered. Kepler distinguished between a geometrical hypothesis – the mathematical model used to generate predictions – and an astronomical hypothesis, the actual path of the planet through the heavens. As geometrical hypotheses, the Ptolemaic, Tychonic and Copernican systems were equivalent; but as astronomical hypotheses they were radically different. It is from this line of thinking that we get, it would seem, the first reference in English to an hypothesis as a theory that needs to be tested. In his 1576 edition of his father’s Prognostication Thomas Digges proposed ‘An Hypothesis or supposed cawse of the variation of the Cumpasse, to be mathematically wayed [i.e. weighed, meaning assessed]’.¹⁹ The implication is that if the hypothesis passes the test it will be promoted to being a true statement. This seems to be the earliest usage of the term ‘hypothesis’ in its standard modern sense, at any rate in English.vii vii For the little group looking for a mathematical pattern in the variation of the compass – what Robert Norman called ‘a Theorik with Hypotheses, and rules for the salving of the apparant irregularitie of the Variation’²⁰ – it was a simple step to adopt the astronomical language of ‘hypotheses’ and give it a new experimental twist.²¹ But this twist effectively marks the birth of a new philosophy of science: a scientific principle is now an hypothesis that has survived the test of experience. Thus Galileo in his ‘Discourse on the Flux and Reflux of the Sea’ of 1616 presents his theory of the tides as an hypothesis which needs to be confirmed or disconfirmed by a systematic programme of observations.²²

Boyle used the word ‘hypothesis’ in this sense over and over again, and even wrote a short paper (never published) on ‘the requisites of a good hypothesis’. Boyle thought of an hypothesis as a useful step towards establishing the truth: a good hypothesis leads to novel predictions which can be tested by experiments. At its best an hypothesis is like the key which enables one to decipher a coded communication: everything now makes sense, and it is evident that this, and this only, is the right solution (exactly the view expressed by Descartes in §43).viii viii Locke wrote a section of the Essay on the ‘true use of hypotheses’. He acknowledged that hypotheses may lead us to new discoveries, but stressed that most (‘I had almost said all’) hypotheses in natural philosophy were no more than very doubtful conjectures.²³

William Wotton, on the other hand, like Newton, generally used the word to refer to arguments that are false or unsatisfactory. For Wotton, to say an argument is an hypothesis is to reject it, for if it really explained all the phenomena it would no longer be an hypothesis. And we find a third use, as in Descartes’ §45: the use of ‘hypothesis’ to refer to an argument that is acknowledged to be false but held in some way to be useful. Osiander, in his anonymous introduction to Copernicus’s On the Revolutions, insisted that Copernicus should only be read as presenting an hypothesis, not as describing how the world really is. Bellarmine told Galileo that he could talk about Copernicanism if he did so hypothetically – Copernicanism being, as far as Bellarmine was concerned, untrue.²⁴ Descartes, following in this tradition, used the word in §45 to refer to principles that ought, for theological reasons, to be acknowledged as false, but that are helpful if one pretends they might be true.ix ix ²⁵

There is a futher use of the word ‘hypothesis’ that we must note. In Gilbert’s On magnetism (1600) the word is used in a purely conventional way in the main body of the text, to refer, for example, to the Copernican hypothesis. But something strange happens in the preface:

[N]othing hath been set down in these books which hath not been explored and many times performed and repeated amongst us. Many things in our reasonings and hypotheses will, perchance, at first sight, seem rather hard, when they are foreign to the commonly received opinion; yet I doubt not but that hereafter they will yet obtain authority from the demonstrations [i.e. experiments] themselves … [W]e but seldom quote ancient Greek authors in our support, because … our doctrine magnetical is at variance with most of their principles and dogmas … [O]ur age hath detected and brought to light very many things which they, were they now alive, would gladly have accepted. Wherefore we also have not hesitated to expound in convincing [probabilibus] hypotheses those things which we have discovered by long experience.²⁶

Gilbert here uses the word ‘hypothesis’ as we would use the word ‘theory’; we assume that an hypothesis awaits confirmation or disconfirmation, but Gilbert’s hypotheses derive from and are confirmed by a long sequence of experiments. They are new additions to secure knowledge; they are, in our terms, theories. We find the same usage in Galileo. In his book on sunspots (1613) he refers to his claim that the moon is opaque and mountainous as a true hypothesis, confirmed by sensory experience.²⁷

Thus the standard modern meaning of ‘hypothesis’, as an explanation that may in due course be tested and which, if confirmed, will be elevated to the status of a theory, did not become firmly established until the 1660s.²⁸ In 1660 Robert Boyle described an experiment proposed by Christopher Wren that ‘would discover the truth or erroneousness of the Cartesian Hypothesis concerning the Ebbing and Flowing of the Sea’;²⁹ Power’s Experimental Philosophy of 1664 uses the word frequently; then in 1665 Hooke prefaced his Micrographia with a dedicatory letter to the Royal Society: ‘The Rules YOU have prescrib’d YOUR selves in YOUR Philosophical Progress do seem the best that have ever yet been practis’d. And particularly that of avoiding Dogmatizing, and the espousal of any Hypothesis not sufficiently grounded and confirm’d by Experiments.’ From this point on ‘hypothesis’, meaning a conjecture or query (to use Hooke’s terms) which could be confirmed or disconfirmed by observation or experiment, became central to the terminology of the new science. Indeed one can say that ‘hypothesis’ only really acquired its modern sense after the foundation of the Royal Society.

These various meanings of ‘hypothesis’ serve to explain its peculiar distribution through seventeenth-century texts. Most mathematicians – Galileo, Pascal, Descartes, Newton – were familiar with the word’s use in technical astronomy, and tended to avoid it in other contexts. But once it became common to refer to Copernicanism as an hypothesis, then other hypotheses – magnetical, atomic, mechanical – multiplied. These were the big theories of the new science; within them smaller hypotheses, such as Digges’s account of the declination of the compass needle, or Boyle’s account of the spring of the air, could be neatly packed.

But the term was not uncontroversial, particularly because Descartes had acknowledged that his hypotheses might be (indeed in some cases must be) false. Newton wrote, in the second edition of the Principia (1713) hypotheses non fingo, and we know that he himself would have translated this as ‘I do not feign hypotheses’ – fingo and ‘feign’ here mean ‘imagine’, which is the core meaning of the word ‘feign’ in the seventeenth century.³⁰ x x Thus both Copernicus and Francis Bacon wrote of astronomers ‘feigning’ eccentrics and epicycles – they meant these are imaginary entities.xi xi ³¹ So what Newton meant was ‘I do not invent imaginary entities in order to explain natural properties.’xii xii In the Discourse on Method (1637) Descartes had dismissed Aristotelian philosophy as ‘speculative’; his own philosophy would get at the truth by proposing explanations (hypotheses, we would say) that could then be tested experimentally.³² In the Principles of Philosophy (1644), however, he retreated from this position. It would often, he acknowledged, be impossible to choose between competing explanations because one could not see what was actually happening within the invisible world of particles out of which our visible world was constructed. Just as a clockmaker, looking at a clock from the outside, could imagine various ways in which the machinery might be configured, so the philosopher must acknowledge that there might be several equally good explanations of a natural process; it was not always possible to devise a test to choose between them.³³ It was this process of making up explanations that might or might not be true that Newton rejected when he insisted hypotheses non fingo. (That the word ‘hypothesis’ was particularly associated with his old enemy, Hooke, will not have been irrelevant.) As far as Newton was concerned the only worthwhile hypotheses were the ones that could be tested: and if they survived testing they ceased to be hypotheses. Gilbert’s and Galileo’s use of ‘hypothesis’ to refer not to a claim that might be true, but to one that we could be sure was true, would have made no sense to him, just as it seems peculiar to us.

§ 3

Pascal’s Puy-de-Dôme experiment explained the height of the mercury in a barometer by showing that it was directly related to the weight of the air. It made visible a causal relationship: the weight of the air and the weight of the mercury balanced each other. From the point of view of a conventional seventeenth-century philosopher, this was a peculiar sort of explanation. As far as Aristotle was concerned, as we saw in Chapter 3, causal explanations had four components: the formal cause, the final cause, the material cause and the efficient cause. In Pascal’s account of why the mercury does not descend in the Torricellian tube the formal and material causes are so attenuated as to be uninteresting, and the final cause has disappeared completely. You can substitute water or wine for mercury, so the exact substance is irrelevant; any liquid will do. You can substitute lead piping for glass, so again the material cause is irrelevant; any pipe sealed at one end will work. The mercury has no natural tendency to stand up in a column, so there is no final cause at work here. There is only an efficient cause: the balance of weights; and a structure or form that makes the balance possible: a sealed tube up-ended in a bath of mercury. For an Aristotelian, there is only one discipline that isolates efficient causes and structures and ignores all others, and that discipline is mechanics. Pascal’s explanation is a mechanical explanation, and its oddity is that it extends the scope of mechanical explanations from the artificial world of levers and pulleys to the natural world of gases and liquids. Moreover, like any mechanical explanation, Pascal’s can be expressed mathematically, either as a measurement (pounds per square inch; or, which amounts to the same thing, the height of the column of mercury) or as a ratio (since the barometer is a balance, the ratio of the two weights is 1:1, but carrying the barometer to the top of the Puy-de-Dôme shows that y metres of air equals in weight x cm of mercury). This is why Boyle’s contribution to the vacuum debate was entitled New Experiments Physico-mechanical: mechanics is now being used to explain physics.

Pascal’s Puy-de-Dôme experiment seems pretty straightforward to us, but that is because we are used to modern physics. To Aristotelians, it did not seem to offer any sort of explanation of what was happening, just as it seems to us conceptually confused to say (as Aristotelians did) that inanimate objects have goals or purposes. Pascal’s explanation looks right to us; to an Aristotelian, it looked all wrong, which is why Aristotelians (and most intellectuals in Pascal’s day were still Aristotelians) tried to substitute explanations in terms of nature abhorring a vacuum and so trying to prevent one coming into existence. It is hard to reconstruct in our minds a mental universe where Pascal’s explanation seems obviously unsatisfactory and an explanation in terms of nature’s purposes seems obviously preferable.

The problem for the Aristotelians was that they could not fashion an explanation that would successfully predict the outcome of the Puy-de-Dôme experiment. Why should nature abhor a vacuum less at the top of a mountain than at the bottom? Pascal could answer this question, and they could not. Pascal’s explanation could be tested and be shown to work. But to acknowledge it as a good explanation philosophers had to change their definition of what constituted an explanation; they had to learn to satisfy themselves with the sort of explanations that mathematicians were accustomed to providing. Even people who thought Pascal’s explanation was a bad one could see that he could make successful predictions (that the height of a column of water in a Torricellian tube would be fourteen times the height of a column of mercury, for example), and they could not.

Let us take another example, one familiar to Pascal: Galileo’s ‘law’ (as we call it) of fall. Galileo showed that (in the absence of air resistance) all falling objects accelerate at the same rate, and that one can therefore predict the distance travelled in any time by a falling body, and its terminal velocity; indeed, these are related in such a way that the units of measurement are irrelevant. The distance travelled is proportional to the square of the elapsed time, whether you are measuring in feet and seconds or kilometres and Hail Marys (it is an accident that we have only one standard, universal system for measuring time and several systems for measuring distance, but early modern peoples did use informal measures of duration, such as the Hail Mary). Galileo’s law of fall describes in mathematical terms what happens when bodies fall under ideal conditions; but it does not explain anything. It does not even offer (as Pascal’s vacuum experiments do) a mechanical explanation. It tells you what to measure and enables you to predict, but it provides no answer to the question ‘Why?’

If science explains things, this is not science. What makes it science is not that it provides an explanation but that it provides reliable predictions in the form of a mathematical model. Accepting Galileo’s law of fall as good science thus involves an even more radical step away from an Aristotelian conception of science than does accepting Pascal’s account of why the mercury stands tall in the barometer. You may think that this is simply because Galileo’s law is incomplete: Newton’s theory of gravity provides an explanation both of Galileo’s law of fall and of Kepler’s laws of planetary motion. That is partly true, but Newton has absolutely no explanation of what gravity is or how it works; as we have seen, he admits as much. The theory of gravity simply makes possible reliable predictions across a wider field. The problem of explanation has been moved, not solved. Consequently, Huygens’ response to Newton’s theory of gravity was straightforward: ‘I had not thought … of this regulated diminution of gravity, namely that it was in inverse ratio to the squares of the distances from the centre: which is a new and remarkable property of gravity, of which the reason is well worth looking for.’³⁴ Huygens was still looking for explanations; Newton had left the world of explanation and entered a new world, the world of theory.

Scientific explanations are not (at least not so far) complete: they come to a halt, often abruptly. A scientific law marks the point beyond which there are no explanations, although further explanations sometimes come along later. Aristotelian science was not like this: Aristotelian philosophers had no sense that their knowledge was incomplete in important respects, and they thus had a different measure of success from a Galileo or a Pascal. For them, the proof that their system of knowledge was successful was that there was nothing it could not explain, although the explanations often look circular to us now: Molière in The Imaginary Invalid (1673) mocked the idea that one could explain why opium puts people to sleep by saying it was because ‘there is in it a dormitive power whose nature it is to lull the senses to sleep.’ Such explanations look foolish after Pascal, but not before.

For a Galileo, or a Pascal, or a Newton what mattered was being able to make successful predictions where such predictions had previously been impossible. But this involved acknowledging the limits of their knowledge. Aristotelian philosophers looked backwards, assuming Aristotle had known everything that needed to be known; the new scientists looked forward, aiming to expand the limited range of topics in which they could make satisfactory predictions. One reason why the new science made progress and the old philosophy did not is that it was conscious of being imperfect and incomplete.

§ 4

What is science? James Bryant Conant, who has a good claim to be the founder of modern history of science (he was Kuhn’s mentor) defined it as ‘a series of concepts or conceptual schemes (theories) arising out of experiment or observation and leading to new experiments and observations’.³⁵ Science is thus an interactive process between theory on the one hand and observation (our old friend ‘experience’) on the other. In astronomy, this process really gets under way with Tycho Brahe; in physics, with Pascal. We can trace it clearly through Newton’s notebooks, even if he compresses it in his first publication. It would seem evident that this extraordinary transformation in the nature of knowledge must be reflected in the language of science: and it is, although the language in which we speak about science has become so completely second nature to us that a key aspect of this linguistic adaptation has become almost completely invisible.³⁶ The adaptation itself is, once one has realized that it must be there, easy to identify and, once identified, its importance is evident.

A helpful way of beginning is to look up the word théorie in a series of French dictionaries.³⁷ It is not until the end of the nineteenth century that we find (in Littré’s great dictionary) the obvious modern meaning, with examples given of the theories of heat and electricity. Previously, ‘theory’ is defined as speculative rather than practical knowledge (the etymological origin of the word is in a Greek word for looking or spectating), with one particular additional usage noted: la théorie des planètes, the mathematical models for the movement of the planets. If we look for the words ‘theory’/théorie/teoria in Galileo, Pascal, Descartes, Hobbes, Arnauld and Locke, we find nothing,xiii xiii while in Hume we find the word used in its modern sense frequently – and more and more so as time goes by.

In English, in the sixteenth century, the word ‘theory’ (or ‘theoric’; the words are used interchangeably) is used as we would expect from our inspection of French dictionaries: on the one hand to refer to speculative or abstract knowledge, usually in opposition to practice (thus musicians learn both the theory and practice of music, and gunners learn the theory and practice of gunnery), and on the other to refer to the theory of the planets. References to the theories of Ptolemy and Copernicus are thus references to their mathematical modelling of the cosmos. The first example I can find of the word being used in the modern sense, without an implied reference to a mathematical model, is in Bacon’s Sylva sylvarum (1627), when he is criticizing Galileo’s explanation of the tides:

Galilaeus noteth it well; That if an Open Trough, wherein Water is, be driven faster than the Water can follow, the Water gathereth upon an heape, towards the Hinder End, where the Motion began; Which he supposeth, (holding confidently the Motion of the Earth,) to be the Cause of the Ebbing and Flowing of the Ocean; Because the Earth ouer-runneth the Water. Which Theory, though it be false, yet the first Experiment is true.xiv xiv ³⁸

It is presumably from Bacon that this new meaning of the word spread.xv xv We find it in 1649 and 1650 in translations of and commentary on van Helmont, and in 1653 in a translation of and commentary on Descartes: in each case there is no equivalent in the original.³⁹ Boyle announces in 1660 that he is going to offer new experiments regarding the vacuum, but not new theories;xvi xvi in 1662 he proudly announces a new ‘theory’ (the word is his), which we now call Boyle’s law.⁴⁰ The first occurrence of the word in its new sense (that is, not as a contrast between theory and practice, nor as a mathematical model) in the Philosophical Transactions of the Royal Society appears to be in Oldenburg’s editorial introduction to an explanation of the tides by John Wallis (Wallis writes of an hypothesis, an essay and a surmise, but not of a theory; in the index to the volume, this is ‘a new theory’); the second in Robert Boyle’s ‘Tryals proposed to Dr Lower’ regarding blood transfusions in animals.⁴¹ In Sprat’s History (1667) the word takes on its full, modern range of meaning: even the scholastics are now said to have had theories, and the production of new theories is now as important a part of the new science as the performance of experiments.⁴² Newton’s letter to the Royal Society of 1672 was, as we have seen, given by Oldenburg the title ‘A Letter of Mr Isaac Newton, Professor of the Mathematicks in the University of Cambridge; Containing His New Theory about Light and Colors’,xvii xvii and the phrase ‘new theory’ runs through the titles of the ensuing correspondence: his Opticks (1704) declares itself to be a study in ‘the Theory of Light’.xviii xviii ⁴³ Optics was traditionally a branch of mathematics, and Boyle’s law is a mathematical relationship, but Hooke writes not only of ‘the true Theory of Elasticity or Springiness’ but also of his own theory of flame, where there is no mathematics involved.⁴⁴ The word used in its new sense first appears in the title of a book in Thomas Burnet’s Telluris theoria sacra (1681), translated as The Theory of the Earth in 1684, and followed in 1696 by William Whiston’s A New Theory of the Earth. In French the new usage seems to have been adopted first by the mathematicians (Johann Bernoulli, Nouvelle théorie du centre d’oscillation, 1714), but it quickly spread more generally: Voltaire’s Élémens de la philosophie de Newton (1738) discusses ‘la théorie de la lumière’. George Berkeley is translated into Italian in 1732: Saggio d’una nuova teoria sopra la visione.

The new sense of the word ‘theory’ is fundamental to an understanding of what the new science claimed to do. Traditionally, philosophy had concerned itself with scientia, true knowledge, but mathematicians practising astronomy had been content with mathematical models – hypotheses, theories – which might or might not correspond to reality but which fitted more or less exactly with the phenomena. Mathematical theories were not explanations, they were conceptual systems for making predictions. The new theory that Boyle announced relating to the pressure of gases (1662), or Newton’s new theory of light (1672) were not explanations – they did not answer the question why; they were concepts that enabled one successfully to predict the outcome of experimental procedures and to identify processes in the natural world. Moreover, the word ‘theory’ carried with it a useful ambiguity: it could refer either to an established truth (which is how Newton used the word) or to a viable hypothesis, thus fudging the differences between those who wanted to claim indisputable truth and those who wanted to make tentative knowledge claims.

In adopting the term ‘theory’ the scientists were thus freeing themselves from the philosophers’ preoccupation with truth in so far as it implied knowledge of causes and of what Aristotelian philosophers called substances, or forms. Locke and Newton insisted that we could have no knowledge of substance (suppose the world is made up of atoms – we can have no idea of their size or shape); we could have knowledge only of properties (oak is hard, balsa is soft, and so forth). For knowledge of substance Newton substituted conceptual models that worked reliably and accurately. Philosophers of science right through to the present day have been preoccupied with what is called ‘realism’, the question of whether science is true; what they have failed to notice is that the founding of modern science was accompanied by an escape from the old notion of true knowledge (scientia) and its replacement by the concept of ‘theory’.xix xix The adoption of the word marks the break between the classical traditions of philosophy and mathematics, which were concerned with deduction and with true knowledge of substances, and modern science, which is concerned with viable theories. Locke’s Essay (1690) symbolizes this shift in its title. It is not a book about knowledge (which is now thought of as largely beyond human capacity), but it is an Essay concerning Humane Understanding: even the word ‘essay’ implies that understanding is necessarily provisional. In a crucial passage in the epistle to the reader he writes of the understanding:

that as it is the most elevated Faculty of the Soul, so it is employed with a greater, and more constant Delight than any of the other. Its searches after Truth, are a sort of Hawking and Hunting, wherein the very pursuit makes a great part of the Pleasure. Every step the Mind takes in its Progress towards Knowledge, makes some xx xx Discovery, which is not only new, but the best too, for the time at least.

Thus knowledge, in so far as we have it, is not absolute but progressive, not definitive but provisional. We make progress, but, unlike those who go hawking and hunting, we may never catch our prey.

It follows that even Galileo was never more than a reluctant scientist, for he always sought the certainty of deduction; rather, modern science begins with Bacon’s re-description of Galileo’s demonstration of the movement of the Earth as a ‘theory’. By the 1660s the standard terminology for discussing science in England included ‘facts’ and ‘evidence’ (from the law; we will discuss ‘evidence’ in the next chapter), and ‘hypotheses’ and ‘theories’ (from astronomy). Science had been invented. The first book to contain these four words, all used in their modern senses, along with ‘experiment’, also used in its modern sense, was, it would seem, Walter Charleton’s paraphrase of van Helmont, the Ternary of Paradoxes of 1649. Charleton was a deliberate and self-conscious innovator in linguistic usage: the Oxford English Dictionary quotes him 151 times as the first entry under a definition (he is recorded as the first to use ‘projectile’, ‘pathologist’ and, alas mistakenly, ‘erotic’).⁴⁵ But none of the usages which immediately concern us were new with him, and indeed he insisted on the remarkable merits of English, on

the Venerable Majesty of our Mother Tongue; out of which, I am ready to assert, may be spun as fine and fit a garment, for the most spruce Conceptions of the Minde to appeare in publick in, as out of any other in the World: especially, since the Carmination or refinement of it, by the skill and sweat of those two Heroicall Wits, the Lord St Alban [Francis Bacon], and the now flourishing Dr Browne; out of whose incomparable Writings may be selected a Volume of such full and significant Expressions, as if uprightly fathomed by the utmost Extent of the sublimest Thought, may well serve to stagger that Partiall Axiome of some Schoolemen, that the Latin is the most symphoniacall and Concordant Language of the Rationall Soule.⁴⁶

Charleton’s language did not meet with the approval of his contemporaries, and he opens his next publication, Deliramenti catarrhi (1650), with a lengthy and bitter diatribe against his thick-skulled detractors whose depraved appetites have rendered them, he declares, ‘fit to digest nothing, but crude Sallads gathered in the Poets Elizium, and soft Romances, oyled with the effeminate Extracts of the Stage, and spiced with some new French-English idioms’ rather than his own masculine idiolect. But Charleton was one of the most active members of the Royal Society in its early years, and his idiolect, tamed and domesticated by Boyle and Sprat, has become the language of science. Where the old philosophy had laid claim to indisputable certainties, the new one modelled itself on astronomy and the law, disciplines in which facts and evidence had long been marshalled in order to generate reliable, even incontrovertible, hypotheses and theories.