6.2
VALUE AT RISK
VAR is a risk management statistic that describes the size of an investment. It was originally developed to combine different types of investments into a single measure of size. For example, describing the combined size of a $15 million stock investment and 15,000 crude oil futures is difficult. The cost to enter the transaction is not a good measure of size—the stock investment required $15 million in cash, and the crude oil investment didn’t require any money down except for a refundable margin deposit. It isn’t immediately clear which of the two investments is larger and more risky unless some analysis is performed.1
VAR addresses this by describing the combination of investments by something that they have in common—daily changes in value. Daily changes in value are also known as earnings or P&L. While risk management practices vary widely, size is one of the most important components of risk, and almost all risk management is at least partially based around a VAR methodology.
VAR is a “big picture” summary of the combined trading risk of an organization. It is a way of taking a lot of trades and understanding how they interact. This involves breaking down trades into a simple common denominator that is general enough to describe almost any type of trade. However, because it is a summary, VAR can ignore or obscure details that may be important to managing a trading operation. Risk management involves paying attention to both the big picture and to details. As a result, VAR is only part of the story. However, it is an important part of the story, since size is the headline of almost every risk report.
Because of its simplicity, VAR is the primary tool used to describe trading. Its popularity is largely based on the fact that the result of a VAR analysis is a single number, so it is easy to read the results every day. VAR analysis is almost always done in conjunction with other types of more detailed analysis.
There are two parts commonly associated with a VAR analysis—mark-to-market accounting (discussed in Chapter 6.1) and an analysis of P&L volatility. Typically, the term risk of a portfolio is synonymous with its P&L volatility.
A High-Level Summary
The purpose of VAR is to give a simple description of risk. For example, a VAR report might be “once a month the trading desk can be expected to lose at least one million dollars over a one-day period.” This description is both meaningful and short enough to be conveyed to a large audience. As a single number, it is simple enough to use in daily reports and easy to examine for trends. For example, if the VAR had decreased by $20 million in the past week, this would represent a significant change in the risk of a portfolio.
There are four parts to a VAR description:
1. The first part of VAR is the description of the frequency at which some event will occur. Since there are approximately 20 trading days in a month, the frequency of a once a month daily move is 1 day out of 20. Translating that to percentages, a 1-in-20 chance means an event that occurs 5 percent of the time. More commonly, this is described as exceeding the 95th percentile of samples. A value that exceeds 99 percent of samples would occur about two and a half times a year.
2. The second part of VAR is a description of the time horizon of the expected move. In this example, the change in P&L is measured over a one-day period. Another possible time horizon might be a weekly move in P&L.
3. The third part of the description is the sidedness of the move. In the example, the measure is looking at the size of losses, so it is a one-sided VAR. If the report were describing the possible size of profits or losses, then it would be a two-sided VAR.
4. Finally, the last part of VAR is a description of the magnitude of the move. The magnitude of the expected move in the example was up or down by a million dollars.
Because it is so simple, a VAR report does not include a lot of details. For example, it doesn’t give any information about what will happen if the price of oil doubles or the stock market crashes. It also doesn’t give any information about how bad things could get in the event of a natural disaster or financial crisis. VAR is not a worst-case event either—VAR gives the minimum threshold for a move that can be expected with some frequency. In the example, a daily profit or loss of at least a million dollars was expected once a month. However, the report does not give a lot of insight into whether the move is likely to be a $1 million, $2 million, or $10 million.
Calculating VAR
Standard definitions of risk are based on the concept that prices can be assigned to assets through mark-to-market accounting and that those price changes lead to either profits or losses. Given that assumption, it is possible to define the risk of a portfolio as the expected volatility of its profits and losses. In this way, P&L provides a common denominator for almost any type of investment.
VAR summarizes the risk of a portfolio by predicting the size of P&L movements that will occur with a specific frequency. It will use a single number to describe either a distribution or a bunch of distributions added together. For example, since there are approximately 20 days in a month, a P&L movement at the least as big as the one at the 95 percent frequency can be expected to occur, on average, at least once a month. As a result, a 95 percent level might be chosen to describe the entire distribution. As shown in Figure 6.2.1, there are two main steps to calculating a VAR number.
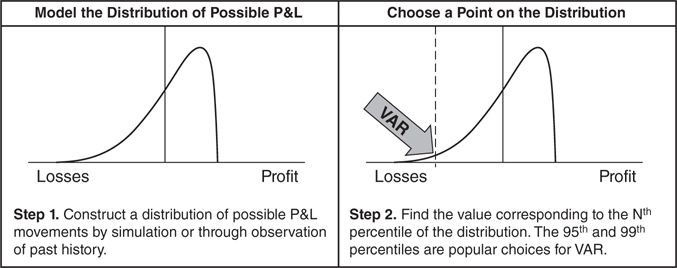
Figure 6.2.1 Constructing VAR
Not everyone uses the same frequency for VAR—some people prefer points that are more likely to be accurate and can be checked commonly while others prefer numbers that are more representative of a worst-case scenario. However, by picking a single point, VAR produces a simpler estimate of risk than having to use an entire distribution of predicted results.
VAR gives up accuracy for simplicity. In many cases, different assets can have the same VAR (Figure 6.2.2).
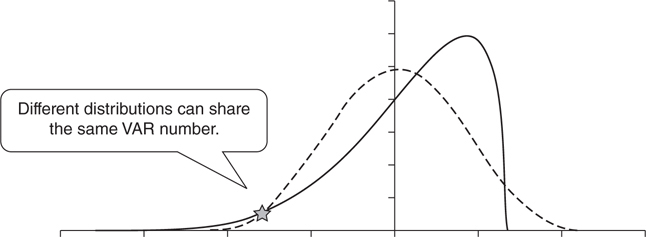
Figure 6.2.2 VAR for two assets
The methodology for calculating the percentile also can vary between firms. Some risk managers prefer to examine only losses; others prefer to look at the volatility of both profits and losses (Figure 6.2.3). If only losses are examined, the VAR is called a one-sided VAR. If both profits and losses are examined, it is called a two-sided VAR. A two-sided VAR will force an asset to have the single VAR regardless of whether it is long or short; it is largely a measure of volatility. One-sided VAR is more commonly used than two-sided VAR because risk managers often want to use VAR to calculate worst-case scenarios or potential losses in stress events.
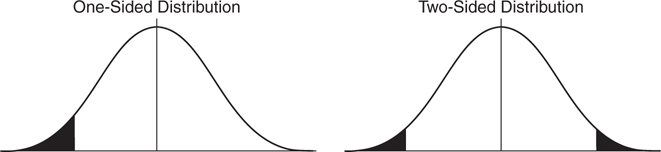
Figure 6.2.3 One-sided and two-sided VAR distributions
Portfolio VAR
On a portfolio level, when multiple assets are combined, VAR becomes more complicated. This is due to the need to incorporate diversification. Diversification means that when two equal sized assets are combined, the combination of the two assets is less risky than either asset alone. This is because the assets may not move together and some of the extreme moves may partially cancel out. For example, when one is losing a lot of money, the other might be doing nothing or gaining money.
The amount of diversification gained by combining multiple assets depends on the relationship between the assets. At one extreme, if two assets are perfectly correlated, perhaps two identical crude oil contracts, then there is no diversification benefit. The risk of the combination will be twice as large as the risk of a single contract. At the other extreme, perfect negative correlation, the assets might be identical but with the opposite positions. For example, an agreement to buy a barrel of crude oil will offset the risk of an agreement to sell a barrel of crude oil.
Mathematically, combining the VAR of multiple assets can be done in two ways—observed/simulated VAR or parametric VAR. With observed/simulated VAR, the risk manager will construct a portfolio and value it over past data or some simulation of possible future price movements. The distribution of possible earnings can be directly sampled to identify VAR. With parametric VAR, each asset can be modeled as a well-known statistical distribution (like a normal distribution) and combined.
Parametric VAR is often based on the assumptions that assets have normally distributed returns. This makes it easy to find the risk of an entire portfolio because normal distributions are only based on two parameters (mean and standard deviation). One of those, the average return, can generally be approximated as zero for financial assets.
From a terminology perspective, volatility is typically abbreviated by the lowercase Greek letter sigma (σ). It is a synonym for the standard deviation of a portfolio. Variance is the square of the volatility. It is a synonym for mean square error and typically is abbreviated as sigma squared (σ2). The variance of a portfolio can be calculated as the sum of the component variances plus a correlation adjustment (Figure 6.2.4).

Figure 6.2.4 Variance of correlated assets
Weaknesses of VAR
Because VAR is a single number, it has some limitations—it abstracts away the fundamental behavior of a portfolio. Typically, P&L is not normally distributed—there isn’t an equal chance of making and losing money. Many energy assets—particularly the ones that can be modeled by options—have asymmetrical payoffs.
For example, a peaking power plant is going to lay idle for most of the year—it will lose money regularly whenever it is inactive. In all but the summer months, small operational charges will accumulate daily. A couple times a year—usually hot summer afternoons—the power plant will have the opportunity to make large windfall profits as it is pressed into duty (Figure 6.2.5). This is an example of a portfolio that benefits from volatility.
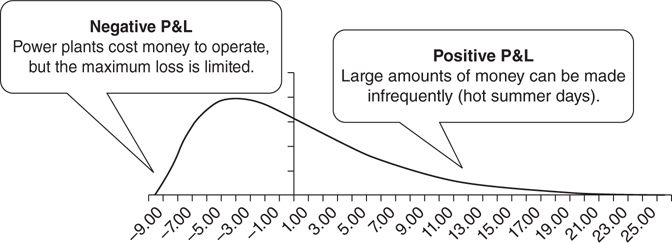
Figure 6.2.5 Asymmetric P&L
Stress Testing
It is often necessary to augment VAR with additional tests called stress tests. VAR is an approximation. It is a trade-off between simplicity and insightfulness. Being simple means that it is straightforward to implement and can be regularly examined by business leaders. However, VAR is not going to handle all types of portfolios well. Sometimes additional analysis will be required. There are so many possible special cases that no general model will be able to address them all. This doesn’t make VAR worthless, just limited. It is useful precisely because it is a simple measure. Some common types of stress testing are to identify what might happen under certain scenarios. For example, it would be possible to track and report expected losses in a financial crisis or a natural disaster alongside VAR on a daily basis.





