24
ANTIQUITY AND THE MIDDLE AGES

Thomas J. Mathiesen

A full treatment of the philosophy of music in antiquity, let alone the Middle Ages, would need to take into account not only the familiar “ancient” classical cultures of Greece and Rome but also those of eastern Asia, India, Mesopotamia, and Egypt. Inasmuch as even a cursory overview of all these cultures would be impossible in a short chapter, the Pythagorean tradition will be a useful place to start: first, because Pythagoras himself has been credited with coining the terms “philosophy” and “philosopher”; and, second, because the tradition absorbed important elements of many ancient cultures, as well as unquestionably exerting an enormous influence on the musical philosophy of classical antiquity and the Middle Ages.

Pythagoras and the Pythagoreans

The historical Pythagoras is an elusive character. Born perhaps on Samos, he is presumed to have lived between 570 and 480 bce. According to his biographers, he was educated by Hermodamas of Samos, Thales, and Anaximander of Miletus, as well as by the learned figures he encountered in his travels in the Near East and Egypt (and possibly even in India). After some years of teaching on Samos following his return to the island, he emigrated to Croton in southern Italy where he attracted a large community of followers. Unrest eventually arose, and Pythagoras emigrated to Metapontum and remained there until his death, the precise date and circumstances of which have been matters of dispute, even among the early Pythagoreans.

According to Heraclides Ponticus (fl. fourth century bce), Pythagoras was the first to use the term “philosophy” (philosophia) and to call himself a “philosopher” (philosophos) because “no one except god is wise [sophos]” (Diogenes Laertius Proem. 12). In other words, Pythagoras “called ‘fond of wisdom’ – that is, ‘philosophos’ – those who, regarding all else as nothing, ardently contemplated the nature of things” (Cicero Tusculanae disputationes 5.3.8).

Pythagoras taught his students privately (and secretly) rather than developing his ideas systematically in a series of treatises, but many of his teachings were preserved in the writings of his followers, who split into two groups (probably in the fifth century bce) – the acousmatics and the mathematicians. The acousmatics were particularly interested in Pythagoras’s teachings in the area of ritual life (e.g. eschatology, diet, sacrifice, purification, burial, reincarnation, and so on) while the mathematicians were interested in the four primary Pythagorean scientific disciplines (geometry, astronomy, arithmetic, and music), which Pythagoras is supposed to have developed from his studies with the Egyptians and Chaldeans. The mathematicians regarded it as their particular task to disseminate and develop these disciplines (Archytas fr. 1; Aristotle Metaphysics 1.5).

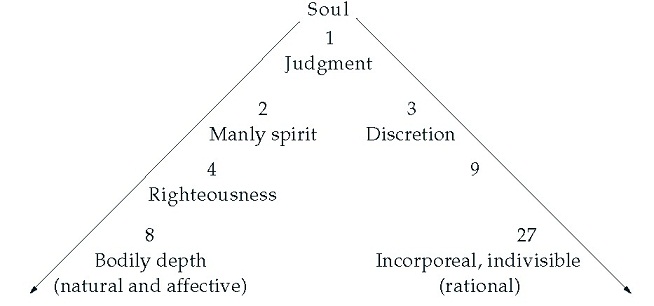
The Pythagoreans (and presumably Pythagoras himself) regarded number as central to all knowledge: “everything that can be known has a Number; for it is impossible to grasp anything with the mind or to recognize it without this” (Philolaus fr. 4). In particular, the series of the first four numbers, the tetraktys of the decad, held significance because it embodies all the musical consonances (the octave, 2:1; the fifth, 3:2; the fourth, 4:3; the twelfth, 3:1; and the fifteenth, 4:1) and all the geometric elements (point, 1; line, 2; plane, 3; and solid, 4); moreover, the sum of the first four numbers returns to the perfection of 1, now in the base 10 (1 + 2 + 3 + 4 = 10).

According to legend, Pythagoras discovered the numerical basis of the musical consonances when walking by a blacksmith’s shop: he heard the consonant sounds of the octave, fifth, and fourth; noticed that the various pitches producing the consonances corresponded to the weights of the hammers (12, 9, 8, and 6); replicated these sounds by suspending the weights from strings; and noted the ratios between the weights. He is then supposed to have observed these same ratios in the lengths of strings, pipes, and so on. As it happens, unison strings under these proportional tensions (whether produced by weights or any other means) do not sound these intervals, which actually result from the proportional resonance of unison strings. Nevertheless, the basic consonant ratios embodied in the first four numbers remained inviolable, with a very few notable exceptions, throughout antiquity and the Middle Ages.

The Pythagoreans viewed these musical consonances and their ratios as broadly paradigmatic: “they took the elements of numbers to be the elements of everything and the whole heaven to be harmonia and number” (Aristotle Metaphysics 1.5). From this, the notion of the cosmos as a musical harmony emerged (including the harmony of the spheres in Plato Republic 10.616c–17c) and concomitantly the conception of music (mousikê) as a science that reveals the secrets of nature and exerts a powerful force on the character (ethos) of individuals and society as a whole, as is conveyed in the widely repeated story of Pythagoras calming an inebriated (or lustful) youth by changing the harmonia (on this term, see below and Mathiesen 2001a) of the music he was hearing and in Socrates’ argument against musical innovation as a threat to the fundamental structure of the state (Plato Republic 4.424b–c). In a real sense, music and philosophy are inexorably linked in the Pythagorean tradition.

Plato and Aristotle

The influence of the Pythagorean tradition is strong in the work of Plato (c.429–347 bce), especially in Timaeus but also in Republic and Laws. The Timaeus (34b–37c; see Plato 1998b), for example, makes frequent use of the term harmonia and its related forms in describing the parts of the universal soul in terms of Pythagorean musical ratios, while in Republic, harmonia is used both in the characterization of various ethnic musical types – Dorian, Phrygian, Lydian, and so on (3.398c–403c; see Plato 1998a) – and in reference to the proper state of the individual soul, as when Socrates says: “he who best blends gymnastics with music (mousikê) and applies them in the most measured way to the soul is the one we should most rightly consider to be the most perfectly musical and harmonious” (Plato Republic 3.412a). Republic also includes the famous Myth of Er, in which a Siren on each orbit in the cosmos (seven planetary and an outer orbit of fixed stars) produces a single pitch, the eight of them together forming “a single harmonia” (10.616d– 17d). (For a fuller discussion, see Chapter 28, in “Plato,” in this volume.)

Aristotle (384–322 bce) and the Aristotelian Problemata have much to say about music, but the material is more often historical or technical rather than philosophical. Aristotle’s On the Heavens, however, is devoted to a refutation of the Pythagorean “harmony of the spheres” (De caelo 2.9), while Metaphysics 14.6 debunks the notion of number as reality. In Book VIII of Politics, Aristotle turns his attention to the power of music to amuse and relax, instill ethical virtue, and stimulate the intellect (see Aristotle 1998). He acknowledges the powerful influence of music, but his view of music is less dogmatic than Plato’s: for Aristotle, the propriety of music (and education in music) is a relative matter, depending on time, place, purpose, age, and station.

Aristoxenus

Aristoxenus of Tarentum (c.350–310 bce), Aristotle’s student, seems to have been the first to develop a comprehensive phenomenology of music, leading one recent scholar to call him “the founder of musicology” (Gibson 2005: 2). Unfortunately, his treatises on harmonics (the phenomena of musical sound) and rhythmics do not survive intact, and some parts of his phenomenology can only be conjectured from treatments (often critical) written in later antiquity.

Aristoxenus clearly identifies his study of harmonics as in accord with Aristotle’s third type of science, the theoretical, which transcends the limitations of sensory experience in the exercise of pure reason (Topics 6.6, Metaphysics 1.1, and Nicomachean Ethics 10.7). Recalling Aristotle’s method in Physics, Aristoxenus begins by defining the constituent parts of musical reality: motion, pitch, compass, notes, intervals, genera, scales, musical line (melos), synthesis (i.e. the way in which notes and intervals, like letters and words, are placed in natural order), and position or placement of the voice. Later on, these constituent parts are recast as a set of seven categories (notes, intervals, genera, scales, tonoi, modulation, and melic composition [melopoiïa]), framed by hearing and intellect on the one hand and comprehension on the other. The phenomena, he says, cannot be properly grasped without a sharp sense of hearing, and their function cannot be understood without intellect. Beyond this, because music passes through time, it is both a Becoming and a Having Become. Thus, in order to have musical comprehension, it is necessary to have a sense of the Becoming and a memory of the Having Become.

In his definition of the three basic genera of melodic lines (enharmonic, chromatic, and diatonic), Aristoxenus abandons traditional Pythagorean ratios in favor of a geometric idealization in which two fixed notes – hypate and mese – defining the interval of a fourth (not, however, specified as a Pythagorean interval in the ratio 4:3) surround two other notes – parhypate and lichanos – that define six specific shades by moving within a spatially defined area, measured in parts of a tone (see Figure 24.1).

This extraordinarily bold conception was routinely attacked and derided by theorists throughout antiquity and the Middle Ages as empirically faulty and mathematically impossible, but Aristoxenus was well aware that musical phenomena had not been and could not be adequately explained by the limited >means of Pythagorean mathematics. By applying a geometric model, Aristoxenus recognized the possibility of transcending these limits. His larger philosophical view seems to have escaped even his followers, who tended to reduce his system to a series of simple descriptive categories, but his application and development of Aristotelian principles and categories established a philosophical alternative to the Pythagorean (and Platonic) view of music. (For a fuller treatment of Aristoxenus, see Mathiesen 1999: 294–344.)

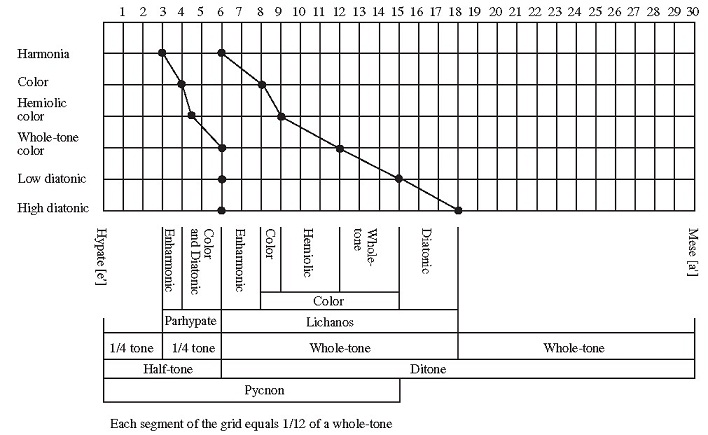
Figure 24.1 The Aristoxenian shades (Mathiesen 1999: 313)

Epicureans and Skeptics

Epicurean and Skeptic philosophers generally rejected the idea that music represented anything beyond itself or held any special power to affect human character (ethos). In Book IV of his fragmentary treatise De musica, the Epicurean Philodemus (c.110–c.40 bce) summarizes and systematically refutes each argument of the Stoic Diogenes the Babylonian (c.240–152 bce), who represents a synthesis of Pythagorean, Platonic, and Aristotelian viewpoints. For Philodemus, music is irrational and, at best, a simple pleasure, invented by man. It has no metaphysical significance and manifests no ethical effects. A similar type of treatment is provided by the Skeptic Sextus Empiricus (fl. second century ce), who reviews and debunks the various traditional claims for music, after which he demonstrates that music cannot even be an object of study because it is predicated on elements that cannot be demonstrated to exist (see Sextus Empiricus 1998).

Early Latin writers: Cicero and Varro

Although there are many musical references in Latin literature from the second century bce through the imperial period, the majority of these are allegorical, metaphoric, technical, or historical; with the exception of Cicero (106–43 bce) and Varro (116–27 bce), musical philosophy as such seems to have been left to writers in Greek. Cicero’s view of music generally accorded with Philodemus, but he also developed his own treatment of the harmony of the spheres in Somnium Scipionis (Republic 6.9–29; cf. De natura deorum 3.27), which would be highly influential as transmitted throughout the Middle Ages together with an extensive commentary by Macrobius. Further echoes of Plato appear in Cicero’s Laws 2.15.38–39, which offers brief comments on musical ethos. Varro’s encyclopedic treatment of the seven liberal arts (in the order grammar, dialectic, rhetoric, geometry, arithmetic, astronomy, and music, as later followed by Martianus Capella) plus medicine and architecture has not been preserved, but references to him appear in the writings of Pliny, Quintilian, Censorinus, Augustine, Cassiodorus, Isidore of Seville, and others. The famous definition “music is the science of effectively modulating the voice,” found in Censorinus’s De die natali 10 and repeated in various forms in many other places, is commonly but insecurely attributed to Varro.

Philo Judaeus

In the first century ce, Philo Judaeus (c.20 bce–c.50 ce) attempted a synthesis of pagan and Jewish philosophy in his allegorical method of expounding scripture – a method in which music and number played a significant role. In his view, the beautiful things of the world were based on prefigurations that were part of God’s creation (De opificio mundi 3–6). Because everything in the cosmos is numerically related, the arts should lead to philosophy and ultimately to God. Thus, musical harmonia, as an imitation of cosmic harmony, enables a recognition of this higher harmony that can in turn lead to a transcendent state (De somniis 1.35–37; De opificio mundi 53–54, 69–71). In a similar manner, the lyre serves as a metaphor for the harmonious soul, which is a “concord of virtues and the beauties in nature” (Quod deus sit immutabilis 24.4–5). Philo’s allegorical method (emerging from a long tradition of allegorical interpretations of Homer and Hesiod) influenced Origen and Sts Ambrose, Jerome, Augustine, and Gregory, eventually becoming a standard for Biblical exegesis as well as for the interpretation of Greek and Roman secular literature. One of the important philosophical streams from antiquity to the Middle Ages, it nevertheless remains somewhat peripheral to the mainstream of musical philosophy because it is so closely linked with theology and the aesthetic dimension of religious experience.

Greek writers of later antiquity

All the traditions of musical philosophy retained separate identities in later antiquity, but the Pythagorean/Platonic and Aristotelian/Aristoxenian traditions merged to some extent in treatises such as De musica attributed to Plutarch of Chaeronea (c.50–c.120), the Manuale harmonices of Nicomachus of Gerasa (fl. late first–early second century), and the Harmonica introductio of Gaudentius (fl. late third or early fourth century; see Gaudentius 1998), all of which provided treatments of Pythagorean mathematics and music combined with historical and technical details of considerable interest to historians of music theory. Other writers of the same period, such as Cleonides and Theon of Smyrna, generally disregard philosophical aspects in providing primarily technical treatments, respectively, of the Aristoxenian and Platonic traditions. None of these shorter treatises, however, can compare with the two capstones of later Greek musical philosophy: the Harmonica by the Alexandrian scientist Claudius Ptolemy (c.90–161), who attempted a critique and developmental reconciliation of Pythagorean and Aristoxenian music theory, together with a consideration of the musical features of the cosmos; and the De musica of the neo-Platonist Aristides Quintilianus (fl. late third–early fourth century), perhaps the most “intricate and elaborately unified philosophical discourse in which music provides a paradigm for the order of the soul and the universe” (Mathiesen 1999: 525; for a fuller treatment of all these figures, see Mathiesen 1999: chs. 4–6).

Plutarch

Musical references abound in the Moralia of Plutarch, but two of the treatises are especially important in the present context: the unquestionably authentic De animae procreatione in Timaeo, essentially a commentary on Plato’s Timaeus; and the pseudonymous De musica, written in the form of a dialogue among a practitioner, a “theorist,” and a precentor. De animae procreatione 27–33 provides a detailed and useful exegesis of the musical ratios and mathematical means that appear in Plato’s psychogony, leading to the conclusion that the ratios and numbers used by the Demiurge represent “the musicality and harmonia of the soul herself with herself, by which she, engendered with myriad goods, has filled the heaven” (1030c). Likewise, in De musica, the practical and historical discussion of Lysias is extended by the theorist Soterichus into the realm of Pythagorean mathematics and music as he describes the ways in which the Platonic ratios of Timaeus 35b–36b should be assigned to specific musical notes in the famous interlocking Pythagorean harmonia (Figure 24.2)

Following further consideration of the natures of the Unlimited, the Limited, and the Even-Odd (cf. Philolaus fr. 1–3), Soterichus observes that music is elevating, instructive, and useful. In summarizing the disciplines of harmonics and rhythmics, he moves from his predominantly Pythagorean position to draw on Aristoxenus in his recognition that the mind relies on a sharp sense of hearing in order to understand the continuity of effects and form critical judgments about the nature and ethos of music. The precentor Onesicrates caps the dialogue by returning the discussion to the Pythagorean realm, concluding that neither the universe nor the motion of the stars could have been established without music because God has arranged everything in accord with harmonia.

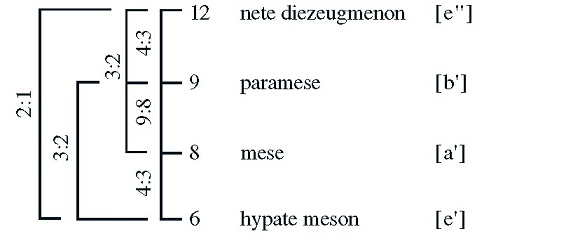
The mese (8) provides the harmonic mean between
the nete diezeugmenon (12) and the hypate meson
(6); the paramese (9) provides the arithmetic mean.

Figure 24.2 The description in De musica 22 (1138e–1139b) (Mathiesen 1999: 313)

Nicomachus of Gerasa

The writings of Nicomachus of Gerasa are among the most important sources for the tradition of Pythagorean mathematics and musical philosophy, especially his Introductio arithmetica, which survives in Greek and in a Latin translation by A. M. S. Boethius; his Introductio musica, which though lost in Greek is generally thought to be the source for the first four books of Boethius’s De institutione musica (see below), the most influential work on music in Latin from at least the Carolingian period until well into the Renaissance; and his little Manuale harmonices and a few additional fragments. The Manuale harmonices, written in the form of a letter to a noble lady, is essentially a series of unrelated summaries that nonetheless preserve important Pythagorean source material. The third “chapter,” for example, presents the planetary harmony as a prototype for the earliest scale of earthly music, which was originally a heptachord in imitation of the higher harmony. In the following chapters, Nicomachus explains how sound and number are related, how the planetary heptachord was expanded into an octave by Pythagoras, how Pythagoras discovered the basic harmonic ratios, how the mathematical means of the Timaeus can be understood, how the Pythagorean Philolaus constructed the harmonia of the octave (Philolaus fr. 6), and how the notes and tetrachords of the Greek musical system evolved from the old heptachord into their current arrangement.

Claudius Ptolemy

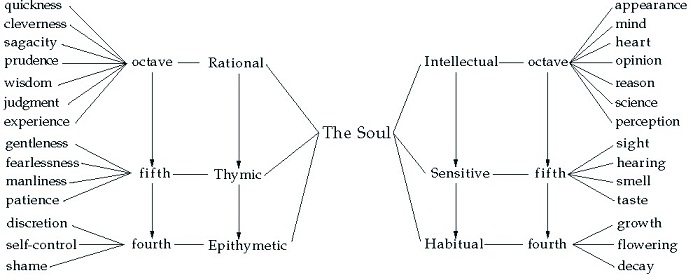
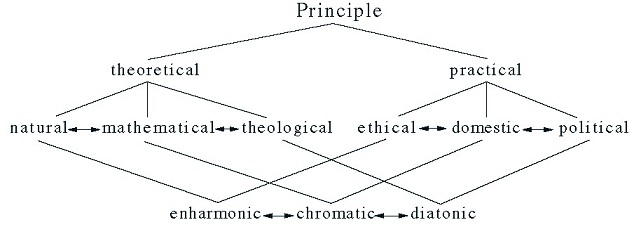
The Harmonica of Claudius Ptolemy, like De musica of Aristides Quintilianus, is arranged in three books, but the second and third books were either left incomplete at his death (as one of the scholia states) or partially lost at an early date. As it survives today in three somewhat different versions, Books I and II of the Harmonica explore both the Pythagorean and Aristoxenian traditions, which are then reformulated by Ptolemy himself to propose a more coherent and consistent system; the third book, which represents the work of Ptolemy’s later redactors, relates the technical details of music to the order of the universe, addressing such topics as the harmoniousness of all things; relationships among consonant musical intervals, the parts of the soul, the primary virtues, and the aspects of the zodiac; and affinities among the sequence of notes and tetrachords in the Greek scale, the various genera, the tonoi (on this term, see Mathiesen 2001b), and the organization of the planetary spheres in the cosmos. Ptolemy does not provide illustrations of these relationships, but Figures 24.3 and 24.4 can be constructed from his descriptions.

All the parts in Figure 24.3 form a concord: in the soul, this is righteousness, and the entire harmonia of the system is the disposition of the philosopher. The arrangement in Figure 24.4 complements the threefold division of the soul and relates the various sciences to the three musical genera. Ptolemy provides only vague reasons for the associations with the enharmonic and diatonic; for the chromatic, he emphasizes the importance of mathematics as a necessary intermediary in understanding the relationship between nature and the god, domestic action as an essential link between ethics and politics. All these interlocking relationships naturally lead to the conclusion that the various tonoi can affect the disposition of the soul, and Ptolemy (or his redactors) conclude Book III by showing the relationships among the various tonoi, the planetary spheres, and the zodiac.

Figure 24.3 Ptolemy’s construction of the soul, based on Harmonica 3.5 (Mathiesen 1999: 481)

Figure 24.4 Ptolemy’s construction of the soul, based on Harmonica 3.6 (Mathiesen 1999: 482)

Aristides Quintilianus

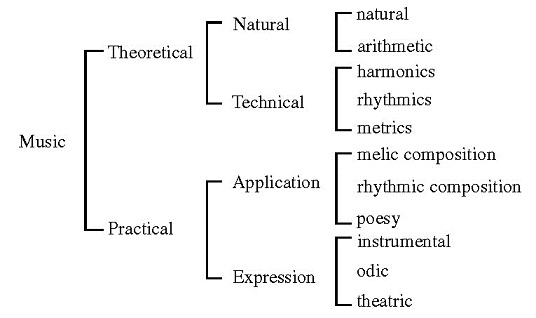
Aristides Quintilianus’s De musica is a more systematic work: every technical detail of the Aristoxenian categories of harmonics, rhythmics, and metrics laid out in Book I (for the section on harmonics, see Aristides Quintilianus 1998) is related in one way or another in Book II to the effect of music on ethos and its role in education, and all of this material is then related to the soul and the order of the universe in Book III. For Aristides Quintilianus, music is an art transcending time and physical nature that reveals the order of the soul and the universe, as he makes clear in his initial definitions of music, the last of which marks out a neo-Platonist epistemology: “Music is a science of melos and of those things contingent to melos. Some define it as follows: ‘the theoretical and practical art of perfect and instrumental melos’; and others thus: ‘an art of the seemly in sounds and motions.’ But we define it more fully and in accordance with our thesis: ‘knowledge of the seemly in bodies and motions’” (De musica 1.4). These definitions lead to his famous classification of music (Figure 24.5).

Building upon the treatment of the Technical and Application subclasses in Book I, Aristides Quintilianus devotes Book II to the subclass of Expression in three topics, beginning with the soul and the use of music in education (based on Plato’s Phaedrus, Timaeus, Republic, and Laws; Aristotle’s Politics; and Cicero’s Republic). He then considers the actualization of music and ways in which music influences behavior through its delivery and the sympathetic resonance of its masculine, feminine, and medial qualities with those of the soul (drawing on Damon of Athens, an elusive figure on whom Plato may have relied for many of his observations about music). This in turn leads to the ways in which musical instruments themselves possess genders and communicate ethical characteristics.

In its treatment of the remaining subclass, the Natural, Book III explains the ultimate goal of music, as anticipated at the very beginning of the treatise (1.1): “it [music] explains both the nature of numbers and the variety of proportions; it gradually reveals the harmoniai that are, through these, in all bodies; and . . . it is able to supply the ratios of the soul – the soul of each person separately and, as well, even the soul of the universe.” Book III is divided into the two parts of the Natural subclass of music, the Arithmetic part reviewing the elements of Pythagorean musical mathematics, possibly drawn from Plutarch’s De animae procreatione (see above) and Theon of Smyrna, while the Natural part relates “each particular to the universe altogether” (3.9). Every musical element (the genera, individual notes, tetrachords, intervals, scales, tonoi, etc.) is associated with some natural element (geometric shapes, five senses, four elements plus the ether, four seasons, the gestation of animals, the four triangles of the zodiac, the astrological actualities, and so on), leading to the relationships among the soul of the universe, the harmonic numbers and means, the virtues, and individual souls, all of which is essentially a gloss on Plato’s Timaeus 35a–c (Figure 24.6)

Figure 24.5 Aristides Quintilianus’ subclasses of music in De musica 1.5 (Mathiesen 1999: 527)

Figure 24.6 Aristides Quintilianus’s design of the soul in De musica 3.24 (Mathiesen 1999: 575)

Book III further notes that different types of melody may be seen as paralleling the two types of future (recalling Plotinus’s Enneads II.3 [52], ch. 9, and III.1 [3], ch. 1; Plato’s Laws 4 and 11 and Cicero’s Republic 10.14–16): conjunct melody moving in sequential order is likened to the “what-will-be”; disjunct melody to the “what-may-be.” Modulation in music, like other types of changes that occur in nature, can thus be further likened to a change of the “what-may-be.” With all its paradigmatic qualities, Aristides Quintilianus concludes that music provides an agreeable preliminary study to philosophy as her “greatest consort and attendant.” Thus, “we must afford to both philosophy and music their proper worth and honor; and we must unite their conjunction as most fit and legitimate” (De musica 3.27).

Latin writers of later antiquity

Latin writers of the first centuries of the Common Era were generally uninterested in musical speculation or a philosophy of music, and as the Latin West began to lose a first-hand knowledge of Greek, authors – insofar as they wished to speak of music at all – increasingly relied on intermediate encyclopedic works such as the Disciplinae of Varro, Vitruvius’s De architectura, and Pliny’s Naturalis historia, and on Cicero, Seneca, and Quintilian as accessible alternatives to Plato and Aristotle. In these early centuries, only St. Augustine (354–430) and Anicius Manlius Severinus Boethius (c.480–525/26) devoted entire treatises to music, but several more centuries would pass before these treatises would begin to exert a substantial impact on medieval musical thought.

Augustine

The first five books of Augustine’s De musica (written prior to his conversion) are devoted to a definition of music and a study of rhythm, relying on number and proportion. The sixth book (written after his conversion) is entirely different in style, tone, and content: here, number and proportion are projected from the corporeal to the incorporeal. Music has a sensory (and sensuous) dimension, but it also causes the soul to imitate the harmony of number in proportion, leading it to a love of God. By absorbing the neo-Platonic view of music and adapting it to Christianity, Augustine (in parallel with other Fathers of the Church, East and West) provides a compelling argument for music not only in Christian worship but also as a legitimate field for philosophical and theological study. These roles are pursued in two types of medieval musicography: the so-called cantus tradition of early medieval music theory, which evolves into the tradition of musica practica, and the tradition of musica theorica or musica speculativa.

Boethius

Boethius, fearing that knowledge of the Greek intellectual and scientific tradition was being lost in the decline of civilization, intended to undertake paraphrase translations of the major Greek texts in the four Pythagorean scientific disciplines (which he called the quadrivium); all of Aristotle’s works on logic, ethics, and physics; and all of Plato, as well as showing the inherent harmony of these philosophical schools. He was unable to carry out such an ambitious program but did translate Porphyrius’s Isagoge, most of Aristotle’s Organon (with commentaries), and Pythagorean treatises on arithmetic and music by or based on Nicomachus (see above), all of this in addition to numerous theological works and The Consolation of Philosophy, his most famous work, written at the close of his life.

Book I of De institutione musica introduces the study of music as understood by the Pythagoreans, laying out a threefold division of musica mundana, humana, and instrumentalis and the distinction between the practitioner of music (cantor) and the true musicus, “one who exhibits the faculty of forming judgments according to speculation or reason relative and appropriate to music” (Boethius 1989: 51). The first four books are devoted to musica instrumentalis (i.e. the elements of harmonics and other principles of Greek music theory). Books II and III draw on Boethius’s earlier De institutione arithmetica to demonstrate the Pythagorean mathematical tenets of Book I, while Book IV is devoted to a detailed (although somewhat confused) treatment of musical notation, the three genera of melody, and the “modes [modi], also called tropoi or tonoi.” Book IV, in particular, had a profound influence on the system of modes (or tones) applied to the medieval system of classifying liturgical chant. Book V, which is incomplete, is based on the first book of Ptolemy’s Harmonica and thus, as noted earlier, provides a sort of reconciliation of the Platonic and Aristotelian traditions, one of Boethius’s aims in his grand intellectual project.

It seems that Boethius intended to include the second and third books of Ptolemy’s Harmonica as Books VI and VII; had this been done, De institutione musica would indeed have ended with treatments of musica humana (the blending of the elements of the body and the soul (see Figures 24.3 and 24.4 above)) and musica mundana (the music of the cosmos). Nevertheless, even without this material, De institutione musica becomes the fundamental text for the study of musica within the quadrivium and is inescapable throughout the entire medieval tradition of musica theorica, into the Renaissance, while Boethius himself comes to be seen as an archetypal musicus.

Other authors

Apart from Augustine and Boethius, the most important Latin authors of the first seven centuries of the Common Era who made more than passing mention of music in their treatises include Censorinus (De die natali), Calcidius (In Timaeum Platonis), Macrobius (In somnium Scipionis), Martianus Capella (De nuptiis Philologiae et Mercurii), Cassiodorus (Institutiones; see Cassiodorus 1998), and Isidore of Seville (Etymologiae; see Isidore 1998). All of them convey some version of Pythagoras’s discovery of the harmonic numbers, and some of them also include Pythagorean references to the harmony of the spheres (especially Calcidius and Macrobius, as would be expected) and the ability of music to influence behavior. Pythagorean and Aristoxenian references are frequently found together, sometimes conscientiously contrasted (as in Censorinus), sometimes without comment (as in Martianus Capella). These are highly eclectic works in which the musical content is primarily an intellectual adornment. Nevertheless, all of them were widely read in the Middle Ages and exerted considerable influence on later musical thought. (For a fuller treatment of all these figures, see Mathiesen 1999: ch. 7.)

The Carolingian Renaissance and beyond

The period following the death of Isidore (d. 636) until the establishment of the universities at Bologna, Paris, Oxford, and Cambridge in the eleventh and twelfth centuries was not propitious for further developments in musical philosophy in the East or West. The school of philosophy in Athens was closed in 529, and the university at Constantinople was replaced in the seventh century by the Ecumenical College (controlled by the Church), which was closed in turn during the Iconoclast controversies in the eighth and ninth centuries. Emperor Justinian (r. 527–65) and his successors were preoccupied with the control (political and ecclesiastical) of the Western territories, the rise of Islam, and the depredations of Iconoclasm, which left little time for an interest in philosophy, literature, and the ancient sciences.

The ninth century, however, was a period of intellectual renewal – in the East under the Macedonian dynasty (867–1056), in the West following the coronation of Charlemagne as Holy Roman Emperor in 800, and in the Islamic empire with the establishment of the House of Wisdom (832) by the caliph al-Ma’mūn. Unfortunately, a short chapter such as this must limit itself to the barest outline of developments in the West, leaving it to readers to pursue the various figures and subjects, according to their interests (see the respective articles in Sadie 2001 for further information on almost all of the following figures; their names are given as in that reference work).

Invited by Charlemagne in 781 to join the palace school at Aachen, Alcuin of York (c.735–804) became Charlemagne’s personal tutor and author of his educational program, including the Admonitio generalis of 789, which specifies the curriculum for the church schools to be established throughout the kingdom and – later – empire. Alcuin emphasized the study of the seven artes as the basis for philosophy and theology, which helped insure their acceptance as legitimate subjects in a Christian context, leading in turn to a renewed interest in the work of Martianus Capella and Boethius. The importance of music, in particular, was stressed by Johannes Scotus Eriugena (or Erigena; c.810–c.877), who undertook a fully comprehensive philosophy in De divisione naturae, as well as translations of the pseudonymous neo-Platonic De caelesti hierarchia (in which the orders of angels replace the sirens or muses in a new celestial harmony) and De divinis nominibus, both attributed (in 532) to Dionysius the Areopagite. Since, for Johannes, music and the universe are related through harmonia (De divisione naturae 3), art aids human beings in returning to the beautiful oneness of God (De divinis nominibus 4.7).

With music fully established in the Carolingian curriculum as one of the artes and as central to establishing and codifying a uniform liturgy throughout the empire, there was a demand for treatments explaining the theoretical principles of music while finding ways to make use of existing principles (frequently glossed with scriptural parallels) to address current practical issues, such as the organization of chant into a series of eight “tones” (four “authentic” and four “plagal”); classification of chants within the tones according to their differentiae; relationships of the eight tones to the Greek tonoi; definition of pitches and intervals, located through mathematical principles; relationship of the tones one to another by characteristic species of intervallic structure in a defining octave, fifth, or fourth; parsing musical structures into phrases, clauses, and sentences; rhythm and meter; systems of notation to assist in defining and stabilizing individual chants; polyphony (organum); and pedagogy. These treatments drew heavily on Boethius, the Latin grammarians, and to a lesser extent Macrobius, Censorinus, Martianus Capella, and Isidore. Thus, they reflected the approaches characteristic of these authors of late antiquity, as described above.

By the eleventh century, many of the practical issues had been addressed, especially those of definition and classification, and in the following centuries (until the mid-fifteenth), musical writings expanded in various different directions, some of which were broadly philosophical (e.g. those involving the classification of knowledge by William of Conches, Hugh of St. Victor, Alan of Lille, Raoul de Longchamp, Dominicus Gundissalinus, etc.; or those influenced – positively or negatively – by the revival of Aristotelianism such as Robert Grosseteste, Robert Kilwardby, Albertus Magnus, Thomas Aquinas, and Roger Bacon); some were practical and pedagogical (e.g. treatises by Guido of Arezzo, Johannes Cotto Afflighemensis, Johannes de Garlandia, Franco of Cologne, Johannes de Muris, Robert de Handlo, Marchetto da Padova, and various anonymous authors), although many of these contain philosophical analogies and observations, exhibit an interest in the identification and classification of musical genres (e.g. Johannes de Grocheio’s De musica), or are adaptations of earlier works (e.g. Johannes de Muris’s Musica speculativa, essentially an abridgment of Books I–III of Boethius’s De institutione musica); and some attempted grand summae, perhaps influenced by Vincent de Beauvais or Aquinas (e.g. Hieronymus de Moravia, Walter Odington, Jacobus of Liège, John of Tewkesbury, Ugolino of Orvieto, and others). There was also a growing concern with the relationship between time and music (emerging from earlier treatments of rhythmics and metrics), especially within polyphonic compositions where the various lines might measure different simultaneous times. Thus, proportions and the nature of numbers, which had previously been considered primarily in regard to sound, play an increasing role in explaining the ever more complicated relationships of counterpoint.

Medieval interests in harmonia, mode and tonos, the influence of music on behavior, the measurement of time, the nature of sound, definitions of consonance and dissonance, the place of music in education and society, the harmony of the spheres, and so on, did not die out by any means with the rise of humanism, but by the mid-fifteenth century, writers concerned with music, whether they were philosophers such as Marsilio Ficino, pedagogues such as Vittorino da Feltre and Giorgio Anselmi, or theorists such as Johannes Gallicus, had found new sources of inspiration and a new approach to philosophy and music.

See also Music theory and philosophy (Chapter 46), Plato (Chapter 28), and Rhythm, melody, and harmony (Chapter 3).

References

Aristides Quintilianus (1998) “From On Music,” in Strunk, pp. 47–66.

Aristotle (1998) “From the Politics,” in Strunk, pp. 23–34.

Boethius, A.M.S. (1989) Fundamentals of Music, ed. C.V. Palisca, trans. C.M. Bower, New Haven: Yale University Press.

Cassiodorus (1998) “From Fundamentals of Sacred and Secular Learning,” in Strunk, pp. 143–48.

Gaudentius (1998) “Harmonic Introduction,” in Strunk, pp. 66–85.

Gibson, S. (2005) Aristoxenus of Tarentum and the Birth of Musicology, New York: Routledge.

Isidore of Seville (1998) “From the Etymologies,” in Strunk, pp. 149–55.

Mathiesen, T.J. (1999) Apollo’s Lyre: Greek Music and Music Theory in Antiquity and the Middle Ages, Lincoln: University of Nebraska Press.

—— (2001a) “Harmonia,” in Sadie, vol. 10, pp. 851.

—— (2001b) “Tonos,” in Sadie, vol. 25, p. 608.

Plato (1998a) “From the Republic,” in Strunk, pp. 9–19.

—— (1998b) “From the Timaeus,” in Strunk, pp. 19–23.

Sadie, S. (ed.) (2001) The New Grove Dictionary of Music and Musicians, 2nd edn, London: Macmillan.

Sextus Empiricus (1998) “Against the Musicians,” in Strunk, pp. 94–109.

Strunk, O. (ed.) (1998) Source Readings in Music History, rev. edn L. Treitler, New York: Norton.