| 7 | Measuring the Circle The Story of π |
The number we call π (pronounced "pie'", like the dessert or pizza) has a long and varied history. That symbol didn't originally represent a number; it's just the Greek letter that corresponds to our letter p. But the number it now labels was well known to the ancient Greeks. Long, long ago, they and others before them recognized that circles had a special, useful property: The circumference of any circle divided by its diameter always comes out to be the same number. If we agree to call that number π, then this handy fact translates into the familiar formula C = πd.
In other words, the ratio of the circumference to the diameter of a circle is always the same. We think of it as a constant — a number that stays the same regardless of how the other numbers in the situation may change. The scholars of ancient times also knew that this same constant ratio showed up in another basic property of circles: The area inside a circle is always that constant times the square of the radius. That is, A = πr2. In particular, if a circle has radius 1 unit (inch, foot, meter, mile, light year, or whatever), then the area inside that circle is exactly equal to π units.
Because the circle shape is so important for so many things we humans make and use, from wheels and gears to clocks and rockets and telescopes, the constant in these two formulas is a number well worth knowing. But what is it, exactly?
From a historical viewpoint, the fascinating, troubling word here is "exactly." Finding its value has been a mystery that people of many different civilizations have worked on and puzzled over for hundreds of years. Here are a few examples:
ca. 1650 B.C. — The Rhind Papyrus, from ancient Egypt, approximated the area of a unit circle as 
ca. 240 B.C.— Archimedes showed that it is between 
and 
Heron later popularized the use of 
in many practical contexts.
ca. 150 A.D.— Ptolemy, a Greek astronomer, used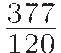 
for it.
ca. 480 — The Chinese scholar Zu Chongzhi used 
for it.
ca. 500 — The Indian mathematician Āryabhaṭa used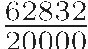 
for it.
ca. 1600 — A decimal value for it was computed to 35 places.
1706 — William Jones, a British mathematician, first used the Greek letter π as the name of this number. That symbol was adopted by the great Swiss mathematician Leonhard Euler in his publications of the 1730s and 1740s, and by the end of the century it had become the common name of this constant.
1873 — William Shanks of England computed, by hand, a decimal value for π to 607 places. It took him more than 15 years. Digits after the 527th are incorrect, but no one noticed the error for almost a century!
1949 — John von Neumann used the U.S. government's ENIAC computer to work out π to 2035 decimal places (in 70 hours).
1987 — Prof. Yasumasa Kanada of the University of Tokyo worked out π to 134,217,000 decimal places on an NEC SX-2 supercomputer.
1991 — Gregory and David Chudnovsky calculated π to 2,260,321,336 decimal places in 250 hours, using a home-built supercomputer in their New York City apartment. (This many digits, printed in a single line of ordinary newspaper type, would stretch from New York to Hollywood, California!)1
2002 — Prof. Kanada's team computed π to 1,241,100,000,000 decimal places! This number is almost 550 times as long as the one the Chudnovskys found. As a line of ordinary type, it would extend more than 1,500,000 miles — more than three trips to the Moon and back.
Yet none of these results is the exact value of π.
About 1765 (when America was working up to the Revolutionary War), a German mathematician named Johann Lambert proved that π is an irrational number; that is, it cannot be expressed exactly as a common fraction (the ratio of two whole numbers). Among other things, this means that no decimal expression, no matter how far it is extended, will ever exactly equal π. But we can find decimals as close as we want, if we're willing to be patient and do enough work.
In fact, just a few decimal places are good enough for almost all practical purposes. The same is true for many of the approximations that were used even before decimals were invented. To illustrate this, we'll calculate the circumference of a circular lake with a diameter of exactly 1 kilometer (about 0.62 miles) using the historical approximations of π listed above, and compare the results to what we get using a modern calculator:
Even the crudest of these approximations, from more than 3600 years ago, is off by less than 1%. The rest of them miss the "real" circumference of the lake by a truly insignificant amount. So why do people bother to calculate π to thousands or millions or billions of decimal places? Is there any possible value to spending all that time and effort? Maybe so. There are many deep questions about irrational numbers that we cannot yet answer. We can prove that their decimal expansions are infinite and do not repeat any finite sequence of digits without interruption from some point on. But is there some subtle pattern in this sequence of digits? Do all ten digits appear with equal frequency, or do certain digits occur more often than others? Do certain strings of digits appear in some predictable way?
We do not even know enough yet to know precisely what questions are worthwhile. Sometimes a seemingly insignificant point leads the way to broad, new insights. And then there are questions about the hardware and software being used to generate these immense strings of digits: How can we make their capacities bigger, their speed faster, their accuracy more reliable'' A problem such as generating the digits of π provides a proving ground for technological improvement.
Nevertheless, probably the most honest explanation of such persistence is simple human curiosity about the unknown. Virtually any problem without an easy solution will lure at least a few people to pursue it, sometimes obsessively. The history of both the progress and the folly of the human race is dotted with the achievements and the misadventures of such people. Not knowing in advance which questions will lead which way adds a risk factor that makes them more inviting. In mathematics, as in any sport, overcoming the challenges of the untried and the unknown is its own reward.
The first 1000 decimal places of π
For a Closer Look: Beckmann's [11] is a readable book about the history of π. Also worth looking at is [14], which collects many articles, including some of the original sources (for example, it contains a sampling from Shanks's original publication). The latest information about Prof. Kanada's computations can be found at the Kanada Laboratory home page.
1 The story of the Chudnovskys and their amazing machine appears in "The Mountains of Pi." a profile by R. Preston published in The New Yorker in 1992. See [144].