If we could rewind the tape of evolution and start it all over again, would things look pretty much the same or radically different? Would fish and birds still look like … fish and birds? Would dogs and cats still walk the Earth? Would human beings still rule the world? Or would our planet be populated by a mind-blowing menagerie of exotic creatures that would make the most unbridled works of science fiction seem tame?
Put another way: Should biological life have evolved as we know it or is our world just one possibility, the way the dice just happened to fall?
The late Harvard paleontologist and evolutionary biologist Stephen Jay Gould famously argued that starting over would produce far different results. In his seminal 1989 book, Wonderful Life: The Burgess Shale and the Nature of History, he wrote:
I call this experiment “replaying life’s tape.” You press the rewind button and, making sure you thoroughly erase everything that actually happened, go back to any time and place in the past—say, to the seas of the Burgess Shale. Then let the tape run again and see if the repetition looks at all like the original. If each replay strongly resembles life’s actual pathway, then we must conclude that what really happened pretty much had to occur. But suppose that the experimental versions all yield sensible results strikingly different from the actual history of life? What could we then say about the predictability of self-conscious intelligence? or of mammals? or of life on land? or simply of multicellular persistence for 600 million difficult years?
Gould’s point was that a high level of chance has been involved in determining which organisms have survived and evolved over the course of Earth’s history. This is likely so. From the meteors that caused mass extinctions to the vagaries of local conditions that rewarded particular adaptations in certain species, the unexpected and unpredictable have left indelible marks.
Nevertheless, increasing numbers of biologists are acknowledging that there are some boundaries—structural constraints and organizational possibilities—that reduce the pool of potential outcomes. There is a growing awareness that some general design rules should always govern the form of any animal life. An assumption behind natural selection, after all, is that some designs work better than others. What it doesn’t tell us is: What are the principles that make them work better? What does “work” mean? What does “better” mean?
Those questions have long hung in the air, creating vast pools of observations awaiting explanation. As we noted in the preceding chapter, scientists have known for quite some time about the predictable branching pattern of blood vessels and river basins. What they couldn’t figure out was why this should be so. As a result, they have avoided the question or, like Gould, focused on the influence of chance and nondeterminism. Taking a step back, we can see that this is no explanation at all. Chance and accident are the opposite of rationality; they are not knowledge but an acknowledgment of its absence. “Chance” is a code word for saying there is too much conflicting data, too many variables for us to make sense of the whole. It is an admission that we cannot see the pattern, which is the opposite of randomness and noise.
Human beings, however, abhor uncertainty, so we have transformed this intellectual impotence into the certainty of doctrine and dogma. Our ancestors ascribed much of what they couldn’t explain to the actions of invisible forces, divine and otherwise. Presto, we had the answer for everything we couldn’t explain. Even the contradictions—Why would a benign God allow suffering?—could be dismissed with the knowing claim that He acts in mysterious ways. Even as modern science has developed the tools to account for large swaths of natural phenomena, it has embraced the notion of nondeterminism to provide a sense of order, and control, over still-puzzling forces. It is an explanation that explains very little, turning mystery into science. Old habits die hard.
It was the best we could do—until now. Just as Newton decoded the once obscure laws of motion and modern medicine has shown that antibiotics are a far more effective treatment for infection than bleeding, the constructal law is another step in our ongoing effort to understand the world around us. It reveals that design in nature is not the result of chance but of a universal law.
In this chapter we will see how the constructal law provides a very different answer to Gould’s fundamental question: If we rewound and replayed “life’s tape,” the evolving designs of animals (and everything else) would not be radically different. We will do this by examining the three main types of animal locomotion: swimming, running, and flying. This was one of the first areas I explored after discovering the constructal law because it directly addresses its fundamental tenets. Locomotion is movement. If the constructal law is truly a principle of physics, if flow access is the key to design, then I should be able to use it to predict not only the designs of inanimate phenomena—such as river basins, lightning bolts, and lava flows—but also the design of animate phenomena such as fish, land animals, and birds. In the process, I would have strong evidence for a unifying theory of design in nature.
Animal locomotion was also a fruitful area of study because the prevailing view in science is that unbridgeable differences exist among these three forms of movement. No one would confuse a shark slicing through the water with a rabbit hopping across the ground or a hawk gliding through the air. The constructal law allowed me to challenge this position by casting old questions in a new light. Instead of focusing on all that separates these different travelers, I zeroed in on the defining characteristic they have in common: All are vehicles for moving mass (their bodies, and what flows through their bodies). Thus, all should have evolved in strikingly similar ways to facilitate their flow of mass across the landscape.
Life is movement. Every living system performs better when the power that is required for maintaining its movement is minimized. Just as lightning bolts and river basins should generate treelike structures to reduce thermodynamic imperfection and increase flow access, animals should have evolved to cover a greater distance for less effort, which means per unit of useful energy derived from food.
This should be true in every respect, allowing us to predict everything, from the size of their hearts and the shapes of the blood vessels to the frequency with which they move their tails, legs, or wings to the paths they cut across water, ground, and air. The traits that have emerged, the evolutionary changes that have persisted as well as the behaviors that are learned, should facilitate flow. And, if better flow is the fundamental tendency that accounts for shape and structure, then we should see the limits of accident and chance and the power of predictable pattern.
Here’s what I found.
Animals move in such seemingly different ways that scientists have long considered the three main types of locomotion to be distinct. Runners and fliers have weight, for example, whereas swimmers are neutrally buoyant. The wings of birds are structurally different from the limbs of antelopes and the tails of fish. The flapping motion of a bird’s wings is unlike the hopping motions of the legs of a land animal and the undulating body of a swimming one. Birds and fish in cruising mode seem to move at a constant altitude or depth, whereas runners hop up and down. Hitting the ground during running is far different from moving against water.
Complicating the picture even further is the great diversity of body sizes, shapes, and speeds found in even a single form of locomotion. We see large and small birds and fast and slow ones; birds that walk a lot and ones that do not; birds that fly alone and those that fly in flocks. Comparing the buzzing wings of a mosquito to the majestic flight of a great blue heron would lead most people to conclude that very different processes are at work. And, let’s be frank, scientists have furthered this line of thinking because diversity means that the expert on butterflies has no reason to fear the fame of the expert on blackbirds, much less the specialist on fish. The distinguished professor of aeronautical engineering does not have to give credit to those who developed his science under the name of shipbuilding centuries earlier. Diversity is also very lucrative. Jobs, salaries, prestige, and opportunities in science—with its area-specific language, concepts, books, journals, libraries, university departments, academies, and awards—depend on specialization.
Examined in toto, the design of nature contradicts this approach. Numerous investigators have found that there are strong convergences in certain functional characteristics of swimmers, runners, and fliers. Just as scaling laws inform the structure of river basins, blood vessels, lungs, and a host of other phenomena, predictable patterns appear across the board in animals. Many of these involve the strong correlation between an animal’s size (its body mass) and its movement. Broadly speaking, the correlation is this: Larger animals are faster, their bodies undulate less frequently, and they are stronger (that is, their muscles exert larger forces) than smaller ones.
Consider once more the mosquito. It may flap its wings up to 1,000 times a second just to move a few meters. The great blue heron, by contrast, flaps its wings leisurely every few seconds at cruising speeds of between 20 and 30 miles per hour. Similarly, the guppies we keep in our fish tanks must move their tails rapidly to travel across the tiny distances of their watery domains, while blue sharks can reach speeds of up to 25 miles an hour by undulating their tails with long, powerful sweeps. Size really does matter.
What is most astonishing is that this correlation between body mass and movement holds true not just for every group of similar animals—all swimmers, runners, or fliers—but uniformly across the animal kingdom. Thus, the stride frequency of land animals scales with approximately the same relation to body mass as the swimming frequency of fish; the speed of running animals scales with approximately the same relation to mass as the speed of flying birds. Put another way, if we know an animal’s body mass, we can calculate how frequently it swings its tail, moves its legs, or flaps its wings. In addition, the force output of the muscles of swimmers, runners, and fliers can be calculated from their weight: It is, for all of them, roughly equal to twice their body weight.
In an attempt to explain these consistent features of animal design, biologists have concentrated on potentially common constraining factors, such as muscle contraction speed, or structural-failure limits. These findings are descriptive, not predictive: They tell us what we see but not why this should be so before we see it. The constructal law provides meaning to this experience, enabling us to discover the relationship between mass and movement, using theory—a purely mental viewing—to predict what their designs should look like.
We start with a basic fact: It takes fuel or food to produce the work that powers every engine. The fuel or food generates an amount of heat. A significant fraction of this heat—called useful energy, available energy, or exergy—is in principle available to be converted into work. The bad news is that neither animals nor heat engines can fully convert the useful energy into work.
Some of the useful energy is lost because of many features of imperfection (flows that overcome resistances, heat currents that flow across finite temperature differences, etc.). This happens everywhere, before the animal or engine produces work from useful energy (exergy), and after (we will discuss this in greater detail in chapter 10). With the produced work, cars, people, and birds battle wind and gravity among other things; the water in rivers rubs against the hard earth and against other obstacles that would slow it down. This is how the precious fraction of useful energy that had become work is ultimately destroyed. All of it.
A well-designed flow configuration cannot obliterate imperfection. But it can reduce its global effect so that more useful energy is made available for moving the mass on the landscape. This is achieved by a better and better distribution of imperfections. To evolve toward a balance of the various imperfections, the components of the flow design must be distributed in certain ways. A river basin, for example, configures and reconfigures itself so that the water is discharged more and more easily from the entire plain to the mouth of the river. The bifurcated structure of lungs, the round tube shape of pipes, and the cracking pattern of drying mudflats are all designs that distribute their resistances so that globally the flow system becomes less and less imperfect.
Animals travel on the surface of the Earth as do rivers, winds, and ocean currents (Figure 19). All are engines that generate work to move mass in an environment filled with things (brakes) that oppose their movement. They move in different ways for different purposes, but the effective expenditure of useful energy is important over a lifetime. Like everything that flows, animal locomotion represents the tendency of moving objects to overcome obstacles, chiefly from gravity and the friction against air, water, and land.
The constructal law predicts that, if we rewound Gould’s tape of life, fish, terrestrial animals, and birds should always manifest designs that allow them to move their mass farther for a given amount of useful energy that is derived from food. More power, more speed, farther, faster; these are measurable manifestations that invoke the word “better.” This is the time arrow, the design direction of all the other flows that cover the Earth.
Figure 19. Several configurations that facilitate the circuit executed by water in nature: raindrops, tree-shaped river basins and deltas, trees and forests, the flow of animal mass (swimming, running, flying), and turbulent structure.
As is customary in science, for our analysis of locomotion we group animals together by basic body types. In the simplest model possible (the one that represents all the bodies), the animal body has a single length scale (Lb) and a body mass scale (M). First, here is what “scale” means. To measure the length of a housefly, we use the unit millimeter. To measure its weight, we use milligrams. This same scale applies to other insects. The Lb for a sparrow is measured in centimeters and its M in grams. The same is true for hummingbirds, so that hummingbirds and sparrows are said to have the same scale. Moving up in size, the Lb of a goose is measured in meters, its M in kilograms. Inside each scale we find a large number of animals and things that line up to be measured in the same way. For example, the kilogram scale of mass unites the goose with the duck, owl, vulture, and toy airplane.
This concept of scale is important because it underscores the fact that we are examining broad phenomena. Some sparrows fly faster than others; an obese man cannot run as fast as an Olympic sprinter—a myriad of factors, including cold and warm habitat or a weakness for ice cream, determine variation within a group. Nevertheless, the entire community of sparrows exhibits predictable flight characteristics just as, broadly speaking, human beings move their legs at a predictable rate and run at a predictable speed.
Now let’s focus on an imaginary flying body, using the constructal law to predict what its design should look like to reduce the effects of thermodynamic imperfection—as well as the broader prediction that animals are built for movement. Just as river basins put the right channels in the right places to move more water for less useful energy, flying bodies should flap their wings with the right rhythm to enable them to achieve the right speed to move their mass a greater and greater distance.
We note that a flying body is a study in deception. At cruising altitude it appears to glide across the sky, riding gently on the wind, straight as an arrow. This lovely image is, alas, an illusion. Its passage is not a steady movement at a constant altitude. Its trajectory, instead, is a saw-toothed horizontal line with a tooth size dictated by the flapping stroke (Figure 20). It rises with the downward stroke that works against the force of gravity and then falls as the effect of this effort wanes. The essential point is that as its cruising speed increases, this vertical loss decreases but its horizontal loss increases due to mounting air friction. To see this for yourself, next time you’re a passenger in a car going 30 miles an hour, stick your hand, tilted slightly up, out the window. In addition to the resistance of the wind, you feel that same wind lifting your hand (which is acting as a makeshift wing). Now have the driver increase the speed to 60. Even as you feel the wind pushing your hand back, requiring more force to keep it steady, you also feel much greater lift.
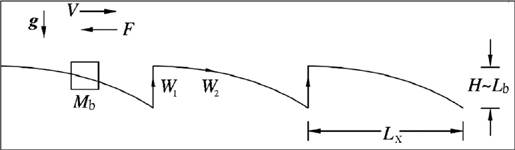
Figure 20. The periodic trajectory of a flying animal shows the factors considered in predicting animal locomotion from the constructal law. The saw-tooth pattern results because flying velocity (V) is composed of alternating work done to overcome vertical loss (W1) and to overcome horizontal loss (W2). W1 is found by multiplying body mass (M), gravity (g), and the height the body falls during the cycle (H), the latter of which scales with body length (Lb). W2 is the product of the force of air drag (FD) and the distance traveled per cycle (Lx).
To fly at a constant altitude, a body spends useful energy to overcome vertical and horizontal loss. Neither loss can be avoided completely. However, the constructal law predicts that they should be balanced against each other so that their sum is made smaller and smaller through the selection of a rhythm in which the work of repositioning the body vertically is matched by the work of advancing the body horizontally. Balance should be achieved by wing flapping such that the flying speed is just right. This special distribution of imperfections is flight itself.
Flying, then, is a rhythm, a sequence of beats tapped out by the wings. For example, if you think of a bird, during a cycle—defined as one downward and upward wingbeat—the bird must perform work in two ways: in the vertical direction (W1) and in the horizontal direction (W2). At cruising altitude, the vertical work necessary in order to lift the body back to a height equivalent to its body or wing length scale (Lb) is W1 ~ MgLb, where Mg is the weight of the body, g is the gravitational acceleration (9.81 meters per second squared), and the symbol ~ means “of the same scale as” or “approximately equal to.”
Meanwhile, horizontal work is necessary in order to penetrate the surrounding medium (air). This work is equal to the drag force (F) times the distance traveled during one cycle of wing flapping (Lx), namely W2 ~ FLx. The horizontal travel Lx is equal to the cruising speed V times the timescale of one cycle.
Combining these formulas, we find that the total work spent to cover a distance is the sum of two losses: the vertical work done per unit of travel and the horizontal work done per unit of travel.
The constructal law predicts that the design of birds should reflect the tendency to mitigate these two losses. How should it do this? Given that the mass of the flying body is fixed, it should lift itself at the right rhythm to achieve the right speed to minimize the sum of the horizontal and the vertical loss, for an object its size.
Returning to our drawing board, these formulas reveal the simple scaling laws that we can use to design our imaginary bird. To mitigate these two losses, speed should be proportional to body mass raised to the power of 1/6, or V ~ M1/6. For birds, the flapping frequencies should be proportional to body mass raised to the power of minus 1/6.
With these equations, the constructal law predicts that larger birds should fly faster than smaller ones and that heavier birds must do more work to travel the same distance as lighter ones, so that they must eat more food than lighter birds. It also predicts that larger birds should flap their wings more slowly than smaller birds or insects. This should be true for all flying bodies.
With the V ~ M1/6 formula (Figure 21), we predict that a 10-kilogram bird should have a speed on the order of 20 meters per second. For a 1-gram insect, the same formula predicts a speed on the order of 5 meters per second. These are just scales, orders of magnitude for vultures or mosquitoes; they are approximate but correct. The scatter of the speed data in each group (insects, birds, airplanes) can be discussed further based on differences in body shape, wing slenderness, and lifestyle (terrestrial versus migratory birds).
When I tested my findings in the real world, I found that these predictions agreed well with observations over the entire range of flying bodies—insects, birds, and airplanes (Figure 21). That is, the secret of the design of flight can be explained completely by looking at how every body balances thermodynamic imperfections to achieve flight.
Figure 21. The characteristic speeds of all the bodies that fly (insects, birds, human-and-machine species) next to the constructal speed versus body mass raised to the 1/6 power.
I wrote the constructal theory of animal flight on a whim, while finishing the manuscript for my 2000 book, Shape and Structure, from Engineering to Nature. In September 2004, I was invited by Professors Ewald R. Weibel and Hans Hoppeler, from the University of Bern, to present the constructal law at a biologists’ conference in Ascona, Switzerland. I used the prediction of flight as one of the many examples of how the constructal law accounts for design generation and evolution throughout nature, both animate and inanimate.
Another speaker at this conference was James H. Marden, a biologist from Pennsylvania State University. During the coffee break following my early-morning lecture about flight, he said we should try to predict the scales of running in the same way. We accomplished this, with pencil and paper, before the lunch break.
We found that if we treat running in the same way as flying—as an effort to move efficiently against the forces of gravity and air and ground friction—we can also predict the speeds and stride frequencies of all runners. Running is, essentially, a form of jerky flight. Instead of flapping their wings to lift their bodies, runners use their legs to spring off the ground (Figure 22). At their apogee, runners’ legs are airborne; they are flying ever so briefly. Like birds, their trajectory is saw-toothed, closer to a cycloid. Also like birds, runners encounter two losses of useful energy: vertically, as gravity pulls them back to Earth, and horizontally, to overcome friction against the ground and the surrounding air.
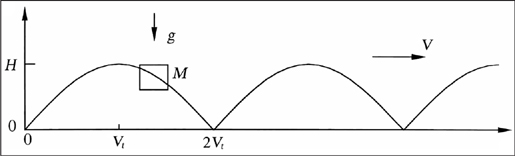
Figure 22. In the periodic trajectory of a running animal, the distance of each stride is the animal’s velocity (V) multiplied by the time (t) of frictionless fall from the height of the run (H). Therefore, t is equivalent to H divided by gravity (g), raised to the 1/2 power. The stride length and H both scale with the body length, and the body mass (M) is approximated by the body density multiplied by the body length cubed.
The vertical and horizontal losses compete, and when they are in balance, their sum is lower than when they are not in balance. Here’s the amazing fact that would be a strange coincidence if it weren’t the outcome of the constructal law. Just as with birds, we can use the constructal law to predict the runner’s speed and stride frequency if we know the body mass (M). What’s more, this formula is essentially the same as the one we found for flight: Speed is proportional to M1/6 and the stride frequency proportional to M−1/6. As with birds, this scaling law allows runners to cover greater distances for a smaller amount of useful energy spent. As we will see in chapter 4, my student Jordan Charles and I applied this finding to swimmers and runners and predicted that world records must fall as champions become bigger, taller, and more slender. The stereotype of the big galoot is a myth. All other things (talent, training, etc.) being equal, bigger athletes go faster.
Another surprise comes from the calculation of the force necessary to lift the body off the ground. For both runners and fliers, the average force exerted over the stride or stroke cycle should be twice the body weight. This agrees with the force-weight measurements across all body sizes, for all animals that fly and run (Figure 23, bottom). These findings underscore the fact that what we are witnessing is not coincidence but pattern.
So far we have seen that running is similar to flying. What about swimming? Jim Marden and I thought about this for three months following our meeting in Ascona. The obvious answer is no, because the movements of the neutrally buoyant bodies of swimmers seem to have nothing to do with gravity. Before the constructal law, this view was dogma across the range of sciences and prevented the emergence of a unifying physics theory of locomotion that includes swimming.
Yes, fish are neutrally buoyant when they float in place. But when they move horizontally, they must push against something, and that something is the Earth. The ground resists everything that moves relative to it, even though swimmers and fliers do not touch it. It serves as a reference against which all moving bodies push. Archimedes declared, “Give me but one firm spot on which to stand, and I will move the Earth.” He was right, and this is why swimming is no different from running and flying. Running and flying evolved from swimming as animal movement spread from water to land to the air.
This design is obvious with birds and land animals, as they fight the vertical loss caused by gravity. Birds push down and back against the air to lift themselves, just as runners push down and back against the ground to spring forward. Swimmers—and for that matter everything that moves under or on top of the water, from boats to submarines—must also push and move their bodies relative to the ground by performing work against gravity and friction.
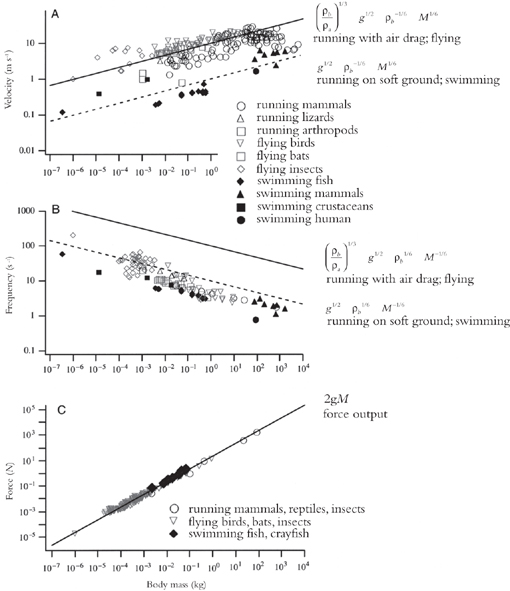
Figure 23. Theoretical predictions from the constructal law are compared with the velocities, frequencies of strokes or strides, and force outputs of a variety of animals. Solid lines in these log-scale graphs show the predicted velocity (A) or frequency (B) of animals based on body mass for flying animals or running animals where the ground is hard and thus the main frictional loss is due to air drag. Dashed lines show the predicted velocity (A) or frequency (B) of animals based on body mass for swimming animals or running animals where the ground is soft and thus the main frictional loss is due to ground deformation. A dotted line indicates the predicted force output, based on body mass (C). The theoretical predictions ignore factors between 0.1 and 10, and so are expected to be accurate within an order of magnitude.
As high school science, common sense, and daily experience make clear, two things cannot occupy the same space simultaneously. To move forward, the swimmer must displace the water in front of it (Figure 24). To advance horizontally by one body length, the swimmer must lift an amount of water equal to its own size to a height approximately equal to its body length. This amount of water must be raised—against the force of gravity—because a net upward displacement is the only way that water can flow around an animal, or any moving object.
Why must the water move up and not down? Because the water surface is deformable and the lake bottom is rigid. The only place the displaced water can move is to the surface, where it pushes through the air and creates a wave. This asymmetry has escaped scientists because most fish are small and swim deep. The water that fish lift is spread out over such an immense area that by the time the displaced water reaches the surface the effect is minuscule—though high-tech systems on satellites are able to detect a moving submarine by the tiny change in the surface water height over a large area.

Figure 24. In order to make forward progress, a fish must move water out of the way, and the only direction the water can go is up. In order to move one body length (L, or Lb) at a certain velocity (V), a fish with body mass Mb must move an equivalent mass of water (Mw). This mass of water can then be thought of as moving downward to occupy the space now vacated by the fish. The work required to move the water mass upward (W1) is approximated by multiplying Mb with L and gravity (g). During the same interval, the fish must do work in order to advance horizontally (W2), that is, proportional to the force of water drag (FD) and the distance traveled per cycle, which in this case is the body length (L).
Those of us who do not own such a detection system can observe this lifting of the surface when fish cavort near the surface and the water seems to boil. It is even easier to see as a boat slices across a lake. Its bow creates a wave that lifts above the surface of the water. You can create the same effect by filling a tub and skimming your finger across the top. The work you do to move your finger across the top causes the displaced water to rise against the pull of gravity, as it exerts two efforts: lifting water (W1) and rubbing against it (W2).
What has not been fully appreciated before the constructal law is that this vertical work is significant and is fundamental to the physics of swimming at all depths. Thus, even though some animals do not touch the ground, they must use it to propel themselves forward horizontally. The flapping of the bird’s wings produces jets of air that eventually push against the ground and increase the pressure that the ground supports. The water lifted by the swimming fish induces a local elevation of the water surface and consequently a greater pressure on the lake bottom. The ground feels and reacts against everything that moves, regardless of the medium in which a particular body is moving. The lake bottom feels the movement of the fish.
With this, the constructal law shows how swimming is the same as running and flying. It is no surprise, then, that the predicted speeds of all swimmers are also proportional to M1/6, just like the speeds of runners and fliers (Figure 23). The same pencil-and-paper analysis shows that the frequency (flapping, fishtailing, stride) should vary as M−1/6: Large animals undulate their bodies less frequently than smaller ones. Bigger fish will flap their tails less often than smaller fish; bigger birds will flap their wings less frequently than smaller ones, and bigger land animals will have less frequent strides than smaller ones.
The correlation between locomotion and body mass that we see in all animals is only part of the puzzle. The principles that govern animal locomotion also predict the flow design of other natural phenomena. The fact that gravity and lifting water are essential in swimming leads to the observation that fish advance horizontally with the same speed as the wave generated by the lifted water.
Bigger waves have higher speeds. The constructal law proclaims that we should be able to predict their speed from their size because these mindless blobs of water should also generate designs that allow them to get from here to there efficiently. Indeed, the study of water waves has shown that their horizontal speed is approximately the same as the speed of free fall from a vertical height that is comparable with the length scale of the wave. The speed at which a three-foot wave moves toward the shore is approximately the same speed at which three feet of water falls to the surface. Just as bigger animals are faster than smaller ones because they fall forward faster, taller and longer waves move horizontally more quickly than shorter ones. Furthermore, if we replace the length scale of the water wave with the length scale of the body of the fish, we obtain the speeds of all swimming bodies. This quite stunning fact is discovered when we consider that animal mass density is roughly the same as the density of water.
This similarity in density between animals and water helps us see the evolutionary connection between the animate and inanimate world. Animals are really just blobs of water; all animals came from water and spread the water on land and in the air. The innumerable waves that the winds and the ocean ceaselessly create allow us to witness evolution. They are manifestations of the process that occurred over vast periods of time to create the far more complicated structures we call fish, land animals, and birds.
Note that the predictions of constructal theory are consistent not only for waves and animals but also for man-made machines. The force–mass relation of engineered motors is the same as that of fliers, runners, and swimmers. The constructal theory of animal flight also predicts the speeds of airplanes—bigger planes are faster—and unites the animate with the inanimate. And why shouldn’t they be united? They, too, confront the same problem as animals and waves: trying to move on Earth against the forces of gravity and friction. They are us—the human-and-machine species.
When we see animal locomotion as a design to move mass on Earth, other puzzles become clear. Let’s start with an obvious observation that leads to a surprising conclusion: Larger animals must perform more work (force times distance) to travel the same distance as smaller ones. When the work of lifting weight (W1) matches the work of overcoming horizontal drag (W2), the total work per distance traveled during the cycle (L) is of the same scale as the weight of the lifted mass (Mg).
In addition, an animal’s metabolic rate (the amount of food it needs to perform that work) can also be predicted from its size by using the constructal law. It, too, increases with body mass. That is, larger animals must eat more food, at a rate that is proportional to Mk—where k is the slope of the food versus M curve when plotted on a log-log graph. The constructal law showed that the exponent k must vary between 2/3 and 3/4. Thus, the constructal law allows us to predict, for the first time, a simple formula where k is not unique for determining the caloric needs of all animals.
The fact that bigger animals need more energy to move their mass than smaller ones is hardly front-page news. The headline here is that larger animals are more efficient as mass vehicles than smaller ones. Using the constructal law, we discovered this by combining our two earlier findings: The amount of food eaten per distance traveled is proportional to Mk (for clarity we set k = 3/4) divided by the animal speed (which is proportional to M1/6). It follows from this that the animal food requirement per unit distance is proportional to M7/12. Furthermore, the food required per unit distance and unit of animal mass decreases in proportion to M−5/12 as the size of the animal increases.
For example, if an elephant weighs 1,000 kilograms (kg) and moves 1 kilometer (km), then its food intake for 1 kg of transported mass is proportional to 1,000−5/12 = 0.0562. If the same 1 kg of animal mass is transported the same distance by 100 jackals each weighing 10 kg, then the food required by the 1 kg is proportional to 10−5/12 = 0.383. What counts is the ratio between the two food requirements, namely 0.0562/0.383, which is approximately 1/7. The conclusion is that the 1 kg of animal mass travels on elephants at only 1/7 of the food cost of the 1 kg on jackals.
This fact illuminates two more big ideas. First, it provides a theoretical physics basis for the economies-of-scale phenomenon noted throughout engineering, economics, logistics, and business. The efficiency of moving something in bulk increases with size (Lorente and Bejan 2010). Second, it underscores the idea that there is a direction of evolution toward improvement of how things move. Just as raindrops occur before rivers, smaller animals appeared on Earth before larger ones—single-cell beings before elephants, mosquito-size insects before great blue herons. Using the constructal law we see the indisputable trend toward not only more movement but also more efficient movement. This time arrow is a major step that we will explore in greater depth in chapter 9.
Here is another puzzle that is elucidated by the constructal law: the sizes of organs of animals and components of vehicles. All animals have characteristic organ sizes: Larger organs on larger animals are so characteristic that all animals appear to have been constructed by assembling the same components in the same proportions of sizes. For example, the hearts of mammals weigh roughly 0.5 percent of the whole animal. Why?
Figure 25. The organ of an animal or vehicle destroys useful energy in two ways, and both depend on the size of the organ. The cost (the useful energy destroyed) due to the flows through blood vessels and other flow constrictions decreases as the organ size increases. The cost of carrying the organ on the animal increases in proportion with the organ mass. The total cost is minimal when the organ size is such that one cost balances the other.
Imagine that the size of the heart is free to vary (Figure 25). The larger it is, the less constrictive its flow passages are, and consequently the work spent on pumping the flow is smaller. At the same time, the work spent in order to carry the organ increases in proportion with the size of the heart. The sum of the two work requirements is minimal when one work cost matches the other. This “optimal distribution of imperfection” pinpoints the organ size.
This is an important theoretical step, because it predicts the necessity of characteristic-size organs. When examined in isolation, the organ appears to be too small, that is, too constrictive to its flows. From this comes the frequent declarations that the organ is a mistake, that is, that “nature makes mistakes.” Yes, if we were designing the heart in isolation, we might make it bigger and heavier, constructing wider pipes for the better flow of blood. But the heart is one component of a larger flow system (the animal), and we predict that it should evolve to have the right size and right weight to enhance the performance of the entire animal to move more easily on the map. These are not “mistakes.” When examined as an integral part of the moving animal, the natural and imperfect organ is the one that (along with the other natural and imperfect organs) makes a good animal—an efficient construct for moving animal mass on Earth.
Because it is a principle of physics, operating everywhere all the time, the constructal law makes us think holistically. Nothing lives in isolation; every flow is part of other flow systems. If we consider a bird in flight, we can see its influence on at least three different levels at once: internally, externally, and behaviorally.
If we dissect the bird to examine its internal organs, we find that the round cross sections of its blood vessels and the shape of its heart and muscles reflect this universal tendency to facilitate the flow of blood, air, food, and stresses. Around its body, feathers minimize heat leaks and friction so that the bird can move its mass more and more efficiently. We note that many birds migrate together. They fly in a V-shaped formation because this means that only the lead bird must fly unprotected into the wind. Those behind it fly in its slipstream, where there is less air friction, enabling them to move at the same speed with less effort. This is also why the large pack of riders in a bike race (the peloton) is almost always able to reel in the few riders who break away early in the race. The individual in the group does not have to work as hard as the solo rider.
This travel pattern also provides efficiency in another way. As the lead bird flaps its wings, it pushes air down. This action creates an air wave (known as a vortex street), pushing displaced air up slightly to the outside of the flapping wing. The following bird positions itself so as to be carried along by this rising pocket of air. The same holds true for the succession of birds in the line and explains the V-like formation. The birds (and the bicycle racers) also rotate their position in the formation by taking turns at the very front. The constructal design of the formation demands this feature, in the same way that the design of the knife blade demands a sharp edge all the time. The formation is the whole animal, the “flying carpet” in which the individual fliers are the organs, and the rotation to the front is the rhythm, the intermittent breathing in the life of the whole.
The same principle explains why fish travel in schools. Each fish displaces water as it swims. Where there was water, now there is fish. As a fish swims, the water behind flows forward to fill the space the fish just occupied. The next fish, by situating itself within a body length of the fish in front of it, is carried forward by the movement of the water, allowing it to expend less useful energy to cover the same distance. (Bike racers also take advantage of this, propelled forward by the air that surges from behind into the space vacated by the rider in front.) The benefits of this effect are realized only if the bird, fish, or cyclist is not too close or too far behind—that is, within a body length. Knowing this, we can predict the design of groups of animals on the move. This mental viewing is applicable across the board. The hull of the ship and its water waves, the submarine and its Bernoulli head, the geese and the V-shaped air waves on which the flock glides, the strings of racing cyclists and cars embedded in the slipstream (another air wave)—they all lift mass and go with the flow.
In sum, the constructal law predicts complex features that have evolved as animal design. In response to Stephen Jay Gould’s question, the constructal law proclaims that if the tape of evolution were rewound and if swimmers, runners, and fliers appeared again, their shapes and structures should produce the same types of speeds, stroke-stride frequencies, and force outputs of these forms of locomotion as exist today. Their circulatory systems would still have a tree-shaped design; their organs would still have characteristic sizes; and, when useful, they would follow movement and migration patterns. Because evolution has a single direction in time—to facilitate the movement of mass—the designs that accomplish this are predictable.
Determinism and randomness find a home under this same law of physics. Up close, we are awed by diversity; the differences between a duck and a goose, much less between animate and inanimate phenomena, are innumerable. But from a distance, the overall patterns of design are easy to see. Earlier we noted how observable differences in the three main types of animal locomotion have led to the prevailing view that they are fundamentally dissimilar. As we have just seen, the constructal law enables us to recognize that they are fundamentally the same. They are united by the basic tendency to balance thermodynamic imperfections, to generate configurations that balance resistances and reduce their combined effect. This is, of course, the same tendency revealed in the evolving design of river basins and lightning bolts, of you and of me.