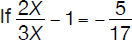The only reason for time is so that everything doesn’t happen at once.
—Albert Einstein
The answers to the problems in this chapter can be found in Chapter 10.
If
0 ≤ x ≤ y
and
(x + y)2 – (x – y)2 ≥ 36
what is the smallest possible value of y?
Two printing presses, M and N, working together can complete a job in 4 hours. Working alone, press M can do the job in 20 hours. How many hours will press N take to do the job by itself?
How many sides does a polygon have if the measure of each interior angle is 5 times the degree measure of each exterior angle?
Five people shared a prize of $100. Each one received a whole number of dollars and no two people received the same amount.
If the largest share was $30 and the smallest one $15, what is the most money that the person with the 3rd largest share could have received?
At time t = 0, a ball was thrown upward from an initial height of 10 ft. Until the ball hit the ground, its height (in feet) after t seconds was given by the function
h(t) = a – (b – 2t)2,
where a and b are positive constants.
If the ball reached its maximum height of 110 ft at time t = 5 seconds, what was the height, in feet, of the ball at time t = 2.5 seconds?
In an amusement park, regulations require that a child be between 30" and 50" tall to ride a specific attraction. Which of the following inequalities can be used to determine whether or not a child’s height h satisfies the regulation for this ride.
(A) | h – 10 | < 50
(B) | h – 20 | < 40
(C) | h – 30 | < 10
(D) | h – 40 | < 10
(E) | h – 45 | < 5
A jar contains 21 marbles: 6 red, 7 blue, and 8 green. If you remove one marble at a time, randomly, what is the minimum number that you must remove to be certain that you have at least 3 marbles of each color?
The number of victories per player of a tennis team is given in the following table:
| # victories | # players |
| 0 | 3 |
| 1 | 6 |
| 2 | 2 |
| 3 | 1 |
A new player joined the team and—as a result—the average number of victories per player became the median number of victories per player.
How many matches did the new player win?
If N + 2 is a multiple of 7, what is the remainder when N is divided by 7?
At a party, a catering company was paid to provide one sub sandwich for every 3 people, one bottle of soda for every 4 people, and one large ice cream cake for every 24 people. If the total number of subs, bottles of soda, and cakes was “N”, then—in terms of N—how many people were at the party?
In a survey of 50 people, 25 people subscribed to newspaper X, 35 people subscribed to newspaper Y, and 20 people subscribed to newspaper Z. For any two of the newspapers, 6 people subscribed to both newspapers but not the third one. If 2 people in the survey did not subscribe to any of the newspapers, how many people subscribed to all three newspapers?
If
2x – 3y = 6
3x – 2y + z = 9
then
x + y + z = ?
The average of three consecutive integers is N. Which of the following must be true?
I. N is an integer.
II. One of the numbers is equal to N.
III. The average of two of the three numbers is N.
| x | f(x) |
| 0 | m |
| 1 | 40 |
| 2 | n |
If f(x) is a linear function defined according to the table above, what is the value of m + n?
The distribution of grades on the final exam in math is shown below:
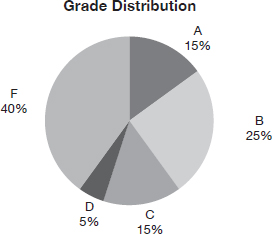
The total number of participating students is 1,000. What percent of the students who failed the exam would have had to pass it, in order for the percent of students passing the exam to be at least 90%?
X is the set of positive integers less than 18; Y is the set of positive integers that contain the digit 3; Z is the set of primes.
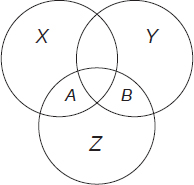
1. How many numbers are members of the region labeled A?
2. Which numbers less than 45 are members of the region labeled B?
Jason’s lock combination consists of three, 2-digit numbers. Each set of numbers satisfies exactly one of the following conditions:
• one number is odd
• one number is a multiple of 6
• one number represents the day of the month Jason was born
Which of the following could be a combination to Jason’s lock:
(A) 24-19-36
(B) 22-20-21
(C) 30-28-26
(D) 19-18-21
(E) 21-20-18
Two propositions were put forward for voting by a city council. Of the 33 city council members, 15 voted for proposition X, 25 voted for proposition Y, and 12 voted for both propositions. Which of the following statements must be true?
I. Ten members voted for proposition Y but not for proposition X.
II. Five members voted against both propositions.
III. Sixteen members voted for one proposition and against the other proposition.
(A) I only
(B) II only
(C) I & II only
(D) I & III only
(E) II & III only
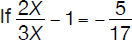
What digit does X represent?
a × 33 + b × 32 + c × 3 + d = 49
Each letter in the equation above represents a digit that is less than or equal to 2. What four-digit number does abcd represent?
A basketball team has 15 players. Each player shot 100 free throws, and the average number of baskets made was 80. If the lowest and the highest scores were eliminated, the average number of baskets for the remaining players was 82. What is the smallest number of baskets anyone on the team could have made?