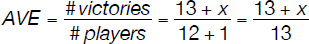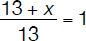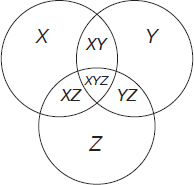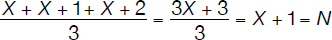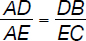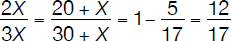Chapter 10
Solutions to Problems in Chapter 9
Computers are incredibly fast, accurate, and stupid. Human beings are incredibly slow, inaccurate, and brilliant. Together they are powerful beyond imagination
—Albert Einstein
Solution 180: 3
We first need to write an equation expressing y as a function of x using the second inequality:
x2 + 2xy + y2 – x2 + 2xy – y2 ≥ 36
or
4xy ≥ 36
and thus
y ≥ 9/x
Maximizing the value of y requires that we minimize (use the smallest possible value of) x. Given that 0 ≤ x ≤ y, the smallest value of x happens to be y and we substitute that value in the expression of y to obtain
y ≥ 9/y
or
y2 ≥ 9
Given that y is a positive number, this results in
y ≥ 3
and thus the smallest value of y is 3.
Solution 181: 5
Observation #1: The number of hours a printing press is in action and its contribution (as in % of work done) to completing the job are directly proportional quantities (more hours, higher percentage of work done).
Observation #2: If more than one printing press is used, their work (percentage of job done) is cumulative.
With these in mind, we can set up the problem to outline the relationship (direct proportionality) among printing presses being used, the number of hours they operate, and the fraction of the task (job) completed during that time:
M + N……4 [hours] ……1 [complete the job]
and
M………20 [hours] ……1 [complete the job]
N……… x [hours] ……1 [complete the job]
Because these quantities are directly proportional, one can write
M………1 [hour] …… 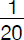 [fraction of job completed]
[fraction of job completed]
N1………1 [hour] …… 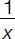 [fraction of job completed]
[fraction of job completed]
M + N………1 [hour] 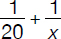 [fraction of job completed]
[fraction of job completed]
M + N………4 [hours] 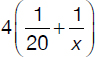 [fraction of job completed]
[fraction of job completed]
Let’s now compare the first and the last relationships shown above. The result is a first degree equation in x:
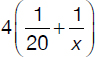
Note that all calculations have been postponed until the last step. It is now easy to see how simplifications can reduce calculations to a minimum, in this case to no calculations at all as simplifying the fraction should not require a calculator:
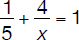
or
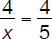
or x = 5 [hours]
Solution 182: 12
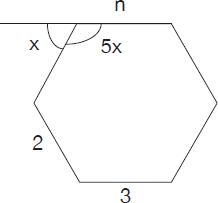
The fact that the ratio of each interior angle to its corresponding exterior one is constant (and equal to 5) indicates that all (interior) angle are equal, therefore the polygon is equilateral (regular).
First, we should calculate the measure of each interior angle of the polygon by noticing that
x + 5x = 6x = 180°
x = 30° (measure of exterior angle)
5x = 150° (measure of interior angle)
The total number of sides of the polygon (n) can then be obtained by writing an equation that gives us the sum of its interior angles using
1. the general formula derived in Problem 52, and
2. the calculated angle measure for its interior angles:
(n – 2) × 180° = n × 150°
n × 180° – 360° = n × 150°
n × 30° = 360°
n = 12
Solution 183: 19
Let the numbers (in ascending order) be: 15, x, y, z, 30:
15 < x < y < z < 30
Their sum is 100. As a result
x + y + z = 100 – 15 – 30 = 55
The number representing the 3rd largest share is y given by
y = 55 – (x + z)
To maximize the value of y, one has to minimize the value of (x + z). The minimum value for x is 16. The minimum value for z is y + 1. We can now rewrite the equation above as
y = 55 – (16 + y + 1) = 38 – y
2y = 38
y = 19
Solution 184: 85
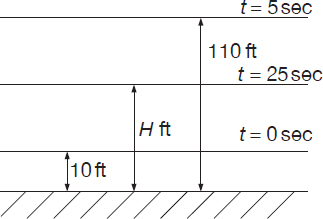
Let the value of the function at t = 2.5 sec be H:
h(2.5) = H
If we consider the motion equation (described above) at times 0, 2.5, and 5 seconds, respectively, we can write the following equations (with all heights being expressed in ft):
h(0) = 10 = a – b2 (Equation 1)
h(2.5) = H = a – (b – 5)2 = a – b2 + 10b – 25 (Equation 2)
h(5) = 110 = a – (b–10)2 = a – b2 + 20b – 100 (Equation 3)
From equation 1, we substitute 10 for a – b2 in equation 3:
110 = 10 + 20b – 100 or b = 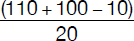 = 10
= 10
Substituting the values for a – b2 and b obtained above in equation 2, one obtains:
H = 10 + 10 × 10 – 25 = 10 + 100 – 25 = 85 [ft]
Solution 185: D
By definition (see Section 3.28 on absolute value),
|h – a| = h – a; if h > a
|h – a| = 0; if h = a
|h – a| = -h + a; if h < a
As a result, the general inequality |h – a| < b can be written
h – a < b for h > a or a < h < a + b
–h + a < b for h < a or a – b < h < a
Combining the two inequalities above results in:
a – b < h < a + b
Because the problem states the condition 30 < h < 50, it follows that
a – b = 30
a + b = 50
or
a = 40
b = 10
and therefore the solution is D.
Solution 186: 18
The key word in the question above is the word “certain.” In the context of this problem, it means that the result has to be 100% accurate under any circumstances and thus it implies that one has to assume the worst-case scenario. That leads us to an outcome where the first 15 marbles are not of the color of the marbles of which we have the least: red. Consequently, the first marbles removed are green (8) and blue (7). In addition and to satisfy the condition that the outcome contains at least 3 marbles of each color, we need to remove 3 red marbles for a total of 18 marbles.
Solution 187: 0
Let’s first write in ascending order the 13 (0 × 3 + 1 × 6 + 2 × 2 + 3 × 1) numbers of victories for each one of the 12 (3 + 6 + 2 + 1) players:
0 0 0 1 1 1 1 1 1 2 2 3
It is easy to notice/calculate the median number of victories per player as being 1. Let’s assume the number of victories of the new player is x. The average number of victories per player taking into account the new addition to the team is
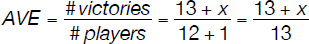
and this is equal to the median number of victories per player. It is now easy to assess that whether
x = 0
x = 1
x = 2
x = 3
x = > 3
and we place anyone of these values in its corresponding position in the sequence of numbers (victories) in ascending order shown above, the median value of the sequence will not change, therefore it is still 1. As a result,
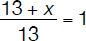
and therefore the total number of matches won by the new player (x) must be 0.
Solution 188: 5
Translating English to algebra, we write the equations that capture the information given in the text of the problem as follows:
N + 2 = 7 × A or N = 7 × A – 2
and
N = 7 × B + R
where A and B are integers, and R is the remainder of dividing N by 7 (R < 7).
Combining the two underlined equations above leads to
7 × A – 2 = 7 × B + R
or
R = 7 × (A – B) – 2
If we interpret the equation above as “R is a multiple of 7 minus 2” and take into account that R < 7, the only acceptable value for R is
7 – 2 = 5
Solution 189: 8N/5
Let the numbers of subs, bottles of soda, and (ice cream) cakes be S, B, and C, respectively. According to the problem statement,
S + B + C = N (Equation 1)
At the same time, with the notation introduced above and translating the information/data to algebra, one can write
3S = 4B = 24C = number of people attending the party (Equation 2)
One has to assume that everybody was treated equally, in other words, each person
1. ate a sub, drank soda, and had a slice of cake, and
2. at the end of the party there were no leftovers.
From the second equation, we have that
S = 8C and B = 6C
We now substitute 8C and 6C for S and B in the first equation to obtain
8C + 6C + C = N
or
C = N/15
For the formula that gives us total number of guests attending the party, we’ll use “24C” and as a result,
Total Number of People Attending the Party = 
Solution 190: 7
To capture information relevant to solving this problem (i.e., all categories of subscribers), let’s use the following notations:
X = number of people who subscribed to newspaper X and only X
Y = number of people who subscribed to newspaper Y and only Y
Z = number of people who subscribed to newspaper Z and only Z
XY = number of people who subscribed to newspapers X and Y
YZ = number of people who subscribed to newspapers Y and Z
ZX = number of people who subscribed to newspapers Z and X
XYZ = number of people who subscribed to all three newspapers
Note that in the above notations XY ≠ X × Y,XYZ ≠ X × Y × Z, etc.
Solution #1 (using algebra only)
With the notations introduced above, using the translation of English to algebra technique, we obtain the following equations:
25 = X + XY + ZX + XYZ (Equation 1)
35 = Y + XY + YZ + XYZ (Equation 2)
20 = Z + ZX + YZ + XYZ (Equation 3)
(for the number of people who subscribed to newspapers X, Y, and Z, respectively)
50 = X + Y + Z + XY + YZ +ZX + XYZ + 2 (Equation 4)
(for the total number of people who participated in the survey)
Observation will play an important role in determining the next steps to work with the above equations. Inspecting the four equations above, for example, may suggest as a way to simplify the equations to simply add the Equations 1, 2, and 3 thus obtaining Equation 5:
80 = X + Y + Z + 2(XY + YZ + ZX) + 3XYZ (Equation 5)
Now if you subtract Equation 4 from 5, you obtain Equation 6.
30 = XY + YZ + ZX + 2XYZ – 2 (Equation 6)
The fact that “for any two of the newspapers, 6 people subscribed to both newspapers but not the third one” translates into Equation 7:
XY = YZ = ZX = 6 (Equation 7)
Substituting Equation 7 in 6 gives us
30 = 6 + 6 + 6 + 2XYZ – 2
or
2XYZ = 14
or
XYZ = 7
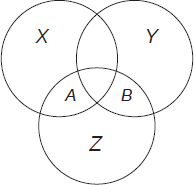
Solution #2 (using Venn diagrams and algebra)
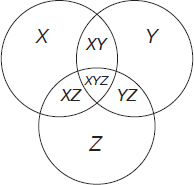
From the above Venn diagram—in which each oval represents the number of people who subscribed to newspapers X, Y, and Z, respectively—one can write the following equations:
25 = X + XY + ZX + XYZ
35 = Y + XY + YZ + XYZ
20 = Z + ZX + YZ + XYZ
(for the number of people who subscribed to magazines X, Y, and Z, respectively) and
50 = X + Y + Z + XY + YZ +ZX + XYZ + 2
(for the total number of people who participated in the survey)
For the rest, we’ll follow the same steps used in the first solution (add the first three equations to obtain):
80 = X + Y + Z + 2(XY + YZ + ZX) + 3XYZ
and subtracting the fourth equation from the result leading to
30 = XY + YZ + ZX + 2XYZ – 2
Substituting 6 for XY, YZ, and ZX in the above equation gives us the total number of subscribers to all three newspapers (X, Y, and Z) as being
XYZ = 7
Solution 191: 3
We should recall from algebra that to solve for three unknowns (i.e., x, y, and z), we need three (independent) equations. The fact that we only have two should discourage us from using a standard way of working with sets of equations (i.e., the substitution technique/approach) because we won’t be able to solve for x, y, and z.
Based on this observation and given that we are asked to calculate the sum of the three unknowns, we conclude that it has to be done through a combination of the two given equations (multiplying each side by -1):
2x – 3y = 6
3x – 2y + z = 9
After taking note of the coefficients used in each equation, it’s easy to observe that if we change signs in the first equation:
-2x + 3y = -6
and add it to the second equation, the latter becomes
3x – 2y + z – 2x + 3y = 9 – 6
or
x + y + z = 3
Solution 192: I, II, and III
Let the three consecutive integers be
X, X + 1, X + 2
The average of the three numbers is
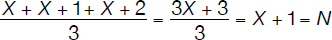
X + 1 is an integer and so is N. Consequently statement/condition I is true.
N = X + 1, which is one of the consecutive integers (the middle one) and as such, statement II is also true.
The average of the first and the third integers (X and X + 2) is the middle integer (X + 1). As a result, statement III is true too.
In conclusion, statements I, II, and III are all true.
Solution 193: 80
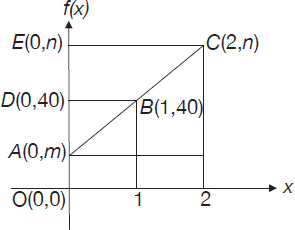
The table in Problem 193 is illustrated in the figure above where f(x) is represented in the x-y coordinate system.
This representation shows the symmetry of the problem and allows us to observe a simple way to convert the information given to us into equations. Triangles ΔABD and ΔACE are similar.
As a result, the following relationship between their sides can be written:
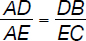
or

80 – 2m = n – m
and the result is:
n + m = 80
Solution 194: 75
Let the population of students who passed and failed the test be P and F, respectively. The percentages of students who passed and failed were
A + B + C + D = 15% + 25% + 15% + 5% = 60%
100% – P = 40%
thus
P = 60% of 1000 = 0.6 × 1000 = 600
F = 40% of 1000 = 0.4 × 1000 = 400
Because the objective is to increase the percentage of passing students from 60% to 90% (i.e., the number of passing students would increase from 600 to 900), it follows that 300 students out of the 400 students who initially failed the test would have to pass. We can set this up as follows:
400…………………100%
300…………………x%
Cross multiplication leads to x = 30,000/400% = 75%, therefore 75% of the students who initially failed would have to subsequently pass in order for the passing student population to increase from 60% to 90%.
Solution 195: 5 and 4
Based on the definitions given in the text of the problem, the sets of numbers in question are:
X: 1, 2, 3, 4, …, 16, 17
Y: 3, 13, 23, 30, 31, 32, 33, …, 39, 43, 53, …
Z: 2, 3, 5, 7, 11, 13, 17, 19, …
Note that the numbers of region A are numbers that belong to the intersection of regions X and Z from which we need to subtract what regions X, Y, and Z have in common—the intersection of X, Y, and Z. Consequently, the numbers that belong to region A are:
{2, 3, 5, 7, 11, 13, 17} – {3, 13} = {2, 5, 7, 11, 17}
to find that region A has 5 numbers.
Moving now to region B, its content is made up of numbers less than 45 that represent the intersection of sets Y and Z from which we need to subtract the intersection of all sets—X, Y, and Z. As a result, region B includes the following set of numbers:
{3, 13, 23, 31, 37, 43}–{3, 13} = {23, 31, 37, 43}
Therefore, region B has four numbers.
Solution 196: E
Note the key word “exactly” — meaning that when we look at the options A through E, no number should satisfy more than one of the three conditions.
With this in mind,
We eliminate “A” because two numbers are multiple of 6 (24 and 36).
We eliminate “B” because none of the three numbers is a multiple of 6.
We eliminate “C” because none of the three numbers is odd.
We eliminate “D” because two numbers in the sequence are odd.
We choose “E” because only one number is a multiple of 6 (18) and one is odd (21), with the third one (20) being neither and therefore could be assumed to be Jason’s day of birth
The result is therefore E.
Solution 197: E
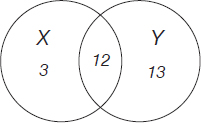
The above Venn diagram captures the information given in the text of the problem.
As exemplified in Problems 190 and 195, one way to approach this problem is by identifying all categories of players:
• council members who voted for X and against Y (15 –12 = 3),
• council members who voted for Y and against X (25 – 12 = 13), and
• council members who voted for both X and Y (12).
The remaining number,
33 – 3 – 13 – 12 = 5
represents a final category of council members, the one identified in the problem as “members who voted against both propositions.”
As a result, we already validated that condition II is true.
Condition I is false as, according to the Venn diagram, 13 (not 10) council members voted for Y and against X.
Condition III is true as the number of council members who voted for one proposition and against the other is equal to the members who voted for X and against Y (3) plus the members who voted for Y and against X (13): 16.
The correct answer is E.
Solution 198: 4
Note that X is a “digit” (i.e., an integer equal to 0, 1, 2,…, or 9) and consequently
5X ≠ 5 × X
The correct representation of unknown digits is done via representation of base 10 numbers (numbers in the base 10 numeral system). For example, when using base 10, you would write
1952 as 1 × 103 + 9 x 102 + 5 x 101 + 2
and
8A5B3 as 8 x 104 + A x 103 + 5 x 102 + B x 101 + 3
By the same token,
2X = 20 + X and 3X = 30 + X
and, as a result, the initial equation can be rewritten as
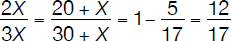
340 + 17 × X = 360 + 12 × X
5 × X = 20
X = 4
Solution 199: 1211
One way to solve this problem is by combining trial-and-error and observation. Let’s just start by noticing that each digit (a, b, c, or d) can take on only one of the following values: 0, 1, 2. In addition, it will help if we rewrite the equation as:
27 × a + 9 × b + 3 × c + d = 49
Observation #1: a cannot be 2 (27 × 2 = 54 > 49) or 0 (even if we used maximum values for b, c, and d, the sum of the remaining terms will still be less than 49). As a result, a = 1, and the equation gets simplified to
9 × b + 3 × c + d = 49 – 27 = 22
Observation #2: b cannot be 1 as assigning maximum values to the remaining digits will still not add up to 22. Consequently b = 2 and the equation gets further simplified to
3 × c + d = 22 – 9 × 2 = 4
Observation #3: c cannot be 0 or 2 as this would result in d = 4 (whereas d can only be 0, 1, or 2) or d < 0. Thus, c = 1 and therefore d = 4 – 3 = 1.
The four digit number (abcd) that satisfied the given equation is therefore
1211
Solution 200: 34
Let’s consider the number of baskets made by the worst and the best performers on the team as being L and H, respectively, and the total number of baskets made by each player on the team except the worst and the best performers as being X. With this notation and translating the text of the problems to algebra, we obtain the following equations:
L + X + H = 15 × 80 = 1200
X = 13 × 82 = 1066
Substituting 1066 for X in the first equation gives us
L + H = 1200 – 1066 = 134
To minimize L—as to obtain the “smallest number of baskets anyone could have made”—we have to maximize H, and given that the maximum value for H is 100, it follows that
L = 134 – H = 134 – 100 = 34
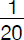 [fraction of job completed]
[fraction of job completed]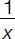 [fraction of job completed]
[fraction of job completed]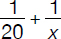 [fraction of job completed]
[fraction of job completed]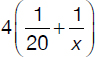 [fraction of job completed]
[fraction of job completed]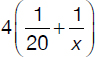
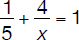
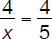


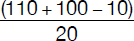 = 10
= 10