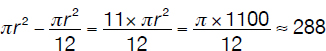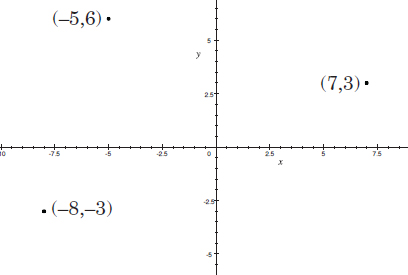
It’s not that I’m so smart, it’s just that I stay with problems longer.
—Albert Einstein
Definition: The Cartesian coordinate system, or rectangular coordinate system, is used to determine each point uniquely in a plane through two numbers, usually called the x-coordinate and the y-coordinate of the point. To define the coordinates, two perpendicular directed lines (the x-axis or abscissa, and the y-axis or ordinate), are specified, as well as the unit length, which is marked off on the two axes.
Example:
See Problems 44, 45, 55, 66, 67, 74, and 193 for sample problems using this system.
Definition: Lines in a Cartesian plane can be described algebraically by linear equations and linear functions. In two dimensions, the characteristic equation is often given in the slope-intercept form:
y = mx + b
where:
m is the slope of the line (see below)
b is the y-intercept of the line
x is the independent variable of the function y.
Example:
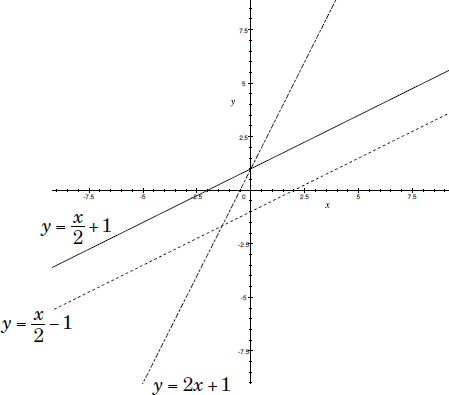
See Problems 44, 45, 74, and 175 for sample problems.
Definition: One of the most important properties of straight lines is their angle from the horizontal plane. This concept is called “slope.”
Examples: Consider points A and B of coordinates (x1, y1) and (x2, y2), respectively. By definition, the slope of the line passing though A and B is
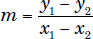
If two lines of slopes m1 and m2, respectively, are perpendicular to each other,
m1 × m2 = –1
If the two lines are parallel to each other,
m1 = m2
See Problems 44, 45, 74, and 136 for sample problems.
Definition: Let d be the distance from point A (x1, y1) to point B (x2, y2). (AB is a line segment.)
Example:
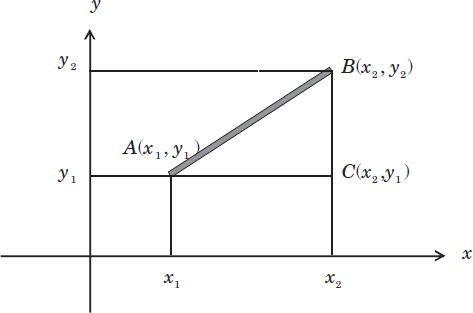
In the figure above, the Pythagorean Theorem gives us a relationship among the hypotenuse and the other two sides of the triangle ΔABC, so that
AB 2 = d 2 = AC 2 + BC 2 = (x2 – x1)2 + (y2 – y1)2
The formula for the distance is therefore:
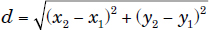
See Problem 55 for a sample problem.
Definition: The midpoint is the point that divides a line segment into two segments of equal length.
Example: If AM = BM then M = midpoint. In general, if the coordinates of A and B are (x1, y1) and (x2, y2), respectively, the coordinates of M are
Rectangle ABCD lies in the xy-coordinate plane so that its sides are not parallel to the axes. What is the product of the slopes of all four sides of rectangle ABCD?
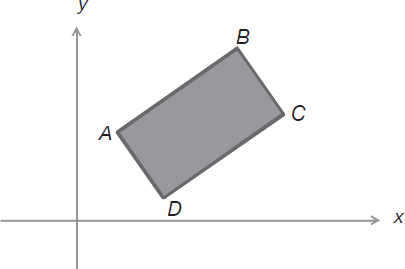
Let the slopes of the four sides of the rectangle ABCD be
m1, m2, m3, m4
Using the property of slopes of perpendicular lines, it follows that
m1 × m2 = –1
m3 × m4 = –1
Consequently,
m1 × m2 × m3 × m4 = 1
In the xy-coordinate plane, the graph
x = y2 – 9
intersects line l at (0, a) and (7, b). What is the greatest slope of l?
First, we calculate a and b taking into account the fact that the two points, (0, a) and (7, b), satisfy the equation of the graph, or
0 = a2 – 9
7 = b2 – 9
Solving for a and b results in
a = ± 3
b = ± 4
The slope of l is given by
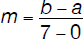
To obtain the greatest value of the slope one needs to maximize the above expression,
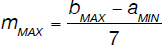
or, from the values of a and b calculated above,
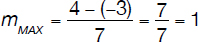
Find the value of p so that (–2, 2.5) is the midpoint between (p, 2) and (–1, 3).
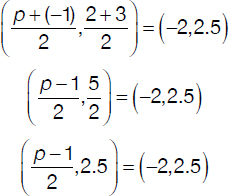
This reduces to needing to figure out what p is, in order to make the x-values work:
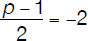
p –1 = –4
p = –3
So the answer is
p = –3
Definition: An angle is a shape formed by two lines/rays (“the legs”) diverging from a common point (“the vertex”).
Example: The intersection of two line segments, AB and BC:
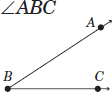
See Problems 48, 49, 51, 61, 63, 65, 67, and 182 for sample problems.
Definition: The point of intersection or the common point at which two lines/rays are joined.
Example:
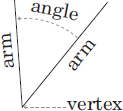
See Problems 48, 49, 51, 61, 63, 65, 67, and 182 for sample problems.
Definition: An angle that measures < 90°.
Example:
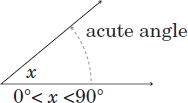
See Problems 48, 49, 67, and 182 for sample problems.
Definition: An angle that measures > 90° but < 180°.
Example:
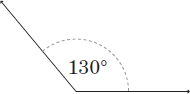
See problems 47, 61, and 182 for sample problems.
For any pair of parallel lines 1 and 2, that are both intersected by a third line, such as line 3 in the diagram below, angle A and angle D are called alternate interior angles. Alternate interior angles have the same degree measurement. Angle B and angle C are also alternate interior angles.
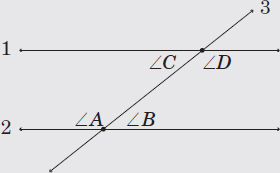
For any pair of parallel lines 1 and 2, that are both intersected by a third line, such as line 3 in the diagram below, angle A and angle D are called alternate exterior angles. Alternate exterior angles have the same degree measurement. Angle B and angle C are also alternate exterior angles.
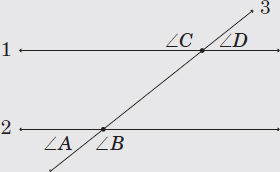
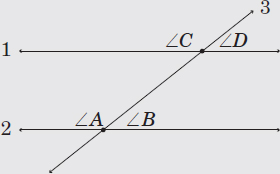
For any pair of parallel lines 1 and 2, that are both intersected by a third line, such as line 3 in the diagram below, angle A and angle C are called corresponding angles. Corresponding angles have the same degree of measurement. Angle B and angle D are also corresponding angles.
An angle bisector is a ray that divides an angle into two equal angles. The gray ray on the right is the angle bisector of the angle on the left.
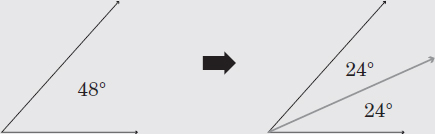
The gray ray on the right is the angle bisector of the angle on the left.
Definition: Two opposite angles formed by two intersecting lines; they are congruent (i.e., their measures are equal).
Example:
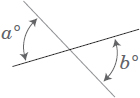
See Problems 47, 63, 65, and 84 for sample problems.
Definition: Angles whose measures have a sum of 180°
Examples:
Example #1:
Example #2:
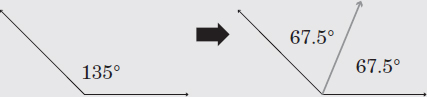
The measure of one of the angles in the figure below is 135°. Calculate the measures of the remaining angles.
If the measure of one angle is 135°, the opposite one will have the same measure by virtue of being vertical angles. The measure of the adjacent angle will be 180° – 135° = 45° as they are supplementary angles. As a result, the measures of the four angles will be
45°, 135°, 45°, 135°
Calculate the measures of the angles a and b in the figure below:
Given that x and y are complementary and x and 140° are supplementary,
x + 140° = 180° → x = 40°
x + y = 90° → y = 90° – x = 50°
140° = exterior angle = 90° + a → a = 50°
b + x + a = 180° → b = 180° – 40° – 50° = 90°
Note: b doesn’t appear to be a right angle but it turns out it is. This is an example reinforcing the rule that in geometry, unless specified in the problem or clearly indicated in the figure, you should treat every diagram as not drawn to scale.
Definition: Two angles whose measures add up to 90°.
Examples:
See Problem 48 for a sample problem.
Definition: A straight angle is the angle formed by a straight line; its measure is 180°.
Example:
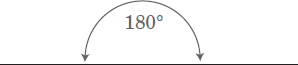
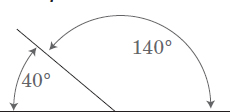
Calculate angle b:
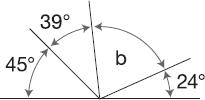
In this diagram angle b is simply 180°. Then, take away the sum of the other angles.
Sum of known angles = 45° + 39° + 24° = 108°
The measure of Angle b = 180° – 108° = 72°
Definition: A right angle is an angle with a measure of 90°.
Example:
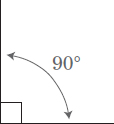
Given a right angle, what is the measure of its supplementary angle?
180° –90° = 90°
The supplementary of a right angle is also a right angle.
Definition: An exterior angle is an angle formed by one side of a triangle and the extension of another side; its measure is equal to the sum of the measures of the two opposite interior angles (because they have the same supplementary angle; in the example below, 30°).
Example:
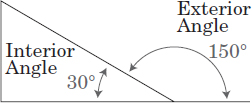
In ΔDEF, an exterior angle at F is represented by 8x + 15. If the two non-adjacent interior angles are represented by 4x + 5 and 3x + 20, find the value of x.
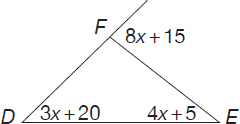
8x + 15 = (4x + 5) + (3x + 20)
8x + 15 = 7x + 25
8x = 7x + 10
x = 10
Definition: A closed geometric figure made up of line segments.
Examples:
Convex:
Concave:
Calculate the sum of the interior angle measures of the polygon shown below.
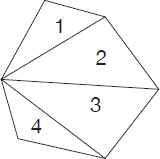
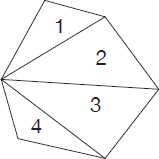
Subdivide the polygon into triangles. The number of triangles obtained is 4. The required measure is
4 × 180° = 720°
Note: A formula can be easily derived based on the observation that there is only one parameter that describes the above figure (i.e., n = number of sides/internal angles/vertices). Based on the solution obtained above (n = 6), by extrapolation, the formula that gives the measure of the sum of interior angles in a polygon of n sides is:
(n–2) × 180°
Definition: Line segment inside a polygon drawn from one vertex to another.
Example: A diagonal is a line segment connecting nonadjacent vertices of a polygon.
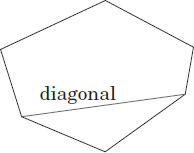
Calculate the number of diagonals in an n-gon (a polygon with n sides).
Let us begin by drawing all diagonals from one vertex of the polygon. In the example above and in Problem 52, the number of diagonals is 3. If we consider a quadrilateral (a polygon with 4 sides), from one vertex we can draw only one diagonal. In a pentagon, we would be able to draw two diagonals. Analyzing these examples and extrapolating to polygons with “n” sides leads us to the conclusion that the number of diagonals that can be drawn from one vertex in an n-gon is equal to the number of sides (n) minus 3.
To calculate the total number of diagonals in an n-gon we now need to multiply the number of diagonals drawn from a vertex with the total number of vertices and divide by 2 to avoid counting diagonals connecting two vertices twice.
As a result, the formula for the total (maximum) number of diagonals in an n-gon is
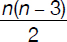
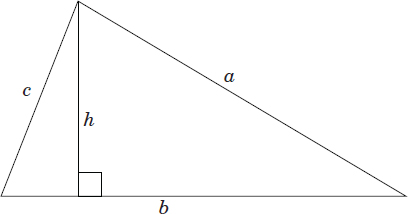
Definition: A triangle is a polygon with three sides.
Example:
Perimeter: p = a + b + c
Area: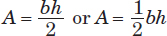 
Two sides of a triangle are 4 and 13. If the third side is an integer, find the largest possible value for the perimeter of this triangle.
Let the third side be x. It follows (see Problem 18) that
13 – 4 < x < 13 + 4
9 < x < 17
The largest possible value of the perimeter of this triangle is obtained by considering the largest (integer) value for x, or 16. As a result, the answer is:
4 + 13 + 16 = 33
Definition: A triangle in which angles are all acute.
Example:
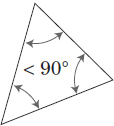
See Problem 56 for a sample problem.
Definition: A triangle with one obtuse and two acute angles.
Example:
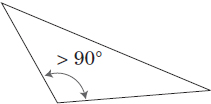
See Problem 61 for a sample problem.
Definition: A triangle with a right angle and two obtuse (and complementary) ones.
Example:
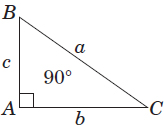
Pythagorean Theorem: a2 = b2 + c2
The 30/60/90 triangle rule: Measure of Angle C = 30°, then a = 2c
See Problems 55 and 59 for sample problems.
Definition: Triangle characterized by having three equal sides and angles (each therefore measuring 60°).
Example:
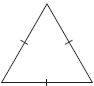
See Problem 57 for a sample problem.
Definition: Triangles having two sides of equal length; the angles opposite the equal sides are also equal.
Example:
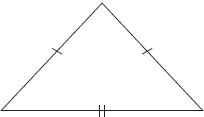
See Problems 58 and 59 for sample problems.
The right triangle shown below has an area of 25. Find its hypotenuse.
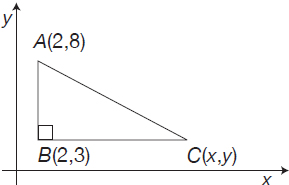
Because the x coordinates of points A and B are equal, segment AB is parallel to the y axis. Because BC is perpendicular to AB, then BC is parallel to the x axis and therefore the y coordinate of point C is equal to 3. We now need to find the x coordinate of point C using the area as follows (d = distance):
area = 25 = (½) d(A, B) × d(B, C)
d(A, B) = 8 – 3 = 5
d(B, C) = |x – 2|
We now substitute d(A, B) and d(B, C) in the area formula above to obtain
25 = (½) (5) |x – 2|
We solve the above as follows
|x – 2| = 10
x = 12 and x = –8
We select x = 12 because point C is to the right of point B and therefore its x coordinate is greater than 2.
We now have the coordinates of points A and C and we can next find the hypotenuse using the distance formula.
Hypotenuse = d(A, C) =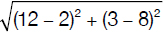 
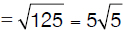
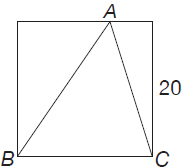
Triangle ABC shown below is inscribed inside a square of side 20 cm. Find the area of the triangle
By definition, the area of the triangle =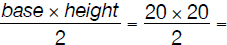 
200 cm2
Find the area of an equilateral triangle that has sides equal to 10 cm.
Let A, B, and C be the vertices of the equilateral triangle and M the midpoint of segment BC. Because the triangle is equilateral, ΔAMC is a right triangle. Let us find h, the height of ΔABC using the Pythagorean theorem.
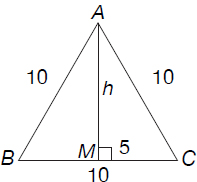
h2 + 52 = 102
Solving the above equation for h leads to:
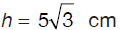
We now find the area using the formula:
area = 
× base × height = × 10 ×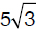 
=
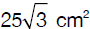
In an isosceles triangle, the measure of angle A is 30 degrees greater than that of angle B. Calculate the largest value of the measure of angle C.
An isosceles triangle has two angles equal in size. The relationship between the measures of the angles A and B is summarized as follows:
A = B + 30°
Option #1: C = A > B
Let’s now calculate the measures of all angles.
C = A = B + 30°
A + B + C = B + 30° + B + B + 30° = 180°
3 x B = 120° or B = 40°
Thus
A = 70° ; B = 40°; C = 70°
Option #2: A > B = C
A = B + 30°
B = C
A + B + C = B + 30° + B + B = 180°
3 x B = 150° or B = 50°
Thus
A = 80° ; B = 50°; C = 50°
What kind of triangles are obtained by dividing the area of a square with a diagonal? What are the measures of their angles?
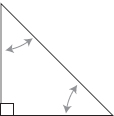
The two triangles obtained are “right isosceles.” The measure of the two equal angles is:
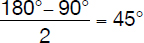
Definition: The longest side of a right triangle (opposite to the right angle); the other sides are called “legs.”
Example:
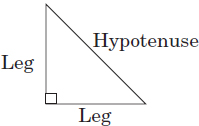
Compare the areas of the triangle (A1) and rectangle (A2) shown below. Indicate which area is the largest.
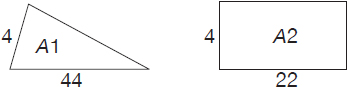
It makes sense to start with the formula that gives us the area of the triangle (A1):
Redrawing the triangle helps:
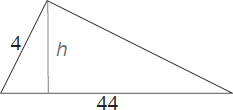
Rewriting the equation above leads to
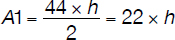
One should notice that comparing “22 x h” and “88” is equivalent to comparing “h” and “4”. As a result, it’s easy to observe that we are know comparing a side (h) and the hypotenuse (4) of the triangle on the left. Given that the hypotenuse is longer than any sides,
h < 4
one concludes that the area of the triangle is less than 88 (see also Problem 1) or
A1 < 88 = 4 x 22 = A2
And thus the answer is A2 .
Definition: Triangles that have the same size and shape.
Examples: Any one of the following four rules can be used to prove that two triangles are congruent:
• Side-Angle-Side (SAS) states that if two sides and the included angle are congruent to two sides and the included angle of a second triangle, the two triangles are congruent. An included angle is an angle created by two sides of a triangle.
• Side-Side-Side (SSS) states that if three sides of one triangle are congruent to three sides of a second triangle, the two triangles are congruent.
• Angle-Side-Angle (ASA) states that if two angles and the included side of one triangle are congruent to two angles and the included side of another triangle, the triangles are congruent. An included side is a side that is common to (between) two angles. For example, in the figure used in Problem 63, segments AP and PD are included sides between a 90° angle and angles BPA and CPD, respectively.
• Angle-Angle-Side (AAS) states that if two angles and a nonincluded side of one triangle are congruent to two angles and the corresponding nonincluded side of another triangle, the two triangles are congruent.
Note that when two triangles are congruent, all six pairs of corresponding parts (angles and sides) are congruent. This statement is referred to as the CPCTC rule (corresponding parts of congruent triangles are congruent).
Is triangle ΔPQR congruent to triangle ΔSTV by SAS? Explain.
Segment PQ is congruent to segment ST because PQ = ST = 4.
Angle Q is congruent to angle T because angle Q = angle T = 100 degrees.
Segment QR is congruent to segment TV because QR = TV = 5.
Thus, triangle ΔPQR is congruent to triangle ΔSTV by Side-Angle-Side.
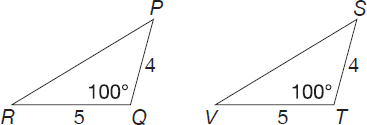
Show that triangle ΔQYN is congruent to triangle ΔQYP.
Segment QN is congruent to segment QP and segment YN is congruent to segment YP because that information is given in the figure.
Segment YQ is congruent to segment YQ by the Reflexive Property of Congruence, which says any figure is congruent to itself.
Thus, triangle ΔQYN is congruent to triangle ΔQYP by Side-Side-Side.
Show that triangle ΔBAP is congruent to triangle ΔCDP.
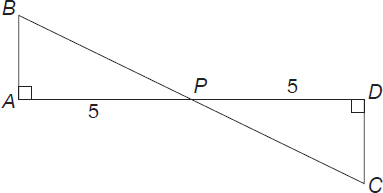
Angle A is congruent to angle D because they are both right angles.
Segment AP is congruent to segment DP because both have measures of 5.
Angle BPA and angle CPD are congruent because vertical angles are congruent.
Thus, triangle ΔBAP is congruent to triangle ΔCDP by Angle-Side-Angle.
Show that triangle ΔCAB is congruent to triangle ΔZYX. C
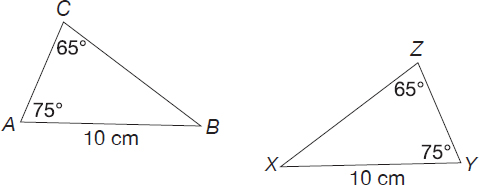
Angle A and angle Y are congruent because that information is given in the figure.
Angle C is congruent to angle Z because that information is given in the figure.
Segment AB corresponds to segment XY and they are congruent because that information is given in the figure.
Thus, triangle ΔCAB is congruent to triangle Δ ZYX by Angle-Angle-Side.
Prove that segment BC is congruent to segment CE.
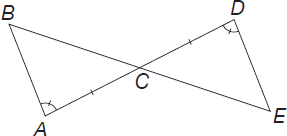
First, you have to prove that triangle ΔCAB is congruent to triangle ΔCDE.
Angle A is congruent to angle D because that information is given in the figure.
Segment AC is congruent to segment CD because that information is given in the figure.
Angle BCA is congruent to angle DCE because vertical angles are congruent.
Triangle ΔCAB is congruent to triangle ΔCDE by Angle-Side-Angle.
Now that we know the triangles are congruent, we also know that all corresponding parts must be congruent. Therefore, segment BC is congruent to segment CE by CPCTC.
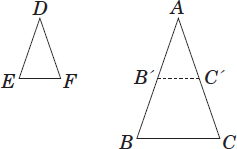
Definition: Triangles that have the same shape, with each corresponding pair of angles having the same measure.
Example:
Which of the following sets of numbers could represent the sides of the triangle ΔABC shown below?
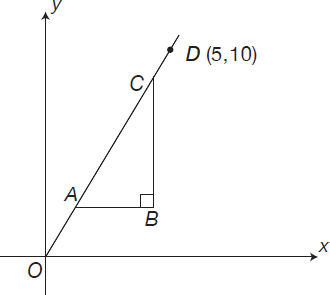
(A) 2,6,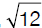 
(B) 2,5,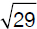 
(C) 3,6,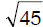 
(D) 3, 5, 6
(E) 5,10,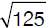 
The triangle ΔABC is a right triangle, so
AC2 = AB2 + BC2 (Pythagorean Theorem)
As a result, we can eliminate all answers that do not satisfy the above equation (A and D). In addition, E has to be ruled out since
AB < 5 and BC < 10
To pick the correct answer between B and C, one notices that by drawing a perpendicular from D to Ox, one obtains two similar triangles, ΔABC and ΔOED.
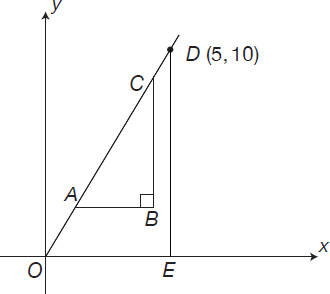
As a result,
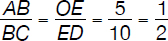
Because the ratio of the two sides of triangle ΔABC must be 1:2, the correct answer is C.
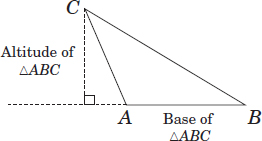
Definition: Altitude (height) is perpendicular from a vertex to the opposite side of the triangle.
Example:
In the figure below, AB is parallel with CD, BC is parallel with DA, and AB = BC. Calculate the perimeter of ABCD.
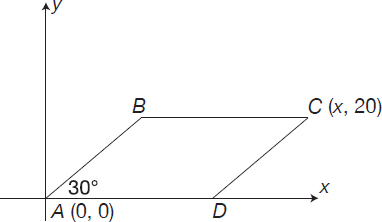
AB being parallel with CD and BC with DA results in AB = CD and BC = DA, so ABCD is a parallelogram. Given that two adjacent sides are equal (AB = BC), all sides are equal:
AB = BC = CD = DA
and thus the perimeter of ABCD = 4 x AB.
From the figure below
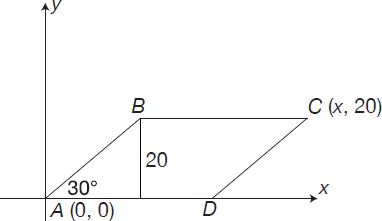
AB = 2 x 20 = 40 (the site opposing a 30° angle in a right triangle is half the hypotenuse). As a consequence, the perimeter of ABCD = 4 x 40 = 160.
Definition: Quadrilaterals are two-dimensional geometric figures (polygons) with 4 sides and 2 diagonals, with 4 interior angles with a sum equaling 360 degrees.
Examples:
Special Quadrilaterals
 |
A parallelogram has 2 parallel pairs of opposite sides. |
 |
A rectangle has 2 pairs of opposite sides parallel, and 4 right angles. It also is a parallelogram, because it has 2 pairs of parallel sides. |
 |
A square has 2 pairs of parallel sides and 4 right angles, and all 4 sides are equal. It also is a rectangle and a parallelogram. |
 |
A rhombus is defined as a parallelogram with 4 equal sides. Is a rhombus always a rectangle? No, because a rhombus does not have to have 4 right angles. |
 |
Trapezoids only have 1 pair of parallel sides. It’s a type of quadrilateral that is not a parallelogram. |
 |
Kites have 2 pairs of adjacent sides that are equal. |
We can use a Venn diagram to group the types of quadrilaterals.
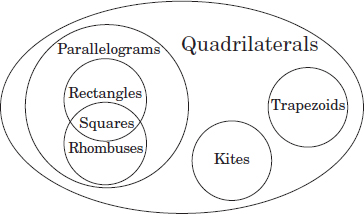
From this diagram, one can see that a square is a quadrilateral, a parallelogram, a rectangle, and a rhombus!
Is a rectangle always a rhombus? No, because all four sides of a rectangle don’t have to be equal. However, the sets of rectangles and rhombuses do intersect, and their intersection is the set of squares—all squares are both a rectangle and a rhombus.
Is a trapezoid a parallelogram? No, because a trapezoid has only one pair of parallel sides. That is why we must show the set of trapezoids in a separate circle on the Venn diagram.
What about kites? Kites are quadrilaterals that can be parallelograms. If their two pairs of sides are equal, they become a rhombus, and if their angles are equal, they become a square.
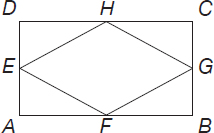
E, F, G, and H are the midpoints of the sides of rectangle ABCD. AB and BC are equal to 12 and 16, respectively. Calculate the difference between the area and the perimeter of quadrilateral EFGH.
Each side of the quadrilateral EFGH is the hypotenuse of a right triangle whose sides are equal to half the lengths of the sides of the rectangular ABCD (i.e., 6 and 8). As a result,
EF = FG = GH = HE = 62 + 82 = 36 + 64 = 10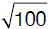0 = 
= 10
(The quadrilateral EFGH is therefore a rhombus.)
The perimeter of EFGH = 4 × 10 = 40
Note that the corner triangles are equal (using the side-angle-side rule, i.e., right triangles having equal sides) and the area of each one is:
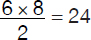
Area of EFGH = Area of ABCD –4 × Area of a corner triangle The area of EFGH = 12 × 16 – 4 × 24 = 192 – 96 = 96
The difference between the area and the perimeter of EFGH is therefore
96–40 = 56.
Definition: Quadrilateral with opposite angles of equal measure and opposite sides of equal length.
Example:
| Perimeter: p = b + b + c + c | Area: A = bh |
| or p = 2b + 2c |
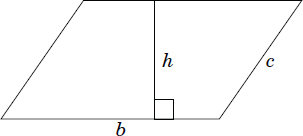
See Problem 67 for a sample problem.
Definition: Parallelogram in which all angles are right angles.
Example:
| Perimeter: p = 2(l + w) | Area: A = lw |
| or p = 2l + 2w |
See Problems 70, 132, and 150 for sample problems.
Definition: Rectangle in which the length of all sides are equal (it is sufficient to say that it is a parallelogram with equal adjacent sides).
Example:
Area = L2 where L is the side length
See Problems 70, 106, and 132 for sample problems.
The diagonals of ABCD (see below), AC = 30 and BD = 40, are perpendicular to each other and AB = 15. Calculate the area of ABCD.
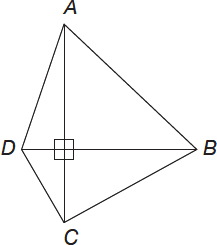
Solution #1
Observe that the area of ABCD is actually half the area of the rectangle shown below:
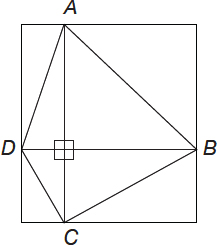
therefore the area of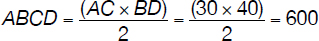 
Solution #2
Using notations shown in the figure below (see also Problem 5),
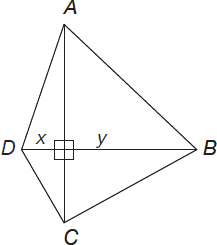
Area of ABCD = Area of ΔACD + Area of ΔABC =
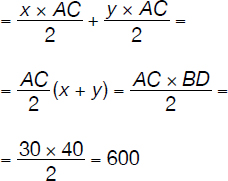
Definition: The perimeter (of a polygon) is the sum of the lengths of its sides.
Example: For a square with side length = L, the perimeter = 4L.
The areas of two squares with sides representing the length and the width of a rectangle are 100 and 64 inches, respectively. Calculate the perimeter of the rectangle.
Given a rectangle with length = L and width = W, its perimeter (P) is 2 x (L + W). With these notations, we can write the following equations:
L =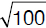 
= 10
W = 
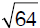= 8
P = 2 x (L + W) = 36
Definition: A regular (or equilateral) polygon is one with sides that all have the same length and angles that all have the same measure.
Example: A polygon with 5 equal sides:
Calculate the angles of a regular polygon with 8 sides.
The internal angles of a regular polygon are equal. The sum of the measures of the internal angles is
(n –2) X 180° = 6 × 180° = 1080° (see also Problem 52)
The measure of each angle is
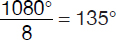
Definition: The two-dimensional geometric figure that includes all of the points that are at the same distance from one fixed point called the center.
Example:
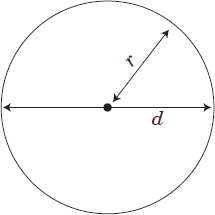
Perimeter: C = πd or C = 2πr
(Circumference)
Area: A = πr2
Note: The value of π is 3.1415926 (to 7 decimal places)
The figure above shows a circle inscribed in a square (i.e., the sides of the square are tangent to the circle).
If the radius of the circle (r) is 8 and the length of each side of the square (L) is π, calculate the ratio of
1. the circumferences of the circle and the square
2. the areas of the circle and the square
The circle:
Circumference = 2πr
Area = πr2
The square:
Circumference = 4π
Area = π2
The required ratios are:
ratio of circumferences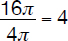 
ratio of areas =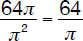 
Definition: The diameter (of a circle) is a line segment that passes through the center and has its endpoints on the circle; it’s the longest line segment that can be drawn in a circle.
Example:
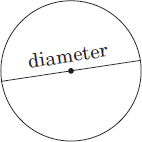
See Problem 73 for a sample problem.
Definition: The radius (of a circle) is a line segment extending from the center to a point on the circle).
Example:
The area of a circle is 314 cm2. Calculate an approximate value for its diameter.
Let the diameter of the circle be d.
A = π × r2 = 314
π = 3.141… ≃ 3.14
d = 2 × r = 2 ×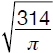 
≃
≃ 2 ×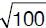 
= 20 [cm]
Definition: The arc of a circle is a part of a circle measured in degrees or units of length; it consists of two points of the circle and all of the points between them.
Example: An arc is a part of the circumference/edge of a circle.
Arc = connected section of the circumference of a circle.
Arcs are measured in two ways: as the measure of the central angle, or as the length of the arc itself.
Measurement by central angle (degrees):
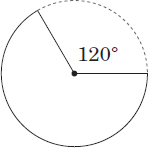
The dotted arc (minor arc) measures 120°.
The black arc (major arc) measures 240°.
Measurement by arc length (radians):
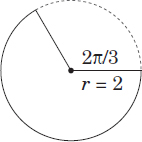
Formula: s = rθ
s = arc length
r = radius of the circle
θ = measure of the central angle in radians
Gray arc: r = 2 and θ = 2π/3, so s = 4π/3
Black arc: r = 2 and θ = 4π/3, so s = 8π/3
Definition: A tangent is a line that touches a curve at a point without crossing over. Formally, it is a line that intersects a curve at a point where the slope of the curve equals the slope of the line.
Example:
See Problem 74 for a sample problem.
Definition: A line that intersects a circle at exactly one point; it’s always perpendicular to the radius that contains the one point of the line that touches the circle (i.e., to the point of tangency).
Example:
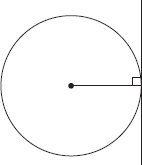
A line (n) is tangent to a circle in A(5,1). The circle’s center is ?O(4,2). Calculate the slope of line (n).
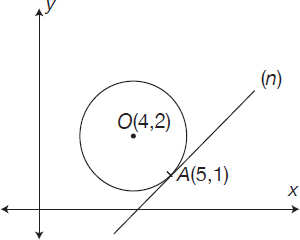
Because line (n) is tangent to the circle in A, the line passes through O (the center of the circle) and A is perpendicular to line (n). If two lines are perpendicular to each other, the product of their slopes (see Section 5.3) is equal to –1, so
Slope of (n) × slope of OA = –1
Solution #1:
Slope of OA =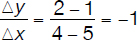 
Slope of (n) =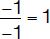 
Solution #2 (for students who tend to overanalyze but this is an overkill):
Using the general equation of a line (y = mx + b) twice for OA—as (4, 2) and (5, 1) both belong to line segment OA—leads to:
2 = 4m + b
1 = 5m + b
If one subtracts the first equation from the second, the result is
–1 = m
Thus, the slope of (n)
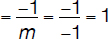
Definition: The circumference of a circle is the distance/length around the circle (perimeter).
Example: Circumference also means a complete circular arc (the distance around the outside of a circle).
Circumference: C = πd
or C = 2πr
(d = diameter)
Area: A = πr 2
See Problems 75 and 165 for sample problems.
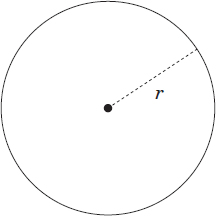
Definition: A central angle is an angle that has its vertex at the center of the circle.
Example:
See Problems 75 and 165 for sample problems.
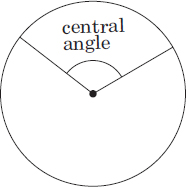
Definition: See illustration under example below.
Example:
The shaded area is called a sector. The part of the circumference of the circle that is on the edge of the sector is called an arc.
Let us denote the measure of the central angle (A), the area of the sector, and the arc length by MCA, AS, and AL, respectively.
| MCA | Sector Area | Arc Length |
| 360° | πr2 | 2πr |
| A° | AS | AL |
Given that the above quantities are directly proportional, the formulas for AS and AL corresponding to a central angle with a measure of A° is:
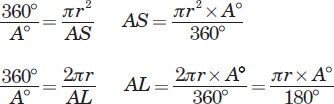
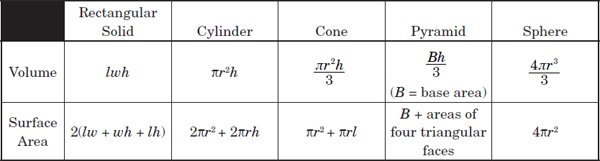
The following table summarizes useful solid geometry formulas.
One slice is cut and removed from a cake of circular shape with area equal to 100π cm2. Assuming the top view of it corresponds to the gray sector shown in the diagram on p. 119, and considering the problem as being twodimensional (i.e., the thickness of the cake is negligible compared to the radius), calculate with approximation (1) the perimeter (circumference) and (2) area of the leftover piece assuming the measure of the central angle A to be 30°.
The radius of the circle is
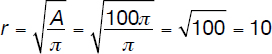
The arc length corresponding to a central angle of 30° is
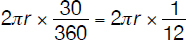
1. The perimeter/circumference of the “remaining” cake is
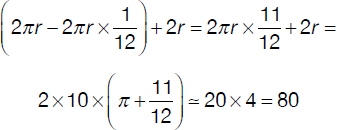
The area of the arc sector corresponding to the “slice” is
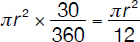
2. The area of the “remaining” cake is
