You cannot teach a man anything; you can only help him discover it in himself.
—Galileo Galilei
Definition: Integers are whole numbers, their negatives, and zero.
Example: …, -3, -2, -1, 0, 1, 2, 3, …
Integers are useful in comparing a direction associated with certain events. Suppose I take five steps forward: this could be viewed as a positive 5. If instead, I take 8 steps backward, we might consider this a -8. Temperature is another way negative numbers are used. On a cold day, the temperature might be 10 degrees Celsius below zero, or -10°C.
We can compare two different integers by looking at their positions on the number line (see p. 29). For any two different places on the number line, the integer on the right is greater than the integer on the left. Note that every positive integer is greater than any negative integer. For example:
6 > -9 -2 > -8 0 > -5 -2 < 1 8 < 11 -7 < -5 -10 < 0
Definition: An odd number is an integer that is not divisible by 2. An even number is an integer divisible by 2 (without a remainder). Note that even numbers include 0.
Examples:
Odd: …, -5, -3, -1, 1, 3, 5, …
Even: …, -4, -2, 0, 2, 4, …
Here are a few hints to remember about odd and even numbers:
• odd × odd = odd
• even × even = even
• odd × even = even × odd = even
Definition: Integers that follow in sequence, where the difference between two successive integers is 1.
Example: … -3, -2, -1, 0, 1, 2, 3, …
Representation of
consecutive integers x, x + 1, x + 2, x + 3, …
consecutive even/odd integers x, x + 2, x + 4, x + 6, …
Given three consecutive integers, if the sum of the first and third integers is increased by 8, the result is 5 less than triple the second integer. Find the three consecutive integers.
Let the three consecutive integers be x, x + 1, x + 2. Translating the first sentence to algebra leads to:
x + (x + 2) + 8 = 3(x + 1) – 5
2x + 10 = 3x – 2
or
x = 12, with the three consecutive integers being 12, 13, and 14
Definition: A line used to graphically represent the relationships between numbers: integers, fractions, or decimals. On this line, a number is placed in relation to other numbers.
Example:
Note that numbers always increase as one moves to the right.
If p + 1 is a multiple of 3, what is the greatest multiple of 3 that is less than p + 1?
This is one of those “easy” problems that good students have difficulty solving as, many times, great minds have a tendency to complicate things more than one should (i.e., to overanalyze).
The keys to solving this problem are:
• coming to grips with the fact that “p + 1” is a number and students should not try to solve for “p,” and
• understanding the importance (in the context of this problem) of the adjective “greatest.”
Placing our number (p + 1) on a number line (see diagram below) is strongly encouraged, as it will provide instant help, especially to those who have a good visual memory.
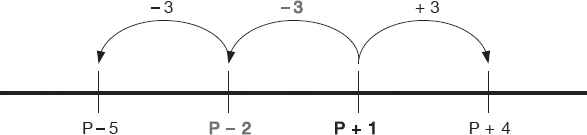
By illustrating the position of a few consecutive multiples of 3 (to include p + 1) and the mechanics of shifting from a particular one to the preceding or the next one, it is easy to pick the correct answer: The “greatest multiple of 3 that is less than p + 1” is p – 2.
If n + 1 is a multiple of 5, what is the smallest multiple of 5 that is greater than n + 1?
The previous multiple of 5 on the number line, or the “greatest multiple of 5 that is less than n + 1” is
n + 1 – 5 = n – 4
The next multiple of 5 on the number line—the “smallest multiple of 5 that is greater than n + 1” — is obtained by adding 5:
n + 1 + 5 = n + 6
Definition: One number is reciprocal of another number if their product is 1 (i.e., the reciprocal of a number = 1 divided by the number).
Example: Reciprocal of x is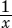 
Find the reciprocal of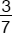 
.
Definition: Positive integers that can evenly be divided into the number (i.e., there is no remainder).
Example: The factors of 36 are: 1, 2, 3, 4, 6, 12, 18, 36 (i.e., the numbers that can be divided evenly into 36 or the numbers that 36 is divisible by).
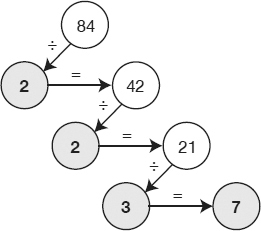
What are the factors of 84?
The factors of 84 are: 1 (a factor of everything); 2, 3, 7 (the distinct prime factors; we actually have 2 twice; see below and also the section on prime numbers); 4, 6, 14, 21 (products of two prime factors); 12, 28, 42 (products of three prime factors); and 84 (product of all the prime factors). A diagram can help to explain this, as shown below.
Definition: Factors that two (or more) numbers have in common.
Examples:
The factors of 12 are: 1, 2, 3, 4, 6, 12
The factors of 36 are: 1, 2, 3, 4, 6, 12, 18, 36
Common factors of 12 and 36 are: 1, 2, 3, 4, 6, 12
See next topic for sample problems.
Definition: The largest common factor of two (or more) numbers.
Examples: GCF of 12 and 36 is 12
Find the GCF of 36 and 54.
The factors of 36 are 1, 2, 3, 4, 6, 9, 12, 18, and 36.
The factors of 54 are 1, 2, 3, 6, 9, 18, 27, and 54.
The common factors of 36 and 54 are 1, 2, 3, 6, 9, and 18.
Among the numbers above that are common factors of both 36 and 54, 18 is the greatest common factor.
Definition: A number that is a multiple of all of the given numbers (multiples that are common to two or more numbers).
Examples:
Common multiples of 6 and 16: 48, 96, …
Common multiples of 12, 14, 15: 420, 840, …
Find the common multiples of 4 and 6.
Multiples of 4 are: 4, 8, 12, 16, 20, 24, 28, 32, 36 …
Multiples of 6 are: 6, 12, 18, 24, 30, 36, …
So, the common multiples of 4 and 6 are: 12, 24, 36, …
Definition: The smallest multiple of two (or more) numbers (the smallest number that is a multiple of both).
Examples:
LCM of 6 and 16 is 48
LCM of 12, 14, 15 is 420
Calculate the LCM of 3 and 4.
Multiples of 3: 3, 6, 9, 
15, 18, 21,
…
Multiples of 4: 4, 8, 16, 20, 28, …
The LCM of 3 and 4 is 12.
Definition: The GCD of two or more integers is the largest integer that is a factor of each of them. Note that this term is similar to GCF. In addition, the same abbreviation is used for the Greatest Common Denominator, a concept necessary to add or subtract fractions.
Examples:
GCD of 12 and 18 is 6
GCD of 12 and 36 is 12
Calculate the GCD of two positive integers a and b, a ≥ b.
Use Euclid’s division algorithm:
Compute the remainder c of dividing a by b.
If the remainder c is zero, b is the greatest common divisor. If c is not zero, replace a with b and b with the remainder c. Go back to step (1).
For example, to solve this, try plugging in numbers for a and b, such as a = 18 and b = 12. Following the two-step approach shown above then leads you to compute the remainder c by dividing a by b:
18 ÷ 12 = 1 and c = 6
c = 6, so you move to the next step and replace a with b and b with the remainder, or a = 12 and b = c = 6; a ÷ b = 12 ÷ 6 = 2 and (the new) c = 0, thus GCD = b = 6
Definition: A prime number is a positive integer greater than 1 that is only divisible by the number 1 and by itself; in other words, it has exactly two whole number factors: itself and the number 1. Note that even though it is divisible by 1 and by itself, 1 is not a prime number.
Example: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, …
Two sides of a triangle are 6 and 20. Find a prime number that could be its third side.
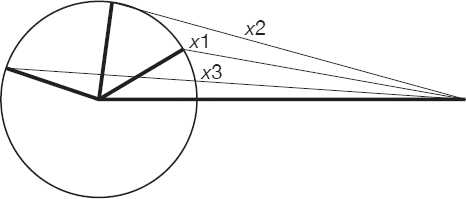
Let the third side of the triangle be x. In the figure above, three different lengths (x1, x2, x3) for x were shown to illustrate the fact that the range of its values is not only limited but also well defined.
The sum of the two sides of a triangle will always be greater than the third side (“x1, x2, x3” in the figure above). As a result, given a triangle with sides “6,” “20,” and “x,” one can write the following inequalities:
6 + 20 > x or x < 26
x + 6 > 20 or x > 14
x + 20 > 6 or x > –14
Combining the above inequalities, leads to
14 < x < 26
There are three prime numbers that satisfy the last double inequality. Any of the three is a correct answer: 17, 19, or 23
Definition: Mathematical relationship between two quantities expressed as the quotient of those quantities.
Example: The ratio of a and b is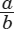 
Let a = 6 (dividend) and b = 2 (divisor) then
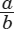= a ÷ b = 6 ÷ 2 = 3 (quotient)
The measures of the three angles in a triangle are in the ratio 1:2:6. Calculate their measures.
Let the measures of the three angles be A, B, and C, and A + B + C = 180°. Given that A:B:C is 1:2:6, it follows that A, B, C can be expressed as x:2x:6x
Consequently:
A + B + C = x + 2x + 6x = 9x = 180°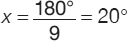
Thus:
A = x = 20°
B = 2x = 40°
C = 6x = 120°
Definition: Percent (%) is a ratio in which the second quantity is the number 100. It is the number of hundredths or parts out of 100. Percentage means parts per 100 (i.e., a way of expressing a number as a fraction of 100).
Example: Percent is a ubiquitous concept in the math sections of the SAT. Although very few advanced students will ever mention it as a difficult topic, I found it to be not as trivial as one might think—probably because its widest usage in problem solving is prone to a straightforward application of the formula used to define it or a variation of it. The results, however, are usually a mixed bag, particularly when the concept is used in problems with a level of difficulty rated as “medium” or “hard.” The following is an approach to a better understanding of this concept, emphasizing its roots and applicability.
For example, Johnny does a very good job working at McDonald’s during his summer vacation and after his first month, his boss tells him: “Congratulations, starting next month your monthly salary will increase by $150.”
Sounds a little awkward, doesn’t it? Wouldn’t it sound more realistic if his boss were to say: “Congratulations, you just got yourself a 5% raise!”
What is the moral of this story?
Two different ways of expression were used to deliver the same message. The latter sounds more realistic, maybe because it is consistent with our perpetual quest to simplify the language we used in a casual/colloquial conversation.
We can use percentages to quantify the (percent of) change when a quantity goes up or down. Comparing the amount of change to the original amount gives us a simple method to compare quantities in general.
A common approach to solving problems using this concept is based on answering two questions:
Q1: Which are the two quantities to be compared?
Q2: Which one of the two quantities represents the reference (i.e., 100%)?
The above approach will be used to solve three SAT problems rated “easy,” “medium,” and “hard,” respectively. By using the same methodology, the above qualifiers become irrelevant as the problems will seem almost identical in terms of their degree of difficulty.
What percent of 8 is 20?
The answers to the two strategic questions (Q1 and Q2) above are:
A1: 8 and 20
A2: 8
A2 tells us that our reference is 8, therefore we are asked to compare 20 against 8. As such, we say that 8 represents 100% and 20 represents x%, and all we need to do is calculate x. The problem can be now set up in a manner that applies the concept of directly proportional numbers, for example:
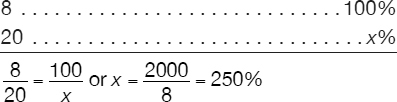
The answer is 20 is/represents 250% of 8.
If a is 25% of b, then b is greater than a by what percent?
The answers to the two strategic questions (Q1 and Q2) above are:
A1:a and b
A2: a
A2 tells us that our reference is a, therefore we are asked to compare b against a. As such, we say that a represents 100% and b represents x% and all we need to do is calculate x. The problem can be now set up in a manner that applies the concept of directly proportional numbers:
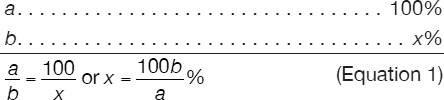
In addition, the problem states that “a is 25% of b” or “a = 25% of b” or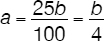 
(Equation 2)
Combining (Equation 1) and (Equation 2) by substituting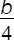 
for a in (1) leads to:
x = 100 × ¼ or x = 400%
Given that a = 100% and b = 400%, the answer is the difference, or b is greater than a by 300%
The stock price of a company fell by 20%. By how much does it have to rise to get back to the initial value?
We first need to identify the quantities to be compared using percents. Assume the initial value of the company’s stock to be S. This value we were told dropped by 20%. As a result, the new value of the company’s stock is 0.80 × S. This value will then have to go back up to the initial value: S.
The answers to the two strategic questions (Q1 and Q2) above are:
A1: (0.80 × S) and S
A2: 0.80 × S
A2 tells us that our reference is 0.80 × S, therefore we are asked to compare S against 0.80 × S. As such, we say that 0.80 × S represents 100% and S represents y% and all we need to do is calculate y. The problem can be now set up in a manner that applies the concept of directly proportional numbers:
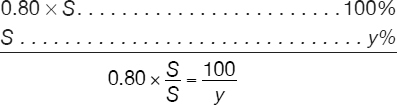
or
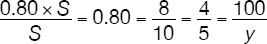
Thus:
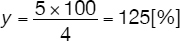
We showed that if 0.80 × S = 100% then S = 125% and thus we calculated that S is greater than 0.80 × S by the difference: 25%. Therefore, to get back to the original value, the stock will have to rise by 25%.
Definition: Proportion is an equation in which two ratios are set equal to each other.
Examples:
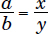
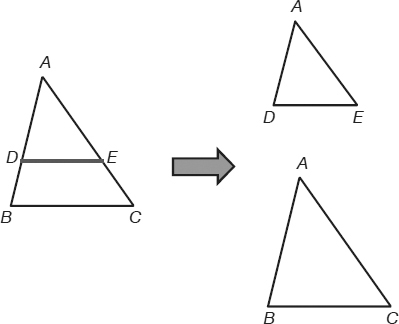
If ΔADE and ΔABC are similar, then
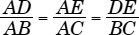
Also see Problems 66 and 93 for more on proportion.
Definition: Quantities in which ratios are constant; in other words, if one increases, the ones “directly proportional” with it also will increase. This also can be defined as quantities related such that if one increases, the other also will increase proportionally.
Example:
If quantities expressed by the values A and B are directly proportional,
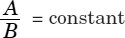
(A and B are directly proportional if B = kA where k is a constant)
See topic below for sample problems.
Definition: Quantities in which the product is constant; in other words, if one increases, the ones “inversely” proportional with it will decrease. This also can be defined as quantities related such that if one increases, the other will decrease proportionally.
Example:
If quantities expressed by the values A and B are inversely proportional,
A × B = constant
(A and B are inversely proportional if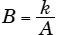 
where k is a constant)
John needs 20 days to paint a house. George works twice as fast as John. The two painters, John and George, work together for 2 days. After that, George had to work on a different project and John continued to work by himself for another 3 days after which time he was reassigned to another project while George was asked to return to this work site. How many days will George need to complete the work?
If John needs 20 days to paint the house and George works twice faster than John, then George will only need 10 days to finish the same paint job.
Given the direct proportionality between the number of days worked and the ratio of work being done vs. total work, in one day, John and George will complete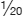 
and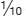 
of the work, respectively. Working together for 2 days, they will paint twice as much and this leads to:
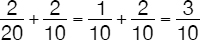
of the total work. Working alone for another 3 days, John will contribute another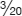 
of work for a total of
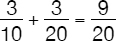
of the work needed. That means that George was left to complete the remaining
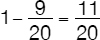
of the total work. Given that he can paint 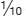of the house in one day, the number of days he will need to complete the work is
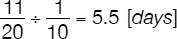
Also see Problem 7 for more on direct and inverse proportions.
Definition: Ordered, finite/infinite list of numbers/terms (usually following a specific pattern), separated by commas.
Examples:
First term = -3; every term thereafter is obtained by adding 5, or
-3, 2, 7, 12, 17, …
First term is 5; every term thereafter is obtained by multiplying the previous one by 3, or
5, 15, 45, 135, …
In general, if one has a sequence (an arithmetic sequence; see Section 3.19) of N consecutive numbers of which the first and the last ones are known, one can find their sum by using the formula: Sum = N(First Number + Last Number)/2
Note: The derivation is quite simple if you pair up the first and the last, the second and the one before last, and so forth and you notice that the sum of each pair is the same. Thus, the total sum is the sum of a pair multiplied by the number of pairs (N/2).
Calculate the sum of all integers from 1 to 100 without using a calculator.
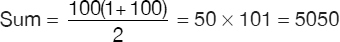
Definition: Sequence in which the difference between any two consecutive terms is the same (i.e., d in the example below).
Example: 2, 7, 12, 17, … where d = 7 – 2 = 12 – 7 = 17 – 12 =
Given an arithmetic sequence:
a1, a2, a3, ………… an
by definition, a general term k is equal to the previous term (k – 1) + d, or
ak = ak-1 + d
The relationship between term n and the first term of the sequence is:
a2 = a1 + d = a1 +1d
a3 = a2 + d = a1 + 2d
a4 = a3 + d = a1 + 3d
an = a1 + (n – 1)d
The first term of a sequence of numbers is –4. Every term thereafter is obtained by adding 5. What is the value of the 401st term of the sequence?
(A) 1995
(B) 2005
(C) 1999
(D) 2001
(E) 1996
In general, problems with sequences (arithmetic or geometric) require calculation of a higher ranked term given that the first term is known and so is the formula for subsequent terms.
Applying the formula that calculates the “next term” and working your way up to the required term, one term at a time is not recommended. (Keep in mind that this is a timed test in which you have on the average a little more than a minute to solve a problem.)
The recommended solution will have to be based on a way to identify a pattern for the calculation of a general term and extrapolate it to the rank in question.
Solution A
To solve the problem as it is presented to us (i.e., as a multiple-choice problem), writing a few terms should help us discover the pattern. The results are captured in the table below.
| Rank | Term |
| 1 | –4 |
| 2 | 1 |
| 3 | 6 |
| 4 | 11 |
| 5 | 16 |
| … | … |
| 401 | ? |
Looking at the above results should provide enough ammunition to our observational skills to notice that all odd terms end in 6 (except for the first one) and even terms in 1. Thus, given that 401 is an odd rank, the corresponding term will have to end in 6. The only answer that ends in 6 is 1996 and as a result, the correct answer is E.
Solution B
I will present next a more general method to solve this problem. Although this method will require more time than the one presented as Solution A, it has the merit of solving this and similar problems in a generic and a more general way, including instances where they are given in the open-ended format.
| Rank | Term (formula) |
| 1 | –4 |
| 2 | –4 + 5 × 1 |
| 3 | –4 + 5 × 2 |
| 4 | –4 + 5 × 3 |
| 5 | –4 + 5 × 4 |
| … | … |
| N | ? |
By observation, the formula for the nth rank is:
–4 + 5 × (n –1)
When n = 401, the above formula allows us to calculate the 401st term, or
–4 + 5 × (401 – 1) = –4 + 2000 = 1996
The correct result is E.
Definition: Sequence in which the ratio between any two consecutive terms is the same (i.e., r in the example below).
Example:
3,6,12,24,48,…
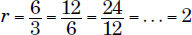
In general, given a geometric sequence
a1, a2, a3, ………… an
by definition, a general term k is equal with the previous term (k – 1) multiplied by r, or
ak = (ak-1)r
The relationship between term n and the first term of the sequence is:
an = a1 (rn-1)
The first term of a sequence is 5. Every term thereafter is obtained by multiplying the previous one by 3. What is the value of the 5th term of the sequence?
n = 5
the 5th term = 5 × 35–1 = 405
Definition: Collection of things referred to as “elements” or “members” of the set.
Examples:
set A = {1, 3, 5, 7, 9}
set B = {3, 9, 10, 11}
Write the set of numbers that do not belong to the domain (see Section 4.9) of the function.
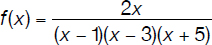
These are the values of x for which the denominator of f(x) is equal to 0, or
X ∈ {–5,1,3}
Definition: Set that includes all elements of the sets entering the union.
Examples:
The union of two sets A and B, written A ∪ B, is the set of elements that are either in set A, set B, or both. For sets A and B defined in Section 3.21, their union is therefore
A ∪ B = {1, 3, 5, 7, 9, 10, 11}
The union of A and B is represented by the shaded area in the diagram shown below.
Definition: A set that includes only the elements that the sets entering the union have in common.
Example: The intersection of two sets A and B, written A ∩ B, is the set of elements which are in both A and B.
A ∩ B = {3, 9}
The intersection of A and B is represented by the shaded area in the diagram shown below.
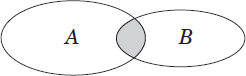
Definition: Diagrams that show all possible logical relations between a finite (in SAT problems, two, maximum three) collections of sets.
Example:
A Venn diagram uses overlapping circles/ovals to show relationships between groups of objects.
In this example, sets A, B, and C, have common elements.
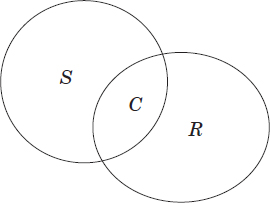
In a high school class, it is mandatory for all students to belong to a language club. The languages offered are Spanish and Russian. S students are enrolled in a Spanish club, R students in a Russian club, and C students are enrolled in both. What is the ratio between students enrolled in the Spanish club but not in the Russian club and the total student population?
The Venn diagram describing the above problem is:
The requested ratio is:
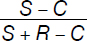
Definition: The factorial of n is the number of ways in which the n elements of a group can be ordered.
Example: The factorial of a number n represented by n! is the product of the natural numbers up to and including n: n! = 1 × 2 × … × (n – 2) × (n – 1) × n
A cafeteria has a lunch special consisting of soup or salad; a sandwich; coffee, tea, or a nonalcoholic beverage; and a dessert. If the menu lists 2 soups, 3 salads, 6 sandwiches, and 10 desserts, how many different lunches can one choose?
The group of four elements the combinations of which we need to calculate (see also Section 3.27) is:
soup/salad, sandwich, coffee/tea/beverage, dessert
The corresponding numbers involved in the combinations are:
2/3, 6, 1/1/1, 10
The number of different lunches is:
(2 + 3) × 6 × (1 + 1 + 1) × 10 = 5 × 6 × 3 × 10 = 900
Definition: A possible selection of a certain number of objects taken from a group with regard to order. (The number of ways a given set of things can be arranged, where order is considered to make a difference.)
Example: The permutation n Pr is the number of subgroups of size r that can be taken from a set with n elements. It is calculated as follows:
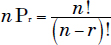
Calculate the permutations (i.e., total number of combinations) of two letters that can be formed from a group of three letters: A, B, C.
The number of permutations is:
and the groups are:
AB, AC, BC, BA, CA, CB
Definition: A possible selection of a certain number of objects taken from a group without regard to order.
Example: Combinations: nCr is the number of unordered subgroups of size r that are selected from a set of size n. It is calculated as follows:
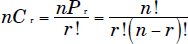
Note that the difference between permutations and combinations consists in the fact that subgroups selected from a given set are ordered and unordered, respectively.
How many combinations of two letters can be formed from a set of three letters: A, B, and C?
The number of combinations is given by:
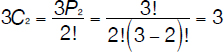
and the groups are:
AB, AC, BC
The order in which we wrote the letters is of no concern; that is, AB could be written BA, but we would still have only one combination of the letters A and B.
Definition: The absolute value of a number a, denoted as | a |, is the distance (i.e., always a positive number) between a and 0 on the number line.
Examples:
| a | = a ; if a > 0
| a | = 0 ; if a = 0
| a | = -a; if a < 0
| 8 | = 8 and | -8 | = 8
Simplify | 2 + 3(–4) |
| 2 + 3(–4) | = | 2 – 12 | = | –10 | = 10
Simplify –| –4 |
–4| = –(4) = –4
Simplify –| (–2)2 |
–| (–2)2 | = –| 4 | = –4
Simplify (–| –2 |)2
(–| –2 |)2 = (–(2))2 = (–2)2 = 4
10 This book uses a number system to delineate the various math topics we’ll be covering. When you take the practice test and create an analysis of your results, you’ll receive recommendations that will show you which numbered sections of the book you can revisit to try to improve your score.