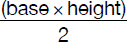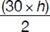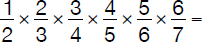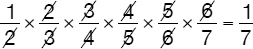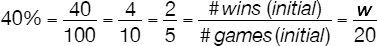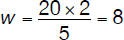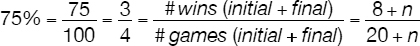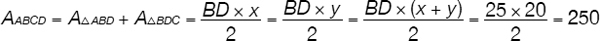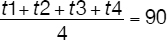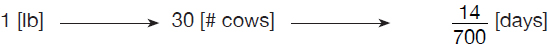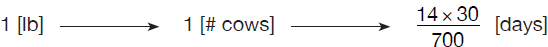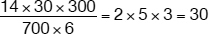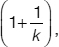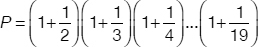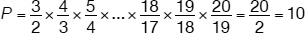Chapter 2
Test Preparation Strategies and Advice
How Too Much “Strategy” Can Be Hazardous to Your Performance
There is only one corner of the universe you can be certain of improving and that’s your own self.
—Aldous Huxley
There is far too much printed advice on “strategy” in approaching test preparation. For the SAT math section, unfortunately, a large percentage of it is based on pseudo/quasi-scientific methodologies such as “how to guess right,” “how to solve problems via trial and error,” and similar tropes. The danger of emphasizing the importance of strategy is that it shifts attention from the fundamental thing that is required in math preparation—the realization that there is no substitute for the need to acquire the knowledge and skills that are essential in problem solving.
My extensive experience in test preparation has revealed three major areas on which test scores depend: factual knowledge, analytic/critical thinking skills, and concentration skills.
Factual Knowledge
There has not been, is not, and will never be a consensus on how much memorization of factual knowledge is necessary for a well-rounded education. There certainly is a decent body of knowledge that you are expected to master in preparation for the math section of the SAT tests. That begins with “simple” concepts (e.g., arithmetic operations, definitions of two-dimensional geometric figures, etc.) and ends with more sophisticated math concepts such as compound probabilities. Average and above-average students are not expected to have significant gaps in their factual knowledge or math background.
Analytic/Critical Thinking Skills
One may refer to these as the glue that keeps together our body of knowledge and the catalyst that gives us the ability to put it to use in solving real-life problems. This is what is missing when a student cannot solve a problem and yet has the same theoretical background as someone who shows him how to solve it. “Gosh, how come I didn’t see that?” is the typical reaction, noticing that finding a solution did not require the use of a “magic” formula or, for that matter, any factual knowledge with which the student was not familiar. Possession of these skills is paramount to achieving excellence in any profession, not only in those with mathematical or scientific/engineering orientations. These skills are the main reason why nobody should ever be justified in downplaying the role of math in our general education.
The following problem outlines the importance of analytic skills in problem solving.
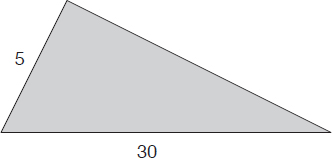
Problem 1
Given the triangle shown, select the correct answer from the following:
(A) Area of triangle is less than 75
(B) Area of triangle is equal to 75
(C) Area of triangle is greater than 75
(D) Area of triangle is either greater than or equal to 75
(E) There is not sufficient data to calculate the area of the triangle.
Solution 1
Note that this is basically a quantitative-analysis-type problem3 that requires that we compare a variable, the area of the triangle, with the number 75.
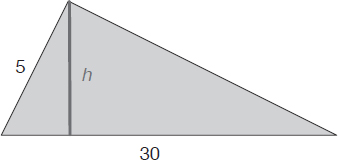
After drawing the height of the triangle (h), the formula that gives us the area of the triangle is:
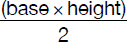
The steps described below lead us to a simplification of the problem whereby what we are left to compare is “h” and “5” (much better/simpler task than comparing “area of triangle” and “75”). The following comparisons are equivalent:
| Area of triangle |
vs. |
75 |
 |
vs. |
75 |
| 15 × h |
vs. |
75 |
| h |
vs. |
5 |
The notations we added to the figure, emphasizing the fact that “h” is perpendicular to the base of the triangle, should easily point out the fact that the two elements we need to compare are the sides of the newly created right triangle. Because “h” is a side and “5” is the hypotenuse, and because the latter is longer than any of the sides of the triangle, it follows that
h < 5
and thus the area of the triangle < 75 and the answer is A.
Note that the only factual knowledge required to solve this problem was the formula for the area of a triangle and the property of right triangles according to which, the hypotenuse is the longest of the sides.
Concentration Skills
To understand the role that concentration plays in taking the SAT test, try to answer the question: “When is the last time you sat down and worked on anything for almost 4 hours4?” Considering that for most students, a candid answer is “never,” one should wonder how come there is so little interest in or emphasis on this aspect of test preparation in most preparatory books available on the market.
In my experience, this is the primary reason for underachievement by above-average students (a category that includes the not-doing-well-on-tests type).
If someone wants to run a marathon, that person needs to prepare/practice for it! No matter how good of an athlete a student is in a different sport, running a marathon requires a unique combination of skills in the areas of endurance and effort optimization.
I suggest two ways to address this issue and improve one’s concentration skills:
• A time window equal to the duration of the test (3 hours 45 minutes) should be periodically allotted to taking a complete test (SAT Verbal and Math). That, of course, would require a distraction-free environment (e.g., no phone calls, background music, snacks, etc.).
• Students should change the approach they use in dealing with their homework. Imagine that all homework (say, preparation for a chemistry test, some reading for geography, and a couple of exercises in French) would be treated as one monolithic task. That would require the same distraction-free environment and need to work nonstop until everything that has to do with the next day’s homework is accomplished. In this way, not only the quality of homework is expected to increase (with a positive impact on grades) but also the students will be indirectly practicing for their SAT by improving their concentration skills.
A balanced combination of the strategies outlined above has proved to have a positive impact on students’ concentration skills.
An Approach to Test Preparation
Those are my principles, and if you don’t like them … well, I have others.
—Groucho Marx
The “Test-After-Test” Approach
This is the most common approach to test preparation and it involves either taking “mock” tests or solving problems from disparate sections of real tests using books such those published by the College Entrance Examination Board. The former allows the student to emulate the test experience by taking complete tests within the actual test’s time limit.
In addition to the problem-solving experience and the exposure to the wide range of math topics and degrees of difficulty, this approach also is useful for allowing you to get a glimpse into the “real thing” and experience the impact of time constraints on your performance.
The “Identification of Weaknesses/Gaps” Approach
Books like those published by Barron’s offer students a set of tools that while complementing the “test-after-test” approach also should fill in the gaps and add more efficiency to the test preparation process.
This approach uses books that take the math required for the test and group it by topics. Major topics are then divided up into subtopics, each of which is prefaced by a summary of the theoretical concepts involved. This way, you do not have to rely on different textbooks for refreshing your memory. Following that, exercises and problems dealing with that particular topic are given to complete the preparation-by-topic exercise. The proper selection of the book is paramount. The type of book mentioned above distinguishes itself by offering a good selection of real5 problems (i.e., problems given in real tests), grouped by topic and type (i.e., multiple choice and open-ended), and by—occasionally—adding a challenge component by dropping most of the problems that in a real test would be considered “easy.” This way, the average problem published in some of these books is more challenging than the average one obtained from a real test. This should be seen as good news because it gives students the opportunity to challenge themselves in the preparatory environment, making the real test an easier than expected examination experience.
This “targeted” approach should be used to identify weaknesses and gaps in theory, problem content, and problem types. It is extremely useful in adding efficiency to the process of test preparation, especially if you have already taken the test once and you’re concentrating on improving your scores. In the time spent for preparation between test dates, emphasis should be on how to maximize the efficiency of the time spent to improve performance.
The “Take-the-Challenge” Approach
You should constantly challenge yourself when preparing for the SAT. Here are some suggestions:
• Skip problems that look easy and/or revolve around topics with which you are comfortable.
• When practicing working on a section of a real test, skip the first two thirds of the test (typically, first = easy; second = medium; third = hard problems).
• Solve more word and open-ended problems (i.e., problems that traditionally fall into the hard category).
• Solve more problems on topics that are not easy; statistically, these could be topics such as probabilities, geometric and arithmetic sequences, Venn diagrams, and so forth.
I recommend all the above techniques be used alternatively. However, the time ratio spent on using them should be slightly in favor of a combination of the second and third approaches with a more accurate definition depending on your specific needs that you or your instructor/tutor have detected.
Do Calculators Really Help?
Man’s mind stretched by a new idea never goes back to its original dimensions.
—Oliver Wendell Holmes
Not necessarily! None of the math problems given on the SAT were designed to require the use of a calculator. It also is doubtful that calculators even help students solve the problems more quickly. In addition, they can be seen as a hindrance to the thinking process and a potential long-term hazard because of their “addictive” nature.
The popular belief is that calculators help us solve problems in less time than what we would need without using them. In the case of SAT problems, this is false!
A student taking the SAT test is like a marathon runner. She will be engaged in an endurance exercise and success depends very much on her ability to perform consistently well for the whole duration of the test. Setting aside the mental preparation involved, marathon runners need to warm up their muscles and bring them to a level of performance that can be sustained for the entire duration of the race. When they feel dehydrated, for example, they do not stop to take a sip of water but rather grab a cup held out to them by officials and drink it while continuing to run at the same pace. Stopping would be extremely detrimental to them as it would cool off the muscles and change the body chemistry to the one required when resting, and getting back into the race would require starting the whole cycle from the beginning, making them lose precious time and stamina.
Being engaged in a mental/intellectual exercise, such as taking an SAT test, is, in many ways, analogous to running a marathon. When it comes to “warming up” and sustaining the effort for the duration of the exercise, it is our “neurons,” our mind, that need to carry us throughout the 3-hour-plus test maintaining the same (a constant) high level of concentration and performance ability. Each time we make use of a calculator, we stop the thinking process.
As an example, consider the following problem:
Problem 2
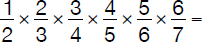
Solution 2
The students who tend to make too much use of calculators would waste no time and start calculating the above expression without paying any attention to the numerators and denominators of the above fractions. That is an example where too much reliance on calculators becomes a hindrance to the thinking process. A quick glimpse at the fractions in question should result in the observation that all but one denominator and numerator remain (i.e., “7” and “1,” respectively) after the others were cancelled off diagonally.
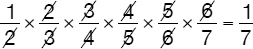
In addition, using the calculator for simple operations that we could do in our heads (a) makes us hesitant and increases our dependency on calculators and (b) gives our mind, presumably warmed up for the mental exercise of taking the test, an unnecessary and detrimental break.
Problems like Problem 8 (see p. 20) also can be used to back up the argument against exaggerated use of calculators.
Too Much Memorization?
Intelligence is not the ability to store information, but to know where to find it.
—Albert Einstein
There is a popular belief that memory is extremely important in solving math problems. Many times, this complements the idea (popular with those who do not quite see a connection between algebra and the real world) that algebra is an abstract, stand-alone science.
Both theories are false. Although some memorization is needed in order to acquire the required body of math knowledge, a thorough understanding of the fundamentals should lead to a more lasting mastery of math concepts. Understanding well the definitions, and how certain concepts, rules, and theorems were derived and the rationale behind them, should eliminate the excessive reliance on memory.
As an example, let us consider the task of calculating the sum of interior angles of any two-dimensional, geometric figure (i.e., a polygon). The only thing that we need to remember is what the answer would be should the polygon have three sides (i.e., be a triangle): 180°. Then, the area of the polygon should be divided up into triangles. It does not matter where and how we start. The sum of the interior angles of the polygon is equal to the number of triangles obtained times 180°. This shows that memorizing the formula, (n – 1) × 180°, where n = number of sides, is not necessary, as we can derive it easily using the approach described above (also see Problem 52 on p. 87).
I strongly recommend that you make an effort to apply logic in understanding various math concepts and rely less on rote memorization, which may lead to a mechanical approach to problem solving.
Ubiquitous Algebra
Q: So how do you find America? A: Turn left at Greenland.
—The Beatles
Algebra, far from being an abstract, stand-alone science, should be seen as a set of tools that mathematicians have devised to help them (and us) solve real-life problems. These are the problems (and a vast majority of problems fall into this category) that invariably require a translation of the text into a language better suited to capture and summarize all information given to us in a succinct form (i.e., allow translation of English to algebra).
This paradigm, while emphasizing the importance of algebraic skills, leads to a three-step approach to problem solving:
1. Read the problem, define the unknowns/variables, and identify them with letters (e.g., x, y, z).
2. With the notations introduced at Step #1, translate the text of the problem into algebra by writing the relationships between known and unknown data (i.e., the equations).
3. Solve the equations using techniques learned in algebra (e.g., substitution).
An example follows in Problem 3.
Problem 3
Anna has five times as many marbles as Bob. If Anna gives Bob seven marbles, Anna will be left with six more marbles than Bob. What is the total number of marbles that Anna and Bob have?
Solution 3
1. Let the number of marbles originally in Anna’s and Bob’s possession be “A” and “B,” respectively.
2. Translation of the first sentence leads to:
A = 5 × B
Translation of the second sentence leads to:
A – 7 = B + 7 + 6
3. We are now left with the easier task (after simplifying and rearranging the second equation in Step #2) of solving the following set of equations:
A = 5 × B
A = B + 20
Solving by substitution leads to 5B = B + 20, or 4B = 20, or
B = 5 and A = 25
The result (A + B) is 30.
Fast Math
Sometimes it’s a little better to travel than to arrive.
—Robert Pirsig
Many students have a “timing” problem. They can solve most of the SAT problems but tend to never be able to finish the math sections in the time allotted by the College Board. Keep in mind that, on average, a student will only have a little more than a minute per problem. Speeding up problem solving can be achieved via a two-prong strategy.
Common Approach
A common approach to problem solving saves time by minimizing the transition time intervals between problems dealing with different topics. Whether the problem is about solving a set of equations (algebra) or involves angle relationships in a geometric figure (geometry) or probabilities, if we could approach it in the same way (i.e., via a process involving the same sequence of logical steps), we will be saving time!
One way to standardize the way we solve math problems is by dividing up the work into three distinct tasks:
• read and understand well the information/data provided;
• identify variables that together with the information/data provided are relevant to and will play a role in solving the problem; and
• define a strategy/approach to problem solving based on input data and relevant variables, then implement it.
The first task is a crucial step in solving math problems and, most of the time, when one is not able to do so (i.e., one gets stuck in the middle of the problem), the reason is that some relevant information was left out or misunderstood.
Note that the ability to accomplish the third task either in its entirety or in a timely manner has a lot to do with how well the input data was understood, captured, and summarized either in memory or, preferably, on paper. An example of such a strategy is shown in the previous section, where the concept of translation of English to algebra is discussed and illustrated in Problem 3.
Here are other examples:
Problem 4
A soccer team has played 20 games and has won 40% of them. What is the minimum number of additional games the team must win to finish the season winning 75% of the games it has played?
Solution 4
Relevant Data/Information:
• number of games played = 20
• percentage of wins = 40%
• goal: percentage of wins = 75%
• need to calculate minimum number of additional games
Variables
• let w be the number of initial wins (that led to the 40% performance)
• let n be the number of additional games to be played that, consistent with the meaning given by using the adjective minimum above, also are “wins”
With this information, we can begin to solve the problem:
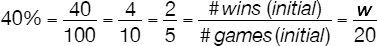
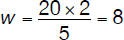
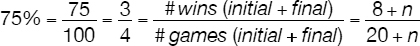
60 + 3n = 32 + 4n
60 – 32 = n
n = 28
Thus, to improve its wining performance from 40% to 75%, the team will have to play (and win) 28 additional games.
Problem 5
In the geometric figure shown below, AC is perpendicular to BD, AC = 20 and BD = 25. Calculate the area of ABCD.
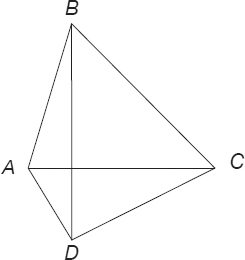
Solution 5
Relevant Data/Information
• AC is perpendicular to BD
• AC = 20
• BD = 25
Variables
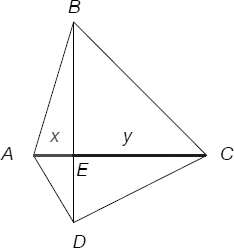
• x = AE
• y = EC
The area of ABCD can be calculated as the sum of the areas of two triangles, either (1) ΔABD and ΔDBC or (2) ΔABC and ΔACD. This is a symmetrical problem and as such, either approach will lead to the correct answer.
Assume we pursue option (1): area of ABCD = area of ΔABD + area of ΔDBC, or
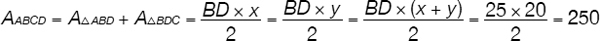
where x and y are the heights of triangles ABD and DBC respectively, and x + y = AC = 20
Problem 6
Eric’s average of four tests is 90. Which of the following cannot be the number of tests on which he earned exactly 90 points?
(A) 0
(B) 1
(C) 2
(D) 3
(E) 4
Solution 6
Relevant Data/Information
• the average of 4 tests is 90
• the answer must represent the number of tests whose score cannot be exactly 90
Variables
• let the 4 test scores be t1, t2, t3, t4
Let’s apply the definition of average:
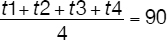
or
t1+t2+t3+t4 = 4 × 90 = 360
By elimination (starting with A), we rule out “0,” “1,” and “2” as—in each case—we can easily find 4, 3, and 2 numbers, respectively, whose sum is 360 and that are different from 90.
If “D” were the answer, then
t1 = t2 = t3 = 90
and
t1 + t2 + t3 = 3 × 90 = 270
or
t4 = 360–270 = 90
Thus, the fourth score would also be 90, validating D (3) as the unique solution.
Minimum Calculations
Most problems rated “medium” or “hard” cannot be solved in one step. In those cases, calculations, when possible, should not be done at every intermediate step but rather carried over to the very last logical step of the solution. When pursuing this strategy, the total number of calculations per problem will be dramatically reduced. As a consequence, the odds of making a mistake will diminish (fewer calculations/operations = fewer mistakes) and the overall timing will be reduced.
Problem 7
If 700 pounds of hay will feed 30 cows for 2 weeks, for how many days will 300 pounds of hay feed 6 cows?
(A) 10
(B) 20
(C) 30
(D) 40
(E) 50
Solution 7
Observation #1: For constant number of days during which food supplies are sufficient, the quantity of food and number of days are directly proportional quantities (“more food, more days”).
Observation #2: If quantity of food is constant, the number of cows and number of days are inversely proportional quantities (“more cows, fewer days”).
We’ll set up the problem in a manner that outlines the relationship (direct proportionality) among quantity of hay, number of cows, and number of days:

Because these quantities are directly/inversely proportional, one can write
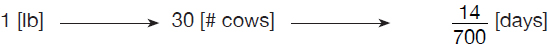
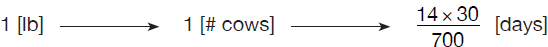

Note that all calculations have been postponed until the last step. It is now easy to see how simplifications can reduce calculations to a minimum, in this case to “no” calculations at all as simplifying the fraction should not require a calculator:
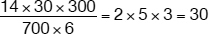
Thus, the correct answer is “C.”
Problem 8
If each factor in the product shown below has the form
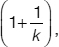
where k represents all of the consecutive integers from 2 to 19, what is the value of P?
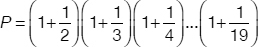
Solution 8
Rewrite a few factors at the beginning and at the end of the expression given for P:
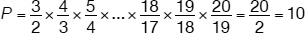
By simplifying/reducing the fractions—as shown above—with no need to use a calculator, the number of calculations is reduced to one: 20/2. The answer, therefore, is 10.
Reading Comprehension
There is a blurry line between the skills required to solve certain math problems (e.g., word problems) and the reading comprehension skills emphasized in various aspects of the verbal sections of the SAT test. As a result, a student who struggles in reading comprehension will not do well in math, in particular in those math sections with a relatively high concentration of hard problems and/or word problems.
Final Tips for Better Learning
• Use pencil and scratch paper.
• Constantly identify your weaknesses and gaps; you really want to allocate more time dealing with them.
• What you do at school (or in any afterschool test preparatory environment) should complement work done at home.
• Be candid with yourself (it is so easy to be in denial!) and, if applicable, your instructor/tutor; there is no such thing as a “stupid question”!
• Challenge yourself constantly; make it “harder” during the preparation stages so that the real test will appear “easier” than anticipated; be creative in trying to do so by spending more time solving “hard” problems (e.g., open-ended problems tend to be in that category and so are word problems).
• If you are confident in your mastery of theory, skip it! Solve Problems 9 through 79 in Part II and read the theory (and/or go over examples) only when you have second thoughts on how good your understanding of that particular topic is.
• Last but not least: Read books! You’ll increase your reading comprehension skills.
PSAT vs. SAT
Confusion of goals and perfection of means seems, in my opinion, to characterize our age.
—Albert Einstein
The “Preliminary” SAT (PSAT) implies that this test is meant to give the student a preliminary idea of how well he or she will do on the SAT6. Although the PSAT is indeed designed as a warm-up for the SAT, it has taken on an importance of its own because of its use by the National Merit Program. Hence, one sees the acronym NMSQT (National Merit Scholarship Qualifying Test) alongside PSAT7.
The following is an attempt to succinctly characterize the difference between the PSAT and SAT.
General
The PSAT is a preparatory/practice tool for the SAT. Its capability to assess students’ skills at a given point in time and, in particular, its capacity to predict their performance in the SAT, while widely advertised, are controversial claims still open for debate.
The NMSQT factor is probably the most important reason for students to consider taking the PSAT. High scorers on the PSAT (≥ 95th percentile) may qualify for a National Merit Scholarship and Letters of Commendations, prestigious achievements that would certainly enhance a college applicant’s chances for admission.
Prepare for the PSAT
The math contents of PSAT and SAT are—for the most part—similar. The PSAT is known to exclude some topics that a majority of first-semester juniors have not covered, most notably (some) Algebra II-type problems. The math sections are fewer (2 versus 3) and shorter (typically two, 25-minute sections versus three, 20-, 25-, and 25-minute sections) in the PSAT than in the SAT, respectively.
Given that the PSAT (1) requires much the same knowledge8 and (2) has the same question types (multiple-choice and grid-in/open-ended), virtually all of the strategies and techniques that apply to the SAT also apply to the PSAT. (That explains the absence of books dedicated exclusively to PSAT preparation!)
The average SAT problem has a slightly higher level of difficulty than its PSAT counterpart and is therefore more challenging. Like in sports, accept the challenge and the results will award you for that (not to mention getting an early start on preparation for the “ultimate” test: the SAT).
Content
Content wise, these two tests pretty much mirror each other, with the SAT rightfully claiming a slightly higher level of difficulty. To quantify it in detail and in an objective way is, surprisingly, not a trivial matter. What does not seem to be a matter of interpretation, though, is the characterization that “the SAT is a more difficult test than the PSAT” because:
• The newly added essay on the SAT is not required on the PSAT.
• Although difficult Algebra II problems are few on the SAT, they are absent altogether on the PSAT.
• The SAT is longer than the PSAT (see below) and thus requires better concentration skills and stamina.
Timing
The tests are timed and the allotted time is 3 hours 45 minutes versus 2 hours and 10 minutes, for the SAT and the PSAT, respectively.
Grading
There is one order of magnitude difference in the way the scores in these two tests are calculated. Each math section of the tests is scored from 200 to 800 and from 20 to 809, in the SAT and the PSAT, respectively.