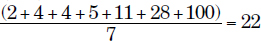
Thunder is impressive, but it is lightning that does the work.
—Mark Twain
Definition: The average/arithmetic mean of a list of values is the sum of the values divided by the number of values in the list.
Examples:
Example #1 (odd amount of numbers):
2, 4, 4, 5, 11, 28, 100
Average =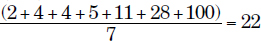
Example #2 (even amount of numbers):
2, 4, 4, 5, 11, 14, 28, 100
Average =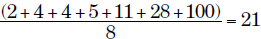 
See Problems 76, 123, 141, 146, and 179 for sample problems.
Definition: The median is the middle value of a list of ordered numbers.
Examples: Based on the examples given for “average/arithmetic mean” (Section 6.1):
Example #1: 5
Example #2: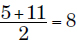 
Note: When a list contains an even number of values, the median is the average of the two values positioned in the middle of the ordered list.
See Problems 76, 111, and 146 for sample problems.
Definition: Mode (of a list of values) is the value or values that appear the greatest number of times.
Examples: Based on the examples given for “average/arithmetic mean” (Section 6.1):
Example #1: 4
Example #2: 4
A number is added to the following list of numbers:
4, 6, 10, 10
Calculate the new addition to the list given that the average is equal to the median value of the list. In addition, calculate the mode of the complete list.
Let the new number be N. The average value of the sequence is
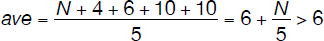
If N < 6, the median is 6 and the condition that the average = median value is not satisfied.
Option 1: 6 < N < 10; median = N, thus
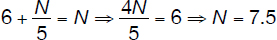
Option 2: N > 10; median = 10, thus
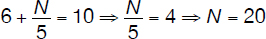
For both options, the mode of the sequence is 10.
Definition: The weighted average is the average of two or more groups that do not all have the same number of members.
Example: Calculating the weighted average is devising a method of computing a kind of arithmetic mean of a set of numbers in which some elements of the set carry more importance (weight) than others.
Grades are often computed using a weighted average. Suppose that homework counts 10%, quizzes 20%, and tests 70%. Calculate Pat’s overall grade if her average/total grades in homework, quizzes, and tests were 92, 68, and 81, respectively.
Pat’s overall grade = (0.10 x 92) + (0.20 x 68) + (0.70 x 81) = 79.5
Definition: The probability that an event will occur is a number between 0 and 1, inclusive. It’s usually written as a fraction and indicates how likely it is that the event will happen. If the event is certain, its probability is 1. If an event is impossible, its probability is 0.
Example:
Let P(A) be the probability of event A to occur:
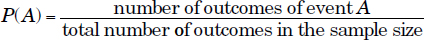
Four basic rules of probabilities apply:
1. For any event A, 0 ≤ P (A) ≤ 1.
2. P (impossible event) = 0. Also written P (empty set) = 0 or P (∅) = 0.
3. P (sure event) = 1. Also written P(S) = 1, where S is the sample space.
4. P (not A) = 1 – P(A) or P (complement of A) = 1 – P(A) or P(AC) = 1 – P(A) or P(Ā) = 1 – P(A).
A jar contains only black and white marbles. If 1 marble is removed at random, the probability that it is black is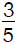 
. After putting another 100 black marbles in the jar, the probability of drawing a black marble is 
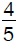. How many marbles were originally in the jar?
Let PB be the probability of drawing a black marble. If the original number of black and white marbles were B and W, respectively, using the definition of probabilities one can write that
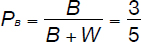
If 100 black marbles are added to the mix, the probability of drawing a black marble is
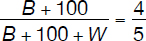
Let’s now combine and solve the two equations above for B and W:
5B = 3B + 3W
5B + 500 = 4B + 4W + 400
or
2B = 3W
B = 4W – 100
If one multiplies the second equation by 2 and substitutes 3W for 2B from the first equation, one obtains
2B = 8W – 200 = 3W or 5W = 200.
Consequently, W = 40 and B =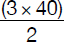 
= 60. The original number of black and white marbles in the jar was
B + W = 100
Definition: Events are independent if the outcome of either event has no effect on the other.
Examples: Independent events are those for which the probability of any one event occurring is unaffected by the occurrence or nonoccurrence of any of the other events. Two separate tosses of a fair coin are independent events. The result of the first toss has no effect on the probability of heads or tails on the second toss.
An opaque jar contains 5 red, 4 yellow, and 6 green candies. A child is allowed to pick two candies. What is the probability (1) of getting a green followed by a red candy and (2) of getting a red and then either a green or a yellow candy?
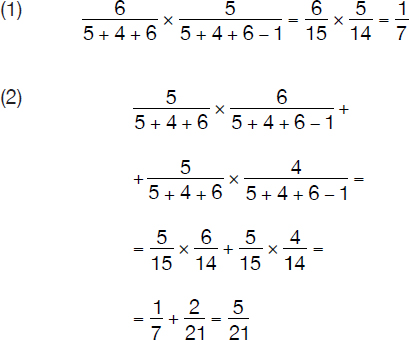
Note: “AND” = × (multiplication) and “OR” = + (addition)