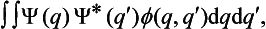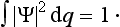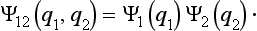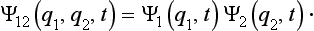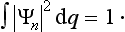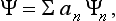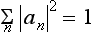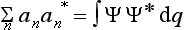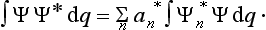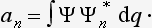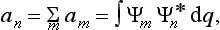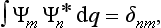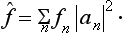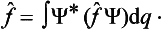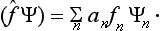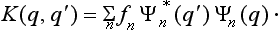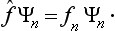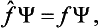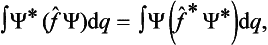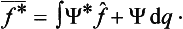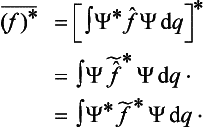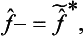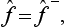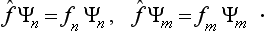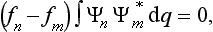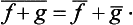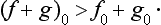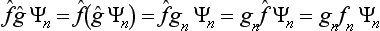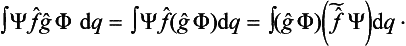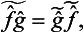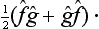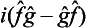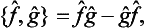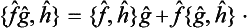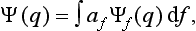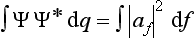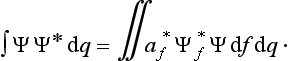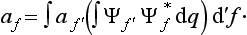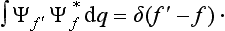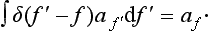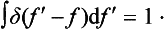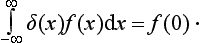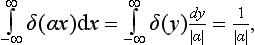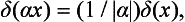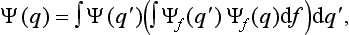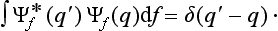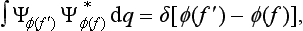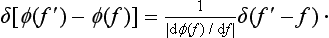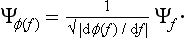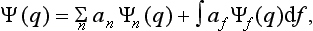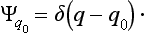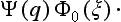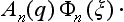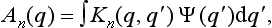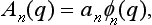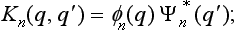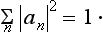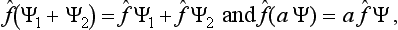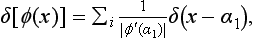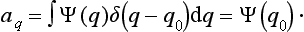THE BASIC CONCEPTS OF QUANTUM MECHANICS
§1 The uncertainty principle
When we attempt to apply classical mechanics and electrodynamics to explain atomic phenomena, they lead to results which are in obvious conflict with experiment. This is very clearly seen from the contradiction obtained on applying ordinary electrodynamics to a model of an atom in which the electrons move round the nucleus in classical orbits. During such motion, as in any accelerated motion of charges, the electrons would have to emit electromagnetic waves continually. By this emission, the electrons would lose their energy, and this would eventually cause them to fall into the nucleus. Thus, according to classical electrodynamics, the atom would be unstable, which does not at all agree with reality.
This marked contradiction between theory and experiment indicates that the construction of a theory applicable to atomic phenomena—that is, phenomena occurring in particles of very small mass at very small distances—demands a fundamental modification of the basic physical concepts and laws.
As a starting-point for an investigation of these modifications, it is convenient to take the experimentally observed phenomenon known as electron diffraction.† It is found that, when a homogeneous beam of electrons passes through a crystal, the emergent beam exhibits a pattern of alternate maxima and minima of intensity, wholly similar to the diffraction pattern observed in the diffraction of electromagnetic waves. Thus, under certain conditions, the behaviour of material particles—in this case, the electrons—displays features belonging to wave processes.
How markedly this phenomenon contradicts the usual ideas of motion is best seen from the following imaginary experiment, an idealization of the experiment of electron diffraction by a crystal. Let us imagine a screen impermeable to electrons, in which two slits are cut. On observing the passage of a beam of electrons‡ through one of the slits, the other being covered, we obtain, on a continuous screen placed behind the slit, some pattern of intensity distribution; in the same way, by uncovering the second slit and covering the first, we obtain another pattern. On observing the passage of the beam through both slits, we should expect, on the basis of ordinary classical ideas, a pattern which is a simple superposition of the other two: each electron, moving in its path, passes through one of the slits and has no effect on the electrons passing through the other slit. The phenomenon of electron diffraction shows, however, that in reality we obtain a diffraction pattern which, owing to interference, does not at all correspond to the sum of the patterns given by each slit separately. It is clear that this result can in no way be reconciled with the idea that electrons move in paths.
Thus the mechanics which governs atomic phenomena—quantum mechanics or wave mechanics—must be based on ideas of motion which are fundamentally different from those of classical mechanics. In quantum mechanics there is no such concept as the path of a particle. This forms the content of what is called the uncertainty principle, one of the fundamental principles of quantum mechanics, discovered by W. Heisenberg in 1927.†
In that it rejects the ordinary ideas of classical mechanics, the uncertainty principle might be said to be negative in content. Of course, this principle in itself does not suffice as a basis on which to construct a new mechanics of particles. Such a theory must naturally be founded on some positive assertions, which we shall discuss below (§2). However, in order to formulate these assertions, we must first ascertain the statement of the problems which confront quantum mechanics. To do so, we first examine the special nature of the interrelation between quantum mechanics and classical mechanics. A more general theory can usually be formulated in a logically complete manner, independently of a less general theory which forms a limiting case of it. Thus, relativistic mechanics can be constructed on the basis of its own fundamental principles, without any reference to Newtonian mechanics. It is in principle impossible, however, to formulate the basic concepts of quantum mechanics without using classical mechanics. The fact that an electron‡ has no definite path means that it has also, in itself, no other dynamical characteristics.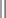
Hence it is clear that, for a system composed only of quantum objects, it would be entirely impossible to construct any logically independent mechanics. The possibility of a quantitative description of the motion of an electron requires the presence also of physical objects which obey classical mechanics to a sufficient degree of accuracy. If an electron interacts with such a “classical object”, the state of the latter is, generally speaking, altered. The nature and magnitude of this change depend on the state of the electron, and therefore may serve to characterize it quantitatively.
In this connection the “classical object” is usually called apparatus, and its interaction with the electron is spoken of as measurement. However, it must be emphasized that we are here not discussing a process of measurement in which the physicist-observer takes part. By measurement, in quantum mechanics, we understand any process of interaction between classical and quantum objects, occurring apart from and independently of any observer. The importance of the concept of measurement in quantum mechanics was elucidated by N. Bohr.
We have defined “apparatus” as a physical object which is governed, with sufficient accuracy, by classical mechanics. Such, for instance, is a body of large enough mass. However, it must not be supposed that apparatus is necessarily macroscopic. Under certain conditions, the part of apparatus may also be taken by an object which is microscopic, since the idea of “with sufficient accuracy” depends on the actual problem proposed. Thus, the motion of an electron in a Wilson chamber is observed by means of the cloudy track which it leaves, and the thickness of this is large compared with atomic dimensions; when the path is determined with such low accuracy, the electron is an entirely classical object.
Thus quantum mechanics occupies a very unusual place among physical theories: it contains classical mechanics as a limiting case, yet at the same time it requires this limiting case for its own formulation.
We may now formulate the problem of quantum mechanics. A typical problem consists in predicting the result of a subsequent measurement from the known results of previous measurements. Moreover, we shall see later that, in comparison with classical mechanics, quantum mechanics, generally speaking, restricts the range of values which can be taken by various physical quantities (for example, energy): that is, the values which can be obtained as a result of measuring the quantity concerned. The methods of quantum mechanics must enable us to determine these admissible values.
The measuring process has in quantum mechanics a very important property: it always affects the electron subjected to it, and it is in principle impossible to make its effect arbitrarily small, for a given accuracy of measurement. The more exact the measurement, the stronger the effect exerted by it, and only in measurements of very low accuracy can the effect on the measured object be small. This property of measurements is logically related to the fact that the dynamical characteristics of the electron appear only as a result of the measurement itself. It is clear that, if the effect of the measuring process on the object of it could be made arbitrarily small, this would mean that the measured quantity has in itself a definite value independent of the measurement.
Among the various kinds of measurement, the measurement of the coordinates of the electron plays a fundamental part. Within the limits of applicability of quantum mechanics, a measurement of the coordinates of an electron can always be performed† with any desired accuracy.
Let us suppose that, at definite time intervals Δt, successive measurements of the coordinates of an electron are made. The results will not in general lie on a smooth curve. On the contrary, the more accurately the measurements are made, the more discontinuous and disorderly will be the variation of their results, in accordance with the non-existence of a path of the electron. A fairly smooth path is obtained only if the coordinates of the electron are measured with a low degree of accuracy, as for instance from the condensation of vapour droplets in a Wilson chamber.
If now, leaving the accuracy of the measurements unchanged, we diminish the intervals δt between measurements, then adjacent measurements, of course, give neighbouring values of the coordinates. However, the results of a series of successive measurements, though they lie in a small region of space, will be distributed in this region in a wholly irregular manner, lying on no smooth curve. In particular, as δt tends to zero, the results of adjacent measurements by no means tend to lie on one straight line.
This circumstance shows that, in quantum mechanics, there is no such concept as the velocity of a particle in the classical sense of the word, i.e. the limit to which the difference of the coordinates at two instants, divided by the interval δt between these instants, tends as δt tends to zero. However, we shall see later that in quantum mechanics, nevertheless, a reasonable definition of the velocity of a particle at a given instant can be constructed, and this velocity passes into the classical velocity as we pass to classical mechanics. But whereas in classical mechanics a particle has definite coordinates and velocity at any given instant, in quantum mechanics the situation is entirely different. If, as a result of measurement, the electron is found to have definite coordinates, then it has no definite velocity whatever. Conversely, if the electron has a definite velocity, it cannot have a definite position in space. For the simultaneous existence of the coordinates and velocity would mean the existence of a definite path, which the electron has not. Thus, in quantum mechanics, the coordinates and velocity of an electron are quantities which cannot be simultaneously measured exactly, i.e. they cannot simultaneously have definite values. We may say that the coordinates and velocity of the electron are quantities which do not exist simultaneously. In what follows we shall derive the quantitative relation which determines the possibility of an inexact measurement of the coordinates and velocity at the same instant.
A complete description of the state of a physical system in classical mechanics is effected by stating all its coordinates and velocities at a given instant; with these initial data, the equations of motion completely determine the behaviour of the system at all subsequent instants. In quantum mechanics such a description is in principle impossible, since the coordinates and the corresponding velocities cannot exist simultaneously. Thus a description of the state of a quantum system is effected by means of a smaller number of quantities than in classical mechanics, i.e. it is less detailed than a classical description.
A very important consequence follows from this regarding the nature of the predictions made in quantum mechanics. Whereas a classical description suffices to predict the future motion of a mechanical system with complete accuracy, the less detailed description given in quantum mechanics evidently cannot be enough to do this. This means that, even if an electron is in a state described in the most complete manner possible in quantum mechanics, its behaviour at subsequent instants is still in principle uncertain. Hence quantum mechanics cannot make completely definite predictions concerning the future behaviour of the electron. For a given initial state of the electron, a subsequent measurement can give various results. The problem in quantum mechanics consists in determining the probability of obtaining various results on performing this measurement. It is understood, of course, that in some cases the probability of a given result of measurement may be equal to unity, i.e. certainty, so that the result of that measurement is unique.
All measuring processes in quantum mechanics may be divided into two classes. In one, which contains the majority of measurements, we find those which do not, in any state of the system, lead with certainty to a unique result. The other class contains measurements such that for every possible result of measurement there is a state in which the measurement leads with certainty to that result. These latter measurements, which may be called predictable, play an important part in quantum mechanics. The quantitative characteristics of a state which are determined by such measurements are what are called physical quantities in quantum mechanics. If in some state a measurement gives with certainty a unique result, we shall say that in this state the corresponding physical quantity has a definite value. In future we shall always understand the expression “physical quantity” in the sense given here.
We shall often find in what follows that by no means every set of physical quantities in quantum mechanics can be measured simultaneously, i.e. can all have definite values at the same time. We have already mentioned one example, namely the velocity and coordinates of an electron. An important part is played in quantum mechanics by sets of physical quantities having the following property: these quantities can be measured simultaneously, but if they simultaneously have definite values, no other physical quantity (not being a function of these) can have a definite value in that state. We shall speak of such sets of physical quantities as complete sets.
Any description of the state of an electron arises as a result of some measurement. We shall now formulate the meaning of a complete description of a state in quantum mechanics. Completely described states occur as a result of the simultaneous measurement of a complete set of physical quantities. From the results of such a measurement we can, in particular, determine the probability of various results of any subsequent measurement, regardless of the history of the electron prior to the first measurement.
From now on (except in §14) we shall understand by the states of a quantum system just these completely described states.
§2 The principle of superposition
The radical change in the physical concepts of motion in quantum mechanics as compared with classical mechanics demands, of course, an equally radical change in the mathematical formalism of the theory. We must therefore consider first of all the way in which states are described in quantum mechanics.
We shall denote by q the set of coordinates of a quantum system, and by dq the product of the differentials of these coordinates. This dq is called an element of volume in the configuration space of the system; for one particle, dq coincides with an element of volume dV in ordinary space.
The basis of the mathematical formalism of quantum mechanics lies in the proposition that the state of a system can be described by a definite (in general complex) function Ψ(q) of the coordinates. The square of the modulus of this function determines the probability distribution of the values of the coordinates: |Ψ|2dq is the probability that a measurement performed on the system will find the values of the coordinates to be in the element dq of configuration space. The function Ψ is called the wave function of the system.†
A knowledge of the wave function allows us, in principle, to calculate the probability of the various results of any measurement (not necessarily of the coordinates) also. All these probabilities are determined by expressions bilinear in Ψ and Ψ*. The most general form of such an expression is
where the function φ(q, q′) depends on the nature and the result of the measurement, and the integration is extended over all configuration space. The probability ΨΨ* of various values of the coordinates is itself an expression of this type.‡
The state of the system, and with it the wave function, in general varies with time. In this sense the wave function can be regarded as a function of time also. If the wave function is known at some initial instant, then, from the very meaning of the concept of complete description of a state, it is in principle determined at every succeeding instant. The actual dependence of the wave function on time is determined by equations which will be derived later.
The sum of the probabilities of all possible values of the coordinates of the system must, by definition, be equal to unity. It is therefore necessary that the result of integrating |Ψ|2 over all configuration space should be equal to unity:
This equation is what is called the normalization condition for wave functions. If the integral of |Ψ|2 converges, then by choosing an appropriate constant coefficient the function Ψ can always be, as we say, normalized. However, we shall see later that the integral of |Ψ|2 may diverge, and then Ψ cannot be normalized by the condition (2.2). In such cases |Ψ|2 does not, of course, determine the absolute values of the probability of the coordinates, but the ratio of the values of |Ψ|2 at two different points of configuration space determines the relative probability of the corresponding values of the coordinates.
Since all quantities calculated by means of the wave function, and having a direct physical meaning, are of the form (2.1), in which Ψ appears multiplied by Ψ*, it is clear that the normalized wave function is determined only to within a constant phase factor of the form eiα (where α is any real number). This indeterminacy is in principle irremovable; it is, however, unimportant, since it has no effect upon any physical results.
The positive content of quantum mechanics is founded on a series of propositions concerning the properties of the wave function. These are as follows.
Suppose that, in a state with wave function Ψ1(q), some measurement leads with certainty to a definite result (result 1), while in a state with Ψ2(q) it leads to result 2. Then it is assumed that every linear combination of Ψ1 and Ψ2, i.e. every function of the form c1 Ψ1 + c2 Ψ2 (where c1 and c2 are constants), gives a state in which that measurement leads to either result 1 or result 2. Moreover, we can assert that, if we know the time dependence of the states, which for the one case is given by the function Ψ1(q, t), and for the other by Ψ2(q, t), then any linear combination also gives a possible dependence of a state on time. These propositions constitute what is called the principle of superposition of states, the chief positive principle of quantum mechanics. In particular, it follows from this principle that all equations satisfied by wave functions must be linear in Ψ.
Let us consider a system composed of two parts, and suppose that the state of this system is given in such a way that each of its parts is completely described.† Then we can say that the probabilities of the coordinates of the first part are independent of the probabilities of the coordinates q2 of the second part, and therefore the probability distribution for the whole system should be equal to the product of the probabilities of its parts. This means that the wave function Ψ12(q1, q2) of the system can be represented in the form of a product of the wave functions Ψ1(q1) and Ψ2(q2) of its parts:
If the two parts do not interact, then this relation between the wave function of the system and those of its parts will be maintained at future instants also, i.e. we can write
§3 Operators
Let us consider some physical quantity f which characterizes the state of a quantum system. Strictly, we should speak in the following discussion not of one quantity, but of a complete set of them at the same time. However, the discussion is not essentially changed by this, and for brevity and simplicity we shall work below in terms of only one physical quantity.
The values which a given physical quantity can take are called in quantum mechanics its eigenvalues, and the set of these is referred to as the spectrum of eigenvalues of the given quantity. In classical mechanics, generally speaking, quantities run through a continuous series of values. In quantum mechanics also there are physical quantities (for instance, the coordinates) whose eigenvalues occupy a continuous range; in such cases we speak of a continuous spectrum of eigenvalues. As well as such quantities, however, there exist in quantum mechanics others whose eigenvalues form some discrete set; in such cases we speak of a discrete spectrum.
We shall suppose for simplicity that the quantity f considered here has a discrete spectrum; the case of a continuous spectrum will be discussed in §5. The eigenvalues of the quantity f are denoted by fn, where the suffix n takes the values 0, 1, 2, 3, … We also denote the wave function of the system, in the state where the quantity f has the value fn, by Ψn. The wave functions Ψn are called the eigenfunctions of the given physical quantity f. Each of these functions is supposed normalized, so that
If the system is in some arbitrary state with wave function Ψ, a measurement of the quantity f carried out on it will give as a result one of the eigenvalues fn. In accordance with the principle of superposition, we can assert that the wave function Ψ must be a linear combination of those eigenfunctions Ψn which correspond to the values fn that can be obtained, with probability different from zero, when a measurement is made on the system and it is in the state considered. Hence, in the general case of an arbitrary state, the function Ψ can be represented in the form of a series
where the summation extends over all n, and the an are some constant coefficients.
Thus we reach the conclusion that any wave function can be, as we say, expanded in terms of the eigenfunctions of any physical quantity. A set of functions in terms of which such an expansion can be made is called a complete (or closed) set.
The expansion (3.2) makes it possible to determine the probability of finding (i.e. the probability of getting the corresponding result on measurement), in a system in a state with wave function Ψ, any given value fn of the quantity f. For, according to what was said in the previous section, these probabilities must be determined by some expressions bilinear in Ψ and Ψ*, and therefore must be bilinear in an and an*. Furthermore, these expressions must, of course, be positive. Finally, the probability of the value fn must become unity if the system is in a state with wave function Ψ = Ψn, and must become zero if there is no term containing Ψn in the expansion (3.2) of the wave function Ψ. The only essentially positive quantity satisfying these conditions is the square of the modulus of the coefficient an. Thus we reach the result that the squared modulus |an|2 of each coefficient in the expansion (3.2) determines the probability of the corresponding value fn of the quantity f in the state with wave function Ψ. The sum of the probabilities of all possible values fn must be equal to unity; in other words, the relation
must hold.
If the function Ψ were not normalized, then the relation (3.3) would not hold either. The sum Σ |an|2 would then be given by some expression bilinear in Ψ and Ψ*, and becoming unity when Ψ was normalized. Only the integral ∫ ΨΨ* dq is such an expression. Thus the equation
must hold.
On the other hand, multiplying by Ψ the expansion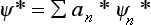 
of the function Ψ* (the complex conjugate of Ψ), and integrating, we obtain
Comparing this with (3.4), we have
from which we derive the following formula determining the coefficients an in the expansion of the function Ψ in terms of the eigenfunctions Ψn:
If we substitute here from (3.2), we obtain
from which it is evident that the eigenfunctions must satisfy the conditions
where δnm = 1 for n = m and δnm = 0 for n ≠ m. The fact that the integrals of the products Ψm Ψn* with m ≠ n vanish is called the orthogonality of the functions Ψn. Thus the set of eigenfunctions Ψn forms a complete set of normalized and orthogonal (or, for brevity, orthonormal) functions.
We shall now introduce the concept of the mean value f of the quantity f in the given state. In accordance with the usual definition of mean values, we define f as the sum of all the eigenvalues fn of the given quantity, each multiplied by the corresponding probability |an|2. Thus
We shall write f in the form of an expression which does not contain the coefficients an in the expansion of the function Ψ, but this function itself. Since the products anan* appear in (3.7), it is clear that the required expression must be bilinear in Ψ and Ψ*. We introduce a mathematical operator, which we denote† by f and define as follows. Let (fΨ) denote the result of the operator f acting on the function Ψ. We define f in such a way that the integral of the product of (fΨ) and the complex conjugate function Ψ* is equal to the mean value f:
It is easily seen that, in the general case, the operator f is a linear‡integral operator. For, using the expression (3.5) for an, we can rewrite the definition (3.7) of the mean value in the form
Comparing this with (3.8), we see that the result of the operator f acting on the function Ψ has the form
If we substitute here the expression (3.5) for an, we find that f is an integral operator of the form
where the function K (q, q′) (called the kernel of the operator) is
Thus, for every physical quantity in quantum mechanics, there is a definite corresponding linear operator.
It is seen from (3.9) that, if the function Ψ is one of the eigenfunctions Ψn(so that all the an except one are zero), then, when the operator f acts on it, this function is simply multiplied by the corresponding eigenvalue fn:
(In what follows we shall always omit the parentheses in the expression (fΨ), where this cannot cause any misunderstanding; the operator is taken to act on the expression which follows it.) Thus we can say that the eigenfunctions of the given physical quantity f are the solutions of the equation
where f is a constant, and the eigenvalues are the values of this constant for which the above equation has solutions satisfying the required conditions. As we shall see below, the form of the operators for various physical quantities can be determined from direct physical considerations, and then the above property of the operators enables us to find the eigenfunctions and eigenvalues by solving the equations fΨ = fΨ.
Both the eigenvalues of a real physical quantity and its mean value in every state are real. This imposes a restriction on the corresponding operators. Equating the expression (3.8) to its complex conjugate, we obtain the relation
where f* denotes the operator which is the complex conjugate of f.† This relation does not hold in general for an arbitrary linear operator, so that it is a restriction on the form of the operator f. For an arbitrary operator f we can find what is called the transposed operator f, defined in such a way that
where Ψ and Φ are two different functions. If we take, as the function Φ, the function Ψ* which is the complex conjugate of Ψ, then a comparison with (3.13) shows that we must have
Operators satisfying this condition are said to be Hermitian.‡ Thus the operators corresponding, in the mathematical formalism of quantum mechanics, to real physical quantities must be Hermitian.
We can formally consider complex physical quantities also, i.e. those whose eigenvalues are complex. Let f be such a quantity. Then we can introduce its complex conjugate quantity f*, whose eigenvalues are the complex conjugates of those of f. We denote by f+ the operator corresponding to the quantity f*. It is called the Hermitian conjugate of the operator f and, in general, will be different from the definition of the operator f*: the mean value of the quantity f* in a state Ψ is
Equating these two expressions gives
from which it is clear that 
is in general not the same as f*.
The condition (3.15) can now be written
i.e. the operator of a real physical quantity is the same as its Hermitian conjugate (Hermitian operators are also called self-conjugate).
We shall show how the orthogonality of the eigenfunctions of an Hermitian operator corresponding to different eigenvalues can be directly proved. Let fn and fm be two different eigenvalues of the real quantity f, and Ψn, Ψm the corresponding eigenfunctions:
Multiplying both sides of the first of these equations by Ψm*, and both sides of the complex conjugate of the second by Ψn, and subtracting corresponding terms, we find
We integrate both sides of this equation over q. Since f* = f, by (3.14) the integral on the left-hand side of the equation is zero, so that we have
whence, since fn ≠ fm, we obtain the required orthogonality property of the functions Ψn and Ψm.
We have spoken here of only one physical quantity f, whereas, as we said at the beginning of this section, we should have spoken of a complete set of simultaneously measurable physical quantities. We should then have found that to each of these quantities f, g, … there corresponds its operator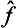 
, ĝ, …, The eigenfunctions Ψn then correspond to states in which all the quantities concerned have definite values, i.e. they correspond to definite sets of eigenvalues fn, gn, …, and are simultaneous solutions of the system of equations
§4 Addition and multiplication of operators
If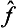 
and ĝ are the operators corresponding to two physical quantities f and g, the sum f+g has a corresponding operator 
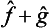. However, the significance of adding different physical quantities in quantum mechanics depends considerably on whether the quantities are or are not simultaneously measurable. If f and g are simultaneously measurable, the operators 
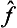and ĝ have common eigenfunctions, which are also eigenfunctions of the operator 
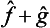, and the eigenvalues of the latter operator are equal to the sums fn + gn. But if f and g cannot simultaneously take definite values, their sum f+g has a more restricted significance. We can assert only that the mean value of this quantity in any state is equal to the sum of the mean values of the separate quantities:
The eigenvalues and eigenfunctions of the operator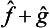 
will not, in general, now bear any relation to those of the quantities f and g. It is evident that, if the operators 
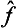and ĝ are Hermitian, the operator 
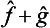will be so too, so that its eigenvalues are real and are equal to those of the new quantity f + g thus defined.
The following theorem should be noted. Let f0 and g0 be the smallest eigenvalues of the quantities f and g, and (f+g)0 that of the quantity f+g. Then
The equality holds if f and g can be measured simultaneously. The proof follows from the obvious fact that the mean value of a quantity is always greater than or equal to its least eigenvalue. In a state in which the quantity f+g has the value (f+g)0 we have 
, and since, on the other hand, 
, we arrive at the inequality (4.2).
Next, let f and g once more be quantities that can be measured simultaneously. Besides their sum, we can also introduce the concept of their product as being a quantity whose eigenvalues are equal to the products of those of the quantities f and g. It is easy to see that, to this quantity, there corresponds an operator whose effect consists of the successive action on the function of first one and then the other operator. Such an operator is represented mathematically by the product of the operators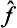 
and ĝ. For, if Ψn are the eigenfunctions common to the operators 
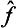and ĝ, we have
the symbol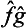 
denotes an operator whose effect on a function Ψ consists of the successive action first of the operator ĝ on the function Ψ and then of the operator 
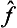on the function ĝΨ). We could equally well take the operator 
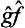instead of 
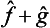, the former differing from the latter in the order of its factors. It is obvious that the result of the action of either of these operators on the functions Ψn will be the same. Since, however, every wave function Ψ can be represented as a linear combination of the functions Ψn, it follows that the result of the action of the operators 
and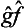 
on an arbitrary function will also be the same. This fact can be written in the form of the symbolic equation 
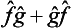or
Two such operators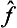 
and ĝ are said to be commutative, or to commute with each other. Thus we arrive at the important result: if two quantities f and g can simultaneously take definite values, then their operators commute with each other.
The converse theorem can also be proved (§11): if the operators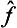 
and ĝ commute, then all their eigenfunctions can be taken common to both; physically, this means that the corresponding physical quantities can be measured simultaneously. Thus the commutability of the operators is a necessary and sufficient condition for the physical quantities to be simultaneously measurable.
A particular case of the product of operators is an operator raised to some power. From the above discussion we can deduce that the eigenvalues of an operator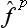 
(where p is an integer) are equal to the pth powers of the eigenvalues of the operator 
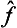. Any function φ(
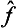) of an operator can be defined as an operator whose eigenvalues are equal to the same function φ(
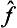) of the eigenvalues of the operator 
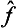. If the function φ(
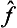) can be expanded as a Taylor series, this expresses the effect of the operator φ(
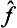) in terms of those of various powers 
.
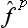In particular, the operator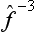 
is called the inverse of the operator 
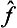. It is evident that the successive action of the operators 
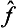and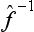 
on any function leaves the latter unchanged, i.e. 
.
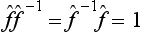If the quantities f and g cannot be measured simultaneously, the concept of their product does not have the same direct meaning. This appears in the fact that the operator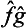 
is not Hermitian in this case, and hence cannot correspond to any real physical quantity. For, by the definition of the transpose of an operator we can write
Here the operator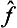 
acts only on the function Ψ, and the operator ĝ on Φ, so that the integrand is a simple product of two functions ĝΦ and 
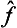Ψ. Again using the definition of the transpose of an operator, we can write
Thus we obtain an integral in which the functions Ψ and Φ have changed places as compared with the original one. In other words, the operator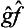 
is the transpose of 
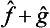, and we can write
i.e. the transpose of the product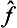 
ĝ is the product of the transposes of the factors written in the opposite order. Taking the complex conjugate of both sides of equation (4.4), we have
If each of the operators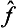 
and ĝ is Hermitian, then 
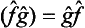. It follows from this that the operator 
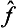ĝ is Hermitian if and only if the factors 
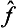and ĝ commute.
We note that, from the products 
ĝ and ĝ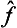
of two non-commuting Hermitian operators, we can form an Hermitian operator, the symmetrized product
It is easy to see that the difference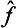 
ĝ—ĝ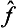
is an anti-Hermitian operator (i.e. one for which the transpose is equal to the complex conjugate taken with the opposite sign). It can be made Hermitian by multiplying by i; thus
is again an Hermitian operator.
In what follows we shall sometimes use for brevity the notation
called the commutator of these operators. It is easily seen that
We notice that, if {
, ĥ} = 0 and {ĝ, ĥ) = 0, it does not in general follow that 
and ĝ commute.
§5 The continuous spectrum
All the relations given in §§3 and 4, describing the properties of the eigenfunctions of a discrete spectrum, can be generalized without difficulty to the case of a continuous spectrum of eigenvalues.
Let f be a physical quantity having a continuous spectrum. We shall denote its eigenvalues by the same letter f simply, and the corresponding eigenfunctions by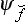 
. Just as an arbitrary wave function Ψ can be expanded in a series (3.2) of eigenfunctions of a quantity having a discrete spectrum, it can also be expanded (this time as an integral) in terms of the complete set of eigenfunctions of a quantity with a continuous spectrum This expansion has the form
where the integration is extended over the whole range of values that can be taken by the quantity f.
The subject of the normalization of the eigenfunctions of a continuous spectrum is more complex than in the case of a discrete spectrum. The requirement that the integral of the squared modulus of the function should be equal to unity cannot here be satisfied, as we shall see below. Instead, we try to normalize the functions Ψf in such a way that |af|2 df is the probability that the physical quantity concerned, in the state described by the wave function Ψ, has a value between f and f + df. Since the sum of the probabilities of all possible values of f must be equal to unity, we have
(similarly to the relation (3.3) for a discrete spectrum).
Proceeding in exactly the same way as in the derivation of formula (3.5), and using the same arguments, we can write, firstly,
and, secondly,
By comparing these two expressions we find the formula which determines the expansion coefficients,
in exact analogy to (3.5).
To derive the normalization condition, we now substitute (5.1) in (5.3), and obtain
This relation must hold for arbitrary af, and therefore must be satisfied identically. For this to be so, it is necessary that, first of all, the coefficient of af, in the integrand (i.e. the integral ∫ Ψf Ψf* dq) should be zero for all f′ ≠ f. For f′ = f, this coefficient must become infinite (otherwise the integral over f′ would vanish). Thus the integral ∫ Ψf′ Ψf* dq is a function of the difference f′ − f, which becomes zero for values of the argument different from zero and is infinite when the argument is zero. We denote this function by δ(f′ − f):
The manner in which the function δ(f′− f) becomes infinite for f′ − f = 0 is determined by the fact that we must have
It is clear that, for this to be so, we must have
The function thus defined is called a delta function, and was first used in theoretical physics by P. A. M. Dirac. We shall write out once more the formulae which define it. They are
while
We can take as limits of integration any numbers such that x = 0 lies between them. If f (x) is some function continuous at x = 0, then
This formula can be written in the more general form
where the range of integration includes the point x = a, and f (x) is continuous at x = a. It is also evident that
i.e. the delta function is even. Finally, writing
we can deduce that
where α is any constant.
The formula (5.4) gives the normalization rule for the eigenfunctions of a continuous spectrum; it replaces the condition (3.6) for a discrete spectrum. We see that the functions Ψf and Ψf′ with f ≠ f′ are, as before, orthogonal. However, the integrals of the squared moduli |Ψf|2 of the functions diverge for a continuous spectrum.
The functions Ψf(q) satisfy still another relation similar to (5.4). To derive this, we substitute (5.3) in (5.1), which gives
whence we can at once deduce that we must have
There is, of course, an analogous relation for a discrete spectrum:
Comparing the pair of formulae (5.1), (5.4) with the pair (5.3), (5.11), we see that, on the one hand, the function Ψ(q) can be expanded in terms of the functions Ψf(q) with expansion coefficients af and, on the other hand, formula (5.3) represents an entirely analogous expansion of the function af ≡ a (f) in terms of the functions Ψf*(q), while the Ψ(q) play the part of expansion coefficients. The function a (f), like Ψ(q), completely determines the state of the system; it is sometimes called a wave function in the f representation (while the function Ψ(q) is called a wave function in the q representation). Just as |Ψ(q) |2 determines the probability for the system to have coordinates lying in a given interval dq, so |a (f)|2 determines the probability for the values of the quantity f to lie in a given interval df. On the one hand, the functions Ψf(q) are the eigenfunctions of the quantity f in the q representation; on the other hand, their complex conjugates are the eigenfunctions of the coordinate q in the f representation.
Let φ(f) be some function of the quantity f, such that φ and f are related in a one-to-one manner. Each of the functions Ψf(q) can then be regarded as an eigenfunction of the quantity φ. Here, however, the normalization of these functions must be changed: the eigenfunctions Ψφ(q) of the quantity φ must be normalized by the condition
whereas the functions Ψf, are normalized by the condition (5.4). The argument of the delta function becomes zero only for f′ = f. As f′ approaches f, we have φ(f′)-φ(f) = [dφ(f)/df]. (f′-f). By (5.10) we can therefore write†
Comparing this with (5.4), we see that the functions Ψφ and Ψf are related by
There are also physical quantities which in one range of values have a discrete spectrum, and in another a continuous spectrum. For the eigenfunctions of such a quantity all the relations derived in this and the previous sections are, of course, true. It need only be noted that the complete set of functions is formed by combining the eigenfunctions of both spectra. Hence the expansion of an arbitrary wave function in terms of the eigenfunctions of such a quantity has the form
where the sum is taken over the discrete spectrum and the integral over the whole continuous spectrum.
The coordinate q itself is an example of a quantity having a continuous spectrum. It is easy to see that the operator corresponding to it is simply multiplication by q. For, since the probability of the various values of the coordinate is determined by the square |Ψ(q)|2, the mean value of the coordinate is
Comparison of this with the definition (3.8) of an operator shows that†
The eigenfunctions of this operator must be determined, according to the usual rule, by the equation qΨq0 = q0Ψq0, where q0 temporarily denotes the actual values of the coordinate as distinct from the variable q. Since this equation can be satisfied either by Ψq0 = 0 or by q = q0, it is clear that the eigenfunctions which satisfy the normalization condition are‡
§6 The passage to the limiting case of classical mechanics
Quantum mechanics contains classical mechanics in the form of a certain limiting case. The question arises as to how this passage to the limit is made.
In quantum mechanics an electron is described by a wave function which determines the various values of its coordinates; of this function we so far know only that it is the solution of a certain linear partial differential equation. In classical mechanics, on the other hand, an electron is regarded as a material particle, moving in a path which is completely determined by the equations of motion. There is an interrelation, somewhat similar to that between quantum and classical mechanics, in electrodynamics between wave optics and geometrical optics. In wave optics, the electromagnetic waves are described by the electric and magnetic field vectors, which satisfy a definite system of linear differential equations, namely Maxwell’s equations. In geometrical optics, however, the propagation of light along definite paths, or rays, is considered. Such an analogy enables us to see that the passage from quantum mechanics to the limit of classical mechanics occurs similarly to the passage from wave optics to geometrical optics.
Let us recall how this latter transition is made mathematically (see Fields, §53). Let u be any of the field components in the electromagnetic wave. It can be written in the form u = aeiφ (with a and φ real), where a is called the amplitude and φ the phase of the wave (called in geometrical optics the eikonal). The limiting case of geometrical optics corresponds to small wavelengths; this is expressed mathematically by saying that φ varies by a large amount over short distances; this means, in particular, that it can be supposed large in absolute value.
Similarly, we start from the hypothesis that, to the limiting case of classical mechanics, there correspond in quantum mechanics wave functions of the form Ψ = aeiφ, where a is a slowly varying function and φ takes large values. As is well known, the path of a particle can be determined in mechanics by means of the variational principle, according to which what is called the action S of a mechanical system must take its least possible value (the principle of least action). In geometrical optics the path of the rays is determined by what is called Fermat’s principle, according to which the optical path length of the ray, i.e. the difference between its phases at the beginning and end of the path, must take its least (or greatest) possible value.
On the basis of this analogy, we can assert that the phase φ of the wave function, in the limiting (classical) case, must be proportional to the mechanical action S of the physical system considered, i.e. we must have S = constant × φ. The constant of proportionality is called Planck’s constant† and is denoted by ħ. It has the dimensions of action (since φ is dimensionless) and has the value
Thus, the wave function of an “almost classical” (or, as we say, quasiclassical) physical system has the form
Planck’s constant ħ plays a fundamental part in all quantum phenomena. Its relative value (compared with other quantities of the same dimensions) determines the “extent of quantization” of a given physical system. The transition from quantum mechanics to classical mechanics, corresponding to large phase, can be formally described as a passage to the limit ħ → 0 (just as the transition from wave optics to geometrical optics corresponds to a passage to the limit of zero wavelength, λ → 0).
We have ascertained the limiting form of the wave function, but the question still remains how it is related to classical motion in a path. In general, the motion described by the wave function does not tend to motion in a definite path. Its connection with classical motion is that, if at some initial instant the wave function, and with it the probability distribution of the coordinates, is given, then at subsequent instants this distribution will change according to the laws of classical mechanics (for a more detailed discussion of this, see the end of §17).
In order to obtain motion in a definite path, we must start from a wave function of a particular form, which is perceptibly different from zero only in a very small region of space (what is called a wave packet); the dimensions of this region must tend to zero with ħ. Then we can say that, in the quasiclassical case, the wave packet will move in space along a classical path of a particle.
Finally, quantum-mechanical operators must reduce, in the limit, simply to multiplication by the corresponding physical quantity.
§7 The wave function and measurements
Let us again return to the process of measurement, whose properties have been qualitatively discussed in §1; we shall show how these properties are related to the mathematical formalism of quantum mechanics.
We consider a system consisting of two parts: a classical apparatus and an electron (regarded as a quantum object). The process of measurement consists in these two parts’ coming into interaction with each other, as a result of which the apparatus passes from its initial state into some other; from this change of state we draw conclusions concerning the state of the electron. The states of the apparatus are distinguished by the values of some physical quantity (or quantities) characterizing it—the “readings of the apparatus”. We conventionally denote this quantity by g, and its eigenvalues by gn; these take in general, in accordance with the classical nature of the apparatus, a continuous range of values, but we shall—merely in order to simplify the subsequent formulae—suppose the spectrum discrete. The states of the apparatus are described by means of quasi-classical wave functions, which we shall denote by Ψn(ξ), where the suffix n corresponds to the “reading” gn of the apparatus, and ξ denotes the set of its coordinates. The classical nature of the apparatus appears in the fact that, at any given instant, we can say with certainty that it is in one of the known states Ψn with some definite value of the quantity g; for a quantum system such an assertion would, of course, be unjustified.
Let φ0(ξ) be the wave function of the initial state of the apparatus (before the measurement), and Ψ(q) some arbitrary normalized initial wave function of the electron (q denoting its coordinates). These functions describe the state of the apparatus and of the electron independently, and therefore the initial wave function of the whole system is the product
Next, the apparatus and the electron interact with each other. Applying the equations of quantum mechanics, we can in principle follow the change of the wave function of the system with time. After the measuring process it may not, of course, be a product of functions of ξ and q. Expanding the wave function in terms of the eigenfunctions φn of the apparatus (which form a complete set of functions), we obtain a sum of the form
where the An(q) are some functions of q.
The classical nature of the apparatus, and the double role of classical mechanics as both the limiting case and the foundation of quantum mechanics, now make their appearance. As has been said above, the classical nature of the apparatus means that, at any instant, the quantity g (the “reading of the apparatus“) has some definite value. This enables us to say that the state of the system apparatus + electron after the measurement will in actual fact be described, not by the entire sum (7.2), but by only the one term which corresponds to the “reading” gn of the apparatus,
It follows from this that An(q) is proportional to the wave function of the electron after the measurement. It is not the wave function itself, as is seen from the fact that the function An(q) is not normalized. It contains both information concerning the properties of the resulting state of the electron and the probability (determined by the initial state of the system) of the occurrence of the nth “reading” of the apparatus.
Since the equations of quantum mechanics are linear, the relation between An(q) and the initial wave function of the electron Ψ(q) is in general given by some linear integral operator:
with a kernel Kn{q, q′) which characterizes the measurement process concerned.
We shall suppose that the measurement concerned is such that it gives a complete description of the state of the electron. In other words (see §1), in the resulting state the probabilities of all the quantities must be independent of the previous state of the electron (before the measurement). Mathematically, this means that the form of the functions An(q) must be determined by the measuring process itself, and does not depend on the initial wave function Ψ(q) of the electron. Thus the An must have the form
where the φn are definite functions, which we suppose normalized, and only the constants an depend on Ψ(q). In the integral relation (7.4) this corresponds to a kernel Kn(q, q′) which is a product of a function of q and a function of q′:
then the linear relation between the constants an and the function Ψ(q) is
where the Ψn(q) are certain functions depending on the process of measurement.
The functions φn(q) are the normalized wave functions of the electron after measurement. Thus we see how the mathematical formalism of the theory reflects the possibility of finding by measurement a state of the electron described by a definite wave function.
If the measurement is made on an electron with a given wave function Ψ(q), the constants an have a simple physical meaning: in accordance with the usual rules, |an|2 is the probability that the measurement will give the nth result. The sum of the probabilities of all results is equal to unity:
In order that equations (7.7) and (7.8) should hold for an arbitrary normalized function Ψ(q), it is necessary (cf. §3) that an arbitrary function Ψ(q) can be expanded in terms of the functions Ψn(q). This means that the functions Ψn(q) form a complete set of normalized and orthogonal functions.
If the initial wave function of the electron coincides with one of the functions Ψn(q), then the corresponding constant an is evidently equal to unity, while all the others are zero. In other words, a measurement made on an electron in the state Ψn(q) gives with certainty the nth result.
All these properties of the functions Ψn(q) show that they are the eigenfunctions of some physical quantity (denoted by f) which characterizes the electron, and the measurement concerned can be spoken of as a measurement of this quantity.
It is very important to notice that the functions Ψn(q) do not, in general, coincide with the functions φn(q); the latter are in general not even mutually orthogonal, and do not form a set of eigenfunctions of any operator. This expresses the fact that the results of measurements in quantum mechanics cannot be reproduced. If the electron was in a state Ψn(q), then a measurement of the quantity f carried out on it leads with certainty to the value fn. After the measurement, however, the electron is in a state φn(q) different from its initial one, and in this state the quantity f does not in general take any definite value. Hence, on carrying out a second measurement on the electron immediately after the first, we should obtain for f a value which did not agree with that obtained from the first measurement.† To predict (in the sense of calculating probabilities) the result of the second measurement from the known result of the first, we must take from the first measurement the wave function φn(q) of the state in which it resulted, and from the second measurement the wave function Ψn(q) of the state whose probability is required. This means that from the equations of quantum mechanics we determine the wave function φn(q, t) which, at the instant when the first measurement is made, is equal to φn(q); the probability of the mth result of the second measurement, made at time t, is then given by the squared modulus of the integral ∫ φn(q, t)Ψm* (q) dq.
We see that the measuring process in quantum mechanics has a “two-faced” character: it plays different parts with respect to the past and future of the electron. With respect to the past, it “verifies” the probabilities of the various possible results predicted from the state brought about by the previous measurement. With respect to the future, it brings about a new state (see also §44). Thus the very nature of the process of measurement involves a far-reaching principle of irreversibility.
This irreversibility is of fundamental significance. We shall see later (at the end of §18) that the basic equations of quantum mechanics are in themselves symmetrical with respect to a change in the sign of the time; here quantum mechanics does not differ from classical mechanics. The irreversibility of the process of measurement, however, causes the two directions of time to be physically non-equivalent, i.e. creates a difference between the future and the past.
†The phenomenon of electron diffraction was in fact discovered after quantum mechanics was invented. In our discussion, however, we shall not adhere to the historical sequence of development of the theory, but shall endeavour to construct it in such a way that the connection between the basic principles of quantum mechanics and the experimentally observed phenomena is most clearly shown.
‡The beam is supposed so rarefied that the interaction of the particles in it plays no part.
†It is of interest to note that the complete mathematical formalism of quantum mechanics was constructed by W. Heisenberg and E. Schrödinger in 1925–6, before the discovery of the uncertainty principle, which revealed the physical content of this formalism.
‡In this and the following sections we shall, for brevity, speak of “an electron”, meaning in general any object of a quantum nature, i.e. a particle or system of particles obeying quantum mechanics and not classical mechanics.
We refer to quantities which characterize the motion of the electron, and not to those, such as the charge and the mass, which relate to it as a particle; these are parameters.
†Once again we emphasize that, in speaking of “performing a measurement”, we refer to the interaction of an electron with a classical “apparatus”, which in no way presupposes the presence of an external observer.
†It was first introduced into quantum mechanics by Schrödinger in 1926.
‡It is obtained from (2.1) when φ(q, q′) = δ(q − q0) δ(q′ − q0), where δ denotes the delta function, defined in §5 below; q0 denotes the value of the coordinates whose probability is required.
†This, of course, means that the state of the whole system is completely described also. However, we emphasize that the converse statement is by no means true: a complete description of the state of the whole system does not in general completely determine the states of its individual parts (see also §14).
†By convention, we shall always denote operators by letters with circumflexes.
‡An operator is said to be linear if it has the properties
where Ψ1 and Ψ2, are arbitrary functions and a is an arbitrary constant.
†By definition, if for the operator f we have fΨ = φ, then the complex conjugate operator f* is that for which we have f* Ψ* = φ*.
‡For a linear integral operator of the form (3.10), the Hermitian condition means that the kernel of the operator must be such that K (q, q′) = K*(q′, q).
†In general, if φ(x) is some one-valued function (the inverse function need not be one-valued), we have
where ai are the roots of the equation φ(x) = 0.
†In future we shall always, for simplicity, write operators which amount to multiplication by some quantity in the form of that quantity itself.
‡The expansion coefficients for an arbitrary function Ψ in terms of these eigenfunctions are
The probability that the value of the coordinate lies in a given interval dq0 is
as it should be.
†It was introduced into physics by M. Planck in 1900. The constant ħ which we use everywhere in this book, is, strictly speaking, Planck’s constant divided by 2π; this is Dirac’s notation.
†There is, however, an important exception to the statement that results of measurements cannot be reproduced: the one quantity the result of whose measurement can be exactly reproduced is the coordinate. Two measurements of the coordinates of an electron, made at a sufficiently small interval of time, must give neighbouring values; if this were not so, it would mean that the electron had an infinite velocity. Mathematically, this is related to the fact that the coordinate commutes with the operator of the interaction energy between the electron and the apparatus, since this energy is (in non-relativistic theory) a function of the coordinates only.