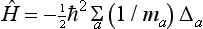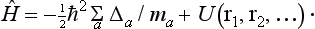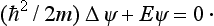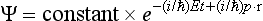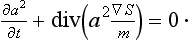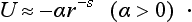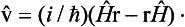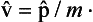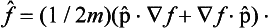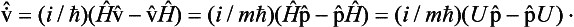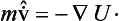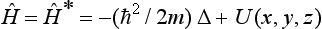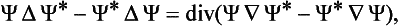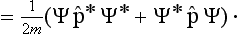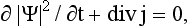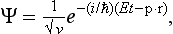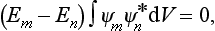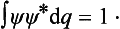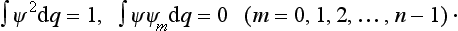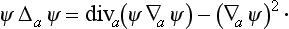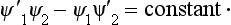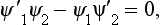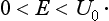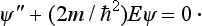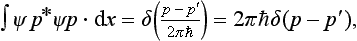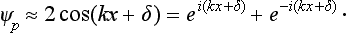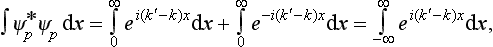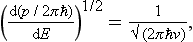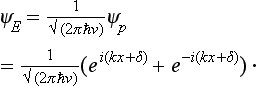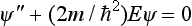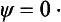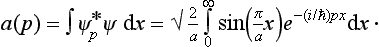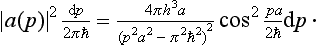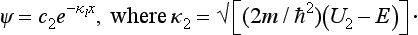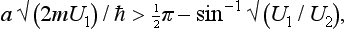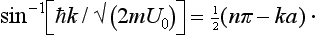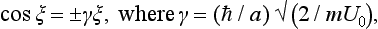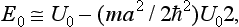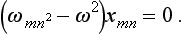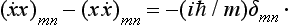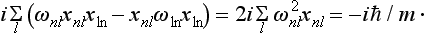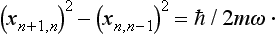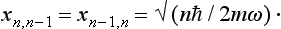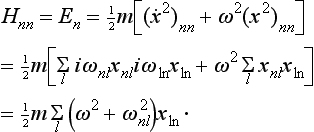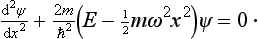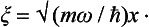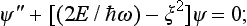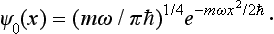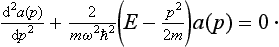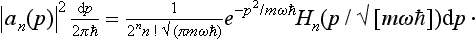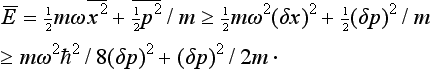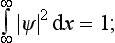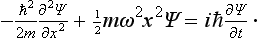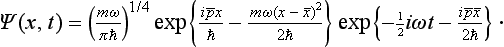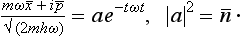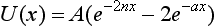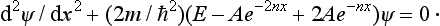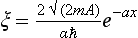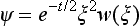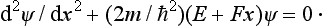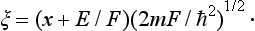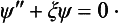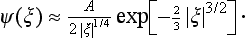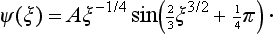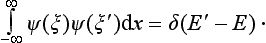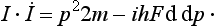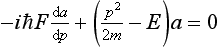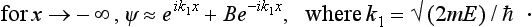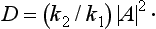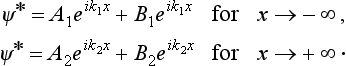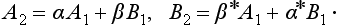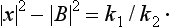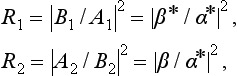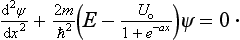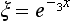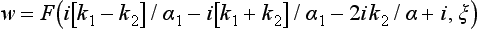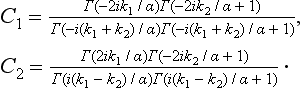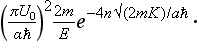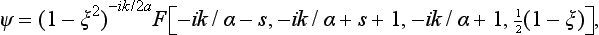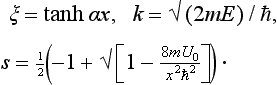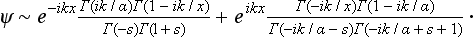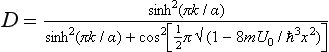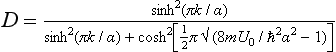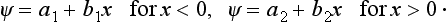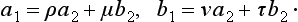SCHRODINGER’S EQUATION
§17 Schrödinger’s equation
The form of the Hamiltonian for a free particle is established by the general requirements imposed by the homogeneity and isotropy of space and by Galileo’s relativity principle. In classical mechanics, these requirements lead to a quadratic dependence of the energy of the particle on its momentum: E = p2/2m, where the constant m is called the mass of the particle (see Mechanics, §4). In quantum mechanics, the same requirements lead to a corresponding relation for the energy and momentum eigenvalues, these quantities being conserved and simultaneously measurable (for a free particle).
If the relation E = p2/2m holds for every eigenvalue of the energy and momentum, the same relation must hold for their operators also:
Substituting here from (15.2), we obtain the Hamiltonian of a freely moving particle in the form
where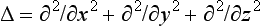 
is the Laplacian operator.
The Hamiltonian of a system of non-interacting particles is equal to the sum of the Hamiltonians of the separate particles:
(the suffix a is the number of the particle; Δa is the Laplacian operator in which the differentiation is with respect to the coordinates of the ath particle).
In classical (non-relativistic) mechanics, the interaction of particles is described by an additive term in the Hamiltonian, the potential energy of the interaction U (r1, r2, …), which is a function of the coordinates of the particles. By adding a similar function to the Hamiltonian of the system, the interaction of particles can be represented in quantum mechanics:†
The first term can be regarded as the operator of the kinetic energy and the second as that of the potential energy. In particular, the Hamiltonian for a single particle in an external field is
where U (x, y, z) is the potential energy of the particle in the external field.
Substituting the expressions (17.2) to 17.5) in the general equation (8.1), we obtain the wave equations for the corresponding systems. We shall write out here the wave equation for a particle in an external field:
The equation (10.2), which determines the stationary states, takes the form
The equations (17.6) and (17.7) were obtained by Schrödinger in 1926 and are called Schrödinger’s equations.
For a free particle, equation (17.7) has the form
This equation has solutions finite in all space for any positive value of the energy E. For states with definite directions of motion, these solutions are eigenfunctions of the momentum operator, with E = p2/2m. The complete (time-dependent) wave functions of such stationary states are
Each such function, a plane wave, describes a state in which the particle has a definite energy E and momentum p. The angular frequency of this wave is E/ħ and its wave vector k = p/ħ; the corresponding wavelength 2πħ/s is called the de Broglie wavelength of the particle.†
The energy spectrum of a freely moving particle is thus found to be continuous, extending from zero to +∞. Each of these eigenvalues (except E = 0) is degenerate, and the degeneracy is infinite. For there corresponds to every value of E, different from zero, an infinite number of eigenfunctions (17.9), differing in the direction of the vector p, which has a constant absolute magnitude.
Let us enquire how the passage to the limit of classical mechanics occurs in Schrödinger’s equation, considering for simplicity only a single particle in an external field. Substituting in Schrödinger’s equation (17.6) the limiting expression (6.1) for the wave function,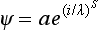 
, we obtain, on performing the differentiation,
In this equation there are purely real and purely imaginary terms (we recall that S and a are real); equating each separately to zero, we obtain two equations
Neglecting the term containing 
in the first of these equations, we obtain
that is; the classical Hamilton—Jacobi equation for the action S of a particle, as it should be. We see, incidentally, that, as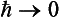 
, classical mechanics is valid as far as quantities of the first (and not only the zero) order in ħ inclusive.
The second equation obtained above, on multiplication by 2a, can be rewritten in the form
This equation has an obvious physical meaning: a2 is the probability density for finding the particle at some point in space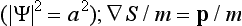 
is the classical velocity v of the particle. Hence equation (17.11) is simply the equation of continuity, which shows that the probability density “moves” according to the laws of classical mechanics with the classical velocity v at every point.
PROBLEM
Find the transformation law for the wave function in a Galilean transformation.
SOLUTION.
Let us apply the transformation to the wave function for free motion of a particle (a plane wave). Since any function ψ can be expanded in plane waves, this will also give the transformation law for any wave function.
The plane waves in the frames of reference K and K′ (K′ moving with velocity V relative to K) are
where r = r′ + Vt; the particle momenta and energies in the two frames are related by
(see Mechanics, §8). Substitution of these expressions in ψ gives
This formula does not contain the parameters of the free motion of the particle, and gives the required general transformation law for the wave function of any state of the particle. For a system of particles, the exponent in (1) contains a summation over the particles.
§18 The fundamental properties of Schrödinger’s equation
The conditions which must be satisfied by solutions of Schrödinger’s equation are very general in character. First of all. the wave function must be single-valued and continuous in all space. The requirement of continuity is maintained even in cases where the field U (x, y, z) itself has a surface of discontinuity. At such a surface both the wave function and its derivatives must remain continuous. The continuity of the derivatives, however, does not hold if there is some surface beyond which the potential energy U becomes infinite. A particle cannot penetrate at all into a region of space where 
, i.e. we must have ψ = 0 everywhere in this region. The continuity of ψ means that ψ vanishes at the boundary of this region; the derivatives of ψ, however, in general are discontinuous in this case.
If the field U (x, y, z) nowhere becomes infinite, then the wave function also must be finite in all space. The same condition must hold in cases where U becomes infinite at some point but does so only as 1/rs with s < 2 (see also §35).
Let Umin be the least value of the function U (x, y, z). Since the Hamiltonian of a particle is the sum of two terms, the operators of the kinetic energy (
) and of the potential energy, the mean value ê of the energy in any state is equal to the sum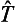 
+ 
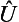. But all the eigenvalues of the operator 
(which is the Hamiltonian of a free particle) are positive; hence the mean value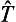 
≥ 0. Recalling also the obvious inequality 
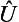> Umin, we find that Ē > Umin. Since this inequality holds for any state, it is clear that it is valid for all the eigenvalues of the energy:
Let us consider a particle moving in an external field which vanishes at infinity; we define the function U (x, y, z), in the usual way, so that it vanishes at infinity. It is easy to see that the spectrum of negative eigenvalues of the energy will then be discrete, i.e. all states with E < 0 in a field which vanishes at infinity are bound states. For, in the stationary states of a continuous spectrum, which correspond to infinite motion, the particle reaches infinity (see §10); however, at sufficiently large distances the field may be neglected, the motion of the particle may be regarded as free, and the energy of a freely moving particle can only be positive.
The positive eigenvalues, on the other hand, form a continuous spectrum and correspond to an infinite motion; for E > 0, Schrödinger’s equation in general has no solutions (in the field concerned) for which the integral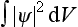 
converges.†
Attention must be drawn to the fact that, in quantum mechanics, a particle in a finite motion may be found in those regions of space where E < U; the probability |ψ|2 of finding the particle tends rapidly to zero as the distance into such a region increases, yet it differs from zero at all finite distances. Here there is a fundamental difference from classical mechanics, in which a particle cannot penetrate into a region where U > E. In classical mechanics the impossibility of penetrating into this region is related to the fact that, for E < U, the kinetic energy would be negative, that is, the velocity would be imaginary. In quantum mechanics, the eigenvalues of the kinetic energy are likewise positive; nevertheless, we do not reach a contradiction here, since, if by a process of measurement a particle is localized at some definite point of space, the state of the particle is changed, as a result of this process, in such a way that it ceases in general to have any definite kinetic energy.
If U (x, y, z) < 0 in all space (and U → 0 at infinity), then, by the inequality (18.1), we have En > 0. Since, on the other hand, for E > 0 the spectrum must be continuous, we conclude that, in this case, the discrete spectrum is absent altogether, i.e. only an infinite motion of the particle is possible.
Let us suppose that, at some point (which we take as origin), U tends to −∞ in the manner
We consider a wave function finite in some small region (of radius r0) about the origin, and equal to zero outside this region. The uncertainty in the values of the coordinates of a particle in such a wave packet is of the order of r0; hence the uncertainty in the value of the momentum is 
ħ/r0. The mean value of the kinetic energy in this state is of the order of ħ2/mr02, and the mean value of the potential energy is 
. Let us first suppose that s < 2. Then the sum
takes arbitrarily larpe negative values for sufficiently small r0. If, however, the mean energy can take such values, this always means that the energy has negative eigenvalues which are arbitrarily large in absolute value. The motion of the particle in a very small region of space near the origin corresponds to the energy levels with large |E|. The “normal” state corresponds to a particle at the origin itself, i.e. the particle “falls” to the point r = 0.
If, however, s < 2, the energy cannot take arbitrarily large negative values. The discrete spectrum begins at some finite negative value. In this case the particle does not fall to the centre. It should be mentioned that, in classical mechanics, the fall of a particle to the centre would be possible in principle in any attractive field (i.e. for any positive s). The case s = 2 will be specially considered in § 35.
Next, let us investigate how the nature of the energy spectrum depends on the behaviour of the field at large distances. We suppose that, as r → ∞, the potential energy, which is negative, tends to zero according to the power law (18.2) (r is now large in this formula), and consider a wave packet “filling” a spherical shell of large radius r0 and thickness 
. Then the order of magnitude of the kinetic energy is again 
, and of the potential energy, 
. We increase r0, at the same time increasing δr, in such a way that δr increases proportionally to r0. If s < 2, then the sum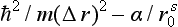 
becomes negative for sufficiently large r0. Hence it follows that there are stationary states of negative energy, in which the particle may be found, with a fair probability, at large distances from the origin. This, however, means that there are levels of arbitrarily small negative energy (it must be recalled that the wave functions rapidly tend to zero in the region of space where U > E). Thus, in this case, the discrete spectrum contains an infinite number of levels, which become denser and denser towards the level E = 0.
If the field diminishes as −1/rs at infinity, with s > 2, then there are not levels of arbitrarily small negative energy. The discrete spectrum terminates at a level with a non-zero absolute value, so that the total number of levels is finite.
Schrödinger’s equation for the wave functions ψ of stationary states is real, as are the conditions imposed on its solution. Hence its solutions can always be taken as real.† The eigenfunctions of non-degenerate values of the energy are automatically real, apart from the unimportant phase factor. For ψ* satisfies the same equation as ψ, and therefore must also be an eigenfunction for the same value of the energy; hence, if this value is not degenerate, ψ and ψ* must be essentially the same, i.e. they can differ only by a constant factor (of modulus unity). The wave functions corresponding to the same degenerate energy level need not be real, however, but by a suitable choice of linear combinations of them we can always obtain a set of real functions.
The complete (time-dependent) wave functions ψ are determined by an equation in whose coefficients i appears. This equation, however, retains the same form if we replace t in it by −t and at the same time take the complex conjugate.‡ Hence we can always choose the functions ψ in such a way that ψ and ψ* differ only by the sign of the time.
As is well known, the equations of classical mechanics are unchanged by time reversal, i.e. when the sign of the time is reversed. In quantum mechanics, the symmetry with respect to the two directions of time is expressed, as we see, in the invariance of the wave equation when the sign of t is changed and ψ is simultaneously replaced by ψ*. However, it must be recalled that this symmetry here relates only to the equation, and not to the concept of measurement itself, which plays a fundamental part in quantum mechanics (as we have explained in detail in §7).
§19 The current density
In classical mechanics the velocity v of a particle is related to its momentum by p = mv. A similar relation holds between the corresponding operators in quantum mechanics, as we should expect. This is easily shown by calculating the operator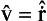 
by the general rule (9.2) for the differentiation of operators with respect to time:
Using the expression (17.5) for Ĥ and formula (16.5), we obtain
Similar relations will clearly hold between the eigenvalues of the velocity and momentum, and between their mean values in any state.
The velocity, like the momentum of a particle, cannot have a definite value simultaneously with the coordinates. But the velocity multiplied by an infinitely short time interval dt gives the displacement of the particle in the time dt. Hence the fact that the velocity cannot exist at the same time as the coordinates means that, if the particle is at a definite point in space at some instant, it has no definite position at an infinitely close subsequent instant.
We may notice a useful formula for the operator 
of the derivative, with respect to time, of some quantity f (r) which is a function of the radius vector of the particle. Bearing in mind that f commutes with U (r), we find
Using (16.4), we can write
Thus we obtain the required expression:
Next, let us find the acceleration operator. We have
Using formula (16.4), we find
This operator equation is exactly the same in form as the equation of motion (Newton’s equation) in classical mechanics.
The integral ∫|ψ|2 dV, taken over some finite volume V, is the probability of finding the particle in this volume. Let us calculate the derivative of this probability with respect to time. We have
Substituting here
and using the identity
where j denotes the vector†
The integral of div j can be transformed by Gauss’s theorem into an integral over the closed surface which bounds the volume V:
It is seen from this that the vector j may be called the probability current density vector, or simply the current density. The integral of this vector over a surface is the probability that the particle will cross the surface during unit time. The vector j and the probability density |ψ|2 satisfy the equation
which is analogous to the classical equation of continuity.
The wave function of free motion (the plane wave (17.9)) can be normalized so as to describe a flow of particles with unit current density (in which, on average, one particle crosses a unit cross-section of the flow per unit time). This function is then
where v is the velocity of the particle, since substitution of this in (19.4) gives j = p/mv, i.e. a unit vector in the direction of the motion.
It is useful to show how the orthogonality of the wave functions of states with different energies follows immediately from Schrödinger’s equation. Let ψm and ψn be two such functions; they satisfy the equations
We multiply the first of these by ψn* and the second by ψm and subtract corresponding terms; this gives
If we now integrate both sides of this equation over all space, the right-hand side, on transformation by Gauss’s theorem, reduces to zero, and we obtain
whence, by the hypothesis Em ≠ En, there follows the required orthogonality relation
§20 The variational principle
Schrödinger’s equation, in the general form Ĥψ = Eψ, can be obtained from, the variational principle
Since ψ is complex, we can vary ψ and ψ* independently. Varying ψ*, we have
whence, because δψ* is arbitrary, we obtain the required equation Ĥψ = Eψ. The variation of ψ gives nothing different. For, varying ψ and using the fact that the operator Ĥ is Hermitian, we have
from which we obtain the complex conjugate equation Ĥ*ψ* = Eψ*.
The variational principle (20.1) requires an unconditional extremum of the integral. It can be stated in a different form by regarding E as a Lagrangian multiplier in a problem with the conditional extremum requirement
the condition being
The least value of the integral in (20.2) (with the condition (20.3)) is the first eigenvalue of the energy, i.e. the energy E0 of the normal state. The function ψ which gives this minimum is accordingly the wave function ψ0 of the normal state.† The wave functions ψn (n > 0) of the other stationary states correspond only to an extremum, and not to a true minimum of the integral.
In order to obtain, from the condition that the integral in (20.2) is a minimum, the wave function ψ1 and the energy E1 of the state next to the normal one, we must restrict our choice to those functions ψ which satisfy not only the normalization condition (20.3) but also the condition of orthogonality with the wave function ψ0 of the normal state: ∫ψψ0 dq = 0. In general, if the wave functions ψ0, ψ1, …, ψn−1 of the first n states (arranged in order of increasing energy) are known, the wave function of the next state gives a minimum of the integral in (20.2) with the additional conditions
We shall give here some general theorems which can be proved from the variational principle.†
The wave function ψ0 of the normal state does not become zero (or, as we say, has no nodes) for any finite values of the coordinates.‡ In other words, it has the same sign in all space. Hence, it follows that the wave functions ψn (n > 0) of the other stationary states, being orthogonal to ψ0, must have nodes (if ψn is also of constant sign, the integral ∫ψ0ψn dq cannot vanish).
Next, from the fact that ψ0 has no nodes, it follows that the normal energy level cannot be degenerate. For, suppose the contrary to be true, and let ψ0, ψ0 be two different eigenfunctions corresponding to the level E0. Any linear combination cψ0+c′ψ0′ will also be an eigenfunction; but by choosing the appropriate constants c, c′, we can always make this function vanish at any given point in space, i.e. we can obtain an eigenfunction with nodes.
If the motion takes place in a bounded region of space, we must have ψ = 0 at the boundary of this region (see §18). To determine the energy levels, it is necessary to find, from the variational principle, the minimum value of the integral in (20.2) with this boundary condition. The theorem that the wave function of the normal state has no nodes means in this case that ψ0 does not vanish anywhere inside this region.
We notice that, as the dimensions of the region containing the motion increase, all the energy levels En decrease; this follows immediately from the fact that an extension of the region increases the range of functions which can make the integral a minimum, and consequently the least value of the integral can only diminish.
for the states of the discrete spectrum of a particle system may be transformed into another expression which is more convenient in practice. In the first term of the integrand we write
The integral of diva (ψ
aψ) over all space is transformed into an integral over an infinitely distant closed surface, and since the wave functions of the states of a discrete spectrum tend to zero sufficiently rapidly at infinity, this integral vanishes. Thus
§21 General properties of motion in one dimension
If the potential energy of a particle depends on only one coordinate (x), then the wave function can be sought as the product of a function of y and z and a function of x only. The former of these is determined by Schrödinger’s equation for free motion, and the second by the one-dimensional Schrödinger’s equation
Similar one-dimensional equations are evidently obtained for the problem of motion in a field whose potential energy is U (x, y, z) = U1(x) + U2(y) + U3(z), i.e. can be written as a sum of functions each of which depends on only one of the coordinates. In §§22–24 we shall discuss a number of actual examples of such “one-dimensional” motion. Here we shall obtain some general properties of the motion.
We shall show first of all that, in a one-dimensional problem, none of the energy levels of a discrete spectrum is degenerate. To prove this, suppose the contrary to be true, and let ψ1 and ψ2 be two different eigenfunctions corresponding to the same value of the energy. Since both of these satisfy the same equation (21.1), we have
or ψ1″ψ2−ψ1ψ2″ = 0 (the prime denotes differentiation with respect to x). Integrating this relation, we find
Since ψ1 = ψ2 = 0 at infinity, the constant must be zero, and so
or ψ1′/ψ1 = ψ2′/ψ2. Integrating again, we obtain ψ1 = constant ×ψ2, i.e. the two functions are essentially identical.
The following theorem (called the oscillation theorem) may be stated for the wave functions ψn(x) of a discrete spectrum. The function ψn(x) corresponding to the (n + 1)th eigenvalue En (the eigenvalues being arranged in order of magnitude), vanishes n times (for finite† values of x).
We shall suppose that the function U (x) tends to finite limiting values as x → ± ∞ (though it need not be a monotonic function). We take the limiting value U (+∞) as the zero of energy (i.e. we put U (+∞) = 0), and we denote U (−∞) by U0, supposing that U0 > 0. The discrete spectrum lies in the range of energy values for which the particle cannot move off to infinity; for this to be so, the energy must be less than both limiting values U (±∞), i.e. it must be negative:
and we must, of course, have in any case E > Umin, i.e. the function U (x) must have at least one minimum with Umin < 0.
Let us now consider the range of positive energy values less than U0:
In this range the spectrum will be continuous, and the motion of the particle in the corresponding stationary states will be infinite, the particle moving off towards x = +∞. It is easy to see that none of the eigenvalues of the energy in this part of the spectrum is degenerate either. To show this, it is sufficient to notice that the proof given above (for the discrete spectrum) still holds if the functions ψ1, ψ2 are zero at only one infinity (in the present case they tend to zero as x → −∞).
For sufficiently large positive values of x, we can neglect U (x) in Schrödinger’s equation (21.1):
This equation has real solutions in the form of a stationary plane wave
where a and δ are constants, and the wave number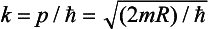
. This formula determines the asymptotic form (for x → +∞) of the wave functions of the non-degenerate energy levels in the range (21.4) of the continuous spectrum. For large negative values of x, Schrödinger’s equation is
The solution which does not become infinite as x → −∞ is
This is the asymptotic form of the wave function as x → −∞. Thus the wave function decreases exponentially in the region where E < U.
the spectrum will be continuous, and the motion will be infinite in both directions. In this part of the spectrum all the levels are doubly degenerate. This follows from the fact that the corresponding wave functions are determined by the second-order equation (21.1), and both of the two independent solutions of this equation satisfy the necessary conditions at infinity (whereas, for instance, in the previous case one of the solutions became infinite as x → −∞, and therefore had to be rejected). The asymptotic form of the wave function as x → +∞ is
and similarly for x → −∞. The term eikx corresponds to a particle moving to the right, and e−ikx corresponds to one moving to the left.
Let us suppose that the function U (x) is even [U (−x) = U (x)]. Then Schrödinger’s equation (21.1) is unchanged when the sign of the coordinate is reversed. It follows that, if ψ(x) is some solution of this equation, then ψ(−x) is also a solution, and coincides with ψ(x) apart from a constant factor: ψ(−x) = cψ(x). Changing the sign of x again, we obtain ψ(x) = c2ψ(x), whence c = ±1. Thus, for a potential energy which is symmetrical (relative to x = 0), the wave functions of the stationary states must be either even [ψ(−x) = ψ(x)] or odd [ψ −(x) = −ψ(x)].† In particular, the wave function of the ground state is even, since it cannot have a node, while an odd function always vanishes for x = 0 [ψ(0) = −ψ(0) = 0].
To normalize the wave functions of one-dimensional motion (in a continuous spectrum), there is a simple method of determining the normalization coefficient directly from the asymptotic expression for the wave function for large values of |x|.
Let us consider the wave function of a motion infinite in one direction, x → + ∞. The normalization integral diverges as x → ∞ (as x → − ∞, the function decreases exponentially, so that the integral rapidly converges). Hence, to determine the normalization constant, we can replace ψ by its asymptotic value (for large positive x), and perform the integration, taking as the lower limit any finite value of x, say zero; this amounts to neglecting a finite quantity in comparison with an infinite one. We shall show that the wave function normalized by the condition
where p is the momentum of the particle at infinity, must have the asymptotic form (21.5) with a = 2:
Since we do not intend to verify the orthogonality of the functions corresponding to different p, on substituting the functions (21.10) in the normalization integral we shall suppose the momenta p and p′ to be arbitrarily close; we can therefore put δ = δ′ (in general δ is a function of p). Next, we retain in the integrand only those terms which diverge for p = p′; in other words, we omit terms containing the factor e±i (k+k)′x. Thus we obtain
which, from (15.7), is the same as (21.9).
The change to normalization by the delta function of energy is effected, in accordance with (5.14), by multiplying ψp by
where v is the velocity of the particle at infinity. Thus
The current density is ½πħ in each of the travelling waves that make up the stationary wave (21.11). Thus we can formulate the following rule for the normalization of the wave function for a motion infinite in one direction by the delta function of energy: having represented the asymptotic expression for the wave function in the form of a sum of two plane waves travelling in opposite directions, we must choose the normalization coefficient in such a way that the current density in the wave travelling towards (or away from) the origin is ½πħ.
Similarly, we can obtain an analogous rule for normalizing the wave functions of a motion infinite in both directions. The wave function will be normalized by the delta function of energy if the sum of the probability currents in the waves travelling towards the origin from x = +∞ and x = −∞ is ½πħ.
§22 The potential well
As a simple example of one-dimensional motion, let us consider motion in a square potential well, i.e. in a field where U (x) has the form shown in Fig. 1 (p. 64): U (x) = 0 for 0 < x < a, U (x) = U0 for x < 0 and x > a. It is evident a priori that for E < U0 the spectrum will be discrete, while for E > U0 we have a continuous spectrum of doubly degenerate levels.
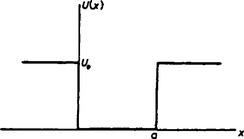
FIG. 1
In the region 0 < x < a we have Schrödinger’s equation
(the prime denotes differentiation with respect to x), while in the region outside the well
For x = 0 and x = a the solutions of these equations must be continuous together with their derivatives, while for x = ±∞ the solution of equation (22.2) must remain finite (for the discrete spectrum when E < U0, it must vanish).
For E < U0, the solution of equation (22.2) which vanishes at infinity is
the signs − and + in the exponent refer to the regions x > a and x < 0 respectively. The probability |ψ|2 of finding the particle decreases exponentially in the region where E < U (x). Instead of the continuity of ψ and ψ′ at the edge of the potential well, it is convenient to require the continuity of ψ and of its logarithmic derivative ψ′ψ. Taking account of (22.3), we obtain the boundary condition in the form
We shall not pause here to determine the energy levels in a well of arbitrary depth U0 (see Problem 2), and shall analyse fully only the limiting case of infinitely high walls (U0 → ∞).
For U0 = ∞, the motion takes place only between the points x = 0 and x = a and, as was pointed out in §18, the boundary condition at these points is
(It is easy to see that this condition is also obtained from the general condition (22.4). For, when U0 → ∞, we have also κ → ∞ and hence ψ′ψ → ∞; since ψ′ cannot become infinite, it follows that ψ = 0.) We seek a solution of equation (22.1) inside the well in the form
The condition ψ = 0 for x = 0 gives δ = 0, and then the same condition for x = a gives sin ka = 0, whence ka = nπ, n being a positive integer,† or
This determines the energy levels of a particle in a potential well. The normalized wave functions of the stationary states are
From these results we can immediately write down the energy levels for a particle in a rectangular “potential box”, i.e. for three-dimensional motion in a field whose potential energy U = 0 for 0 < x < a, 0 < y < b, 0 < z < c and U = ∞ outside this region. In fact, these levels are given by the sums
and the corresponding wave functions by the products
It may be noted that the energy E0 of the ground state is, by (22.7) or (22.9), of the order of ħ2/ml2, where l is the linear dimension of the region in which the particle moves. This result is in accordance with the uncertainty relation; when the uncertainty in the coordinate is l, the uncertainty in the momentum, and therefore the order of magnitude of the momentum itself, is ħ/l. The corresponding energy is (ħ/l)2/m.
PROBLEMS
Determine the probability distribution for various values of the momentum for the normal state of a particle in an infinitely deep square potential well.
SOLUTION.
The coefficients a (p) in the expansion of the function ψ1 (22.8) in terms of the eigenfunctions of the momentum are
Calculating the integral and squaring its modulus, we obtain the required probability distribution:
SOLUTION.
The spectrum of energy values E < U1, which we shall consider, is discrete. In the region x < 0 the wave function is
Inside the well (0 < x < a) we look for ψ in the form
The condition of the continuity of ψ′/ψ at the edges of the well gives the equations
or
Eliminating δ, we obtain the transcendental equation
(where n = 1, 2, 3, …, and the values of the inverse sine are taken between 0 and ½ π), whose roots determine the energy levels E = k2ħ2/2m. For each n there is in general one root; the values of n number the levels in order of increasing energy.
Since the argument of the inverse sine cannot exceed unity, it is clear that the values of k can lie only in the range from 0 to √2m U1/ħ2). The left-hand side of equation (1) increases monotonically with k, and the right-hand side decreases monotonically. Hence it is necessary, for a root of equation (1) to exist, that for 
the right-hand side should be less than the left-hand side. In particular, the inequality
which is obtained for n = 1, is the condition that at least one energy level exists in the well. We tee that for given and unequal U1 U2, there are always widths a of the well which are so small that there is no discrete energy level. For U1 = U2, the condition (2) is evidently always satisfied.
For U1 = U2 = Ua (a symmetrical well), equation (1) reduces to
Introducing the variable ξ = ½ ka, we obtain for odd n the equation
and those roots of this equation must be taken for which tan ξ > 0. For even n we obtain the equation
and we must take those roots for which tan ξ < 0. The roots of these two equations determine the energy levels 
. The number of levels is finite when γ ≠ 0.
In particular, for a shallow well in which U0 
ħ2/ma2, we have γ 
1 and equation (5) has no root. Equation (4) has one root (with the upper sign on the right-hand side),
. Thus the well contains only one energy level,
which is near the top of the well.
PROBLEM 3.
Determine the pressure exerted on the walls of a rectangular “potential box” by a particle inside it.
SOLUTION.
The force on the the wall perpendicular to the x-axis is the mean value of the derivative −∂H/∂a of the Hamilton’s function of the particle with respect to the length of the box in the direction of the x-axis. The pressure is obtained by dividing this force by the area bc of the wall. According to the formula (11.16), the required mean value is found by differentiating the eigenvalue (22.9) of the energy. The result is
§23 The linear oscillator
Let us consider a particle executing small oscillations in one dimension (what is called a linear oscillator). The potential energy of such a particle is ½mω2x2, where ω is, in classical mechanics, the characteristic (angular) frequency of the oscillations. Accordingly, the Hamiltonian of the oscillator is
Since the potential energy becomes infinite for x = ± ∞, the particle can have only a finite motion, and the energy eigenvalue spectrum is entirely discrete.
Let us determine the energy levels of the oscillator, using the matrix method†. We shall start from the equations of motion in the form (19.3); in this case they give
In matrix form, this equation reads
For the matrix elements of the acceleration we have, according to (11.8), 
. Hence we obtain
Hence it is evident that all the matrix elements xmn vanish except those for which ωmn = ω or ωmn = −ω. We number all the stationary states so that the frequencies ± ω correspond to transitions 
, i.e.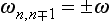 
. Then the only non-zero matrix elements are xn, n±1.
We shall suppose that the wave functions ψn are taken real. Since x is a real quantity, all the matrix elements xmn are real. The Hermitian condition (11.10) now shows that the matrix xmn is symmetrical:
To calculate the matrix elements of the coordinate which are different from zero, we use the commutation rule
written in the matrix form
By the matrix multiplication rule (11.12) we hence have for m = n
In this sum, only the terms with l = n ± 1 are different from zero, so that we have
From this equation we deduce that the quantities (xn+1,n)2 form an arithmetic progression, which is unbounded above, but is certainly bounded below, since it can contain only positive terms. Since we have as yet fixed only the relative positions of the numbers n of the states, but not their absolute values, we can arbitrarily choose the value of n corresponding to the first (normal) state of the oscillator, and put this value equal to zero. Accordingly x0,−1 must be regarded as being zero identically, and the application of equations (23.3) with n = 0, 1, … successively leads to the result
Thus we finally obtain the following expression for the matrix elements of the coordinate which are different from zero:†
The matrix of the operator Ĥ is diagonal, and the matrix elements Hnn are the required eigenvalues En of the energy of the oscillator. To calculate them, we write
In the sum over l, only the terms with l = n±1 are different from zero; substituting (23.4), we obtain
Thus the energy levels of the oscillator lie at equal intervals of ħω from one another. The energy of the normal state (n = 0) is ½ħω; we call attention to the fact that it is not zero.
The result (23.5) can also be obtained by solving Schrödinger’s equation. For an oscillator, this has the form
Here it is convenient to introduce, instead of the coordinate x, the dimensionless variable ξ by the relation
Then we have the equation
here the prime denotes differentiation with respect to ξ.
For large ξ, we can neglect 2E/ħω in comparison with ξ2; the equation ψ″ = ξ2ψ has the asymptotic integrals 
(for differentiation of this function gives ψ″ = ξ2ψ on neglecting terms of order less than that of the term retained). Since the wave function ψ must remain finite as ξ → ±∞, the index must be taken with the minus sign. It is therefore natural to make in equation (23.8) the substitution
For the function 
we obtain the equation (with the notation (2E/ħω) −1 = 2n; since we already know that E > 0, we have n > −½)
where the function 
must be finite for all finite ξ, and for ξ → ±∞ must not tend to infinity more rapidly than every finite power of ξ (in order that the function ψ should tend to zero).
Such solutions of equation (23.10) exist only for positive integral (and zero) values of n (see §a of the Mathematical Appendices); this gives the eigenvalues (23.5) for the energy, which we know already. The solutions of equation (23.10) corresponding to various integral values of n are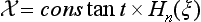 
, where Hn(ξ) are what are called Hermite polynomials; these are polynomials of the nth degree in ξ, defined by the formula
Determining the constants so that the functions ψn satisfy the normalization condition
we obtain (see (a.7))
Thus the wave function of the normal state is
It has no zeros for finite x, which is as it should be.
By calculating the integrals 
, we can determine the matrix elements of the coordinate; this calculation leads, of course, to the same values (23.4).
Finally, we shall show how the wave functions ψn may be calculated by the matrix method. We notice that, in the matrices of the operators 
, the only elements different from zero are
Using the general formula (11.11), and taking into account the fact that ψ−1 ≡ 0, we conclude that
After substituting the expression 
, we obtain the equation
whose normalized solution is (23.13). And, since
we obtain the recurrence formula
when this is applied n times to the function (23.13), we obtain the expression (23.12) for the normalized functions ψn.
PROBLEMS
SOLUTION.
Instead of expanding the wave function of the stationary state in terms of the eigenfunctions of momentum, it is simpler in the case of the oscillator to start directly from Schrödinger’s equation in the momentum representation. Substituting in (23.1) the coordinate operator 
(15.12), we obtain the Hamiltonian in the p representation,
The corresponding Schrödinger’s equation Ĥa (p) = Ea (p) for the wave function a (p) in the momentum representation is
This equation is of exactly the same form as (23.6); hence its solutions can be written down at once by analogy with (23.12). Thus we find the required probability distribution to be
PROBLEM 2.
Determine the lower limit of the possible values of the energy of an oscillator, using the uncertainty relation (16.7).
SOLUTION.
Since 
, (16.7) gives for the mean value of the energy of the oscillator
On determining the minimum value of this expression (regarded as a function of δp), we find the lower limit of the mean values of the energy, and therefore that of all possible values:
PROBLEM 3.
Find the wave functions of the states of a linear oscillator that minimize the uncertainty relation, i.e. in which the standard deviations of the coordinate and momentum in the wave packet are related by δp δx = ½ħ (E. Schrödinger 1926).†
SOLUTION.
The required wave functions must have the form
Their dependence on the coordinate at any instant is in accordance with (16.8),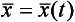 
and 
, and therefore for the mean values 
being the mean values of the coordinate and the momentum; according to (19.3), we have, for a linear oscillator (U = ½m ω2x2),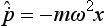
or
i.e. the function 
satisfies the classical equation of motion. The constant factor in (1) is determined by the normalization condition
in addition to this factor, ψ may contain a phase factor with a time-dependent phase φ(t). The unknown constant δx and the unknown function φ(t) are found by substituting (1) in the wave equation
With (2), the substitution gives
Hence (δx) 2 = ħ/2mω and
Thus we have finally
When 
and 
, this becomes ψ0(x)e−iωt/2, the wave function of the oscillator ground state.
The mean energy of the oscillator in a coherent state is
the quantity 
is the mean “number” of quanta ħω in the state. We see that the coherent state is completely specified by the function 
(t) satisfying the classical equation (2). The general form of this, function may be given as
The function (3) can be expanded in wave functions of the stationary states of the oscillator:
The coefficients in this expansion are (cf. §41, Problem 1)
The probability for the oscillator to be in the nth state is therefore
the Poisson distribution.
PROBLEM 4.
Determine the energy levels for a particle moving in a field of potential energy (Fig. 3)
(P. M. Morse).
FIG. 3
SOLUTION.
The spectrum of positive eigenvalues of the energy is continuous (and the levels are not degenerate), while the spectrum of negative eigenvalues is discrete.
We introduce a new variable
(taking values from 0 to ∞) and the notation (we consider the discrete spectrum, so that E < 0)
Schrödinger’s equation then takes the form
As ξ → ∞, the function ψ behaves asymptotically as e±iξ, while as ξ → 0 it is proportional to ξ±s. From considerations of finiteness we must choose the solution which behaves as e−iξ as ξ → ∞ and as ξs as ξ → 0. We make the substitution
and obtain for w the equation
which has to be solved with the conditions that w is finite as ξ → 0, while as ξ → ∞, w tends to infinity not more rapidly than every finite power of ξ. Equation (2) is the equation for a confluent hypergeometric function (see §d of the Mathematical Appendices):
A solution satisfying the required conditions is obtained for non-negative integral n (when the function F reduces to a polynomial). According to the definitions (1), we thus obtain for the energy levels the values
where n takes positive integral values from zero to the greatest value for which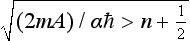 
(so that the parameter s is positive in accordance with its definition). Thus the discrete spectrum contains only a limited number of levels. If 
, there is no discrete spectrum at all.
SOLUTION.
The spectrum of positive eigenvalues of the energy is continuous, while that of negative values is discrete; we shall consider the latter. Schrödinger’s equation is
We put ξ = tanh ax and use the notation
obtaining
This is the equation of the associated Legendre polynomials; it can be brought to hypergeometric form by making the substitution ψ = (1 − ξ2)ε/2 w (ξ) and temporarily changing the variable to u = ½(1 − ξ):
The solution finite for ξ = 1 (i.e. for x = ∞) is
If ψ remains finite for ξ = −1 (i.e. for x = −∞), we must have ∈ − s = −n, where n = 0, 1, 2, …; then F is a polynomial of degree n, which is finite for ξ = −1. Thus the energy levels are determined by s − ∈ = n, or
There is a finite number of levels, determined by the condition ∈ > 0, i.e. n < s.
§24 Motion in a homogeneous field
Let us consider the motion of a particle in a homogeneous external field. We take the direction of the field as the axis of x; let F be the force acting on the particle in this field. In an electric field of intensity E, this force is F = eE, where e is the charge on the particle.
The potential energy of the particle in the homogeneous field is of the form U = −Fx+constant; choosing the constant so that U = 0 for x = 0, we have U = −Fx. Schrödinger’s equation for this problem is
Since U tends to + ∞ as x − ∞, and vice versa, it is clear that the energy levels form a continuous spectrum occupying the whole range of energy values E from −∞ to +∞. None of these eigenvalues is degenerate, and they correspond to motion which is finite towards x = −∞ and infinite towards X = +∞.
Instead of the coordinate x, we introduce the dimensionless variable
Equation (24.1) then takes the form
This equation does not contain the energy parameter. Hence, if we obtain a solution of it which satisfies the necessary conditions of finiteness, we at once have the eigenfunction for arbitrary values of the energy.
The solution of equation (24.3) which is finite for all x has the form (see §b of the Mathematical Appendices)
where
is called the Airy function, while A is a normalization factor which we shall determine below.
As ξ → −∞, the function ψ(ξ) tends exponentially to zero. The asymptotic expression which determines ψ(ξ) for large negative values of ξ is (see (b.4))
For large positive values of ξ, the asymptotic expression for ψ(ξ) is (see (b.5))†
Using the general rule (5.4) for the normalization of eigenfunctions of a continuous spectrum, let us reduce the function (24.4) to the form normalized by the delta function of energy, for which
In §21 we gave a simple method of determining the normalization coefficient by means of the asymptotic expression for the wave functions. Following this method, we represent the function (24.6) as the sum of two travelling waves:
The current density, calculated from each of these two terms, is
and equating this to ½πħ we find
§25 The transmission coefficient
Let us consider the motion of particles in a field of the type shown in Fig. 5: U (x) increases monotonically from one constant limit (U = 0 as x → −∞) to another (U = U0 as x +∞). According to classical mechanics, a particle of energy E < U0 moving in such a field from left to right, on reaching such a “potential wall”, is reflected from it, and begins to move in the opposite direction; if. however, E > U0, the particle continues to move in its original direction, though with diminished velocity. In quantum mechanics, a new phenomenon appears: even for E > U0, the particle may be reflected from the potential wall. The probability of reflection must in principle be calculated as follows.
FIG. 5
Let the particle be moving from left to right. For large positive values of x, the wave function must describe a particle which has passed “above the wall” and is moving in the positive direction of x, i.e. it must have the asymptotic form
and A is a constant. To find the solution of Schrödinger’s equation which satisfies this boundary condition, we calculate the asymptotic expression for x → −∞; it is a linear combination of the two solutions of the equation of free motion, i.e. it has the form
The first term corresponds to a particle incident on the wall (we suppose ψ normalized so that the coefficient of this term is unity); the second term represents a particle reflected from the wail. The probability current density in the incident wave is k1, in the reflected wave k1|B|2, and in the transmitted wave k2|A|2. We define the transmission coefficient D of the particle as the ratio of the probability current density in the transmitted wave to that in the incident wave:
Similarly we can define the reflection coefficient R as the ratio of the density in the reflected wave to that in the incident wave. Evidently R = 1 − D:
(this relation between A and B is automatically satisfied).
If the particle moves from left to right with energy E < U0, then k2 is purely imaginary, and the wave function decreases exponentially as x → +∞. The reflected current is equal to the incident one, i.e. we have “total reflection” of the particle from the potential wall. We emphasize, however, that in this case the probability of finding the particle in the region where E < U is still different from zero, though it diminishes rapidly as x increases.
In the general case of an arbitrary stationary state (with energy E > U0), the asymptotic form of the wave function is given, both for x → −∞ and for x → +∞, by a sum of waves propagated in each direction:
Since these expressions are asymptotic forms of the same solution of a linear differential equation, there must be a linear relation between the coefficients A1, B1 and A2, B2. Let A2 = αA1 + βB1, where α, β are constants (in general complex) which depend on the specific form of the field U (x). The corresponding relation for B2 can then be written down from the fact that Schrödinger’s equation is real. This shows that, if ψ is a solution of a given Schrödinger’s equation, the complex conjugate function ψ* is also a solution. The asymptotic forms
differ from (25.5) only in the nomenclature of the constant coefficients; we therefore have B2* = αB1* + βA1* or B2 = α*B1 + β*A1. Thus the coefficients in (25.5) are related by equations of the form
The condition of constant current along the x-axis leads to the relation
Expressing A2, B2 in terms of A1, B1 by (25.6), we find
Using the relation (25.6), we can show, in particular, that the reflection coefficients are equal (for a given energy E > U0) for particles moving in the positive and negative directions of the x-axis; the former case corresponds to putting B2 = 0 in (25.5), and the latter case to A1 = 0. In these two cases, B1/A1 = −β*/α* and A2/B2 = β/α* respectively. The corresponding reflection coefficients are
whence it is clear that R1 = R2.
It is natural to call B1/A1 = −β*/α* and A2/B2 = β/α* the reflection amplitudes for motion in the positive and negative directions respectively. They are equal in modulus but may have different phase factors.
PROBLEMS
Determine the reflection coefficient of a particle from a rectangular potential wall (Fig. 6); the energy of the particle E > U0.
FIG. 6
SOLUTION.
Throughout the region x > 0, the wave function has the form (25.1), while in the region x < 0 its form is (25.2). The constants A and B are determined from the condition that ψ and dψ/dx are continuous at x = 0:
whence
The reflection coefficient† is (25.4)
For E = U0 (k2 = 0), R becomes unity, while for E → ∞ it tends to zero as (U0/4E)2.
PROBLEM 2.
Determine the transmission coefficient for a rectangular potential barrier (Fig. 7).
FIG. 7
SOLUTION.
Let E be greater than U0, and suppose that the incident particle is moving from left to right. Then we have for the wave function in the different regions expressions of the form
(on the side x > a there can be only the transmitted wave, propagated in the positive direction of x). The constants A, B, B′ and C are determined from the conditions of continuity of ψ and dψ/dx at the points x = 0 and a. The transmission coefficient is determined as D = k1|C|2/k1 = |C|2. On calculating this, we obtain
For E < U0, k2 is a purely imaginary quantity; the corresponding expression for D is obtained by replacing k2 by iκ2 where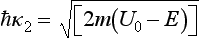 
:
PROBLEM 3.
Determine the reflection coefficient for a potential wall defined by the formula U (x) = U0/(1 +e−ax) (Fig. 5); the energy of the particle is E > U0.
SOLUTION.
We have to find a solution which, as x → + ∞, has the form
We introduce a new variable
(which takes values from − ∞ to 0), and seek a solution of the form
where w (ξ) tends to a constant as ξ → 0 (i.e. as x → ∞). For w (ξ) we find an equation of hypergeometric type:
which has as its solution the hypergeometric function
(we omit a constant factor). As ξ → 0, this function tends to 1, i.e. it satisfies the condition imposed.
The asymptotic form of the function ψ as ξ → −∞ (i.e. x → −∞) is †
where
The required reflection coefficient is R = |C2/C1|2 on calculating it by means of the well known formula
we have
For E = U0 (k2 = 0), R becomes unity, while for ER→ it tends to zero as
In the limiting case of classical mechanics. R becomes zero, as it should.
PROBLEM 4.
Determine the transmission coefficient for a potential barrier defined by the formula
(Fig. 8); the energy of the particle is E < U0.
FIG. 8
SOLUTION.
The Schrödinger’s equation is the same as that obtained in the solution of Problem 5, §23; it is necessary merely to alter the sign of U0 and to regard the energy E now as positive. A similar calculation gives the solution
where
This solution satisfies the condition that, as x → ∞ (i.e. as 
), the wave function should include only the transmitted wave (elkx). The asymptotic form of the wave function as x → −∞ (ξ → −1) is found by transforming the hypergeometric function with the aid of formula (e.7):
Taking the squared modulus of the ratio of coefficients in this function, we obtain the following expression for the transmission coefficient D = 1 − R:
(if 8mU0/ħ2α2 < 1), or
(if 8mU0/ħ2α2 > 1). The first of these formulae holds also for the case U0 < 0, i.e. when the particle is passing over a potential well instead of a potential barrier. It is interesting to note that in that case D = 1 if 1 +8m|U0|/ħ2α2 = (2n + 1)2; thus, for certain values of the depth |U0| of the well, particles passing over it are not reflected. This is evident from equation (2), where the term in elkx vanishes for positive integral s.
PROBLEM 5.
Determine how the transmission coefficient tends to zero as E → 0, assuming that the potential energy U (x) decreases rapidly at distances |x| a, where a is the dimension of the interaction region.
SOLUTION.
For distances k |x| 1, E can be neglected in Schrödinger’s equation. If also |x| a, the potential energy can also be neglected, and the equation becomes − (ħ2/2m) d2ψ/dx2 = 0; the solution of this may be written as
The relation between a1, b1 and a2, b2 can be found by solving the equation at distances |x| a. It is linear:
The coefficients ρ, μ, v and τ are real and independent of the energy, which does not appear in the equation.† The solution (1) must be the same as the first two terms in the expansion of (25.1) and (25.2) in powers of x, so that
Substituting these in (2) and solving for A, we get, for small k, A ≈ 2ik/v, whence D ≈ 4k2/v2 E. The transmission coefficient thus tends to zero in proportion to the particle energy. This is of course true for the examples in Problems 2 and 4.
†This statement is, of course, not a logical consequence of the basic principles of quantum mechanics, and is to be regarded as a deduction from experiment.
†The idea of a wave related to a particle was first introduced by L. de Broglie in 1924.
†However, it must be mentioned that, for some particular mathematical forms of the function U (x, y, z) (which have no physical significance), a discrete set of values may be absent from the otherwise continuous spectrum.
†These assertions are not valid for systems in a magnetic field.
‡It is assumed that the potential energy U does not depend explicitly on the time: the system is either closed or in a constant (non-magnetic) field.
†If ψ is written as |ψ|eia, then 
†In the rest of this section we shall suppose the wave functions ψ to be real; they can always be so chosen (if there is no magnetic field).
†The proof of theorems concerning the zeros of eigenfunctions (see also §21) is given by M. A. Lavrent’ev and L. A. Lyusternik, The Calculus of Variations (Kurs variatsionnogo ischislemya), 2nd edition, chapter IX, Moscow, 1950; R. Courant and D. Hubert, Methods of Mathematical Physics, volume I, chapter VI, Interscience, New York, 1953.
‡This theorem and its consequences are not in general valid for the wave functions of systems consisting of several identical particles (see the end of §63).
†If the particle can be found only on a limited segment of the x-axis, we must consider the zeros of ψn(x) within that segment.
†In this discussion it is assumed that the stationary state is not degenerate, i.e. the motion is not infinite in both directions. Otherwise, when the sign of x is changed, two wave functions belonging to the energy level concerned may be transformed into each other. In this case, however, although the wave functions of the stationary states need not be even or odd, they can always be made so (by choosing appropriate linear combinations of the original functions).
†For n = 0 we should have ψ = 0 identically.
†This was done by Heisenberg in 1925, before Schrödinger’s discovery of the wave equation.
†We choose the indeterminate phases xn (see the second footnote to §11) so as to obtain the plus sign in front of the radical in all the matrix elements (23.4). Such a choice is always possible for a matrix in which only those elements are different from zero which correspond to transitions between states with adjacent numbers.
†These are called coherent states.
†It may be noted, by way of anticipation, that the asymptotic expressions (24.5) and (24.6) correspond to the quasi-classical expressions for the wave function in the classically inaccessible and accessible regions (§47).
†In the limiting case of classical mechanics, the reflection coefficient must become zero. The expression obtained here, however, does not contain the quantum constant at all. This apparent contradiction is explained as follows. The classical limiting case is that in which the de Broglie wavelength of the particle λ ħ/p is small in comparison with the characteristic dimensions of the problem, i.e. the distances over which the field U (x) changes noticeably. In the schematic example considered, however, this distance is zero (at the point x = 0), so that the passage to the limit cannot be effected.
†See formula (e.6), in each of whose two terms we must take only the first term of the expansion, i.e. replace the hypergeometric functions of 1/z by unity.
†Since the flux is constant, ρτ − ρτ-μv = 1.