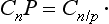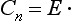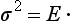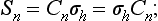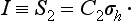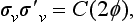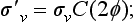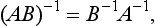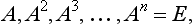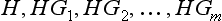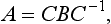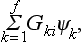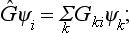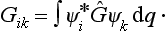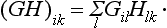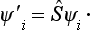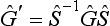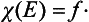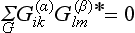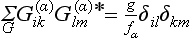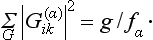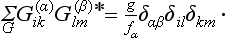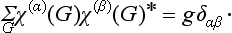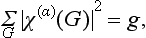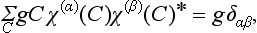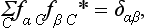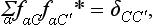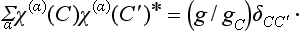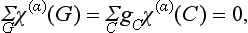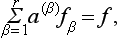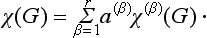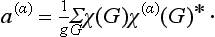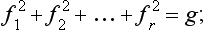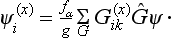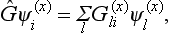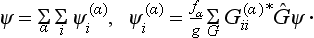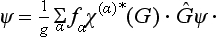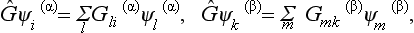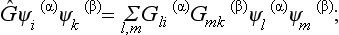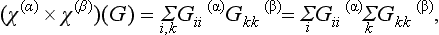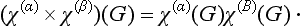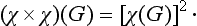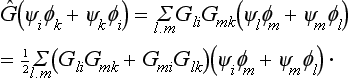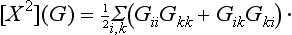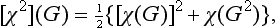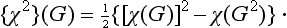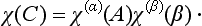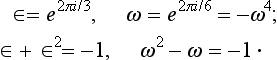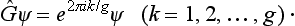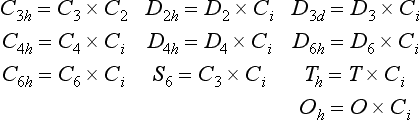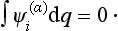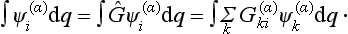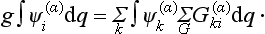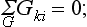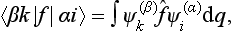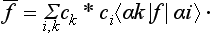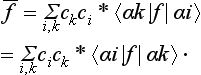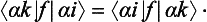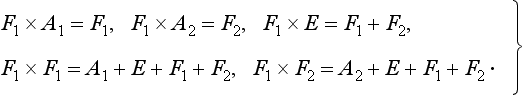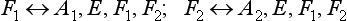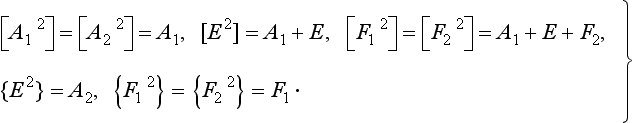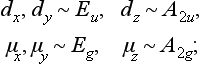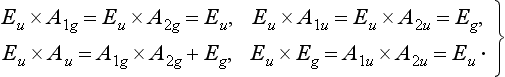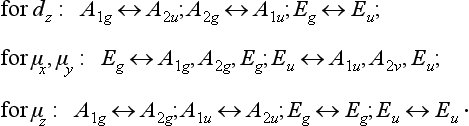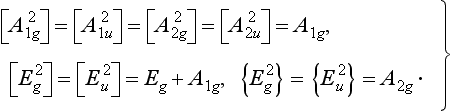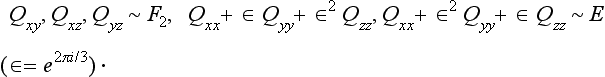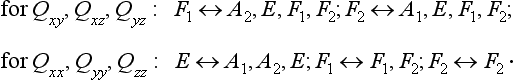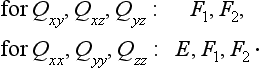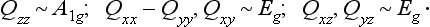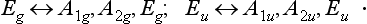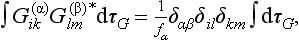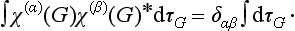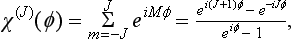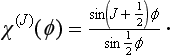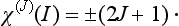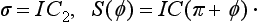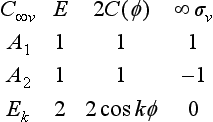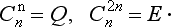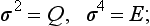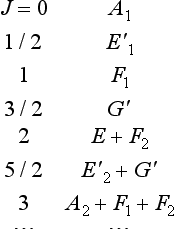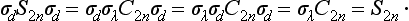THE THEORY OF SYMMETRY
§91 Symmetry transformations
The classification of terms in the polyatomic molecule is fundamentally related to its symmetry, as in the diatomic molecule. Hence we shall begin by examining the types of symmetry which a molecule can have.
The symmetry of a body is determined by the assembly of all those rearrangements after which the body is unaltered; these rearrangements are called symmetry transformations. Any possible symmetry transformation can be represented as a combination of one or more of the three fundamental types of transformation. These three essentially different types are: the rotation of the body through a definite angle about some axis, the reflection of it in some plane, and the parallel displacement of the body over some distance. Of these, the last evidently is applicable only to an infinite medium (a crystal lattice). A body of finite dimensions (in particular, a molecule) can be symmetrical only with respect to rotations and reflections.
If the body is unaltered on rotation through an angle 2Π/n about some axis, then that axis is said to be an axis of symmetry of the nth order. The number n can take any integral value: n = 2, 3, …. The value n = 1 corresponds to a rotation through an angle of 2Π or, what is the same thing, of 0, i.e. it corresponds to an identical transformation. We shall symbolically denote by Cn the operation of rotation through an angle 2Π/n about a given axis. Repeating this operation two, three, … times, we obtain rotations through angles 2(2Π/n), 3(2Π/n), …, which also leave the body unaltered; these rotations may be denoted by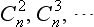 
. It is obvious that, if p divides n,
In particular, performing the rotation n times, we return to the initial position, i.e. we effect an identical transformation. The latter is customarily denoted by E, so that we can write
If the body is left unaltered by a reflection in some plane, this plane is said to be a plane of symmetry. We shall denote by the symbol σ the operation of reflection in a plane. It is evident that a double reflection in the same plane is the identical transformation:
A simultaneous application of the two transformations (rotation and reflection) gives what are called the rotary—reflection axes. A body has a rotary—reflection axis of the nth order if it is left unaltered by a rotation through an angle 2π/n about this axis, followed by a reflection in a plane perpendicular to the axis (Fig. 32). It is easy to see that this is a new form of symmetry only when n is even. For, if n is odd, an n-fold repetition of the rotary—reflection transformation would be equivalent to a simple reflection in a plane perpendicular to the axis (since the angle of rotation is 2π, while an odd number of reflections in the same plane amounts to a simple reflection). Repeating this transformation a further n times, we have as a result that the rotary—reflection axis reduces to the simultaneous presence of an axis of symmetry of the nth order and an independent plane of symmetry perpendicular to this axis. If, however, n is even, an n-fold repetition of the rotary—reflection transformation returns the body to its initial position.
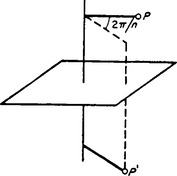
FIG. 32
We denote the rotary—reflection transformation by the symbol Sn. Denoting by σh a reflection in a plane perpendicular to a given axis, we can put, by definition,
the order in which the operations Cn and σh are performed clearly does not affect the result.
An important particular case is a rotary—reflection axis of the second order. It is easy to see that a rotation through an angle π, followed by a reflection in a plane perpendicular to the axis of rotation, is the inversion transformation, whereby a point P of the body is carried into another point P′, lying on the continuation of the line which joins P to the intersection O of the axis and the plane, and such that the distances OP and OP′ are the same. A body symmetrical with respect to this transformation is said to have a centre of symmetry. We shall denote the operation of inversion by I, so that we have
It is also evident that Iσh = C2, IC2 = σh; in other words, an axis of the second order, a plane of symmetry perpendicular to it and a centre of symmetry at their point of intersection are mutually dependent: if any two of these elements are present, the third is automatically present also.
We shall now give various purely geometrical properties of rotations and reflections which it is useful to bear in mind in studying the symmetry of bodies.
A product of two rotations about axes intersecting at some point is a rotation about some third axis also passing through that point. A product of two reflections in intersecting planes is equivalent to a rotation; the axis of this rotation is evidently the line of intersection of the planes, while the angle of rotation is easily seen, by a simple geometrical construction, to be twice the angle between the two planes. If we denote a rotation through an angle φ about an axis by C (φ), and reflections in two planes passing through that axis by the symbols† σv and σ′v, the above statement can be written as
where φ is the angle between the two planes. It must be noted that the order in which the two reflections are performed is not immaterial. The transformation σvσ′v gives a rotation in the direction from the plane of σ′v to that of σv; on interchanging the factors we have a rotation in the opposite direction. Multiplying equation (91.6) on the left by σv, we obtain
in other words, the operation of rotation, followed by reflection in a plane passing through the axis, is equivalent to a reflection in another plane intersecting the first at half the angle of rotation. In particular, it follows from this that an axis of symmetry of the second order and two mutually perpendicular planes of symmetry passing through it are mutually dependent; if two of them are present, so is the third.
We shall show that the product of rotations through an angle π about two axes intersecting at an angle φ (Oa and Ob in Fig. 33) is a rotation through an angle 2φ about an axis perpendicular to the first two (PP′ in Fig. 33). For it is obvious that the resulting transformation is also a rotation; after the first rotation (about Oa) the point P is carried into P′, and after the second (about Ob) it returns to its original position. This means that the line PP′ remains fixed, and is therefore an axis of rotation. To determine the angle of rotation, it is sufficient to note that, in the first rotation, the axis Oa remains fixed, while after the second it takes the position Oa′, which makes an angle 2φ with Oa. In the same way we can see that, when the order of the two transformations is reversed, we obtain a rotation in the opposite direction.
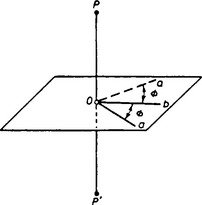
FIG. 33
Although the result of two successive transformations in general depends on the order in which they are performed, in some cases the order of operations is immaterial: the transformations commute. This is so for the following transformations:
(1) Two rotations about the same axis.
(2) Two reflections in mutually perpendicular planes (equivalent to a rotation through π about their line of intersection).
(3) Two rotations through π about mutually perpendicular axes (equivalent to a rotation through π about the third perpendicular axis).
(4) A rotation and a reflection in a plane perpendicular to the axis of rotation.
(5) Any rotation or reflection and an inversion with respect to a point lying on the axis of rotation or in the plane of reflection; this follows from (1) and (4).
§92 Transformation groups
The set of all the symmetry transformations for a given body is called its symmetry transformation group (or simply its symmetry group.) Hitherto we have spoken of these transformations as geometrical rearrangements of the body. However, in quantum-mechanical applications it is more convenient to regard symmetry transformations as transformations of the coordinates which leave the Hamiltonian of the system in question invariant. It is obvious that, if the system is left unaltered by some rotation or reflection, the corresponding transformation of the coordinates does not change its Schrödinger’s equation. Thus we shall speak of a transformation group with respect to which a given Schrödinger’s equation is invariant.†
Symmetry groups are conveniently studied with the help of the general mathematical techniques of what is called group theory, the fundamentals of which we shall explain below. At first we shall consider groups, each of which contains a finite number of transformations (known as finite groups). Each of the transformations forming a group is said to be an element of the group.
Symmetry groups have the following important properties. Each group contains the identical transformation E (called the unit element of the group). The elements of a group can be multiplied by one another; by the product of two (or more) transformations we mean the result of applying them in succession. It is obvious that the product of any two elements of a group is also an element of that group. For the multiplication of elements we have the associative law (AB)C = A (BC), where A, B, C are elements of a group. There is evidently no general commutative law; in general, AB ≠ BA. For each element A of a group there is in the same group an inverse element A−1 (the inverse transformation), such that AA−1 = E. In some cases an element may be its own inverse; in particular, E−1 = E. It is evident that mutually inverse elements A and A−1 commute.
The element inverse to the product AB of two elements is
and similarly for the product of a greater number of elements; this is easily seen by effecting the multiplication and using the associative law.
If all the elements of a group commute, the group is said to be Abelian. A particular case of Abelian groups is formed by what are called cyclic groups. By a cyclic group we mean a group, all of whose elements can be obtained by raising one of them to successive powers, i.e. a group consisting of the elements
where n is some integer.
Let G be some group.† If we can separate from it some set of elements H such that the latter is itself a group, then the group H is called a sub-group of the group G. A given element of a group may appear in several of its sub-groups.
By taking any element A of a group and raising it to successive powers, we finally obtain the unit element (since the total number of elements in the group is finite). If n is the smallest number for which An = E, then n is called the order of the element A, and the set of elements A, A2, …, An = E is called the period of A. The period is denoted by {A}; it is itself a group, i.e. it is a sub-group of the original group, and is cyclic.
In order to find whether a given set of elements of a group is a sub-group of it, it is sufficient to find whether, on multiplying any two of its elements, we obtain another element of the set. For in that case we have, together with each element A, all its powers, including An−1 (where n is the order of A), which is the inverse of A (since An−1 A = An = E); and there will obviously be a unit element.
The total number of elements in a group is called its order. It is easy to see that the order of a sub-group is a factor of the order of the whole group. To show this, let us consider a sub-group H of a group G, and let G1 be some element of G which does not belong to H. Multiplying all the elements of H (on the right, say) by G1, we obtain a set (or complex, as it is called) of elements, denoted by HG1. All the elements of this complex clearly belong to the group G. However, none of them belongs to H; for, if for any two elements Ha, Hb belonging to H we had HaG1 = Hb, it would follow that G1 = Ha−1Hb, i.e. G1 would also belong to the sub-group H, which is contrary to hypothesis. Similarly we can show that, if G2 is an element of G not belonging to H or to HG1, none of the elements of the complex HG2 will belong to H or to HG1. Continuing this process, we finally exhaust all the elements contained in the finite group G. Thus all the elements are divided among the complexes (called the cosets of H in G)
each of which contains H elements, H being the order of the sub-group H. Hence it follows that the order g of the group G is g = hm, and this proves the theorem. The integer m = g/H is called the index of the sub-group H in the group G.
If the order of a group is a prime number, it follows at once from the above that the group has no sub-groups (except itself and E). The converse theorem is also valid: a group having no sub-groups is of prime order and in addition must be cyclic (since otherwise it would contain elements whose period would form a sub-group).
We shall now introduce the important concept of conjugate elements. Two elements A and B are said to be conjugate if
where C is also an element of the group; multiplying this equation on the right by C and on the left by C−1, we have the converse equation B = C−1AC. An important property of conjugate elements is that, if A is conjugate to B, and B to C, then A is conjugate to C; for, if B = P−1AP, C = Q−1BQ (P and Q being elements of the group), it follows that C = (PQ)−1A (PQ). For this reason we can speak of sets of conjugate elements of a group. Such sets are called classes of conjugate elements, or simply classes, of the group. Each class is completely determined by any one element A of it; for, given A, we obtain the whole class by forming the products GAG−1, where G is successively every element of the group (of course, this may give each element of the class several times). Thus we can divide the whole group into classes; each element of the group can clearly appear in only one class. The unit element of the group is a class by itself, since for every element of the group GEG−1 = E. If the group is Abelian, each of its elements is a class by itself; since all the elements, by definition, commute, each element is conjugate only to itself. We emphasize that a class of a group (not being E) is not a sub-group of it; this is evident from the fact that it does not contain a unit element.
All the elements of a given class are of the same order. For, if n is the order of the element A (so that An = E), then for a conjugate element B = CAC−1 we have (CAC−1)n = CAnC−1 = E.
Let H be a sub-group of G, and G1 an element of G not belonging to H. It is easy to see that the set of elements G1HG1−1 has all the properties of a group, i.e. it also is a sub-group of the group G. The sub-groups H and G1HG1−1 are said to be conjugate; each element of one is conjugate to one element of the other. By giving G1 various values, we obtain a series of conjugate sub-groups, which may partly coincide. It may happen that all the sub-groups conjugate to H are H itself. In this case H is called a normal divisor or invariant sub-group of the group G. Thus, for example, every sub-group of an Abelian group is clearly a normal divisor of it.
Let us consider a group A with n elements A, A′, A″, …, and a group B with m elements B, B′, B″, …, and suppose that all the elements of A (apart from the unit E) are different from those of B but commute with them. If we multiply every element of group A by every element of group B, we obtain a set of nm elements, which also form a group. For, for any two elements of this set we have AB. A’B′ = AA′. BB′ = A″B″, i.e. another element of the set. The group of order nm thus obtained is denoted by A × B, and is called the direct product of the groups A and B.
Finally, we shall introduce the concept of the isomorphism of groups. Two groups A and B of the same order are said to be isomorphous if we can establish a one-to-one correspondence between their elements, such that, if the element B corresponds to the element A, and B′ to A′, then B″ = BB′ corresponds to A″ = AA′. Two such groups, considered in the abstract, clearly have identical properties, though the actual meaning of their elements may be different.
§93 Point groups
Transformations which appear in the symmetry group of a body of finite dimensions (in particular, a molecule) must be such that at least one point of the body remains fixed when any of these transformations is applied. In other words, all axes and planes of symmetry of a molecule must have at least one common point of intersection. For a successive rotation of the body about two non-intersecting axes or a reflection in two non-intersecting planes results in a translation of the body, which obviously cannot then be left unaltered. Symmetry groups having the above property are called point groups.
Before going on to construct the possible types of point group, we shall explain a simple geometrical procedure whereby the elements of a group may be easily divided into classes. Let Oa be some axis, and let the element A of the group be a rotation through a definite angle about this axis. Next, let G be a transformation (rotation or reflection) in the same group, which on being applied to the same axis Oa carries it to the position Ob. We shall show that the element B = GAG−1 then corresponds to a rotation about the axis Ob through the same angle as that of the rotation about Oa to which the element A corresponds. For, let us consider the effect of the transformation GAG−1 on the axis Ob itself. The transformation G−1 inverse to G carries the axis Ob to the position Oa, so that the subsequent rotation A leaves it in this position; finally, G carries it back to its initial position. Thus the axis Ob remains fixed, so that B is a rotation about this axis. Since A and B belong to the same class, their orders are the same; this means that they effect rotations through the same angle.
Thus we reach the result that two rotations through the same angle belong to the same class if there is, among the elements of the group, a transformation whereby one axis of rotation can be carried into the other. In exactly the same way, we can show that two reflections in different planes belong to the same class if some transformation in the group carries one plane into the other. The axes or planes of symmetry whose directions can be carried into each other are said to be equivalent.
Some additional comments are necessary in the case where both rotations are about the same axis. The element inverse to the rotation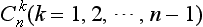 
about an axis of symmetry of the nth order is the element 
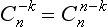, i.e. a rotation through an angle (n −k)2π/n in the same direction or, what is the same thing, a rotation through an angle 2kπ/n in the opposite direction. If, among the transformations in the group, there is a rotation through an angle π about a perpendicular axis (this rotation reverses the direction of the axis under consideration), then, by the general rule proved above, the rotations Cnk and Cn−k belong to the same class. A reflection σH in a plane perpendicular to the axis also reverses its direction; however, it must be borne in mind that the reflection also changes the direction of rotation. Hence the existence of σH does not render Cnk and Cn−k conjugate. A reflection σv in a plane passing through the axis, on the other hand, does not change the direction of the axis, but changes the direction of rotation, and therefore Cn−k = σvCnkσv, so that Cnk and Cn−k belong to the same class if such a plane of symmetry exists. If rotations about an axis through the same angle in opposite directions are conjugate, we shall call it bilateral.
The determination of the classes of a point group is often facilitated by the following rule. Let G be some group not containing the inversion I, and Ci a group consisting of the two elements I and E. Then the direct product G × Ci is a group containing twice as many elements as G; half of them are the same as the elements of the group G, while the remainder are obtained by multiplying the latter by I. Since I commutes with any other transformation of a point group, it is clear that the group G × Ci contains twice as many classes as G; to each class A of the group G there correspond the two classes A and AI in the group G × Ci. In particular, the inversion I always forms a class by itself.
Let us now go on to enumerate all possible point groups. We shall construct these by starting from the simplest ones and adding new elements of symmetry. We shall denote point groups by bold italic Latin letters with appropriate suffixes.
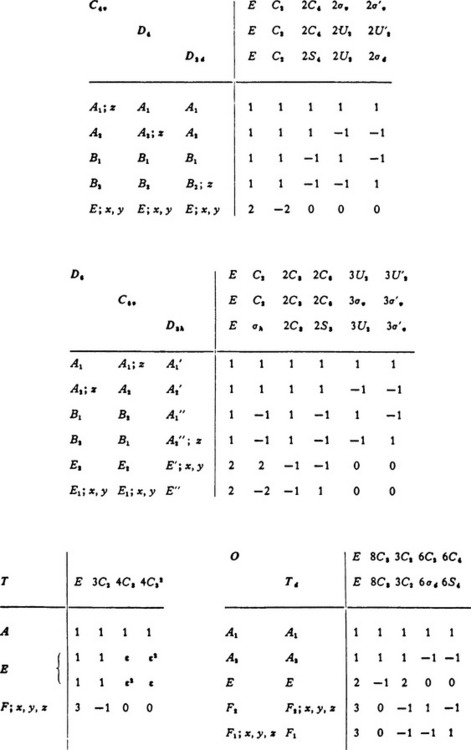
The simplest type of symmetry has a single axis of symmetry of the nth order. The group Cn is the group of rotations about an axis of the nth order. This group is evidently cyclic. Each of its n elements forms a class by itself. The group C1 contains only the identical transformation E, and corresponds to the absence of any symmetry.
The group S2n is the group of rotary—reflections about a rotary—reflection axis of even order 2n. It contains 2n elements and is evidently cyclic. In particular, the group S2 contains only two elements, E and I; it is also denoted by Ci. We may note also that, if the order of a group is a number of the form 2n = 4p + 2, inversion is among its elements; it is clear that (S4p+2)2p+1 = C2 σH = I. Such a group can be written as a direct product S4p+2 = C2p+1 xCi; it is also denoted by C2p+1,i.
These groups are obtained by adding to an axis of symmetry of the nth order a plane of symmetry perpendicular to it. The group Cnh contains 2n elements: n rotations of the group Cn and n rotary—reflection transformations Cnkσh, k = 1, 2, …, n (including the reflection CnnΣĤ = σh). All the elements of the group commute, i.e. it is Abelian; the number of classes is the same as the number of elements. If n is even (n = 2p), the group contains a centre of symmetry (since C2ppσh = C2ΣĤ = I). The simplest group, C1Ĥ, contains only two elements, E and σh; it is also denoted by Cs.
If we add to an axis of symmetry of the nth order a plane of symmetry passing through it, this automatically gives another n − 1 planes intersecting along the axis at angles of π/n, as follows at once from the geometrical theorem† (91.7). The group Cnv thus obtained therefore contains 2n elements: n rotations about the axis of the nth order, and n reflections σv in vertical planes. Figure 34 shows, as an example, the systems of axes and planes of symmetry for the groups C3v, and C4v.
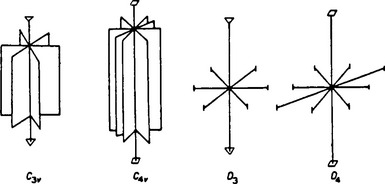
FIG. 34
To determine the classes, we notice that, because of the presence of planes of symmetry passing through the axis, the latter is bilateral. The actual distribution of the elements among the classes depends on whether n is even or odd.
If n is odd (n = 2p + 1), successive rotations C2p+1 carry each of the planes successively into each of the other 2p planes, so that all the planes of symmetry are equivalent, and the reflections in them belong to a single class. Among rotations about the axis there are 2p operations apart from the identity, and these are conjugate in pairs, forming p classes each of two elements (C2p+1k and C2p+1−k, k = 1, 2, …, p); moreover, E forms an extra class. Thus there are p + 2 classes altogether.
If, on the other hand, n is even (n = 2p), only every alternate plane can be interchanged by successive rotations C2p; two adjacent planes cannot be carried into each other. Thus there are two sets of p equivalent planes, and accordingly two classes of p elements (reflections) each. Of the rotations about the axis, C2p2p = E and C2pp = C2 each form a class by themselves, while the remaining 2p −2 rotations are conjugate in pairs and give another p − 1 classes, each of two elements. The group C2p, v thus has p + 3 classes altogether.
If we add to an axis of symmetry of the nth order an axis of the second order perpendicular to it, this involves the appearance of a further n −1 such axes, so that there are altogether n horizontal axes of the second order, intersecting at angles π/n. The resulting group Dn contains 2n elements: n rotations about an axis of the nth order, and n rotations through an angle π about horizontal axes (we shall denote the latter by U2, reserving the notation C2 for a rotation through an angle π about a vertical axis). Fig. 34 shows, as an example, the systems of axes for the groups D3 and D4.
In an exactly similar manner to case IV, we may verify that the axis of the nth order is bilateral, while the horizontal axes of the second order are all equivalent if n is odd, or form two non-equivalent sets if n is even. Consequently, the group D2p has the following p + 3 classes: E, 2 classes each of p rotations U2, the rotation C2, and p − 1 classes each of two rotations about the vertical axis. The group D2p+1, on the other hand, has p+2 classes: E, 2p + 1 rotations U2, and p classes each of two rotations about the vertical axis.
An important particular case is the group D2. Its system of axes is composed of three mutually perpendicular axes of the second order. This group is also denoted by V.
If we add to the system of axes of a group Dn horizontal plane of symmetry passing through the n axes of the second order, n vertical planes automatically appear, each of which passes through the vertical axis and one of the horizontal axes. The group Dnh thus obtained contains 4n elements; besides the 2n elements of the group Dn, it contains also n reflections σv and n rotary—reflection transformations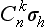 
. Figure 35 shows the system of axes and planes for the group D3h.
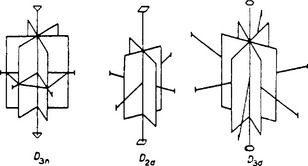
FIG. 35
The reflection σh commutes with all the other elements of the group; hence we can write Dnh as the direct product Dnh = Dn × Cs, where Cs is the group consisting of the two elements E and σh. For even n the inversion operation is among the elements of the group, and we can also write D2ph = D2p × Ci.
Hence it follows that the number of classes in the group Dnh is twice the number in the group Dn. Half of them are the same as those of the group Dn (rotations about axes), while the remainder are obtained by multiplying these by σh. The reflections σv in vertical planes all belong to a single class (if n is odd) or form two classes (if n is even). The rotary—reflection transformations σhCnk and σhCn−k are conjugate in pairs.
There is another way of adding planes of symmetry to the system of axes of the group Dn. This is to draw vertical planes through the axis of the nth order, midway between each adjacent pair of horizontal axes of the second order. The adding of one such plane again involves the appearance of another (n −1) planes. The system of axes and planes of symmetry thus obtained determines the group Dnd. Figure 35 shows the axes and planes for the groups D2d and D3d.
The group Dnd contains 4n elements. To the 2n elements of the group Dn are added n reflections in the vertical planes (denoted by σd—the “diagonal” planes) and n transformations of the form G = U2σd. In order to ascertain the nature of these latter, we notice that the rotation U2 can, by (91.6), be written in the form U2 = σhΣv, where Σv is a reflection in the vertical plane passing through the corresponding axis of the second order. Then G = σhΣvΣd (the transformations Σv, σh alone are not, of course, among the elements of the group). Since the planes of the reflections Σv and Σd intersect along an axis of the nth order, forming an angle (2k + 1)Π/2n, where k = 1, …, (n − 1) (since here the angle between adjacent planes is Π/2n), it follows that, by (91.6), we have ΣvΣd = C2n2k+1. Thus we find that G = σhC2n2k + 1 = S2n2k−1, i.e. these elements are rotary—reflection transformations about the vertical axis, which is consequently not a simple axis of symmetry of the nth order, but a rotary—reflection axis of the 2nth order.
The diagonal planes reflect two adjacent horizontal axes of the second order into each other; hence, in the groups under consideration, all axes of the second order are equivalent (for both even and odd n). Similarly, all diagonal planes are equivalent. The rotary—reflection transformations S2n2k+1 and S2n−2k−1 are conjugate in pairs.†
Applying these considerations to the group D2p, d, we find that it contains the following 2p + 3 classes: E, the rotation C2 about the axis of the nth order, (p − 1) classes each of two conjugate rotations about the same axis, one class of the 2p rotations U2, one class of 2p reflections Σd, and p classes each of two rotary—reflection transformations.
For odd n (= 2p + 1), inversion is among the elements of the group; this is seen from the fact that, in this case, one of the horizontal axes is perpendicular to a vertical plane. Hence we can write D2p+1,d = D2p+1 × Ci, so that the group D2p+1,d contains 2p + 4 classes, which are obtained at once from the p + 2 classes of the group D2p+1.
VIII The group T (the tetrahedron group)
The system of axes of this group is the system of axes of symmetry of a tetrahedron. It can be obtained by adding to the system of axes of the group V four oblique axes of the third order, rotations about which carry the three axes of the second order into one another. This system of axes is conveniently represented by showing the three axes of the second order as passing through the centres of opposite faces of a cube, and those of the third order as the spatial diagonals of the cube. Figure 36 shows the position of these axes in a cube and in a tetrahedron (one axis of each type is shown).
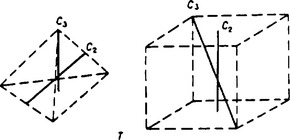
FIG. 36
The three axes of the second order are mutually equivalent. The axes of the third order are also equivalent, since they are carried into one another by the rotations C2, but they are not bilateral axes. Hence it follows that the twelve elements in the group T are divided into four classes: E, the three rotations C2, the four rotations C3 and the four rotations C32.
This group contains all the symmetry transformations of the tetrahedron. Its system of axes and planes can be obtained by adding to the axes of the group T planes of symmetry, each of which passes through one axis of the second order and two of the third order. The axes of the second order thereby become rotary—reflection axes of the fourth order (as in the case of the group D2d). This system is conveniently represented by showing the three rotary—reflection axes as passing through the centres of opposite faces of a cube, the four axes of the third order as its spatial diagonals, and the six planes of symmetry as passing through each pair of opposite edges (Fig. 37 shows one of each kind of axis and one plane).
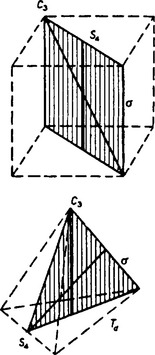
FIG. 37
Since the planes of symmetry are vertical with respect to the axes of the third order, the latter are bilateral axes. All the axes and planes of a given kind are equivalent. Hence the 24 elements of this group are divided into the following five classes: E, eight rotations C3 and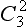 
, six reflections in planes, six rotary—reflection transformations S4 and 
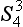, and three rotations 
.
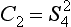This group is obtained from T by adding a centre of symmetry: Th = T × Ci. As a result, three mutually perpendicular planes of symmetry appear, passing through each pair of axes of the second order, and the axes of the third order become rotary—reflection axes of the sixth order (Fig. 38 shows one of each kind of axis and one plane).
FIG. 38
The group contains 24 elements divided among eight classes, which are obtained at once from those of the group T.
XI The group O (the octahedron group)
The system of axes of this group is the system of axes of symmetry of a cube: three axes of the fourth order pass through the centres of opposite faces, four axes of the third order through opposite corners, and six axes of the second order through the midpoints of opposite edges (Fig. 39).
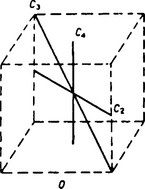
FIG. 39
It is easy to see that all the axes of a given order are equivalent, and each of them is bilateral. Hence the 24 elements are divided among the following five classes: E, eight rotations C3 and C32, six rotations C4 and C43, three rotations C42 and six rotations C2.
This is the group of all symmetry transformations of the cube.† It is obtained by adding to the group O a centre of symmetry: Oh = O × Ci. The axes of the third order in the group O are thereby converted into rotary—reflection axes of the sixth order (the spatial diagonals of the cube); in addition, another six planes of symmetry appear, passing through each pair of opposite edges, and three planes parallel to the faces of the cube (Fig. 40). The group contains 48 elements divided among ten classes, which can be at once obtained from those of the group O; five classes are the same as those of the group O, while the remainder are: I, eight rotary—reflection transformations S6 and S65, six rotary—reflection transformations C4σh, C43σh about axes of the fourth order, three reflections σh in planes horizontal with respect to the axes of the fourth order, and six reflections Σv in planes vertical with respect to these axes.
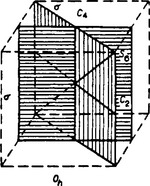
FIG. 40
XIII, XIV The groups Y, Yh (the icosahedron groups)
These groups occur only exceptionally in Nature as symmetry groups of molecules. Hence we shall here only mention that Y is a group of 60 rotations about the axes of symmetry of the icosahedron (a regular solid with twenty triangular faces) or of the pentagonal dodecahedron (a regular solid with twelve pentagonal faces); there are six axes of the fifth order, ten of the third and fifteen of the second. The group Yh is obtained by adding a centre of symmetry: Yh = Y × Ci, and is the complete group of symmetry transformations of the above-mentioned polyhedra.
This exhausts all possible types of point group containing a finite number of elements. In addition, we must consider what are called continuous point groups, which contain an infinite number of elements. This we shall do in §98.
§94 Representations of groups
Let us consider any symmetry group, and let Ψ1 be some one-valued function of the coordinates in the configuration space of the physical system concerned. Under the transformation of the coordinate system which corresponds to an element G of the group, this function is changed into some other function. On performing in turn all the g transformations in the group (g being the order of the group), we in general obtain g different functions from Ψ1. For certain Ψ1, however, some of these functions may be linearly dependent. As a result we obtain some number f (< g) of linearly independent functions Ψ1, Ψ2, …, Ψf, which are transformed into linear combinations of one another under the transformations belonging to the group in question. In other words, as a result of the transformation G, each of the functions Ψi (i = 1, 2, 3, …, f) is changed into a linear combination of the form
where the Gik are constants depending on the transformation G. The array of these constants is called the matrix of the transformation.†
In this connection it is convenient to regard the elements G of the group as operators acting on the functions Ψi, so that we can write
the functions Ψi can always be chosen so as to be orthonormal. Then the concept of the matrix of the transformation is the same as that of the matrix of the operator, in the form defined in §11:
To the product of two elements G and Ĥ of the group there corresponds the matrix obtained from the matrices of G and Ĥ by the ordinary rule of matrix multiplication (11.12):
The set of matrices of all the elements in a group is called a representation of the group. The functions Ψ1 …, Ψf with respect to which these matrices are defined are called the basis of the representation. The number f of these functions gives what is called the dimension of the representation.
Let us consider the integrals ∫Ψi*Ψk dq. Since the integration is taken over all space, it is evident that the values of the integrals are unchanged by any rotation or reflection of the coordinate system. That is, the symmetry transformations do not destroy the orthonormality of the base functions, and therefore the operators Ĝ are unitary (see §12).‡ Accordingly, the matrices which represent the elements of a group in a representation with an orthonormalized basis are also unitary.
Suppose that we perform on the system of functions Ψ1, …,Ψf the linear unitary transformation
This gives a new system of functions Ψ′1, …,Ψ′f, which are also orthonormal (see §12).† If we now take, as the basis of the representation, the functions Ψ′i, we obtain a new representation of the same dimension. Such representations, obtained from one another by a linear transformation of their base functions, are said to be equivalent; it is evident that they are not essentially different.
The matrices of equivalent representations can be simply expressed in terms of one another. According to (12.7), the matrix of the operator Ĝ in the new representation is the matrix of the operator
in the old representation.
The sum of the diagonal elements (i.e. the trace) of the matrix representing an element G of a group is called its character; we shall denote it by χ(G). It is a very important result that the characters of the matrices of equivalent representations are the same (see (12.11)). This circumstance gives particular importance to the description of group representations by stating their characters: it enables us to distinguish at once the fundamentally different representations from those which are equivalent. Henceforward we shall regard as different representations only those which are not equivalent.
If we take S in (94.5) to be that element of the group which relates the conjugate elements G and G′, we have the result that, in any given representation of a group, the characters of the matrices representing elements of the same class are the same.
The identical transformation corresponds to the unit element E of the group. Hence the matrix representing the latter is diagonal in every representation, and the diagonal elements are unity. The character χ(E) is consequently just the dimension of the representation:
Let us consider some representation of dimension f. It may happen that, as a result of a suitable linear transformation (94.4), the base functions divide into sets of f1, f2, … functions (f1 + f2 + … = f), in such a way that, when any element of the group acts on them, the functions in each set are transformed only into combinations of themselves, and do not involve functions from other sets. In such a case the representation in question is said to be reducible.
If, on the other hand, the number of base functions that are transformed only into combinations of themselves cannot be reduced by any linear transformation of them, the representation which they give is said to be irreducible. Any reducible representation can, as we say, be decomposed into irreducible ones. This means that, by the appropriate linear transformation, the base functions divide into several sets, of which each is transformed by some irreducible representation when the elements of the group act on it. Here it may be found that several different sets transform by the same irreducible representation; in such a case this irreducible representation is said to be contained so many times in the reducible one.
Irreducible representations are an important characteristic of a group, and play a fundamental part in all quantum-mechanical applications of group theory. We shall give the chief properties of irreducible representations.†
It may be shown that the number of different irreducible representations of a group is equal to the number r of classes in the group. We shall distinguish the characters of the various irreducible representations by indices; the characters of the matrices of the element G in the representations are χ(1)(G), χ(2)(G), …, χ(r)(G).
The matrix elements of irreducible representations satisfy a number of orthogonality relations. First of all, for two different irreducible representations the relations
hold, where α and β (α ≠ β) refer to the two irreducible representations, and the summation is taken over all the elements of the group. For any irreducible representation the relations
hold, i.e. only the sums of the squared moduli of the matrix elements are not zero:
The relations (94.7), (94.8) can be combined in the form
In particular, we can obtain from this an important orthogonality relation for the characters of the representations. Summing both sides of equation (94.9) over equal values of the suffixes i, k and l, m, we have
i.e. the sum of the squared moduli of the characters of an irreducible representation is equal to the order of the group. We may notice that this relation can be used as a criterion of the irreducibility of a representation; for a reducible representation, this sum is always greater than g (for instance, it is ng if the representation contains n different irreducible parts).
It also follows from (94.10) that the equality of the characters of two irreducible representations is not only a necessary but also a sufficient condition for them to be equivalent.
Since the characters of elements of the same class are equal, the sum (94.10) actually contains only r independent terms, and can be written in the form
where the summation is over the r classes of the group (arbitrarily denoted by C) and gc is the number of elements in class C.
Since the number of irreducible representations is equal to the number of classes, the quantities fαC = √(gc/g)χ(α)(C) form a square matrix of r2 quantities.
The orthogonality relations for the first suffix,
then automatically give those for the second suffix,
Hence, besides (94.11), we have
Among the irreducible representations of any group there is always a trivial one, given by a single base function invariant under all the transformations in the group: This one-dimensional representation is called the unit representation; in it, all characters are unity. If one of the representations in the orthogonality relation (94.10) or (94.11) is the unit representation, the other is such that
i.e. the sum of the characters of all the elements of the group is zero for every irreducible representation.
The relation (94.10) enables any reducible representation to be very easily decomposed into irreducible ones if the characters of both are known. Let χ(G) be the characters of some reducible representation of dimension f, and let the numbers a(1), a(2), …, a(r) indicate how many times the corresponding irreducible representations are contained in it, so that
where fβ are the dimensions of the irreducible representations. Then the characters χ(G) can be written
Multiplying this equation by χ(α)(G)* and summing over all G, we have by (94.10)
Let us consider a representation of dimension f = g, given by the g functions ĜΨ, Ψ being some general function of the coordinates (so that all the g functions ĜΨ obtained from it are linearly independent); such a representation is said to be regular. It is clear that none of the matrices of this representation will contain any diagonal elements, with the exception of the matrix corresponding to the unit element; hence χ(G) = 0 for G ≠ E, while χ(E) = g. Decomposing this representation into irreducible ones, we have for the numbers a(α), by (94.16), the values a(α) = (1/g)gf(x) = i.e. each irreducible representation is contained in the reducible one under consideration as many times as its dimension. Substituting this in (94.14), we find the relation
the sum of the squared dimensions of the irreducible representations of a group is equal to its order.† Hence it follows, in particular, that for Abelian groups (where r = g) all the irreducible representations are of dimension one (f1 = f2 = … = fr = 1).
We may also remark, without proof, that the dimensions of the irreducible representations of a group divide its order.
In practice, the decomposition of a regular representation into irreducible parts is made by means of the formula
It is easy to verify that the functions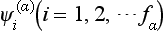 
represented by this formula with a given value of k are transformed according to
i.e. they are a basis of the αth irreducible representation. By giving various values to k we obtain in this way fα different sets of base functions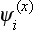 
for one irreducible representation, in accordance with the fact that each irreducible representation appears fα times in the regular representation.
Any function Ψ may be written as a sum of functions transformed by the irreducible representations of the group. This problem is solved by the formulae
To prove this, we substitute the second formula in the first and calculate the sum over i, obtaining
Since the dimensions fα coincide with the characters χ(α)(E) of the unit element of the group, we can use the orthogonality relation (94.12) to show that the sum in (94.20) is non-zero (and equal to g) only if G is the unit element of the group. Hence the right-hand side of (94.20) is identically equal to Ψ.
Let us consider two different systems of functions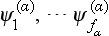 
, which form two irreducible representations of a group. By forming the products 
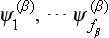we obtain a system of fαfβ new functions, which can serve as the basis for a new representation of dimension fαfβ. This representation is called the direct product or Kronecker product of the other two; it is irreducible only if fα or fβ is unity. It is easy to see that the characters of the direct product are equal to the products of the characters of the two component representations. For, if
then
hence we have for the characters, which we denote by (χ(α) × χ(β)(G),
i.e.
The two irreducible representations so multiplied may, in particular, be the same; in this case we have two different sets of functions Ψ1, …, Ψf and φ1, …, φf giving the same representation, while the direct product of the representation with itself is given by the f2 functions ΨiΨk, and has the characters
This reducible representation can be at once decomposed into two representations of smaller dimension (although these are, in general, themselves reducible). One of them is given by the ½f (f + 1) functions Ψiφk + Ψkφi, the other by the ½f (f − 1) functions Ψiφk − Ψkφi, i ≠ k; it is evident that the functions in each of these sets are transformed only into combinations of themselves. The former is called the symmetric product of the representation with itself, and its characters are denoted by the symbol [χ2](G); the latter is called the antisymmetric product, and its characters are denoted by {χ2} (G). To determine the characters of the symmetric product, we write
Hence we have for the character
But Σi Gii = χ(G), and Σi, k GikGki = χ(G2); thus we finally obtain the formula
which enables us to determine the characters of the symmetric product of a representation with itself from the characters of the representation. In an exactly similar manner, we find for the characters of the antisymmetric product the formula†
If the functions Ψi and φi are the same, we can evidently construct from them only the symmetric product, formed by the squares Ψi2 and the products ΨiΨk, i ≠ k. In applications, symmetric products of higher orders are also encountered; their characters may be obtained in a similar manner.
An important property of direct products is the following. The decomposition of the direct product of two different irreducible representations into irreducible parts contains the unit representation (and only once) only if the representations multiplied together are complex conjugates. For real representations, the unit representation is present only in the direct product of an irreducible representation with itself, and is of course in the symmetric part. In order to know whether the unit representation is present in the representation (94.21), we simply sum its characters with respect to G and divide the result by the order g of the group, in accordance with (94.16). The conclusion stated then follows at once from the orthogonality relations (94.10).
Finally, we shall make a few remarks regarding the irreducible representations of a group which is the direct product of two other groups (not to be confused with the direct product of two representations of the same group). If the functions Ψi(α) give an irreducible representation of the group A, and the functions φκ(β) give one of the group B, the products φκ(β)Ψi(α) are the basis of an fαfβ-dimensional representation of the group A × B, and this representation is irreducible. The characters of this representation are obtained by multiplying the corresponding characters of the original representations (cf. the derivation of formula (94.21)); to an element C = AB of the group A × B there corresponds the character
Multiplying together in this way all the irreducible representations of the groups A and B, we obtain all the irreducible representations of the group A × B.
§95 Irreducible representations of point groups
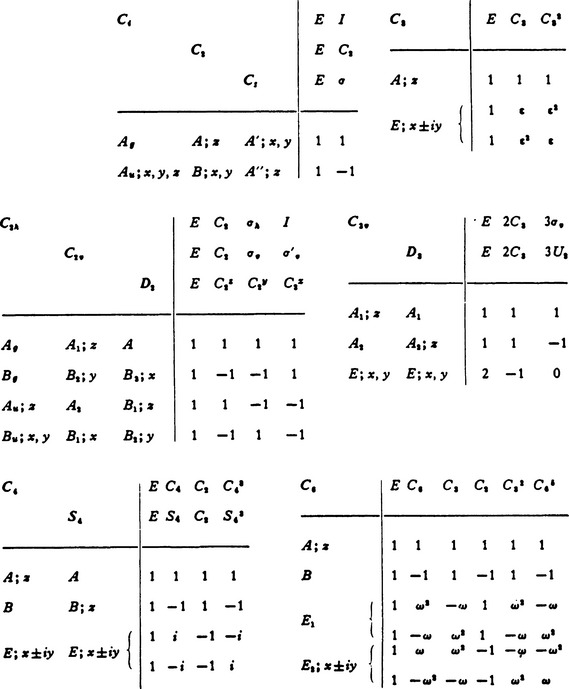
Let us pass now to the actual determination of the irreducible representations of point groups. The great majority of molecules have axes of symmetry only of the second, third, fourth or sixth order. Hence we shall not consider the icosahedron groups Y, YĤ; we shall examine the groups Cn, Cnh, Cnv, Dn, Dnh only for the values n = 1, 2, 3, 4, 6, and the groups S2n, Dnd only for n = 1, 2, 3.
The characters of the representations of these groups are shown in Table 7. Isomorphous groups have the same representations and are given together. The numbers in front of the symbols for the elements of a group in the upper rows show the numbers of elements in the corresponding classes (see §93). The left-hand columns show the conventional names usually given to the representations. The one-dimensional representations are denoted by the letters A, B, the two-dimensional ones by E, and the three-dimensional ones by F; the notation E for a two-dimensional irreducible representation should not be confused with the unit element of a group.† The base functions of A representations are symmetric, and those of B representations antisymmetric, with respect to rotations about a principal axis of the nth order. The functions of different symmetry with respect to a reflection σh are distinguished by the number of primes (one or two), while the suffixes g and u show the symmetry with respect to inversion. Beside the symbols for the representations are placed the letters x, y, z; these show the representations by which the coordinates themselves are transformed. The z-axis is always taken along the principal axis of symmetry. The letters ∈ and ω denote
The simplest problem is to determine the irreducible representations for the cyclic groups (Cn, Sn). A cyclic group, like any Abelian group, has only one-dimensional representations. Let G be a generating element of the group (i.e. one which, on being raised to successive powers, gives all the elements of the group). Since Gg = E (where g is the order of the group), it is clear that, when the operator ĝ acts on a base function Ψ, the latter can be multiplied only by 11/2, i.e.†
The group C2Ĥ (and the isomorphous groups C2v and D2) is Abelian, so that all its irreducible representations are one-dimensional, and the characters can only be ± 1 (since the square of every element is E).
Next we consider the group C3v. As compared with the group C3, the reflections σv in vertical planes (all belonging to one class) are here added. A function invariant with respect to rotation about the axis (a base function of the representation A of the group C3) may be either symmetric or antisymmetric with respect to the reflections σv. Functions multiplied by ∈ and ∈2 under the rotation C3, on the other hand (base functions of the complex conjugate representations E), change into each other on reflection.‡ It follows from these considerations that the group C3v, (and D3, which is isomorphous with it) has two one-dimensional irreducible representations and one two-dimensional, with the characters shown in the table. The fact that we have indeed found all the irreducible representations may be seen from the result 12+12+22 = 6, which is the order of the group.
Similar considerations give the characters of the representations of other groups of the same type (C4v, C6v).
The group T is obtained from the group D2 ≡ V by adding rotations about four oblique axes of the third order. A function invariant with respect to transformations of the group V (a basis of the representation A) can be multiplied, under the rotation C3, by 1, ∈ or ∈2. The base functions of the three one-dimensional representations B1, B2, B3 of the group V change into one another under rotations about the axes of the third order (this is seen, for example, if we take as these functions the coordinates x, y, z themselves). Thus we obtain three one-dimensional irreducible representations and one three-dimensional (12+12+12+32 = 12).
Finally, let us consider the isomorphous groups O and Td. The group Td is obtained from the group T by adding reflections σd in planes each of which passes through two axes of the third order. A base function of the unit representation A of the group T may be symmetric or antisymmetric with respect to these reflections (which all belong to one class), and this gives two one-dimensional representations of the group Td. Functions multiplied by ∈ or ∈2 under a rotation about an axis of the third order (the basis of the complex conjugate representations E of the group T) change into each other on reflection in a plane passing through this axis, so that one two-dimensional representation is obtained. Finally, of three base functions of the representation F of the group T, one is transformed into itself on reflection (and can either remain unaltered or change sign), while the other two change into each other. Thus we have altogether two one-dimensional representations, one two-dimensional and two three-dimensional.†
The representations of the remaining point groups in which we are interested can be obtained immediately from those already given, if we notice that the remaining groups are direct products of those already considered with the group Ci (or Ci):
Each of these direct products has twice as many irreducible representations as the original group, half of them being symmetric (denoted by the suffix g) and the other half antisymmetric (suffix u) with respect to inversion. The characters of these representations are obtained from those of the representations of the original group by multiplying by ±1 (in accordance with the rule (94.24)). Thus, for instance, we have for the group D3d the representations:
§96 Irreducible representations and the classification of terms
The quantum-mechanical applications of group theory are based on the fact that the Schrödinger’s equation for a physical system (an atom or molecule) is invariant with respect to symmetry transformations of the system.† It follows at once from this that, on applying the elements of a group to a function satisfying Schrödinger’s equation for some value of the energy (an eigenvalue), we must again obtain solutions of the same equation for the same value of the energy. In other words, under a symmetry transformation the wave functions of the stationary states of the system belonging to a given energy level transform into linear combinations of one another, i.e. they give some representation of the group. An important fact is that this representation is irreducible. For functions which are invariably transformed into linear combinations of themselves under symmetry transformations must belong to the same energy level; the equality of the eigenvalues of the energy corresponding to several groups of functions (into which the basis of a reducible representation can be divided), which are not transformed into combinations of one another, would be an improbable coincidence.‡
Thus, to each energy level of the system, there corresponds some irreducible representation of its symmetry group. The dimension of this representation determines the degree of degeneracy of the level concerned, i.e. the number of different states with the energy in question. The fixing of the irreducible representation determines all the symmetry properties of the given state, i.e. its behaviour with respect to the various symmetry transformations.
Irreducible representations of dimension greater than one are found only in groups containing non-commuting elements; Abelian groups have only one-dimensional irreducible representations. It is apposite to recall here that the relation between degeneracy and the presence of operators which do not commute with one another (but do commute with the Hamiltonian) has already been found above from considerations unrelated to group theory (§10).
The following important reservation should be made regarding all these statements. As has already been pointed out (§18), the symmetry (valid in the absence of a magnetic field) with respect to a change in the sign of the time has, in quantum mechanics, the result that complex conjugate wave functions must belong to the same eigenvalue of the energy. Hence it follows that, if some set of functions and the set of complex conjugate functions give different (non-equivalent) irreducible representations of a group, these two complex conjugate representations must be regarded as forming together a single “physically irreducible” representation of twice the dimension. This will be assumed below. In the preceding section we had examples of such representations. Thus the group C3 has only one-dimensional representations; however, two of these are complex conjugates, and correspond physically to doubly degenerate energy levels. (In the presence of a magnetic field there is no symmetry with respect to a change in the sign of the time, and hence complex conjugate representations correspond to different energy levels.)†
Let us suppose that a physical system is subjected to the action of some perturbation (i.e. the system is placed in an external field). The question arises to what extent the perturbation can result in a splitting of the degenerate levels. The external field has itself a certain symmetry.‡ If this symmetry is the same as or higher
than that of the unperturbed system, the symmetry of the perturbed Hamiltonian Ĥ = Ĥ0+
is the same as the symmetry of the unperturbed operator Ĥ0. It is clear that, in this case, no splitting of the degenerate levels occurs. If, however, the symmetry of the perturbation is lower than that of the unperturbed system, then the symmetry of the Hamiltonian Ĥ is the same as that of the perturbation 
, The wave functions which gave an irreducible representation of the symmetry group of the operator Ĥ0 will also give a representation of the symmetry group of the perturbed operator Ĥ, but this representation may be reducible, and this means that the degenerate level is split.
We shall show by means of an example how the mathematical techniques of group theory enable us to solve the problem of the splitting of any given level.
Let the unperturbed system have symmetry Td, and let us consider a triply degenerate level corresponding to the irreducible representation F2 of this group. The characters of this representation are
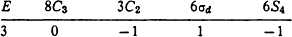
Let us assume that the system is subjected to the action of a perturbation with symmetry C3v (with the third-order axis coinciding with one of those of the group Td). The three wave functions of the degenerate level give a representation of the group C3v (which is a sub-group of the group Td), and the characters of this representation are equal to those of the same elements in the original representation of the group Td, i.e.
| E | 2C3 | 3σv |
| 3 | 0 | 1 |
This representation, however, is reducible. Knowing the characters of the irreducible representations of the group C3v, it is easy to decompose it into irreducible parts, using the general rule (94.16). Thus we find that it consists of the representations A1 and E of the group C3v. The triply degenerate level F2 is therefore split into one non-degenerate level A1 and one doubly degenerate level E. If the same system is subjected to the action of a perturbation of symmetry C2v, which is also a sub-group of the group Td, then the wave functions of the same level F2 give a representation with characters
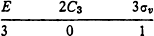
Decomposing this into irreducible parts, we find that it contains the representations A1, B1, B2 Thus in this case the level is completely split into three non-degenerate levels.
§97 Selection rules for matrix elements
Group theory not only enables us to carry out a classification of the terms of any symmetrical physical system, but also gives us a simple method of finding the selection rules for the matrix elements of the various quantities which characterize the system.
This method is based on the following general theorem. Let Ψi(α) be one of the base functions of an irreducible (non-unit) representation of a symmetry group Then the integral of this function over all space† vanishes identically:
The proof is based on the evident fact that the integral over all space is invariant with respect to any transformation of the coordinate system, including any symmetry transformation. Hence
We sum this equation over all the elements of the group. The integral on the left is simply multiplied by g, the order of the group, and we have
However, for any non-unit irreducible representation we have identically
this is a particular case of the orthogonality relations (94.7), when one of the irreducible representations is the unit representation. This proves the theorem.
If Ψ is a function belonging to the basis of some reducible representation of a group, the integral ∫ Ψ dq will be zero except when this representation contains the unit representation. This theorem is a direct consequence of the previous one.
The matrix elements of a physical quantity f are given by the integrals
where the indices α and β distinguish different energy levels of the system, and the suffixes i, k denumerate wave functions belonging to the same degenerate level.† We denote the irreducible representations of the symmetry group of the system concerned that are given by the functions Ψi(α) and Ψk(β) by the symbols D(α) and D(β), and by Df the representation of the same group that corresponds to the symmetry of the quantity f; this representation depends on the tensor character of f. For example, if f is a true scalar, then its operator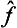 
is invariant under all the symmetry transformations, and Df is the unit representation. The same occurs for a pseudoscalar quantity if the group contains only axes of symmetry, but if there are also reflections, Df is not the unit representation, though its dimension is unity. If f is a vector, then Df is a representation given by the three vector components that are transformed into combinations of each other; this representation is in general different for polar and axial vectors.
The products Ψk(β)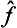
Ψi(α) give the representation that is the direct product D(β) × Df × D(α). The matrix elements are non-zero if this representation contains the unit representation or, equivalently, if the direct product D(β) × D(α) contains Df. In practice, it is more convenient to decompose into irreducible parts the product D(α) × Df; this gives us immediately all the types D(β) of states for transitions into which (from a state of the type D(α)) the matrix elements are not zero.
In the simplest case of a scalar quantity, for which Df is the unit representation, it then follows immediately that the matrix elements are non-zero only for transitions between states of the same type: the direct product D(α) × D(β) of two different irreducible representations does not contain the unit representation, but the latter is always present in the direct product of an irreducible representation with itself. This is most general statement of a theorem of which particular cases have already been met with.
The matrix elements diagonal with respect to energy, i.e. those for transitions between states belonging to the same term (as opposed to transitions between states belonging to two different terms of the same type), need special treatment. In this case we have only one set of functions Ψ1(α), Ψ2(α), …, not two different ones. The selection rules here are found by different methods, depending on the behaviour of the quantity f under time reversal.
Let us consider a state described by a wave function of the form Ψ = ΣciΨi(α). The mean value of f in this state is given by the sum
In the state with the complex conjugate wave function Ψ* = Σ ci*Ψi(α), we have
If f is invariant under time reversal, the two states not only belong to the same energy level but must also have the same value of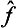 
. Since the coefficients ci are arbitrary, this means that
Hence, in order to find the selection rules, we must consider not the direct product D(α) × D(α) as a whole, but only its symmetric part [D(x)2]; there are non-zero matrix elements if [D(α)2] contains Df.†
If, however, f changes sign under time reversal, the change from Ψ to Ψ* has to be accompanied by a change in the sign of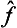 
. Hence we find by the same method that
In this case, therefore, the selection rules are determined by the decomposition of the antisymmetric part of the direct product, {D(α)2}.
PROBLEMS
Find the selection rules for the matrix elements of the electric and magnetic dipole moments d and μ when symmetry O is present.
Solution
The group O includes no reflections; the polar vector d and the axial vector μ are therefore transformed by the same irreducible representation, F1. The decompositions of the direct products of F1 with the other representations of the group O are
Hence the non-zero non-diagonal (with respect to energy) matrix elements are those for the transitions
The symmetric and antisymmetric products of the irreducible representations of the group O are
The symmetric products do not contain F1; hence there are no diagonal (with respect to energy) matrix elements of the vector d (which is invariant under time reversal). The magnetic moment, which changes sign under time reversal, has diagonal matrix elements for the states F1 and F2.
Solution
The vectors d and μ have different transformation laws in the group D3d:
here and in the Problems below, the symbol ∼ stands for the words “is transformed by the representation”. We have
Hence the non-diagonal matrix elements of dx, dy are non-zero for the transitions Eu ↔ A1g, A2g, Eg; Eg↔A1u, A2u, Eu. In the same way we find the selection rules
The symmetric and antisymmetric products of the irreducible representations of the group D3d are
Hence we see that there are no diagonal (with respect to energy) matrix elements for any of the components d; for the vector μ there are diagonal matrix elements of μz for transitions between states belonging to a degenerate level of the type Eg or Eu.
PROBLEM 3
Find the selection rules for the matrix elements of the electric quadrupole moment tensor Qik when symmetry O is present.
Solution
The components of the tensor Qik (a symmetrical tensor with the sum Qii equal to zero) with respect to group O are transformed by the laws
Decomposing the direct products of F2 and E with all the representations of the group, we find the selection rules for the non-diagonal matrix elements:
The diagonal matrix elements exist (as we see from (2)) in the following states:
Solution
The transformation laws of the components Qik with respect to the group D3d are
Qzz behaves as a scalar. Decomposing the direct products of Eg with all the representations of the group, we find the selection rules for the non-diagonal matrix elements of the remaining components Qik:
The diagonal elements are non-zero (as we see from (4)) only for the states Eq and Eu.
§98 Continuous groups
As well as the finite point groups enumerated in §93, there exist also what are called continuous point groups, having an infinite number of elements. These are the groups of axial and spherical symmetry.
The simplest axial symmetry group is the group C∞, which contains rotations C (φ) through any angle φ about the axis of symmetry; this is called the two-dimensional rotation group. It may be regarded as the limiting case of the groups Cn as n → ∞. Similarly, as limiting cases of the groups Cnh, Cnv, Dn, Dnh we obtain the continuous groups C∞h, C∞v, D∞, D∞h.
A molecule has axial symmetry only if it consists of atoms lying in a straight line. If it meets this condition, but is asymmetric about its midpoint, its point group will be the group C∞v, which, besides rotations about the axis, contains also reflections σv in any plane passing through the axis. If, on the other hand, the molecule is symmetrical about its midpoint, its point group will be D∞h = C∞v × Ci. The groups C∞, C∞h, D∞ cannot appear as the symmetry groups of a molecule.
The group of complete spherical symmetry contains rotations through any angle about any axis passing through the centre, and reflections in any plane passing through the centre; this group, which we shall denote by Kh, is the symmetry group of a single atom. It contains as a sub-group the group K of all spatial rotations (called the three-dimensional rotation group, or simply the rotation group). The group Kh can be obtained from the group K by adding a centre of symmetry (Kh = K × Ci).
The elements of a continuous point group may be distinguished by one or more parameters which take a continuous range of values. Thus, in the rotation group, the parameters might be the three Eulerian angles, which define a rotation of the coordinates.
The general properties of finite groups described in §92, and the concepts appertaining to them (sub-groups, conjugate elements, classes, etc.), can be at once generalized to continuous groups. Of course, the statements which directly concern the order of the group (for instance, that the order of a sub-group divides the order of the group) are no longer meaningful.
In the group C∞v all planes of symmetry are equivalent, so that all reflections σv form a single class with a continuous series of elements; the axis of symmetry is bilateral, so that there is a continuous series of classes, each containing two elements C (±φ). The classes of the group D∞h are obtained at once from those of the group C∞v, since D∞h = C∞v × Ci.
In the rotation group K, all axes are equivalent and bilateral; hence the classes of this group are rotations through an angle of fixed absolute magnitude |φ| about any axis. The classes of the group Kh are obtained at once from those of the group K.
The concept of representations, reducible and irreducible, can also be immediately generalized to continuous groups. Each irreducible representation contains an infinite sequence of matrices, but the number of base functions transformed into combinations of one another (the dimension of the representation) is finite. These functions may always be chosen so as to make the representation unitary. The number of different irreducible representations of a continuous group is infinite, but they form a discrete sequence, i.e. they can be numbered successively. For the matrix elements and characters of these representations there are orthogonality relations which generalize the corresponding ones for finite groups. Instead of (94.9), we now have
and instead of (94.10)
The integration in these formulae is what is called an invariant integration over the group; the element dτG is expressed in terms of the parameters of the group and their differentials in such a way as to remain an element when subjected to any transformation in the group.† For example, in the rotation group we can take dτG = sin β dα dβ dγ, where α, β and γ are the Eulerian angles, which define a rotation of the system of coordinates (§58); in this case, ∫dτG = 8π2.
We have already found, in essence, the irreducible representations of the three-dimensional rotation group (without using the terminology of group theory), when determining the eigenvalues and eigenfunctions of the total angular momentum. For the angular momentum component operators are (apart from a constant factor) the operators of infinitely small rotations,‡ and the eigenvalues of the angular momentum characterize the behaviour of the wave functions with respect to spatial rotations. To a value j of the angular momentum there correspond 2j + 1 different eigenfunctions Ψjm, differing in the values of the component m of the angular momentum and all belonging to one (2j + 1)-fold degenerate energy level. Under rotations of the coordinate system, these functions are transformed into linear combinations of themselves, and thus give irreducible representations of the rotation group. Thus, from the group-theory point of view, the numbers j number the irreducible representations of the rotation group, and one (2j + 1)-dimensional representation corresponds to each j. The number j takes integral and half-integral values, so that the dimension 2j + 1 of the representations takes all the integral values 1, 2, 3, ….
The base functions of these representations have been, in essence, investigated in §§56 and 57, and the matrices of the representations have been found in §58. The basis of a representation of given j is formed by the 2j + 1 independent components of a symmetrical spinor of rank 2j (which are equivalent to the set of 2j + 1 functions Ψjm).
The irreducible representations of the rotation group which correspond to half-integral values of j are distinguished by an important property. Under a rotation through 2π, the base functions of the representations change sign (being components of a spinor of odd rank). Since, however, a rotation through 2π is the same as the unit element of the group, we reach the result that representations with half-integral j are, as we say, two-valued; to each element of the group (a rotation through an angle φ, 0 ≤ φ ≤ 2π, about some axis) there correspond in such a representation not one but two matrices, with characters differing in sign.†
An isolated atom has, as we have already remarked, the symmetry Kh = K × Ci. Hence, from the group-theory point of view, there corresponds to each term of the atom some irreducible representation of the rotation group K (determining the value of the total angular momentum J of the atom) and an irreducible representation of the group Ci (determining the parity of the state).‡
When the atom is placed in an external electric field, its energy levels are split. The number of different levels resulting and the symmetry of the corresponding states can be determined by the method described in §96. It is necessary to decompose the (2J + 1)-dimensional representation of the symmetry group of the external field (given by the functions ΨJM) into irreducible representations of this group. This requires a knowledge of the characters of the representation given by the functions ΨJM.
Since the characters of the irreducible representations of elements of one class are the same, it is sufficient to consider rotations about the z-axis. By a rotation through an angle φ about this axis the wave functions ΨJM are, as we know, multiplied by ei, Mφ, where M is the component of the angular momentum along this axis. The transformation matrix for the functions ΨJM will therefore be diagonal, with character
or†
With respect to inversion I, all the functions ΨJM with different M behave in the same way, being multiplied by +1 or − 1 according as the state of the atom is even or odd. Hence the character
Finally, the characters corresponding to reflection in a plane σ and rotary reflection through an angle φ are found by writing these symmetry transformations as
Let us pause to consider also the irreducible representations of the axial symmetry group C∞v, This problem has, in essence, been solved when we ascertained the classification of the electron terms of a diatomic molecule having this symmetry C∞r (i.e. when the two atoms are different). To the terms 0+ and 0− (with ω = 0) there correspond two one-dimensional irreducible representations: the unit representation A1 and the representation A2, in which the base function is invariant under all rotations and changes sign under reflections in planes σv, while to the doubly degenerate terms with Ω = 1, 2, … there correspond two-dimensional representations denoted by E1, E2, …. Under a rotation through an angle φ about the axis, the base functions are multiplied by e±iΩφ, while on reflection in planes σv they change into each other. The characters of these representations are
The irreducible representations of the group D∞h = C∞v × Ci are obtained at once from those of the group C∞v. (and correspond to the classification of the terms of a diatomic molecule composed of like nuclei).
If we take half-integral values for Ω, the functions e±iΩφ give two-valued irreducible representations of the group C∞v, corresponding to the terms of the molecule having half-integral spin.†
§99 Two-valued representations of finite point groups
To the states of a system with half-integral spin (and therefore half-integral total angular momentum) there correspond two-valued representations of the point symmetry group of the system. This is a general property of spinors, and therefore holds for both continuous and finite point groups. The necessity thus arises of finding the two-valued irreducible representations of finite point groups.
As we have already remarked, the two-valued representations are not really true representations of a group. In particular, the relations discussed in §94 do not apply to them, and where all irreducible representations were considered in these relations (for example, in the relation (94.17) for the sum of the squared dimensions of the irreducible representations), only the true one-valued representations were meant.
To find the two-valued representations, it is convenient to employ the following artifice (H. A. Bethe 1929). We introduce, in a purely formal manner, the concept of a new element of the group (denoted by Q); this is a rotation through an angle of 2π about an arbitrary axis, and is not the unit element, but gives the latter when applied twice: Q2 = E. Accordingly, rotations Cn about the axes of symmetry of the nth order will give identical transformations only after being applied 2n times (and not n times):
The inversion I, being an element which commutes with all rotations, must give E as before on being applied twice. A twofold reflection in a plane, however, gives Q, not E:
this follows, since the reflection can be written in the form σh = IC2. As a result we obtain a set of elements forming some fictitious point symmetry group, whose order is twice that of the original group; such groups we shall call double point groups. The two-valued representations of the actual point group will clearly be one-valued (i.e. true) representations of the corresponding double group, so that they can be found by the usual methods.
The number of classes in the double group is greater than in the original group (but not, in general, twice as great). The element Q commutes with all the other elements of the group,† and hence always forms a class by itself. If the axis of symmetry is bilateral, the elements Cnk and Cn2n-k = QCnn-k are conjugate in the double group. Hence, when axes of the second order are present, the distribution of the elements among classes depends also on whether these axes are bilateral (in ordinary point groups this is unimportant, since C2 is the same as the opposite rotation C2−1).
Thus, for instance, in the group T the axes of the second order are equivalent, and each of them is bilateral, while the axes of the third order are equivalent but not bilateral. Hence the 24 elements of the double group‡ T′ are distributed in seven classes: E, Q, the class of three rotations C2 and three C2Q, and the classes 4C3, 4C32, 4C3Q, 4C32Q.
The irreducible representations of a double point group include, firstly, representations which are the same as the one-valued representations of the simple group (a unit matrix corresponding to both Q and E); secondly, the two-valued representations of the simple group, a negative unit matrix corresponding to Q. It is these latter representations in which we are now interested.
The double groups Cn′ (n = 1, 2, 3, 4, 6) and S4′, like the corresponding simple groups, are cyclic. All their irreducible representations are one-dimensional, and can be found without difficulty as shown in §95.
The irreducible representations of the groups Dn′ (or Cnv′, which are isomorphous with them) can be found by the same method as for the corresponding simple groups. These representations are given by functions of the form e±ikφ, where φ is the angle of rotation about an axis of the nth order, and k is given half-integral values (the integral values correspond to the ordinary one-valued representations). Rotations about horizontal axes of the second order change these functions into one another, while the rotation Cn multiplies them by e±2Πik/n.
It is a little less easy to find the representations of the double cubic groups. The 24 elements of the group T′ are divided among seven classes. Hence there are altogether seven irreducible representations, of which four are the same as those of the simple group T. The sum of the squared dimensions of the remaining three representations must be 12, and hence we find that they are all two-dimensional. Since the elements C2 and C2Q belong to the same class, χ(C2) = χ(C2Q) = −χ(C2), whence we conclude that χ(C2) = 0 in all three representations. Next, at least one of the three representations must be real, since complex representations can occur only in conjugate pairs. Let us consider this representation, and suppose that the matrix of the element C3 is brought to diagonal form, with diagonal elements a1, a2. Since C33 = Q, a13 = a23 = − 1. In order that χ(C3) = a1+a2 may be real, we must take a1 = eΠi/3, a2 = e−Πi/3. Hence we find that χ(C3) = 1, χ(C32) = a12 + a22 = −1. Thus one of the required representations is obtained. By comparing its direct products with the two complex conjugate one-dimensional representations of the group T, we find the other two representations.
By means of similar arguments, which we shall not pause to give here, we may find the representations of the group O′. Table 8 gives the characters of the representations of the double groups mentioned above. Only those representations are shown which correspond to two-valued representations of the ordinary groups. The isomorphous double groups have the same representations.
The remaining point groups are isomorphous with those we have considered, or else are obtained by direct multiplication of the latter by the group Ci, so that their representations do not need to be specially calculated.
For the same reasons as for ordinary representations, two complex conjugate two-valued representations must be regarded as one physically irreducible representation of twice the dimension. It is necessary to pair one-dimensional two-valued representations even when they have real characters. For (see §60) in systems with half-integral spin, complex conjugate wave functions are linearly independent. Hence, if we have a two-valued one-dimensional representation† with real characters (given by some function Ψ then, although the complex conjugate function Ψ* is transformed by an equivalent representation, we can nevertheless see that Ψ and Ψ* are linearly independent. Since, on the other hand, the complex conjugate wave functions must belong to the same energy level, we see that in physical applications this representation must be doubled.
The whole of the discussion in §97 concerning the method of finding the selection rules for the matrix elements of various physical quantities f remains valid for states of a system with half-integral spin, except as regards the matrix elements diagonal with respect to energy. On repeating the analysis at the end of §97 but with formulae ‡
PROBLEM
Determine how the levels of an atom (with given values of the total angular momentum J) are split when it is placed in a field having the cubic symmetry† O.
SOLUTION
The wave functions of the states of an atom with angular momentum J and various values MJ give a (2J + 1)-dimensional reducible representation of the group O, with characters determined by the formula (98.3). Decomposing this representation into irreducible parts (one-valued for integral J and two-valued for half-integral J), we at once find the required splitting (cf. §96). We shall list the irreducible parts of the representations corresponding to the first few values of J:
†The suffix v customarily denotes a reflection in a plane passing through a given axis (a “vertical” plane), and the suffix h a reflection in a plane perpendicular to the axis (a “horizontal” plane).
†This point of view enables us to include in our considerations not only the rotation and reflection groups discussed here, but also other types of transformation which leave Schrödinger’s equation unaltered. These include the interchange of the coordinates of identical particles forming part of the system considered (a molecule or atom). The set of all possible permutations of identical particles in a given system is called its permutation group (we have already met these permutations in §63). The general properties of groups given below apply to permutation groups also; we shall not pause to study this type of group in more detail here. The following remark should be made concerning the notation which we use in this chapter. Symmetry transformations are essentially operators just like those which we consider all through the book. They ought, therefore, to be denoted by letters with circumflexes. We do not do this, in view of the generally accepted notation, and because this omission cannot lead to misunderstandings in the present chapter. For the same reason we denote the identical transformation by the customary symbol E, and not by 1, which would correspond to the notation in the other chapters. Lastly, the inversion operator is denoted in this chapter by I, instead of P as in §30, although the latter is customary in recent literature on quantum mechanics.
†We shall denote groups by bold italic letters.
†In a finite group, there cannot be two planes of symmetry intersecting at an angle which is not a rational fraction of 2π. If there were two such planes, it would follow that there were an infinite number of other planes of symmetry, intersecting along the same line and obtained by reflecting one plane in the other ad infinitum. In other words, if there are two such planes, there must be complete axial symmetry.
†For we have
†The groups T, Td, Th, O, Oh are called cubic groups.
†Since the functions Ψi are assumed one-valued, a definite matrix corresponds to each element of the group.
‡In this argument it is important that the integrals are either equal to zero (for i § k), or definitely not zero (for i = k) because the integrand |Ψi|2 is positive.
†From (12.12), the unitarity of the transformations implies that the sum of the squared moduli of the base functions is invariant.
†The proof of these properties may be found in any textbook on group theory.
†It may be mentioned that, for point groups, equation (94.17) for given r and g can in practice be satisfied in only one way by a set of integers f1, …, fr.
†It is useful to note that, for representations of dimension 2, the characters {x2}(G) are equal to the determinants of the linear transformations G, as can easily be shown by direct calculation.
†The reason why two complex conjugate one-dimensional representations are shown as one two-dimensional one is explained in §96.
†For the point group Cn we can, for example, take as the functions Ψ the functions eikφ, k = 1, 2, … n, where φ is the angle of rotation about the axis, measured from some fixed direction.
‡These functions may, for example, be taken as Ψ1 = eiφ, Ψ2 = e−iφ. On reflection in a vertical plane, φ changes sign.
†Irreducible representations of higher dimension (4 and 5) occur in the icosahedron groups.
†The methods of group theory were first applied in quantum mechanics by E. P. Wigner (1926).
‡Provided that there is no special reason for this. Reference may be made here to the “accidental” degeneracy that arises because the Hamiltonian of a system can have a higher symmetry than the purely geometrical symmetry considered in the present chapter (see the end of §36).
†Strictly speaking, the fact that the characters are real (i.e. that the complex conjugate representations are equivalent) is not a sufficient condition for the possibility of choosing real base functions of the representation of the group. For irreducible representations of point groups, however, it is sufficient (though not for the “double” point groups; see §99).
‡For example, in the case of the energy levels of the d and f shells of ions in a crystal lattice which interact slightly with the surrounding atoms, the perturbation (the external field) is the field acting on an ion due to the other atoms.
If a symmetry group Ĥ is a sub-group of the group G, we say that Ĥ corresponds to a lower symmetry and G to a higher symmetry. It is evident that the symmetry of the sum of two expressions, one of which has the symmetry of G and the other that of H, is the lower symmetry, that of Ĥ.
†That is, the configuration space of the physical system concerned.
†Since the base functions can be taken as real when “physically irreducible” representations are used, we do not distinguish in (97.2) between the wave functions and their complex conjugates.
†The product [D(α)2]) always contains the unit representation, so that the diagonal elements (and non-diagonal elements between states of the same type) are non-zero for a scalar quantity.
†The statements made here about the properties of irreducible representations of continuous groups are valid only if the integrals (98.1) and (98.2) converge; in particular, the “volume of the group” ∫ dτG must be finite. This condition is satisfied for continuous point groups (but not, for instance, for the Lorentz group which occurs in the relativistic theory).
‡In mathematical terms, these operators are the generators of the rotation group.
†It must be mentioned that two-valued representations of a group are not representations in the true sense of the word, since they are not given by one-valued base functions; sec also §99.
‡Moreover, the Hamiltonian of the atom is invariant with respect to interchanges of the electrons In the non-relativistic approximation, the coordinate and spin wave functions are separable, and we can speak of representations of the permutation group that are given by the coordinate functions. If the irreducible representation of the permutation group is given, the total spin S of the atom is determined (§63). When the relativistic interactions are taken into account, however, the separation of the wave functions into coordinate and spin parts is not possible. The symmetry with respect to simultaneous interchange of the coordinates and spins of the particles does not characterize the term, since Pauli’s principle admits only those total wave functions which are antisymmetric with respect to all the electrons. This is in accordance with the fact that, when the relativistic interactions are taken into account, the spin is not, strictly speaking, conserved; only the total angular momentum J is conserved.
†To avoid misunderstanding, it should be emphasized that this formula corresponds to a parametrization of the group elements other than that by the Eulerian angles: the transformation is specified by the direction of the axis of rotation and the angle φ of the rotation about the axis. It can be shown that, with this parametrization, the integration in (98.2), for example, is to be taken over 2(1 −cos φ)dφ do, where do is the element of solid angle for the direction of the axis of rotation.
†Contrary to the result for the three-dimensional rotation group, it would here be possible, by a suitable choice of fractional values of Ω, to obtain not only one-valued and two-valued representations, but also those of three or more values. However, the physically possible eigenvalues of the angular momentum, which is the operator of an infinitely small rotation, are determined by the representations of the aforementioned three-dimensional rotation group. Hence the three (or more)-valued representations of the two-dimensional rotation group (and of any finite symmetry group), though mathematically determinate, are without physical significance.
†This is obvious for rotations and inversion; for a reflection in a plane, it follows since the reflection can be represented as the product of an inversion and a rotation.
‡We distinguish the double groups by primes to the symbols for the ordinary groups. The groups S2′ ≡ Ci′, S6′ ≡ C3i′, however, which contain the inversion I, are Abelian but not cyclic.
†Such representations are found in the group Cn for odd n; the characters are χ(Cnk) = (−1)b
‡In connection with the application of these rules, it may be noted that for two-valued representations the unit representation is in the antisymmetric, not the symmetric, product of the representation with itself. For a two-valued representation with dimension 2, the product {D(α)2}) is just the unit representation.
†For example, an atom in a crystal lattice. The presence or absence of a centre of symmetry in the symmetry group of the external field is immaterial to this problem, since the behaviour of the wave function on inversion (the parity of the level) is unrelated to the angular momentum J.