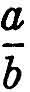is small if a is small compared with b. This still of course has the rather vague sense which is attached to all these words.This is not supposed to be a book about geometry. This subject is to be dealt with in another book in the same series. But it is impossible to avoid saying something about it. Numerical ideas and geometrical ideas have been wrapped up together for thousands of years, and they cannot be separated entirely now. For the Greeks, geometry was the primary subject. A Greek writer pictured a product of two numbers as an area, and a product of three numbers as a volume. A formula in which four numbers were multiplied together was offered with a slight apology, as it did not correspond to any geometrical figure which could be visualized.
To-day, books which do not profess to deal with geometry are full of geometrical terms. Numbers are often called points, equations are called curves, and so on. We shall therefore say something about this subject. At the same time, we shall try to make our theories about numbers stand on their own feet. We shall use geometrical ideas as suggestions how to proceed, and as providing picturesque language, rather than as the real basis of our theories.
Geometry originally meant “land measurement.” It arises generally from our attempts to give an account of the rigid non-interpenetrating objects with which we are familiar in the physical world. These objects force themselves on our senses, but it is not easy to think accurately about them. It is not simply that it is difficult to measure them exactly; it is impossible. Our measuring instruments, and indeed our senses, are coarse-grained. Objects which are sufficiently close together become indistinguishable, whatever aids to nature we employ in trying to separate them for observation. If we try to measure physical objects by dividing them up, we can do so up to a point; beyond this, they cease to be what they at first appeared. Divide a wooden foot-rule into twelve parts, and each is a wooden inch. Divide it into 101000 parts and each is … what?
All this makes it very difficult to think in a reasonable way about the physical world. Actually we take refuge in thoughts about ideal systems which represent the physical world to our minds, but which, because they are constructed in our thoughts, are not subject to the awkwardness of physical objects. The name “geometry” has become transferred to the study of such ideal systems. Many such systems are very interesting in themselves, quite apart from the question whether they represent anything in physical space.
In geometry we consider things which we call “points,” “lines” and so on. In our mental construction we may say that a point is anything which has certain properties which are required by the system, without specifying, or indeed being interested in the question what a point actually is. In this method of procedure, the question whether our assumptions are consistent, i.e., whether there could be anything with the assigned properties, is an important and sometimes a difficult one. But there is another way of thinking of geometry. We have already constructed one ideal system, that of numbers, and we can use them as the materials out of which to build our geometry. If we have already agreed about numbers, no further difficulties about existence arise; it is just a question whether numbers have properties which are interesting as a geometry. It turns out that this is so.
As the “points,” the original elements of our geometry, we take the numbers, namely, the integers and fractions so far defined. This is reasonable because a “point” is an idealization of “a well-defined place,” and a well-defined place is usually defined e.g., as “five yards along the path from where we are now.” In fact measurement can hardly be done without counting.
The next step consists of describing properties of numbers by words which originally had a physical significance, and which therefore establish in our minds a correlation between our number-system and our ideas of the physical space which we intend it to represent.
The idea of a large number is familiar, but the meaning of the word “large” depends on the context; 30 is a large score for a side at Rugby football, but not at cricket; 100 is a large individual score at cricket, but £100 a year is not a large income, and so on. In mathematics, we say that a number b is large compared with a number a if b can be divided into a large number of a’s, with or without remainder. “Large” still has a rather vague sense; but it often refers to an indefinitely increasing scale of largeness—b is large compared with a, c is large compared with b, and so on.
“Small” is the opposite of “large”; a is small compared with b if b is large compared with a.
Transferring our attention to fractions, we say that the fraction 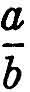is small if a is small compared with b. This still of course has the rather vague sense which is attached to all these words.
The difference between the fractions 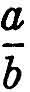and 
is 
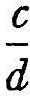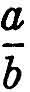and we say that is near to 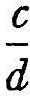if 
is small. This use of the word “near” confers a geometrical meaning on our fractions. It is not inseparable from them, but I do not suppose that anyone actually thinks about fractions without visualizing them as marks on a ruler or in some geometrical way of this kind. Thus for purposes of thought and calculation we replace a ruler of unit length by the system of fractions 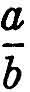with a < b. The particles of which the ruler is composed lie in a certain order along it, and so do the fractions lie in a certain order. Every particle has other particles very near to it on each side, and this is also true of the fractions, since 
and 
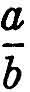are very near to if n is very large. But of course the ideal system goes beyond the physical system in this matter of divisibility; by making n larger and larger we can make and as near as we like to 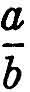. We may thus say that the ideal system constructed of the fractions is infinitely fine-grained. As a representation of physical objects this is perhaps a defect, but a limitation on the fineness of the grain would introduce serious difficulties in calculation, just as a limitation on the largeness of numbers would.
The system of geometry in which a point is specified by means of a number, or is even identified with the number, was invented by the famous philosopher and mathematician Descartes. It is known as Cartesian geometry.
We saw above that the fractions correspond to the points along a ruler. If we think of all the fractions 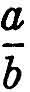, in which a may be less than or greater than b, or negative, these will correspond to a ruler extending to infinity in both directions. We call this system a one-dimensional Cartesian geometry.
According to this definition, the geometry is just the system of numbers; but it is intended to, and does, call up in our minds a picture of a sort of space, like the spaces of the physical world. There are problems of two different kinds about a system of geometry; whether just as a system it has interesting properties, and whether it corresponds to anything in physical space.
One-dimensional Cartesian geometry is not a very exciting subject; and a one-dimensional physical world would be rather lacking in interesting features. The inhabitants would be situated like beads on a wire or trucks on a railway-line. All one could do would be to move backwards and forwards. The behaviour of one’s next-door neighbours would be even more important than it is in ordinary life.
A two-dimensional space is a space such as the floor of a room. Many people must remember constructing a sort of two-dimensional world on the nursery floor. The inhabitants are toys which are only allowed to move by sliding along the floor, and must not be lifted up. A hollow square of bricks lying on the floor makes a house, which the inhabitants can only enter or leave by opening a “door.” If this system has three-dimensional aspects, we agree to ignore them. It is true that we can see down into the “house” from above, but from the point of view of the inhabitants we must be regarded as supernatural beings. If we throw something into the house from above, this must seem to have suddenly appeared inside a closed room, and must be regarded with horror by the inhabitants as a supernatural event.
Any place on the floor can be specified by measuring its distance from one wall, and also its distance from a second wall making an angle with the first. That is, two measurements are required. I am using the word “distance” here in a popular and rather vague sense. Later on this word will be given an official meaning in our theory. But it presumably conveys some idea to the reader, and we must be content for the moment to leave it at that.
The two measurements which specify a place on the floor give us two numbers, say x and y; that is, the point is specified by means of a number-pair (x, y). The numbers x and y are called the co-ordinates of the point. If we are building an ideal system, or geometry, in which points are numbers, the points of the system will be the number-pairs (x, y). These number-pairs must not be confused with those of Chapter IV, for which the bracket notation has now been abandoned. As we do not want to “add” or “multiply” points, there are no such rules of operation for these number-pairs.
The system consisting of the number-pairs (x, y) is called a two-dimensional Cartesian geometry.
This system is usually represented by a figure drawn on paper in the following way. A line, called the x-axis, is drawn across the paper, and another, called the y-axis, is drawn up and down the paper. These intersect at a point called the origin, and usually marked 0. They are (mentally) extended indefinitely in both directions, and divide the paper (or plane) into four regions called quadrants. The number or point (x, y) is represented by a point on the paper distant x units to the right of the y-axis (or to the left, if x is negative), and y units above the x-axis (or below, if y is negative). Thus in the top right-hand quadrant both x and y are positive.
I assume that the reader has learnt something about the “points” and “straight lines” in Euclidean geometry. A geometrical straight line is a mental construct which is supposed to represent the straight edges of physical objects. In Euclidean geometry, a straight line is really defined by the properties we assign to it.
In the Cartesian system we have identified “point” with “number,” or “number-pair (x, y),” if we are in two dimensions. We must now consider what corresponds in this system to a straight line.
One of the characteristic principles of Euclidean geometry is that of similar figures. Two triangles, for example, are said to be similar if their corresponding sides are proportional and their corresponding angles are equal.
If ABC and A′B′C′ are similar triangles, the former being the smaller, ABC is just a map of A′B′C′ on a smaller scale. In fact any small map is usually “similar” to the country of which it is a map. Of course in the case of a flat map of the earth, this is not strictly accurate, since the earth is round. The idea of similarity is really an extension to any size of the properties of scale drawings with which we are familiar.
There are systems of geometry in which similar figures on different scales do not exist. For example it can be shown that on the surface of a sphere there cannot be similar figures on different scales.
In the figure p. 66, APQ is a straight line intersecting the x-axis at A. Let P be (x, y), so that OB = x, and BP = y. Similarly let Q be (x′, y′), so that OC = x′ and CQ = y′.
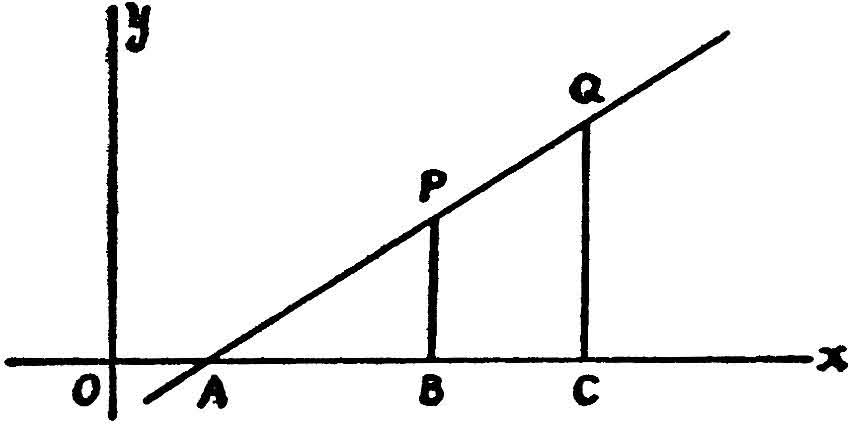
In this figure ABP and ACQ are similar triangles, and consequently corresponding sides will be proportional. Thus
If OA is of length a, then AB = OB − OA = x − a, and similarly AC = x′ − a. The above relation is therefore equivalent to
So if we took another point R on the line, of co-ordinates (x″, y″), we should find that y″/(x″ − a) is also equal to the above expressions; in other words, y/(x − a) has the same value for all points (x, y) on the line; it is a constant, i.e. it depends only on the position of the line, and not on the particular point P, Q, R, … chosen on it.
If it has the value c, then
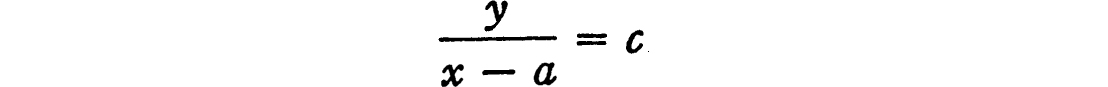
or
y = c(x − a).
This relation is known as the equation of the straight line. It is, as we have seen, determined by the position of the line; and conversely, if the equation is given, the position of the line can be found.
If we think of an equation as something to be solved, well, we can solve it; i.e., if x is given we can determine y from the equation, or if y is given, we can solve it for x; the solution is
It is easy to write down the equations of some special straight lines. The equation of the x-axis is y = 0. A straight line above the x-axis, everywhere at a distance 1 above it, is y = 1. These should be obvious from the definitions. Another example is the equation of the straight line which bisects the angle between the x-axis and the y-axis. Its equation is y = x; this expresses the fact that any point on the bisector is equidistant from the two axes.
From the point of view of algebra, the characteristic feature of the equation of a straight line is that it does not contain any squares or products of x and y, but merely constant multiples of x and y. We express this property by saying that the equation is linear. The general form of a linear equation is lx + my + n = 0, where l, m and n are constants. The constant l which multiplies the variable x is called the coefficient of x; and similarly m is the coefficient of y.
A straight line, in our system, must be defined officially to be what the above argument suggests. It is the set of all number-pairs (x, y) such that a linear equation lx + my + n = 0, with constant coefficients l, m, n, is satisfied.
We must point out also that two equations such as x + y + 1 = 0, and 2x + 2y + 2 = 0, in which the coefficients and the constant term in one are proportional to those in the other, are thought of as corresponding to the same straight line. For the same value of x, each of them gives the same value of y, so that they correspond to the same figure in the diagram.
One often sees statements such as “a straight line has length but no breadth,” and people sometimes wonder how anything can exist which is so lacking in solidity as to have no breadth at all. It is clear of course that such a statement cannot apply to the “straight lines” of the physical world. A line drawn on paper certainly has breadth, and even the boundary between two areas of different colours always has a certain vagueness if we examine it closely enough. In theoretical geometry, a straight line is just something we think of. In Cartesian geometry, what we think of is really a number. For example, one of the straight lines of the Cartesian plane is x = 1; and in the case of this line what it comes to is simply that any number is exactly equal to 1, or not equal to 1 at all. Two numbers are either the same or different. They may be nearly equal, but they do not merge imperceptibly into one another.
We want to define something in our system of geometry which corresponds to the ordinary idea of distance in physical space. In one-dimensional geometry, the “distance” between the “points” represented by the numbers x and x′ can be defined as being their difference, x′ − x. This is reasonable, since if the points coincide the distance between them should vanish, while if they differ greatly it should be large. If we do not want to attach a directional meaning to the distance, we must take it to be x′ − x or x − x′, whichever is positive.
In two-dimensional geometry, that is, the geometry of number-pairs (x, y), we want to define the distance between the point P represented by (x, y), and the point Q represented by (x′, y′). Consider first the case in which the two y’s are the same, so that Q is (x′ y′). In this case, following the suggestion of one-dimensional geometry, it is natural to define the distance between P and Q to be x − x′ or x′ − x, whichever is positive. If also x = x′ then the two points are identical, and the distance between them conveniently reduces to 0.
Similarly if the two points considered are (x, y) and (x, y′), with the same x, the distance between them is defined to be y − y′ or y′ − y, whichever is positive.
To proceed to the general case, in which x is not equal to x′ and y is not equal to y′, we have to borrow some ideas from Euclidean geometry. We shall assume in particular that the reader knows the famous theorem of Pythagoras, about the sides of a right-angled triangle. We do this as a purely temporary measure, in order to suggest some interesting formulae. Later it is these formulae themselves which will provide our official definitions.
The theorem of Pythagoras is that the square on the hypotenuse of a right-angled triangle is equal to the sum of the squares on the other two sides. If PQR is such a triangle, with R as the right angle, this means that PQ2 = PR2 + QR2. Now in Cartesian geometry, a straight line joining two points (x, y) and (x′, y), with the same y, is usually thought of as being at right angles to one joining two points (x, y) and (x, y′) with the same x. If P is (x, y), Q is (x′, y′), and R is (x′, y), then, according to this, PR will be at right angles to RQ.
If we are to reproduce in our Cartesian system Euclid’s idea of distance and so also Pythagoras’ theorem, we must therefore define the square of the distance between the points P(x, y) and Q(x′, y′) to be
(x − x′)2 + (y − y′)2.
This definition applies to any two points in the plane; for example if y′ = y, so that Q coincides with R, it reduces to (x − x′)2, as we should expect.
For the time being, we do not define “distance,” but only “square of distance.” The reader may think that this is a curious way to proceed, but the definition of distance presents difficulties which we are not yet in a position to surmount. If it makes the reader feel any better about this, we could call square-of-distance “separation” or something of the kind. We should then have defined the separation between two points, and its relation to the distance (if there is one) must be left over for the moment.
In Euclidean geometry, parallel straight lines are straight lines which never meet. We have to see what this corresponds to in Cartesian geometry. Suppose that the two lines are represented by the equations
lx + my + n = 0 and l′x + m′y + n′ = 0.
Then they are parallel if l/l′ = m/m′, i.e., lm′ = l′m. For example
x + 2y + 1 = 0 and 3x + 6y + 2 = 0
are parallel.
To prove this, let us suppose that the two lines do meet; i.e. that there are numbers x and y such that both equations are true. Then we shall also have
l′(lx + my + n) − l(l′x + m′y + n′) = 0.
On multiplying out, it is seen that the coefficient of x is zero, and so is the coefficient of y, in view of the relation lm′ = l′m. All that is left is l′n − ln′ = 0. But, if this is true, then l, m, and n are proportional to l′, m′ and n′, so that the two lines are identical. If we exclude this case, the assumption that the two lines meet leads to a contradiction, and so cannot be true.
We can of course avoid an appeal to the principles of Euclidean geometry by taking the relation lm′ = l′m as the definition of parallelism. This in fact is the most convenient official definition in a number-geometry. But some such argument as the above is needed in order to show how the official definition arises.
Perpendicular straight lines are straight lines at right angles. But what is a right angle?
Practical men always knew what a right angle was. It was the angle of a tile such that four identical tiles would always fit together exactly on a flat floor, whichever way round you took them. In an ideal system it is, however, not quite so easy to define a right angle.
Again we shall borrow an idea from Euclid. In Euclid, if PO is perpendicular to AOB, AO being equal to OB, then PA = PB. Now let AOB be represented by the equation lx + my = 0, and let A be (m, −l), and B(−m, l). Let OP be represented by the equation l′x + m′y = 0, and let P be (m′, −l′). Then the squared-distance PA2 is (m′ − m)2 + (l′ − l)2, and the squared-distance PB2 is (m′ + m)2 + (l′ + l)2. Written in full, these are l2 + l′2 + m2 + m′2 − 2ll′ − 2mm′ and l2 + l′ + m2 + m′2 + 2ll′ + 2mm′ respectively, and the difference between them is 4ll′ + 4mm′. They are equal if this is zero, or, what comes to the same thing, if ll′ + mm′ = 0.
This can therefore be taken as our official definition of perpendicular lines. For example, 3x + 4y = 0 is perpendicular to 4x − 3y = 0. If we consider equations with a constant term, it is easily seen that this does not enter into the argument; for example, 3x + 4y + 1 = 0 is perpendicular to 4x − 3y + 2 = 0.
As a particular case, the lines x = 0 and y = 0, i.e., the “axes,” are perpendicular, since they correspond to the values l = 1, m = 0, l′ = 0, m′ = 1. This does not necessarily mean that the axes must be represented by lines drawn on paper at right angles, in the popular sense. It is usual and convenient to do so, but, if we stick faithfully to our “official” definition, axes drawn in any other way ought to do equally well.
In Euclidean geometry, a circle consists of all those points which are at the same given distance from a fixed point. In our system, we must say that the point P, or (x, y), lies on a circle with centre C, or (a, b), if the separation or square-of-distance between P and C is a constant. If the constant is denoted by k, this means that x and y are connected by the relation
(x − a)2 + (y − b)2 = k.
This is the equation of the circle. It corresponds in the Cartesian analysis to the circle, in the same way that the equations previously considered corresponded to straight lines. The constant k corresponds to the square of the radius in Euclid’s system; the radius itself, like “distance,” is left undefined for the moment.
There are many other interesting curves in plane geometry which correspond to simple equations connecting x and y. For example, the equation y2 = x represents a parabola, celebrated as the path of a projectile (though this parabola is lying on its side). The equation x2 + 4y2 = 1 represents an ellipse, celebrated as the orbit in which a planet moves round the sun. The equations x2 − y2 = 1 and xy = 1 represent hyperbolas. All these are the curves which have been studied since ancient times under the name of conic sections.
Life in three dimensions is perhaps too familiar to require description here. What we have to do is to represent by a mathematical system the space occupied by solid objects such as ourselves.
Consider an object in an ordinary room. Its position can be specified by stating the point on the floor which it is vertically above and its height above the floor. The point on the floor is fixed by two measurements from the walls, say x and y. Let its height above the floor be z. Then the position of the object is specified by the set of three numbers (x, y, z).
In solid or three-dimensional Cartesian geometry we therefore identify a point with such a set of three numbers. All the ideas of two-dimensional Cartesian geometry extend easily to three-dimensional geometry. Without going into details, we can say that a plane in solid geometry is represented by an equation of the form
lx + my + nz = c
where l, m, n and c are constants. The squared-distance between two points (x, y, z) and (x′, y′, z′) is defined to be
(x − x′)2 + (y − y′)2 + (z − z′)2.
The equation of a sphere is of the form
(x − a)2 + (y − b)2 +(z − c)2 = k.
Naturally much more can happen in three dimensions than in two, so that three-dimensional or solid geometry is more exciting, if more complicated than two-dimensional or flat geometry.
If it is true that poltergeists can throw solid objects into closed rooms, presumably they require a fourth dimension in which to do it. This is a situation with which (as mathematicians) we are perfectly prepared to cope. We have merely to add a fourth co-ordinate, and identify a point with a set of four numbers, say (x, y, z, w). This provides us with a four-dimensional Cartesian geometry. It is impossible to visualize it, but as a mathematical system it is not much more difficult to handle than three-dimensional geometry. In fact we can introduce any number of dimensions in the same way.
There is another way in which four-dimensional geometry has been used to represent physical space. We can represent time as a fourth dimension. The “points” of this geometry do not correspond to points in space, but to point-events. A point-event is specified by four numbers (x, y, z, t), where t is the time at which the event (supposed instantaneous) occurs. Thus (1, 2, 3, 4) would mean that something happened at the place (1, 2, 3) at 4 o’clock (if t represents the time in hours).
It might be supposed that the association of time with space in this way would serve no useful purpose, since time is usually thought of as something of quite a different kind from space; but in the formulae of relativity this is found not to be true, and it is “space-time” taken as a whole which the relativists always think about.