. In fact it is easily seen that any two straight lines meet in a point, unless the coefficients of x in the two equations are proportional to the coefficients of y. Such equations correspond to parallel lines, which, of course, never meet.We return now to two-dimensional geometry. In Euclidean plane geometry, we are specially interested in the points at which straight lines and circles intersect or meet. We have to consider what corresponds to “intersection” in Cartesian geometry.
Consider for example the two straight lines represented by the equations
x − y = 1, 2x − y = 3.
It is easily verified that each of these equations is satisfied if we take x = 2 and y = 1; that is, the point (2, 1) lies on each line, and is therefore their “point of intersection.” Another example is
x − 2y = 1, 2x − y = 4,
which meet at the point . In fact it is easily seen that any two straight lines meet in a point, unless the coefficients of x in the two equations are proportional to the coefficients of y. Such equations correspond to parallel lines, which, of course, never meet.
Now consider the question of the intersection of a straight line and a circle. Take for example the circle with centre at the origin and squared-radius 4. (Naturally the radius, when it is defined, will be 2.) The squared-distance of the point (x, y) from the “origin” (0, 0) is, by definition, x2 + y2; and for every point on the circle this is equal to the square of the radius, i.e., it is 4. Thus the co-ordinates (x, y) of every point on the circle satisfy the relation x2 + y2 = 4; in other words, this is the equation of the circle.
Let us take as our straight line the bisector of the angle between the axes, which, as we have previously seen, is represented by the equation y = x. This line passes through the centre of the circle. If the mathematics of the situation is to correspond at all to the way in which we visualize it, or to the figures which we draw to represent it, the straight line and the circle certainly ought to intersect.
Now since y = x on the straight line, at a point of intersection we must have x2 + x2 = 4, i.e., 2x2 = 4, so that x2 = 2. It is therefore a question of finding a number x whose square is 2. Clearly such an x cannot be an integer, and we must suppose that it is a fraction, say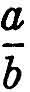 
. We may suppose this fraction reduced to its lowest terms, i.e., that any factors common to a and b have been removed by cancelling; then a and b have no common factor. We thus want To 
= 2, i.e., a2 = 2b2.
Now 2b2 is an even number (a number of which 2 is a factor is called even, a number of which it is not a factor is called odd). Hence a2 must be an even number, and so also a must be an even number, since the square of an odd number is clearly odd. So a has 2 as a factor, i.e., it is of the form 2c, where c is another integer. On the other hand, b is an odd number, because we have supposed that a and b have no common factor, and so b cannot have the factor 2.
Our equation can now be written as 4c2 = 2b2, and hence, dividing each side by 2,
2c2 = b2.
But this shows that b2 is an even number, and so also that b is an even number.
We have thus arrived at a complete contradiction; the argument shows in one way that b is an odd number, and in another way that it is an even number. Something has gone wrong. The only way back to sanity lies in abandoning the assumption that the equation x2 = 2 has a solution. We must admit that it has not.
The result is that, in spite of appearances, the straight line and the circle never meet. Each finds its way through a gap in the other. The existence of such gaps shows that our number-system has grave defects as a way of representing the continuous objects or motions of physical space.
The whole matter can, of course be put into non-geometrical language. A number whose square is equal to a given number is called the square root of the latter. What we have just proved is that there is no exact square root of 2. Actually there is nothing exceptional about 2; 3, 5, 6, 7, 8, and in fact most other numbers have not got square roots.
Now it is very inconvenient to have to admit that there is no square root of 2. Not only does this lead to strange geometrical situations, but it would mean that in all sorts of algebraical problems we should have to distinguish between different cases, according to whether certain numbers had square roots or not. Practically speaking, if 2 has not got a square root it is necessary to invent one.
We have seen that it is impossible to solve the equation 
with integers a and b. It is however possible to divide all fractions 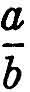, in which a and b are positive, into two classes, according to whether 
is less than 2 or greater than 2. Naturally every number of the former class will be less than every number of the latter class.
A division of all the numbers (i.e., integers and fractions) into two classes, as in the above case, every number of one class being less than every number of the other class, is called a section. The simplest way to attach a meaning to the square root of 2 is to define it as being the section defined above. It would do equally well if we defined it to be the lower class, i.e., the class of numbers a/b with a2 < 2b2, or the corresponding upper class, but there is no reason to prefer one to the other. Whether we call it a section or one class or the other only makes a slight difference to the language to be used, the situation in any case being substantially the same.
We denote the square root of a number x by 
Thus for example 
This curious symbol was once an r, but it has become worn down by constant use.
Naturally the square root of any positive number can be defined in the same way as the square root of 2. For example, the square root of 3 is the section of all numbers a/b into two classes, such that a2 < 3b2 in the lower class, and a2 > 3b2 in the upper class. To be quite consistent, we ought even to define the square root of a number such as 4, which has a square root in the ordinary sense, in this way. The square root of 4 would be the section of all numbers a/b into two classes such that a2 < 4b2 in the lower class, and a2 > 4b2 in the upper class; or, what comes to the same thing, such that a < 2b in the lower class, and a > 2b in the upper class. This may seem a very cumbrous way of getting at something very simple, but it simplifies the logic of the situation.
It must be admitted that we have not been able to define 
in so simple, or it may seem in so satisfactory a way as, for example, 
and it might be thought that, if there are gaps in the sequence of numbers, it would be more honest just to say so. Actually the definition which we have given does all that is required of the definition of a number. Consider for example the sum of the two numbers 
and 
With each of them there is associated a lower class of numbers in the above way, viz., the numbers 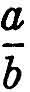such that a2 < 2b2, and the numbers 
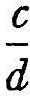such that c2 < 3d2. Now form the class of numbers 
. These numbers are the lower class of a new “section,” which is 
Similarly 
is defined by the section of which the numbers 
form the lower class.
We usually think of 
as something having a
definite numerical value; it is given in tables as
1.4142136 …
Such “values” are apt to make us suppose that is something more concrete than a “section,” but this would be a delusion. All that the above “value” means is that the numbers
are members of the lower class of the section defining 
and that, if we go on far enough with this sequence (whatever it may be), we shall get as near as we like to members of the upper class.
It is convenient to have names by which to distinguish between the integers and fractions used so far, and numbers of the new kind which have just been introduced. We call the integers and fractions rational numbers, and all others irrational numbers. Thus 
is rational, 
is irrational. The reader must get used to using words, with which he is familiar in other connections, as the technical terms of mathematics, of course with different meanings. It might be clearer if we put the technical terms in inverted commas and spoke of “rational” and “irrational” numbers; but it is too late to try to introduce this convention now. We can only ask the reader to insert inverted commas mentally for himself, wherever they are appropriate. I hope the reader will agree at any rate that “irrational” numbers are not irrational, in the dictionary sense of “not in accordance with reason.”
The set of all the rational and irrational numbers form the complete set of numbers which are required for ordinary calculation. It might be thought for one awful moment that, if we operated again with irrational numbers in the same way as we did with rational numbers, we should come upon a new class of super-irrationals, and so on endlessly. But this is not so. Nothing fresh emerges from this process. The irrational numbers already defined are the only ones which exist.
The extension of the idea of number to include irrational numbers leads to a corresponding extension of Cartesian geometry. Previously, a point in Cartesian two-dimensional geometry was a number-pair (x, y), where x and y were both rational. We now consider also as points number-pairs (x, y), where either x or y or both may be irrational.
This enables us to complete our geometry in a very satisfactory way. For example, in the problem of the intersection of the straight line y = x with the circle x2 + y2 = 4, we can now say that they intersect at the point 
they also intersect at the point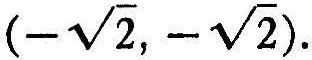 
This corresponds exactly to what we should expect from a figure, in which the straight line and circle certainly look as if they intersected in two points.
It is now possible also to define the distance between any two points in Cartesian geometry. In two dimensions, the distance between the points (x, y) and (x′, y′) is
It is the square root of what we previously called the “separation.” For example, the distance between the point (1, 1) and the “origin” (0, 0) is 
In the previous system this distance did not exist, because it was not a rational number. The introduction of irrational numbers enables us to make general statements about lengths and distances as we should like to, without concerning ourselves about the nature of their particular values.
In three dimensions, the distance between the points (x, y, z) and (x′, y′, z′) is of course
We can even define distance in four or more dimensions in a similar way.
The discovery that irrational numbers are required to make geometry do what is expected of it was made by the ancient Greeks. It is one of their most important contributions to mathematics.
The whole apparatus of algebraical formulae extends at once to irrational numbers. For example, a formula such as a2 − b2 = (a − b) × (a + b), proved first when a and b are integers, and next when they are fractions, is now seen to be equally true when one or both of a and b are irrational. In fact the rules of operation with irrational numbers are just the same as those for operations with rational numbers, and such a formula is simply a consequence of these rules, and not of the particular nature of the numbers a and b.
As an example of the advantages of the use of irrational numbers in algebra, let us take the following theorem: the arithmetical mean of any two positive numbers cannot be less than their geometrical mean. The arithmetical mean of two numbers a and b is 
and their geometrical mean is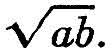 
Expressed as a formula, the theorem is 
The very expression of such a theorem requires the use of irrational numbers; even if a and b are taken to be rational, 
will usually not be rational, so that the theorem has no meaning in the domain of rational numbers, unless a and b are connected in a special way so that is rational. Of course one can get rid of irrationals by squaring each side of the inequality, and replacing it by 
This is in fact what we did in discussing inequalities in Chapter III. We proved there that (a + b)2 ≥ 4ab for any two positive integers a and b. But now we can replace a and b either by fractions or by irrationals, and we can also divide by 4 and take the square root of each side. The theorem of the arithmetical and geometrical means as we have stated it then follows.
The theorem stated here, involving two numbers, is only a particular case of a theorem involving any number of numbers. Suppose that we are considering n numbers a1, a2, … an. Then their arithmetical mean is (a1 + a2 + ··· + an)/n, and their geometrical mean is the nth root of a1a2 … an (i.e., the number whose nth. power is a1a2 … an). The general theorem is still that the arithmetical mean is not less than the geometrical mean. This is a famous theorem of which several different proofs are known, but they are too complicated to be given here.