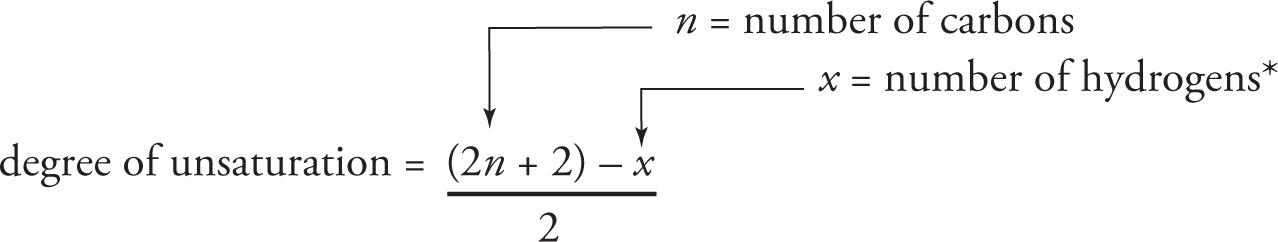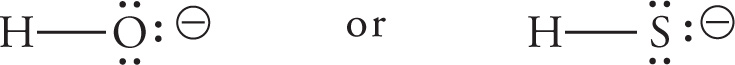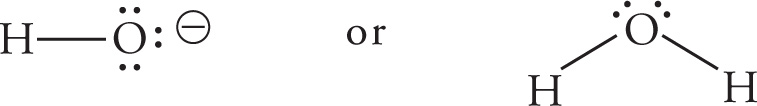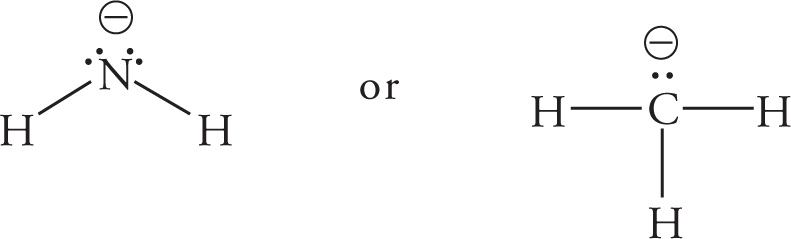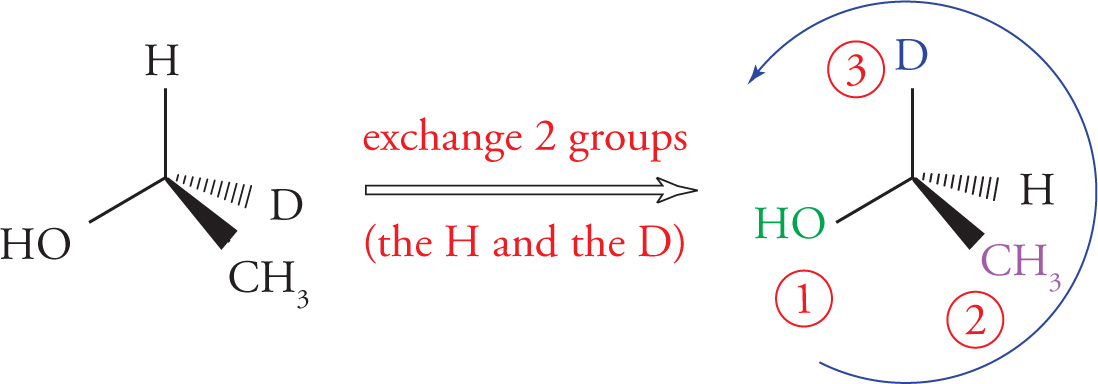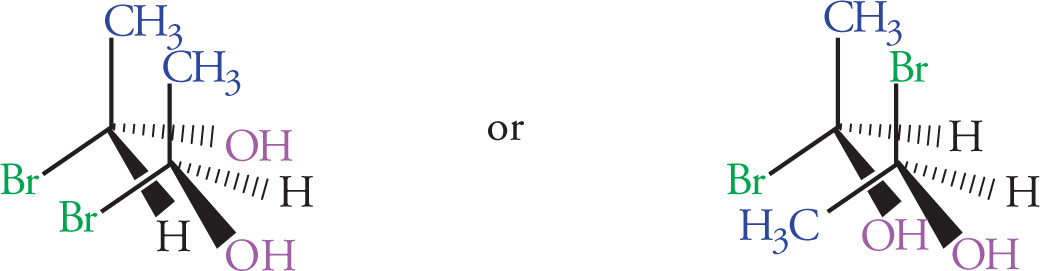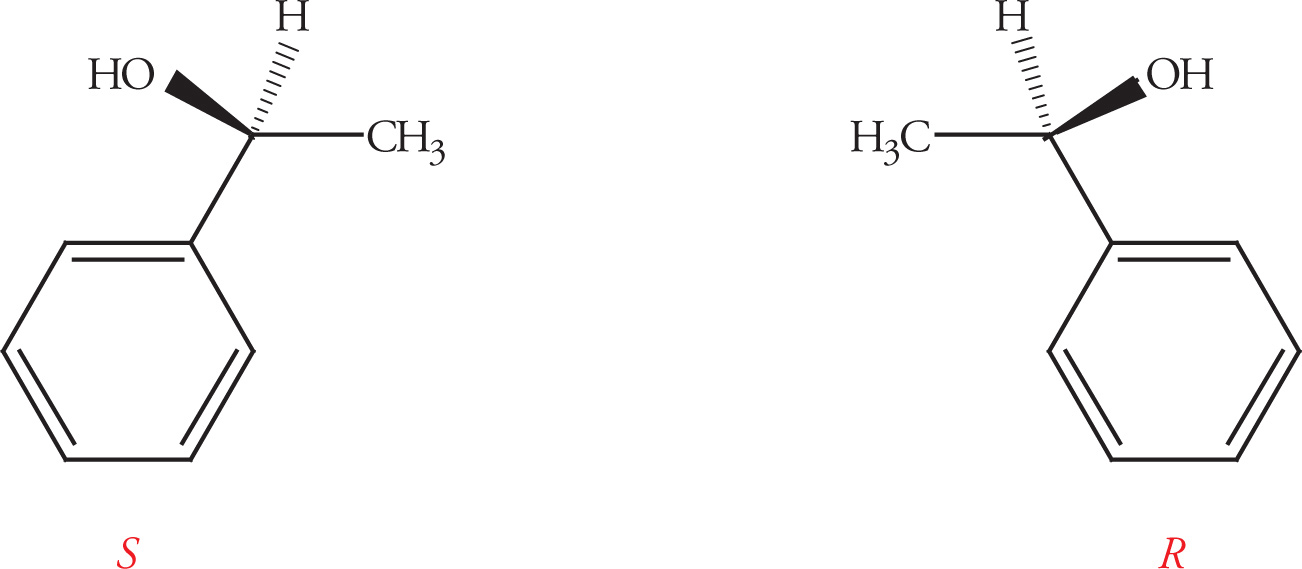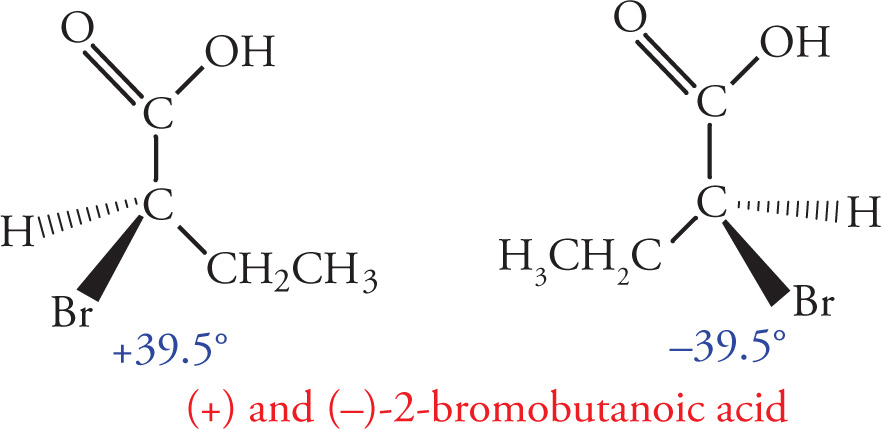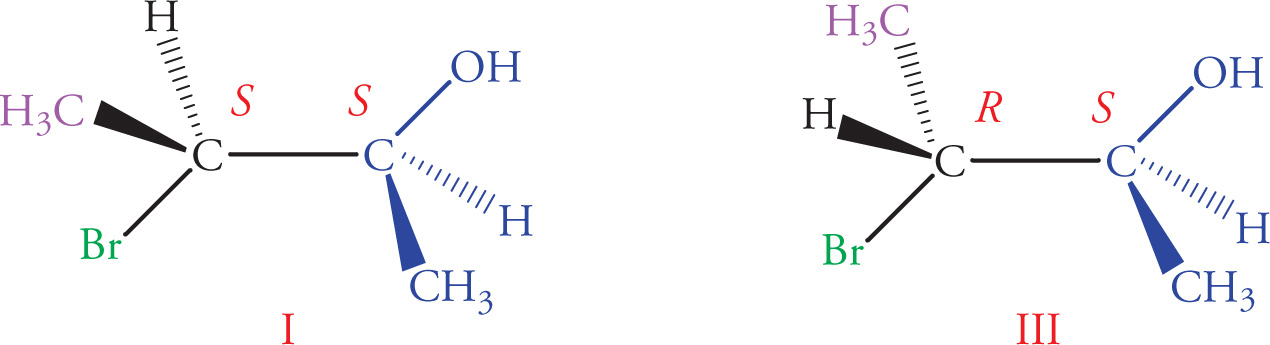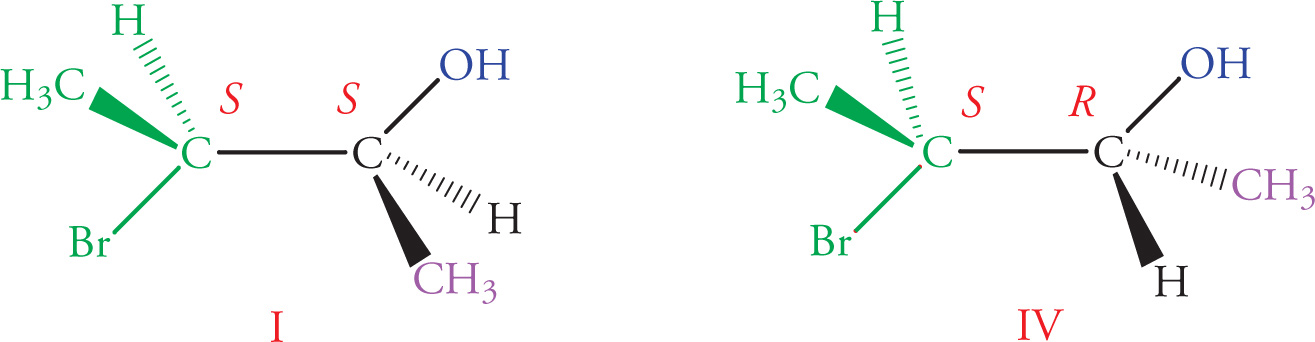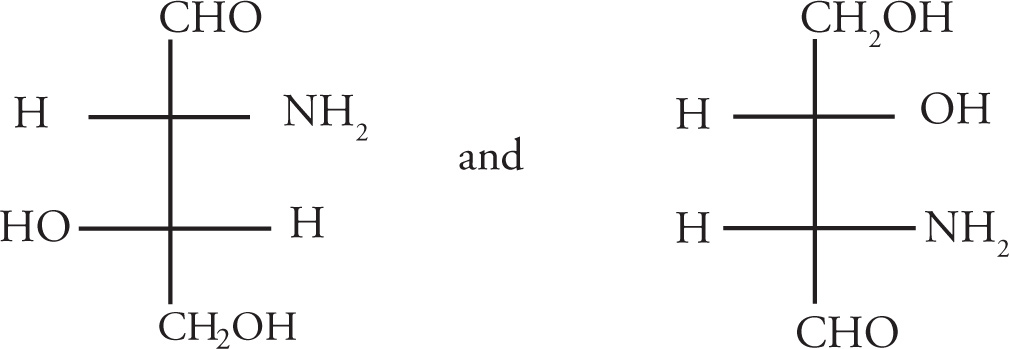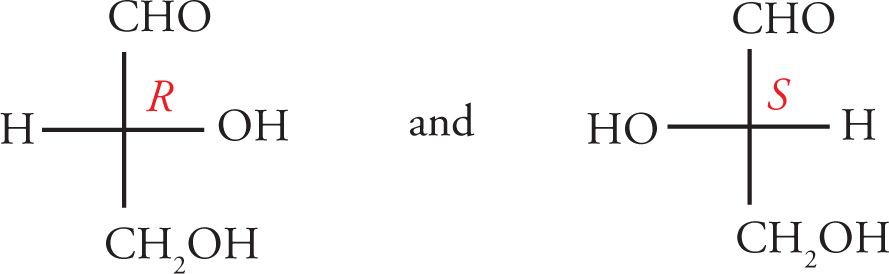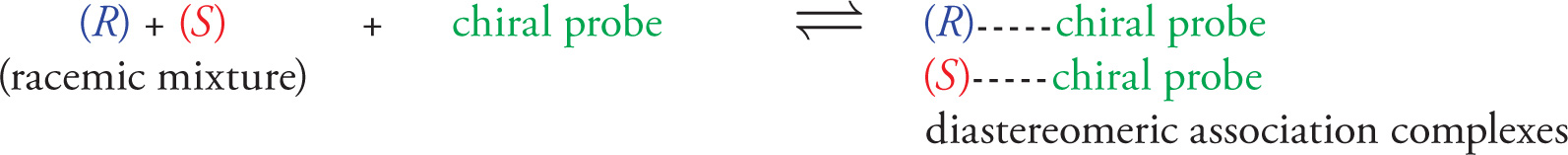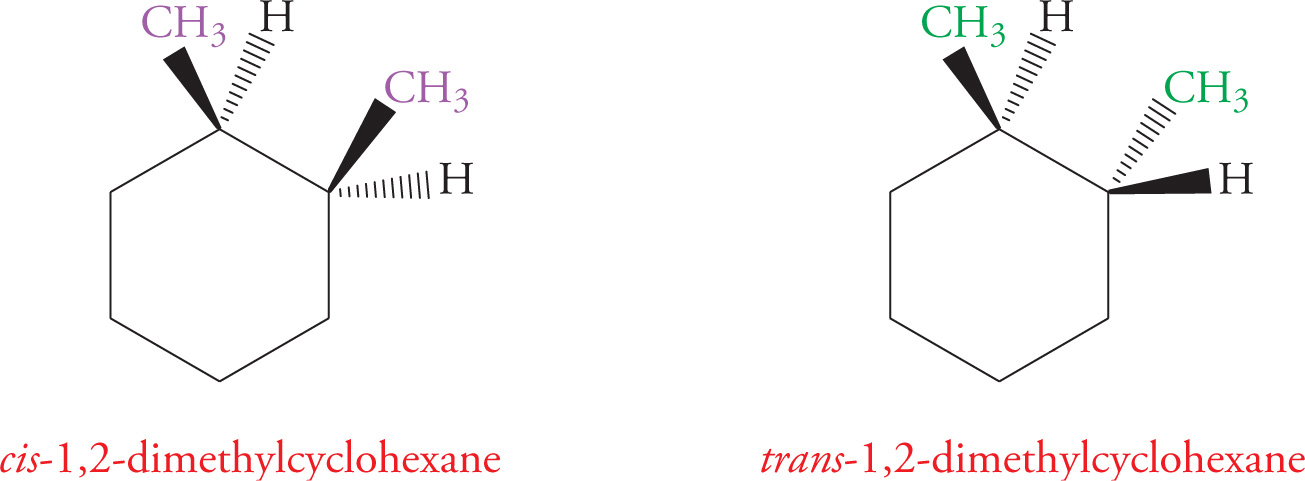Chapter 4
Structure and Stability
4.1 THE ORGANIC CHEMIST’S TOOLBOX
In the following chapters, we will frequently discuss several fundamental principles necessary to understand the reactivity of organic molecules. These “tools” are collected here.
Structural Formulas
By definition, an organic molecule is said to be saturated if it contains no π bonds and no rings; it is unsaturated if it has at least one π bond or a ring. A saturated compound with n carbon atoms has exactly 2n + 2 hydrogen atoms, while an unsaturated compound with n carbon atoms has fewer than 2n + 2 hydrogens.
* x represents the number of hydrogens and any monovalent atoms (such as the halogens: F, Cl, Br, or I).
Since the number of oxygens has no effect, it is ignored.
For nitrogen-containing compounds, replace each N by 1 C and 1 H when using this formula.
4-Chlorobutene (C4H7Cl) also has one degree of unsaturation, but the number of hydrogens is different. Each halogen atom (fluorine, chlorine, bromine, iodine) or other monovalent atom “replaces” one hydrogen atom, so d = [(2 × 4 + 2)−(7 + 1)]/2 = 1:
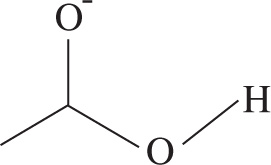
Methoxyethene (C3H6O) also has one degree of unsaturation. Since a divalent atom can take the place of a methylene group, it doesn’t affect the degree of unsaturation, and can be ignored. The calculation for this formula, then, should look like this: [(2 × 3 + 2) − 6]/2 = 1
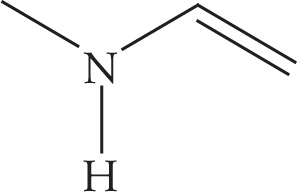
Methyl vinyl amine (C3H7N) has one degree of unsaturation as well. Each nitrogen (or other trivalent atom) “replaces” one carbon and one hydrogen atom. Therefore, adjust the formula to be C4H8, then do the calculation. The new formula thus gives d = [(2 × 4 + 2) − 8]/2 = 1:
Example 4-1: Determine the degree of unsaturation of each of these molecules. Which, if any, are saturated?
(a) C6H8
(b) C4H6O
(c) C20H30O
(d) C3H8O
(e) C3H5Br
(a) d = [(2 × 6 + 2) − 8]/2 = 3.
(b) Just ignore the O, and find that d = [(2 × 4 + 2) − 6]/2 = 2.
(c) Ignoring the O, we get d = [(2 × 20 + 2) − 30]/2 = 6.
(d) Ignore the O, and find that d = [(2 × 3 + 2) − 8]/2 = 0. This molecule is saturated.
(e) Since Br is a halogen, we treat it like a hydrogen, so d = [(2 × 3 + 2) − (5 + 1)]/2 = 1.
Hybridization
Although hybridization theory is covered in more detail in the MCAT General Chemistry Review, it’s useful here to briefly outline how to determine an atom’s hybridization.
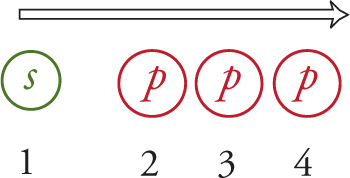
So, since the carbon atom in methane must provide four orbitals, we just count: 1 … 2…3 … 4:
Therefore, the hybridization of the carbon atom in methane is s + p + p + p, which is written as sp3. The sum of the exponents in the hybridization nomenclature tells us how many orbitals of this type are used. So, in methane, there are 1 + 3 = 4 hybrid orbitals. The following table gives the hybridization of the central atom for each of the orbital geometries:
Reaction Intermediates
Some organic reactions proceed through carbocations (carbonium ions), while others make use of carbanions.
It’s essential to understand the stabilities of reaction intermediates, because generally the reactivity of a molecule is inversely related to its stability. This means the molecules that are more stable are less reactive, while higher energy species will be more reactive. This theme will resurface over and over again in organic chemistry, and is a useful rule of thumb to keep in mind when you need to predict how a reaction might proceed.
Inductive Effects
All substituent groups surrounding a reaction intermediate can be thought of as electron-withdrawing groups or electron-donating groups. Electron-withdrawing groups pull electrons toward themselves through σ bonds. Electron-donating groups donate (push) electron density away from themselves through σ bonds. Groups more electronegative than carbon tend to withdraw, while groups less electronegative than carbon tend to donate. On the MCAT, alkyl substituents are always electron-donating groups.
Electron-donating groups tend to stabilize electron-deficient intermediates (carbocations), while electron-withdrawing groups tend to stabilize electron-rich intermediates (carbanions). The stabilization of reaction intermediates by the sharing of electrons through σ bonds is called the inductive effect.
An alternative explanation would be to consider the stability of the conjugate bases of these acids.
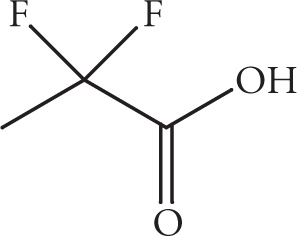
The chlorine atoms in the trichloroacetate anion distribute the negative charge better, making it more stable than the acetate anion. Therefore, because trichloroacetate anion is a weaker base (is more stable) than acetate anion, trichloroacetic acid is a stronger acid than acetic acid. Acidity will be reviewed in more detail a bit later in the Toolbox.
Resonance Stabilization
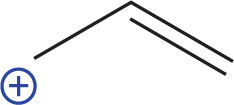
While induction works through σ bonds, resonance stabilization occurs in conjugated π systems. A conjugated system is one containing three or more atoms that each bear a p orbital. These orbitals are aligned so they are all parallel, creating the possibility of delocalized electrons.
The electrons in the π bond can interact with the empty p orbital on the carbon bearing the positive charge. This is illustrated by the following resonance structures:
The electron density is spread out—delocalized—over the entire 3-carbon framework in order to stabilize the carbocation. So, we might say of the allyl cation that both the electrons and the positive charge are delocalized.
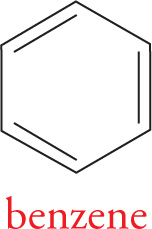
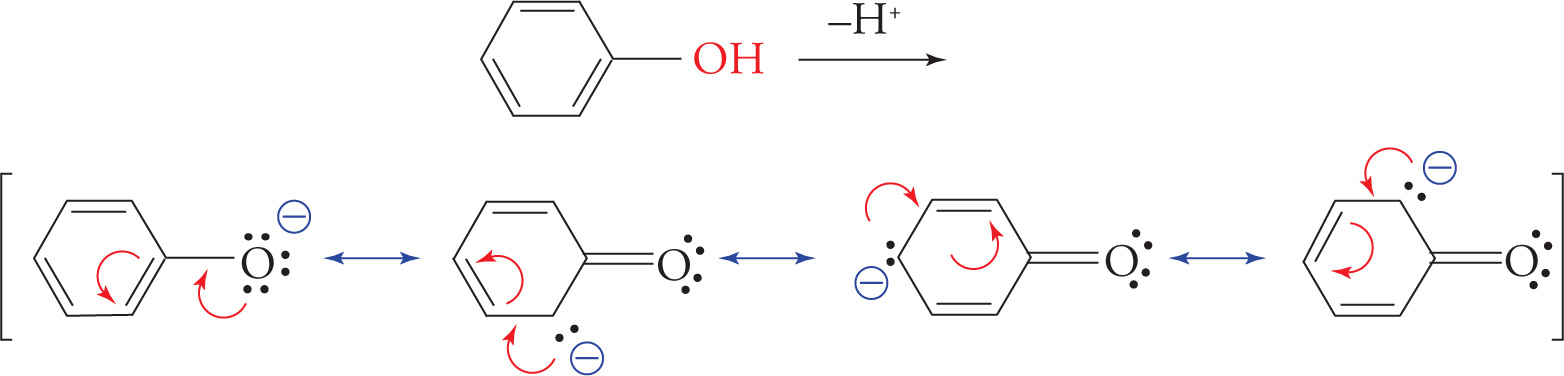
Thus one might expect two distinct carbon-carbon bond lengths: one for the single bonds, and one for the double bonds. Yet experimental data clearly demonstrate that all the C—C bond lengths are identical in benzene. All the carbons of benzene are sp2 hybridized, so they each have an unhybridized p orbital. Two structures can be drawn for benzene, which differ only in the location of the π bonds. The true structure of benzene is best pictured as a resonance hybrid of these structures. Perhaps a better representation of benzene shows both resonance contributors, like this:
Notice that these resonance structures differ only in the arrangement of their π electrons, not in the locations of the atoms. All six unhybridized p orbitals are aligned parallel with one another. This alignment of adjacent unhybridized p orbitals allows for delocalization of π electrons over the entire ring. Whenever we have a delocalized π system (aligned p orbitals), resonance structures can be drawn.
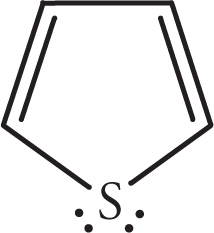
Here the sulfur atom has two pairs of non-bonding electrons. Notice that these electrons are one atom away from two π bonds. One pair of these electrons is actually in an unhybridized p orbital, such that it can be delocalized into the cyclic π system. Here are the representative resonance structures:
The other pair of electrons, however, is in a hybrid orbital and cannot delocalize into the π system. Here the delocalization of sulfur’s electrons imparts aromatic stability to the molecule. The hybridization of the sulfur is therefore most correctly represented as sp2.
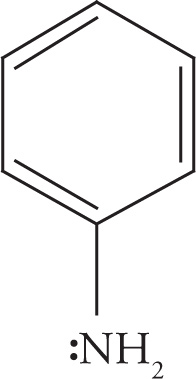
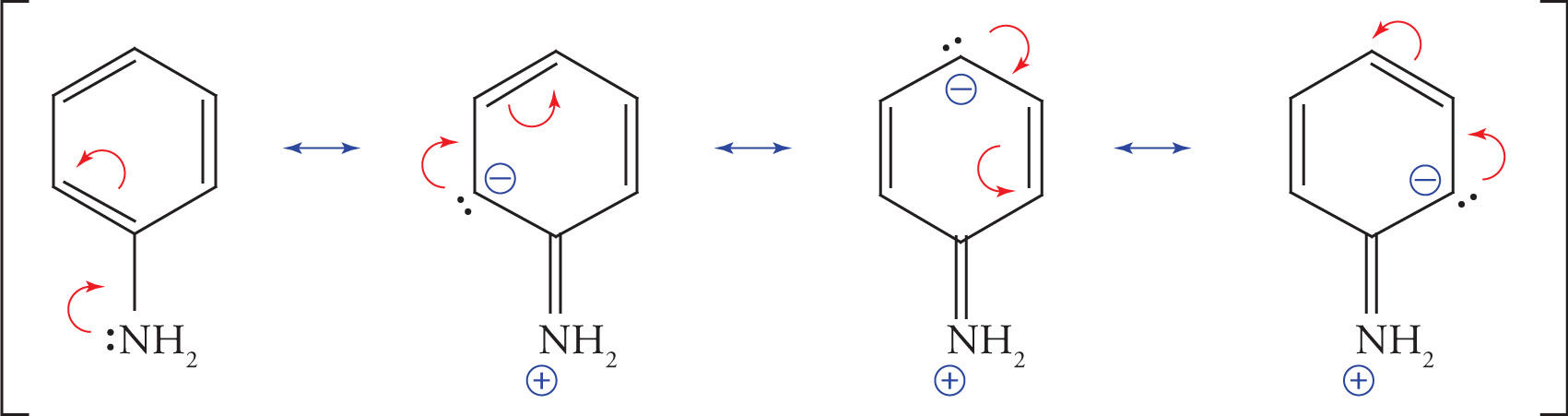
The nitrogen in aniline has an unshared electron pair that is one atom removed from a cyclic π system. Again these electrons can be delocalized by overlap of the lone pair-containing orbital with the p orbitals of the benzene ring. This can be demonstrated by the following resonance structures:
In this case, the delocalization of the nitrogen’s electrons disrupts the aromaticity of the benzene ring and is therefore less favorable. Experimental determination of the nitrogen’s bond angles reveals that they are actually intermediate between 120° and 109°, so the hybridization of the nitrogen can best be described not as sp2 or sp3, but as something intermediate between them. The important point, however, is that the electrons are at least somewhat delocalized into the π system. Therefore, the nitrogen’s hybridization is not strictly sp3.
(a) i) sp2, 120° ii) sp2, 120° iii) sp2, 120° (The lone pair is delocalized, so it’s not counted.) iv) sp3, 109° v) sp2, 120° vi) sp2, 120°
(b) i) sp3, 109° ii) sp3, 109° iii) sp3, 109°
(c) i) sp3, 109° ii) sp2, 120° iii) sp3, 109°
(d) i) sp2, 120° ii) sp2, 120° iii) sp2, 120° iv) sp2, 120°
(e) i) sp3, 109° ii) sp3, 109° iii) sp2, 120° iv) sp, 180° v) sp, 180°
(f) i) sp3, 109° ii) sp, 180° iii) sp3, 109° iv) sp3, 109°
1. Resonance structures can never be drawn through atoms that are truly sp3 hybridized. Remember that an sp3-hybridized atom is one with a total of four σ bonds and/or lone electron pairs.
No resonance structures possible!
No resonance structures are possible with these electrons.
No resonance structures are possible with these electrons.
2. Resonance structures usually involve electrons that are adjacent to (one atom away from) a π bond or an unhybridized p orbital. Here are some examples of molecules that are resonance stabilized:
3. Resonance structures of lowest energy are the most important. Remember that the evaluation of resonance structure stability involves three main criteria:
a. Resonance contributors in which the octet rule is satisfied for all atoms are more important than ones in which it is not. This is the most important of the three criteria listed here and takes priority over items b and c below.
b. Resonance contributors that minimize separation of charge (formal charge) are better than those with a large separation of charge.
c. In structures with formal charge(s), the more important resonance contributor has negative charges on the more electronegative atom(s), and positive charge(s) on the less electronegative atom(s).
Now that we can identify valid resonance structures of any given molecule and rank those resonance structures based on their relative energies, let’s use this information to demonstrate the close relationship between stability and reactivity by examining acidity.
Acidity
While acids and bases will be covered in detail in Chapter 11 of the MCAT General Chemistry Review, we will now examine how the organic chemistry principles we’ve just discussed can help explain the acidity of a compound, as well as help us understand the relative acidity of several functional groups.
Electronegativity Effects
For example, let’s compare the acidity of an alcohol like propanol and an alkane like propane. If we compare the stability of each conjugate base, we find that the alkoxide ion is a relatively stable species compared to the carbanion since the negative charge is located on the very electronegative oxygen atom rather than on a carbon atom.
Therefore, alcohols are considerably more acidic than hydrocarbons.
Resonance Effects
Let’s next compare the relative acidities of propanol and propanoic acid.
In the carboxylate ion, the electrons on the negatively charged oxygen are adjacent to a π bond and can therefore be delocalized. This leads to greater stability of the carboxylate anion and thus to higher acidity of the conjugate acid.
Note that the two resonance structures of the carboxylate ion are equivalent, and are therefore of equal energy.
In contrast, the electrons on the oxygen of the propoxide ion below have no adjacent empty p orbital or π system. Therefore, they are localized and highly reactive, making an alkoxide ion a very strong base (much like OH−) and the alcohol a weak acid.
This makes carboxylic acids, as their name suggests, much more acidic than alcohols.
In acetone, the hydrogens next to the carbonyl are acidic because there are two resonance structures for the conjugate base of a ketone. One is stable with the negative charge on oxygen, and one is higher in energy with the negative charge on carbon. Even though it has resonance, it is less acidic than cyclopentanol (see below) because some of the charge resides on the carbon; rank 2nd.
There are no possible resonance structures for this molecule, but the negative charge resides on an electronegative oxygen; rank 3rd.
Four resonance structures are possible for the phenoxide ion because the negative charge on the oxygen is adjacent to a benzene ring. However, they are not all of equivalent energy because the negative charge resides on the less electronegative C in three of the four structures. The delocalization of charge means that a phenol (−OH group attached to a benzene ring) is more acidic than an alkyl alcohol; rank 4th as the strongest acid.
Note that the phenol on the previous page would still be less acidic than a carboxylic acid since both resonance structures of a carboxylate ion have the negative charge on oxygen, rather than the less electronegative carbon in the phenoxide ion.
Inductive Effects
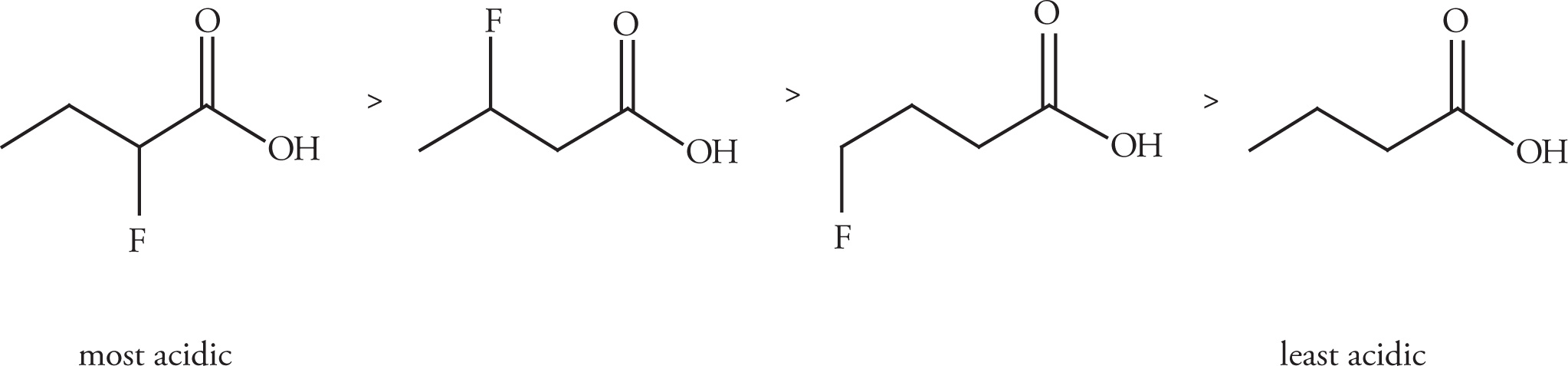
As we’ve just learned, the acidity of carboxylic acids compared to alcohols results from the resonance stability of the carboxylate anion. In addition, Example 4-2 briefly illustrated how electron-withdrawing substituents next to the carboxylic acid group can increase the acidity of this (or any) functional group by increasing the stability of the negative charge on the anion. To expand upon this idea, inductive effects decrease with increasing distance; the closer the electron-withdrawing group is to the acidic proton (or the negative charge on the conjugate base), the greater the stabilizing effect. The following order of acidity for the isomers of fluorobutanoic acid should help clarify this point.
Order of Acidity
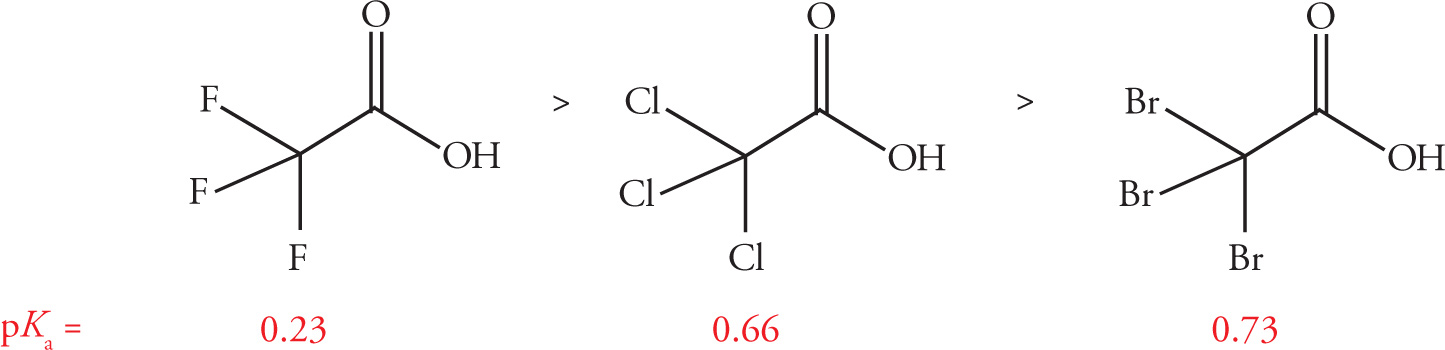
The magnitude of the effect is also dependent on the strength of the electron withdrawing substituent. In general, the more electronegative a substituent is, the greater its inductive effect will be. As shown below, while trifluoro-, trichloro-, and tribromoacetic acid all have substantially lower pKa values than standard acetic acid (pKa = 4.76), the trend in their acidities mirrors the electronegativity of their respective inductive group.
Example 4-5: Rank the following nine compounds in order of decreasing acidity.
Effects of Substituents on Acidity
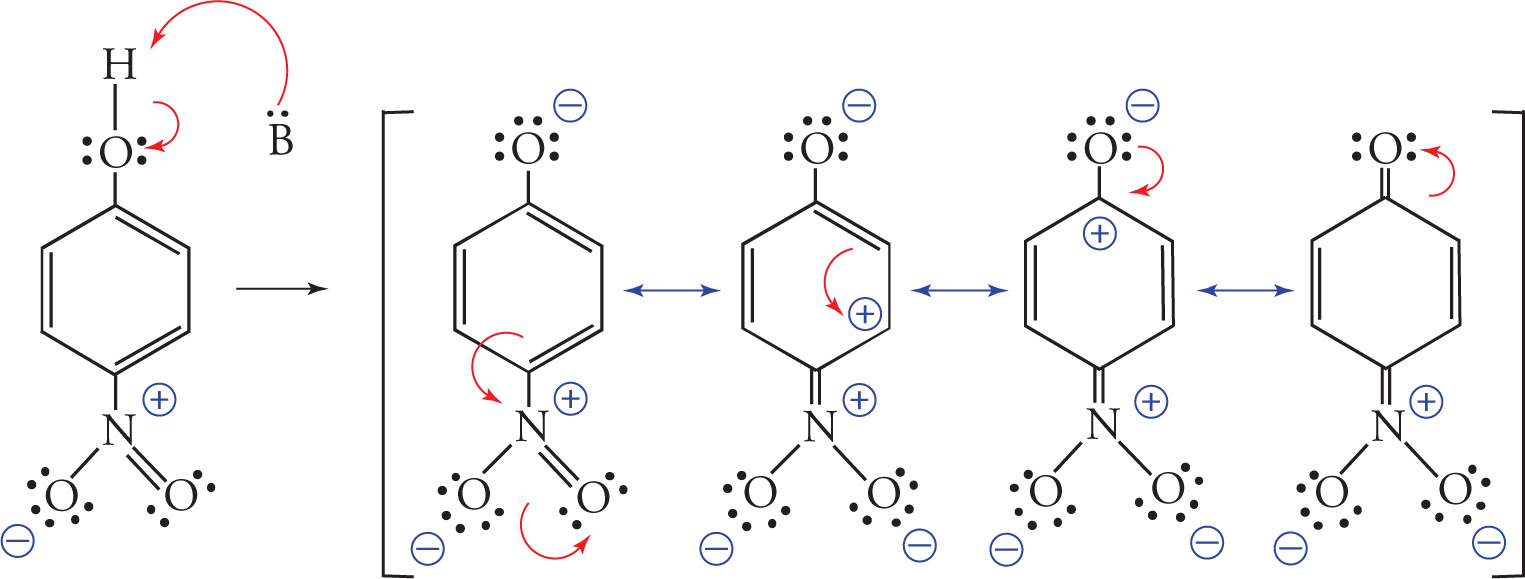
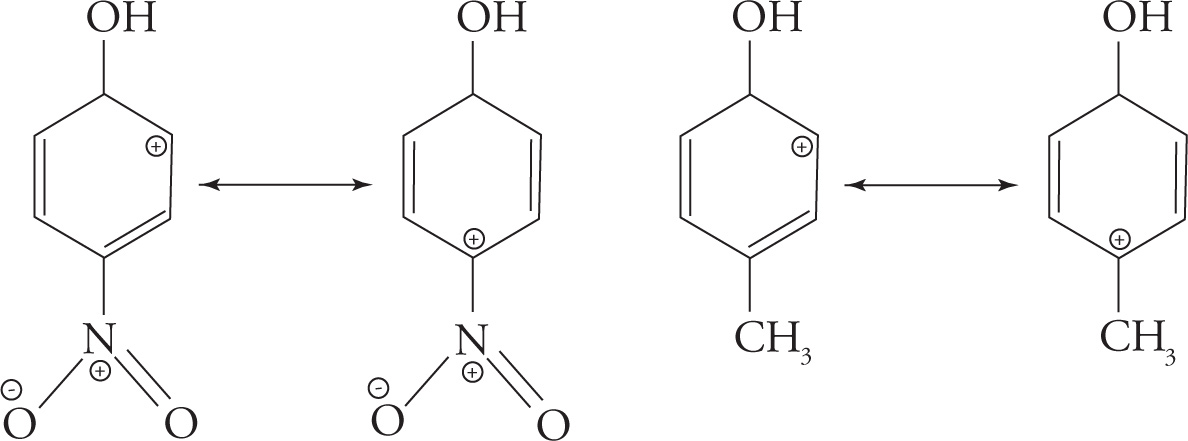
Electron-withdrawing substituents on phenols increase their acidity. As an example, consider para-nitrophenol. The nitro group is strongly electron withdrawing and greatly stabilizes the phenoxide ion through resonance. Once the para-nitrophenol is deprotonated, it’s easy to see how the nitro group can withdraw electrons through the delocalized π system such that the negative charge on the phenoxide oxygen can be delocalized all the way to an oxygen atom of the nitro group. This electron-withdrawing resonance stabilization of the nitro group increases the acidity of para-nitrophenol as compared to a phenol that does not have electron-withdrawing substituents.
On the other hand, consider a substituted phenol that has an electron-donating group rather than an electron-withdrawing group. A good example of this is para-methoxyphenol. Here, it is easy to see how once para-methoxyphenol is deprotonated, the negative charge on the oxygen can be destabilized by the donation of a lone pair of electrons from the methoxy oxygen so a negative charge is placed on a carbon that’s adjacent to the negatively charged phenoxide oxygen. Electron-donating groups tend to destabilize a phenoxide ion and decrease the acidity of substituted phenols.
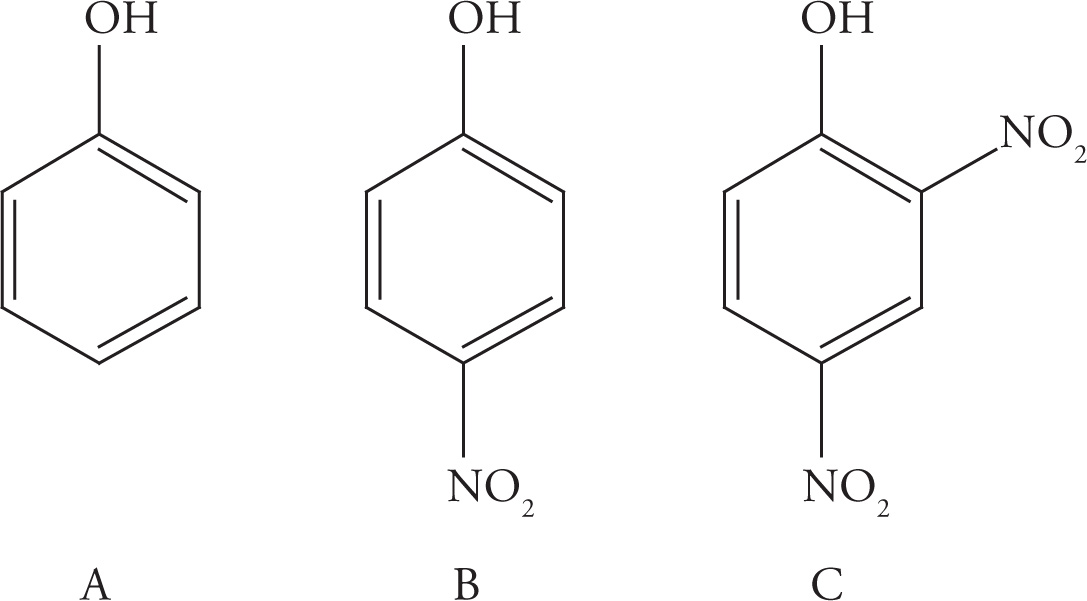
Example 4-6: For each of the following groups of three phenols, rank them in order of decreasing acidity.
(i) C > B > A. Compound C is the most acidic because of the two electron-withdrawing nitro groups. They delocalize the charge of the conjugate base, making C a stronger acid. The para-nitro group in B can also delocalize the charge by resonance, though not as well as the two nitro groups in choice C. Finally, A is the least acidic, since it has no electron-withdrawing groups to stabilize the charge.
(ii) B > A > C. Since the amino group in choice C is similar to the OCH3 group discussed above due to the lone pair of electrons on the N, it is also an electron-donating group. As such, it will decrease the acidity of the phenol, making it the least acidic of the three compounds.
Nucleophiles and Electrophiles
Most organic reactions occur between nucleophiles and electrophiles. Nucleophiles are species that have unshared pairs of electrons or π bonds and, frequently, a negative (or partial negative, δ−) charge. As the name nucleophile implies, they are “nucleus-seeking” or “nucleus-loving” molecules. Since nucleophiles are electron pair donors, they are also known as Lewis bases. Here are some common examples of nucleophiles:
Nucleophilicity is a measure of how “strong” a nucleophile is. There are general trends for relative nucleophilicities:
1. Nucleophilicity increases as negative charge increases. For example, NH2− is more nucleophilic than NH3.
2. Nucleophilicity increases going down the periodic table within a particular group. For example, F− < Cl− < Br− < I−.
3. Nucleophilicity increases going left in the periodic table across a particular period. For example, NH2− is more nucleophilic than OH−.
(a) SH−, since by Trend #2 on the previous page, S is more nucleophilic than O.
(b) OH−, because OH− carries a negative charge, while H2O does not (Trend #1, previous page).
(c) NH2−, since F is more electronegative than N.
(d) CH3−, because N is more electronegative than C.
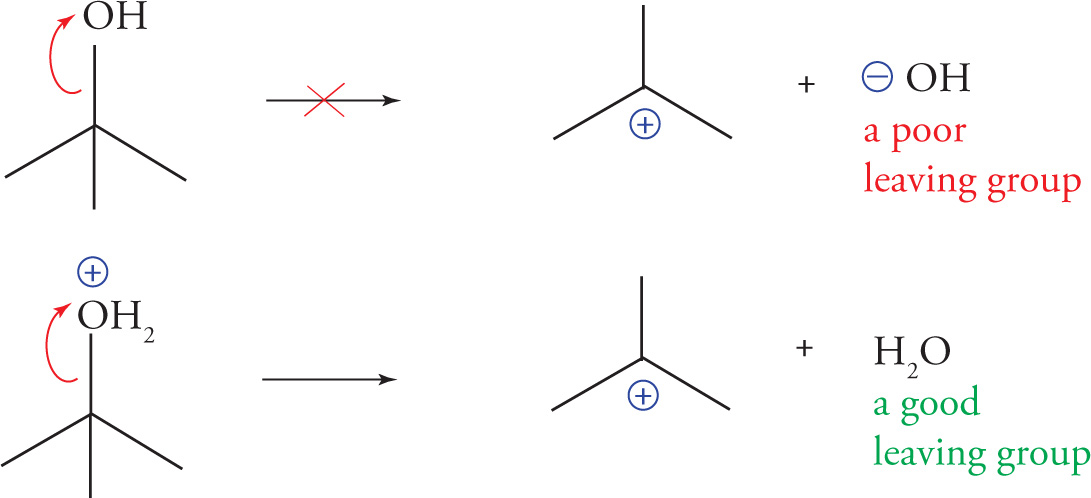
Leaving Groups
While students of organic chemistry often associate the discussion of leaving groups with substitution and elimination reactions, these reaction types are beyond the scope of the MCAT. However, a good understanding of leaving group ability will be useful for several reactions we’ll review in Chapter 6.
Resonance Structures of the Mesylate Leaving Group
Ring Strain
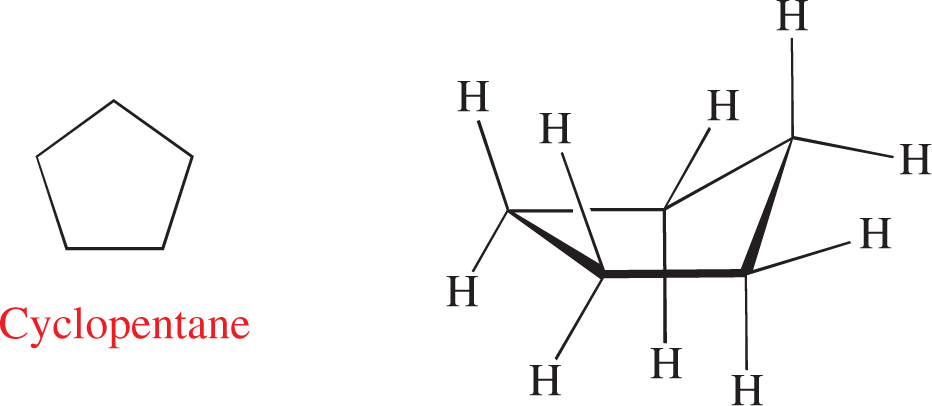
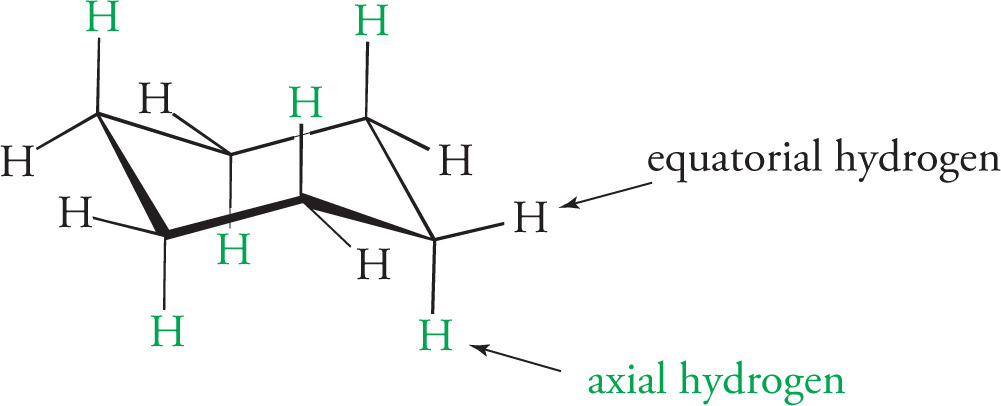
The last item in our toolbox is a feature of organic molecules that, unlike inductive and resonance effects, contributes to instability in a molecule: ring strain. Ring strain arises when bond angles between ring atoms deviate from the ideal angle predicted by the hybridization of the atoms. Let’s examine several cycloalkanes in turn.
Hydrogenation Reactions of Cyclopropane and Cyclobutane
4.2 ISOMERISM
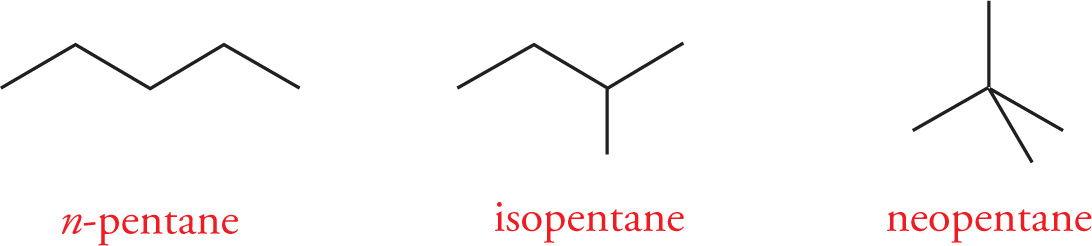
Constitutional Isomerism
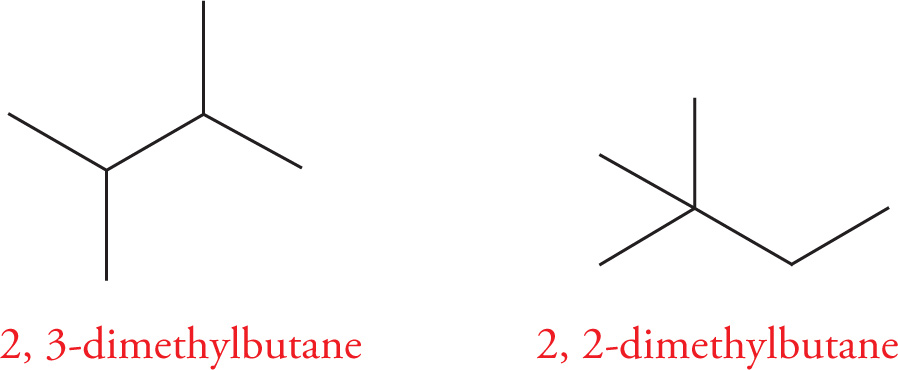
Constitutional (or, less precisely, structural) isomers are compounds that have the same molecular formula but have their atoms connected together differently. Take pentane (C5H12), for example. n-Pentane is a fully-saturated hydrocarbon that has two additional constitutional isomers:
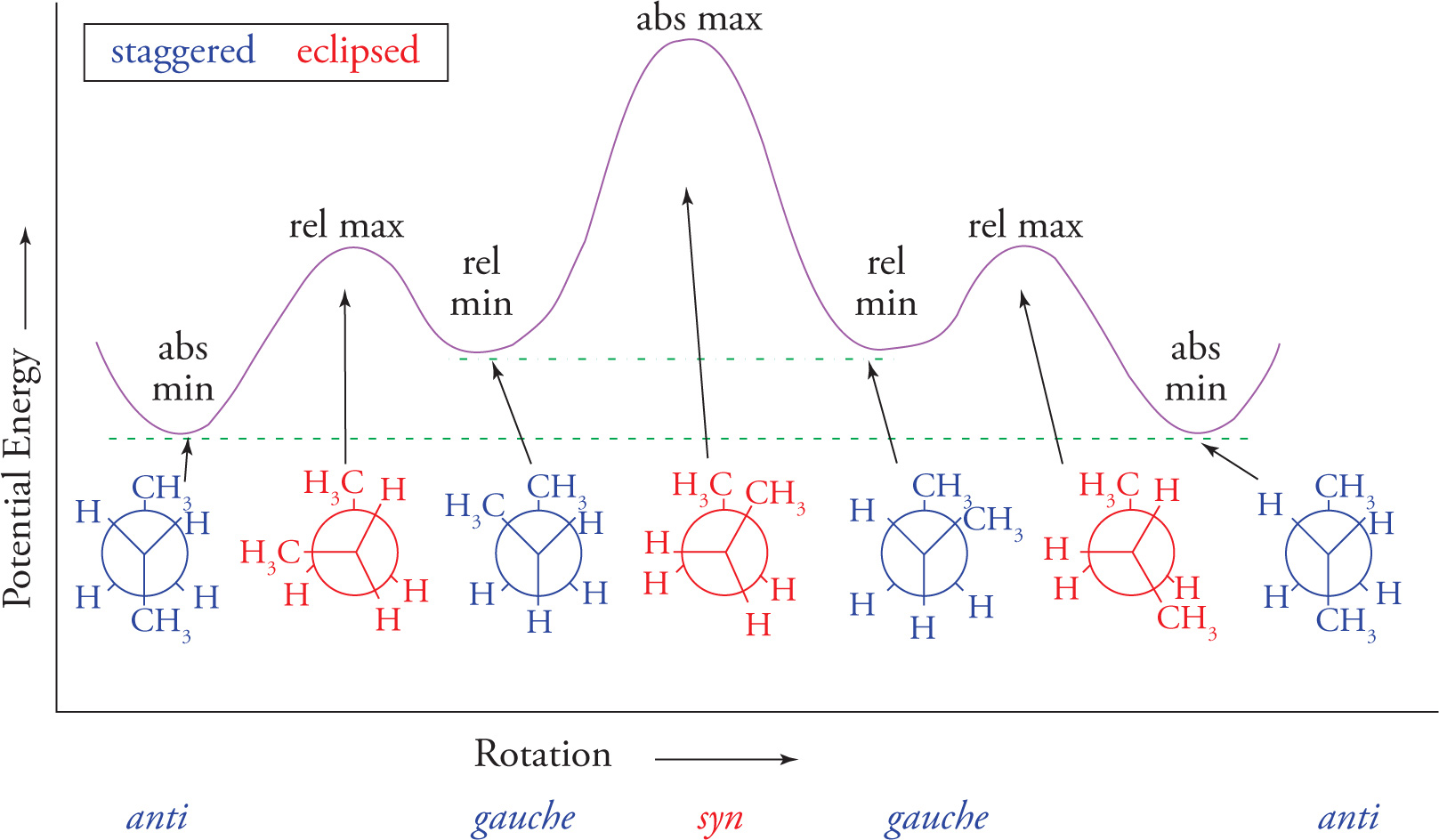
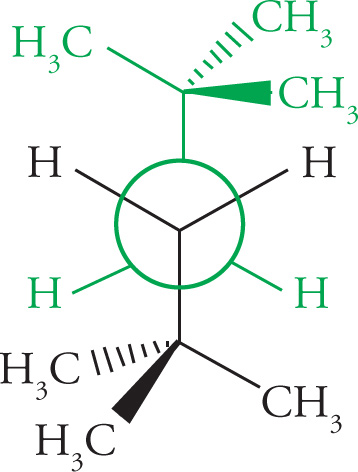
Conformational Isomerism
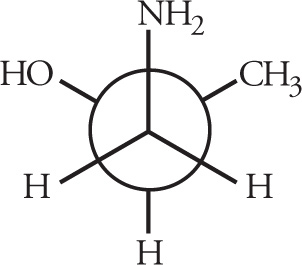
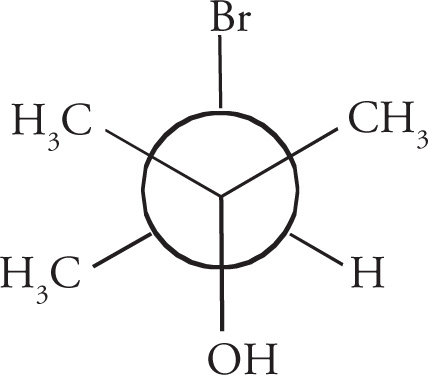
Conformational isomers are compounds that have the same molecular formula and the same atomic connectivity, but differ from one another by rotation about a σ bond. In truth, they are the exact same molecule. For saturated hydrocarbons there are two orientations of σ bonds attached to adjacent sp3 hybridized carbons on which we will concentrate. These are the staggered conformation and the eclipsed conformation. In staggered conformations a σ bond on one carbon bisects the angle formed by two σ bonds on the adjacent carbon. In an eclipsed conformation a σ bond on one carbon directly lines up with a σ bond on an adjacent carbon. Both conformations can be visualized using either the flagged bond notation, or the Newman projection, as shown with ethane (C2H6) below.
The σ bonds should actually directly line up with each other. For clarity here, they are not directly aligned.
(a) 2,2,5,5-tetramethylhexane (about the C3—C4 bond)
(b) 2,2-dimethylpentane (about the C2—C3 bond)
(c) 1,2-ethandiol
(c) In this molecule, the gauche conformation is more stable than the anti conformation, because an intramolecular hydrogen bond can be formed in the gauche but not in the anti conformation.
Stereoisomerism
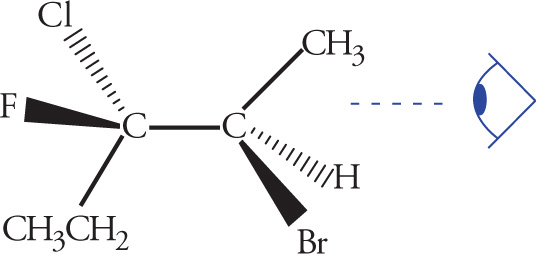
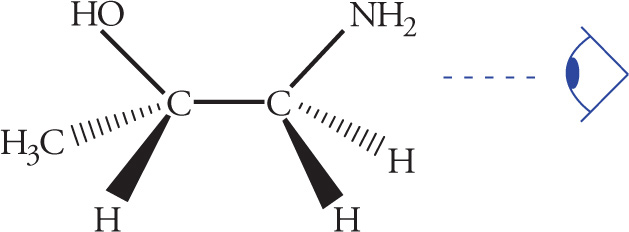
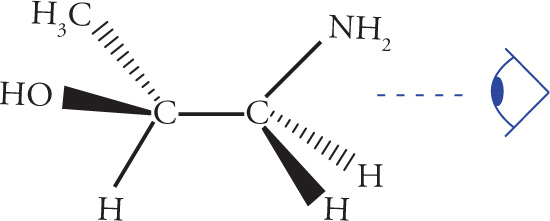
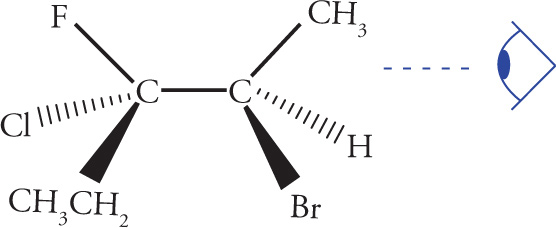
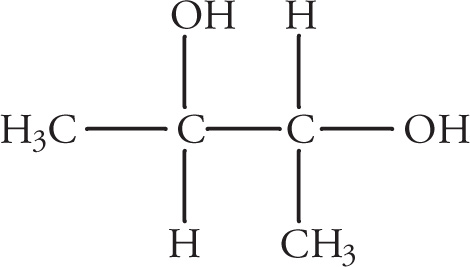
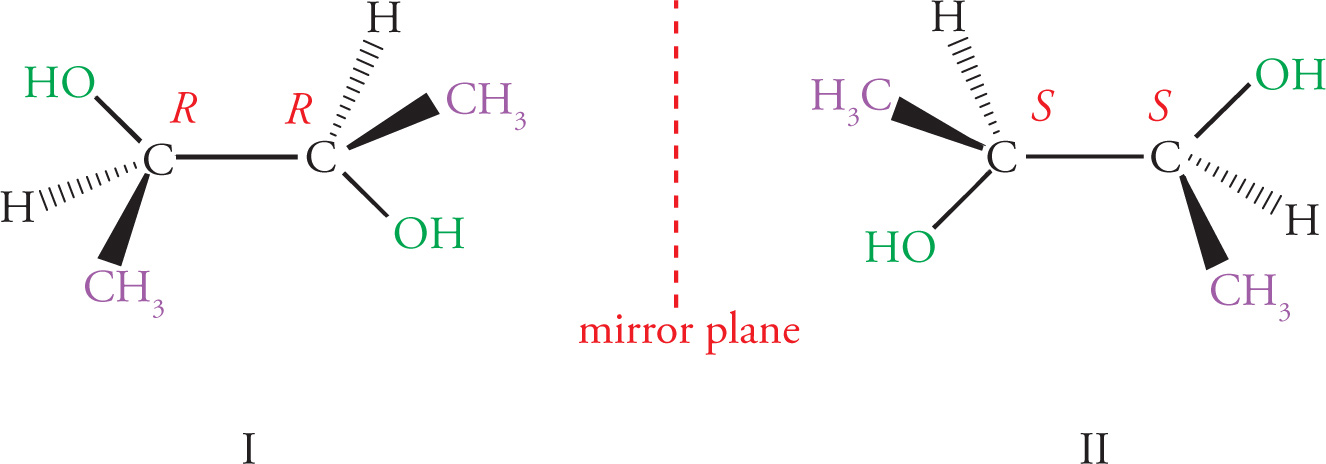
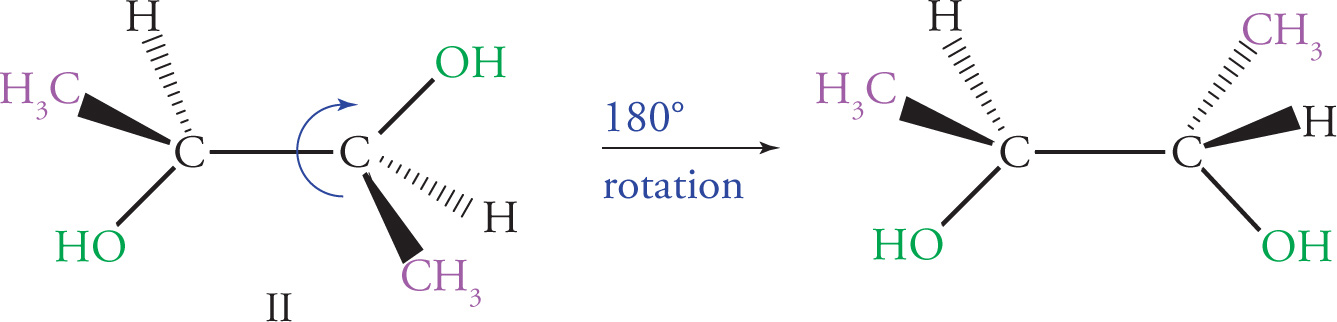
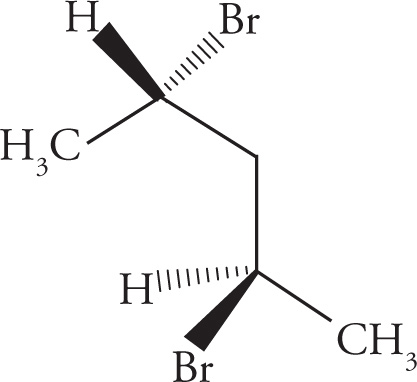
Stereoisomerism is of major importance in organic chemistry, especially when looking at biological molecules, so several questions relating to stereochemistry routinely appear on the MCAT. Stereoisomers are molecules that have the same molecular formula and connectivity but differ from one another only in the spatial arrangement of the atoms. They cannot be interconverted by rotation of σ bonds. For example, consider the following two molecules:
Chirality
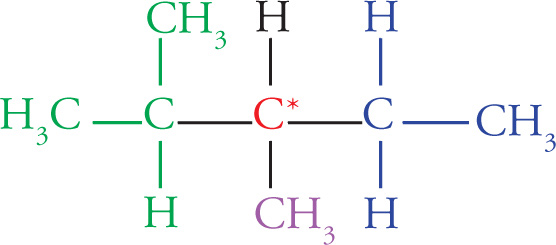
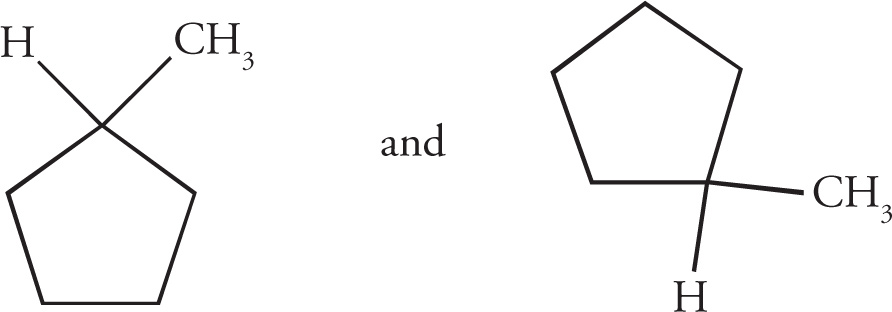
Any molecule that cannot be superimposed on its mirror image is said to be chiral, while a molecule that can be superimposed on its mirror image has a plane of symmetry and is said to be achiral. It’s important that you be able to identify chiral centers. For carbon, a chiral center will have four different groups bonded to it. Note that since a carbon atom has four different groups attached to it, it must be sp3 hybridized with (approximately) 109° bond angles and tetrahedral geometry. Such a carbon atom is also sometimes referred to as a stereocenter, a stereogenic center, or an asymmetric center.
(a) This molecule has no chiral centers.
(b) This molecule has 1 chiral center and, therefore, 2 possible stereoisomers:
(c) There is 1 chiral center and, therefore, 2 possible stereoisomers:
(d) This molecule has 1 chiral center and, therefore, 2 possible stereoisomers:
(e) There are 2 chiral centers and, therefore, 4 possible stereoisomers:
(f) There are 2 chiral centers, which would seem to indicate 4 possible stereoisomers:
However, there are only 3, because the following “2” molecules are actually the same:
(g) This molecule has no chiral centers.
(h) This molecule has 9 chiral centers and, therefore, 29 = 512 possible stereoisomers:
(i) Although there are two chiral centers,
there are 3, not 4 stereoisomers, because—see (f) above—the following “two” molecules are actually the same:
Absolute Configuration
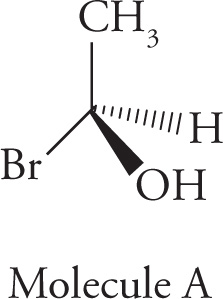
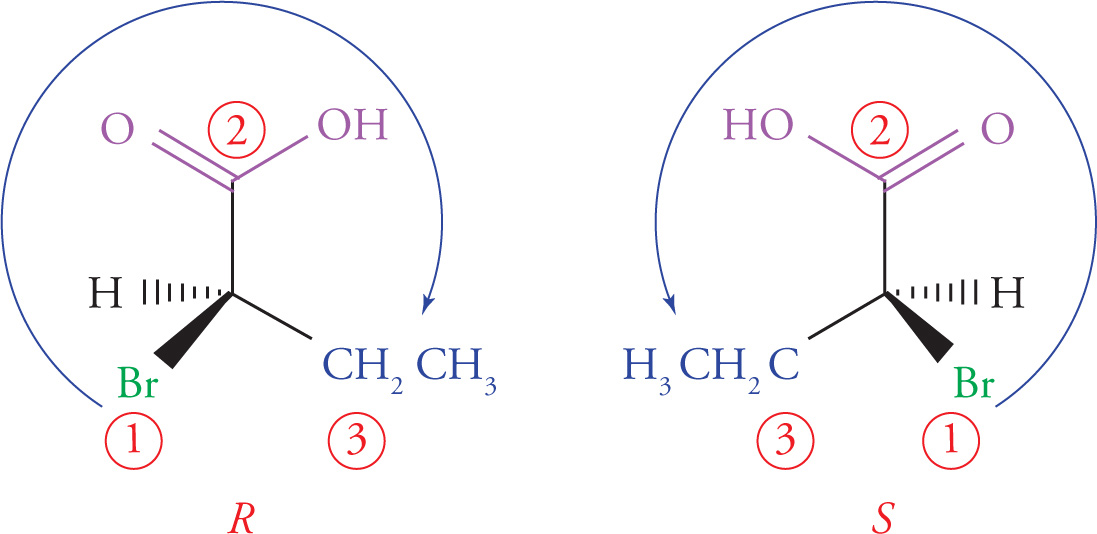
Chiral centers (carbon atoms bearing four different substituents) can be assigned an absolute configuration. There is an arbitrary set of rules for assigning absolute configuration to a stereocenter (known as the Cahn-Ingold-Prelog rules), which can be illustrated using Molecule A:
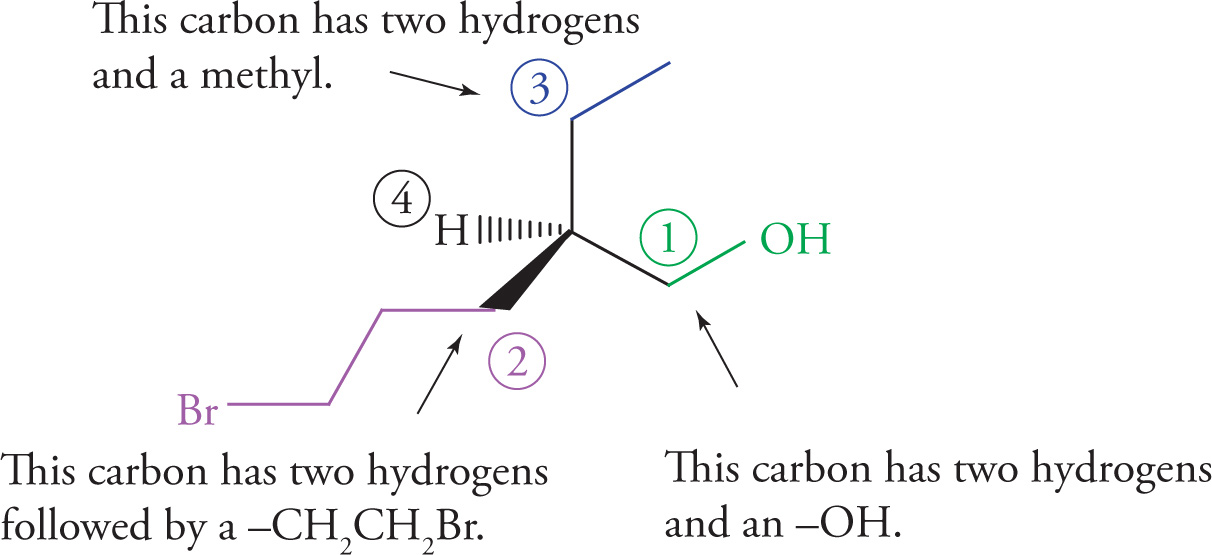
1. Priority is assigned to the four different substituents on the chiral center according to increasing atomic number of the atoms directly attached to the chiral center. Going one atom out from the chiral center, bromine has the highest atomic number and is given highest priority, #1; oxygen is next and is therefore #2; carbon is #3, and the hydrogen is the lowest priority group, #4:
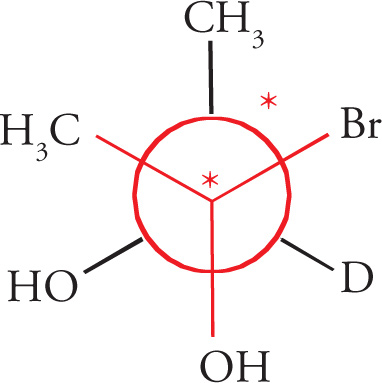
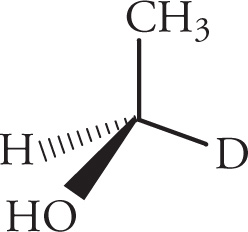
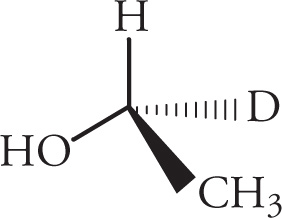
If isotopes are present, then priority among these are assigned on the basis of atomic weight with the higher priority being assigned to the heavier isotope (since they are all of the same atomic number). For example, the isotopes of hydrogen are 1H, 2H = D (deuterium), and 3H = T (tritium), and for the following molecule, we’d assign priorities as shown:
If two identical atoms are attached to a stereocenter, then the next atoms in both chains are examined until a difference is found. Once again this is done by atomic number. Note the following example:
2. A multiple bond is counted as two single bonds for both of the atoms involved. For example:
3. Once priorities have been assigned, the molecule is rotated so that the lowest priority group points directly away from the viewer. Then simply trace a path from the highest priority group to the lowest remaining priority group. If the path traveled is clockwise, then the absolute configuration is R (from the Latin rectus, right). Conversely, if the path traveled is counterclockwise, then the absolute configuration is S (from the Latin sinister, left).
(a) R. Either rotate the molecule so the lowest priority group is in the back,
or simply trace it as it stands and invert the configuration (since the lowest priority group is coming toward you):
(b) R. The lowest priority group is already pointing away from you and the trace is clockwise.
(c) S. Recall Fischer notation for molecules, note that the lowest priority group is pointing away from you, and the trace is counterclockwise.
(d) R. The lowest priority group is neither going into nor coming out of the plane of the page. One method is to rotate the molecule so the lowest priority group is in the back and redraw the molecule. Since the path is traveled clockwise, the configuration is R.
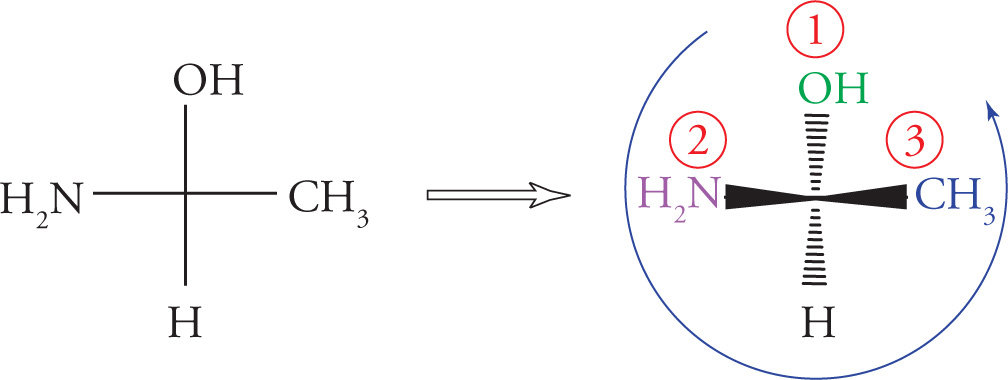
Here’s a trick to help in the rotation of molecules. Exchanging two groups on a chiral center necessarily changes the absolute configuration. So in this case, it is perhaps most convenient to exchange any two groups such that the lowest priority group is going into the page:
Note that this trace is going counterclockwise. Remember, however, that we exchanged two groups (the hydrogen and the deuterium), which necessarily changes the absolute configuration. Since the counterclockwise trace in the altered molecule means an S configuration, the true configuration is R.
(e) Because this molecule is not chiral, we cannot assign it an absolute configuration.
(f) S. Rotate so the lowest priority group is in back,
or exchange two groups, −H and −NH2:
Clockwise trace. But remember that two groups on the chiral center were exchanged, so the absolute configuration of the given molecule is the opposite; therefore, S.
(g) R. Rotate so the lowest priority group is in the back:
Enantiomers
It is important to be able to identify chiral centers because, as we have seen, when there are four different groups attached to a centralized carbon, there are two distinct arrangements or configurations possible for these groups in space. Consider the following two molecules:
Optical Activity
One important property that differs between enantiomers is the manner in which they interact with plane-polarized light. A compound that rotates the plane of polarized light is said to be optically active. A compound that rotates plane-polarized light clockwise is said to be dextrorotatory (d), also denoted by (+), while a compound that rotates plane-polarized light in the counterclockwise direction is said to be levorotatory (l), also denoted by (−). The magnitude of rotation of plane-polarized light for any compound is called its specific rotation. This property is dependent on the structure of the molecule, the concentration of the sample, and the path length through which the light must travel.
Diastereomers
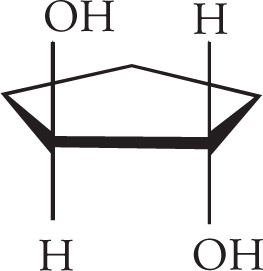
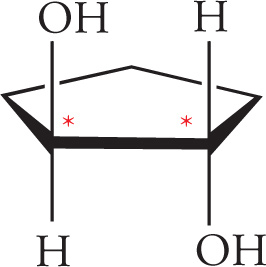
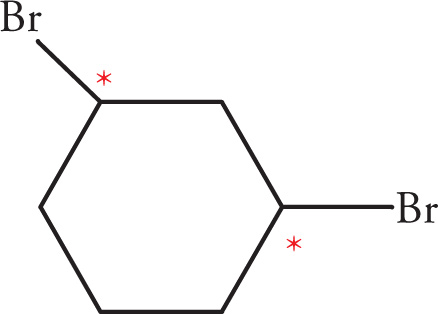
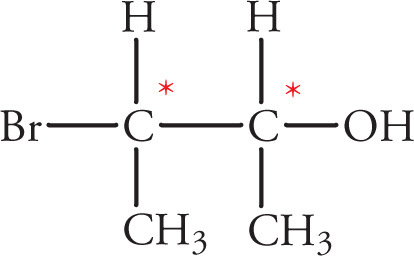
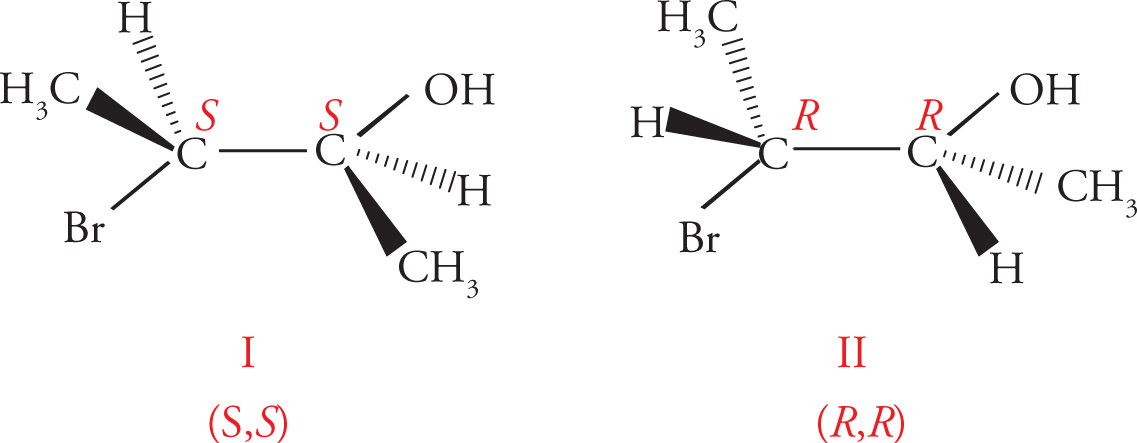
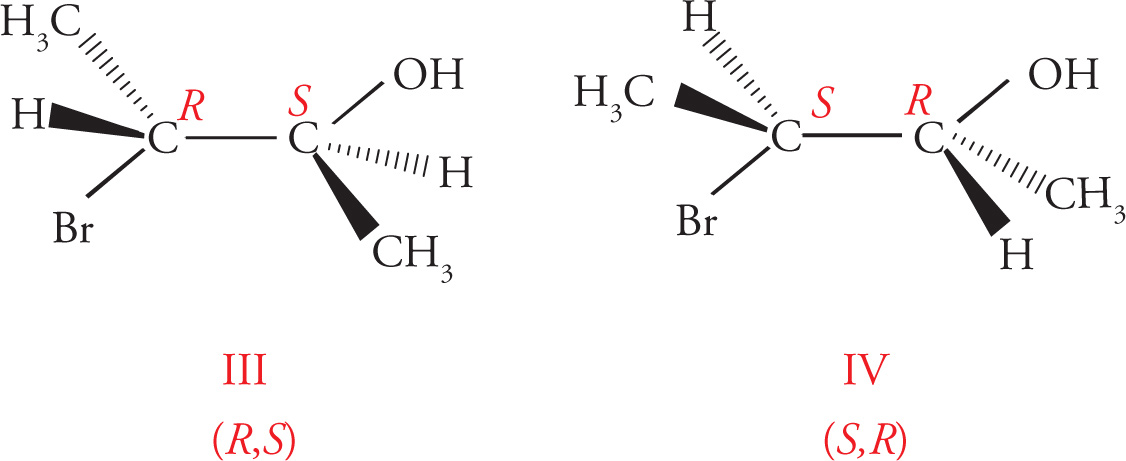
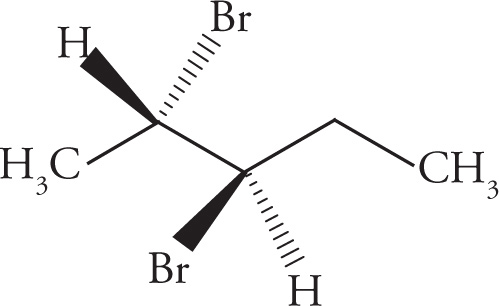
In the preceding discussions on stereoisomerism we have focused on molecules that have only one chiral center. What about molecules with multiple stereocenters? Remember that the number of possible stereoisomers is 2n, where n is the number of chiral centers. If there is one chiral center, then there are two possible stereoisomers: the enantiomeric pair R and S. Two chiral centers means there are four possible stereoisomers. Consider the following molecule (3-bromobutan-2-ol), for example:
(a) The molecules are superimposable and therefore identical.
(b) The molecules are identical. (The left carbon is not a chiral center.)
(c) Diastereomers.
(d) Enantiomers.
(e) Diastereomers.
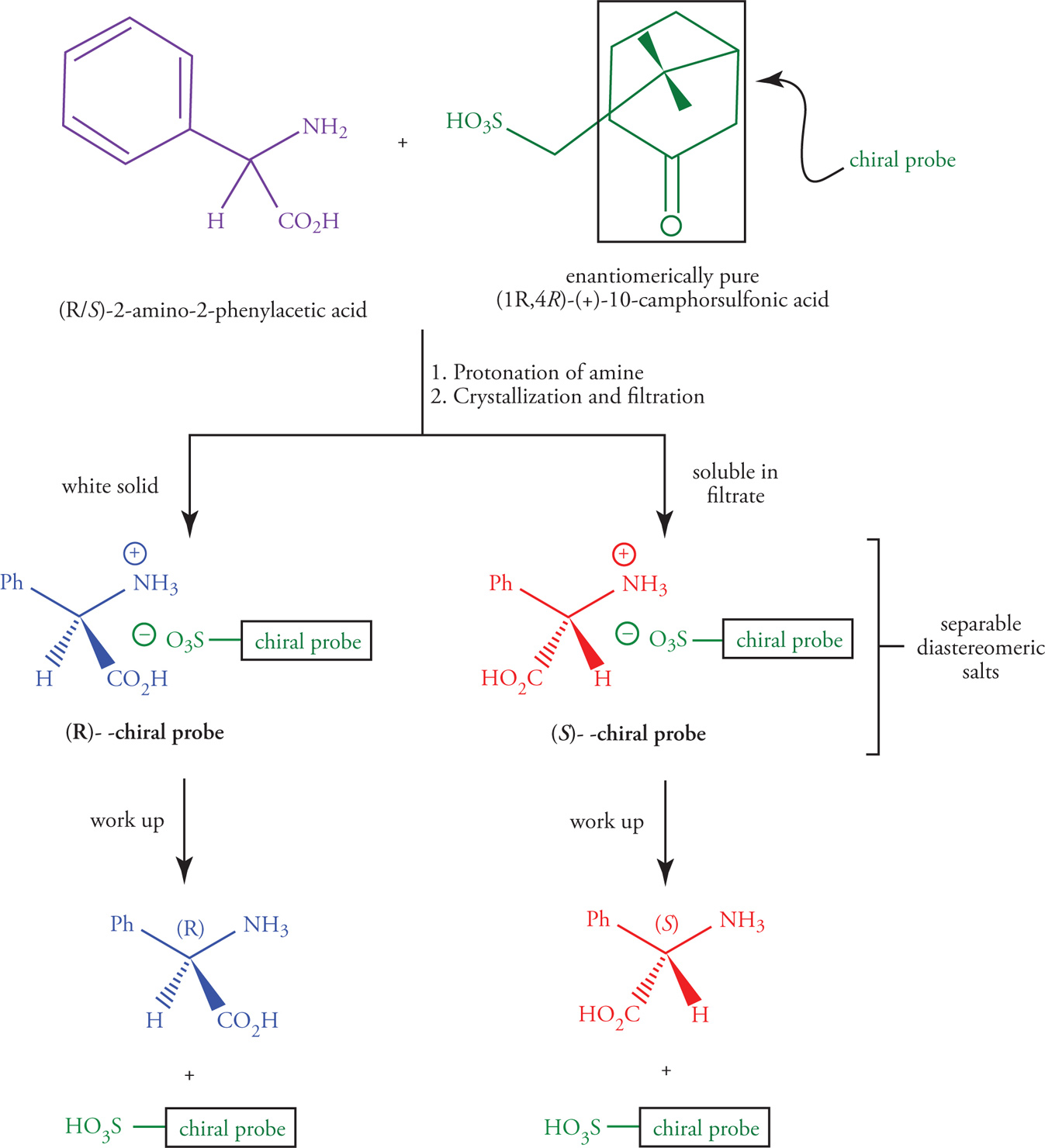
Resolution of Enantiomers
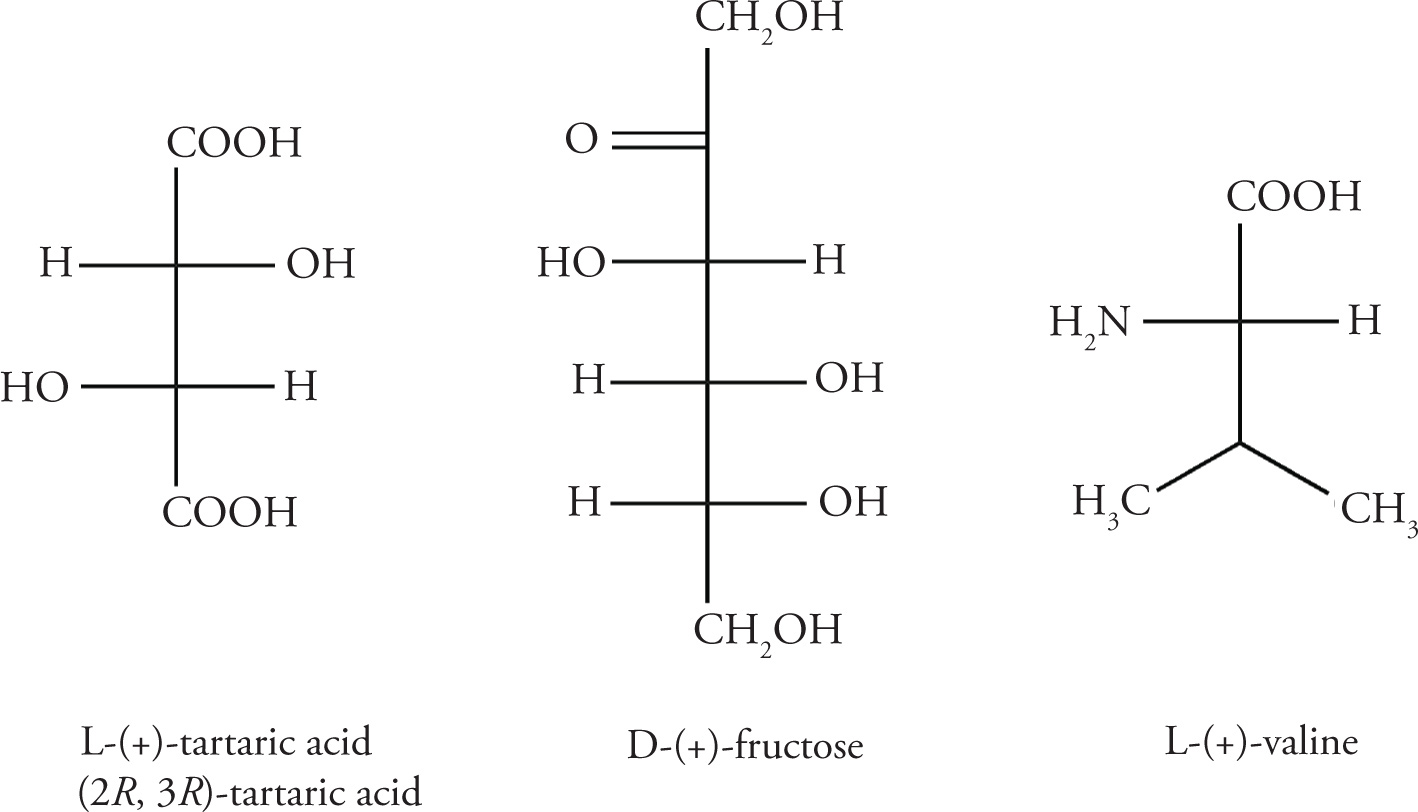
Nature has evolved intricate mechanisms for the bio-synthesis of enantiomerically pure, optically active compounds. For example, L-(+)-tartaric acid, D-(+)-fructose, and L-(+)-valine are all isolated as a single enantiomer from their respective biological sources.
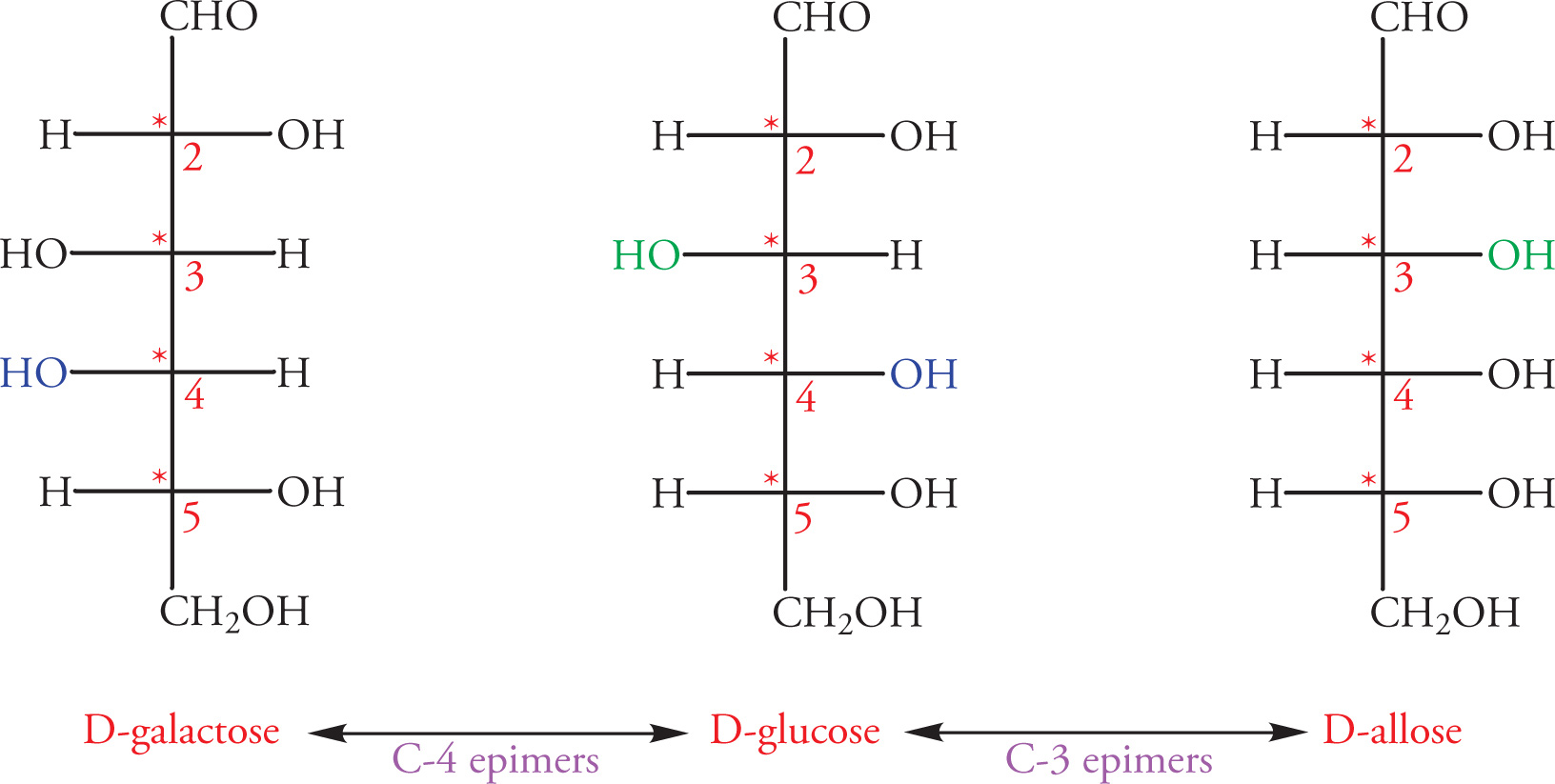
Epimers
Epimers are a subclass of diastereomers that differ in their absolute configuration at a single chiral center (only one stereocenter is inverted). To illustrate epimeric relationships, let’s look at the Fischer projections of some sugars (see Chapter 7):
• R or S = absolute configuration (structure)
• D or L = relative configuration (structure)
• (+) or (−) = observed optical rotation (property)
Anomers
Epimers that form as a result of ring closure are known as anomers. For the MCAT, anomers will be encountered only with regard to sugar chemistry. To illustrate anomerism, consider D-glucose. Open-chain glucose exists in equilibrium with cyclic glucose, known as glucopyranose. Cyclization occurs when the C-5 hydroxyl group attacks the carbonyl (C=O) carbon, C-1. This converts a carbon with three substituents to a carbon with four different substituents. Thus, a new stereocenter is formed (C-1), and it can assume one of two possible forms: with the hydroxyl group down, it is α; with the hydroxyl group up, it is β. It is the orientation at C-1 that distinguishes the two anomers, and C-1 is known as the anomeric center (or anomeric carbon).
Meso Compounds
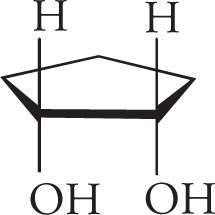
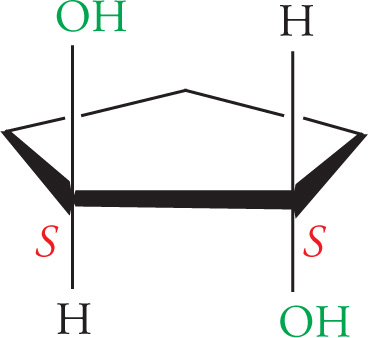
Let’s look at another molecule with more than one stereocenter. Consider 2,3-butanediol:
(a) This molecule is optically active. It has two chiral centers, but no internal mirror plane. Therefore it is not a meso compound and will rotate plane-polarized light.
(b) This molecule is a meso compound due to its two chiral centers and internal mirror plane. It will be optically inactive. Be sure to look for rotations around σ bonds in order to find the mirror planes of some molecules.
(c) This molecule has no chiral centers, so will have no optical activity.
(d) By rotating around the C-2 to C-3 bond to put the molecule into an eclipsed conformation, you can see that there is an internal mirror plane in the molecule. Since C-2 and C-3 are also chiral centers with four different substituents, this is a meso compound, and will be optically inactive.
(e) This molecule has three chiral centers (the two bridgehead carbons are chiral), but no plane of symmetry. It is therefore chiral and optically active.
(f) There is no mirror image in this molecule even though it has two chiral centers (they have the same absolute configuration). It will therefore be optically active.
(g) This molecule does have an internal mirror plane, and its two chiral centers have opposite absolute configurations. It is therefore meso, and not optically active.
Geometric Isomers
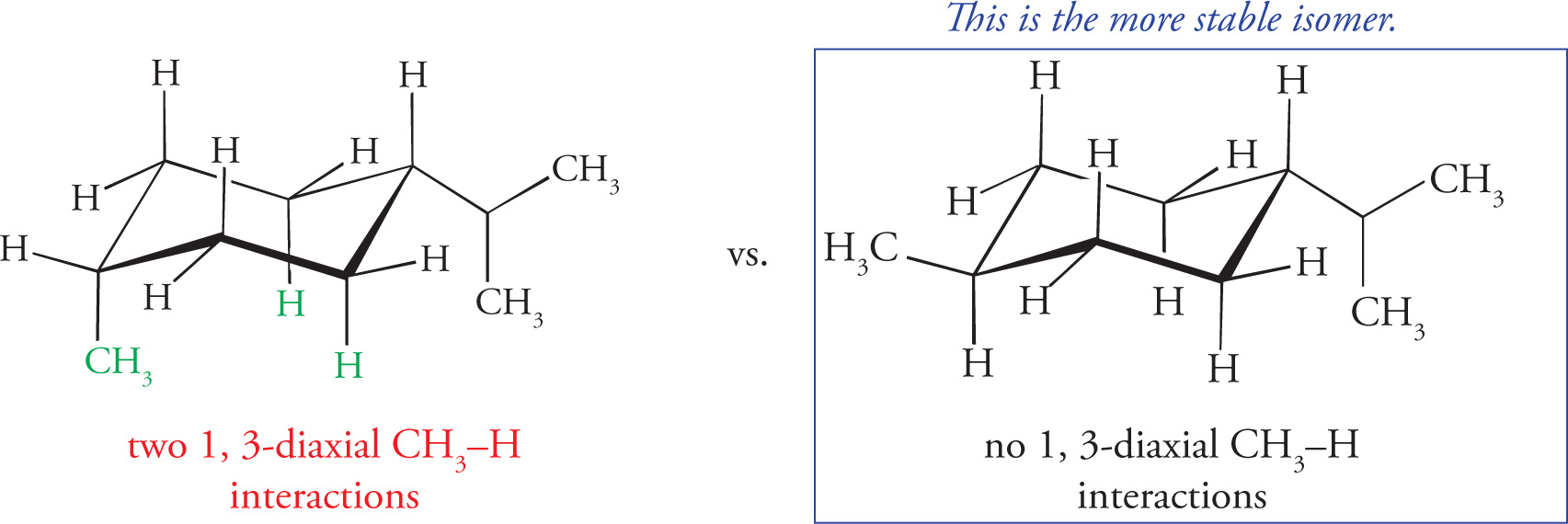
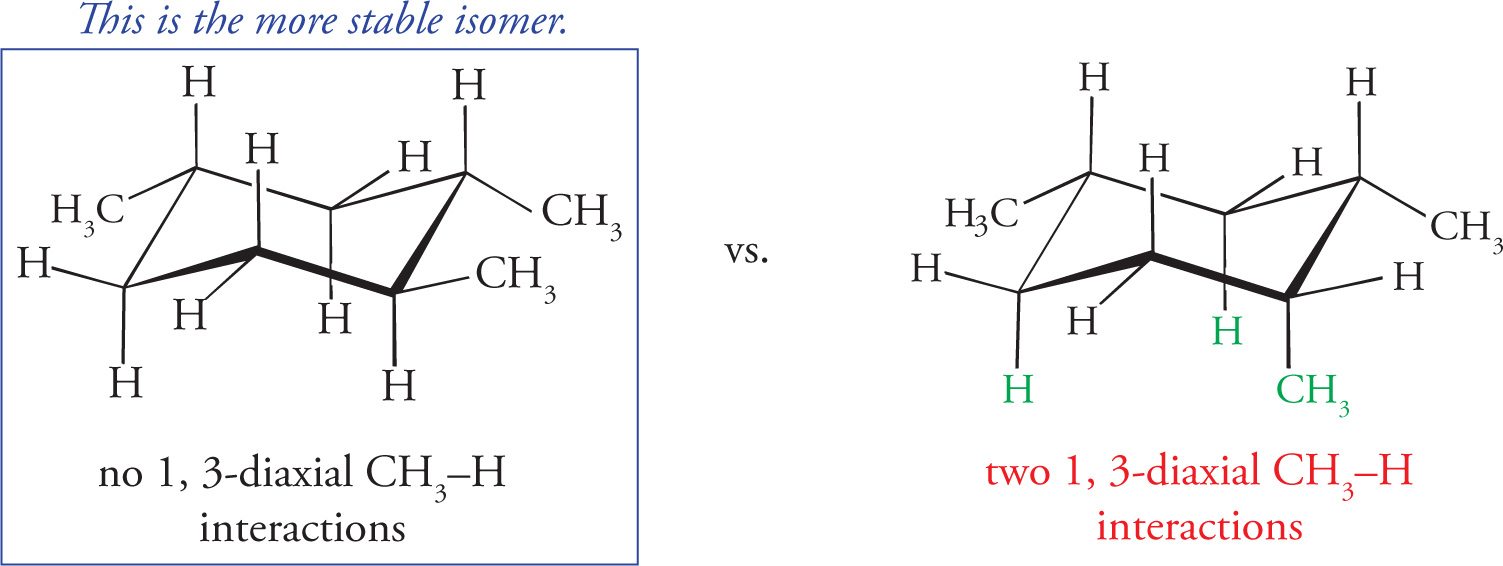
Geometric isomers are diastereomers that differ in orientation of substituents around a ring or a double bond. Cyclic hydrocarbons and double bonds (alkenes) are constrained by their geometry, meaning they do not rotate freely about all bonds. So, there’s a difference between having substituents on the same side of the ring (or double bond) and having substituents on opposite sides. For example, the following are geometric isomers of 1,2-dimethylcyclohexane:
SUMMARY OF ISOMERS
Chapter 4 Summary
• Saturated compounds have the general formula CnH2n+2; unsaturated molecules contain rings or π bonds.
• As the substitution of carbocations increases, so does their stability due to the inductive effect; carbanions are more stable when they are less substituted.
• Resonance stabilization results from the ability of π electrons or charge to move and delocalize through a system of conjugated π bonds or unhybridized p orbitals.
• Brønsted-Lowry acids are proton donors, and are stronger (dissociate more) when their conjugate bases are most stable in solution.
• Acidity of carboxylic acids results from the resonance stability of the carboxylate anion.
• Electron withdrawing groups increase the acidity of carboxylic acids by stabilizing the negative charge of the carboxylate anion via the inductive effect.
• Nucleophiles are Lewis bases and are electron rich, while electrophiles are Lewis acids and are electron deficient.
• Nucleophiles are stronger when negatively charged, less electronegative, or larger in size.
• Leaving groups are more likely to leave as their stability in solution increases (uncharged and/or larger groups are usually better LGs).
• Compounds with the same molecular formula are known as isomers; structural, or constitutional isomers differ by the connectivity of atoms in the molecule.
• Conformational isomers differ by rotation around a σ bond.
• Stereoisomers have the same atom connectivity, but different spatial orientation of atoms.
• Chiral molecules have chiral centers (carbon with four different substituents), are not superimposable on their mirror image, and rotate plane-polarized light.
• Enantiomers are non-superimposable mirror images and have opposite absolute configuration at all chiral centers.
• Enantiomers rotate plane-polarized light an equal magnitude, but in opposite direction, therefore a 50:50 mixture of enantiomers, or a racemic mixture, is not optically active.
• The process of separating a mixture of enantiomers is called resolution, and entails conversion of the racemic mixture into a pair of separable diastereomers temporarily before converting back to the pure, chiral enantiomers.
• Diastereomers are stereoisomers that are not mirror images; they differ in absolute configuration for at least one, but not all carbons.
• Epimers are diastereomers that differ in absolute configuration at only one stereocenter.
• Geometric isomers are diastereomers that are cis/trans (or Z/E) pairs on a ring or double bond. When highest priority groups are on the same side of a ring or bond the molecule is cis (or Z); when they’re on opposite sides, the compound is trans (or E).
• Meso compounds are achiral molecules with chiral centers and an internal mirror plane.
CHAPTER 4 FREESTANDING PRACTICE QUESTIONS
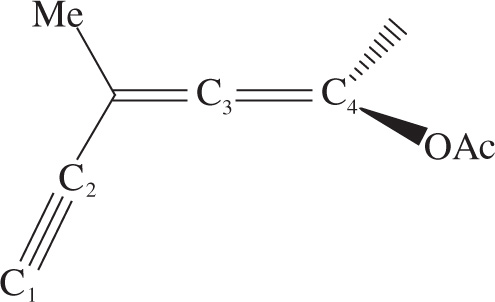
1. In the molecule below, what are the hybridizations of C1, C2, C3, and C4 respectively?
A) sp, sp, sp2, sp2
B) sp, sp, sp, sp2
C) sp2, sp2, sp, sp
D) sp2, sp, sp, sp
2. Which of the following structures represents the most stable possible resonance structure for acetic acid (CH3CO2H)?
3. Rank the conformations of 2-aminoethanol by increasing stability.
A) anti < gauche < eclipsed
B) eclipsed < anti < gauche
C) gauche < anti < eclipsed
D) eclipsed < gauche < anti
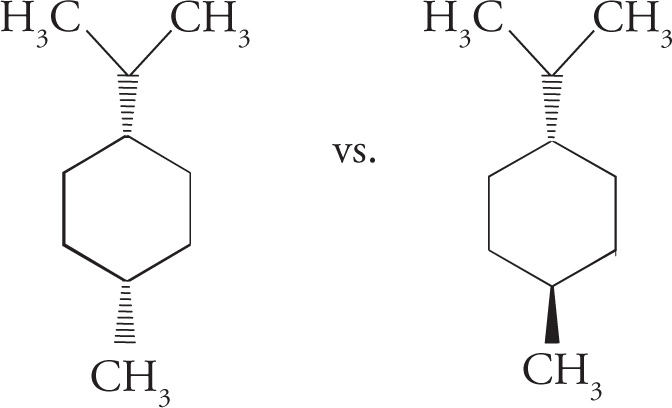
4. The most stable conformation of the following substituted cyclohexane has the methyl groups in which of the following positions?
A) 2 Equatorial and 1 axial
B) All axial
C) All equatorial
D) 2 Axial and 1 equatorial
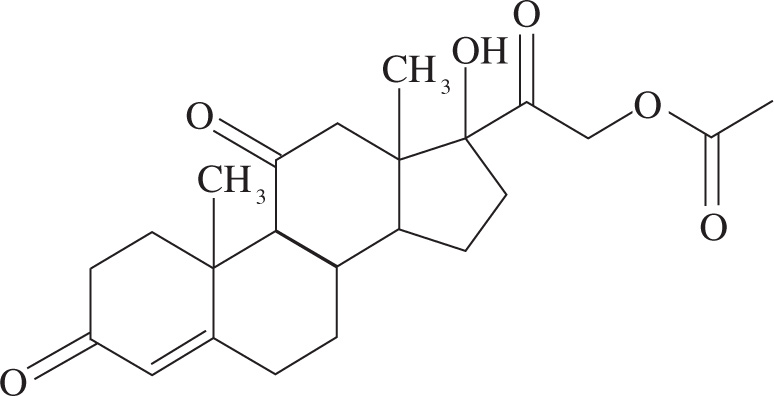
5. How many stereoisomers are possible for cortisone acetate (shown below)?
A) 32
B) 64
C) 128
D) 256
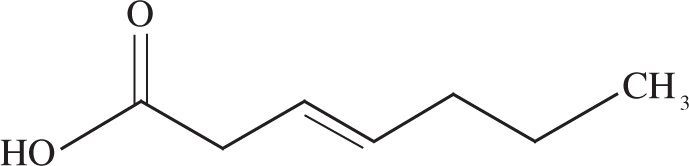
6. What is the correct IUPAC name for the following molecule?
A) (E)-3-heptenoic acid
B) (E)-4-heptenoic acid
C) (Z)-3-heptenoic acid
D) (Z)-4-heptenoic acid
7. Which of the following is the strongest nucleophile?
A) CN−
B) OH−
C) CH3OH
D) NH3
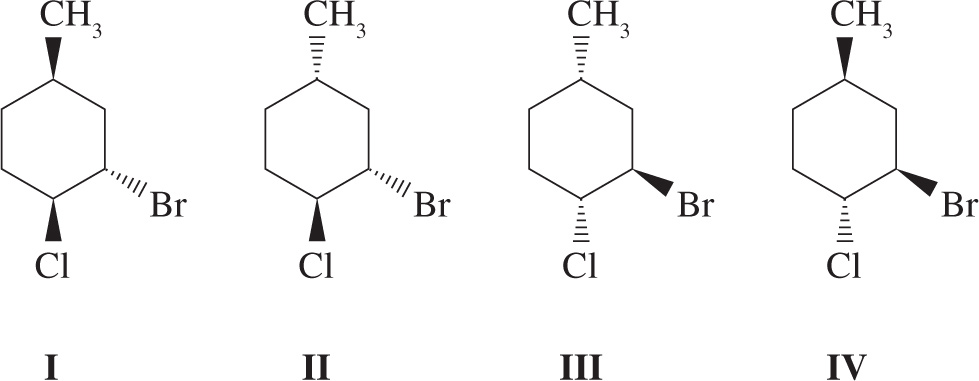
8. Which of the following answer choices lists two pairs of diastereomers?
A) I, III and II, IV
B) I, II and II, III
C) I, III and I, IV
D) II, IV and III, IV
CHAPTER 4 PRACTICE PASSAGE
In mammalian systems, aromatic hydrocarbons are enzymatically metabolized by cytochrome P450 into arene oxides when ingested or inhaled. Arene oxides are compounds in which one of the double bonds of an aromatic ring has been converted into an epoxide. These molecules can rearrange to form phenols, which are harmlessly excreted. As shown in Figure 1, arene oxide rearrangement requires the formation of an intermediate carbocation and subsequent hydride shift.
Figure 1 Arene oxide rearrangement
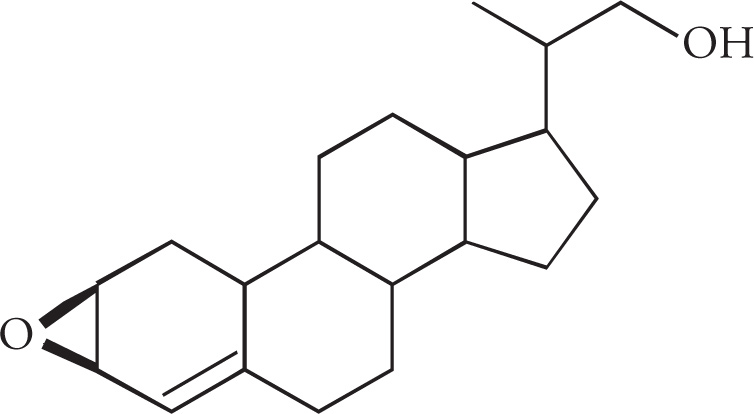
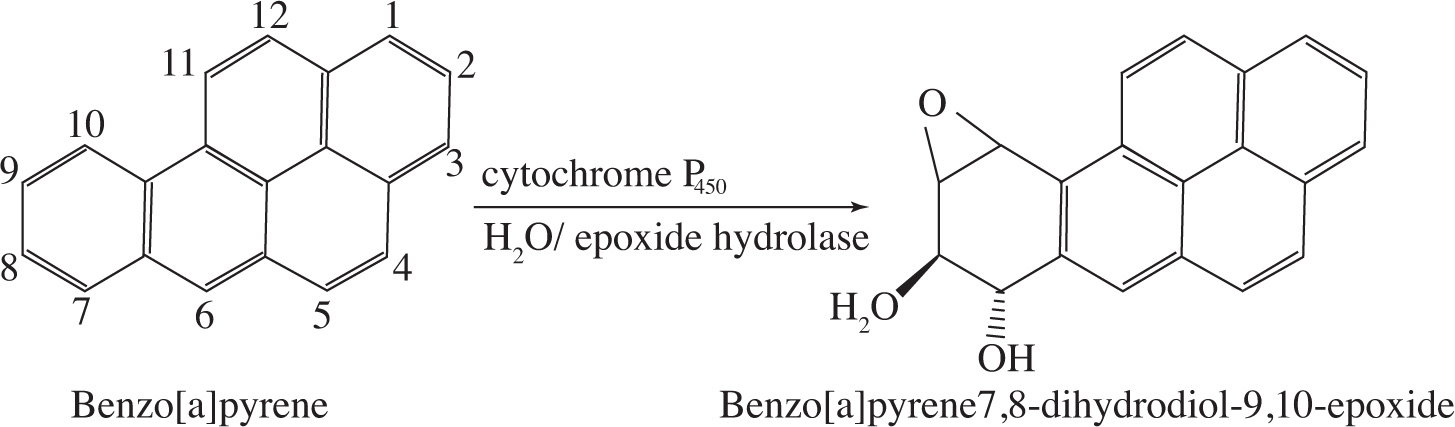
Figure 2 Oxidation of Benzo[a]pyrene
1. Determine the absolute configurations of Carbons 7 and 8 of the diol epoxide shown in Figure 2.
A) 7R, 8R
B) 7R, 8S
C) 7S, 8S
D) 7S, 8R
2. All of the following statements about epoxides are correct EXCEPT:
A) epoxides and ethers bear the same leaving groups.
B) ring strain and torsional strain increase the free energy of an epoxide.
C) epoxide hydrolysis under basic conditions produces trans-1,2-diols.
D) epoxide oxygen atoms are capable of donating hydrogen bonds.
3. Rank the following four substances in order of increasing reactivity with ethylene oxide.
I. Hydroxide
II. Ammonia
III. Methide
IV. Water
A) III < I < II < IV
B) IV < II < I < III
C) IV < II < III < I
D) II < IV < I < III
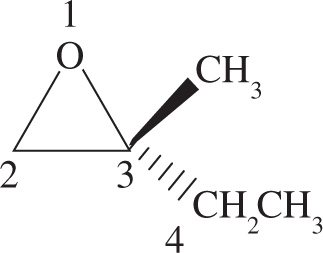
4. Which labeled atom in the molecule shown below would be the fastest site of reaction with a thiolate (R-S−)?
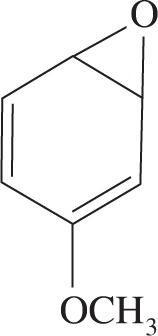
5. Which of the following arene oxides will react as in Figure 1 to form the most stable carbocation intermediate?
SOLUTIONS TO CHAPTER 4 FREESTANDING PRACTICE QUESTIONS
1. B Both C1 and C2 make up the triple bond. They are both sp hybridized so you can eliminate choices C and D. C3 is part of an allene. The bonds that it forms with its neighbors are linear (180°), so it is also sp. You can eliminate choice A, which leaves choice B as the correct choice. C4 has a double bond and two single bonds so it is sp2.
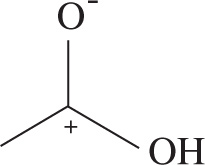
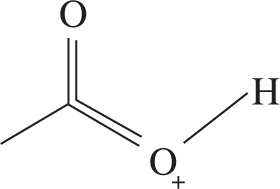
2. B Good resonance structures must do the following: obey the octet rule, accrue the fewest charges possible, and place negative charges on electronegative atoms and positive charges on electropositive atoms (listed in priority). Further, resonance structures don’t represent oxidation or reduction of molecules, and as such the total charge of each structure must be the charge of the molecule. This eliminates choices C and D. Choices A and B are both valid resonance structures, but only choice B places a full octet on all non-H atoms.
3. B Since this is a ranking question, look for obvious extremes and eliminate answers. Choices A and C should be eliminated because the eclipsed conformation is always the least stable due to sterics and electron repulsions in aligned bonds. Choice D is the more enticing answer of the remaining two because the general rule of thumb is that the anti conformation is the most stable because the bulky groups are farthest apart, while they are 60° apart in a gauche conformation. This question is tricky, however, because in this case there is intramolecular hydrogen bonding which can occur in the gauche conformation, making it the most stable one (eliminate choice D).
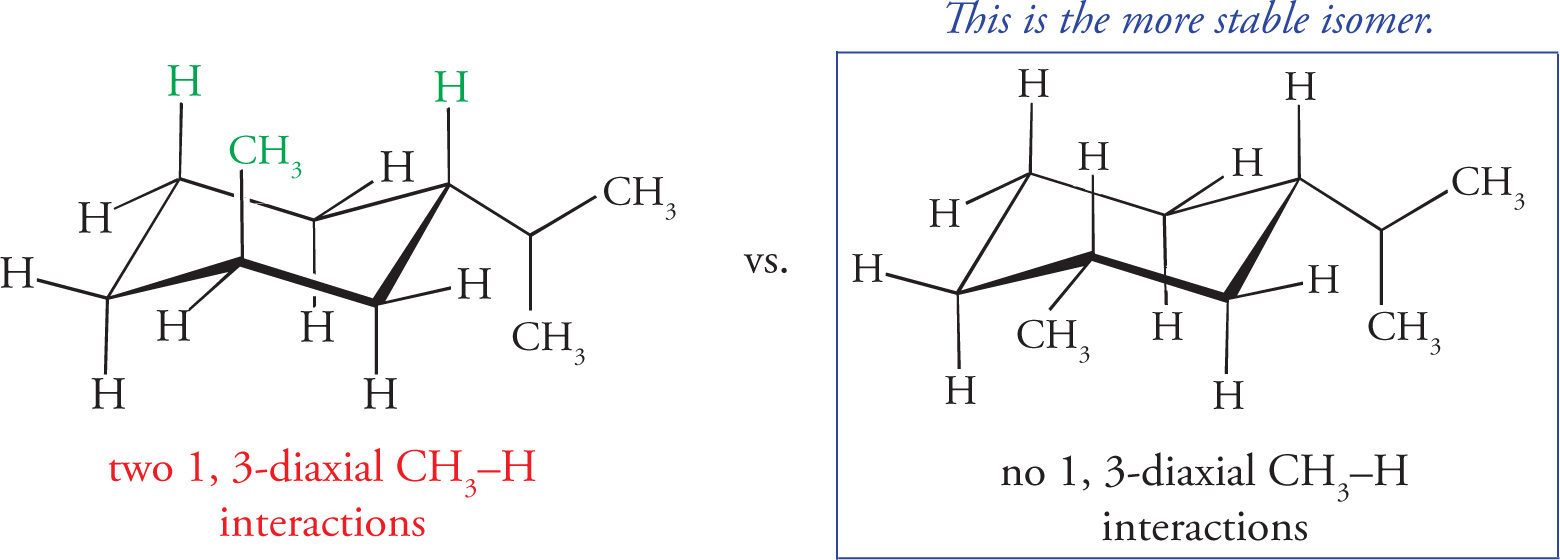
4. A Choice B can be eliminated before analyzing the structure since if all three substituents could be axial, then by a ring flip, all three could also be equatorial. The more stable chair conformation puts substituents in an equatorial position since they are less sterically crowded than those in axial positions. Similarly, if choice A is true of the molecule, then by ring flip, choice D must be also. Therefore choice D should be eliminated since it has more axial substituents. Between choices A and C, only choice A fits the compound shown because the relationship between the methyl groups on Carbons 1 and 2 is trans and the relationship between the methyl groups on Carbons 1 and 4 is cis. In this conformation, the methyl groups on Carbons 1 and 2 would be found in the equatorial position and the methyl group on Carbon 4 would be axial, making A the better choice.
5. B The maximum number of stereoisomers is given by the formula 2n, where n equals the number of stereocenters. Cortisone acetate has six stereocenters and 26 = 64. Five of the six ring junctures are chiral centers (all sp3 carbons), as is the carbon with the OH substituent. Choice A would correspond to five stereocenters, choice C would require seven stereocenters, and choice D would correspond to a compound with eight stereocenters.
6. A When naming a compound, number the carbons starting at the end nearest a functional group (the carboxylic acid in this case). Based on the position of the double bond in the molecule, you can eliminate choices B and D. Since the two largest substituents on each carbon of the double bond are on opposite sides of the bond, the double bond has E stereochemistry; therefore, eliminate choice C.
7. A Nucleophiles are electron rich. While neutral compounds that have lone pairs can be nucleophilic, negatively charged nucleophiles tend to be stronger (eliminate choices C and D). The stronger nucleophile is the more reactive nucleophile; more reactive corresponds to less stable. Therefore, the nucleophile that is less able to stabilize a negative charge will be the stronger nucleophile. For choices A and B, the negative charge resides on the C and O, respectively. Since carbon is less electronegative than oxygen, it is therefore less able to stabilize a negative charge, making cyanide the best nucleophile (eliminate choice B).
8. B Stereoisomers in which all stereocenters are inverted are enantiomers, while stereoisomers with at least one, but not all, inverted chiral centers are diastereomers. Molecules I and III are an enantiomeric pair (eliminate choices A and C); Molecules II and IV are enantiomers as well (eliminate choice D). All other pairs of molecules are diastereomers.
SOLUTIONS TO CHAPTER 4 PRACTICE PASSAGE
1. D
Note that the configuration for Carbon 7 reads as R, but because the hydroxyl group occupies an into-plane position, this assignment is incorrect. One way to get around this is to exchange the hydroxyl group’s position with the hydrogen also on this carbon. Doing so will place the hydroxyl group in a correct position, which results in a clockwise trace. This reads as R but because two groups have been exchanged, the true configuration is S. Once the configuration of Carbon 7 is determined to be S, choices A and B can be eliminated.
2. D Epoxides and ethers all bear an OR leaving group so choice A can be eliminated. Choice B is incorrect because epoxides, due to their 3-point ring structure, possess ring strain and torsional strain, which imparts a relatively high free energy. Epoxide hydrolysis (basic or acidic) will produce trans-1,2-diols, also eliminating choice C. Choice D is the only answer choice consistent with the EXCEPT wording of the question because epoxides are only capable of accepting hydrogen bonds, not donating them.
3. B Each of the four substances listed will act as nucleophiles with ethylene oxide (C2H4O). The strongest nucleophile has a negative charge on the least electronegative atom, which is carbon. Choices B and D both list methide as the strongest nucleophile (eliminate choices A and C). The weakest nucleophile is going to be listed first. The choice is between water and ammonia. Since nitrogen is less electronegative than oxygen, NH3 is a stronger nucleophile than water (eliminate choice D).
4. B Thiolate is a relatively weak base, but a great nucleophile. This means it will be attracted to the electrophilic carbons of the molecule, C-2 and C-3, and effect an epoxide ring opening (eliminate choices A and D). Because the question asks about the fastest site of reaction, the least sterically hindered carbon is the best choice. Thiolate will have easier access to the primary carbon, so eliminate choice C.
5. A The nature of the substituents on each ring act to stabilize or destabilize the carbocation that forms. The methoxy substituent in choice A is an electron-donating group, which will stabilize the carbocation through resonance due to the lone electron pairs on the oxygen.
On the other hand, the nitro group in choice B will destabilize the intermediate since one resonance structure, shown below, puts two atoms with a positive charge next to each other (eliminate choice B). Choice C affords no increase or decrease in stability. Choice D will show mild stabilization due to the inductive donation offered by its methyl group (also shown below).
Overall, choice A shows the strongest carbocation stabilization since resonance effects are generally stronger than inductive ones.