THE REVEREND AND THE SUBMARINE
Q: What do a bicycle, snow, a kangaroo, and a submarine have in common?
A: They’re all important for building a car that can drive itself.
TAKE BICYCLES. BICYCLES are trouble. The sensors on a self-driving car are really good at identifying things like pedestrians and squirrels, which move a lot slower than cars and which look basically the same from every angle. Other cars are a piece of cake; they’re giant reflective blobs of metal that light up like a Christmas tree on radar. But bicycles? Bicycles can be fast or slow, big or small, metal or carbon fiber—and depending on your viewing angle, they can be as wide as a car or as narrow as a book. If you don’t notice the bicycle itself, how can you tell that a bicyclist isn’t just a pedestrian with eccentric posture? And don’t even start on all that swerving. So erratic and impulsive. It’s enough to give a robot a serious headache.
Snow is trouble, too, and not because of traction—robots are smart enough to get winter tires, and they know their own limits. But snow covers lane lines. Snow obscures stop signs. Snow interferes with the laser beams that the car uses to measure distance to nearby objects. To a robot car, snow means sensory deprivation.
As for kangaroos, while other critters may be unpredictable, at least they stay on the ground. But a kangaroo jumps 30 feet at a time. As it bounds up and down, it seems to get bigger and smaller, bigger and smaller in the camera’s field of vision, like a giant rabbit in a kaleidoscope. This is really confusing to a robot. With all those rapid changes in apparent size, how can you tell how far away it is? It’s almost like you need a dedicated kangaroo-range-finding laser—maybe lots of them, since kangaroos travel in … well, zoologists call them “mobs” for a reason.
Then there’s a submarine. We promise we’ll get to that in a minute.
But first, we invite you to reflect on something. Isn’t it astonishing that we’re talking about mobs of kangaroos as one of the big technological problems here—as opposed to, say, getting out of the driveway, or not crashing into your neighbors’ living room? Ask yourself a simple question. If you had to put a loved one in a taxi, would you rather have them driven by a randomly sampled 16-year-old with a driver’s license, or by one of Waymo’s cars? (Waymo is the autonomous-car company spun out of Google.) If you have to think about this question, we encourage you to consider a few facts.1
56% of American teenagers talk on the phone while driving.
In 2015, 2,715 American teenagers died, and 221,313 went to the emergency room, because of car-crash injuries.
Half of all crashes involving teenage drivers are single-vehicle crashes.
In contrast, Waymo’s cars never get distracted. They never drink. They never get tired, and they never text their friends when they should be paying attention to the road. Since 2009, they’ve driven more than 2 million miles on public roads, and in that time they’ve caused only one accident: a fender-bender with a city bus in California, while traveling two miles per hour. All told, Waymo’s per-mile, at-fault accident rate over nine years is 40 times lower than the rate for drivers ages 16–19, and 10 times lower than for drivers ages 50–59. And that’s the prototype.
These numbers predict a clear trajectory in the cultural norms of the future: the notion of allowing a 16-year-old to drive a car will seem absurdly irresponsible. When our descendants learn that this used to be normal, they’ll react the same way people react today upon learning that their grandparents used to drive home without seat belts after drinking four martinis. As for bicycles, snow, and kangaroos? Those are just engineering problems. They’ll be fixed in the near future, perhaps even by the time you read this, and almost surely with the same solution: better data. In AI, data is like water. It’s the universal solvent.
In fact, if you hang out with enough data scientists who work on self-driving cars, you’ll quickly be confronted with a striking question: Has the last Californian to hold a driver’s license already been born?
The Robotics Revolution
Robots have come a long way in a short time.
In the 1950s, the state of the art was Theseus, a life-size autonomous mouse built by Claude Shannon at Bell Labs, and powered by a bank of telephone relays. Theseus the ancient Greek hero entered a labyrinth to slay the Minotaur. Theseus the mouse had more modest ambitions: he entered a 25-square tabletop maze to find a block of cheese. At first he would navigate by trial and error until he found the cheese. After this first triumph, he could find his way back to the cheese from anywhere in the maze, without a mistake.2
In the 1960s and ’70s, there was the Stanford Cart: a wagon-sized vehicle with four small bicycle wheels, an electric motor, and a single TV camera. The Cart began as a test vehicle to study how engineers might control a moon rover remotely from Earth. But it soon morphed into a platform for research on autonomous navigation for a whole generation of robotics students at the Stanford Artificial Intelligence Lab. By 1979, after years of refinement, the Cart could steer itself across a chair-filled room in five hours, without human intervention—quite an achievement for the time.3
And today? Self-driving cars are just the start. Don’t forget about autonomous flying taxis, like the ones the government of Dubai has been testing since September of 2017. Or the autonomous iron mine run by Rio Tinto, in the middle of the Australian outback. Or the autonomous shipping terminal at the Port of Qingdao, in China—six enormous berths spanning two kilometers of coastline, 5.2 million shipping containers a year, hundreds of robot trucks and cranes, and nobody at the wheel.4
One of the most common questions we hear from students in our data-science classes is “How do these robots work?” We’d love to answer that question in all its glory. Alas, we can’t. For one thing, there are so many details that it would take a much longer book, one with lots and lots of equations. Besides, a lot of the details are proprietary. You may have heard, for instance, that Waymo has sued Uber for $1.86 billion over the alleged theft of some of those details—a suit whose outcome, at the time of writing, was unknown.5
Details aside, though, let’s think about the big picture. Here’s an analogy. You can certainly learn the basics of how a plane stays in the air, even if you don’t know how to build a Boeing 787. Similarly, you can understand how a self-driving car navigates its environment, even if you can’t design such a car yourself. That’s exactly the level of understanding you’ll achieve by the end of this chapter, by building on what you’ve already learned about conditional probability.
To get there, we’ll start with a simple, almost childlike question, one fundamental to any autonomous robot—whether it walks, drives, or flies; whether it digs up iron or ferries us to the grocery store; whether it’s the size of a mouse or the size of a container ship. This question, in fact, is so important that it must be asked and answered dozens or even hundreds of times every second.
That question is: Where am I?
In AI, this is called the SLAM problem, for “simultaneous localization and mapping.” The word “simultaneous” is key here. Whether you’re a person or a robot, knowing where you are means doing two things at once: (1) constructing a mental map of an unknown environment, and (2) inferring your own unknown location within that environment. This is a chicken-and-egg problem. Your beliefs about the environment depend on your location, but your beliefs about your location depend on the environment. Neither can be known independently of the other, so it seems logically impossible to infer both at once. Imagine, for example, that you’re trying to get to Times Square having never been to New York before, and we give you directions by telling you that it’s one subway stop north of Penn Station—and then, when you ask where Penn Station is, we tell you that it’s one stop south of Times Square. Now you’re supposed to go find both places without a map. That’s the SLAM problem.
Although it may not seem like it to you, the information you get from your senses about your own location in the world is just about as circular as our directions to Times Square. The cognitive miracle is that you can solve the SLAM problem routinely, with no conscious effort, every time you walk into an unfamiliar room. Neuroscientists don’t fully understand how you do it, but they do know that there’s a lot of very specialized and phylogenetically ancient brain circuitry involved, especially in the hippocampus. And like many capabilities honed by evolution, this one turns out to be really hard to reverse engineer. In AI, this is often called the “Moravec paradox”: the easy things for a five-year-old are the hard things for a machine, and vice versa.*
The current revolution in autonomous robots has become possible only because all the research put into SLAM systems has finally paid off. Robots have gone from dodging chairs to dodging other drivers; from five hours traversing a room to five gigabytes of sensor data per second; from an autonomous mouse that can navigate a 25-square grid to an autonomous car that can navigate millions of miles of public road. SLAM is one of AI’s most smashing success stories. So in this chapter, we’d like to address two SLAM-related questions—one obvious, and one a bit more unexpected.
1. How does a robot car know where it is?
2. How can you become a smarter person by thinking a bit more like a robot car?
The answer to both of these questions involves something called Bayes’s rule. Bayes’s rule is how self-driving cars know where they are on the road—but it’s so much more than that. Bayes’s rule is a profound mathematical insight used every day, in almost every area of science and industry. Moreover, it is a supremely helpful principle for living your day-to-day life in a smarter way—like, for instance, if you want to invest more prudently, or make more informed decisions about medical care. Bayes’s rule provides the single best example of how training yourself to think a bit more like a machine can help you be a wiser, healthier person.
How Is Finding a Submarine like Finding Yourself on the Road?
We can now, at last, return to our earlier promise. We told you that understanding a submarine would be important for getting a car to drive itself. Now let us show you why.
The connection here is Bayes’s rule, which we’ll explain by telling you a story about a submarine. Not a self-driving submarine or anything like that—just a run-of-the-mill nuclear-powered attack submarine called the USS Scorpion. The Scorpion is famous because one day, in 1968, it went missing, somewhere along a stretch of open ocean spanning thousands of miles. This sent the U.S. military into a frenzy; it’s a big deal when a nuclear submarine vanishes. Despite the long odds, navy officials threw everything they had into the search. They combed the ocean for months on end, yet they couldn’t find the Scorpion. Discouraged and hopeless, they were about ready to call it quits.
But one man was too stubborn to give up. His name was John Craven, and he was stubborn because he was convinced that he had probability on his side—and the remarkable thing is that he was right. John Craven and his search team used Bayes’s rule to answer the question “Where is the Scorpion in this big empty ocean?” Once you know how they did it, you’ll understand how a self-driving car uses the same math to answer a very similar question: “Where am I on this big open road?”
The Search for the Scorpion
In February of 1968, the USS Scorpion set sail from Norfolk, Virginia, under the watch of Commander Francis A. Slattery. The Scorpion was a Skipjack-class high-speed attack submarine, the fastest in the American fleet. Like other subs of her class, she played a major role in U.S. military strategy: this was the height of the Cold War, and both the Americans and the Soviets deployed large fleets of these attack subs to locate, track, and—should the unthinkable happen—destroy the other side’s missile submarines.
On this deployment, the Scorpion sailed east, bound for the Mediterranean, where for three months she participated in training exercises alongside the navy’s 6th Fleet. Then, in mid-May, the Scorpion was sent back west, past Gibraltar and out into the Atlantic. There she was ordered to observe Soviet naval vessels operating near the Azores—a remote island chain in the middle of the North Atlantic, about 850 miles off the coast of Portugal—and then to continue west, bound for home. The sub was due back in Norfolk at 1:00 P.M. on Monday, May 27, 1968.
The families of the Scorpion’s 99 crew members had gathered on the docks that day to welcome their loved ones back home. But as 1:00 P.M. came and went, the sub had not yet surfaced. Minutes stretched into hours; day gave way to night. Still the families waited. But there was no sign of the Scorpion.
With growing alarm, the navy ordered a search. By 10:00 P.M. the operation involved 18 ships; by the next morning, 37 ships and 16 long-range patrol aircraft.6 But the odds of a good outcome were slim. The Scorpion had last made contact off the Azores, six days earlier. She could have been anywhere along that 2,670-mile strip of ocean between the Azores and the eastern seaboard. With every passing hour, the chances that the sub could be located, and that rescue gear could be deployed in time, were rapidly fading. At a tense news conference on May 28, President Lyndon Johnson summarized the mood of a nation: “We are all quite distressed.… We have nothing that is encouraging to report.”7
After eight days, the navy was forced to concede the obvious: the 99 men of the crew were declared lost at sea, presumed dead. The navy now turned to the grim task of locating the Scorpion’s final resting place—a tiny needle in a vast haystack stretching three-fourths of the way across the North Atlantic. Although hopes for saving the crew had been dashed, the stakes for finding the sub were still high, and not only for the families of those lost: the Scorpion had carried two nuclear-tipped torpedoes, each capable of sinking an aircraft carrier with a single hit. These dangerous warheads were now somewhere on the bottom of the sea.
John Craven, Bayesian Search Guru
To lead the search, the Pentagon turned to Dr. John Craven, chief scientist in the navy’s Special Projects Office, and the leading guru on finding lost objects in deep water.
Remarkably, Craven had done this kind of thing before. Two years earlier, in 1966, a B-52 bomber had collided in midair with a refueling tanker over the Spanish coast, near the seaside village of Palomares. Both planes crashed, and the B-52’s four hydrogen bombs, each of them 50 times more powerful than the Hiroshima explosion, were scattered for miles. Luckily none of the warheads detonated, and three of the bombs were found immediately. But the fourth bomb was missing and was presumed to have fallen into the sea.
Craven and his team had to ponder many unknown variables about the crash. Had the bomb remained in the plane, or had it fallen out? If the bomb had fallen out, had its parachutes deployed? If the parachutes had deployed, had the winds taken the bomb far out to sea? If so, in what direction, and exactly how far? To sort through this thicket of unknowns, Craven turned to his preferred strategy: Bayesian search. This methodology had been pioneered during World War II, when the Allies used it to help locate German U-boats. But its origins stretched back much further, all the way to a mathematical principle called Bayes’s rule, first worked out in the 1750s.8
Bayesian search has four essential steps. First, you should create a map of prior probabilities over your search grid. These probabilities are “prior” in that they represent your beliefs before you have any data. They combine two sources of information:
• The presearch opinions of various experts. In the case of the missing H-bomb, some of these experts would be familiar with midair crashes, some with nuclear bombs, some with ocean currents, and so forth.
• The capability of your search instruments. For example, suppose that the most plausible scenario puts the lost bomb at the bottom of a deep ocean trench. Despite its plausibility, you might not actually want to begin your search there: the trench is so dark and remote that even if the bomb were there, you’d be unlikely to find it. To draw on a familiar metaphor, a Bayesian search has you start looking for your lost keys using a precise mathematical combination of two factors: where you think you lost them, and where the streetlight is shining brightest.
You can see an example map of prior probabilities in the top panel of Figure 3.1.

Figure 3.1. In Bayesian search, prior beliefs are combined with data from search sensors to yield a set of revised beliefs.
The second step is to search the location of highest prior probability, which is square C5 in Figure 3.1. If you find what you’re looking for, then you’re done. If you don’t, you move on to the third step: revise your beliefs. Suppose you searched around square C5 but found nothing. Now you reduce the probability around square C5 and bump up the probability in the other regions accordingly. Your prior probabilities have now, in light of the new data, become posterior probabilities. You can visualize this by overlaying two maps on top of each other:
• The original map of prior probabilities (top panel).
• The map of sensor-data probabilities (middle panel). These probabilities are low in the regions where you searched and found nothing, but they remain high in the regions where you haven’t searched at all, since you can’t rule them out.
This is the essence of Bayes’s rule: prior belief + facts = revised belief.
Fourth, and finally, you iterate. You repeat steps 2 and 3, always searching in that day’s region of highest probability. If you come up empty, you revise your beliefs. Today’s posterior becomes tomorrow’s prior, day after day, until you find what you’re looking for.
Craven Is Stymied
Unfortunately, Craven and his team never actually got to apply these Bayesian principles to the 1966 search for the missing H-bomb off the coast of Palomares. In a classic military move, the Pentagon had asked Craven to do something important, and then empowered someone else with a higher rank to make his life as difficult as possible. The commanding officer on the scene, Rear Admiral William “Bull Dog” Guest, had a notably different view of the way the search should be conducted. He had little patience for probabilities, Bayes’s rule, or 20-something-year-old math PhDs dressed in corduroy and Oxford cloth. His initial orders to Craven were to prove that the bomb had fallen on land rather than in the sea, so that it would be someone else’s job to find the damned thing. As a result, the search for the Palomares H-bomb was really two searches. There was Craven’s Bayesian “shadow” search, with its slide rules and probability maps, and with updated numbers constantly chattering over the teletype machine as the mathematicians fed remote calculations to a mainframe back in Pennsylvania. But the insights arising from these calculations were ignored in favor of Admiral Guest’s “plan of squares,” which guided the real search.
Eventually, the Palomares H-bomb was found, after it was discovered that a local fisherman had seen the bomb fall into the water under a parachute and could guide the navy to its point of entry. Thus while the search was a success, the Bayesian part of it had been a failure, for the simple reason that it had never been given a chance. Nonetheless, the Palomares incident taught John Craven some valuable lessons—both about the practicalities of conducting a Bayesian search and about how to get support for that search from the military brass.9
Two years later, when he was called upon to find the Scorpion, Craven was ready.
The Search for the Scorpion Continues
When the Scorpion disappeared in May of 1968, Craven and his team of Bayesian-search experts quickly reconvened. At first, their task seemed vastly more daunting than the search for the Palomares bomb. Back then, they’d known to confine the search to a relatively small area in the shallow seas off the coast of southern Spain. Here, the team had to find a submarine two miles underwater, somewhere between Virginia and the Azores, without so much as a single clue.
Luckily, they caught a break. Starting in the early 1960s, the U.S. military had spent $17 billion installing an enormous, highly classified network of underwater microphones throughout the North Atlantic, so that they could track the movements of the Soviet navy. Highly trained technicians at secret listening posts monitored these microphones around the clock. After sniffing around, Craven discovered that one of these listening posts in the Canary Islands had, one day in late May, recorded a very unusual series of 18 underwater sounds. Then he learned that two other listening posts—both of them thousands of miles away, off the coast of Newfoundland—had recorded those very same sounds around the same time. Craven’s team compared these three readings and, by triangulation, worked out that the sounds must have emanated from a very deep part of the Atlantic Ocean, about 400 miles southwest of the Azores. This location fell along the Scorpion’s expected route home. Moreover, the sounds themselves were highly suggestive: a muffled underwater explosion, then 91 seconds of silence, and then 17 further sonic events in rapid succession that, to Craven, sounded like the implosion of various compartments of a submarine as it sank beneath its hull-crush depth.10
This acoustic revelation dramatically narrowed the size of the search area. Still, the team had about 140 square miles of ocean floor to cover, all of it 10,000 feet below the surface, and therefore inaccessible to all but the most advanced submersibles.
The Bayesian search now kicked into high gear. Craven and his team interviewed expert submariners, who came up with nine possible scenarios—a fire on board, a torpedo exploding in its bay, a clandestine Russian attack, and so on—for how the submarine had sunk. They weighed the prior probability of each scenario and ran computer simulations to understand how the submarine’s likely movements might have unfolded under each one. They even blew up depth charges at precise locations, to calibrate the original acoustical data from the listening posts in the Canary Islands and Newfoundland.
Finally, they put all this information together to form a single search-effectiveness probability for each cell on their search grid. This map crystallized thousands upon thousands of hours of interviews, calculations, experiments, and careful thinking. It would have looked something like Figure 3.2.
Predictably, Craven encountered both logistical and bureaucratic difficulties in getting the Pentagon to pay attention to his map of probabilities. Summer came and went. By this point, the search for the Scorpion had been going for over three months, to no avail.
Eventually his cajoling paid off, and the military brass ordered that Craven’s map be used to guide the search. So starting in October, when commanders leading the search aboard the USS Mizar finally got hold of the map, the operation became truly Bayesian. Day by day, the team rigorously searched the region of highest probability, crunched the numbers, and updated the map for tomorrow. And day by day, those numbers were slowly homing in on rectangle F6.

Figure 3.2. A reconstruction of the map of prior probabilities used in the search for the Scorpion.
On October 28, Bayes finally paid off.
The Mizar was in the midst of its fifth cruise and its seventy-fourth individual run over the ocean floor. All of a sudden the ship’s magnetometer spiked, suggesting an anomaly on the sea floor. Cameras were hurriedly deployed to investigate—and sure enough, there she was. Partially buried in the sand, 400 miles from landfall, and two miles below the surface of the sea, the USS Scorpion had been found at last.11
To this day, nobody knows for sure what happened to the Scorpion—or if they do, they’re not talking. The navy’s official version of events cites the accidental explosion of a torpedo or the malfunctioning of a garbage-disposal unit as the two most likely possible causes. Many other explanations have been proposed over the years—and as with any famous mystery, conspiracy theories abound.12
But there was at least one definitive conclusion to come out of the incident: Bayesian search worked brilliantly. As it turned out, the sub’s final resting place lay a mere 260 yards away from rectangle E5, the initial region of highest promise on Craven’s map of prior probabilities. The search team had actually passed over that location on a previous cruise but had missed the telltale signs due to a broken sonar.13

Figure 3.3. A photo of the bow section of the USS Scorpion, taken in 1968 by the crew of the bathyscape Trieste II.
Ponder that for a moment more. Think of how hard it is to find something you’ve lost on a 100-foot stretch of beach, or for that matter in your own living room. Yet when a lone submarine had disappeared somewhere in a 2,600-mile stretch of open ocean, a Bayesian search had pinpointed its location to within 260 yards, only three lengths of the submarine itself. It was a remarkable triumph for Craven’s team—and for Bayes’s rule, the 250-year-old mathematical formula that had served as the search’s guiding principle.
Bayes’s Rule, from Reverend to Robot
Here’s the key mantra we must take away from the story of the Scorpion: all probabilities are really conditional probabilities. In other words, all probabilities are contingent upon what we know. When our knowledge changes, our probabilities must change, too—and Bayes’s rule tells us how to change them.
Bayes’s rule was discovered by an obscure English clergyman named Thomas Bayes. Born in 1701 to a Presbyterian family in London, Bayes showed an early talent for mathematics, but he came of age at a time when religious dissenters were barred from universities in England. Denied the chance to study math at Oxford or Cambridge, he ended up studying theology at the University of Edinburgh instead. This must have seemed like a cruel barrier to Bayes, just as it did to so many others of his era. But there was a peculiar side effect of this discrimination. Because of its intolerant religious policies, England was home to a surprising number of amateur mathematical societies formed by talented Presbyterians who, like Bayes, were barred from English universities, and who therefore created their own homegrown intellectual communities instead. In his forties, Bayes became a member of one such society, in a spa town in Kent called Tunbridge Wells, where he’d taken a job as a minister—and where he came up with the rule that now bears his name, sometime during the 1750s.
Surprisingly, his discovery didn’t make much of an impact at first. Bayes didn’t even publish it during his lifetime; he died in 1761, and his manuscript was read posthumously to the Royal Society in 1763, by his friend Richard Price. There was a brief period around the turn of the nineteenth century when Bayesian ideas flourished, mainly in the hands of the great French mathematician Pierre-Simon Laplace. But upon Laplace’s death in 1827, Bayes’s rule fell into obscurity and irrelevance for more than a century.
Bayesian Updating and Robot Cars
Today, however, Bayes’s rule is back, better than ever, and sitting right behind the steering wheel of every robot car out there.
Bayes’s rule is an equation that tells us how to update our beliefs in light of new information, turning prior probabilities into posterior probabilities. It offers the perfect solution to the robotics problem we discussed earlier: SLAM, or simultaneous localization and mapping. SLAM is an inherently Bayesian problem. As new sensor data arrives, a robot car must update its “mental map” of the surrounding environment—the lane markers, the intersections, the traffic lights, the stop signs, and all the other vehicles on the road—while simultaneously inferring its own uncertain location within that environment. In essence, a robot car “thinks” of itself as a blob of probability, traveling down a Bayesian road.
Before we describe how this works, let’s address one obvious question up front: Why not just navigate using GPS technology, like the kind you have on your smartphone? The problem is that even under ideal conditions, civilian-grade GPS systems are accurate only to about 5 meters—and they’re much worse in tunnels or near tall buildings, where they might err by 30 or 40 meters. Trying to navigate city traffic using GPS alone would be like trying to perform vascular surgery while wearing oven mitts and a blindfold.
So to supplement the information it gets from its GPS receiver, a robot car must turn to a bevy of other sensors. Some of these are plain old video cameras, while others are just like the safety features on most new cars today—for example, bumper-mounted radar, like the kind that beeps at you whenever you’re in danger of backing up into something.
A robot car’s coolest and most useful sensor is called LIDAR, a portmanteau of “light” and “radar” that stands for “light detection and ranging.” Imagine being blindfolded and told to make your way across an unfamiliar room with the help of nothing but a cane. You would probably do this by touch: that is, by using the cane to poke and prod around you, informally measuring the distance to things in your immediate vicinity. If you did this enough times, in all different directions, then you could build up a good mental map of your surroundings.
A LIDAR array works on the same principle: it shoots a laser beam and measures distance by timing how long it takes the light to bounce back. A typical LIDAR array might have 64 individual lasers, each sending out hundreds of thousands of pulses per second. Each laser beam provides detailed information about a very specific direction. So to allow the car to see in all directions, the LIDAR is mounted on the roof, in a rotating assembly that spins roughly 300 times per minute, just like a faster version of the rotating beam on the radar screens from Top Gun. The lasers will therefore point in any one direction about five times every second, giving the car discrete rather than continuous positional updates. In other words, the car sees a world lit not by steady sunshine but by a strobe light—by short flashes of data from its LIDAR and other sensors, each one giving the car a new view of its surroundings, like in Figure 3.4.

Figure 3.4. A LIDAR image of a highway, courtesy of Oregon State University.
Every time the car receives a new burst of data, it uses Bayes’s rule to update its “beliefs” about its location. We can visualize this Bayesian updating process using a map where the road is broken up into little grid cells, each with its own probability. Suppose that you’ve pulled out of the driveway in your autonomous car, and that you’re now 60 seconds into your journey, traveling at about 30 miles per hour. Based on the data up to now, the car has a set of beliefs about its position. This is shown as a map of probabilities in the upper-left panel of Figure 3.5. Now let’s check in with the car one-fifth of a second later, after one sweep of the LIDAR array, 60.2 seconds into your journey. How have those beliefs changed?
There are three steps in the car’s reasoning. The first is what navigation experts call “dead reckoning,” or as we like to call it, “introspection and extrapolation.” Introspection means collecting “internal state” information, like speed, wheel angle, and acceleration; extrapolation means using this information, together with the laws of physics, to forecast the probable movement of the car over the next fraction of a second. The result is a map of prior probabilities for the car’s location 60.2 seconds into the journey, shown in the upper-right panel of the figure above. These probabilities are “prior” because they don’t yet incorporate updated sensor data; we’re in the instant just before the next flash of the strobe.

Figure 3.5. How an autonomous car uses Bayes’s rule to update its beliefs about its location.
You’ll notice two things here: the blob of probability has moved down the road a bit, and it’s been “smeared out” to cover a larger area. This smearing represents the additional uncertainty introduced by extrapolation. For example, if you’re traveling 30 miles per hour, you’d expect to cover about nine feet in 0.2 seconds. But you might actually cover a bit more or less as a result of unanticipated steering, braking, or acceleration.
The car’s second step is to gather data from its external sensors, like its cameras and LIDAR. These provide a reality check on the car’s position, helping to correct the errors introduced by extrapolation. This information is shown in the bottom-left panel of Figure 3.5. You can think of this map as a set of “sensor-only” probabilities—that is, what would the car think about its position based on external sensors alone, in the absence of any prior information?
The car does have prior information, though, and so the third and final step is synthesis. Using Bayes’s rule, the prior probabilities based on extrapolation (from step 1) are combined with the sensor data (from step 2). In the bottom-right panel, you can see this new map of posterior probabilities, which provides a revised answer to the fundamental question: “Where am I?” Crucially, the blob of posterior probabilities is less smeared out than either the prior or the sensor-data probabilities in isolation. Two sources of information typically mean less uncertainty than you’d have from either source alone.
We’ve left out a lot of details here. Here’s the biggest one: in the example above, we pretended that the road was a fixed reference frame, and that the only unknown variable was the car’s location within that frame. That’s the L in SLAM, for “localization.” But don’t forget the M, for “mapping.” In reality, the road itself is unknown, and all its features are subjected to the same Bayesian treatment. Road boundaries, lane lines, pedestrians, other cars, even kangaroos—all are represented as blobs of probability whose locations are constantly being updated with every flash of data from the sensors.
How Bayes’s Rule Can Make You Smarter
Viewed through the lens of Bayes’s rule, finding a lost submarine and finding yourself on the road turn out to be very similar problems. But Bayes’s rule is far bigger than that. In fact, in terms of its applicability to everyday life, it’s one of the most useful equations ever discovered—a perfect mathematical dose of antidogmatism that tells us when to be skeptical and when to be open-minded. Think of all the new information you encounter every day. Bayes’s rule answers a very important question: When should that information change your mind, and by how much?
You might never in your life actually sit down with pencil and paper to work through the math of Bayes’s rule, and that’s totally fine. The point is that, even if you don’t, learning to think about the world a bit like a Bayesian car—in terms of priors, data, and how to combine them—can help you be a wiser person. Here are two key examples.
Bayes’s Rule in Medical Diagnostics
We’ll start with an example with some clear numbers attached—and where even highly trained experts tend to get the answer wrong, because they have failed to apply Bayes’s rule.
Imagine that you are a doctor, and that a 40-year-old woman named Alice comes into your office for a routine screening mammogram. Unfortunately, her mammogram result comes back positive, indicating that she may have breast cancer. But you know from your medical training that no test is perfect, and that Alice may have gotten a false-positive result. What should you tell her about the probability that she has cancer, given her positive mammogram? Here are some facts to help you judge.
• The prevalence of breast cancer among people like Alice is 1%. That is, for every 1,000 40-year-old women who have a routine mammogram, about 10 of them have breast cancer.
• The test has an 80% detection rate: if we give it to 10 women with cancer, it will detect about 8 of those cases, on average.
• The test has a 10% false-positive rate: if we give it to 100 women without breast cancer, it will wrongly flag about 10 of them, on average.
In light of these numbers, what is the posterior probability P(cancer | positive mammogram)?
The answer, according to Bayes’s rule, is quite small: only 7.4%. This number may surprise you. If so, you’re not alone: a shockingly high number of doctors guess something much larger. In one famous study, 100 doctors were given the same information you’ve just been given, and 95 of them estimated that P(cancer | positive mammogram) was somewhere between 70% and 80%.14 They didn’t just get the answer wrong; they were off by a factor of 10.
This example raises two questions. First, why is the posterior probability P(cancer | positive mammogram) only 7.4%, despite the fact that the mammogram is 80% accurate? Second, how could so many doctors get the answer so badly wrong?
The answer to the first question is this: most women who test positive on a mammogram are healthy, because the vast majority of women who receive mammograms in the first place are healthy. Put simply, cancer has a low prior probability. We can visualize this using a waterfall diagram, which is like an “everyday life” version of the probability map that a self-driving car uses to navigate the road. In Figure 3.6, we follow a hypothetical cohort of 1,000 women, each 40 years old, as they receive routine screening mammograms. The left branch shows 10 women (1% of 1,000) who actually have breast cancer. Since the test is 80% accurate, we expect that of these 10 cases, 2 will be missed and 8 will be caught. Meanwhile, the right branch shows 990 patients who are cancer-free. Since the test has a 10% false-positive rate, we expect that about 890 will be cleared and 100 will be wrongly flagged, rounding off slightly.15
So at the bottom of the waterfall, we end up with 1,000 cases, broken down as follows.
• 108 positive mammograms. Of these, 8 are true positives, or cases of cancer that were detected. The remaining 100 are false positives, or healthy women wrongly flagged by the test.
• 892 negative mammograms. Of these, 2 are false negatives, or missed cancer cases. The other 890 are true negatives, or women correctly given a clean bill of health.
Each of these 1,000 cases is equally likely, so we color in their squares with the same light gray. The fact that cancer is relatively unlikely is reflected not by shading but by sheer numbers: only 10 of these 1,000 squares correspond to cases of cancer.
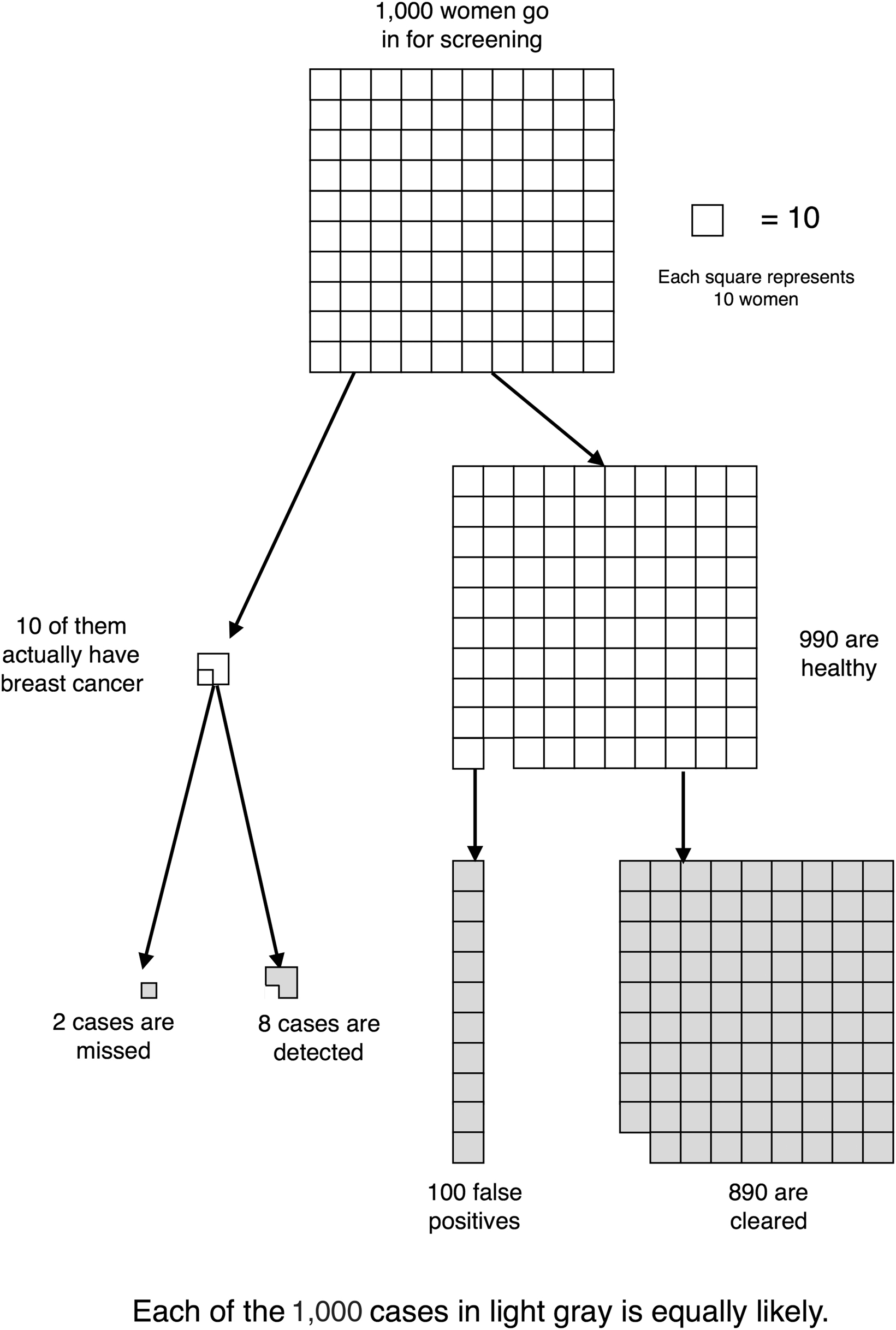
Figure 3.6. A waterfall diagram that follows a hypothetical cohort of 1,000 40-year-old women as they receive routine screening mammograms.
Now let’s use this diagram to think about the situation for your hypothetical patient, Alice. When she first walks into the doctor’s office, you know that Alice will be like one of the 1,000 women at the bottom of the waterfall diagram. You just don’t know which one. When her mammogram comes back positive, now you know that Alice must be like one of the 108 women with the same result. So let’s revisit the diagram and color those 108 cases in a darker gray, while “zeroing out” the other 892 cases by coloring them in white, in Figure 3.6.
Of these 108 positive mammograms, 8 are real cancer cases, while 100 are false positives. Therefore the posterior probability that Alice has cancer, P(cancer | positive mammogram), is about 8/108 ≈ 7.4%.
And that’s Bayes’s rule. The prior probability of cancer was 1%. After you see the data, the posterior probability of cancer becomes 7.4%—a lot higher than the prior, but still a far cry from the 70–80% figure estimated by most doctors. (If you’d like to see this worked out using an actual equation, see the sidebar at the end of the chapter.)
Now let’s turn to the second question we posed earlier. When asked to estimate the posterior probability P(cancer | positive mammogram), why did so many doctors come up with a figure 10 times too high? Basically, the doctors were ignoring the prior probability, a fallacy called “base-rate neglect.” The doctors’ estimates of 70–80% weren’t accounting for the low rate of cancer in the population (1%), which implies that most positive tests will be false positives. Instead, the doctors were focusing on just one number: the fact that the test is “80% accurate,” meaning that it detects 80% of actual cancer cases. They were giving too much credence to the data, and not enough credence to the prior.

Figure 3.7.
There are three morals to this story. First, never ask your doctor, “How accurate is this test?” At best, you’ll get the right answer to the wrong question. Instead ask, “What’s the posterior probability that I have the disease?” (Be prepared for a scowl, though, since your doctor may not know what this is.)
Second, although Bayes’s rule is conventionally expressed as an equation, you rarely need this equation to calculate a posterior probability. Instead, you can just make a waterfall diagram like the one on the previous page, following a hypothetical cohort of subjects through some data-collection process. You’ll get to enjoy the Bayesian omelette without cracking the mathematical egg.
Finally, never neglect the base rate, otherwise known as the prior, when interpreting data. Bayes’s rule says that the right posterior probability is always found by combining data and prior—just the way a robot car navigates the road.
Bayes’s Rule and Investing
In fact, once you become sensitized to the phenomenon of base-rate neglect, you will start to see it everywhere. As our next example shows, it’s an especially important fallacy to watch out for as you contemplate one of the most important financial decisions you will ever make: how to invest for your retirement.
Broadly speaking, there are two popular investment strategies for a retirement portfolio: indexing and gambling. “Gambling” means that you try to pick a winner, by trusting your money to an active fund manager who attempts to outperform the market. “Indexing” means that you give up on trying to beat the market and instead just buy the market, in the form of a broad-based index of stocks like the S&P 500.
Proponents of the gambling strategy argue that it’s entirely possible to beat the market over the long run. Their best argument for that claim is exactly two words long: Warren Buffett. Buffett, also known as the “Oracle of Omaha,” stands alone in the history of investing. His performance numbers are staggering: from 1964 to 2014, an investor in Buffett’s holding company, Berkshire Hathaway, would have turned $10,000 into $182 million. Equally remarkable is Buffett’s consistency: his stock picks have outperformed the S&P 500 over nearly every contiguous five-year period since the mid-1960s. And while Buffett is the most famous Wall Street success story, there have also been others—a handful of true market wizards, from Joel Greenblatt to Peter Lynch, whose track records are way too impressive to be attributable to blind luck. The investors who have identified and trusted these extraordinary fund managers have been richly rewarded.
Yet stacked against the example of these rare geniuses, we find a harsh numerical reality: most fund managers are nothing at all like Warren Buffett. Their performance numbers were especially damning over the 10-year period from 2007 to 2016, a decade that included a historic crash followed by a roaring bull market. These were ideal conditions for smart stock pickers. Yet according to Standard and Poor’s, 86% of actively managed stock funds underperformed their benchmark indices over this period. In Europe, the picture was worse: 98.9% of domestic stock funds, 97% of emerging-market funds, and 97.8% of global stock funds underperformed, net of fees. The active fund managers in the Netherlands took the global prize: 100% of them failed to beat their benchmarks.16
The upshot is that there’s real stock-picking talent out there, but it’s hard to find. So how should these facts affect your investment strategy? Should you settle for an index fund? Or should you gamble on greatness, in the hopes that you can find one of those rare fund managers who truly can beat the market?
If you decide to gamble, then you should be honest with yourself about your goal: to conduct your own Bayesian search for the next Warren Buffett. The possible “search locations” are all the different fund managers competing for your capital, and your “search data” is the information on each manager’s track record. What are the chances that your search can locate one of the rare exceptions, in a vast ocean of fund managers who cannot consistently beat the market?
Alas, Bayes’s rule gives a pretty clear answer: the chances are terrible.
To show why, we’ll appeal to a metaphor that makes the question easy to approach using probability: most mutual fund managers are just flipping coins. In some years they flip heads, and they beat the market. In other years they flip tails, and the market beats them. (Of course, regardless of whether they flip heads or tails, they still charge you fees.) But a rare investor like Warren Buffett is, metaphorically, flipping a coin with heads on both sides. He beats the market year after year, without exception.
Under this metaphor, if we were to compare the 10-year performance of Warren Buffett with that of five regular stock pickers, we might see something like the table below.
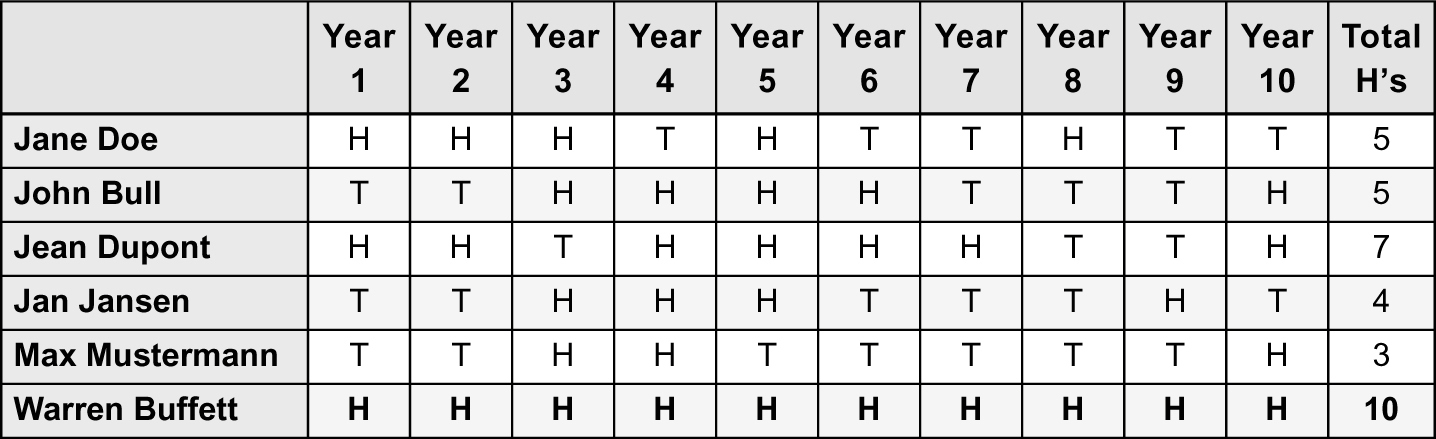
For our five average investors, their performance is just random. But for Buffett, his performance is driven by his superior stock-picking ability—that special two-headed coin he keeps squirreled away in a safe in Omaha, Nebraska. As you can see from the table, his excellent performance clearly stands out from the crowd.
But here’s the problem: on Wall Street, you have to stand out from a much bigger crowd. There aren’t merely five mediocre fund managers out there, flipping coins and charging fees. There are thousands upon thousands of them—and the chances are pretty good that at least a few of them will enjoy long winning streaks, just by chance.
That’s where Bayes’s rule comes in. Imagine a jar containing 1,024 normal coins. Into this jar, a friend places a single two-headed coin. Your friend then gives the jar a good shake, and you draw a single coin at random. You want to know whether your coin has two heads, but it’s against the rules to simply look at both sides: you wouldn’t be able to do that back in the real world, since every fund manager out there will have some great marketing pitch that makes them sound like a two-headed coin. So you’re forced to conduct a statistical test for two-headedness, by flipping the coin 10 times.
Now suppose the coin comes up heads on all 10 flips. In light of the evidence, are you holding the two-headed coin or one of the 1,024 ordinary coins? To answer this question with Bayes’s rule, let’s consider the following facts:
• There are 1,025 coins in the jar: 1,024 are normal, and 1 has two heads.
• The single two-headed coin is guaranteed to come up heads 10 times in a row.
• Any randomly chosen normal coin has probability 1/1024 of coming up heads 10 times in a row. (This is calculated by multiplying ½ by itself 10 times.) Therefore, of the 1,024 normal coins in the jar, we’d expect 1 to come up heads 10 times in a row.
We can tabulate all this information as follows:

This matrix tells us that of the 1,025 coins in the jar, we’d expect two of them to come up heads 10 times in a row. Only one of them is actually the two-headed coin. There’s just a 50% chance that you’re holding it, even after 10 flips.
Now let’s compare this coins-in-a-jar scenario with the kind of marketing language you might hear from a stock picker at an actively managed mutual fund with an above-average track record:
Look at my past performance. I’ve been running my fund for 10 years, and I’ve beaten the market every single year. If I were just one of those average stock pickers at an inferior fund, this would be very unlikely: less than one chance in a thousand.
The math of this scenario is exactly the same as the one involving the big jar of coins. Metaphorically, the fund manager is claiming to be a two-headed coin, on the basis of flipping 10 heads in a row: beating the market every year for 10 years. But from your perspective, things are not so clear. You should recognize that the clever marketing pitch is implicitly conflating two different probabilities: P(10-year winning streak | good stock picker) with P(good stock picker | 10-year winning streak). But remember our key lesson from the story of Abraham Wald: conditional probabilities aren’t symmetric like that.
So is the fund manager lucky or good? Let’s run through the Bayesian calculation under two different prior assumptions. First, suppose you believe that 1% of all stock pickers are true market beaters, and that the other 99% are just flipping coins. Under these assumptions, let’s imagine following a cohort of 10,000 stock pickers over 10 years.
• All 100 excellent stock pickers (1% of 10,000) will beat the market every year.
• A mediocre stock picker has about a 1-in-1,000 chance of beating the market 10 times in a row.† Since there are 9,900 mediocre stock pickers, we’d expect about 10 of them to beat the market all 10 years, just by chance.
So that’s 110 market beaters, of whom 100 were good and 10 were lucky. Therefore, the posterior probability P(market beater | 10-year winning streak) is 100/110, or about 91%.
What if, however, you believed that excellence were much rarer, like P(true market beater) = 1/10,000? Under this prior, the posterior probability ends up being much lower:
• Now there’s only 1 excellent stock picker who beats the market every year.
• Of the 9,999 mediocre stock pickers, we’d again expect about 10 of them to beat the market 10 times in a row, just by chance.
So we have P(market beater | 10-year winning streak) = 1/11, or about 9%.17
Bayes’s rule implies that the right reaction to an investor’s track record depends strongly on the prior probability: whether excellent fund managers are common or rare. Yet all available evidence suggests that true market beaters are exceedingly rare. Recall all those ugly statistics on how few funds exceed their benchmarks in even a single year, much less 10 years in a row.
For the everyday investor, this has one important consequence. There might indeed be great stock pickers out there. But Bayes’s rule implies that, without a very long track record, these geniuses cannot be distinguished reliably from the much larger group of mediocrities who are just getting lucky. Even the genius of Warren Buffett became apparent only over a period of decades. Thus when it comes to the question of searching for a talented fund manager, the lesson of Bayes’s rule is: don’t bother trying. It’s even harder than finding a lost submarine in 2,600 miles of open ocean. You’d almost surely be better off investing in a broad index of stocks and bonds, rather than trying to pick winners.
Nevertheless, hope springs eternal. So in case you find your optimism undiminished by the hard reality of Bayes’s rule, we’ll leave you with this thought. If you’re hoping to find the next Warren Buffett, you will only have a marketing pitch to go by—early in a stock picker’s career, the performance data is almost useless. So tread carefully, or you’ll end up backing the manager with the silver tongue, rather than the golden edge.
Postscript
We first met Bayes’s rule as a principle for finding a lost submarine, and today Bayesian search is a small industry, with entire companies that consult on search-and-rescue operations.18 For example, you might recall the tragedy of Air France Flight 447, which crashed in the Atlantic Ocean on its way from Rio de Janeiro to Paris, in June of 2009. By late 2011, the search for the wreckage had been going on for two fruitless years. Then a Bayesian search firm was hired, a map of probabilities was drawn up, and the plane was found within one week of undersea search.19
Moreover, the main idea of Bayes’s rule—updating your prior knowledge in light of new evidence—applies everywhere, not least behind the wheel of a self-driving car. Biologists use it to help understand the role of our genes in explaining cancer. Astronomers use it to find planets orbiting other stars on the outer fringes of our galaxy. It’s been used to detect doping at the Olympics, to filter spam from your in-box, and to help quadriplegics control robot arms directly with their minds, just like Luke Skywalker.20 And as you’ve seen, it’s essential for navigating the treacherous landscapes of health care and finance.
So Bayes’s rule is much more than just a principle for finding what has been lost. Yes, it helped find the Scorpion, and it helps self-driving cars find themselves on the road. But it can also help you find wisdom in confronting the flood of information you face every day.

