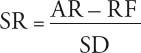
Dieser Anhang liefert die Formeln für die in Kapitel 8 erläuterten Performance-Kennzahlen.
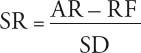
Wobei gilt:
SR = Sharpe Ratio
AR = Average Return (durchschnittliche Rendite, als Näherungswert für die erwartete Rendite)
RF = Risk-free Interest Rate (risikoloser Zinssatz, zum Beispiel die Rendite von Schatzwechseln)
SD = Standard Deviation (Standardabweichung)
Die Standardabweichung wird wie folgt berechnet:
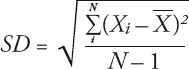
Wobei gilt:
|
= Mittel |
Xi |
= die einzelnen Renditen |
N |
= Anzahl der Renditen |
Wenn man das Sharpe Ratio, wie meist üblich, anhand monatlicher Zahlen berechnet, errechnet sich das annualisierte Sharpe Ratio durch Multiplikation mit der Wurzel aus 12. Man beachte, dass die Rendite eine Durchschnittsrendite ist, keine kumulierte Rendite.
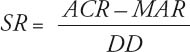
Wobei gilt:
SR |
= Sortino Ratio |
ACR |
= Annual Compounded Return (kumulierte Jahresrendite) |
MAR |
= Minimum Acceptable Return (kleinste akzeptable Rendite, zum Beispiel null, die risikolose Rendite oder der Durchschnitt) |
DD |
= Downside Deviation (Abweichung nach unten) |
Dabei ist DD definiert als:
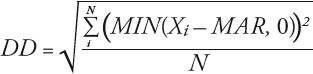
Wobei gilt:
Xi |
= die individuellen Renditen |
MAR |
= Minimum Acceptable Return (kleinste akzeptable Rendite, zum Beispiel null, risikolose Rendite, Durchschnitt) |
N |
= Anzahl der Werte |
Wenn man beispielweise MAR = 0 definiert, werden für die Berechnung von DD nur die Abweichungen in Monaten mit negativen Renditen verwendet (die anderen Monate sind gleich null).
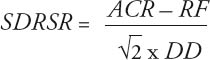
Wobei gilt:
SDRSR |
= Symmetric Downside-Risk Sharpe Ratio |
ACR |
= Annual Compounded Return (kumulierte Jahresrendite) |
RF |
= Risk-free Interest Rate (risikoloser Zinssatz, zum Beispiel die Rendite von Schatzwechseln) |
DD |
= Downside Deviation (Abweichung nach unten) |
Wobei DD definiert ist als:
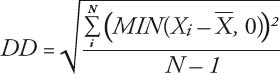
Wobei gilt:
Xi |
= die individuellen Renditen (zum Beispiel das Mittel, null oder die risikolose Rendite) |
|
= Benchmark-Rendite (zum Beispiel das Mittel, null oder die risikolose Rendite) |
Da das SDR Sharpe Ratio nur die Abweichung nach unten beinhaltet, bedeutet die Multiplikation mit der Wurzel aus 2 (aufgrund der Verdoppelung der quadrierten Abweichungen) die Annahme, dass die Abweichung nach oben gleich der Abweichung nach unten (also symmetrisch dazu) ist. Diese ungefähre Ersetzung der Abweichung nach oben ermöglicht es, dass man die Werte des SDR Sharpe Ratio mit Werten des Sharpe Ratio vergleichen kann.
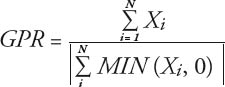
Wobei gilt:
Xi |
= die einzelnen Renditen |
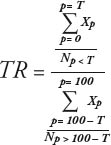
Wobei gilt:
Xp |
= Rendite im Perzentil p |
T |
= Grenz-Perzentil für die Berechnung des Zählers für das Tail Ratio (Implizite Annahme: Niedrigere Perzentil-Ränge bedeuten eine höhere Rendite. Beispielsweise sind die obersten zehn Prozent der Renditen alle Renditen unter T, wobei T = 10). |
Np<T |
= Anzahl der Renditen unter dem Perzentil |
TNp>100–T |
= Anzahl der Renditen über dem Perzentil 100 – T |
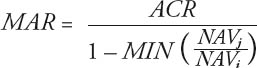
Wobei gilt:
ACR |
= Annual Compounded Return (kumulierte Jahresrendite in Dezimalform) |
NAV |
= Net Asset Value (Nettoinventarwert) |
j > i |
|

Wobei gilt:
ACR |
= Annual Compounded Return (kumulierte Jahresrendite) |
RF |
= Risk-free Return (risikolose Rendite) |
AMR |
= Average Maximum Retracement (größtes durchschnittliches Retracement) = MRi / N |
Wobei gilt:
N |
= Anzahl der Monate |
MRi |
= max(MRPNHi, MRSNLi) |
wobei MRPNHi das maximale Retracement vom vorigen NAV-Hoch aus ist, definiert als:
MRPNHi = (PNHi – NAVi) / PNHi
Wobei gilt:
PNHi |
= voriges NAV-Hoch (vor dem Monat i) |
NAVi |
= NAV am Ende des Monats i |
MRSNLi ist das maximale Retracement zu einem nachfolgenden NAV-Hoch und definiert als:
MRSNLi = (NAVi – SNLi) / NAVi
wobei SNLi das nachfolgende NAV-Tief (nach dem Monat i) ist.