
Sie suchen im Internet nach einem Hotelzimmer in London. Sie finden dasselbe Hotelzimmer auf zwei verschiedenen Websites zu zwei unterschiedlichen Preisen (beide Male einschließlich Steuern):
•Website A: 320
•Website B: 250
Was ist günstiger? Die Antwort scheint auf der Hand zu liegen, tut sie aber nicht. Als ich diese Frage einmal einem Konferenzpublikum stellte, rief ein Teilnehmer zur Antwort: „Kommt darauf an, ob beide inklusive Frühstück sind.“ Ich antwortete: „Das wäre aber ein teures Frühstück.“ Aber zumindest hatte er die richtige Idee, denn die Frage, die ich gestellt hatte, enthielt unvollständige Informationen. Ich hatte nicht gesagt, in welcher Währung die Preise angegeben waren. Wenn nun die 320 Dollar und die 250 Pfund wären? Das würde doch alles ändern, oder?
„Nun ja“, denken Sie jetzt wahrscheinlich, „kein vernünftiger Mensch würde bei einem Preisvergleich die Währung übergehen, also was soll das?“ Der springende Punkt ist, dass Anleger ständig diese Art von Fehler begehen, wenn sie bei der Auswahl von Anlagen nur auf die Rendite achten. Die Renditen ohne die Risiken zu vergleichen ist genauso, als würde man Hotelpreise ohne die Währung vergleichen. Das Risiko ist die Währungsangabe der Rendite.1
Sehen Sie sich die beiden Manager in Tabelle 8.1 an. Welcher bringt die bessere Performance? Wir gehen davon aus, dass die in Kapitel 4 besprochenen versteckten Risiken kein Thema sind und die Standardabweichung somit ein brauchbarer Näherungswert für das Risiko ist. Außerdem gehen wir davon aus, dass die Manager bezüglich der Qualität als gleichwertig gelten.
Viele Anleger würden sich für Manager B entscheiden, weil sie sich überlegen: „Ich bin bereit, das höhere Risiko einzugehen, damit ich das höhere Renditepotenzial bekomme.“ Ist diese Überlegung aber rational? In Tabelle 8.2 nehmen wir eine dritte Investmentalternative hinzu – ein Investment bei Manager A mit einem Schuldenhebel von 300 Prozent.2
Tabelle 8.1
Vergleich zweier Manager

Tabelle 8.2
Erneuter Vergleich der beiden Manager
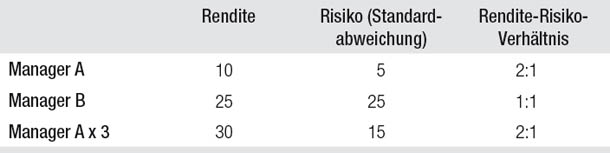
Jetzt weist die gehebelte Investition bei Manager A sowohl eine höhere Rendite als auch ein geringeres Risiko auf als die Investition bei Manager B. Also müssten eigentlich auch risikofreudige Anleger Manager A bevorzugen und einen Hebelfaktor einsetzen, der die Rendite auf das gewünschte Niveau hebt.
Man kann sich das Risiko als Loch vorstellen – je tiefer das Loch, umso größer das Risiko – und die Rendite als Sandhaufen. Die Hebelwirkung ist eine Schaufel, mit der man, falls gewünscht, einen Teil des Sandes aus dem Risikoloch auf den Renditehaufen schaufeln und somit den Ertrag im Austausch gegen ein höheres Risiko steigern kann – ein Kompromiss, den man vielleicht gern eingeht, wenn das Risikoniveau niedriger ist als gewünscht. Um den Vergleich fortzuführen: Durch den Einsatz einer negativen Hebelwirkung (also durch eine Cashposition) ist es auch möglich, Sand vom Renditehaufen in das Risikoloch zu schaufeln und somit das Risiko im Austausch gegen eine geringere Rendite zu senken. In diesem Sinne sind Risiko und Rendite mittels Hebelwirkung vollständig austauschbar.
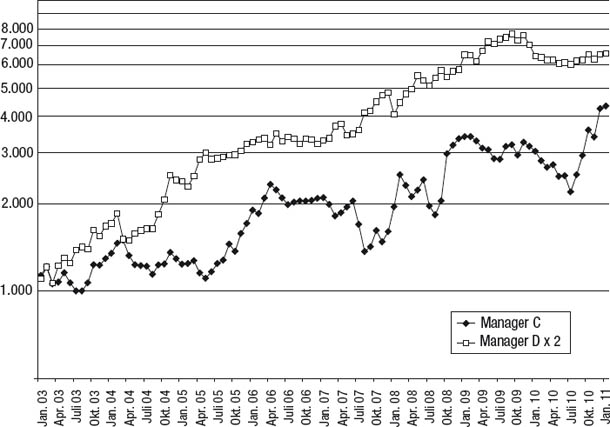
Als Praxisbeispiel zur Veranschaulichung dieses Konzepts vergleichen wir in Abbildung 8.1 zwei konkrete Manager. Angenommen, wir betrachten die frühere Performance als Hinweis auf die potenzielle künftige Performance – zumindest relativ gesehen –, welcher Manager bietet dann das bessere Investment? Es scheint, als wäre die Antwort auf diese Frage unbestimmt: Manager C erzielt zwar eindeutig eine höhere Rendite, aber Manager D weist ein erheblich geringeres Risiko auf, was aus den viel kleineren Drawdowns im gesamten Verlauf des Track Records hervorgeht. Dass es anscheinend unmöglich ist, zu entscheiden, welcher Manager die bessere Performance an den Tag legt, stimmt aber nur in einem oberflächlichen Sinne. In Abbildung 8.2 vergleichen wir wieder die Manager C und D miteinander, aber diesmal gehen wir davon aus, dass das Exposure auf Manager D verdoppelt wird.3 Jetzt wird klar, dass Manager D sowohl hinsichtlich der Rendite als auch hinsichtlich des Risikos überlegen ist, denn er erzielt am Ende einen wesentlich höheren Nettoinventarwert (NAV), dies aber immer noch mit sichtbar kleineren Drawdowns (trotz der Verdopplung des Exposures). Auch wenn Manager C in Abbildung 8.1 am Ende eine höhere Rendite erzielt hat, so könnte man als Anleger doch eine noch höhere Rendite erzielen, indem man doppelt so viel in Manager D investiert – unter Beibehaltung des geringeren Risikos. Daraus kann man die Lehre ziehen, dass die Rendite eine mangelhafte Messlatte ist. Was zählt, ist das Rendite-Risiko-Verhältnis.
Abbildung 8.1
Zwei Wege zur Rendite
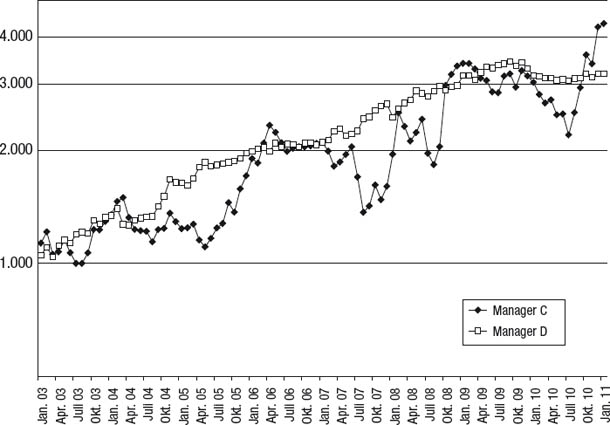
Abbildung 8.2
Doppeltes Exposure auf den weniger riskanten Manager
Und was ist, wenn keine Hebelwirkung als Werkzeug zur Verfügung steht? Was, wenn ein Anleger die Wahl zwischen den Managern C und D aus Abbildung 8.1 hat, aber praktische Hindernisse einer Erhöhung des Exposures auf Manager D im Wege stehen? Dann sind Rendite und Risiko unauflöslich miteinander verbunden und der Anleger muss sich zwischen der höheren Rendite und dem höheren Risiko von Manager C einerseits und der niedrigeren Rendite und dem niedrigeren Risiko von Manager D andererseits entscheiden. Dann mag es scheinen, dass risikotolerante Anleger mit Manager C immer besser fahren. Ein solcher Anleger könnte sich sagen: „Dass Manager C riskanter ist, ist mir egal, solange am Ende die Rendite höher ist.“ Die Schwachstelle dieser Prämisse ist allerdings, dass Anleger, die zum falschen Zeitpunkt mit Manager C anfangen – und das kann leicht passieren –, beträchtliche Verluste statt Gewinne erleben, selbst wenn sie bei dieser Investition bleiben, und erst recht, wenn sie das nicht tun. Je volatiler der Renditeverlauf, umso wahrscheinlicher ist es, dass Anleger das Investment aufgeben, nachdem das Kapital wieder einmal geschrumpft ist, sodass sie die höhere Rendite des Managers gar nicht realisieren. In Echtzeit wissen die Anleger ja nicht, dass sich ihr Investment am Ende wieder erholen wird. Das heißt, obwohl Manager C am Ende einen Vorsprung vor Manager D hat, überstehen viele Anleger die Fahrt gar nicht so lange, dass sie das erfolgreiche Endergebnis erleben (und sogar diejenigen, die es erleben, sind das Investment vielleicht anlässlich eines Ausflugs nach oben eingegangen, was ihre Rendite senkt oder gar eliminiert). Je größer die Volatilität, umso größer der Prozentsatz der Anleger, die ihr Investment mit Verlust kündigen.
Man muss also für gültige Performance-Vergleiche ganz klar risikobereinigte Renditen und nicht nur die Renditen allein verwenden. Im nächsten Abschnitt schauen wir uns ein paar verschiedene Maße für die risikobereinigte Rendite an.
Die Berechnungsformeln für die Performance-Kennzahlen in diesem Abschnitt finden Sie in Anhang B.
Das Sharpe Ratio gehört zu den am meisten verwendeten Kennzahlen für die risikobereinigte Rendite. Es ist definiert als durchschnittliche Überrendite geteilt durch die Standardabweichung. Die Überrendite ist die Rendite, die über die risikolose Rendite hinausgeht (zum Beispiel die Zinsen auf Schatzwechsel). Wenn zum Beispiel die durchschnittliche Jahresrendite acht Prozent und die Zinsen auf Schatzwechsel drei Prozent betragen, beläuft sich die Überrendite auf fünf Prozent. Die Standardabweichung ist ein Maß für die Renditeschwankungen (für eine ausführliche Erklärung siehe in Kapitel 4 den Abschnitt mit der Überschrift „Volatilität als Risikomaß“). Im Prinzip ist das Sharpe Ratio die um die Volatilität der Renditen normalisierte Überrendite.
Das Sharpe Ratio bringt allerdings zwei grundsätzliche Probleme mit sich:
1.Das Maß für die Rendite basiert auf der durchschnittlichen und nicht auf der kumulierten Rendite. Die Rendite, die ein Anleger realisiert, ist die kumulierte Rendite und nicht die durchschnittliche Rendite. Je volatiler die Reihe der einzelnen Renditen, umso mehr weicht die durchschnittliche Rendite von der tatsächlichen (also der kumulierten) Rendite ab. Zum Beispiel würde ein 2-Jahres-Zeitraum mit 50 Prozent Gewinn in einem Jahr und 50 Prozent Verlust im anderen eine durchschnittliche Rendite von null ergeben, aber der Anleger würde in Wirklichkeit einen Verlust von 25 Prozent realisieren (150 % × 50 % = 75 %). Die durchschnittliche kumulierte Jahresrendite von -13,4 Prozent würde hingegen die Wirklichkeit wiedergeben (86,6% × 86,6% = 75%).
2.Das Sharpe Ratio unterscheidet nicht zwischen Volatilität nach oben und nach unten. Das Risikomaß, das im Sharpe Ratio enthalten ist – die Standardabweichung –, spiegelt nicht die Art wider, wie die meisten Anleger das Risiko wahrnehmen. Den Anlegern geht es um Verluste und nicht um die Volatilität. Gegen Volatilität nach unten haben sie etwas, aber Volatilität nach oben gefällt ihnen. Mir sind noch keine Anleger begegnet, die sich darüber beschwert haben, ihre Manager hätten in einem Monat zu viel Gewinn gemacht. Die Standardabweichung und infolgedessen auch das Sharpe Ratio behandeln Volatilität nach oben und nach unten gleich. Diese Eigenschaft kann zu Rangfolgen führen, die den Wahrnehmungen und Vorlieben der meisten Anleger widersprechen.4
Abbildung 8.3 vergleicht zwei Manager, die im dargestellten Zeitraum zwar die gleiche Rendite erzielen, aber sehr unterschiedliche Renditeprofile haben. Welcher Manager erscheint riskanter? Entscheiden Sie sich für eine Antwort, bevor Sie weiterlesen.
Wahrscheinlich meinen Sie, Manager A sei riskanter. Er weist drei Episoden mit Drawdowns von mehr als 20 Prozent auf, wobei der größte 28 Prozent beträgt. Im Unterschied dazu beläuft sich bei Manager B der deutlichste Rückgang vom Gipfel zum Tal auf eher mäßige elf Prozent. Und doch ist die Standardabweichung – die Risikokomponente des Sharpe Ratio – bei Manager B um 30 Prozent höher. Daraus ergibt sich: Obwohl die Manager A und B identische kumulierte Renditen haben und obwohl Manager A viel größere Kapital-Retracements aufweist, ist auch das Sharpe Ratio von Manager A wesentlich höher: 0,71 gegen 0,58 (wenn man einen risikolosen Zinssatz von zwei Prozent annimmt). Wie kommt das? Manager B hat in mehreren Monaten hohe Gewinne verzeichnet und diese Monate treiben seine Standardabweichung kräftig in die Höhe, wodurch sein Sharpe Ratio sinkt. Obwohl die meisten Anleger eindeutig das Risikoprofil von Manager B bevorzugen würden, gibt das Sharpe Ratio mit Bestimmtheit die umgekehrte Rangfolge an.
Abbildung 8.3
Welcher Manager ist riskanter?

Die Möglichkeit, dass eine Diskrepanz zwischen Rangfolgen aufgrund des Sharpe Ratio und den Präferenzen der Anleger bestehen kann, hat dazu geführt, dass andere Kennzahlen für das Verhältnis zwischen Rendite und Risiko erfunden wurden, die versuchen, die Mängel des Sharpe Ratio zu beheben. Bevor wir einige dieser alternativen Kennzahlen besprechen, wollen wir uns aber erst noch mit der Frage befassen: Was bedeutet ein negatives Sharpe Ratio?
Obwohl es üblich ist, dass für Manager, deren Renditen unter der risikolosen Rendite liegen, negative Sharpe Ratios angegeben werden, sind negative Sharpe Ratio absolut bedeutungslos. Wenn das Sharpe Ratio positiv ist, bewirkt eine größere Volatilität (gemessen anhand der Standardabweichung), die ja eine negative Eigenschaft ist, dass das Sharpe Ratio sinkt und so sollte es logischerweise auch sein. Aber wenn das Sharpe Ratio negativ ist, erhöht eine höhere Volatilität seinen Wert – denn wenn man eine negative Rendite durch eine größere Zahl teilt, ergibt sich ein weniger negatives Verhältnis. Vergleiche, die negative Sharpe Ratios beinhalten, können zu absurden Ergebnissen führen. Tabelle 8.3 liefert ein Beispiel dafür. Das Defizit von Manager B gegenüber der risikolosen Rendite ist doppelt so groß wie das von Manager A (-10 Prozent gegen -5 Prozent) und er hat eine viermal so hohe Volatilität. Doch obwohl Manager B sowohl hinsichtlich der Rendite als auch hinsichtlich der Volatilität viel schlechter ist als Manager A, hat er ein höheres (weniger negatives) Sharpe Ratio. Dieses groteske Ergebnis ist eine unmittelbare Folge der Tatsache, dass eine höhere Volatilität bei negativen Sharpe Ratios das Sharpe Ratio erhöht (es weniger negativ macht). Was soll man mit negativen Sharpe Ratios anfangen? Ignorieren.5 Sie sind immer wertlos und oft irreführend.
Das Sortino Ratio behebt beide Probleme, die soeben für das Sharpe Ratio angeführt wurden. Erstens verwendet es die kumulierte Rendite, die die über einen beliebigen Zeitraum tatsächlich realisierte Rendite darstellt, anstelle der arithmetischen Rendite. Zweitens – und das ist noch wichtiger – definiert das Sortino Ratio das Risiko anhand der Abweichung nach unten und berücksichtigt nur Abweichungen unterhalb einer festgelegten „kleinsten akzeptablen Rendite“ (MAR = Minimum Acceptable Return), anstatt wie das Sharpe Ratio die Standardabweichung zu verwenden, die sämtliche Abweichungen nach oben und nach unten beinhaltet. Konkret ist das Sortino Ratio definiert als die über die MAR hinausgehende Überrendite geteilt durch die Abweichung nach unten. Man kann die MAR für die Berechnung des Sortino Ratio zwar auf ein beliebiges Niveau legen, aber normalerweise wird dafür eine der drei folgenden Definitionen verwendet:
1.Null. Es werden Abweichungen für alle negativen Renditen berechnet.
2.Die risikolose Rendite. Es werden die Abweichungen für alle Renditen unterhalb der risikolosen Rendite berechnet.
3.Die durchschnittliche Rendite. Es werden Abweichungen für alle Renditen unterhalb der durchschnittlichen Rendite berechnet.
Die Tatsache, dass das Sortino Ratio eines Managers höher ist als sein Sharpe Ratio, wird häufig als Beleg dafür angeführt, dass die Renditen positiv verschoben seien – es bestehe die Tendenz, dass die Abweichungen nach oben größer als die Abweichungen nach unten sind. Solche Vergleiche sind aber unrichtig. Man kann das Sortino Ratio und das Sharpe Ratio nicht miteinander vergleichen und wie bereits erklärt fällt das Sortino Ratio auch bei Managern höher aus, deren schwerste Verluste größer als ihre höchsten Gewinne sind. Der Grund für das tendenziell höhere Sortino Ratio ist, dass es nur für einen Teil der Renditen Abweichungen berechnet – diejenigen unterhalb der MAR –, aber für die Berechnung der Abweichung nach unten einen Divisor verwendet, der auf der Anzahl aller Abweichungen beruht. Da es zwischen Abweichungen nach oben und nach unten unterscheidet, gibt es die Vorlieben der Anleger wahrscheinlich genauer wieder und ist insofern wohl ein besseres Werkzeug für den Vergleich von Managern. Man sollte ein Sortino Ratio aber nur mit anderen Sortino Ratios vergleichen und niemals mit Sharpe Ratios.
Das Symmetric Downside-Risk Sharpe Ratio Das Symmetric Downside-Risk (SDR = symmetrisches Abwärtsrisiko) Sharpe Ratio wurde von William T. Ziemba entwickelt6 und ähnelt in Absicht und Aufbau dem Sortino Ratio, enthält aber eine entscheidende Anpassung, die die grundsätzliche Aufwärtstendenz des Sortino Ratio im Vergleich zum Sharpe Ratio beseitigt. Das SDR Sharpe Ratio ist definiert als kumulierte Rendite minus risikolose Rendite, geteilt durch die Abweichung nach unten. Die Abweichung nach unten wird ähnlich berechnet wie beim Sortino Ratio, allerdings mit einer entscheidenden Ausnahme: Als Ausgleich dafür, dass zur Berechnung der Abweichung nur Renditen unterhalb eines bestimmten Grenzwerts beitragen, wird ein Multiplikator von 2,0 eingesetzt.7 Man kann die Benchmark für die Berechnung der Abweichung nach unten auf ein beliebiges Niveau legen, dabei gelten aber die gleichen drei Möglichkeiten wie beim Sortino Ratio: null, die risikolose Rendite und die durchschnittliche Rendite. (Ziemba benutzt in seinem Artikel null als Benchmark.) Anders als das Sortino Ratio kann man das SDR Sharpe Ratio (bei Verwendung des Durchschnitts als Benchmark) direkt mit dem Sharpe Ratio vergleichen.8
Das SDR Sharpe Ratio ist (bei allen üblichen Benchmarks) dem Sharpe Ratio vorzuziehen, weil es berücksichtigt, dass Abweichungen nach unten aus Anlegersicht ganz andere Folgen bezüglich des Risikos haben als Abweichungen nach oben. Auch dem Sortino Ratio ist das SDR Sharpe Ratio vorzuziehen, weil es zwar fast identisch berechnet wird 9, aber den entscheidenden Vorteil hat, dass man es direkt mit dem verbreiteten Sharpe Ratio vergleichen kann. Außerdem kann man als Anleger durch den Vergleich des SDR Sharpe Ratios eines Managers mit seinem Sharpe Ratio ein Gefühl dafür bekommen, ob die Renditen des Managers zur positiven oder zur negativen Seite neigen.
Das Gain to Pain Ratio ist die Summe aller Monatsrenditen geteilt durch den Betrag der Summe aller monatlichen Verluste. 10 Diese Performance-Kennzahl gibt das Verhältnis des kumulierten Nettogewinns zu dem kumulierten Nettoverlust an, der realisiert wurde, um den Gewinn zu erzielen. Ein GPR von 1,0 würde beispielsweise bedeuten, dass ein Anleger für die Erzielung seines monatlichen Reingewinns Verluste in gleicher Höhe in Kauf nehmen muss. Das GPR bestraft alle Verluste entsprechend ihrer Größe und die Aufwärtsvolatilität geht positiv ein, denn sie wirkt sich nur auf die Renditekomponente des Verhältnisses aus.
Ein entscheidender Unterschied zwischen dem GPR und Kennzahlen wie dem Sharpe Ratio, dem SDR Sharpe Ratio und dem Sortino Ratio ist, dass es nicht zwischen fünf Verlusten zu jeweils zwei Prozent und einem einzelnen Verlust von zehn Prozent unterscheidet, während sich bei den bisher besprochenen Kennzahlen der einzelne große Verlust stärker auswirkt. Dieser Unterschied ergibt sich daraus, dass bei der Berechnung der Standardabweichung und der Abweichung nach unten für die anderen Verhältniszahlen die Differenz zwischen der Referenzrendite (zum Beispiel dem Durchschnitt, null oder der risikolosen Rendite) und dem Verlust ins Quadrat gesetzt wird. Wenn beispielsweise die Referenzrendite null beträgt, ist das Quadrat eines einzelnen Verlusts fünfmal so groß wie die Summe der Quadrate aus fünf Verlustabweichungen um zwei Prozent (102 = 100; 5 × 22 = 20). Bei der GPR-Berechnung wird hingegen in beiden Fällen 10 zum Nenner addiert. Wenn es einem Anleger egal ist, ob ein bestimmtes Maß an Verlust über mehrere Monate hinweg oder in einem bestimmten Monat entstanden ist, dann ist das GPR ein besseres Maß als das SDR Sharpe Ratio und das Sortino Ratio. Bei einem Anleger, für den ein einzelner großer Verlust schlimmer ist als mehrere Verluste, die zusammen den gleichen Betrag ergeben, wäre das allerdings andersherum.
Zwar wird das GPR normalerweise auf Monatsrenditen angewendet, aber man kann es auch für andere Zeiträume berechnen. Wenn tägliche Zahlen verfügbar sind, kann das GPR dank der zahlreichen Werte eine statistisch sehr signifikante Kennzahl sein. Je länger der Zeitrahmen, umso höher das GPR, denn viele Verluste, die in einem kürzeren Zeitrahmen sichtbar sind, werden über einen längeren Zeitraum geglättet. Nach meiner Erfahrung beträgt das Tages-GPR eines Managers meistens etwa ein Sechstel seines Monats-GPR. Was Monatszahlen angeht, kann man grob sagen, dass GPRs über 1,0 gut und über 1,5 sehr gut sind. Für Tageszahlen belaufen sich die entsprechenden Werte etwa auf 0,17 und 0,25.
Ein Vorteil des GPR gegenüber anderen Verhältnissen ist, dass die Rangfolgen auch bei negativen Renditen korrekt bleiben – das heißt, ein kleineres negatives GPR ist immer besser als ein hohes negatives GPR (was für die anderen Ratios nicht unbedingt gilt). Ein GPR von null bedeutet, dass die Summe aller Gewinne gleich der Summe aller Verluste ist. Der theoretische kleinste Wert des GPRs wäre -1,0 und würde auftreten, wenn es keine Monate mit Gewinn gäbe. Je näher das GPR bei -1,0 liegt, umso kleiner das Verhältnis der Summe aller Gewinne zur Summe aller Verluste. 11
Für den Anleger ist die Frage wichtig, ob die extremen Renditen eines Managers nach oben oder nach unten größer sind. Manager mit häufigen geringen Gewinnen und gelegentlichen hohen Verlusten (Manager mit negativer Schiefe) sind riskanter und weniger wünschenswert als Manager mit häufigen geringen Verlusten und gelegentlichen hohen Gewinnen (Manager mit positiver Schiefe). Es gibt zwar eine statistische Kennzahl für die Schiefe – also für das Ausmaß, in dem der Tail (die Extremereignisse) einer Renditeverteilung auf der rechten (positiven) beziehungsweise auf der linken (negativen) Seite länger ist als bei der symmetrischen Normalverteilung –, aber ihren konkreten Werten lässt sich über ihr Vorzeichen hinaus nur schwer eine intuitive Bedeutung beilegen.
Das Tail Ratio gibt die Tendenz, dass extreme Renditen häufiger auf der positiven oder der negativen Seite auftreten, in Form einer Zahl an, die intuitiv einleuchtet. Das Tail Ratio enthält einen variablen Parameter: den Grenzwert für das obere und das untere Perzentil, die für die Berechnung der Kennzahl verwendet werden. Wenn man diesen Schwellwert beispielsweise auf zehn setzt, entspricht das Tail Ratio dem Durchschnitt aller Renditen im oberen Rendite-Dezil geteilt durch den Durchschnitt aller Renditen im unteren Rendite-Dezil aller Renditen. Bei einer Normalverteilung ergibt sich ein Tail Ratio von 1,0. Ein Tail Ratio deutlich unter 1,0 gibt an, dass die größten Verluste tendenziell größer ausfallen als die größten Gewinne. Ein Ratio deutlich über 1,0 gibt hingegen die umgekehrte Tendenz an. Zum Beispiel würde ein Tail Ratio von 0,5 bedeuten, dass das Ausmaß des durchschnittlichen Verlusts im unteren Dezil doppelt so groß ist wie der durchschnittliche Gewinn im oberen Dezil – und das würde auf einen womöglich sehr riskanten Manager hindeuten.
Das MAR Ratio ist die annualisierte kumulierte Rendite geteilt durch den maximalen Drawdown. Das Calmar Ratio ist exakt das Gleiche, bloß dass sich die Berechnung konkret auf die Zahlen der letzten drei Jahre beschränkt. Diese Verhältniszahlen sind zwar insofern nützlich, als sie sich auf eine Worst-Case-Situation in der Vergangenheit beziehen, aber ihre statistische Signifikanz wird dadurch beeinträchtigt, dass der Divisor nur auf einem einzigen Ereignis basiert. Bei der Anwendung auf längere Track Records benachteiligt das MAR Ratio außerdem Manager mit längeren Track Records massiv, weil mit zunehmender Dauer auch der potenzielle maximale Drawdown wächst. (Beim Calmar Ratio passiert das per definitionem deshalb nicht, weil es nur auf den Zahlen der letzten drei Jahre basiert.) Wie in Kapitel 6 erklärt, sollte man Vergleiche zwischen Managern auf gemeinsame Zeiträume beschränken, und wenn man das MAR verwendet, ist das besonders wichtig.
Das Return Retracement Ratio (RRR = Rendite-Retracement-Verhältnis) ähnelt dem MAR Ratio sowie dem Calmar Ratio insofern, als es die durchschnittliche annualisierte kumulierte Jahresrendite durch ein Maß für ein Retracement (einen Rücklauf) teilt. Der entscheidende Unterschied ist allerdings, dass es nicht auf einem einzigen Retracement beruht (dem größten). Das RRR teilt die Rendite durch das durchschnittliche maximale Retracement (AMR = Average Maximum Retracement), das wiederum auf einer Berechnung des größten Retracements jedes Monats basiert. Das maximale Retracement eines Monats entspricht der jeweils größeren der beiden folgenden Zahlen:
1.Der größtmögliche kumulierte Verlust, den ein investierter Anleger im betreffenden Monat erlitten hätte (der prozentuale Rückgang des NAV vom bisherigen Hoch bis zum Ende des Betrachtungsmonats).
2.Der größtmögliche Verlust, den ein neuer Anleger erlitten hätte, wenn er am Ende des Monats investiert hätte (der prozentuale Rückgang des NAVs vom Ende des Betrachtungsmonats bis zum folgenden niedrigsten NAV).
Für die Bestimmung des maximalen Retracements werden deshalb beide Maße verwendet, weil jedes von beiden in bestimmten Abschnitten des Track Records ein zu geringes Retracement angeben würde. Die erste Bedingung würde unweigerlich in den ersten Monaten des Track Records nur kleine Retracements anzeigen, weil für das Entstehen großer Retracements noch gar keine Möglichkeit bestand. Die zweite Bedingung würde hingegen aus analogen Gründen in späteren Phasen des Track Records zu kleine Retracements ausweisen. Durch Verwendung des jeweils höheren Wertes ist sichergestellt, dass für jeden Monat die Worst-Case-Zahl benutzt wird. Das durchschnittliche maximale Retracement ist der Durchschnitt aller monatlichen maximalen Retracements. Das RRR besitzt eine viel größere statistische Aussagekraft als das MAR Ratio und das Calmar Ratio, weil es auf zahlreichen Datenpunkten (einen für jeden Monat) und nicht nur auf einer einzigen Zahl (dem maximalen Drawdown im gesamten Zeitraum) basiert.
Tabelle 8.4 vergleicht die in Abbildung 8.3 gezeigten Manager A und B bezüglich der besprochenen auf der risikobereinigten Rendite basierenden Performance-Kennzahlen. Interessanterweise führt das Sharpe Ratio, also das mit Abstand am weitesten verbreitete Maß für das Rendite-Risiko-Verhältnis, zu der exakt gegenteiligen Schlussfolgerung aller anderen Kennzahlen. Während das Sharpe Ratio impliziert, dass Manager A hinsichtlich des Verhältnisses zwischen Rendite und Risiko wesentlich überlegen sei, stufen alle anderen Performance-Kennzahlen Manager B höher ein – oft mit großem Abstand. Sie wissen vermutlich noch, dass die kumulierten Renditen der Manager A und B identisch waren und somit der einzige Unterschied zwischen den beiden das Risiko war, auf das man aufgrund ihrer Ertragsverläufe schließen kann. Das Sharpe Ratio, das als Maß für das Risiko die Standardabweichung verwendet, beurteilt Manager B deshalb als riskanter, weil seine Volatilität über alle Monate hinweg höher ist. Allerdings verlief der größte Teil der Volatilität von Manager B nach oben – eine Eigenschaft, die die meisten Anleger als Qualitätsmerkmal und nicht als Fehler betrachten würden. Manager A hatte zwar insgesamt eine geringere Volatilität, aber seine Abwärtsvolatilität war wesentlich größer als die von Manager B – eine Eigenschaft, die die meisten Anleger intuitiv als größeres Risiko empfinden würden. Das Sharpe Ratio unterscheidet nicht zwischen Volatilität nach oben oder nach unten, aber die anderen Kennzahlen für die risikobereinigte Rendite tun das durchaus.
Tabelle 8.4
Ein Vergleich risikobereinigter Rendite-Kennzahlen
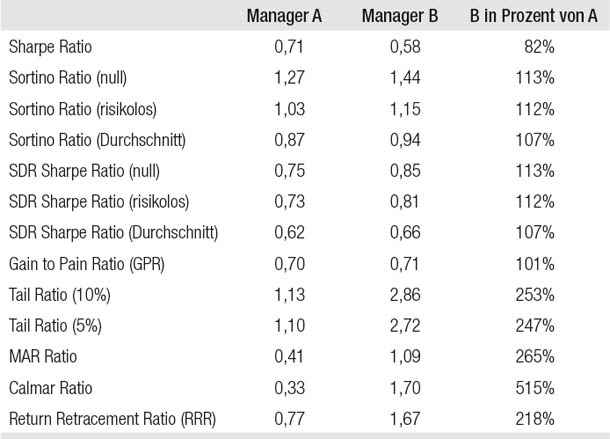
Auch wenn alle Kennzahlen für die risikobereinigte Rendite nur die Volatilität nach unten bestrafen, so tun sie dies doch auf unterschiedliche Arten, die auch unterschiedliche Konsequenzen haben:
•Das Sortino Ratio und das SDR Sharpe Ratio. Diese Verhältnisse bestrafen Renditen unterhalb eines festgelegten Niveaus (zum Beispiel null), wobei das Gewicht der Abweichung nach unten mit zunehmender Abweichung überproportional zunimmt. Deshalb mindert eine einzelne größere Abweichung nach unten das Verhältnis stärker als mehrere kleinere Abweichungen, die zusammen den gleichen Betrag ergeben. Die Reihenfolge der Verlustmonate wirkt sich auf diese Verhältniszahlen nicht aus. Zwei weit voneinander entfernte Verluste von zehn Prozent haben auch dann die gleiche Auswirkung, wenn beispielsweise der zweite zu einem viel größeren Retracement des Kapitals führt.
•Das Gain to Pain Ratio (GPR). Das Gain to Pain Ratio bestraft Abweichungen nach unten direkt proportional zu ihrer Größe. Im Gegensatz zum Sortino Ratio und zum SDR Sharpe Ratio wirkt sich allerdings eine große Abweichung exakt genauso aus wie mehrere kleine Abweichungen, die zusammen den gleichen Betrag ergeben. Dieser Unterschied erklärt, weshalb die Manager A und B laut GPR fast gleichwertig sind, während laut Sortino Ratio und SDR Sharpe Ratio Manager A deutlich schlechter dasteht: Die Verluste von Manager A sind größer und seltener, aber die Summe der Verluste ist bei beiden Managern fast gleich. Was die Reihenfolge der Verluste angeht, ist es beim GPR ähnlich wie beim Sortino Ratio und beim SDR Sharpe Ratio – aufeinanderfolgende oder dicht beieinander liegende Verluste werden nicht stärker bestraft.
•Das Tail Ratio. Das Tail Ratio legt den Schwerpunkt auf die extremsten Gewinne und Verluste. Es hebt sehr gut Manager hervor, deren schwerste Verluste tendenziell größer sind als ihre größten Gewinne. Laut Tail Ratio ist Manager B mit seinen gelegentlichen sehr großen Gewinnen, aber nur mäßigen größten Verlusten dramatisch besser als Manager A, der das umgekehrte Muster an den Tag legt.
•Das MAR Ratio und das Calmar Ratio. Im Gegensatz zu allen vorgenannten Kennzahlen werden diese beiden stark von der Reihenfolge der Renditen beeinflusst. Eine Ballung von Verlusten wirkt sich auf sie viel stärker aus als gleich große Verluste, die über den gesamten Track Record verteilt sind. Allerdings konzentrieren sich beide Kennzahlen nur auf den schwersten Drawdown des Kapitals. Deshalb wirken sich Verluste, die außerhalb des Zeitraums, in dem der schwerste Kapitalverlust vom Hoch zum Tief stattfindet, überhaupt nicht auf diese Verhältniszahlen aus. Da der maximale Drawdown von Manager A viel größer ist als der von Manager B, zeigen diese Verhältnisse daher einen dramatischen Unterschied zwischen den beiden Managern an.
•Das Return Retracement Ratio (RRR). Das RRR ist die einzige Rendite-Risiko-Kennzahl, die sowohl alle Abweichungen nach unten als auch aufeinanderfolgende oder dicht beieinander liegende Verluste bestraft. Im Gegensatz zum MAR Ratio und zum Calmar Ratio, die nur Verluste im Rahmen des maximalen Drawdowns berücksichtigen, beinhaltet die RRR-Berechnung alle Verluste.
Tabelle 8.5
Die Eigenschaften risikobereinigter Performance-Kennzahlen
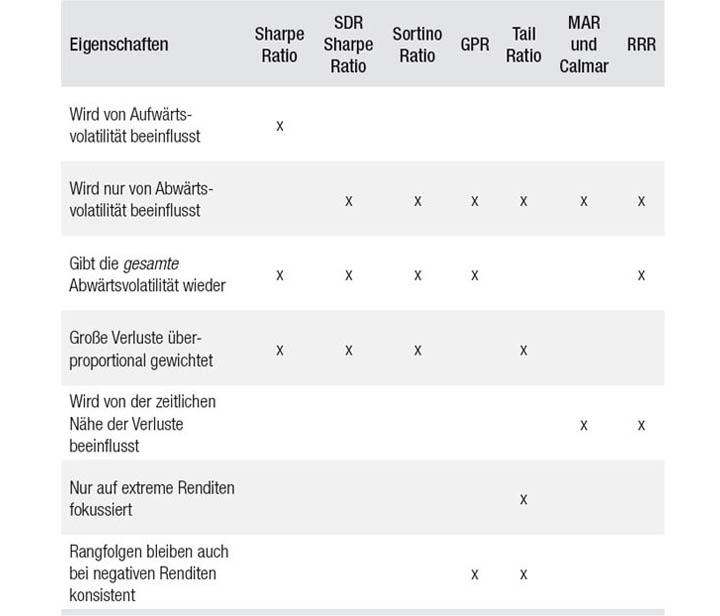
Tabelle 8.5 bietet eine Übersicht über die Eigenschaften der verschiedenen Kennzahlen für die risikobereinigte Rendite.
Zu einem gewissen Grad hängt die Entscheidung, welche Rendite-Risiko-Kennzahl man verwendet, von den Eigenschaften einer Performance-Kennzahl ab, die der individuelle Anleger bevorzugt. Die wichtigsten Vor- und Nachteile der besprochenen Performance-Kennzahlen lassen sich folgendermaßen zusammenfassen:
•Das Sharpe Ratio. Obwohl es die am weitesten verbreitete risikobereinigte Kennzahl ist, passen die von ihm gelieferten Rangfolgen am wenigsten zum intuitiven Risikoempfinden der meisten Menschen, denn es bestraft auch Gewinne.
•Das Sortino Ratio. Dieses Ratio behebt den hauptsächlichen Mangel des Sharpe Ratio dadurch, dass es sich nur auf das Verlustrisiko konzentriert, anstatt das Risiko nach der gesamten Volatilität zu bemessen. Zudem verwendet das Sortino Ratio die kumulierte Rendite, die der tatsächlichen Rendite über den gesamten Zeitraum entspricht, während das Sharpe Ratio die arithmetische Durchschnittsrendite verwendet, bei der das nicht der Fall ist. Ein Nachteil des Sortino Ratio ist, dass man es nicht unmittelbar mit dem Sharpe Ratio vergleichen kann, denn es neigt zu höheren Werten.
•Das SDR Sharpe Ratio. Dieses Verhältnis enthält die gleiche Fehlerkorrektur wie das Sortino Ratio und bietet als zusätzlichen Vorteil eine Anpassung, die direkte Vergleiche mit dem Sharpe Ratio ermöglicht. Ähnlich wie das Sortino Ratio benutzt auch das SDR Sharpe Ratio nicht die arithmetische Durchschnittsrendite, sondern die kumulierte Rendite. Da das SDR Sharpe Ratio fast zur gleichen Rangfolge wie das Sortino Ratio führt und noch den Vorteil hat, dass man es mit dem Sharpe Ratio desselben Managers vergleichen kann, scheint es für alle Anleger die bessere Wahl zu sein. Beide Kennzahlen zu verwenden wäre redundant.
•Das Gain to Pain Ratio (GPR). Ähnlich wie das Sortino Ratio und das SDR Sharpe Ratio bestraft auch das GPR einen Manager nur für Verluste (null Prozent werden auch für das Sortino Ratio und das SDR Sharpe Ratio häufig als kleinste annehmbare Rendite oder als Benchmark gewählt). Das GPR gewichtet Verluste entsprechend ihrem Ausmaß, während bei dem Sortino Ratio und dem SDR Sharpe Ratio größere Verluste stärker gewichtet werden. Anleger, für die ein Monatsverlust von zehn Prozent gleichwertig mit fünf Verlusten à zwei Prozent ist, bevorzugen vielleicht das GPR, während Anlegern, für die ein Monatsverlust von zehn Prozent schlimmer ist, vielleicht das SDR Sharpe Ratio lieber ist.
•Das Tail Ratio. Da das Tail Ratio per definitionem nur einen kleinen Teil aller Renditen berücksichtigt (20 Prozent oder noch weniger), ist es nicht zur alleinigen Verwendung als Maß für die risikobereinigte Rendite gedacht. Dadurch, dass es sich auf extreme Renditen konzentriert, ist es allerdings als Ergänzung zu einer anderen Kennzahl sehr nützlich.
•Das MAR Ratio und das Calmar Ratio. Diese Kennzahlen bestrafen Verluste, die so nahe beieinander liegen, dass sie zum gleichen Drawdown zusammengefasst werden können. Auf die anderen Verhältnisse (außer dem RRR) wirkt sich die Abfolge der Renditen nicht aus. Diese beiden Verhältnisse haben allerdings den Nachteil, dass das Risiko nur durch ein einziges Ereignis definiert ist (den maximalen Drawdown), was ihre statistische Signifikanz und ihre Repräsentativität beeinträchtigt.
•Das Return Retracement Ratio (RRR). Dieses Verhältnis basiert einerseits auf Abweichungen nach unten und wird andererseits von dicht beieinander liegenden Verlusten beeinflusst. Sein großer Vorzug gegenüber dem MAR Ratio und dem Calmar Ratio besteht darin, dass es alle Retracements berücksichtigt und dass die Risikoangabe auf allen Monatszahlen basiert, nicht nur auf einem einzelnen Ereignis und einer einzelnen Zahlenangabe, nämlich dem maximalen Drawdown. Man kann zwar das MAR Ratio und das Calmar Ratio als zusätzliche Kennzahlen zu Rate ziehen, die sich auf eine Worst-Case-Situation beziehen, aber als Maß für das Rendite-Drawdown-Verhältnis ist das RRR vorzuziehen.
Die meisten Menschen dürften der Meinung sein, dass die Performance-Charts in diesem Kapitel ein besseres intuitives Gefühl für die relative Performance (sowohl hinsichtlich der Rendite als auch des Risikos) vermitteln als die Performance-Kennzahlen.
Ein NAV-Chart wie der in Abbildung 8.3 ist eine äußerst nützliche Möglichkeit, einen Track Record zu beurteilen. Der NAV-Chart stellt das kumulierte Wachstum von 1.000 Dollar im Laufe der Zeit dar. So würde etwa ein NAV von 2.000 bedeuten, dass sich die Anfangsinvestition im angegebenen Zeitraum verdoppelt hat. Der NAV kann einen guten intuitiven Eindruck von der früheren Performance vermitteln, sowohl bezüglich der Rendite als auch bezüglich des Risikos. Und wenn man als Anleger nur einen einzigen Maßstab für die Performance überprüfen würde, wäre der NAV-Chart wahrscheinlich der informativste.
Unsere visuelle Wahrnehmung von NAV-Charts mit normaler Skala, die längere Zeiträume darstellen, kann allerdings zu irreführenden Schlüssen führen. Sehen Sie sich Abbildung 8.4 an und beantworten Sie – bevor Sie weiterlesen – die folgenden drei Fragen:
1.War die Rendite in der ersten Hälfte des Track Records oder in der zweiten größer?
2.War der Manager in der ersten oder in der zweiten Hälfte des Track Records riskanter?
3.War seine Rendite-Risiko-Performance in der ersten oder in der zweiten Hälfte des Track Records besser?
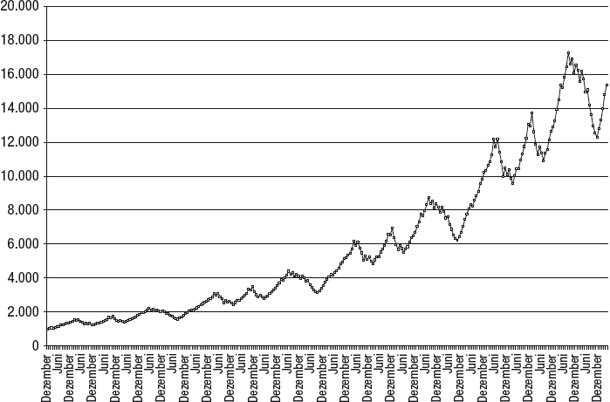
Wenn Sie eine dieser Fragen mit der ersten Hälfte beantwortet haben, liegen Sie falsch. Und wenn Sie eine der Fragen mit der zweiten Hälfte beantwortet haben, liegen Sie ebenso falsch. Die beiden Hälften sind nämlich exakt gleich. Tatsächlich sind sogar alle vier Viertel des Track Records gleich. Abbildung 8.4 wurde so erstellt, dass die in Abbildung 8.3 dargestellten Renditen von Manager A kopiert und viermal hintereinander so zusammengefügt wurden, dass sie die NAV-Entwicklung bei viermal aufeinander folgendem gleichen Renditemuster darstellen. Allerdings scheint es beim Anblick von Abbildung 8.4, als würden sowohl die Rendite als auch die Volatilität im Laufe der Zeit rapide zunehmen. Das tun sie aber nicht. Diese Illusion resultiert aus der Darstellung des NAV-Charts mit einer konventionellen arithmetischen Skala. Auf einer arithmetischen Skala sieht ein Rückgang des NAV um 1.000 immer gleich aus, egal ob er bei 16.000 oder bei 2.000 beginnt. Die beiden Rückgänge unterscheiden sich aber grundlegend: im ersten Fall bescheidene sechs Prozent und im zweiten Fall enorme 50 Prozent. Und die Verzerrung durch die arithmetische Skala wird umso größer, je größer der NAV-Bereich ist. Bei langfristigen Charts ist das oft ein Problem.
Abbildung 8.4
Wie hat sich die Performance im Laufe der Zeit verändert?
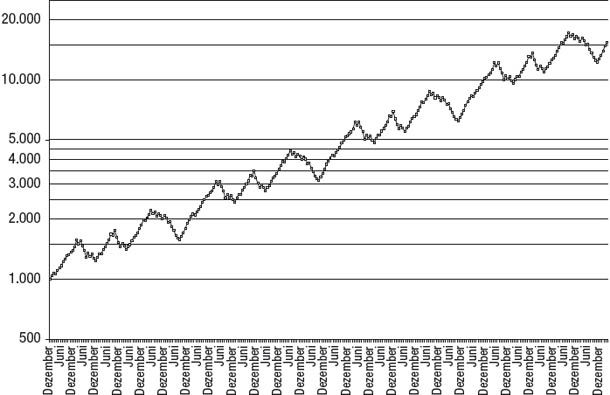
Die ideale Darstellung eines NAV-Charts ist die logarithmische Skala. Auf einer logarithmischen Skala werden die Abstände von Bewegungen eines bestimmten Betrags (zum Beispiel 1.000) mit steigendem Niveau proportional kleiner, sodass prozentual gleiche Bewegungen auf der vertikalen Skala gleich groß erscheinen. Abbildung 8.5 zeigt das gleiche NAV wie Abbildung 8.4, allerdings auf einer logarithmischen Skala. Dass der Chart eine Wiederholung gleicher Muster ist, wird hier erkennbar, weil prozentual gleiche Veränderungen jetzt auch gleich aussehen. Die Moral: Die richtige Darstellungsart für NAV-Charts ist immer die logarithmische Skala und besonders wichtig ist das bei einem großen NAV-Bereich (der in langfristigen Charts verbreiteter ist). Für die Abbildungen 8.1 und 8.2 wurden bereits logarithmische Skalen verwendet, damit die relative Volatilität im zeitlichen Verlauf korrekt dargestellt wurde.
Abbildung 8.5
Logarithmische Skala: Prozentual gleiche Bewegungen sehen auch gleich aus
Der Rolling Window Return Chart oder RWRC zeigt für jeden Monat die Rendite des Zeitraums, nach dem der Chart benannt ist. Beispielsweise zeigt ein 12-Monats-RWRC die 12-Monats-Rendite zu jedem Monatsende (beginnend mit der 12-Monats-Rendite des Track Records). Der RWRC bietet einen klaren visuellen Überblick über die Ergebnisse, die man erzielt hätte, wenn man über einen bestimmten Zeitraum bei einem Manager investiert hätte, und er beantwortet Fragen wie die folgenden: In welchem Bereich hätten sich die Ergebnisse bewegt, wenn man ein Investment bei diesem Manager zwölf Monate lang gehalten hätte? 24 Monate lang? Wie groß war der schwerste Verlust bei einer Haltezeit von zwölf Monaten? Bei einer Haltezeit von 24 Monaten?
In jedem Dezember entspricht die rollierende 12-Monats-Rendite der Jahresrendite. Der wichtige Unterschied besteht jedoch darin, dass der RWRC auch für alle anderen Monate die analogen Renditen angibt. Die Wahrscheinlichkeit, dass der Dezember der Monat des Jahres mit der schlechtesten 12-Monats-Rendite ist, beträgt nur 1:12. Dadurch, dass der RWRC die 12-Monats-Renditen zu allen Monatsenden zeigt, beinhaltet er auch Worst-Case-Ereignisse, die von den Jahresrenditen wahrscheinlich nicht erfasst würden, und liefert somit für Haltezeiten von einem Jahr ein treffenderes Bild. Man kann auch RWRCs für andere Zeiträume berechnen (zum Beispiel für 24 oder 36 Monate).
Abbildung 8.6
Kleiner Unterschied bei der Rendite, großer Unterschied bei der Stabilität der Rendite
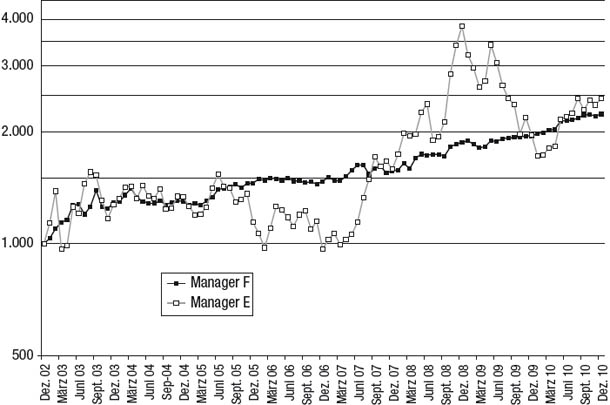
Um zu veranschaulichen, wie man einen RWRC als grafisches Analysewerkzeug verwendet, vergleichen wir in Abbildung 8.6 zwei Manager miteinander, die sich hinsichtlich ihrer Renditen nur leicht voneinander unterscheiden (die kumulierte Jahresrendite von Manager E ist nur um 1,3 Prozent höher), hinsichtlich der Stabilität ihrer Renditen hingegen sehr. Wie in Abbildung 8.7 gezeigt, schwanken die 12-Monats-Renditen von Manager E enorm – zwischen einem schweren Verlust von 49 Prozent und einem spektakulären Gewinn von 142 Prozent. Im Gegensatz dazu bewegen sich die 12-Monats-Renditen von Manager F innerhalb eines viel gemäßigteren Bereichs von -10 bis +29 Prozent (siehe Abbildung 8.8). Bei Anlegern, die geduldig genug waren, mindestens zwölf Monate lang bei Manager F zu bleiben, hätte es nur eine Handvoll Anfangsmonate gegeben, die zu einem Nettoverlust geführt hätten. Anlegern, die bei Manager E investiert hätten, hätte diese Geduld allerdings keinen Trost gebracht, denn sie hätten in mehr als einem Viertel aller 12-Monats-Zeiträume Nettoverluste von mehr als 15 Prozent und in mehreren sogar über 40 Prozent erlitten. Selbst Anleger, die sich bei Manager E auf eine 24-monatige Haltezeit eingelassen hätten, hätten in fast einem Fünftel aller Zeiträume Verluste von mehr als 15 Prozent erlitten (siehe Abbildung 8.9). Im Gegensatz dazu wäre das schlechteste Ergebnis einer Haltezeit von 24 Monaten bei Manager E eine positive Rendite von vier Prozent gewesen (siehe Abbildung 8.10).
Abbildung 8.7
Rollierende 12-Monats-Renditen: Manager E
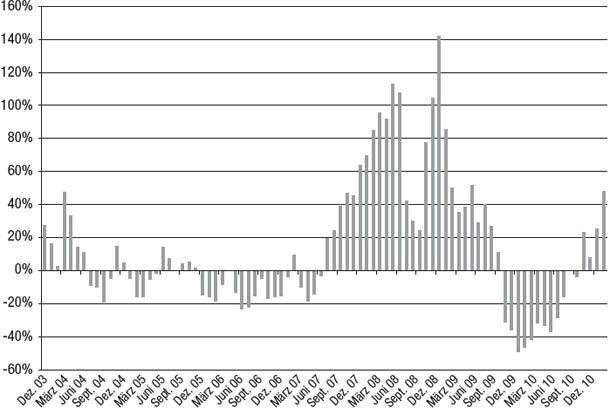
Abbildung 8.8
Rollierende 12-Monats-Renditen: Manager F
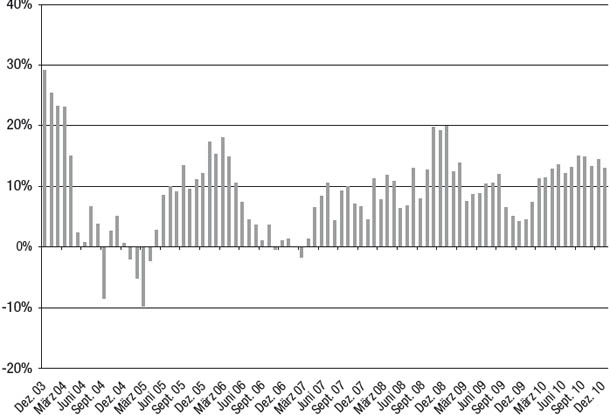
Abbildung 8.9
Rollierende 24-Monats-Renditen: Manager E
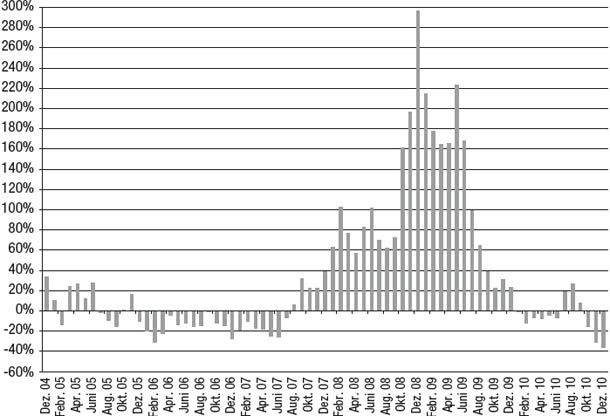
Abbildung 8.10
Rollierende 24-Monats-Renditen: Manager F
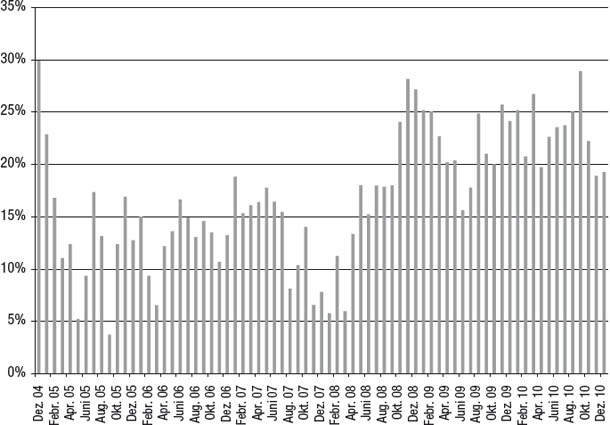
Man kann als Anleger den RWRC einsetzen, um die potenzielle Häufigkeit und Größe von Worst-Case-Ergebnissen abzuschätzen, wenn man Investments anhand seiner Toleranz bezüglich der Haltedauer von Verlustpositionen auswählen will. Beispielsweise sollte ein Anleger, der nicht bereit ist, eine Verlustposition länger als zwölf Monate zu halten, Manager mit einem merklichen Anteil von negativen 12-Monats-Renditen meiden – egal wie gut ihre anderen Performance-Kennzahlen auch sein mögen.
Man kann mit rollierenden Charts auch andere Angaben darstellen als die Rendite. Beispielsweise kann man anhand eines rollierenden Charts der annualisierten Volatilität (tägliche Daten in einem mehrmonatigen Zeitfenster) verwenden, um Manager oder Portfolios hinsichtlich frühzeitiger Anzeichen für einen möglichen Anstieg des Risikos zu überwachen.
Der Underwater Chart zeigt den schlimmsten möglichen kumulierten prozentualen Verlust an, den man als Anleger am Ende jedes Monats hätte erleiden können – dafür geht man davon aus, dass das Investment zum vorangegangenen NAV-Höhepunkt getätigt wurde. Der tiefste Punkt im NAV-Chart ist das maximale Retracement (das Risikomaß, das für das MAR Ratio und das Calmar Ratio verwendet wird). Allerdings bietet der Underwater Chart weitaus mehr Informationen, weil er nicht nur den größtmöglichen Verlust über den gesamten Track Record zeigt (das maximale Retracement), sondern auch den größtmöglichen Verlust am Ende aller anderen Monate des Track Records. Abbildung 8.11 ist der Underwater Chart der beiden in Abbildung 8.6 dargestellten Manager mit sehr verschiedener Stabilität der Renditen. Krasser könnte der Unterschied zwischen den beiden wohl kaum sein. Die Retracements von Manager F sind sehr flach und relativ kurzlebig (ein Anstieg zur 0-Prozent-Linie zeigt ein neues NAV-Hoch an). Die Retracements von Manager E sind hingegen tief und langwierig. Der Underwater Chart bietet eine hervorragende visuelle Darstellung des relativen Risikos eines Investments, die sehr gut zu der Art passt, wie die meisten Anleger das Risiko wahrnehmen.
Abbildung 8.11
Underwater Curve: Manager E und Manager F im Vergleich
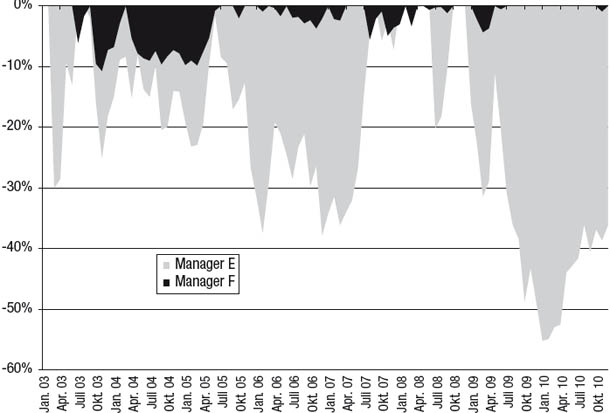
Die Underwater Curve hat allerdings den Mangel, dass das Risiko in den Monaten im ersten Teil des Track Records zu niedrig angegeben wird, weil die Zeit für den Rückblick auf ein früheres NAV-Hoch nicht lange genug ist. Es gibt keine Möglichkeit, den Worst-Case-Verlust für diese frühen Monate wirklichkeitsgetreu darzustellen, weil es dafür einfach keinen Track Record gibt. Außerdem ist die Underwater Curve aus der Sicht des schwersten kumulierten Verlusts konstruiert, den ein bestehender Anleger erleiden könnte. Man kann mit Recht behaupten, dass der schlimmste Verlust eines neuen Anlegers ein noch relevanteres Maß sein dürfte. Eine Lösung, diesen Unzulänglichkeiten der Berechnung der Underwater Curve abzuhelfen, wäre die zusätzliche Berücksichtigung des schwersten Verlusts, den Anleger erlitten hätten, die in jedem Monat eingestiegen wären, wenn man annimmt, sie wären am Punkt des tiefsten nachfolgenden NAV ausgestiegen. Auf diese Weise kann man eine „Zweiwege“-Underwater Curve (2DUC = 2-Direction Underwater Curve) konstruieren, die für jeden Monat den größten der beiden folgendermaßen definierten Verluste zeigt:
1.Der kumulierte Verlust eines bestehenden Anlegers vom vorangegangenen NAV-Höhepunkt aus.
2.Der kumulierte Verlust eines Anlegers, der zum Monatsende investiert hat und zum nächsten NAV-Tief liquidiert hat.
Der Durchschnitt aller Punkte des 2DUC-Charts wäre somit das Risikomaß, das auch für das Rendite-Retracement-Ratio verwendet wird (das durchschnittliche maximale Retracement oder AMR = Average Maximum Retracement). Die Ausflüge von Manager E unter die Wasserlinie werden im 2DUC-Chart noch signifikanter (Abbildung 8.12), sie steigen von einem durchschnittlichen Monatswert von 21 auf ein AMR von 30. Die Underwater Curve von Manager E bleibt auch im 2DUC-Chart mit einem nach wie vor niedrigen Durchschnitt von drei Prozent gedämpft. Der 2DUC-Chart besagt, dass das durchschnittliche Worst-Case-Szenario für Anleger bei Manager F zehnmal so schlimm ausfällt wie bei Manager F. Für eine Differenz der durchschnittlichen kumulierten Jahresrendite von 1,3 Prozent ist das eine Menge zusätzliches Risiko. Es wäre also selbst für den risikotolerantesten Anleger schwierig, aufgrund der Performance die Entscheidung für Manager E statt Manager F zu rechtfertigen.
Abbildung 8.12
2DUC: Manager E und Manager F im Vergleich
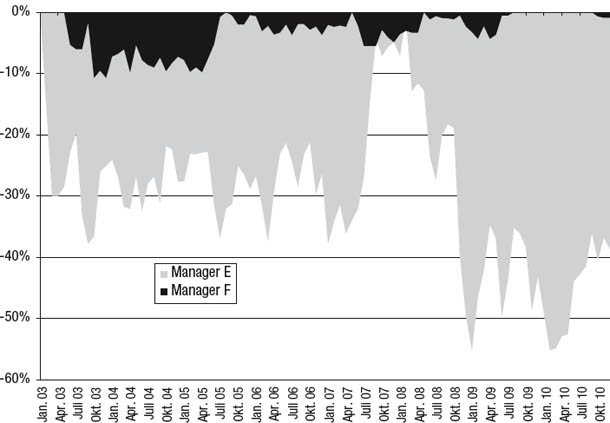
Investment-Missverständnis 23: Die durchschnittliche Jahresrendite ist wahrscheinlich die allerwichtigste Performance-Kennzahl.
In Wirklichkeit: Die Rendite allein ist bedeutungslos, weil sie durch Erhöhung des Risikos jederzeit gesteigert werden kann. Die hauptsächliche Performance-Kennzahl sollte das Rendite-Risiko-Verhältnis sein.
Investment-Missverständnis 24: Für einen risikofreudigen Anleger, der zwei Anlagealternativen abwägt, ist ein Investment mit erwartetem niedrigerem Rendite-Risiko-Verhältnis, aber höherer Rendite einem Investment von gleicher Qualität, aber umgekehrten Eigenschaften häufig vorzuziehen.
In Wirklichkeit: Die Alternative mit dem höheren Rendite-Risiko-Verhältnis kann selbst für risikobereite Anleger die bessere sein, denn durch Hebeleinsatz kann sie in ein Investment mit gleicher Rendite bei geringerem Risiko beziehungsweise höherer Rendite bei gleichem Risiko verwandelt werden.
Investment-Missverständnis 25: Das Sharpe Ratio ist als Rendite-Risiko-Kennzahl die beste Wahl.
In Wirklichkeit: Das Sharpe Ratio ist zwar das am häufigsten verwendete Maß für das Rendite-Risiko-Verhältnis, aber da es nicht zwischen Aufwärts- und Abwärtsvolatilität unterscheidet, passen viele der in diesem Kapitel beschriebenen alternativen Rendite-Risiko-Kennzahlen besser zu der Art, wie die meisten Anleger das Risiko wahrnehmen.
Investment-Missverständnis 26: Wenn das Sortino Ratio höher ist als das Sharpe Ratio, lässt sich daraus schließen, dass die Renditeverteilung des Managers rechtsschief ist (starke Abweichungen nach oben sind wahrscheinlicher als starke Abweichungen nach unten).
In Wirklichkeit: Das Sortino Ratio liefert aufgrund seiner Berechnungsformel tendenziell höhere Werte als das Sharpe Ratio. Diejenige Rendite-Risiko-Kennzahl, die auf dem Verlustrisiko basiert und direkt mit dem Sharpe Ratio vergleichbar ist, ist das auf dem symmetrischen Verlustrisiko basierende SDR Sharpe Ratio (wenn man als Benchmark die durchschnittliche Rendite verwendet). Wenn das SDR Sharpe Ratio deutlich höher ist als das Sharpe Ratio, bedeutet dies, dass die Renditen rechtsschief sind.
Investment-Missverständnis 27: Der maximale Drawdown ist eines der wichtigsten Risikomaße.
In Wirklichkeit: Der größte Nachteil des maximalen Drawdowns ist, dass er nur auf einem einzigen Ereignis basiert. Ein Retracement-Maß, das auf allen Datenpunkten basiert, zum Beispiel das durchschnittliche maximale Retracement (AMR = Average Maximum Retracement), ist viel aussagekräftiger als der maximale Drawdown. Aus diesem Grund ist das Return Retracement Ratio (RRR) Rendite-Risiko-Kennzahlen vorzuziehen, die auf dem maximalen Drawdown basieren (wie MAR, Calmar et cetera).
Investment-Missverständnis 28: Die Größe der Rückgänge im NAV-Chart steht in direkter Beziehung zur Größe der Kapital-Drawdowns.
In Wirklichkeit: Der konventionelle NAV-Chart wird auf einer arithmetischen Skala dargestellt, der zwar die Veränderungen in Dollar exakt wiedergibt, nicht aber die prozentualen Veränderungen. Infolgedessen erscheint der gleiche prozentuale Rückgang größer, wenn der Wert des Investments größer ist. In längerfristigen Charts, die von Anfang bis Ende einen beträchtlichen Wertzuwachs abdecken, erscheinen die Preisbewegungen der jüngeren Vergangenheit daher im Verhältnis zu prozentual gleich großen Bewegungen in weiter zurückliegenden Zeiträumen stark übertrieben. Um diese Verzerrung zu vermeiden, sollten längerfristige NAV-Charts logarithmisch dargestellt werden.
Viele Anleger legen zu viel Wert auf die Rendite. Da man die Rendite jederzeit durch Erhöhung des Exposures (also durch das Eingehen eines höheren Risikos) steigern kann, ist das Rendite-Risiko-Verhältnis ein viel aussagekräftigeres Maß für die Performance. Man kann nämlich eine Anlage mit höherem Rendite-Risiko-Verhältnis und geringerer Rendite als eine Alternativanlage mit gegenteiligen Eigenschaften mithilfe eines Hebels bei geringerem Risiko auf das gleiche Renditeniveau heben. Das Sharpe Ratio ist die mit Abstand am weitesten verbreitete Kennzahl für das Rendite-Risiko-Verhältnis. Allerdings bestraft es Volatilität nach oben genauso wie Volatilität nach unten und das passt nicht zu der Art, wie die meisten Anleger Risiken wahrnehmen. Andere Rendite-Risiko-Kennzahlen, die in diesem Kapitel erläutert wurden und die als Näherung für das Risiko die Verluste in den Fokus nehmen, spiegeln die Art, wie die meisten Anleger Risiken wahrnehmen, besser wider. Man kann als Anleger Tabelle 8.5, die einen Überblick über die Eigenschaften verschiedener Rendite-Risiko-Kennzahlen bietet, für die Auswahl der Performance-Kennzahlen benutzen, die am besten zu ihren Kriterien passen. Man kann die Rendite-Risiko-Kennzahlen auch durch die in diesem Kapitel erläuterten Performance-Charts ergänzen, die in intuitiver, verständlicher Form eine gewaltige Menge an Informationen liefern und den Kern jeder Performance-Analyse bilden sollten. Ich empfehle, bei jeder Beurteilung eines Managers oder eines Fonds folgende Performance-Charts zu verwenden:
•Einen NAV-Chart
•RWRCs über zwölf und 24 Monate
•Einen 2DUC-Chart

Anmerkung: Einige Kennzahlen und Chart-Analysewerkzeuge, die in diesem Kapitel beschrieben werden, habe ich selbst erfunden und daher sind sie in keiner existierenden Software verfügbar. Momentan befasse ich mich mit der Entwicklung einer Onlinesoftware für die Performance-Beurteilung, die alle in diesem Kapitel erläuterten Zahlen und Chart-Werkzeuge enthalten wird. Das Produkt mit dem Namen „Schwager Analytics Module“ dürfte im zweiten Quartal 2013 als Modul für das von Gate 39 Media entwickelte System Clarity Portfolio Viewer erhältlich sein. Das Schwager Analytics Module wird so gestaltet sein, dass es sowohl Portfolios als auch die Investments analysieren kann, aus denen sie bestehen (zum Beispiel Manager, Fonds oder sonstige Investments). Interessierte Leser erhalten unter www.gate39media.com/schwager-analytics weitere Informationen. Im Sinne der Offenlegung: Ich habe ein finanzielles Interesse an diesem Produkt.
1 Wir lassen hier außer Acht, dass höhere Renditen, wie in Kapitel 6 dargelegt, ein negativer Indikator für die künftige Performance sein können, und wir gehen davon aus, dass die Performance-Vergleiche über längere Zeiträume vorgenommen werden, nicht nur auf die jüngere Vergangenheit bezogen – und dass der Anleger Grund zu der Annahme hat, dass die Fähigkeiten des Managers bei dem Performance-Unterschied eine Rolle spielen.
2 Bei Strategien, bei denen eine Margin verwendet wird (zum Beispiel Futures, FX, Optionen), brauchen die Manager nur einen kleinen Anteil der nominalen Investition aufzubringen, um die Margin-Anforderungen zu erfüllen. In solchen Fällen kann man als Anleger häufig das sogenannte Notional Funding [etwa: „fiktive Finanzierung“] nutzen – ein Konto wird mit einem geringeren Geldbetrag als seinem Nennwert finanziert. Zum Beispiel kann ein Anleger auf ein Konto 300.000 Dollar einzahlen und damit Anlagen im Wert von 900.000 Dollar handeln – implizit wird also das Investment im Vergleich zu einem Investment ohne Notional Funding mit 300 Prozent gehebelt. Technisch gesehen stellt das Notional Funding allerdings keinen echten Schuldenhebel dar, obwohl es das Exposure pro investiertem Dollar erhöht, denn dabei wird kein Geld verliehen. Unser Beispiel geht von Notional Funding aus. Bei Strategien, die vollständig finanziert werden müssen, muss man vom gehebelten Anteil der Rendite die Kreditkosten abziehen.
3 Die Manager C und D sind CTAs, die mit Futures handeln, sodass man das erhöhte Exposure durch Notional Funding erzielen könnte (also ohne Hebelwirkung durch Kreditaufnahme). Die in Abbildung 8.1 dargestellten Renditen wurden um die Zinseinnahmen bereinigt, sodass die Verdopplung des Exposures (egal, ob durch Notional Funding oder einen kreditfnanzierten Hebel) alle Renditen fast exakt mit dem Faktor 2 multiplizieren würde. (Wenn die Renditen Zinseinnahmen beinhalten würden, würde die Verdopplung des Exposures die Renditen nicht exakt verdoppeln, denn auf das zusätzliche Exposure würden ja keine Zinseinkünfte anfallen.)
4 Der Gerechtigkeit halber muss man sagen, dass eine hohe Aufwärtsvolatilität ein Hinweis auf eine größere potenzielle Abwärtsvolatilität sein kann und dass das Sharpe Ratio in solchen Fällen ein geeignetes Maß ist. Besonders irreführend ist es allerdings bei der Beurteilung von Strategien, die darauf abzielen, gelegentlich große Gewinne zu erzielen, und dabei das Verlustrisiko straff kontrollieren (also rechtsschiefe Strategien).
5 Und was macht man, wenn man einen Wert braucht, etwa wenn man anhand des Ratios eine Rangfolge von Managern erstellt? In diesem Fall ist es sinnvoll, für die Sortierung zwei Kriterien zu verwenden: Bei positiven Überrenditen benutzt man das Sharpe Ratio, bei negativen Renditen einfach die Überrendite.
6 William T. Ziemba: „The Symmetric Downside Risk Sharpe Ratio“, in: Journal of Portfolio Management (Herbst 2005), S. 108-121.
7 Ziemba hat bei der Definition der Abweichung nach unten den Begriff „Benchmark“ statt MAR verwendet. Wenn man als Benchmark den Median benutzt, geht nur die Hälfte der Renditen in die Berechnung der Abweichung nach unten ein und dann sorgt der Multiplikator von 2,0 für einen exakten Ausgleich. Entscheidet man sich für eine andere Benchmark (zum Beispiel null, die risikolose Rendite oder den Durchschnitt), ist die Anzahl der Punkte unterhalb der Benchmark nicht exakt halb so groß und der Multiplikator von 2,0 liefert nur eine ungefähre Anpassung.
8 Um ganz genau zu sein: Bei einer symmetrischen Verteilung der Renditen liegt das SDR Sharpe Ratio tendenziell leicht unter dem Sharpe Ratio, weil beim SDR Sharpe Ratio die kumulierte Rendite und nicht wie beim Sharpe Ratio die arithmetische Rendite verwendet wird. Und die arithmetische Rendite ist immer größer oder gleich der kumulierten Rendite. Wenn man als Benchmark für die Berechnung der Abweichung nach unten allerdings null oder die risikolose Rendite verwendet, weil man annimmt, dass die durchschnittliche Rendite des Managers höher ist als die risikolose Rendite, neigt das SDR Sharpe Ratio aus zwei Gründen dazu, bei einer symmetrischen Renditeverteilung höher zu sein als das Sharpe Ratio:
1.Dann liegt weniger als die Hälfte der Renditen unter der Benchmark, sodass die Multi-plikation mit 2,0 keinen vollständigen Ausgleich bewirkt.
2.Abweichungen nach unten von der risikolosen Rendite (erst recht von null) sind kleiner als Abweichungen vom Durchschnitt.
Aufgrund dieser beiden Faktoren ist die Abweichung nach unten geringer als die Standardabweichung und daraus ergibt sich, dass das SDR Sharpe Ratio kleiner ist als das Sharpe Ratio.
9 Neben der entscheidenden Einführung des Multiplikators von 2,0, der einen unverfälschten Vergleich zwischen dem SDR Sharpe Ratio und dem Sharpe Ratio ermöglicht, ist der einzige Unterschied zwischen dem SDR Sharpe Ratio und dem Sortino Ratio, dass Ersteres die risiko-lose Rendite von der kumulierten Rendite anstatt von der MAR (die gleich der risikolosen Rendite sein kann oder nicht) abzieht.
10 Das Gain to Pain Ratio (GPR) ist eine Performance-Kennzahl. Ich benutze es seit vielen Jahren. Mir ist keine frühere Verwendung dieser Kennzahl bekannt, allerdings wird dieser Begriff manchmal als Bezeichnung für Rendite-Risiko-Kennzahlen oder Rendite-DrawdownKennzahlen verwendet. Das GPR ähnelt dem Profitfaktor, einer gängigen Kennzahl für die Beurteilung von Handelssystemen. Der Profitfaktor ist die Summe aller profitablen Trades geteilt durch den Betrag der Summe aller verlustbringenden Trades. Er wird allerdings auf Trades angewendet, das GPR hingegen auf Renditen innerhalb bestimmter Zeiträume (zum Beispiel Monatsrenditen). Es lässt sich rechnerisch leicht zeigen, dass der Profitfaktor dem GPR + 1 entspricht und somit zur gleichen Performance-Rangfolge führt wie das GPR. Für quantitativ orientierte Leser, die mit der Omega-Funktion vertraut sind: Die auf null bezogene Omega-Funktion entspricht ebenfalls dem GPR + 1.
11 Das Verhältnis der Summe der Gewinne zur Summe der Verluste entspricht dem GPR + 1. Also würde beispielsweise ein GPR von -0,25 bedeuten, dass das Verhältnis der Summe der Gewinne zur Summe der Verluste 0,75 beträgt.