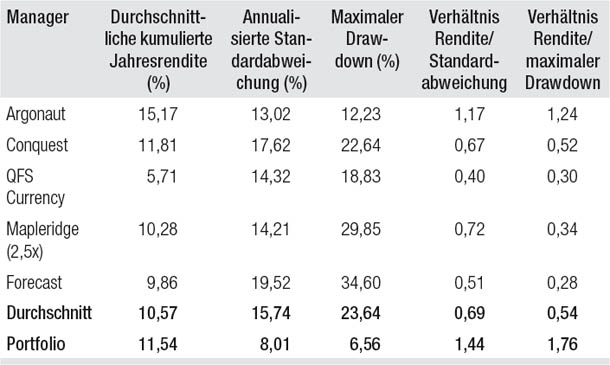
Fred ist Researchanalyst bei einem Dachfonds-Unternehmen und erhält den Auftrag, ein Portfolio aus Futures-, Global-Macro- und Devisenfonds zusammenzustellen. Nach einigem Research erstattet er seinem Chef Sam Bericht und empfiehlt das aus fünf Managern bestehende Portfolio, das in Tabelle 18.1 gezeigt wird. Die fünf Manager haben eine durchschnittliche Jahresrendite von 10,57 Prozent und eine durchschnittliche Standardabweichung von 15,74 Prozent. Ihr durchschnittlicher maximaler Drawdown beträgt 23,64 Prozent. Dank des Diversifizierungseffekts sind diese Zahlen für das Portfolio viel besser: eine Jahresrendite von 11,54 Prozent bei einer Standardabweichung von nur 8,01 Prozent und einem deutlich reduzierten maximalen Drawdown von 6,56 Prozent.
Tabelle 18.1
Die Zahlen eines 5-Manager-Portfolios, Januar 2001 bis Juni 2010

Sam schaut sich den Portfoliovorschlag an und bestellt Fred in sein Büro. „Die Manager, die Sie ausgesucht haben, sind offenbar eine interessante Mischung“, sagt er, „aber Sorgen macht mir, dass das Portfolio nur fünf Manager enthält. Ich würde gerne noch diese zehn Manager hinzunehmen, die ich mir angeschaut habe.“ Er überreicht Fred die Liste der Manager aus Tabelle 18.2.
Dann fährt Sam fort: „Interessanterweise ist die durchschnittliche Rendite meiner zehn Manager fast identisch mit der durchschnittlichen Rendite Ihrer fünf Manager (10,50 und 10,57 Prozent) und die Risikokennzahlen sind fast gleich – die durchschnittliche Standardabweichung ist ein bisschen höher (16,68 statt 15,74 Prozent), dafür aber der durchschnittliche maximale Drawdown ein bisschen niedriger (22,03 Prozent statt 23,64 Prozent). Hinsichtlich der Performance entspricht diese Gruppe von Managern also fast exakt Ihren Managern. Wenn wir sie jedoch hinzunehmen, verdreifacht sich die Anzahl der Manager im Portfolio und wir haben die Diversifizierung, die wir brauchen. Rechnen Sie die Zahlen des kombinierten Portfolios aus 15 Managern aus und kommen Sie dann wieder zu mir.“
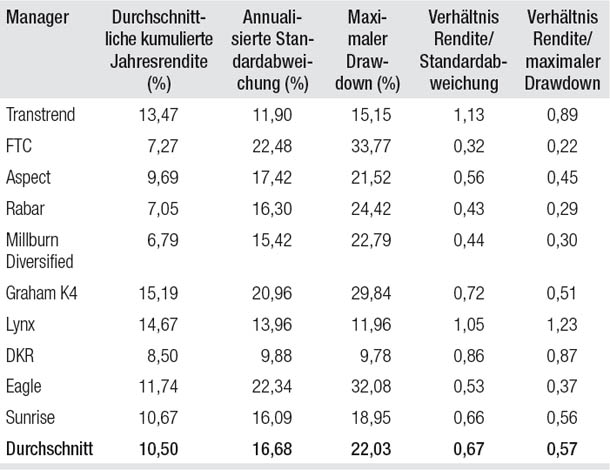
Tabelle 18.2
Die Zahlen bei der Aufnahme von zehn zusätzlichen Managern, Januar 2001 bis Juni 2010
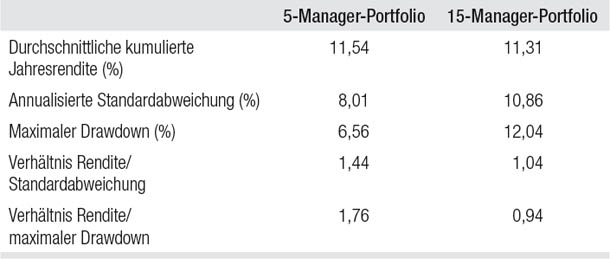
Fred macht die Analyse und stellt zu seiner Überraschung fest, dass die Verdreifachung der Anzahl der Manager das Portfoliorisiko signifikant erhöht, obwohl die Risikokennzahlen der zusätzlichen Manager denen der ursprünglichen Manager entsprechen. Die Ergebnisse sind in Tabelle 18.3 abgebildet. Die durchschnittliche Jahresrendite des Portfolios ändert sich nicht sehr – sie sinkt leicht von 11,5 auf 11,3 Prozent –, aber die Risikokennzahlen verschlechtern sich wesentlich: Die Standardabweichung des Portfolios steigt um mehr als ein Drittel von 8,0 auf 10,9 Prozent und der maximale Drawdown verdoppelt sich annähernd von 6,6 auf 12,0 Prozent.
Tabelle 18.3
Das Portfolio aus 15 Managern und das aus fünf Managern im Vergleich
Was ist passiert? Wieso lässt die Hinzunahme weiterer Manager mit identischer Performance die Volatilität des Portfolios steigen – genau das Gegenteil der Wirkung, die durch die zusätzliche Diversifizierung angestrebt wird? Die Antwort lautet, dass die Diversifizierung nicht nur von der Anzahl der Manager abhängt, sondern auch von dem Grad der Korrelation zwischen den Managern (untereinander und zum gesamten Portfolio). Freds ursprüngliches 5-Manager-Portfolio bestand aus Managern, die fast völlig unkorreliert sind: Die Paar-Korrelation beträgt 0,07. Im Gegensatz dazu setzen alle zehn Manager von Sam ähnliche Strategien ein – systematische Trendfolge – und sind daher sehr eng miteinander korreliert (eine durchschnittliche Paar-Korrelation von 0,69). Infolgedessen reduziert die Hinzunahme dieser Manager das Risiko durch Diversifizierung nicht, sondern wirkt ungefähr so, als würde man eine einzelne überdimensionierte Position in das Portfolio aufnehmen. Wenn Sam stattdessen empfohlen hätte, zu den ursprünglichen fünf einen einzigen Manager mit einer zehnmal so großen Allokation wie die der anderen Manager hinzuzunehmen, hätten wir intuitiv erwartet, dass das Risiko steigt. Die Situation ist aber nicht viel anders, wenn wir statt eines Managers mit der zehnfachen Korrelation zehn hochgradig korrelierte Manager hinzunehmen.
Die Diversifizierung von Freds ursprünglichem Portfolio wäre zwar wegen seines Exposures auf das Zufälligkeitsrisiko und das spezifische Risiko, das ich im vorigen Kapitel erläutert habe, immer noch unbefriedigend, aber immerhin wäre es besser diversifiziert gewesen als das Portfolio aus 15 Managern. Dafür, dass die Diversifizierung funktioniert, ist es entscheidend, dass die zum Portfolio hinzugefügten Investments zu den bereits bestehenden Investments und untereinander im Durchschnitt schwach korreliert sind.
Die Lehre daraus für Anleger lautet, dass man die Diversifizierung eines Multimanager-Portfolios nicht nach der Anzahl der Manager beurteilen darf. Manche Portfoliotypen sind auch dann für eine unbefriedigende Diversifizierung anfällig, wenn die Anzahl der Manager mehr als ausreichend erscheint. Ein Beispiel dafür sind CTA-Portfolios ähnlich dem in der Tabelle gezeigten. Da die meisten CTAs systematische Trendfolgemethoden verwenden und die meisten derartigen Methoden eng miteinander korreliert sind, sind CTA-Portfolios oft sogar dann schlecht diversifiziert, wenn sie eine große Zahl von Managern enthalten. Auch Portfolios aus Long/Short-Aktien-Hedgefonds sind für mangelhafte Diversifizierung anfällig, denn die Mehrzahl der Manager, die diesen Trading-Stil betreiben, ist signifikant zum Aktienmarkt korreliert. Tatsächlich ist es bei manchen Strategien (zum Beispiel bei der Wandelarbitrage) so gut wie unmöglich, ein gut diversifiziertes Portfolio zu erstellen, denn dort hängt die Performance der Manager oft mehr von dem Investment-Umfeld für die Strategie ab als von der Methode des einzelnen Managers.
Und wie kann man als Anleger beurteilen, ob ein Portfolio ungenügend diversifiziert ist? Ein einfaches Maß und eine leicht zu beschaffende Kennzahl ist die durchschnittliche Paar-Korrelation – der Durchschnitt der Paar-Korrelationen aller im Portfolio enthaltenen Manager. Zum Beispiel gibt es bei einem Portfolio aus 20 Managern 190 mögliche Manager-Paarungen und darum 190 Paar-Korrelationen. Der Durchschnitt aus diesen Korrelationen ist ein Indikator für den Diversifizierungsgrad eines Portfolios. Jeder Portfoliomanager sollte problemlos in der Lage sein, einem Anleger die durchschnittliche Paar-Korrelation des Portfolios mitzuteilen. Es gibt zwar keine fest umrissenen Definitionen dafür, was eine angemessene oder unzulängliche Diversifizierung ist. Für die Paar-Korrelation des Portfolios würde ich aber folgende allgemeine Richtwerte vorschlagen: Mehr als 0,50 gibt eine unzureichende Diversifizierung wieder, Werte zwischen 0,30 und 0,50 lassen eine nicht ganz ausreichende Diversifizierung vermuten und eine durchschnittliche Paar-Korrelation unter 0,20 zeigt an, dass die Manager sehr gut diversifiziert sind. Unter gewissen Umständen ist eine unzureichende Diversifizierung allerdings absolut akzeptabel. Konkret gesagt: Wenn ein Portfolio als Bestandteil einer übergeordneten Mischung aus Anlagen betrachtet wird, ist die Tatsache, dass es als eigenständiges Investment nicht angemessen diversifiziert ist, dann kein Problem, wenn es bezüglich der anderen Positionen im Gesamtportfolio des Anlegers eine gute Diversifizierung darstellt.
Investment-Missverständnis 47: Wenn man die Anzahl der Investments in einem Portfolio erhöht, steigert man die Diversifizierung und senkt das Risiko (wenn die zusätzlichen Investments den bestehenden Investments bezüglich der Renditen und der Risiken entsprechen).
In Wirklichkeit: Tatsächlich kann die Erhöhung der Anzahl der Investments das Portfoliorisiko erhöhen, wenn die zusätzlichen Investments zu anderen Positionen im Portfolio oder untereinander stark korreliert sind.
Die Erhöhung der Anzahl der Investments in einem Portfolio kann manchmal zu weniger statt mehr Diversifizierung führen. Die Diversifizierung hängt nämlich sowohl von der Anzahl der Positionen als auch – und das ist noch wichtiger – davon ab, wie wenig sie miteinander korreliert sind. Ein Portfolio mit einer kleinen Anzahl unkorrelierter Positionen ist im Endeffekt besser diversifiziert als ein Portfolio mit vielen signifikant korrelierten Anlagen.