Chapter 5

Number Systems

Objectives

Upon completion of this chapter, you will be able to answer the following questions:

• How do you convert numbers between decimal and binary systems?

• How do you convert numbers between decimal and hexadecimal systems?

Key Terms

This chapter uses the following key terms. You can find the definitions in the glossary at the end of the book.

dotted decimal page 176

binary page 176

hexadecimal page 176

Introduction (5.0)

Guess what? This is the 32-bit binary IPv4 address of a computer in a network: 11000000.10101000.00001010.00001010. This is the IPv4 address for the same computer in dotted decimal: 192.168.10.10. Which one would you rather work with? Addresses get even more complicated with IPv6, where addresses are 128 bits! To make these addresses more manageable, IPv6 uses the hexadecimal system, which includes the numbers 0 to 9 and the letters A to F.

As a network administrator, you must know how to convert binary addresses into dotted decimal and dotted decimal addresses into binary. You also need to know how to convert dotted decimal into hexadecimal and vice versa. (Hint: You still need your binary conversion skills when converting between dotted decimal and hexadecimal.)

They may seem complicated, but these conversions are not that hard when you learn a few tricks. The module that corresponds to this chapter contains an activity called the Binary Game, which will really help you get started. Why wait?

Binary Number System (5.1)

IPv4 addresses are 32-bit addresses expressed in decimal notation. This section discusses the binary number system along with the conversion between the binary and decimal number systems.

Binary and IPv4 Addresses (5.1.1)

IPv4 addresses begin as binary, series of only 1s and 0s. These are difficult to manage, so network administrators convert them to decimal. This section shows you a few ways to do this.

Binary is a numbering system that consists of the digits 0 and 1, called bits. In contrast, the decimal numbering system consists of the digits 0 to 9.

It is important to understand binary because hosts, servers, and network devices use binary addressing. Specifically, they use binary IPv4 addresses, as shown in Figure 5-1, to identify each other.

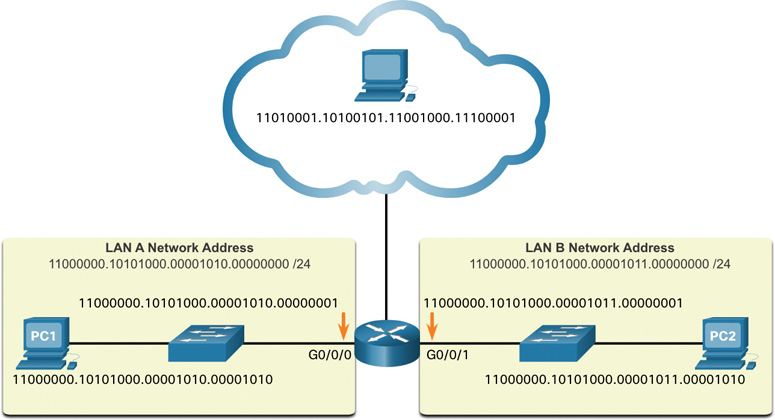
Figure 5-1 IPv4 Address in Binary Format

A figure shows two LAN networks connected to a cloud network via a router. The IPv4 address here are denoted in binary format. On the left is LAN A of network address 11000000.10101000.00001010.00000000/24. It has a PC1 of IP 11000000.10101000.00001010.00001010 which is connected to a router via a switch to the interface G0/0/0 via the gateway address 11000000.10101000.00001010.00000001. On the right is LAN B of network address 11000000.10101000.00001011.00000000/24. It has a PC2 of IP 11000000.10101000.00001011.00001010 which is connected to a router via a switch to the port G0/0/1 via the gateway address 11000000.10101000.00001011.00000001. This router is in turn connected to a cloud network of IP 11010001.10100101.11001000.11100001.

Each address consists of a string of 32 bits, divided into four sections called octets. Each octet contains 8 bits (or 1 byte), and each pair of octets is separated with a dot. For example, PC1 in Figure 5-1 is assigned IPv4 address 11000000.10101000.00001010.00001010. Its default gateway address would be that of the R1 Gigabit Ethernet interface: 11000000.10101000.00001010.00000001.

Binary works well with hosts and network devices. However, it is very challenging for humans to work with. For ease of use by people, IPv4 addresses are commonly expressed in dotted decimal notation. Figure 5-2 shows the same network as Figure 5-1, but here PC1 is assigned the IPv4 address 192.168.10.10, and its default gateway address is 192.168.10.1.

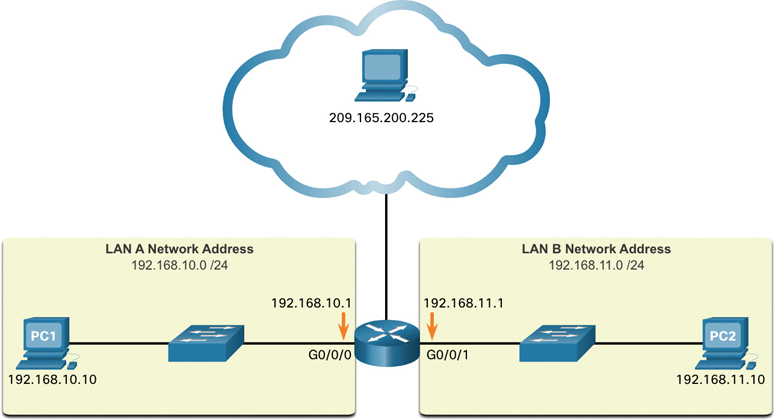
Figure 5-2 IPv4 Addresses in Dotted Decimal Format

A figure shows two LAN networks connected to a cloud network via a router. It is denoted in dotted decimal format. On the left is LAN A of network address 192.168.10.0/24. It has a PC1 of IP 192.168.10.10 which is connected to a router via a switch to the interface G0/0/0 via the gateway address 192.168.10.1. On the right is LAN B of network address 192.168.11.0/24. It has a PC2 of IP 192.168.11.0 which is connected to a router via a switch to the interface G0/0/1 via the gateway address 192.168.11.1. This router is in turn connected to a cloud network of IP 209.165.200.225.

For a solid understanding of network addressing, it is necessary to know binary addressing and gain practical skills converting between binary and dotted decimal IPv4 addresses. The following sections cover how to convert between base 2 (binary) and base 10 (decimal) numbering systems.

Video—Converting Between Binary and Decimal Numbering Systems (5.1.2)

Refer to the online course to view this video.

Binary Positional Notation (5.1.3)

Learning to convert binary to decimal requires an understanding of positional notation. Positional notation means that a digit represents different values depending on the “position” the digit occupies in the sequence of numbers. You already know the most common numbering system, the decimal (base 10) notation system.

The decimal positional notation system operates as described in Table 5-1.

Table 5-1 Decimal Positional Notation

Radix	10	10	10	10
Position in number	3	2	1	0
Calculate	(103)	(102)	(101)	(100)
Positional value	1000	100	10	1

The following bullets describe the rows in Table 5-1:

• Row 1 (radix) is the number base. Decimal notation is based on 10, so the radix is 10.

• Row 2 (position in number) considers the position of the decimal number starting with, from right to left, 0 (1st position), 1 (2nd position), 2 (3rd position), 3 (4th position). These numbers also represent the exponential values used to calculate the positional value in the 4th row.

• Row 3 (calculate) calculates the positional value by taking the radix and raising it by the exponential value of its position in row 2.

Note

n⁰ is = 1.

• Row 4 (positional value) represents units of thousands, hundreds, tens, and ones.

To use the positional system, match a given number to its positional value. The example in Table 5-2 illustrates how positional notation is used with the decimal number 1234.

Table 5-2 Example of Using Decimal Positional Notation

	Thousands	Hundreds	Tens	Ones
Positional Value	1000	100	10	1
Decimal Number (1234)	1	2	3	4
Calculate	1 × 1000	2 × 100	3 × 10	4 × 1
Add Them Up…	1000	+ 200	+ 30	+ 4
Result	1234

In contrast, the binary positional notation operates as described in Table 5-3.

Table 5-3 Binary Positional Notation

Radix	2	2	2	2	2	2	2	2
Position in number	7	6	5	4	3	2	1	0
Calculate	(27)	(26)	(25)	(24)	(23)	(22)	(21)	(20)
Positional value	128	64	32	16	8	4	2	1

The following bullets describe the rows in Table 5-3:

• Row 1 (radix) is the number base. Binary notation is based on 2, so the radix is 2.

• Row 2 (position in number) considers the position of the binary number starting with, from right to left, 0 (1st position), 1 (2nd position), 2 (3rd position), 3 (4th position). These numbers also represent the exponential value use to calculate the positional value in the 4th row.

• Row 3 (calculate) calculates the positional value by taking the radix and raising it by the exponential value of its position in row 2.

Note

n⁰ is = 1.

• Row 4 (positional value) represents units of ones, twos, fours, eights, and so on.

The example in Table 5-4 illustrates how a binary number 11000000 corresponds to the number 192. If the binary number had been 10101000, then the corresponding decimal number would be 168.

Table 5-4 Example of Using Binary Positional Notation

Positional Value	128	64	32	16	8	4	2	1
Binary Number (11000000)	1	1	0	0	0	0	0	0
Calculate	1 × 128	1 × 64	0 × 32	0 × 16	0 × 8	0 × 4	0 × 2	0 × 1
Add Them Up…	128	+ 64	+ 0	+ 0	+ 0	+ 0	+ 0	+ 0
Result	192

Check Your Understanding—Binary Number System (5.1.4)

Refer to the online course to complete this activity.

Convert Binary to Decimal (5.1.5)

To convert a binary IPv4 address to its dotted decimal equivalent, divide the IPv4 address into four 8-bit octets. Then apply the binary positional value to the first octet binary number and calculate accordingly.

For example, say that 11000000.10101000.00001011.00001010 is the binary IPv4 address of a host. To convert the binary address to decimal, start with the first octet, as shown in Table 5-5. Enter the 8-bit binary number under the positional value of row 1 and then calculate to produce the decimal number 192. This number goes into the first octet of the dotted decimal notation.

Table 5-5 Converting 11000000 to Decimal

Positional Value	128	64	32	16	8	4	2	1
Binary Number (11000000)	1	1	0	0	0	0	0	0
Calculate	1 × 128	1 × 64	0 × 32	0 × 16	0 × 8	0 × 4	0 × 2	0 × 1
Add Them Up…	128	+ 64	+ 0	+ 0	+ 0	+ 0	+ 0	+ 0
Result	192

Next, convert the second octet of 10101000 as shown in Table 5-6. The resulting decimal value is 168, and it goes into the second octet.

Table 5-6 Converting 10101000 to Decimal

Positional Value	128	64	32	16	8	4	2	1
Binary Number (10101000)	1	0	1	0	1	0	0	0
Calculate	1 × 128	0 × 64	1 × 32	0 × 16	1 × 8	0 × 4	0 × 2	0 × 1
Add Them Up…	128	+ 0	+ 32	+ 0	+ 8	+ 0	+ 0	+ 0
Result	168

Convert the third octet of 00001011 as shown in Table 5-7.

Table 5-7 Converting 00001011 to Decimal

Positional Value	128	64	32	16	8	4	2	1
Binary Number (00001011)	0	0	0	0	1	0	1	1
Calculate	0 × 128	0 × 64	0 × 32	0 × 16	1 × 8	0 × 4	1 × 2	1 × 1
Add Them Up…	0	+ 0	+ 0	+ 0	+ 8	+ 0	+ 2	+ 1
Result	11

Convert the fourth octet of 00001010 as shown in Table 5-8. This completes the IP address and produces the dotted decimal result 192.168.11.10.

Table 5-8 Converting 00001010 to Decimal

Positional Value	128	64	32	16	8	4	2	1
Binary Number (00001010)	0	0	0	0	1	0	1	0
Calculate	0 × 128	0 × 64	0 × 32	0 × 16	1 × 8	0 × 4	1 × 2	0 × 1
Add Them Up…	0	+ 0	+ 0	+ 0	+ 8	+ 0	+ 2	+ 0
Result	10

Activity—Binary to Decimal Conversions (5.1.6)

This activity allows you to practice 8-bit binary to decimal conversion as much as necessary. We recommend that you work with this tool until you are able to do the conversion without error. Convert the binary number shown in the octet to its decimal value.

Refer to the online course to complete this activity.

Decimal to Binary Conversion (5.1.7)

It is also necessary to understand how to convert a dotted decimal IPv4 address to binary. A useful tool is the binary positional value table. Figures 5-3 through 5-10 show examples of this type of table. The following steps walk through how to use this table to do the conversion:

Step 1. In Figure 5-3, is the decimal number of the octet (n) equal to or greater than the most significant bit (128)?

• If no, then enter binary 0 in the 128 positional value.

• If yes, then add a binary 1 in the 128 positional value and subtract 128 from the decimal number.

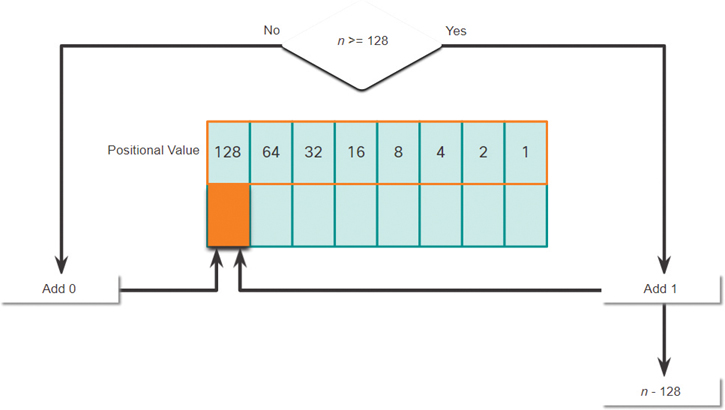
Figure 5-3 128 Positional Value

A decimal to binary conversion method using the binary positional value table is given. The binary positional value table contains two rows. The first row includes the positional values 1 to 128 from right to left. The second row has empty cells to be filled with the binary equivalent of each digit in the decimal octet. The process starts at 128th positional value. If the octet n is greater than or equal to 128, then, a binary 1 is to be added at the 128th binary position. After this, the subtraction of a decimal value of 128 is to be made from the decimal octet n. If the octet is less than or equal to 128, then, a "0" is to be added at the 128th binary position.

Step 2. In Figure 5-4, is the decimal number of the octet (n) equal to or greater than the next most significant bit (64)?

• If no, then enter binary 0 in the 64 positional value.

• If yes, then add a binary 1 in the 64 positional value and subtract 64 from the decimal number.

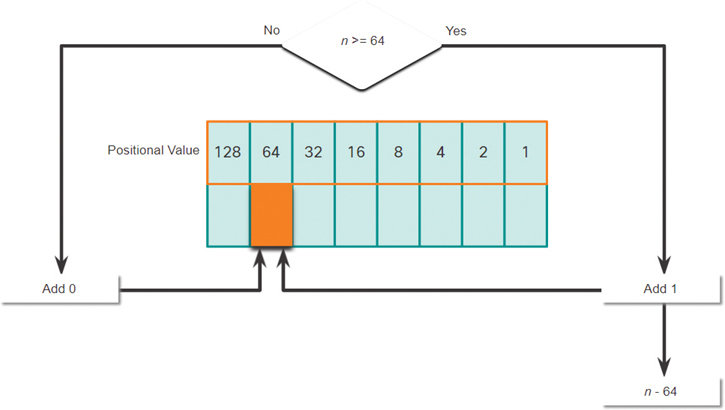
Figure 5-4 64 Positional Value

A decimal to binary conversion method using the binary positional value table is given. The binary positional value table contains two rows. The first row includes the positional values 1 to 128 from right to left. The second row has empty cells to be filled with the binary equivalent of each digit in the decimal octet. The process takes place at the 64th positional value. If the octet n is greater than or equal to 64, then, a binary 1 is to be added at the 64th binary position. After this, the subtraction of a decimal value of 64 is to be made from the decimal octet n. If the octet is less than or equal to 64, then, a "0" is to be added at the 64th binary position.

Step 3. In Figure 5-5, is the decimal number of the octet (n) equal to or greater than the next most significant bit (32)?

• If no, then enter binary 0 in the 32 positional value.

• If yes, then add a binary 1 in the 32 positional value and subtract 32 from the decimal number.

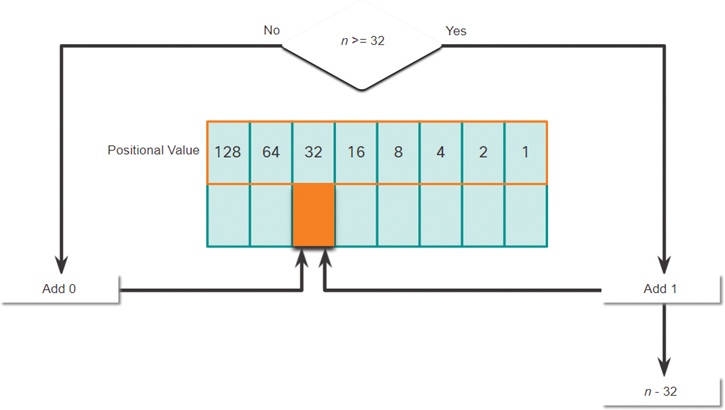
Figure 5-5 32 Positional Value

A decimal to binary conversion method using the binary positional value table is given. The binary positional value table contains two rows. The first row includes the positional values 1 to 128 from right to left. The second row has empty cells to be filled with the binary equivalent of each digit in the decimal octet. The process takes place at 32nd positional value. If the octet n is greater than or equal to 32, then, a binary 1 is to be added at the 32nd binary position. After this, the subtraction of a decimal value of 32 is to be made from the decimal octet n. If the octet is less than or equal to 32, then, a "0" is to be added at the 32nd binary position.

Step 4. In Figure 5-6, is the decimal number of the octet (n) equal to or greater than the next most significant bit (16)?

• If no, then enter binary 0 in the 16 positional value.

• If yes, then add a binary 1 in the 16 positional value and subtract 16 from the decimal number.

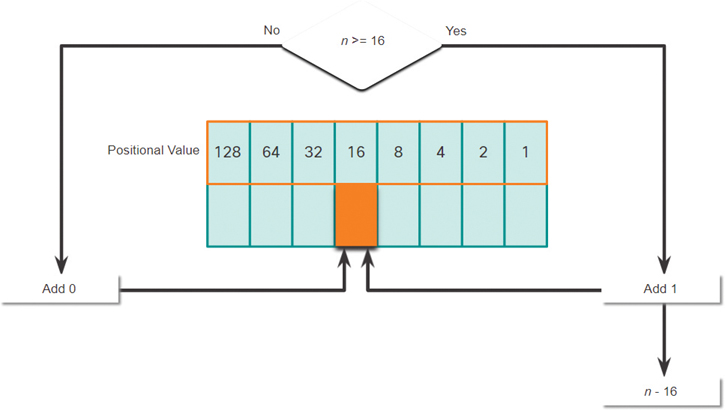
Figure 5-6 16 Positional Value

A decimal to binary conversion method using the binary positional value table is given. The binary positional value table contains two rows. The first row includes the positional values 1 to 128 from right to left. The second row has empty cells to be filled with the binary equivalent of each digit in the decimal octet. The process takes place at the 16th positional value. If the octet n is greater than or equal to 16, then, a binary 1 is to be added at the 16th binary position. After this, the subtraction of a decimal value of 16 is to be made from the decimal octet n. If the octet is less than or equal to 16, then, a "0" is to be added at the 16th binary position.

Step 5. In Figure 5-7, is the decimal number of the octet (n) equal to or greater than the next most significant bit (8)?

• If no, then enter binary 0 in the 8 positional value.

• If yes, then add a binary 1 in the 8 positional value and subtract 8 from the decimal number.

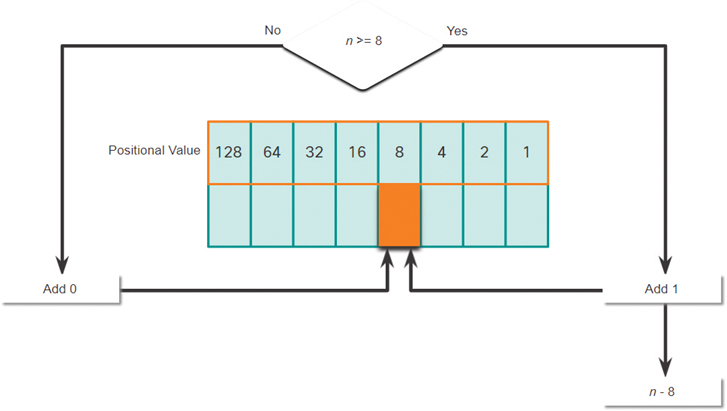
Figure 5-7 8 Positional Value

A decimal to binary conversion method using the binary positional value table is given. The binary positional value table contains two rows. The first row includes the positional values 1 to 128 from right to left. The second row has empty cells to be filled with the binary equivalent of each digit in the decimal octet. The process takes place at 8th positional value. If the octet n is greater than or equal to 8, then, a binary 1 is to be added at the 8th binary position. After this, the subtraction of a decimal value of 8 is to be made from the decimal octet n. If the octet is less than or equal to 8, then, a "0" is to be added at the 8th binary position.

Step 6. In Figure 5-8, is the decimal number of the octet (n) equal to or greater than the next most significant bit (4)?

• If no, then enter binary 0 in the 4 positional value.

• If yes, then add a binary 1 in the 4 positional value and subtract 4 from the decimal number.

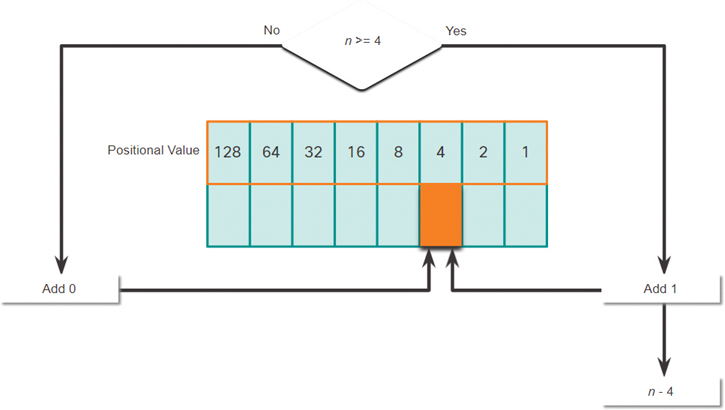
Figure 5-8 4 Positional Value

A decimal to binary conversion method using the binary positional value table is given. The binary positional value table contains two rows. The first row includes the positional values 1 to 128 from right to left. The second row has empty cells to be filled with the binary equivalent of each digit in the decimal octet. The process takes place at 4th positional value. If the octet n is greater than or equal to 4, then, a binary 1 is to be added at the 4th binary position. After this, the subtraction of a decimal value of 4 is to be made from the decimal octet n. If the octet is less than or equal to 4, then, a "0" is to be added at the 4th binary position.

Step 7. In Figure 5-9, is the decimal number of the octet (n) equal to or greater than the next most significant bit (2)?

• If no, then enter binary 0 in the 2 positional value.

• If yes, then add a binary 1 in the 2 positional value and subtract 2 from the decimal number.

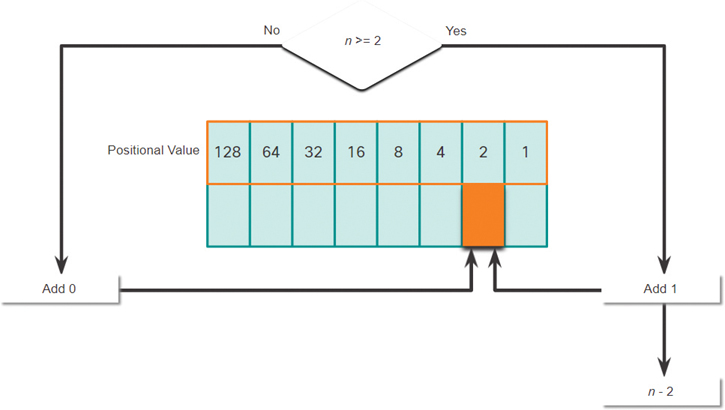
Figure 5-9 2 Positional Value

A decimal to binary conversion method using the binary positional value table is given. The binary positional value table contains two rows. The first row includes the positional values 1 to 128 from right to left. The second row has empty cells to be filled with the binary equivalent of each digit in the decimal octet. The process takes place at 2nd positional value. If the octet n is greater than or equal to 2, then, a binary 1 is to be added at the 2nd binary position. After this, the subtraction of a decimal value of 2 is to be made from the decimal octet n. If the octet is less than or equal to 2, then, a "0" is to be added at the 2nd binary position.

Step 8. In Figure 5-10, is the decimal number of the octet (n) equal to or greater than the last most significant bit (1)?

• If no, then enter binary 0 in the 1 positional value.

• If yes, then add a binary 1 in the 1 positional value and subtract 1 from the last decimal number.

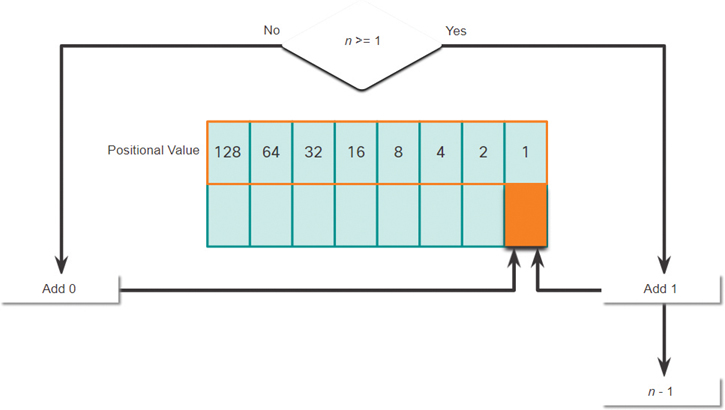
Figure 5-10 1 Positional Value

A decimal to binary conversion method using the binary positional value table is given. The binary positional value table contains two rows. The first row includes the positional values 1 to 128 from right to left. The second row has empty cells to be filled with the binary equivalent of each digit in the decimal octet. The process takes place at 1st positional value. If the octet n is greater than or equal to 1, then, a binary 1 is to be added at the 1st binary position. After this, the subtraction of a decimal value of 1 is to be made from the decimal octet n. If the octet is less than or equal to 1, then, a "0" is to be added at the 1st binary position.

Decimal to Binary Conversion Example (5.1.8)

To help understand the process of converting from decimal to binary, consider the IP address 192.168.11.10.

The first octet number, 192, is converted to binary using the previously explained positional notation process.

It is possible to bypass the process of subtraction with easier or smaller decimal numbers. For instance, notice that it is fairly easy to calculate the third octet converted to a binary number without actually going through the subtraction process (8 + 2 = 10). The binary value of the third octet is 00001010.

The fourth octet is 11 (8 + 2 + 1). The binary value of the fourth octet is 00001011.

Converting between binary and decimal may seem challenging at first, but with practice, it should become easier over time.

Figures 5-11 through 5-21 illustrate the steps to convert the IP address 192.168.10.11 into binary:

Step 1. In Figure 5-11, is the first octet number 192 equal to or greater than the high-order bit 128?

• Yes it is, so add a 1 to the high-order positional value to represent 128.

• Subtract 128 from 192 to produce a remainder of 64.

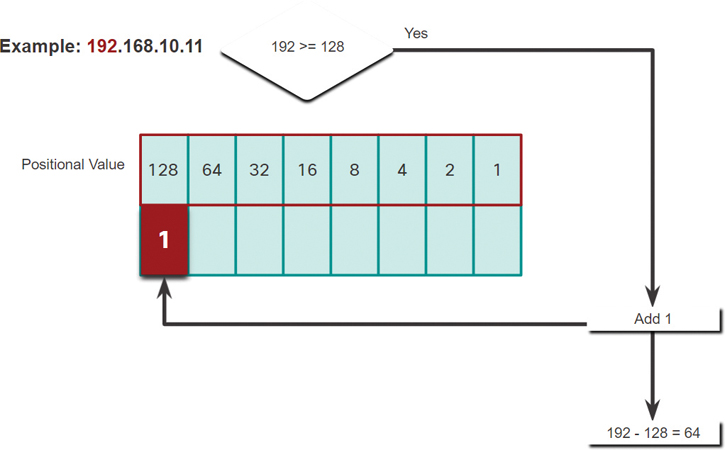
Figure 5-11 Step 1

A decimal to binary conversion method using the binary positional value table is given for the first octet of IP 192.168.10.11. The binary positional value table contains two rows. The first row includes the positional values 1 to 128 from right to left. The second row has empty cells to be filled with the binary equivalent of each digit in the decimal octet. The process takes place at 128th positional value. Here, the octet 192 is greater than 128, therefore, a binary 1 is added at the 128th positional value. After which, the subtraction of a decimal value of 128 is made from the decimal octet 192, The remainder here is 64.

Step 2. In Figure 5-12, is the remainder 64 equal to or greater than the next high-order bit 64?

• It is equal, so add a 1 to next high-order positional value.

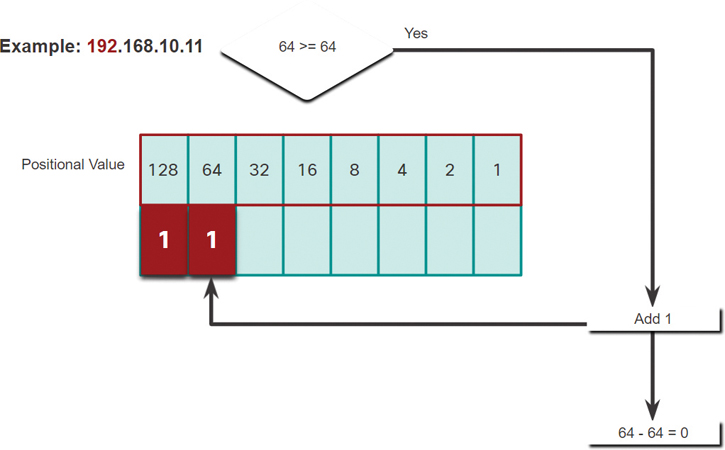
Figure 5-12 Step 2

A decimal to binary conversion method for remainder 64, obtained from step 1, using the binary positional value table is shown. The binary positional value table contains two rows. The first row includes the positional values 1 to 128 from right to left. The second row has empty cells to be filled with the binary equivalent of each digit in the decimal octet. A binary value of 1, obtained from the previous step is present at the 128th positional value. The process takes place at the 64th positional value. Here, in step 2, the octet 64 is equal to 64, therefore, a binary 1 is added at the 64th positional value. After this, the subtraction of a decimal value of 64 is made from the decimal octet 64. The remainder is 0.

Step 3. In Figure 5-13, since there is no remainder, enter binary 0 in the remaining positional values.

• The binary value of the first octet is 11000000.

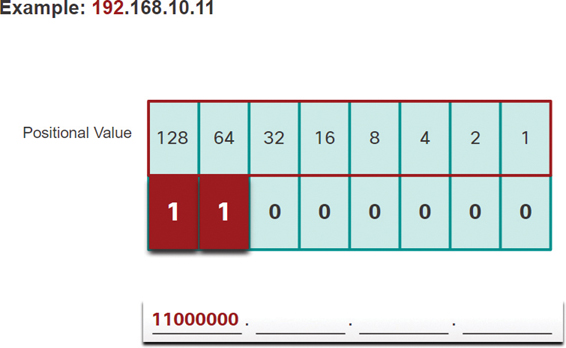
Figure 5-13 Step 3

A decimal to binary conversion method using the binary positional value table for the remainder 0, obtained from step 2 is shown. The binary positional value table contains two rows. The first row includes the positional values 1 to 128 from right to left. In the second row, the binary equivalent of each digit in the decimal octet is filled. The binary values at 128th and 64th positional values are 1. Since the remainder is 0, the binary entry for the remaining positional values is 0. Therefore, the binary value of the first octet is 11000000.

Step 4. In Figure 5-14, is the second octet number 168 equal to or greater than the high-order bit 128?

• Yes it is, so add a 1 to the high-order positional value to represent 128.

• Subtract 128 from 168 to produce a remainder of 40.

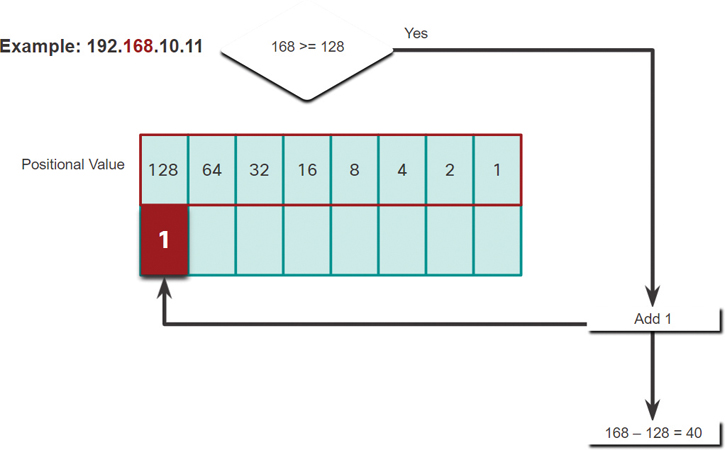
Figure 5-14 Step 4

A decimal to binary conversion method using the binary positional value table is given for the second octet of IP 192.168.10.11. The binary positional value table contains two rows. The first row includes the positional values 1 to 128 from right to left. The second row has empty cells to be filled with the binary equivalent of each digit in the decimal octet. The process takes place at 128th positional value. Here, the octet 168 is greater than 128. Therefore, a binary 1 is added at the 128th binary positional value. After which, a subtraction of a decimal value of 128 is made from the decimal octet 168. The remainder here is 40.

Step 5. In Figure 5-15, is the remainder 40 equal to or greater than the next high-order bit 64?

• No it is not, so enter a binary 0 in the positional value.

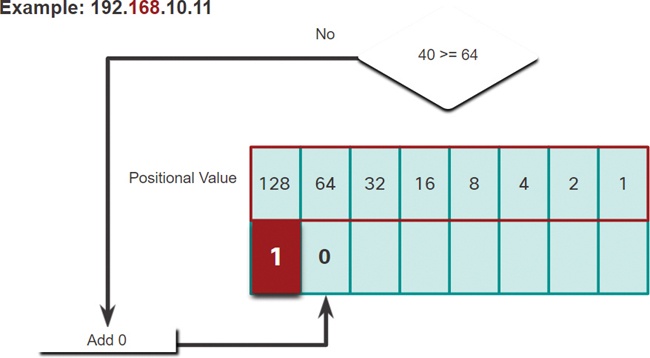
Figure 5-15 Step 5

The next step of a decimal to binary conversion method using the binary positional value table is given for the second octet of IP 192.168.10.11. The binary positional value table contains two rows. The first row includes the positional values 1 to 128 from right to left. The second row has empty cells to be filled with the binary equivalent of each digit in the decimal octet. A binary 1, obtained from the previous step is present at the 128th positional value. Here, the process takes place at 64th positional value. Here, the octet 40 is lesser than 64. Therefore, a binary 0 is added at the 64th positional value.

Step 6. In Figure 5-16, is the remainder 40 equal to or greater than the next high-order bit 32?

• Yes it is, so add a 1 to the high-order positional value to represent 32.

• Subtract 32 from 40 to produce a remainder of 8.

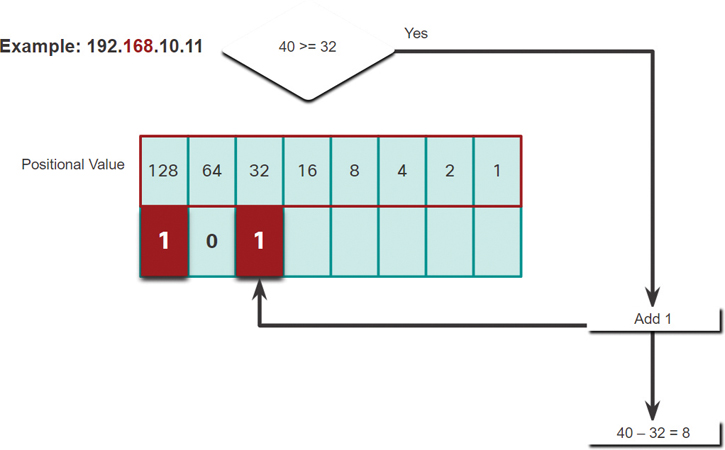
Figure 5-16 Step 6

The next step of a decimal to binary conversion method using the binary positional value table is given for the second octet of IP 192.168.10.11. The binary positional value table contains two rows. The first row includes the positional values 1 to 128 from right to left. The second row has cells that are to be filled with the binary equivalent of each digit in the decimal octet. The binary 1, and binary 0 obtained from the previous steps are present at the 128th and 64th positional values respectively. Here, the process takes place at 32nd positional value. The octet 40 is greater than 32, therefore, a binary 1 is added at the 32nd binary position. After which, a subtraction of a decimal value of 32 is to be made from the decimal octet 40. The remainder obtained here is 8.

Step 7. In Figure 5-17, is the remainder 8 equal to or greater than the next high-order bit 16?

• No it is not, so enter a binary 0 in the positional value.

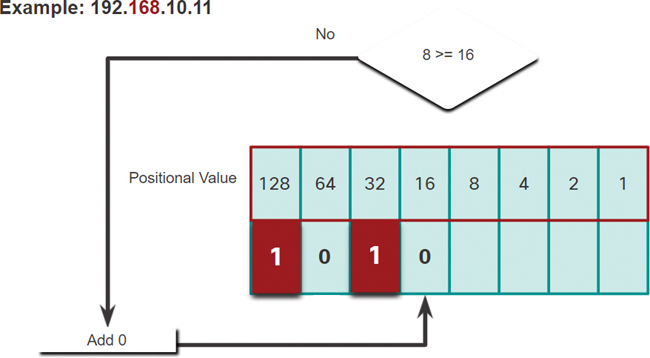
Figure 5-17 Step 7

The next step of a decimal to binary conversion method using the binary positional value table is given for the second octet of IP 192.168.10.11. The binary positional value table contains two rows. The first row includes the positional values 1 to 128 from right to left. The second row has cells that are to be filled with the binary equivalent of each digit in the decimal octet. Binaries 1, 0, and 1 obtained from the previous steps are present at the 128th, 64th, and 32nd positional values respectively. Here, the process takes place at 16th positional value. Here, the octet 8 is lesser than16. Therefore, a binary 0 is added at the 16th positional value.

Step 8. In Figure 5-18, is the remainder 8 equal to or greater than the next high-order bit 8?

• It is equal, so add a 1 to next high-order positional value.

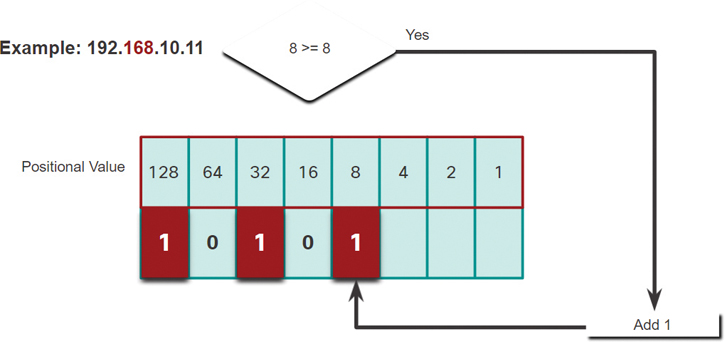
Figure 5-18 Step 8

The next step of a decimal to binary conversion method using the binary positional value table is given for the second octet of IP 192.168.10.11. The binary positional value table contains two rows. The first row includes the positional values 1 to 128 from right to left. The second row has cells to be filled with the binary equivalent of each digit in the decimal octet. Binaries 1, 0, 1, and 0 obtained from the previous steps are present at the 128th, 64th, 32nd, and 16th positional values respectively. Here, the process takes place at 8th positional value. Here, the octet 8 is equal to 8. Therefore, a binary 1 is added at the 8th positional value.

Step 9. In Figure 5-19, since there is no remainder, enter binary 0 in the remaining positional values.

• The binary value of the second octet is 10101000.

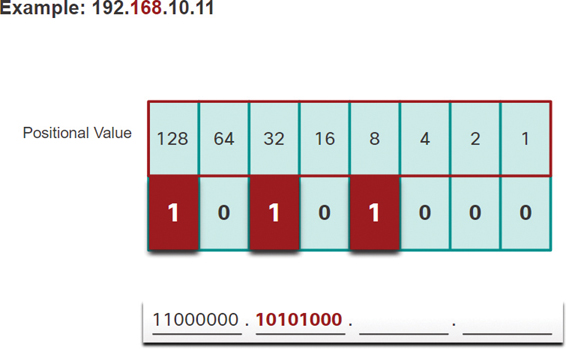
Figure 5-19 Step 9

A decimal to binary conversion method using the binary positional value table for the second octet is given. The binary positional value table contains two rows. The first row includes the positional values 1 to 128 from right to left. In the second row, binary equivalent of each digit in the decimal octet is filled. The obtained binary values are 1, 0, 1, 0, and 1 in the 128th, 64th, 32nd, 16th, and 8th positional values respectively. The binary entry for the remaining positional values is 0. Therefore, the binary value of the second octet is 10101000.

Step 10. In Figure 5-20, the binary value of the third octet is 00001010.

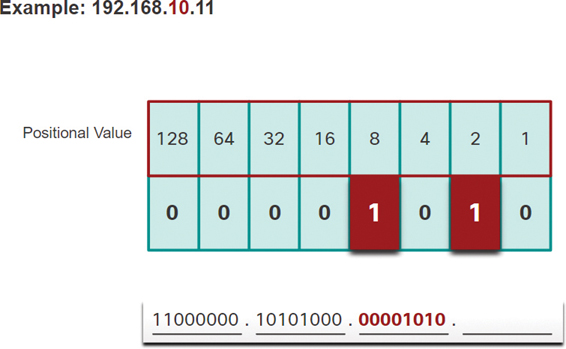
Figure 5-20 Step 10

A decimal to binary conversion method using the binary positional value table for the third octet is given. The binary positional value table contains two rows. The first row includes the positional values 1 to 128 from right to left. In the second row, binary equivalent of each digit in the decimal octet is to be filled. The obtained binary values are 0, 0, 0, 0, 1, 0, 1, and 0 in the positional values from left to right. Therefore, the binary value of the third octet is 00001010.

Step 11. In Figure 5-21, the binary value of the fourth octet is 00001011.

Figure 5-21 Step 11

A decimal to binary conversion method using the binary positional value table for the fourth octet is given. The binary positional value table contains two rows. The first row includes the positional values 1 to 128 from right to left. In the second row, binary equivalent of each digit in the decimal octet is to be filled. The obtained binary values are 0, 0, 0, 0, 1, 0, 1, and 1 in the positional values from left to right. Therefore, the binary value of the fourth octet is 00001011.

Activity—Decimal to Binary Conversions (5.1.9)

This activity allows you to practice decimal conversion to 8-bit binary values. We recommend that you work with this tool until you are able to do the conversion without error. Convert the decimal number shown in the Decimal Value row to its binary bits.

Refer to the online course to complete this activity.

Activity—Binary Game (5.1.10)

Playing this game is a fun way to learn binary numbers for networking.

Game link: Log in to cisco.com and down load the game from https://learningnetwork.cisco.com/docs/DOC-1803 or https://learningnetwork.cisco.com/docs/DOC-11119. (Create a Cisco account if you do not already have one.)

IPv4 Addresses (5.1.11)

As mentioned at the beginning of this section, routers and computers understand only binary, while humans work in decimal. It is important for you to gain a thorough understanding of these two numbering systems and how they are used in networking.

192.168.10.10 is an IP address that is assigned to a computer, as shown in Figure 5-22.

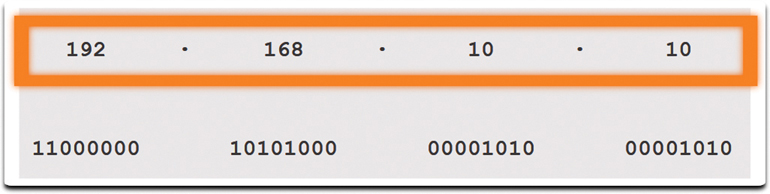
Figure 5-22 Dotted Decimal Address

This address is made up of four different octets, as shown in Figure 5-23.

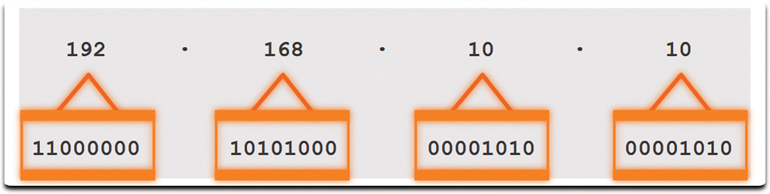
Figure 5-23 Octets

The computer stores the address as the entire 32-bit data stream, as shown in Figure 5-24.

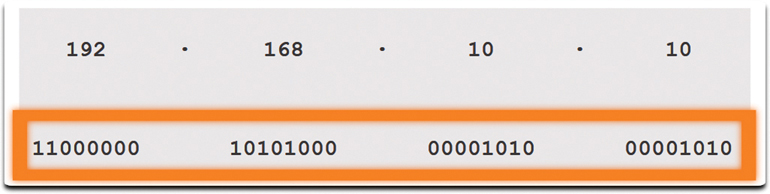
Figure 5-24 32-Bit Address

A figure shows the IP address of a computer and their respective octets. The dotted decimal here is 192.168.10.10. Below this are the following octet sets: for 192- 11000000; 168- 10101000; 10- 00001010; and for 10- 00001010. The octets are highlighted together, which is the 32-bit address 11000000.10101000.00001010.00001010.

Hexadecimal Number System (5.2)

IPv6 addresses are 128-bit addresses expressed in hexadecimal notation. This section discusses the hexadecimal number system along with the conversion between the hexadecimal and decimal number systems.

Hexadecimal and IPv6 Addresses (5.2.1)

Now you know how to convert binary to decimal and decimal to binary. You need that skill to understand IPv4 addressing in a network. But you are just as likely to use IPv6 addresses in a network. To understand IPv6 addresses, you must be able to convert hexadecimal to decimal and vice versa.

Just as decimal is a base 10 number system, hexadecimal is a base 16 system. The base 16 number system uses the digits 0 to 9 and the letters A to F. Figure 5-25 shows the equivalent decimal and hexadecimal values for binary 0000 to 1111.

Figure 5-25 Comparing Decimal, Binary, and Hexadecimal Number Systems

A figure is shown in which the decimal number along with its respective binary and hexadecimal numbers are presented in three tables as follows: 0,0000, and 0; 1,0001, and 1; 2,0010, and 2; 3,0011, and 3; 4,0100, and 4; 5,0101, and 5; 6,0110, and 6; 7,0111, and 7; 8,1000, and 8; 9,1001, and 9; 10,1010, and A; 11,1011, and B; 12,1100, and C; 13,1101, and D; 14,1110, and E; 15,1111, and F respectively.

Binary and hexadecimal work well together because it is easier to express a value as a single hexadecimal digit than as 4 binary bits.

The hexadecimal numbering system is used in networking to represent IP version 6 (IPv6) addresses and Ethernet MAC addresses.

IPv6 addresses are 128 bits in length, and every 4 bits is represented by a single hexadecimal digit, for a total of 32 hexadecimal values. IPv6 addresses are not case-sensitive; they can be written in either lowercase or uppercase.

As shown in Figure 5-26, the preferred format for writing an IPv6 address is x:x:x:x:x:x:x:x, with each x consisting of four hexadecimal values. When referring to 8 bits of an IPv4 address, we use the term octet. In IPv6, a hextet is the unofficial term used to refer to a segment of 16 bits or 4 hexadecimal values. Each x is a single hextet, 16 bits, or 4 hexadecimal digits.

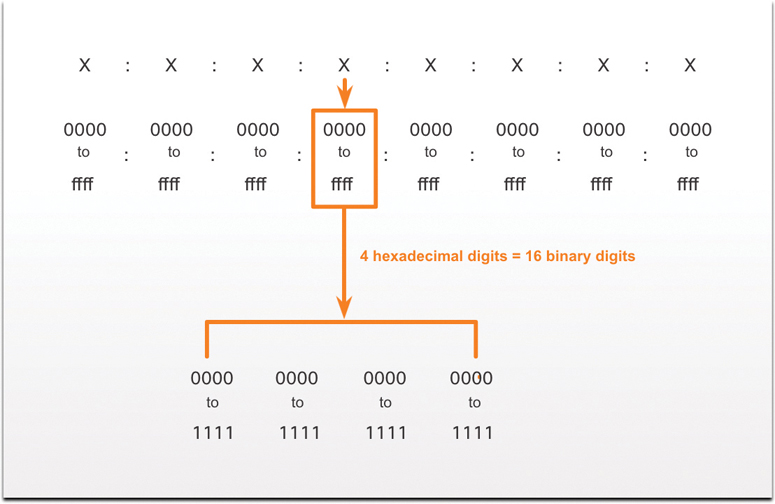
Figure 5-26 Hextets of an IPv6 Address

A figure is shown for the hextets of an IPv6 address. The IP address here is denoted by six sets of X. Each of its binary value is from 0000 to ffff. The fourth binary combination (0000 to ffff) consisting of 4 hexadecimal digits is highlighted and mapped to four combinations of "0000 to 1111" which consists of 16 binary digits.

The sample topology in Figure 5-27 displays IPv6 hexadecimal addresses.

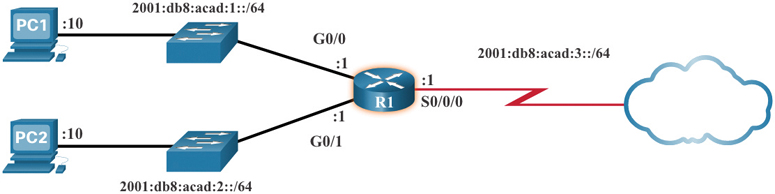
Figure 5-27 Topology with IPv6 Addresses

Two PCs, namely PC1 and PC2 has an IP address ending with :10 are connected to a router via a switch each via ports G0/0 and G0/1 respectively. The interface of the switches are 2001:db8:acad:1::/64 and 2001:db8:acad:2::/64 respectively. A serial connection is present between a cloud network, having interface 2001:db8:acad:3::/64 and the router via port S0/0/0.

Video—Converting Between Hexadecimal and Decimal Numbering Systems (5.2.2)

Refer to the online course to view this video.

Decimal to Hexadecimal Conversions (5.2.3)

Converting decimal numbers to hexadecimal values is a straightforward process that involves the following steps:

Step 1. Convert the decimal number to 8-bit binary strings.

Step 2. Divide the binary strings into groups of four, starting from the rightmost position.

Step 3. Convert each set of 4 binary numbers into the equivalent hexadecimal digit.

Let’s look at an example of converting the decimal number 168 to hexadecimal:

Step 1. 168 in binary is 10101000.

Step 2. 10101000 split into two groups of 4 binary digits is 1010 and 1000.

Step 3. 1010 is hex A, and 1000 is hex 8.

Answer: 168 is A8 in hexadecimal.

Hexadecimal to Decimal Conversion (5.2.4)

Converting hexadecimal numbers to decimal values is also a straightforward process that involves only three steps:

Step 1. Convert the hexadecimal number to 4-bit binary strings.

Step 2. Create 8-bit binary grouping starting from the rightmost position.

Step 3. Convert each 8-bit binary grouping into the equivalent decimal digit.

Here is an example of the steps for converting hex D2 to decimal:

Step 1. D2 in 4-bit binary strings is 1101 and 0010.

Step 2. 1101 and 0010 is 11010010 in an 8-bit grouping.

Step 3. 11010010 in binary is equivalent to 210 in decimal.

Answer: D2 in hexadecimal is 210 in decimal.

Check Your Understanding—Hexadecimal Number System (5.2.5)

Refer to the online course to complete this activity.

Summary (5.3)

The following is a summary of the topics in the chapter and their corresponding online modules.

Binary Number System

Binary is a numbering system that consists of the numbers 0 and 1, called bits. In contrast, the decimal numbering system consists of the numbers 0 to 9. It is important to understand binary because hosts, servers, and network devices use binary addressing—specifically, binary IPv4 addresses—to identify each other. You must know binary addressing and how to convert between binary and dotted decimal IPv4 addresses. In this chapter you learned a few ways to convert decimal to binary and binary to decimal.

Hexadecimal Number System

Just as decimal is a base 10 number system, hexadecimal is a base 16 system. The base 16 number system uses the numbers 0 to 9 and the letters A to F. The hexadecimal numbering system is used in networking to represent IPv6 addresses and Ethernet MAC addresses. IPv6 addresses are 128 bits in length, and every 4 bits is represented by a single hexadecimal digit, for a total of 32 hexadecimal values. To convert hexadecimal to decimal, you must first convert the hexadecimal to binary and then convert the binary to decimal. To convert decimal to hexadecimal, you must also first convert the decimal to binary.

Practice

There are no labs or Packet Tracer activities for this chapter.

Check Your Understanding Questions

Complete all the review questions listed here to test your understanding of the topics and concepts in this chapter. The appendix “Answers to ‘Check Your Understanding’ Questions” lists the answers.

1. What is the binary representation for the decimal number 173?

1. 10100111

2. 10100101

3. 10101101

4. 10110101

2. Which address is the dotted decimal equivalent of the binary address 11101100 00010001 00001100 00001010?

1. 234.17.10.9

2. 234.16.12.10

3. 236.17.12.6

4. 236.17.12.10

3. How many binary bits exist in an IPv6 address?

1. 32

2. 48

3. 64

4. 128

5. 256

4. What is the binary equivalent of the decimal number 232?

1. 11101000

2. 11000110

3. 10011000

4. 11110010

5. Which two statements are correct about IPv4 and IPv6 addresses? (Choose two.)

1. IPv6 addresses are represented by hexadecimal numbers.

2. IPv4 addresses are represented by hexadecimal numbers.

3. IPv6 addresses are 32 bits in length.

4. IPv4 addresses are 32 bits in length.

5. IPv4 addresses are 128 bits in length.

6. IPv6 addresses are 64 bits in length.

6. Which IPv4 address format looks like 201.192.1.14 and was created for ease of use by people?

1. binary

2. dotted decimal

3. hexadecimal

4. ASCII

7. What is the dotted decimal representation of the IPv4 address 11001011.00000000.01110001.11010011?

1. 192.0.2.199

2. 198.51.100.201

3. 203.0.113.211

4. 209.165.201.223

8. What is the decimal equivalent of the binary number 10010101?

1. 149

2. 157

3. 168

4. 192

9. What is the decimal equivalent of the hex number 0x3F? (0x refers to hexadecimal)

1. 63

2. 77

3. 87

4. 93

10. What is the dotted decimal representation of the IPv4 address represented as the binary string 00001010.01100100.00010101.00000001?

1. 10.100.21.1

2. 10.10.20.1

3. 100.10.11.1

4. 100.21.10.1

11. What is the decimal equivalent of 0xC9? (0x refers to hexadecimal)

1. 185

2. 200

3. 201

4. 199

12. Which is a valid hexadecimal number?

1. f

2. g

3. h

4. j

13. What is the binary representation of 0xCA? (0x refers to hexadecimal)

1. 10111010

2. 11010101

3. 11001010

4. 11011010

14. How many bits are in an IPv4 address?

1. 32

2. 64

3. 128

4. 256