I

Discrete Noiseless Systems

1. The Discrete Noiseless Channel

Teletype and telegraphy are two simple examples of a discrete channel for transmitting information. Generally, a discrete channel will mean a system whereby a sequence of choices from a finite set of elementary symbols S₁…S_n can be transmitted from one point to another. Each of the symbols S_i is assumed to have a certain duration in time t_i seconds (not necessarily the same for different S_i, for example the dots and dashes in telegraphy). It is not required that all possible sequences of the S_i be capable of transmission on the system; certain sequences only may be allowed. These will be possible signals for the channel. Thus in telegraphy suppose the symbols are: (1) A dot, consisting of line closure for a unit of time and then line open for a unit of time; (2) A dash, consisting of three time units of closure and one unit open; (3) A letter space consisting of, say, three units of line open; (4) A word space of six units of line open. We might place the restriction on allowable sequences that no spaces follow each other (for if two letter spaces are adjacent, they are identical with a word space). The question we now consider is how one can measure the capacity of such a channel to transmit information.

In the teletype case where all symbols are of the same duration, and any sequence of the 32 symbols is allowed, the answer is easy. Each symbol represents five bits of information. If the system transmits n symbols per second it is natural to say that the channel has a capacity of 5n bits per second. This does not mean that the teletype channel will always be transmitting information at this rate—this is the maximum possible rate and whether or not the actual rate reaches this maximum depends on the source of information which feeds the channel, as will appear later.

In the more general case with different lengths of symbols and constraints on the allowed sequences, we make the following definition: The capacity C of a discrete channel is given by

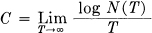
where N(T) is the number of allowed signals of duration T.

It is easily seen that in the teletype case this reduces to the previous result. It can be shown that the limit in question will exist as a finite number in most cases of interest. Suppose all sequences of the symbols S₁,…, S_n are allowed and these symbols have durations t₁,…, t_n. What is the channel capacity? If N(t) represents the number of sequences of duration t we have

N(t) = N(t — t₁) + N(t — t₂) +…+ N(t — t_n).

The total number is equal to the sum of the numbers of sequences ending in S₁, S₂,…, S_n and these are N(t — t₁), N(t — t₂),…, N(t — t_n), respectively. According to a well-known result in finite differences, N(t) is then asymptotic for large t to AX′₀ where A is constant and X₀ is the largest real solution of the characteristic equation:

X^–t₁ + X^–t₂ +…+ X^–t_n = 1

and therefore

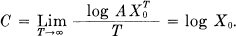
In case there are restrictions on allowed sequences we may still often obtain a difference equation of this type and find C from the characteristic equation. In the telegraphy case mentioned above

N(t) = N(t — 2) + N(t — 4) + N(t — 5) + N(t — 7)

+ N(t — 8) + N(t — 10)

as we see by counting sequences of symbols according to the last or next to the last symbol occurring. Hence C is—log μ₀ where μ₀ is the positive root of 1 = μ² + μ⁴ + μ⁵ + μ⁷ + μ⁸ + μ¹⁰. Solving this we find C = 0.539.

A very general type of restriction which may be placed on allowed sequences is the following: We imagine a number of possible states a_l, a₂,…, a_m. For each state only certain symbols from the set S₁,…, S_n can be transmitted (different subsets for the different states). When one of these has been transmitted the state changes to a new state depending both on the old state and the particular symbol transmitted. The telegraph case is a simple example of this. There are two states depending on whether or not a space was the last symbol transmitted. If so, then only a dot or a dash can be sent next and the state always changes. If not, any symbol can be transmitted and the state changes if a space is sent, otherwise it remains the same. The conditions can be indicated in a linear graph as shown in Fig. 2. The junction points correspond to the states and the lines indicate the symbols possible in a state and the resulting state. In Appendix 1 it is shown that if the conditions on allowed sequences can be described in this form C will exist and can be calculated in accordance with the following result:

Theorem 1: Let 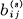be the duration of the s^th symbol which is allowable in state i and leads to stage j. Then the channel capacity C is equal to log W where W is the largest real root of the determinantal equation:

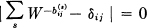
where δ_ij = 1 if i = j and is zero otherwise.

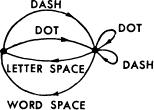
Fig. 2.—Graphical representation of the constraints on telegraph symbols.

For example, in the telegraph case (Fig. 2) the determinant is:

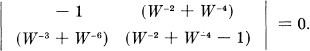
On expansion this leads to the equation given above for this set of constraints.

2. The Discrete Source of Information

We have seen that under very general conditions the logarithm of the number of possible signals in a discrete channel increases linearly with time. The capacity to transmit information can be specified by giving this rate of increase, the number of bits per second required to specify the particular signal used.

We now consider the information source. How is an information source to be described mathematically, and how much information in bits per second is produced in a given source? The main point at issue is the effect of statistical knowledge about the source in reducing the required capacity of the channel, by the use of proper encoding of the information. In telegraphy, for example, the messages to be transmitted consist of sequences of letters. These sequences, however, are not completely random. In general, they form sentences and have the statistical structure of, say, English. The letter E occurs more frequently than Q, the sequence TH more frequently than XP, etc. The existence of this structure allows one to make a saving in time (or channel capacity) by properly encoding the message sequences into signal sequences. This is already done to a limited extent in telegraphy by using the shortest channel symbol, a dot, for the most common English letter E; while the infrequent letters, Q, X, Z are represented by longer sequences of dots and dashes. This idea is carried still further in certain commercial codes where common words and phrases are represented by four- or five-letter code groups with a considerable saving in average time. The standardized greeting and anniversary telegrams now in use extend this to the point of encoding a sentence or two into a relatively short sequence of numbers.

We can think of a discrete source as generating the message, symbol by symbol. It will choose successive symbols according to certain probabilities depending, in general, on preceding choices as well as the particular symbols in question. A physical system, or a mathematical model of a system which produces such a sequence of symbols governed by a set of probabilities, is known as a stochastic process.3 We may consider a discrete source, therefore, to be represented by a stochastic process. Conversely, any stochastic process which produces a discrete sequence of symbols chosen from a finite set may be considered a discrete source. This will include such cases as:

1. Natural written languages such as English, German, Chinese.
2. Continuous information sources that have been rendered discrete by some quantizing process. For example, the quantized speech from a PCM transmitter, or a quantized television signal.
3. Mathematical cases where we merely define abstractly a stochastic process which generates a sequence of symbols. The following are examples of this last type of source.

(A) Suppose we have five letters A, B, C, D, E which are chosen each with probability .2, successive choices being independent. This would lead to a sequence of which the following is a typical example.

B D C B C E C C C A D C B D D A A E C E E A A B B D A E E C A C E E B A E E C B C E A D.

This was constructed with the use of a table of random numbers.⁴

(B) Using the same five letters let the probabilities be .4, .1, .2, .2, .1, respectively, with successive choices independent. A typical message from this source is then:

A A A C D C B D C E A A D A D A C E D A E A D C A B E D A D D C E C A A A A A D.

(C) A more complicated structure is obtained if successive symbols are not chosen independently but their probabilities depend on preceding letters. In the simplest case of this type a choice depends only on the preceding letter and not on ones before that. The statistical structure can then be described by a set of transition probabilities p_i(j), the probability that letter i is followed by letter j. The indices i and j range over all the possible symbols. A second equivalent way of specifying the structure is to give the “digram” probabilities p(i,j), i.e., the relative frequency of the digram i j. The letter frequencies p(i), (the probability of letter i), the transition probabilities p_i(j) and the digram probabilities p(i,j) are related by the following formulas:

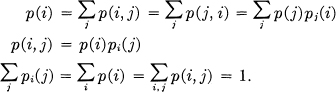
As a specific example suppose there are three letters A, B, C with the probability tables:

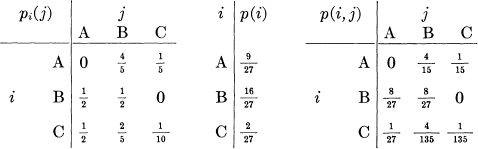
A typical message from this source is the following:

A B B A B A B A B A B A B A B B B A B B B B B A B A B A B A B A B B B A C A C A B B A B B B B A B B A B A C B B B A B A.

The next increase in complexity would involve trigram frequencies but no more. The choice of a letter would depend on the preceding two letters but not on the message before that point. A set of trigram frequencies p(i, j, k) or equivalently a set of transition probabilities p_ij(k) would be required. Continuing in this way one obtains successively more complicated stochastic processes. In the general n-gram case a set of n-gram probabilities p(i₁, i₂,…, i_n) or of transition probabilities p_{i1, i2,…, in–1 (in)} is required to specify the statistical structure.

(D) Stochastic processes can also be defined which produce a text consisting of a sequence of “words.” Suppose there are five letters A, B, C, D, E and 16 “words” in the language with associated probabilities:

Suppose successive “words” are chosen independently and are separated by a space. A typical message might be:

DAB EE A BEBE DEED DEB ADEE ADEE EE DEB BEBE BEBE BEBE ADEE BED DEED DEED CEED ADEE A DEED DEED BEBE CABED BEBE BED DAB DEED ADEB.

If all the words are of finite length this process is equivalent to one of the preceding type, but the description may be simpler in terms of the word structure and probabilities. We may also generalize here and introduce transition probabilities between words, etc.

These artificial languages are useful in constructing simple problems and examples to illustrate various possibilities. We can also approximate to a natural language by means of a series of simple artificial languages. The zero-order approximation is obtained by choosing all letters with the same probability and independently. The first-order approximation is obtained by choosing successive letters independently but each letter having the same probability that it has in the natural language.5 Thus, in the first-order approximation to English, E is chosen with probability .12 (its frequency in normal English) and W with probability .02, but there is no influence between adjacent letters and no tendency to form the preferred digrams such as TH, ED, etc. In the second-order approximation, digram structure is introduced. After a letter is chosen, the next one is chosen in accordance with the frequencies with which the various letters follow the first one. This requires a table of digram frequencies p_i(j). In the third-order approximation, trigram structure is introduced. Each letter is chosen with probabilities which depend on the preceding two letters.

3. The Series of Approximations to English

To give a visual idea of how this series of processes approaches a language, typical sequences in the approximations to English have been constructed and are given below. In all cases we have assumed a 27-symbol “alphabet,” the 26 letters and a space.

1. Zero-order approximation (symbols independent and equiprobable).

   XFOML RXKHRJFFJUJ ZLPWCFWKCYJ FFJEYVKCQSGHYD QPAAMKBZAACIBZLHJQD.

2. First-order approximation (symbols independent but with frequencies of English text).

   OCRO HLI RGWR NMIELWIS EU LL NBNESEBYA TH EEI ALHENHTTPA OOBTTVA NAH BRL.

3. Second-order approximation (digram structure as in English).

   ON IE ANTSOUTINYS ARE T INCTORE ST BE S DEAMY ACHIN D ILONASIVE TUCOOWE AT TEASONARE FUSO TIZIN ANDY TOBE SEACE CTISBE.

4. Third-order approximation (trigram structure as in English).

   IN NO IST LAT WHEY CRATICT FROURE BIRS GROCID PONDENOME OF DEMONSTURES OF THE REPTAGIN IS REGOACTIONA OF CRE.

5. First-order word approximation. Rather than continue with tetragram,…, n-gram structure it is easier and better to jump at this point to word units. Here words are chosen independently but with their appropriate frequencies.

   REPRESENTING AND SPEEDILY IS AN GOOD APT OR COME CAN DIFFERENT NATURAL HERE HE THE A IN CAME THE TO OF TO EXPERT GRAY COME TO FURNISHES THE LINE MESSAGE HAD BE THESE.

6. Second-order word approximation. The word transition probabilities are correct but no further structure is included.

   THE HEAD AND IN FRONTAL ATTACK ON AN ENGLISH WRITER THAT THE CHARACTER OF THIS POINT IS THEREFORE ANOTHER METHOD FOR THE LETTERS THAT THE TIME OF WHO EVER TOLD THE PROBLEM FOR AN UNEXPECTED.

The resemblance to ordinary English text increases quite noticeably at each of the above steps. Note that these samples have reasonably good structure out to about twice the range that is taken into account in their construction. Thus in (3) the statistical process insures reasonable text for two-letter sequences, but four-letter sequences from the sample can usually be fitted into good sentences. In (6) sequences of four or more words can easily be placed in sentences without unusual or strained constructions. The particular sequence of ten words “attack on an English writer that the character of this” is not at all unreasonable. It appears then that a sufficiently complex stochastic process will give a satisfactory representation of a discrete source.

The first two samples were constructed by the use of a book of random numbers in conjunction with (for example 2) a table of letter frequencies. This method might have been continued for (3), (4) and (5), since digram, trigram and word frequency tables are available, but a simpler equivalent method was used. To construct (3) for example, one opens a book at random and selects a letter at random on the page. This letter is recorded. The book is then opened to another page and one reads until this letter is encountered. The succeeding letter is then recorded. Turning to another page this second letter is searched for and the succeeding letter recorded, etc. A similar process was use for (4), (5) and (6). It would be interesting if further approximations could be constructed, but the labor involved becomes enormous at the next stage.

4. Graphical Representation of a Markoff Process

Stochastic processes of the type described above are known mathematically as discrete Markoff processes and have been extensively studied in the literature.6 The general case can be described as follows: There exist a finite number of possible “states” of a system; S₁, S₂,…, S_n. In addition there is a set of transition probabilities, p_i(j), the probability that if the system is in state S_i it will next go to state S_j. To make this Markoff process into an information source we need only assume that a letter is produced for each transition from one state to another. The states will correspond to the “residue of influence” from preceding letters.

The situation can be represented graphically as shown in Figs. 3, 4 and 5. The “states” are the junction points in the graph and the probabilities and letters produced for a transition are given beside the corresponding line. Figure 3 is for the example B in Section 2, while Fig. 4 corresponds to the example C. In Fig. 3 there is only one state since successive letters are independent. In Fig. 4 there are as many states as letters. If a trigram example were constructed there would be at most n² states corresponding to the possible pairs of letters preceding the one being chosen. Figure 5 is a graph for the case of word structure in example D. Here S corresponds to the “space” symbol.

5. Ergodic and Mixed Sources

As we have indicated above a discrete source for our purposes can be considered to be represented by a Markoff process. Among the possible discrete Markoff processes there is a group with special properties of significance in communication theory. This special class consists of the “ergodic” processes and we shall call the corresponding sources ergodic sources. Although a rigorous definition of an ergodic process is somewhat involved, the general idea is simple. In an ergodic process every sequence produced by the process is the same in statistical properties. Thus the letter frequencies, digram frequencies, etc., obtained from particular sequences, will, as the lengths of the sequences increase, approach definite limits independent of the particular sequence. Actually this is not true of every sequence but the set for which it is false has probability zero. Roughly the ergodic property means statistical homogeneity.

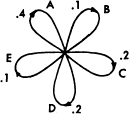
Fig. 3.—A graph corresponding to the source in example B.

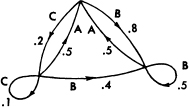
Fig. 4.—A graph corresponding to the source in example C.

Fig. 5.—A graph corresponding to the source in example D.

All the examples of artificial languages given above are ergodic. This property is related to the structure of the corresponding graph. If the graph has the following two properties7 the corresponding process will be ergodic:

1. The graph does not consist of two isolated parts A and B such that it is impossible to go from junction points in part A to junction points in part B along lines of the graph in the direction of arrows and also impossible to go from junctions in part B to junctions in part A.
2. A closed series of lines in the graph with all arrows on the lines pointing in the same orientation will be called a “circuit.” The “length” of a circuit is the number of lines in it. Thus in Fig. 5 series BEBES is a circuit of length 5. The second property required is that the greatest common divisor of the lengths of all circuits in the graph be one.

If the first condition is satisfied but the second one violated by having the greatest common divisor equal to d > 1, the sequences have a certain type of periodic structure. The various sequences fall into d different classes which are statistically the same apart from a shift of the origin (i.e., which letter in the sequence is called letter 1). By a shift of from 0 up to d — 1 any sequence can be made statistically equivalent to any other. A simple example with d = 2 is the following: There are three possible letters a, b, c. Letter a is followed with either b or c with probabilities 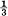and 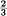respectively. Either b or c is always followed by letter a. Thus a typical sequence is

a b a c a c a c a b a c a b a b a c a c.

This type of situation is not of much importance for our work.

If the first condition is violated the graph may be separated into a set of subgraphs each of which satisfies the first condition. We will assume that the second condition is also satisfied for each subgraph. We have in this case what may be called a “mixed” source made up of a number of pure components. The components correspond to the various subgraphs. If L₁, L₂, L₃,…are the component sources we may write

L = p₁L₁ + p₂L₂ + p₃L₃ +…

where p_i is the probability of the component source L_i.

Physically the situation represented is this: There are several different sources L_l, L₂, L₃,…which are each of homogeneous statistical structure (i.e., they are ergodic). We do not know a priori which is to be used, but once the sequence starts in a given pure component L_i, it continues indefinitely according to the statistical structure of that component.

As an example one may take two of the processes defined above and assume p₁ = .2 and p₂ = .8. A sequence from the mixed source

L = .2L₁ + .8L₂

would be obtained by choosing first L₁ or L₂ with probabilities .2 and .8 and after this choice generating a sequence from whichever was chosen.

Except when the contrary is stated we shall assume a source to be ergodic. This assumption enables one to identify averages along a sequence with averages over the ensemble of possible sequences (the probability of a discrepancy being zero). For example the relative frequency of the letter A in a particular infinite sequence will be, with probability one, equal to its relative frequency in the ensemble of sequences.

If P_i is the probability of state i and p_i(j) the transition probability to state j, then for the process to be stationary it is clear that the P_i must satisfy equilibrium conditions:

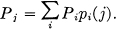
In the ergodic case it can be shown that with any starting conditions the probabilities P_j(N) of being in state j after N symbols, approach the equilibrium values as N → ∞.

6. Choice, Uncertainty and Entropy

We have represented a discrete information source as a Markoff process. Can we define a quantity which will measure, in some sense, how much information is “produced” by such a process, or better, at what rate information is produced?

Suppose we have a set of possible events whose probabilities of occurrence are p₁, p₂,…, p_n. These probabilities are known but that is all we know concerning which event will occur. Can we find a measure of how much “choice” is involved in the selection of the event or of how uncertain we are of the outcome?

If there is such a measure, say H(p₁, p₂,…, p_n), it is reasonable to require of it the following properties:

1. H should be continuous in the p_i.
2. If all the p_i are equal, p_i = 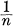, then H should be a monotonic increasing function of n. With equally likely events there is more choice, or uncertainty, when there are more possible events.
3. If a choice be broken down into two successive choices, the original H should be the weighted sum of the individual values of H. The meaning of this is illustrated in Fig. 6. At the left we have three possibilities p₁ = 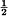, p₂ = 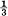, p₃ = . On the right we first choose between two possibilities each with probability 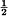, and if the second occurs make another choice with probabilities 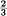, 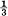. The final results have the same probabilities as before. We require, in this special case, that

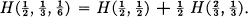
The coefficient 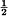is the weighting factor introduced because this second choice only occurs half the time.

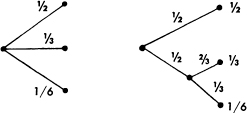
Fig. 6.—Decomposition of a choice from three possibilities.

In Appendix 2, the following result is established:

Theorem 2: The only H satisfying the three above assumptions is of the form:

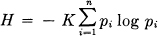
where K is a positive constant.

This theorem, and the assumptions required for its proof, are in no way necessary for the present theory. It is given chiefly to lend a certain plausibility to some of our later definitions. The real justification of these definitions, however, will reside in their implications.

Quantities of the form H = — ∑ p_i log p_i (the constant K merely amounts to a choice of a unit of measure) play a central role in information theory as measures of information, choice and uncertainty. The form of H will be recognized as that of entropy as defined in certain formulations of statistical mechanics8 where p_i is the probability of a system being in cell i of its phase space. H is then, for example, the H in Boltzmann's famous H theorem. We shall call H = — ∑ p_i log p_i the entropy of the set of probabilities p₁,…, p_n. If x is a chance variable we will write H(x) for its entropy; thus x is not an argument of a function but a label for a number, to differentiate it from H(y) say, the entropy of the chance variable y.

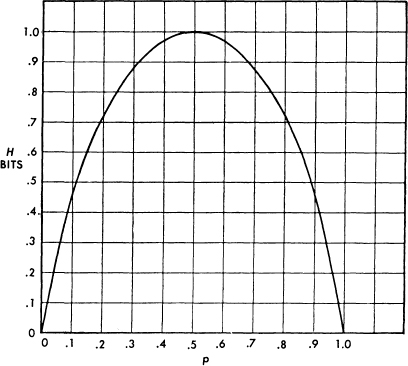
Fig. 7.—Entropy in the case of two possibilities with probabilities ρ and (1 — ρ).

The entropy in the case of two possibilities with probabilities p and q = 1 — p, namely

H = — (p log p + q log q)

is plotted in Fig. 7 as a function of p.

The quantity H has a number of interesting properties which further substantiate it as a reasonable measure of choice or information.

1. H = 0 if and only if all the p_i but one are zero, this one having the value unity. Thus only when we are certain of the outcome does H vanish. Otherwise H is positive.

2. For a given n, H is a maximum and equal to log n when all the p_i are equal, i.e., 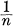. This is also intuitively the most uncertain situation.

3. Suppose there are two events, x and y, in question, with m possibilities for the first and n for the second. Let p(i,j) be the probability of the joint occurrence of i for the first and j for the second. The entropy of the joint event is

while

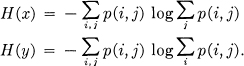
It is easily shown that

H(x, y) ≤ H(x) + H(y)

with equality only if the events are independent (i.e., p(i,j) = p(i) p(j)). The uncertainty of a joint event is less than or equal to the sum of the individual uncertainties.

4. Any change toward equalization of the probabilities p₁, p₂,…, p_n increases H. Thus if p₁ < p₂ and we increase p₁, decreasing p₂ an equal amount so that p₁ and p₂ are more nearly equal, then H increases. More generally, if we perform any “averaging” operation on the p_i of the form

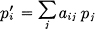
where 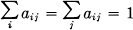, and all a_ij≥0, then H increases (except in the special case where this transformation amounts to no more than a permutation of the p_j with H of course remaining the same).

5. Suppose there are two chance events x and y as in 3, not necessarily independent. For any particular value i that x can assume there is a conditional probability p_i(j) that y has the value j. This is given by

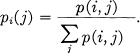
We define the conditional entropy of y, H_x(y) as the average of the entropy of y for each value of x, weighted according to the probability of getting that particular x. That is

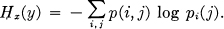
This quantity measures how uncertain we are of y on the average when we know x. Substituting the value of p_i(j) we obtain

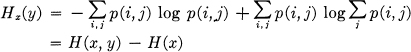
or

H(x, y) = H(x) + H_x(y).

The uncertainty (or entropy) of the joint event x, y is the uncertainty of x plus the uncertainty of y when x is known.

6. From 3 and 5 we have

H(x) + H(y) ≥ H(x,y) = H(x) + H_x(y).

Hence

H(y) ≥ H_x(y).

The uncertainty of y is never increased by knowledge of x. It will be decreased unless x and y are independent events, in which case it is not changed.

7. The Entropy of an Information Source

Consider a discrete source of the finite state type considered above. For each possible state i there will be a set of probabilities p_i(j) of producing the various possible symbols j. Thus there is an entropy H_i for each state. The entropy of the source will be defined as the average of these H_i weighted in accordance with the probability of occurrence of the states in question:

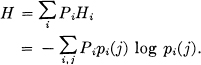
This is the entropy of the source per symbol of text. If the Markoff process is proceeding at a definite time rate there is also an entropy per second.

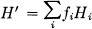
were f_i is the average frequency (occurrences per second) of state i. Clearly

H′ = mH

where m is the average number of symbols produced per second. H or H′ measures the amount of information generated by the source per symbol or per second. If the logarithmic base is 2, they will represent bits per symbol or per second.

If successive symbols are independent then H is simply — ∑ p_i log p_i where p_i is the probability of symbol i. Suppose in this case we consider a long message of N symbols. It will contain with high probability about p₁N occurrences of the first symbol, p₂N occurrences of the second, etc. Hence the probability of this particular message will be roughly

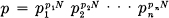
or

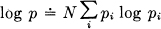
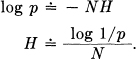
H is thus approximately the logarithm of the reciprocal probability of a typical long sequence divided by the number of symbols in the sequence. The same result holds for any source. Stated more precisely we have (see Appendix 3):

Theorem 3: Given any ∊ > 0 and δ > 0, we can find an N₀ such that the sequences of any length N ≥ N₀ fall into two classes:

1. A set whose total probability is less than ∊.

2. The remainder, all of whose members have probabilities satisfying the inequality

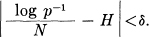
In other words we are almost certain to have 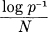very close to H when N is large.

A closely related result deals with the number of sequences of various probabilities. Consider again the sequences of length N and let them be arranged in order of decreasing probability. We define n(q) to be the number we must take from this set starting with the most probable one in order to accumulate a total probability q for those taken.

Theorem 4:

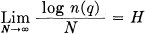
when q does not equal 0 or 1.

We may interpret log n(q) as the number of bits required to specify the sequence when we consider only the most probable sequences with a total probability q. Then 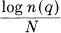is the number of bits per symbol for the specification. The theorem says that for large N this will be independent of q and equal to H. The rate of growth of the logarithm of the number of reasonably probable sequences is given by H, regardless of our interpretation of “reasonably probable.” Due to these results, which are proved in Appendix 3, it is possible for most purposes to treat the long sequences as though there were just 2^HN of them, each with a probability 2^-HN.

The next two theorems show that H and H′ can be determined by limiting operations directly from the statistics of the message sequences, without reference to the states and transition probabilities between states.

Theorem 5: Let p(B_i) be the probability of a sequence B_i of symbols from the source. Let

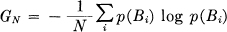
where the sum is over all sequences B_i containing N symbols. Then G_N is a monotonic decreasing function of N and

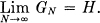
Theorem 6: Let p(B_i, S_j) be the probability of sequence B_i followed by symbol S_j and p_Bi(S_j) = p(B_i, S_j)/p(B_i) be the conditional probability of S_j after B_i. Let.

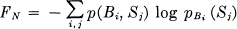
where the sum is over all blocks B_i of N — 1 symbols and over all symbols S_j. Then F_N is a monotonic decreasing function of N,

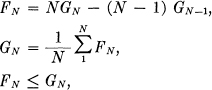
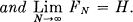
These results are derived in Appendix 3. They show that a series of approximations to H can be obtained by considering only the statistical structure of the sequences extending over 1, 2,…, N symbols. F_N is the better approximation. In fact F_N is the entropy of the N^th order approximation to the source of the type discussed above. If there are no statistical influences extending over more than N symbols, that is if the conditional probability of the next symbol knowing the preceding (N — 1) is not changed by a knowledge of any before that, then F_N = H. F_N of course is the conditional entropy of the next symbol when the (N—1) preceding ones are known, while G_N is the entropy per symbol of blocks of N symbols.

The ratio of the entropy of a source to the maximum value it could have while still restricted to the same symbols will be called its relative entropy. This, as will appear later, is the maximum compression possible when we encode into the same alphabet. One minus the relative entropy is the redundancy. The redundancy of ordinary English, not considering statistical structure over greater distances than about eight letters, is roughly 50%. This means that when we write English half of what we write is determined by the structure of the language and half is chosen freely. The figure 50% was found by several independent methods which all gave results in this neighborhood. One is by calculation of the entropy of the approximations to English. A second method is to delete a certain fraction of the letters from a sample of English text and then let someone attempt to restore them. If they can be restored when 50% are deleted the redundancy must be greater than 50%. A third method depends on certain known results in cryptography.

Two extremes of redundancy in English prose are represented by Basic English and by James Joyce's book Finnegans Wake. The Basic English vocabulary is limited to 850 words and the redundancy is very high. This is reflected in the expansion that occurs when a passage is translated into Basic English. Joyce on the other hand enlarges the vocabulary and is alleged to achieve a compression of semantic content.

The redundancy of a language is related to the existence of crossword puzzles. If the redundancy is zero any sequence of letters is a reasonable text in the language and any two-dimensional array of letters forms a crossword puzzle. If the redundancy is too high the language imposes too many constraints for large crossword puzzles to be possible. A more detailed analysis shows that if we assume the constraints imposed by the language are of a rather chaotic and random nature, large crossword puzzles are just possible when the redundancy is 50%. If the redundancy is 33%, three-dimensional crossword puzzles should be possible, etc.

8. Representation of the Encoding and Decoding Operations

We have yet to represent mathematically the operations performed by the transmitter and receiver in encoding and decoding the information. Either of these will be called a discrete transducer. The input to the transducer is a sequence of input symbols and its output a sequence of output symbols. The transducer may have an internal memory so that its output depends not only on the present input symbol but also on the past history. We assume that the internal memory is finite, i.e., there exist a finite number m of possible states of the transducer and that its output is a function of the present state and the present input symbol. The next state will be a second function of these two quantities. Thus a transducer can be described by two functions:

y_n = f(x_n, α_n)

α_n+1 = g(x_n, α_n)

where:

x_n is the n^th input symbol.

α_n is the state of the transducer when the n^th input symbol is introduced,

y_n is the output symbol (or sequence of output symbols) produced when x_n is introduced if the state is α_n.

If the output symbols of one transducer can be identified with the input symbols of a second, they can be connected in tandem and the result is also a transducer. If there exists a second transducer which operates on the output of the first and recovers the original input, the first transducer will be called non-singular and the second will be called its inverse.

Theorem 7: The output of a finite state transducer driven by a finite state statistical source is a finite state statistical source, with entropy (per unit time) less than or equal to that of the input. If the transducer is non-singular they are equal.

Let α represent the state of the source, which produces a sequence of symbols x_i; and let β be the state of the transducer, which produces, in its output, blocks of symbols y_j. The combined system can be represented by the “product state space” of pairs (α, β). Two points in the space (α₁, β₁) and (α₂, β₂), are connected by a line if α₁ can produce an x which changes β₁ to β₂, and this line is given the probability of that x in this case. The line is labeled with the block of y₁ symbols produced by the transducer. The entropy of the output can be calculated as the weighted sum over the states. If we sum first on β each resulting term is less than or equal to the corresponding term for α, hence the entropy is not increased. If the transducer is non-singular let its output be connected to the inverse transducer. If H′₁, H′₂ and H′₃ are the output entropies of the source, the first and second transducers respectively, then H′₁ ≥ H′₂ ≥ H′₃ = H′₁ and therefore H′₁ =H′₂.

Suppose we have a system of constraints on possible sequences of the type which can be represented by a linear graph as in Fig. 2. If probabilities 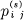were assigned to the various lines connecting state i to state j this would become a source. There is one particular assignment which maximizes the resulting entropy (see Appendix 4).

Theorem 8: Let the system of constraints considered as a channel have a capacity C = log W. If we assign

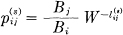
where 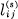is the duration of the s^th symbol leading from state i to state j and the B_i satisfy

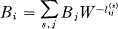
then H is maximized and equal to C.

By proper assignment of the transition probabilities the entropy of symbols on a channel can be maximized at the channel capacity.

9. The Fundamental Theorem for a Noiseless Channel

We will now justify our interpretation of H as the rate of generating information by proving that H determines the channel capacity required with most efficient coding.

Theorem 9: Let a source have entropy H(bits per symbol) and a channel have a capacity C (bits per second). Then it is possible to encode the output of the source in such a way as to transmit at the average rate 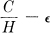symbols per second over the channel where ∊ is arbitrarily small. It is not possible to transmit at an average rate greater than .

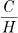The converse part of the theorem, that 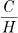cannot be exceeded, may be proved by noting that the entropy of the channel input per second is equal to that of the source, since the transmitter must be non-singular, and also this entropy cannot exceed the channel capacity. Hence H′ ≤ C and the number of symbols per second = H′/H ≤ C/H.

The first part of the theorem will be proved in two different ways. The first method is to consider the set of all sequences of N symbols produced by the source. For N large we can divide these into two groups, one containing less than 2^(H+η)N members and the second containing less than 2^RN members (where R is the logarithm of the number of different symbols) and having a total probability less than μ. As N increases η and μ approach zero. The number of signals of duration T in the channel is greater than 2^(C–θ)T with θ small when T is large. If we choose

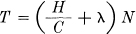
then there will be a sufficient number of sequences of channel symbols for the high probability group when N and T are sufficiently large (however small λ) and also some additional ones. The high probability group is coded in an arbitrary one-to-one way into this set. The remaining sequences are represented by larger sequences, starting and ending with one of the sequences not used for the high probability group. This special sequence acts as a start and stop signal for a different code. In between a sufficient time is allowed to give enough different sequences for all the low probability messages. This will require

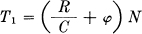
where φ is small. The mean rate of transmission in message symbols per second will then be greater than

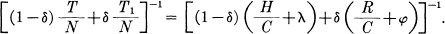
As N increases δ, λ and φ approach zero and the rate approaches .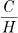

Another method of performing this coding and thereby proving the theorem can be described as follows: Arrange the messages of length N in order of decreasing probability and suppose their probabilities are p₁ ≥ p₂ ≥ p₃…≥ p_n. Let 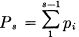; that is P_s is the cumulative probability up to, but not including, p_s. We first encode into a binary system. The binary code for message s is obtained by expanding P_s as a binary number. The expansion is carried out to m_s places, where m_s is the integer satisfying:

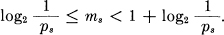
Thus the messages of high probability are represented by short codes and those of low probability by long codes. From these inequalities we have

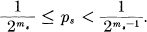
The code for P_s will differ from all succeeding ones in one or more of its m_s places, since all the remaining P_i are at least 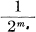larger and their binary expansions therefore differ in the first m_s places. Consequently all the codes are different and it is possible to recover the message from its code. If the channel sequences are not already sequences of binary digits, they can be ascribed binary numbers in an arbitrary fashion and the binary code thus translated into signals suitable for the channel.

The average number H₁ of binary digits used per symbol of original message is easily estimated. We have

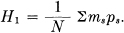
But,

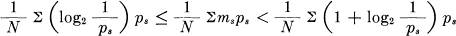
and therefore,

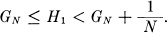
As N increases G_N approaches H, the entropy of the source and H₁ approaches H.

We see from this that the inefficiency in coding, when only a finite delay of N symbols is used, need not be greater than 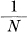plus the difference between the true entropy H and the entropy G_N calculated for sequences of length N. The per cent excess time needed over the ideal is therefore less than

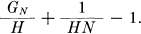
This method of encoding is substantially the same as one found independently by R. M. Fano.9 His method is to arrange the messages of length N in order of decreasing probability. Divide this series into two groups of as nearly equal probability as possible. If the message is in the first group its first binary digit will be 0, otherwise 1. The groups are similarly divided into subsets of nearly equal probability and the particular subset determines the second binary digit. This process is continued until each subset contains only one message. It is easily seen that apart from minor differences (generally in the last digit) this amounts to the same thing as the arithmetic process described above.

10. Discussion and Examples

In order to obtain the maximum power transfer from a generator to a load, a transformer must in general be introduced so that the generator as seen from the load has the load resistance. The situation here is roughly analogous. The transducer which does the encoding should match the source to the channel in a statistical sense. The source as seen from the channel through the transducer should have the same statistical structure as the source which maximizes the entropy in the channel. The content of Theorem 9 is that, although an exact match is not in general possible, we can approximate it as closely as desired. The ratio of the actual rate of transmission to the capacity C may be called the efficiency of the coding system. This is of course equal to the ratio of the actual entropy of the channel symbols to the maximum possible entropy.

In general, ideal or nearly ideal encoding requires a long delay in the transmitter and receiver. In the noiseless case which we have been considering, the main function of this delay is to allow reasonably good matching of probabilities to corresponding lengths of sequences. With a good code the logarithm of the reciprocal probability of a long message must be proportional to the duration of the corresponding signal, in fact

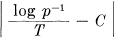
must be small for all but a small fraction of the long messages.

If a source can produce only one particular message its entropy is zero, and no channel is required. For example, a computing machine set up to calculate the successive digits of π produces a definite sequence with no chance element. No channel is required to “transmit” this to another point. One could construct a second machine to compute the same sequence at the point. However, this may be impractical. In such a case we can choose to ignore some or all of the statistical knowledge we have of the source. We might consider the digits of π to be a random sequence in that we construct a system capable of sending any sequence of digits. In a similar way we may choose to use some of our statistical knowledge of English in constructing a code, but not all of it. In such a case we consider the source with the maximum entropy subject to the statistical conditions we wish to retain. The entropy of this source determines the channel capacity which is necessary and sufficient. In the π example the only information retained is that all the digits are chosen from the set 0, 1,…, 9. In the case of English one might wish to use the statistical saving possible due to letter frequencies, but nothing else. The maximum entropy source is then the first approximation to English and its entropy determines the required channel capacity.

As a simple example of some of these results consider a source which produces a sequence of letters chosen from among A, B, C, D with probabilities 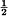, , , , 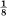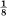successive symbols being chosen independently. We have

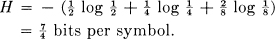
Thus we can approximate a coding system to encode messages from this source into binary digits with an average of 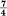binary digit per symbol. In this case we can actually achieve the limiting value by the following code (obtained by the method of the second proof of Theorem 9):

	A	0
	B	10
	C	110
	D	111

The average number of binary digits used in encoding a sequence of N symbols will be

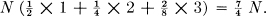
It is easily seen that the binary digits 0, 1 have probabilities 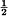, 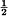so the H for the coded sequences is one bit per symbol. Since, on the average, we have 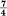binary symbols per original letter, the entropies on a time basis are the same. The maximum possible entropy for the original set is log 4 = 2, occurring when A, B, C, D have probabilities , , , . Hence the relative entropy is 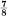. We can translate the binary sequences into the original set of symbols on a two-to-one basis by the following table:

	00	A′
	01	B′
	10	C′
	11	D′

This double process then encodes the original message into the same symbols but with an average compression ratio .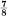

As a second example consider a source which produces a sequence of A's and B's with probability p for A and q for B. If p < < q we have

H = — log p^p(1 — p)^1–p

= — p log p(1 — p)^(1–p)/p

= p log .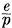

In such a case one can construct a fairly good coding of the message on a 0, 1 channel by sending a special sequence, say 0000, for the infrequent symbol A and then a sequence indicating the number of B's following it. This could be indicated by the binary representation with all numbers containing the special sequence deleted. All numbers up to 16 are represented as usual; 16 is represented by the next binary number after 16 which does not contain four zeros, namely 17 = 10001, etc.

It can be shown that as p → 0 the coding approaches ideal provided the length of the special sequence is properly adjusted.

---

3 See, for example, S. Chandrasekhar, “Stochastic Problems in Physics and Astronomy,” Reviews of Modern Physics, v. 15, No. 1, January 1943, p. 1.

⁴ Kendall and Smith, Tables of Random Sampling Numbers, Cambridge, 1939.

⁵ Letter, digram and trigram frequencies are given in Secret and Urgent by Fletcher Pratt, Blue Ribbon Books, 1939. Word frequencies are tabulated in Relative Frequency of English Speech Sounds, G. Dewey, Harvard University Press, 1923.

⁶ For a detailed treatment see M. Frechet, Methods des fonctions arbitraires. Theorie des énénements en chaine dans le cas d'un nombre fini d'états possibles. Paris, Gauthier Villars, 1938.

⁷ These are restatements in terms of the graph of conditions given in Frechet.

⁸ See, for example, R. C. Tolman, Principles of Statistical Mechanics, Oxford, Clarendon, 1938.

⁹ Technical Report No. 65, The Research Laboratory of Electronics, M.I.T., March 17, 1949.