V

The Rate for a Continuous Source

27. Fidelity Evaluation Functions

In the case of a discrete source of information we were able to determine a definite rate of generating information, namely the entropy of the underlying stochastic process. With a continuous source the situation is considerably more involved. In the first place a continuously variable quantity can assume an infinite number of values and requires, therefore, an infinite number of binary digits for exact specification. This means that to transmit the output of a continuous source with exact recovery at the receiving point requires, in general, a channel of infinite capacity (in bits per second). Since, ordinarily, channels have a certain amount of noise, and therefore a finite capacity, exact transmission is impossible.

This, however, evades the real issue. Practically, we are not interested in exact transmission when we have a continuous source, but only in transmission to within a certain tolerance. The question is, can we assign a definite rate to a continuous source when we require only a certain fidelity of recovery, measured in a suitable way. Of course, as the fidelity requirements are increased the rate will increase. It will be shown that we can, in very general cases, define such a rate, having the property that it is possible, by properly encoding the information, to transmit it over a channel whose capacity is equal to the rate in question, and satisfy the fidelity requirements. A channel of smaller capacity is insufficient.

It is first necessary to give a general mathematical formulation of the idea of fidelity of transmission. Consider the set of messages of a long duration, say T seconds. The source is described by giving the probability density, P(x), in the associated space, that the source will select the message in question. A given communication system is described (from the external point of view) by giving the conditional probability P_x(y) that if message x is produced by the source the recovered message at the receiving point will be y. The system as a whole (including source and transmission system) is described by the probability function P(x, y) of having message x and final output y. If this function is known, the complete characteristics of the system from the point of view of fidelity are known. Any evaluation of fidelity must correspond mathematically to an operation applied to P(x, y). This operation must at least have the properties of a simple ordering of systems; i.e., it must be possible to say of two systems represented by P₁(x, y) and P₂(x, y) that, according to our fidelity criterion, either (1) the first has higher fidelity, (2) the second has higher fidelity, or (3) they have equal fidelity. This means that a criterion of fidelity can be represented by a numerically valued evaluation function:

v(P(x, y))

whose argument ranges over possible probability functions P(x, y). The function v(P(x, y)) orders communication systems according to fidelity, and for convenience we take lower values of v to correspond to “higher fidelity.”

We will now show that under very general and reasonable assumptions the function v(P(x, y)) can be written in a seemingly much more specialized form, namely as an average of a function ρ(x, y) over the set of possible values of x and y:

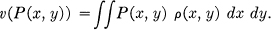
To obtain this we need only assume (1) that the source and system are ergodic so that a very long sample will be, with probability nearly 1, typical of the ensemble, and (2) that the evaluation is “reasonable” in the sense that it is possible, by observing a typical input and output x₁ and y₁, to form a tentative evaluation on the basis of these samples; and if these samples are increased in duration the tentative evaluation will, with probability 1, approach the exact evaluation based on a full knowledge of P(x, y). Let the tentative evaluation be ρ(x, y). Then the function ρ(x, y) approaches (as T → ∞) a constant for almost all (x, y) which are in the high probability region corresponding to the system:

ρ(x, y) → v(P (x, y))

and we may also write

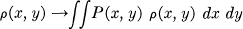
since

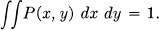
This establishes the desired result.

The function ρ(x, y) has the general nature of a “distance” between x and y.9 It measures how undesirable it is (according to our fidelity criterion) to receive y when x is transmitted. The general result given above can be restated as follows: Any reasonable evaluation can be represented as an average of a distance function over the set of messages and recovered messages x and y weighted according to the probability P(x, y) of getting the pair in question, provided the duration T of the messages be taken sufficiently large.

The following are simple examples of evaluation functions:

1. R.M.S. criterion.

   

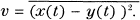
   In this very commonly used measure of fidelity the distance function ρ(x, y) is (apart from a constant factor) the square of the ordinary Euclidean distance between the points x and y in the associated function space.

   

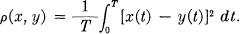
2. Frequency weighted R.M.S. criterion. More generally one can apply different weights to the different frequency components before using an R.M.S. measure of fidelity. This is equivalent to passing the difference x(t) — y(t) through a shaping filter and then determining the average power in the output. Thus let

   e(t) = x(t) — y(t)

   and

   

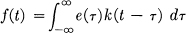
   then

   

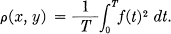
3. Absolute error criterion.

   

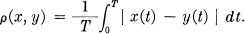
4. The structure of the ear and brain determine implicitly a number of evaluations, appropriate in the case of speech or music transmission. There is, for example, an “intelligibility” criterion in which ρ(x, y) is equal to the relative frequency of incorrectly interpreted words when message x(t) is received as y(t). Although we cannot give an explicit representation of ρ(x, y) in these cases it could, in principle, be determined by sufficient experimentation. Some of its properties follow from well-known experimental results in hearing, e.g., the ear is relatively insensitive to phase and the sensitivity to amplitude and frequency is roughly logarithmic.
5. The discrete case can be considered as a specialization in which we have tacitly assumed an evaluation based on the frequency of errors. The function ρ(x, y) is then defined as the number of symbols in the sequence y differing from the corresponding symbols in x divided by the total number of symbols in x.

28. The Rate for a Source Relative to a Fidelity Evaluation

We are now in a position to define a rate of generating information for a continuous source. We are given P(x) for the source and an evaluation v determined by a distance function ρ(x, y) which will be assumed continuous in both x and y. With a particular system P(x, y) the quality is measured by

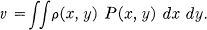
Furthermore the rate of flow of binary digits corresponding to P(x, y) is

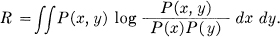
We define the rate R₁ of generating information for a given quality v₁ of reproduction to be the minimum of R when we keep v fixed at v₁ and vary P_x(y). That is:

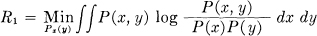
subject to the constraint:

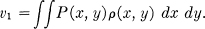
This means that we consider, in effect, all the communication systems that might be used and that transmit with the required fidelity. The rate of transmission in bits per second is calculated for each one and we choose that having the least rate. This latter rate is the rate we assign the source for the fidelity in question.

The justification of this definition lies in the following result:

Theorem 21: If a source has a rate R₁ for a valuation v₁ it is possible to encode the output of the source and transmit it over a channel of capacity C with fidelity as near v₁ as desired provided R₁ ≤ C. This is not possible if R₁ > C.

The last statement in the theorem follows immediately from the definition of R₁ and previous results. If it were not true we could transmit more than C bits per second over a channel of capacity C. The first part of the theorem is proved by a method analogous to that used for Theorem 11. We may, in the first place, divide the (x, y) space into a large number of small cells and represent the situation as a discrete case. This will not change the evaluation function by more than an arbitrarily small amount (when the cells are very small) because of the continuity assumed for ρ(x, y). Suppose that P₁(x, y) is the particular system which minimizes the rate and gives R₁. We choose from the high probability y's a set at random containing

2^{(R₁ + ∊)T}

members where ∊ → 0 as T → ∞. With large T each chosen point will be connected by high probability lines (as in Fig. 10) to a set of x's. A calculation similar to that used in proving Theorem 11 shows that with large T almost all x's are covered by the fans from the chosen y points for almost all choices of the y's. The communication system to be used operates as follows: The selected points are assigned binary numbers. When a message x is originated it will (with probability approaching 1 as T → ∞) lie within at least one of the fans. The corresponding binary number is transmitted (or one of them chosen arbitrarily if there are several) over the channel by suitable coding means to give a small probability of error. Since R₁ ≤ C this is possible. At the receiving point the corresponding y is reconstructed and used as the recovered message.

The evaluation v′₁ for this system can be made arbitrarily close to v₁ by taking T sufficiently large. This is due to the fact that for each long sample of message x(t) and recovered message y(t) the evaluation approaches v₁ (with probability 1).

It is interesting to note that, in this system, the noise in the recovered message is actually produced by a kind of general quantizing at the transmitter and is not produced by the noise in the channel. It is more or less analogous to the quantizing noise in PCM.

29. The Calculation of Rates

The definition of the rate is similar in many respects to the definition of channel capacity. In the former

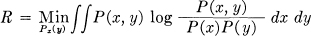
with P_x(y) fixed and possibly one or more other constraints (e.g., an average power limitation) of the form K = ∫∫ P(x, y) λ(x, y) dx dy.

A partial solution of the general maximizing problem for determining the rate of a source can be given. Using Lagrange's method we consider

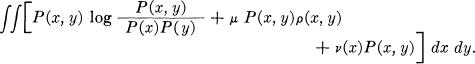
The variational equation (when we take the first variation on P(x, y)) leads to

P_y(x) = B(x) e^{–λρ(x, y)}

where λ is determined to give the required fidelity and B(x) is chosen to satisfy

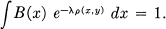
This shows that, with best encoding, the conditional probability of a certain cause for various received y, P_y(x) will decline exponentially with the distance function ρ(x, y) between the x and y in question.

In the special case where the distance function ρ(x, y) depends only on the (vector) difference between x and y,

ρ(x, y) = ρ(x — y)

we have

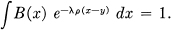
Hence B(x) is constant, say α, and

P_y(x) = αe^{–λρ(x–y)}.

Unfortunately these formal solutions are difficult to evaluate in particular cases and seem to be of little value. In fact, the actual calculation of rates has been carried out in only a few very simple cases.

If the distance function ρ(x, y) is the mean square discrepancy between x and y and the message ensemble is white noise, the rate can be determined. In that case we have

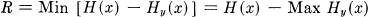
with 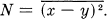But the Max H_y(x) occurs when y − x is a white noise, and is equal to W₁ log 2πeN where W₁ is the bandwidth of the message ensemble. Therefore

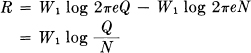
where Q is the average message power. This proves the following:

Theorem 22: The rate for a white noise source of power Q and band W₁ relative to an R.M.S. measure of fidelity is

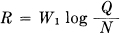
where N is the allowed mean square error between original and recovered messages.

More generally with any message source we can obtain inequalities bounding the rate relative to a mean square error criterion.

Theorem 23: The rate for any source of band W₁ is bounded by

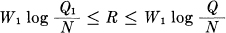
where Q is the average power of the source, Q₁ its entropy power and N the allowed mean square error.

The lower bound follows from the fact that the Max H_y(x) for a given 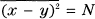occurs in the white noise case. The upper bound results if we place the points (used in the proof of Theorem 21) not in the best way but at random in a sphere of radius .

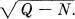Acknowledgments

The writer is indebted to his colleagues at the Laboratories, particularly to Dr. H. W. Bode, Dr. J. R. Pierce, Dr. B. McMillan, and Dr. B. M. Oliver for many helpful suggestions and criticisms during the course of this work. Credit should also be given to Professor N. Wiener, whose elegant solution of the problems of filtering and prediction of stationary ensembles has considerably influenced the writer's thinking in this field.

 

Appendix 1.    The Growth of the Number of Blocks of Symbols with a Finite State Condition

Let N_i (L) be the number of blocks of symbols of length L ending in state i. Then we have

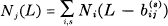
where are the length of the symbols which may be chosen in state i and lead to state j. These are linear difference equations and the behavior as L → ∞ must be of the type

N_j = A_jW^L.

Substituting in the difference equation

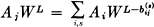
or

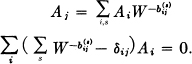
For this to be possible the determinant

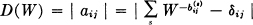
must vanish and this determines W, which is, of course, the largest real root of D = 0.

The quantity C is then given by

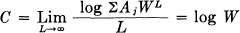
and we also note that the same growth properties result if we require that all blocks start in the same (arbitrarily chosen) state.

Appendix 2.    Derivation of H = — ∑ p_i log p_i

Let 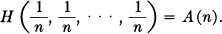From condition (3) we can decompose a choice from s^m equally likely possibilities into a series of m choices each from s equally likely possibilities and obtain

A(s^m) = m A(s).

Similarly

A (t_n) = n A(t).

We can choose n arbitrarily large and find an m to satisfy

s^m ≤ tⁿ < s^(m+1).

Thus, taking logarithms and dividing by n log s,

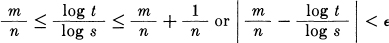
where ∊ is arbitrarily small. Now from the monotonic property of A(n),

A(s^m) ≤ A(tⁿ) ≤ A (s^m+1)

  m A(s) ≤ nA(t) ≤ (m + 1) A (s).

Hence, dividing by nA (s),

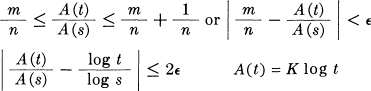
where K must be positive to satisfy (2).

Now suppose we have a choice from n possibilities with commeasurable probabilities 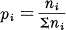where the n_i are integers. We can break down a choice from ∑n_i possibilities into a choice from n possibilities with probabilities p₁,…, p_n and then, if the ith was chosen, a choice from n_i with equal probabilities. Using condition (3) again, we equate the total choice from ∑n_i as computed by two methods

K log Σn_i = H(p₁,…, p_n) + KΣ p_i log n_i.

Hence

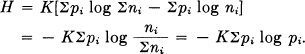
If the p_i are incommeasurable, they may be approximated by rationals and the same expression must hold by our continuity assumption. Thus the expression holds in general. The choice of coefficient K is a matter of convenience and amounts to the choice of a unit of measure.

Appendix 3.    Theorems on Ergodic Sources

We assume the source to be ergodic so that the strong law of large numbers can be applied. Thus the number of times a given path p_ij in the network is traversed in a long sequence of length N is about proportional to the probability of being at i, say P_i, and then choosing this path, P_ip_ijN. If N is large enough the probability of percentage error ± δ in this is less than ∊ so that for all but a set of small probability the actual numbers lie within the limits

(P_ip_ij ± δ)N.

Hence nearly all sequences have a probability p given by

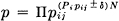
and 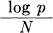is limited by

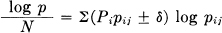
or

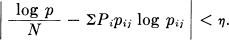
This proves Theorem 3.

Theorem 4 follows immediately from this on calculating upper and lower bounds for n(q) based on the possible range of values of p in Theorem 3.

In the mixed (not ergodic) case if

L = Σ p_iL_i

and the entropies of the components are H₁ ≥ H₂ ≥…≥ H_n
we have the

Theorem: 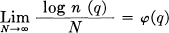is a decreasing step function,

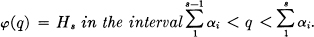
To prove Theorems 5 and 6 first note that F_N is monotonic decreasing because increasing N adds a subscript to a conditional entropy. A simple substitution for p_Bi(S_j) in the definition of F_N shows that

F_N = N G_N — (N — 1) G_N-1

and summing this for all N gives 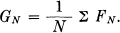Hence G_N ≥ F_N and G_N monotonic decreasing. Also they must approach the same limit. By using Theorem 3 we see that .

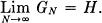Appendix 4.    Maximizing the Rate for a System of Constraints

Suppose we have a set of constraints on sequences of symbols that is of the finite state type and can be represented therefore by a linear graph, as in Fig. 2. Let l_ij^(s) be the lengths of the various symbols that can occur in passing from state i to state j. What distribution of probabilities P_i for the different states and p_ij^(s) for choosing symbol s in state i and going to state j maximizes the rate of generating information under these constraints? The constraints define a discrete channel and the maximum rate must be less than or equal to the capacity C of this channel, since if all blocks of large length were equally likely, this rate would result, and if possible this would be best. We will show that this rate can be achieved by proper choice of the P_i and p_ij^(s). The rate in question is

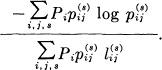
Let

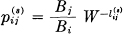
where the B_i satisfy the equations

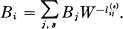
This homogeneous system has a non-vanishing solution since W is such that the determinant of the coefficients is zero:

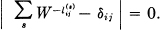
The p_ij^(s) defined thus are satisfactory transition probabilities for in the first place,

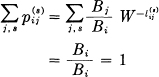
so that the sum of the probabilities from any particular junction point is unity. Furthermore they are non-negative as can be seen from a consideration of the quantities A_i given in Appendix 1. The A_i are necessarily non-negative and the B_i satisfy a similar system of equations but with i and j interchanged. This amounts to reversing the orientation on the lines of the graph.

Substituting the assumed values of p_ij^(s) in the general equation for the rate we obtain

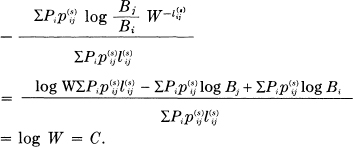
Hence the rate with this set of transition probabilities is C and since this rate could never be exceeded this is the maximum.

Appendix 5

Let S₁ be any measurable subset of the g ensemble, and S₂ the subset of the f ensemble which gives S₁ under the operation T. Then

S₁ = TS₂.

Let H^λ be the operator which shifts all functions in a set by the time λ. Then

H^λS₁ = H^λTS₂ = TH^λS₂

since T is invariant and therefore commutes with H^λ. Hence if m[S] is the probability measure of the set S

m[H^λS₁] = m[TH^λS₂] = m[H^λS₂]

   = m[S₂] = m[S₁]

where the second equality is by definition of measure in the g space, the third since the f ensemble is stationary, and the last by definition of g measure again. This shows that the g ensemble is stationary.

To prove that the ergodic property is preserved under invariant operations, let S₁ be a subset of the g ensemble which is invariant under H^λ, and let S₂ be the set of all functions f which transform into S₁. Then

H^λS₁ = H^λTS₂ = TH^λS₂ = S₁

so that H^λS₂ is included in S₂, for all λ. Now, since

m[H^λS₂] = m[S₂] = m[S₁]

this implies

H^λS₂ = S₂

for all λ with m[S₂] ≠ 0, 1. This contradiction shows that S₁ does not exist.

Appendix 6

The upper bound, 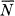₃ ≤ N₁ + N₂, is due to the fact that the maximum possible entropy for a power N₁ + N₂ occurs when we have a white noise of this power. In this case the entropy power is N₁ + N₂.

To obtain the lower bound, suppose we have two distributions in n dimensions p(x_i) and q(x_i) with entropy powers 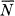₁ and 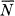₂. What form should p and q have to minimize the entropy power 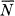₃ of their convolution r(x_i):

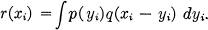
The entropy H₃ of r is given by

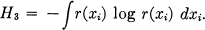
We wish to minimize this subject to the constraints

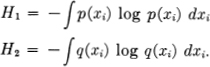
We consider then

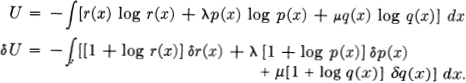
If p(x) is varied at a particular argument x_i = s_i, the variation in r(x) is

δr(x) = q(x_i — s_i)

and

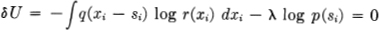
and similarly when q is varied. Hence the conditions for a minimum are

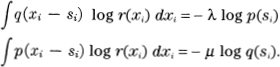
If we multiply the first by p(s_i) and the second by q(s_i) and integrate with respect to s_i we obtain

H₃ = — λ H₁

H₃ = — μ H₂

or solving for λ and μ and replacing in the equations

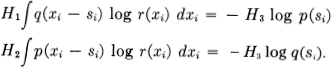
Now suppose p(x_i) and q(x_i) are normal

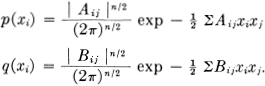
Then r(x_i) will also be normal with quadratic form C_ij. If the inverses of these forms are a_ij, b_ij, c_ij then

c_ij = a_ij + b_ij.

We wish to show that these functions satisfy the minimizing conditions if and only if a_ij = Kb_ij and thus give the minimum H₃ under the constraints. First we have

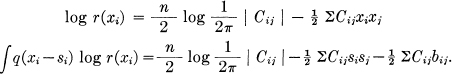
This should equal

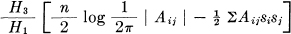
which requires .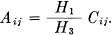

In this case 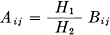and both equations reduce to identities.

Appendix 7

The following will indicate a more general and more rigorous approach to the central definitions of communication theory. Consider a probability measure space whose elements are ordered pairs (x, y). The variables x, y are to be identified as the possible transmitted and received signals of some long duration T. Let us call the set of all points whose x belongs to a subset S₁ of x points the strip over S₁, and similarly the set whose y belong to S₂ the strip over S₂. We divide x and y into a collection of non-overlapping measurable subsets X_i and Y_i approximate to the rate of transmission R by

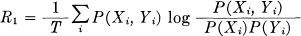
where

P(X_i) is the probability measure of the strip over X_i

P(Y_i) is the probability measure of the strip over Y_i

P(X_i, Y_i) is the probability measure of the intersection of the strips.

A further subdivision can never decrease R₁. For let X₁ be divided into X₁ = X^′₁ + X^″₁ and let

	P(Y1) = a P(X′1) = b P(X″1) = c	P(X1) = b + c P(X′1, Y1) = d P(X″1, Y1) = e
P(X1, Y1) = d + e.

Then in the sum we have replaced (for the X_l, Y₁ intersection)

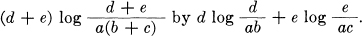
It is easily shown that with the limitation we have on b, c, d, e,

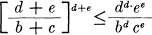
and consequently the sum is increased. Thus the various possible subdivisions form a directed set, with R monotonic increasing with refinement of the subdivision. We may define R unambiguously as the least upper bound for the R₁ and write it

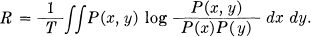
This integral, understood in the above sense, includes both the continuous and discrete cases and of course many others which cannot be represented in either form. It is trivial in this formulation that if x and u are in one-to-one correspondence, the rate from u to y is equal to that from x to y. If v is any function of y (not necessarily with an inverse) then the rate from x to y is greater than or equal to that from x to v since, in the calculation of the approximations, the subdivisions of y are essentially a finer subdivision of those for v. More generally if y and v are related not functionally but statistically, i.e., we have a probability measure space (y,v), then R(x,v) ≤ R(x,y). This means that any operation applied to the received signal, even though it involves statistical elements, does not increase R.

Another notion which should be defined precisely in an abstract formulation of the theory is that of “dimension rate,” that is the average number of dimensions required per second to specify a member of an ensemble. In the band limited case 2W numbers per second are sufficient. A general definition can be framed as follows. Let f_α(t) be an ensemble of functions and let ρ_T[f_α(t), f_β(t)] be a metric measuring the “distance” from f_α to f_β over the time T (for example the R.M.S. discrepancy over this interval). Let N(∊, δ, T) be the least number of elements f which can be chosen such that all elements of the ensemble apart from a set of measure δ are within the distance ∊ of at least one of those chosen. Thus we are covering the space to within ∊ apart from a set of small measure δ. We define the dimension rate λ for the ensemble by the triple limit

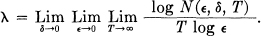
This is a generalization of the measure type definitions of dimension in topology, and agrees with the intuitive dimension rate for simple ensembles where the desired result is obvious.

---

9 It is not a “metric” in the strict sense, however, since in general it does not satisfy either ρ(x, y) = ρ(y, x) or ρ(x, y) + ρ(y, z) ≥ ρ(x, z).