III

Continuous Information

We now consider the case where the signals or the messages or both are continuously variable, in contrast with the discrete nature assumed heretofore. To a considerable extent the continuous case can be obtained through a limiting process from the discrete case by dividing the continuum of messages and signals into a large but finite number of small regions and calculating the various parameters involved on a discrete basis. As the size of the regions is decreased these parameters in general approach as limits the proper values for the continuous case. There are, however, a few new effects that appear and also a general change of emphasis in the direction of specialization of the general results to particular cases.

We will not attempt, in the continuous case, to obtain our results with the greatest generality, or with the extreme rigor of pure mathematics, since this would involve a great deal of abstract measure theory and would obscure the main thread of the analysis. A preliminary study, however, indicates that the theory can be formulated in a completely axiomatic and rigorous manner which includes both the continuous and discrete cases and many others. The occasional liberties taken with limiting processes in the present analysis can be justified in all cases of practical interest.

18. Sets and Ensembles of Functions

We shall have to deal in the continuous case with sets of functions and ensembles of functions. A set of functions, as the name implies, is merely a class or collection of functions, generally of one variable, time. It can be specified by giving an explicit representation of the various functions in the set, or implicitly by giving a property which functions in the set possess and others do not. Some examples are:

1. The set of functions:

   f_θ(t) = sin (t + θ).

   Each particular value of θ determines a particular function in the set.

2. The set of all functions of time containing no frequencies over W cycles per second.
3. The set of all functions limited in band to W and in amplitude to A.
4. The set of all English speech signals as functions of time.

An ensemble of functions is a set of functions together with a probability measure whereby we may determine the probability of a function in the set having certain properties.1 For example with the set,

f_θ(t) = sin (t + θ),

we may give a probability distribution for θ, say P(θ). The set then becomes an ensemble.

Some further examples of ensembles of functions are:

1. A finite set of functions f_k(t) (k = 1, 2,…, n) with the probability of f_k being p_k.
2. A finite dimensional family of functions

   f(α₁, α₂,…, α_n; t)

   with a probability distribution for the parameters α_i:

   p(α₁,…, α_n).

   For example we could consider the ensemble defined by

   

   with the amplitudes a_i distributed normally and independently, and the phases θ_i distributed uniformly (from 0 to 2π) and independently.

3. The ensemble

   

   with the a_i normal and independent all with the same standard deviation 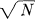. This is a representation of “white” noise, band limited to the band from 0 to W cycles per second and with average power N.2

4. Let points be distributed on the t axis according to a Poisson distribution. At each selected point the function f(t) is placed and the different functions added, giving the ensemble

   

   where the t_k are the points of the Poisson distribution. This ensemble can be considered as a type of impulse or shot noise where all the impulses are identical.

5. The set of English speech functions with the probability measure given by the frequency of occurrence in ordinary use.

An ensemble of functions f_α(t) is stationary if the same ensemble results when all functions are shifted any fixed amount in time. The ensemble

f_θ(t) = sin (t + θ)

is stationary if θ is distributed uniformly from 0 to 2π. If we shift each function by t₁ we obtain

f_θ(t + t₁) = sin (t + t₁ + θ)

       = sin (t + φ)

with φ distributed uniformly from 0 to 2π. Each function has changed but the ensemble as a whole is invariant under the translation. The other examples given above are also stationary.

An ensemble is ergodic if it is stationary, and there is no subset of the functions in the set with a probability different from 0 and 1 which is stationary. The ensemble

sin (t + θ)

is ergodic. No subset of these functions of probability ≠ 0, 1 is transformed into itself under all time translations. On the other hand the ensemble

a sin (t + θ)

with a distributed normally and θ uniform is stationary but not ergodic. The subset of these functions with a between 0 and 1, for example, is stationary, and has a probability not equal to 0 or 1.

Of the examples given, 3 and 4 are ergodic, and 5 may perhaps be considered so. If an ensemble is ergodic we may say roughly that each function in the set is typical of the ensemble. More precisely it is known that with an ergodic ensemble an average of any statistic over the ensemble is equal (with probability 1) to an average over all the time translations of a particular function in the set.3 Roughly speaking, each function can be expected, as time progresses, to go through, with the proper frequency, all the convolutions of any of the functions in the set.

Just as we may perform various operations on numbers or functions to obtain new numbers or functions, we can perform operations on ensembles to obtain new ensembles. Suppose, for example, we have an ensemble of functions f_α(t) and an operator T which gives for each function f_α(t) a resulting function g_α(t) :

g_α(t) = Tf_α(t).

Probability measure is defined for the set g_α(t) by means of that for the set f_α(t). The probability of a certain subset of the g_α(t) functions is equal to that of the subset of the f_α(t) functions which produce members of the given subset of g functions under the operation T. Physically this corresponds to passing the ensemble through some device, for example, a filter, a rectifier or a modulator. The output functions of the device form the ensemble g_α(t).

A device or operator T will be called invariant if shifting the input merely shifts the output, i.e., if

g_α(t) = Tf_α(t).

implies

g_α(t + t₁) = Tf_α(t + t₁)

for all f_α(t) and all t₁. It is easily shown (see Appendix 5) that if T is invariant and the input ensemble is stationary then the output ensemble is stationary. Likewise if the input is ergodic the output will also be ergodic.

A filter or a rectifier is invariant under all time translations. The operation of modulation is not, since the carrier phase gives a certain time structure. However, modulation is invariant under all translations which are multiples of the period of the carrier.

Wiener has pointed out the intimate relation between the invariance of physical devices under time translations and Fourier theory.⁴ He has shown, in fact, that if a device is linear as well as invariant Fourier analysis is then the appropriate mathematical tool for dealing with the problem.

An ensemble of functions is the appropriate mathematical representation of the messages produced by a continuous source (for example, speech), of the signals produced by a transmitter, and of the perturbing noise. Communication theory is properly concerned, as has been emphasized by Wiener, not with operations on particular functions, but with operations on ensembles of functions. A communication system is designed not for a particular speech function and still less for a sine wave, but for the ensemble of speech functions.

19. Band Limited Ensembles of Functions

If a function of time f(t) is limited to the band from 0 to W cycles per second it is completely determined by giving its ordinates at a series of discrete points spaced 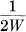seconds apart in the manner indicated by the following result.5

Theorem 13: Let f(t) contain no frequencies over W.

Then

where

In this expansion f(t) is represented as a sum of orthogonal functions. The coefficients X_n of the various terms can be considered as coordinates in an infinite dimensional “function space.” In this space each function corresponds to precisely one point and each point to one function.

A function can be considered to be substantially limited to a time T if all the ordinates X_n outside this interval of time are zero. In this case all but 2TW of the coordinates will be zero. Thus functions limited to a band W and duration T correspond to points in a space of 2TW dimensions.

A subset of the functions of band W and duration T corresponds to a region in this space. For example, the functions whose total energy is less than or equal to E correspond to points in a 2TW dimensional sphere with radius .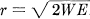

An ensemble of functions of limited duration and band will be represented by a probability distribution p(x₁,…, x_n) in the corresponding n dimensional space. If the ensemble is not limited in time we can consider the 2TW coordinates in a given interval T to represent substantially the part of the function in the interval T and the probability distribution p(x₁,…, x_n) to give the statistical structure of the ensemble for intervals of that duration.

20. Entropy of a Continuous Distribution

The entropy of a discrete set of probabilities p₁,…, p_n has been defined as:

H = — Σ p_i log p_i.

In an analogous manner we define the entropy of a continuous distribution with the density distribution function p(x) by:

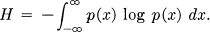
With an n dimensional distribution p(x₁,…, x_n) we have

If we have two arguments x and y (which may themselves be multidimensional) the joint and conditional entropies of p(x, y) are given by

and

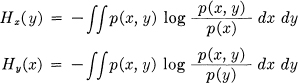
where

The entropies of continuous distributions have most (but not all) of the properties of the discrete case. In particular we have the following:

1. If x is limited to a certain volume v in its space, then H(x) is a maximum and equal to log v when p(x) is constant 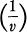in the volume.
2. With any two variables x, y we have

   H(x, y) ≤ H(x) + H(y)

   with equality if (and only if) x and y are independent, i.e., p(x, y) = p(x) p(y) (apart possibly from a set of points of probability zero).

3. Consider a generalized averaging operation of the following type:

   

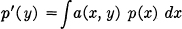
   with

   

   Then the entropy of the averaged distribution p′(y) is equal to or greater than that of the original distribution p(x).

4. We have

   H(x, y) = H(x) + H_x(y) = H(y) + H_y(x)

   and

   H_x(y) ≤ H(y).

5. Let p(x) be a one-dimensional distribution. The form of p(x) giving a maximum entropy subject to the condition that the standard deviation of x be fixed at σ is Gaussian. To show this we must maximize

   

   with

   

   as constraints. This requires, by the calculus of variations, maximizing

   

   The condition for this is

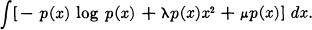
   — 1 — log p(x) + λx² + μ = 0

   and consequently (adjusting the constants to satisfy the constraints)

   

   Similarly in n dimensions, suppose the second order moments of p(x₁,…, x_n) are fixed at A_ij:

   

   Then the maximum entropy occurs (by a similar calculation) when p(x₁…, x_n) is the n dimensional Gaussian distribution with the second order moments A_ij.

6. The entropy of a one-dimensional Gaussian distribution whose standard deviation is σ is given by

   

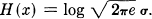
   This is calculated as follows:

   

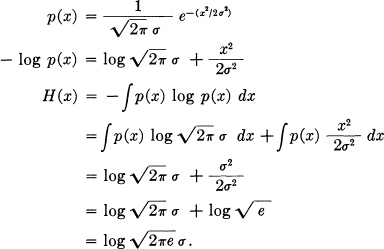
   Similarly the n dimensional Gaussian distribution with associated quadratic form a_ij is given by

   

   and the entropy can be calculated as

   

   where | a_ij | is the determinant whose elements are a_ij.

7. If x is limited to a half line (p(x) = 0 for x ≤ 0) and the first moment of x is fixed at a:

   

   then the maximum entropy occurs when

   

   and is equal to log ea.

8. There is one important difference between the continuous and discrete entropies. In the discrete case the entropy measures in an absolute way the randomness of the chance variable. In the continuous case the measurement is relative to the coordinate system. If we change coordinates the entropy will in general change. In fact if we change to coordinates y₁…y_n the new entropy is given by

   

   where J is the Jacobian of the coordinate transformation. On expanding the logarithm and changing variables to x₁…x_n, we obtain: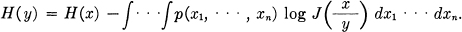

   

   Thus the new entropy is the old entropy less the expected logarithm of the Jacobian. In the continuous case the entropy can be considered a measure of randomness relative to an assumed standard, namely the coordinate system chosen with each small volume element dx₁…dx_n given equal weight. When we change the coordinate system the entropy in the new system measures the randomness when equal volume elements dy₁…dy_n in the new system are given equal weight.

   In spite of this dependence on the coordinate system the entropy concept is as important in the continuous case as the discrete case. This is due to the fact that the derived concepts of information rate and channel capacity depend on the difference of two entropies and this difference does not depend on the coordinate frame, each of the two terms being changed by the same amount.

   The entropy of a continuous distribution can be negative. The scale of measurements sets an arbitrary zero corresponding to a uniform distribution over a unit volume. A distribution which is more confined than this has less entropy and will be negative. The rates and capacities will, however, always be non-negative.

9. A particular case of changing coordinates is the linear transformation

   

   In this case the Jacobian is simply the determinant | a_ij |^-1 and

   H(y) = H(x) + log | a_ij |.

   In the case of a rotation of coordinates (or any measure preserving transformation) J = 1 and H (y) = H(x).

21. Entropy of an Ensemble of Functions

Consider an ergodic ensemble of functions limited to a certain band of width W cycles per second. Let

p(x₁,…, x_n)

be the density distribution function for amplitudes x₁…x_n at n successive sample points. We define the entropy of the ensemble per degree of freedom by

We may also define an entropy H per second by dividing, not by n, but by the time T in seconds for n samples. Since n = 2TW, H = 2WH′.

With white thermal noise p is Gaussian and we have

For a given average power N, white noise has the maximum possible entropy. This follows from the maximizing properties of the Gaussian distribution noted above.

The entropy for a continuous stochastic process has many properties analogous to that for discrete processes. In the discrete case the entropy was related to the logarithm of the probability of long sequences, and to the number of reasonably probable sequences of long length. In the continuous case it is related in a similar fashion to the logarithm of the probability density for a long series of samples, and the volume of reasonably high probability in the function space.

More precisely, if we assume p(x₁,…, x_n) continuous in all the x_i for all n, then for sufficiently large n

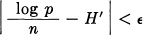
for all choices of (x₁,…, x_n) apart from a set whose total probability is less than δ, with δ and ∊ arbitrarily small. This follows from the ergodic property if we divide the space into a large number of small cells.

The relation of H to volume can be stated as follows: Under the same assumptions consider the n dimensional space corresponding to p(x₁,…, x_n). Let V_n(q) be the smallest volume in this space which includes in its interior a total probability q. Then

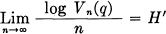
provided q does not equal 0 or 1.

These results show that for large n there is a rather well-defined volume (at least in the logarithmic sense) of high probability, and that within this volume the probability density is relatively uniform (again in the logarithmic sense).

In the white noise case the distribution function is given by

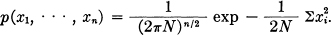
Since this depends only on ∑x_i² the surfaces of equal probability density are spheres and the entire distribution has spherical symmetry. The region of high probability is a sphere of radius . As n → ∞ the probability of being outside a sphere of radius 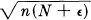approaches zero however small ∊ and times the logarithm of the volume of the sphere approaches log .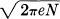

In the continuous case it is convenient to work not with the entropy H of an ensemble but with a derived quantity which we will call the entropy power. This is defined as the power in a white noise limited to the same band as the original ensemble and having the same entropy. In other words if H′ is the entropy of an ensemble its entropy power is

In the geometrical picture this amounts to measuring the high probability volume by the squared radius of a sphere having the same volume. Since white noise has the maximum entropy for a given power, the entropy power of any noise is less than or equal to its actual power.

22. Entropy Loss in Linear Filters

Theorem 14: If an ensemble having an entropy H₁ per degree of freedom in band W is passed through a filter with characteristic Y (f) the output ensemble has an entropy

The operation of the filter is essentially a linear transformation of coordinates. If we think of the different frequency components as the original coordinate system, the new frequency components are merely the old ones multiplied by factors. The coordinate transformation matrix is thus essentially diagonalized in terms of these coordinates. The Jacobian of the transformation is (for n sine and n cosine components)

where the f_i are equally spaced through the band W. This becomes in the limit

Since J is constant its average value is the same quantity and applying the theorem on the change of entropy with a change of coordinates, the result follows. We may also phrase it in terms of the entropy power. Thus if the entropy power of the first ensemble is N₁ that of the second is

TABLE I

The final entropy power is the initial entropy power multiplied by the geometric mean gain of the filter. If the gain is measured in db, then the output entropy power will be increased by the arithmetic mean db gain over W.

In Table I the entropy power loss has been calculated (and also expressed in db) for a number of ideal gain characteristics. The impulsive responses of these filters are also given for W = 1/2π, with phase assumed to be 0.

The entropy loss for many other cases can be obtained from these results. For example the entropy power factor for the first case also applies to any gain characteristic obtained from 1 — ω by a measure preserving transformation of the ω axis. In particular a linearly increasing gain G (ω) = ω, or a “saw tooth” characteristic between 0 and 1 have the same entropy loss. The reciprocal gain has the reciprocal factor. Thus 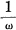has the factor e². Raising the gain to any power raises the factor to this power.

23. Entropy of the Sum of Two Ensembles

If we have two ensembles of functions f_α(t) and g_β(t) we can form a new ensemble by “addition.” Suppose the first ensemble has the probability density function p(x₁,…, x_n) and the second q(x₁,…, x_n). Then the density function for the sum is given by the convolution:

Physically this corresponds to adding the noises or signals represented by the original ensembles of functions.

The following result is derived in Appendix 6.

Theorem 15: Let the average power of two ensembles be N₁ and N₂ and let their entropy powers be ₁ and ₂. Then the entropy power of the sum, ₃, is bounded by

White Gaussian noise has the peculiar property that it can absorb any other noise or signal ensemble which may be added to it with a resultant entropy power approximately equal to the sum of the white noise power and the signal power (measured from the average signal value, which is normally zero), provided the signal power is small, in a certain sense, compared to the noise.

Consider the function space associated with these ensembles having n dimensions. The white noise corresponds to the spherical Gaussian distribution in this space. The signal ensemble corresponds to another probability distribution, not necessarily Gaussian or spherical. Let the second moments of this distribution about its center of gravity be a_ij. That is, if p(x₁,…, x_n) is the density distribution function

where the α_i are the coordinates of the center of gravity. Now α_ij is a positive definite quadratic form, and we can rotate our coordinate system to align it with the principal directions of this form. a_ij is then reduced to diagonal form b_ii. We require that each b_ii be small compared to N, the squared radius of the spherical distribution.

In this case the convolution of the noise and signal produce approximately a Gaussian distribution whose corresponding quadratic form is

N + b_ii.

The entropy power of this distribution is

[II(N + b_ii)]^1/n

or approximately

The last term is the signal power, while the first is the noise power.

---

1In mathematical terminology the functions belong to a measure space whose total measure is unity.

² This representation can be used as a definition of band limited white noise. It has certain advantages in that it involves fewer limiting operations than do definitions that have been used in the past. The name “white noise,” already firmly intrenched in the literature, is perhaps somewhat unfortunate. In optics white light means either any continuous spectrum as contrasted with a point spectrum, or a spectrum which is flat with wavelength (which is not the same as a spectrum flat with frequency).

³ This is the famous ergodic theorem or rather one aspect of this theorem which was proved in somewhat different formulations by Birkhoff, von Neumann, and Koopman, and subsequently generalized by Wiener, Hopf, Hurewicz and others. The literature on ergodic theory is quite extensive and the reader is referred to the papers of these writers for precise and general formulations; e.g., E. Hopf “Ergodentheorie,” Ergebnisse der Mathematic und ihrer Grenzgebiete, v. 5; “On Causality Statistics and Probability,” Journal of Mathematics and Physics, v. XIII, No. 1, 1934; N. Wiener “The Ergodic Theorem,” Duke Mathematical Journal, v. 5, 1939.

⁴ Communication theory is heavily indebted to Wiener for much of its basic philosophy and theory. His classic NDRC report, The Interpolation, Extrapolation, and Smoothing of Stationary Time Series (Wiley, 1949), contains the first clear-cut formulation of communication theory as a statistical problem, the study of operations on time series. This work, although chiefly concerned with the linear prediction and filtering problem, is an important collateral reference in connection with the present paper. We may also refer here to Wiener's Cybernetics (Wiley, 1948), dealing with the general problems of communication and control.

⁵ For a proof of this theorem and further discussion see the author's paper “Communication in the Presence of Noise” published in the Proceedings of the Institute of Radio Engineers, v. 37, No. 1, Jan., 1949, pp. 10-21.