7 Assessment, Feedback, and Meeting the Needs of All Learners

Copyright © Erin Null
Kirk Carlson teaches sixth-grade mathematics. He uses many of the teaching moves we have mentioned earlier, including rich tasks and collaborative grouping, and he balances his curriculum among conceptual understanding, procedural skills, and applications. Surface, deep, and transfer learning are always front and center in his mind as he plans units so that he knows his students are experiencing these phases of learning as they master a mathematical topic. He uses purposeful questions and prompts throughout his student-centered lessons. He and his students use accountable talk to share ideas and make connections. His students know the learning intention and success criteria for each lesson. What helps Kirk with all of this is that he knows his students and their level of understanding at just about any point in time. He does this by intentionally evaluating with both formative and summative assessments, using the information he gets from these assessments to diagnose students’ understandings and misconceptions, and adjusting his instruction based on this information. At the same time, he regularly provides feedback to his students so they are aware of what they need to learn and how they can best accomplish that.
Mr. Carlson often ends his class with an exit ticket designed to quickly assess where students are in their understanding of the topic of the day. They are working on developing conceptual understanding of multiplication of fractions. Today’s exit ticket has two problems and looks like the one in Figure 7.1.
Mr. Carlson collects the tickets as students leave class. He then sits down to quickly sort answers. While all of the students had the correct product for 6 × 5, a few were not clear with their explanations. Some explained that the problem meant 6 groups of 5. Bob and Marty wrote that the problem meant 5 groups of 6. Others skip counted by 5. One skip counted by 6. Work on the second problem varied more. Answers included 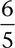
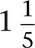
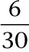
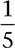
The half piece of paper he collected from each student provided Mr. Carlson with valuable feedback about each student’s understanding or misconceptions, and it also provided information that would help him design tomorrow’s instruction and know which students would need extra support. This is an example of the power of assessment.
In this chapter, we will share our thoughts on the critical role of ongoing assessment and feedback to and from your students, which is so essential to helping students move through the phases of learning toward true mastery of mathematical content. We will begin with how to productively evaluate both your daily assessment of student understanding and summative assessments of student learning in ways that can inform your instruction and offer students feedback. We will also look at ways to differentiate instruction to meet individual needs through thoughtfully planned lessons. We will address intervention by looking at the research on Response to Intervention for students who need extra support and exploring options for students who show advanced ability in doing mathematics. We will address some of the things that we know from research don’t work when it comes to instruction . . . things that have very low impact and you can stop spending time and energy on. Finally, we’ll close with what John has identified as ten teacher mind frames that together summarize a great deal of the “what works” literature in an effort to inspire you to sharpen your tools and have the greatest possible impact on your students’ learning.
Video 7.1 Continual Assessment for Precision Teaching

http://resources.corwin.com/VL-mathematics
Assessing Learning and Providing Feedback
Assessment needs to be a prominent feature of the classroom; unfortunately, it is too often left to the end-of-unit test that informs the teacher and the student very little about what they understand, nor does it allow the teacher an opportunity to adjust his or her instruction to meet students’ needs. As we will discuss, formative and summative assessment are both important and should not be used simply to grade students’ work, but rather to measure progress and compare it with the teaching that has occurred.
Formative Evaluation Embedded in Instruction
Formative evaluation is the process of gathering evidence to inform instruction. In other words, it is a way of thinking about measuring progress in learning and responding to it in teaching. Many teachers may be familiar with this activity by another name—formative assessment. Throughout this book, we prefer to use the terms formative and summative evaluation to describe this process. We argue that any assessment you give may be interpreted formatively or summatively, but when the teacher as the evaluator decides how to interpret where a student is during and after a lesson, and how to improve his or her teaching in response, it is the evaluation of the assessment that matters. Gathering real-time data about where students are in the learning process is critical to making good decisions about the next lesson or teaching move. Mr. Carlson’s exit ticket is a formative assessment. He planned within his instruction to pause at this stage and find out where his students are in their learning. He not only gathered the data, but will use it in his own planning for teaching and will share it with students to inform their learning.
The formative evaluation process has several key elements (Leahy, Lyon, Thompson, & Wiliam, 2005), many of which will be familiar to you by now:
- Clarifying, sharing, and understanding learning intentions and criteria for success
- Engineering effective classroom discussions, activities, and learning tasks that elicit evidence of learning
- Providing feedback that moves learning forward
- Activating learners as instructional resources for one another
- Activating learners as the owners of their own learning
In this section, we will focus on the role of feedback as a tool for moving learning forward. The evidence gathered in the process of formative evaluation serves as feedback to the teacher on the effectiveness of instruction. Teachers, in turn, provide feedback to students and support students in providing feedback to themselves and each other; this feedback moves the learning process forward.
Feedback for the Teacher: Adjusting Instruction
Daily formative evaluation is a chief way for teachers to make instructional decisions about what will occur next. In Chapter 3, we discussed questioning techniques to check for understanding. Other ways to check for understanding are listed in Figure 7.2.
These kinds of activities—when done routinely—offer teachers and students a lot of insight into student understanding. But these remain moment-in-time snapshots if not further contextualized through the administration and analysis of pre- and postassessments and regularly paced progress monitoring. In other words, it’s what we do with it that counts. If assessment is used for nothing more than sorting students, we will continue to achieve the results we have always gotten.
John (Hattie, 2012) speaks of several internal questions that drive learners:
- Where am I going? What are my goals?
- How am I going there? What progress is being made toward the goal?
- Where to next? What activities need to be undertaken next to make better progress? (p. 116)
These are the same three questions teachers must ask about instruction as they make adjustments based on the data they gather from students. When Mr. Carlson realized that students were struggling to explain their reasoning about multiplying 6 times 
Feedback for the Student: Adjusting Learning
Through frequent assessment, teachers discover when students need additional support to continue their learning. The feedback that we as teachers then provide in return can inform them about errors and misconceptions that need to be addressed. We should know our students well and teach to their strengths while closely monitoring learning gaps. Feedback has a powerful impact on student learning, with an effect size of 0.75, placing it in the top ten influences on achievement. When students are engaged in appropriately challenging tasks, they are more likely to respond to feedback because they need feedback to continue growing and learning. Feedback then is designed to close the gap between students’ current level of understanding or performance and the expected level of performance, which we call the success criteria. For feedback to work, teachers have to understand
- students’ current level of performance,
- students’ expected level of performance, and
- actions they can take to close the gap.
It is important to note that grades may not serve as feedback. Studies such as Elawar and Corno (1985) along with Butler (1988) tell us that “the effect of giving both scores and comments [is] the same as the effect of giving scores alone” (Wiliam, 2011, p. 109). Giving scores alone, or scores and comments, does not necessarily lead to the visible learning effect provided by feedback. “To be effective, feedback needs to direct attention to what’s next” (Wiliam, 2011, p. 128). As Brookhart (2008) describes it, feedback needs to be “just-in-time, just-for-me information delivered when and where it can do the most good” (p. 1), and receiving it strengthens students’ metacognitive and self-regulatory skills. When feedback is delivered such that it is timely, specific, understandable, and actionable, students assimilate the language used by the teacher into their own self-talk. In other words, what we say to students, as well as how we say it, contributes to their identity and sense of agency, as well as to their success. Figure 7.3 includes information about the ways in which feedback can vary in terms of timing, amount, mode, and audience.
The feedback we give students at any point in their learning falls into four levels, not all of which are considered optimal (Hattie, 2012):
Feedback about the task:
How well has the task been performed; is it correct or incorrect? For example, when reviewing student work on word problems, the teacher noticed that students often gave solutions as numbers without contexts. They would respond “3” rather than “3 cups of flour are needed to bake the cake.” Feedback might include a note about remembering to include units of measure because “naked numbers” don’t always make sense.
Feedback about the process:
What are the strategies needed to perform the task; are there alternative strategies that can be used? For instance, there are often multiple approaches to solving rich mathematical tasks. Students provide feedback to one another about the strategies they use when they share their approaches to solving the problem.
Self-regulatory feedback:
What is the conditional knowledge and understanding needed to know what you’re doing? This can include self-monitoring, directing the processes and tasks, and strategic thinking. For example, the teacher might provide a broad timeline for completing a large project. One element of feedback to students becomes questions or comments asking them to relate their progress on their specific project to the general timeline. Based on this, students will be reassured that they are making good progress or reminded of necessary steps they have missed.
Feedback about self:
Evaluation and affect about the person. For example, “Excellent job! You are so smart!”
Video 7.2 Feedback That Fosters Learning

http://resources.corwin.com/VL-mathematics
The first two levels, task and process, are more commonly used in classrooms, and we witness teachers using these on a frequent basis. This form of feedback can be most effective when students are working at the task or process level, but if you want to move them toward self-regulation, then more feedback at this level is critical. Effective teachers look for opportunities to give feedback to students by playing back what occurred. Saying to a student, “I can see you had trouble with this part of the task, but then you solved it. What did you do that led to this success?” alerts him to think reflectively about the strategic thinking and action he took to get himself over a hurdle. It also acknowledges to the student that you are listening to what he is doing—and such respect is typically welcomed, builds trust, and leads to students realizing that the feedback is just for them. In doing so, we give students the internal scripts they need to become increasingly self-directed learners.
The third level of feedback—self-regulatory feedback—is one that plays such a prominent role during deep consolidation and transfer of learning. All of these methods offer critical opportunities for teachers to dialogue with students as they delve into increasingly self-directed learning. Consider the power of the self-regulatory feedback that eighth-grade teacher Mr. Bintz from Chapter 5 gave to a student who was having difficulty with the complex problem comparing cell phone plans.
Mr. Bintz: It looks like you’re stuck about how to get started on solving this problem. What strategies have you tried to get moving?
Clemensia: I’ve underlined the important information in the problem and started a list of other things I need to know. I’m just not sure what they’re asking me to do with it.
Mr. Bintz: What do you think an answer to this question would look like? What form would it take?
Clemensia: I think it’s looking for a recommendation about the best cell phone plan. I don’t know what the right evidence is to support my idea.
Mr. Bintz: Let’s think about that. What are some important things to consider when selecting a plan?
Clemensia: I’m not sure.
Mr. Bintz: Then that’s a good thing for you to think about next. Take a look at the information you’ve marked as important, think about how you use your phone, and consider talking with a classmate to help clarify your thinking. I admire how you’re being persistent in working to figure out what this problem is asking and what evidence you’ll need. Let’s talk again tomorrow. You can share what you’ve figured out and the next steps you’ve decided on to help you solve the problem.
Notice that throughout the conversation, the teacher keeps his tone warm and encouraging, yet the focus is on feedback about the task and the process, emphasizing the student’s ability to take action and change the outcomes. To be sure, the discussion took a few minutes to conduct. But the time is well worth it and is critical as students move from deepening their learning to moving into transfer.
Video 7.3 Feedback That Fosters Perseverance

http://resources.corwin.com/VL-mathematics
The fourth level—feedback about self—is employed too often by well-meaning teachers. Although meant to bolster self-esteem, it appears to have a zero to negative impact on learning, especially in discouraging students from engaging in any further revision of their work (Hyland & Hyland, 2001). We want students to think positively about themselves, and praise is a tool that can contribute to positive teacher-student relationships. The message should not be interpreted as “do not give praise”; instead, the message is to separate the praise about a person’s traits from the effort put into a task and into learning.
It’s important that adults don’t withhold their unconditional positive regard for students, but praise that masquerades as feedback can undermine efforts to motivate and encourage. Dweck (2006) has written extensively on the damage that praise about the individual can do in reinforcing a fixed mindset, rather than a growth mindset. Students with a fixed mindset have been conditioned to believe that innate qualities such as intelligence and talent are the keys to success, and they discount the role of effort or their own agency. Although we don’t mean to, too often we communicate our own beliefs in a fixed mindset when we tell students, “You’re so good at math!” instead of saying, “Your problem solving has really improved this quarter. Look at the difference in your scores since the last quarter.” Highlighting progress further builds learners’ sense of agency as they see the relationship between their success and their actions.
Furthermore, feedback focused on something that you already know does little to change understanding. Feedback thrives on errors, which we believe should be expected and celebrated because they are opportunities for learning. If students are not making errors, they have likely previously mastered the learning intention and are not stretching themselves. That said, if they make too many, they may need more help or to start in a different place. Unfortunately, in too many classrooms, students who already know the content are privileged and students who make errors feel shame. In those situations, learning isn’t occurring for students who already know the content; they’ve already learned it. But learning also isn’t occurring for the students who make errors because they hide their errors and avoid feedback. Classrooms have to be safe places for errors to be recognized.
It’s only when the feedback is received and absorbed that it works. The messages that students receive externally become the messages they give themselves. We must make sure that we not only commend learners when and specifically on what they are doing well, but also help them to identify the actions they need to take in order to get back on the path. Asking a learner, “What can you do next to find that answer?” sends an underlying message that she has agency and can take steps. In contrast, telling a learner, “The answer is on page 37,” without giving her an opportunity to resolve what’s blocking her, tells her that you don’t believe she is capable of doing so. Asking students, “What did you understand by the feedback I just gave you?” can reinforce that their interpretation of the feedback is much more critical than just having the teacher give the feedback. Indeed, feedback not listened to is not worth much, which is why so many grades alone have little value—they are not interpreted by the student other than “the work is over!”
Summative Evaluation
Summative evaluation is when we use broader assessments with the purpose of determining what students know and are able to do at a given point in time. In the case of mathematics, they indicate what students know about mathematics content and problem solving. Some types of summative assessment include the following:
- State assessments or standardized tests are used to provide data about student performance in relation to other students. They are usually administered under the same conditions and scored in the same manner for all students. Although they may include a few open-ended tasks, most questions usually have one correct answer and are often in multiple-choice format. These tests allow comparisons to be made among all students taking the test. The scores can also help schools and districts see patterns and make changes to improve student achievement over time. Data returned to teachers and parents are often quite general, reporting student achievement by general topics.
- District benchmark or interim assessments are commercially available or can be written by a group of teachers within a district. They are given at certain points over the course of the academic year. Because these tests are administered under district guidelines, they can vary greatly in how and when they are administered and the format they take. Benchmark assessments are usually used to (1) evaluate where students are in their learning progress and (2) determine whether they are on track to performing well on future assessments, such as standardized or state tests.
- Higher level mathematics courses such as algebra, geometry, statistics, or calculus often include end-of-course summative assessments that are cumulative. A certain percentage of a student’s grade is made up of this test result.
- Unit or chapter tests can come from the mathematics program being used or written by a classroom teacher or group of teachers teaching the grade or course. These tests can take the form of computational examples, application problems, open response, or performance tasks.
Video 7.4 Growth Mindset: The Students’ Perspective

http://resources.corwin.com/VL-mathematics
Assessments such as unit quizzes and tests can be used for evaluation purposes in that they may provide information to support student learning and guiding instruction. We believe that a fundamental part of understanding mathematics is to realize how concepts grow and expand over time. For example, over the past twenty years, the mathematics education community has recognized the importance of developing early algebraic thinking in the elementary grades to build a good foundation as students enter formal algebra courses. Students need to understand the meaning of multiplication in order to really understand division and the idea of inverse operations. There are many examples of these connections based on important concepts that begin as early as kindergarten.
Now consider a second-grade student who is struggling to understand place value and regrouping in subtraction. His teacher gives him extra help in the form of more concrete experiences, and although he is starting to catch on, most of his classmates are progressing and this young boy fails the chapter test. Let’s stop for a minute and consider the impact on this child’s mathematical mindset. He begins to believe he cannot do mathematics, and his parents’ disappointment exacerbates that belief. Is there a way to use the results of the summative assessment, in this case the chapter test, to determine next steps for instruction and for the student?
How can the process of summative evaluation help a teacher determine next steps for instruction? When a student does poorly (even a student who “passes” with a low grade) on a chapter test, we have several choices. We can move him on to the next topic and hope he catches up. The problem with this approach is that the lack of foundational understanding in mathematics compounds. Too often, by the time a student is in middle school, the chances of getting caught up are slim and he likely hates mathematics. Another possibility is to analyze error patterns and misconceptions that a student has and look for extra time to fill in gaps and continue to address misconceptions. This is a good time to share specifics with parents or support personnel within the school so that any opportunity for extra help can focus on exactly what that student needs rather than waste time on nonessential instruction. The third option is to recommend a student for intervention (RTI) support, where a mathematics specialist can address the gaps in depth and the student is given additional time to get this support.
How can the process of summative evaluation help a teacher determine next steps for a student? While diagnosis and remediation are certainly not the main purposes of summative assessment, we should take advantage of any opportunity to provide feedback to students, both their strengths as well as areas that need additional work. Formative evaluation opportunities provide consistent feedback, yet at times, a chapter test can provide a clearer picture for all students (not just struggling students) of areas that may still need some attention.
There are several different ways you can address feedback for students using information that you gather from summative assessments. In general, if the class did well, you might take some time to discuss test items that several students missed. You may want to set up a time to meet individually with students to go over the test. One practice Linda used was to have all students correct any errors on their tests in a pen or pencil of a different color. We all have experienced giving a test that just about everyone in the class botched. That was a sign to us and to our students that we needed to spend more time on those concepts before we moved on. It helped us to know where students still had misconceptions or needed more practice, and it helped the students know where to focus their efforts.
Did you ever take a mathematics test and have to wait a week for it to be graded and returned? That is not fair to students and doesn’t support providing immediate feedback on what students know and don’t know. The point here is that even though a test is a form of summative assessment, students still deserve and should receive timely feedback on what they know or need to learn to be prepared for the next unit of study.
Meeting Individual Needs Through Differentiation
As we all discover in our first years in the classroom, a lesson that works wonderfully for some students is not a good choice for others. Just as “one-size-fits-all” T-shirts don’t fit many people very well, one-size-fits-all instruction tends not to respond to the needs of all learners well. Our challenge as teachers is to differentiate instruction, to provide a thoughtful range of options that make teaching and learning more responsive to individual needs. Differentiation is about finding a balancing point between the need to respond to individual differences among students and the need to keep lessons manageable by not trying to individualize instruction for every learner in the classroom.
Tomlinson (1995) defines differentiated instruction as “the consistent use of a variety of instructional approaches to modify content, process, and/or products in response to the learning readiness and interest of academically diverse students” (p. 80). In this section, we will discuss structures and strategies for differentiation in the regular classroom.
Classroom Structures for Differentiation
A classroom that is structured for differentiation has two key attributes: a wide range of learning resources available to students and a flexible classroom environment. The wide range of learning resources available in a mathematics classroom includes a range of manipulative tools; a range of problem-solving strategies; and, particularly for secondary students, a range of reference/resource materials available to help students solve problems. By having many strategies and tools available, both teachers and students can draw on different tools at different times. In the primary grades, this may mean some students are still working with counters and tally marks for addition and subtraction while others are working with base ten blocks and sketches. By middle school, students should be comfortable with a wide range of problem-solving strategies. These can range from the simple (act it out or make an organized list) to the more complex (generalize or change your point of view). Teachers should deliberately cultivate a classroom environment where a wide range of strategies and tools is available and valued.
As we discussed in Chapter 5, students can be grouped for learning in a variety of ways. Differentiation works most smoothly when the classroom norm is that groups change often and they change based on the learning task at hand; students are used to working collaboratively and they are used to working with different students in their groups. As the teacher develops a menu of instructional options, the flexibility of grouping students in a variety of ways makes implementing the menu a more straightforward task.
Adjusting Instruction to Differentiate
Teachers can differentiate instruction by making adjustments in one or more of three areas: content, process, and product. For teachers just starting to differentiate, we recommend selecting one area for adjustment at a time. Remember, our goal is to be sure each learner is making progress mastering the grade-level standards at an appropriate degree of challenge, working in what Vygotsky (1978) calls the “zone of proximal development.” When students are working on tasks they already know how to do, they may build fluency, but they are likely not learning much that is new. The zone of proximal development is that area where students are challenged, but with adult or peer support can be successful. This area of stretching is where learning happens. Differentiation of instruction is about making sure all students are working within their own zone of proximal development.
When teachers adjust content, they are modifying the mathematics students are working on. Adjusting content does not mean that students are moving more quickly through the standards or are working on standards for a grade level ahead of where they are. Rather, adjusting content means working within grade-level standards to provide different levels of difficulty and complexity that match where students are in the learning process. This may mean using larger or “less friendly” numbers in the word problems students are solving or adjusting the complexity of the problem. Compare these two examples from a third-grade class:
Pablo is getting new carpet for his bedroom, and he needs to know the area of the room. Pablo’s room is 10ʹ wide and 8ʹ long. How many square feet of carpet will Pablo need in his room?
Pablo is getting new carpet for his bedroom and he needs to know the area of the room. Pablo’s room is 9ʹ wide and 8ʹ long. There is also an alcove by the window that is a 5ʹ square. How many square feet of carpet will Pablo need in his room?
Both problems involve multiplication of whole numbers in the context of area, and the numbers are similar in magnitude, within the parameters for third-grade students. For learners who are ready to work in more complex situations, the second problem, with two parts to the room, is more challenging.
When teachers adjust process, they are making adjustments to the strategies students use to access information. Process differentiation in mathematics might mean emphasizing different representations for different groups of students. It is spring in Ms. Corral’s kindergarten class, and the children are working to find a solution to this problem: Juan had four tennis balls and DaShaun had five more. How many tennis balls do the boys have together? For a young child who is still focusing on counting all as a strategy for addition, the teacher provides counters and encourages the child to draw a picture to help the student move to a more visual representation. For another group of students, the teacher might guide the students to use the counting on strategy with a number line to find a solution. Rich mathematical tasks with multiple entry points, such as those discussed in Chapter 3, have great power, in part because they make process differentiation easier. The entire class is working on the same task but using different tools and strategies to find solutions.
Teachers adjust product when they ask students to complete different tasks to show what they have learned. One student might build models of various geometric shapes while another shares pieces of art that include the shapes as components. For students still mastering the attributes of shapes, the challenge of creating models on their own that have the correct attributes is sufficient to move them forward with learning. For a student who already knows the basics about the shapes, recognizing them in the context of art or architecture provides a more difficult task at a more appropriate level of challenge.
Differentiation is often presented as a strategy for meeting the needs of academically and intellectually gifted students, or in the context of this book, those who are top performers in mathematics. These same differentiation strategies can be used to reach back and reinforce a fundamental idea from a previous grade for students who are struggling, while allowing those students who are working at grade level to continue their own progress. The key idea is that the teacher has a practical structure for adapting instruction to meet the needs of the wide range of learners in the classroom.
Intervention
When you hear the term intervention, it is likely you think of models of support for struggling students, and the RTI (Response to Intervention) model is probably the best known model. RTI focuses on providing high-quality instruction and interventions matched to student need, monitoring progress frequently to make decisions about changes in instruction or goals, and applying child response data to important educational decisions. However, we often forget students at the other end of the spectrum, those who have a unique ability or talent in mathematics and intrinsic motivation to explore ideas in mathematics beyond the usual school curriculum. In the next section, we will discuss research-based RTI strategies for mathematics that support visible teaching and learning as well as strategies for meeting the needs of students who show a special aptitude for doing mathematics.
As we have noted before, there is no one right way to teach, and there are a lot of things that teachers do that are effective. Teaching is about making adjustments and trying to determine what will work for a particular group of students. Designing learning opportunities, monitoring for impact, and then making adjustments are the hallmarks of effective teachers. But there are more formal ways to monitor impact.
Response to Intervention (RTI)
The evidence for Response to Intervention is significant; it’s one of the top influences studied thus far, with an effect size of 1.07. In other words, it works (e.g., VanDerHeyden, McLaughlin, Algina, & Snyder, 2012). There are several components of an effective RTI effort that combine to produce the impact seen in the studies. These include universal screening, quality core instruction, progress monitoring, and supplemental and intensive interventions (Lembke, Hampton, & Beyers, 2012). We know that the earlier students who need support are identified and attended to, the greater the success rate for those students. Entire books have been written on RTI (Gersten & Newman-Gonchar, 2011), so this section will highlight only the key components necessary for teachers to understand.
RTI focuses efforts on providing evidence-based interventions for students who do not respond to quality core instruction (also known as Tier 1). This quality core instruction includes differentiated experiences discussed earlier. In the language of RTI, students can receive Tier 2 or Tier 3 interventions, or a combination of both. This multitiered system of support can result in improved student learning. It requires that teachers notice when students do not respond (when the impact is insufficient) and then change the instruction or intervention to reach the desired outcome. The two levels of response are as follows:
- Tier 2: Also known as supplemental interventions
- Tier 3: Also known as intensive interventions
The following questions posed by Gresham and Little (2012) offer guidance on what to consider when implementing RTI at the district, school, or classroom level.
- What are the critical mathematical concepts and skills to be learned by all students?
- How do the current resources in my classroom address the selected lesson’s mathematical concepts and skills of the standard I am to teach?
- What prior mathematical knowledge do students need or have to master to reach the content standard?
- What may be sources of difficulty and confusion for the students?
- How can this lesson build on students’ prior mathematical knowledge and experiences?
- What will students think and do in response to the instructional lesson?
- What scaffolding and support can I provide to meet the needs of all learners through differentiating instruction and accommodating individuals?
- Which questions, resources, strategies, activities, examples, and so on will clarify and/or extend conceptual learning by students?
- Which grouping arrangements, accommodations, adaptations, use of levels of learning, cognitive/metacognitive strategies, and/or technology are needed for whole/small groups of students?
- How can I make the mathematical learning task less complex without changing the goal?
- What kinds of data are available and will help us assess students’ mathematics progress toward the set mathematical goals?
- How will I check for mathematical conceptual understanding and depth of mathematical knowledge?
In the IES Practice Guide, Assisting Students Struggling With Mathematics: Response to Intervention (RtI) for Elementary and Middle Schools (Gersten et al., 2009), a committee of mathematics researchers and practitioners with expertise on this topic proposed eight recommendations based on the best available research evidence. A brief summary of each recommendation follows.
Recommendation 1: Screen all students to identify those at risk for potential mathematics difficulties and provide interventions to students identified as at risk.
For RTI efforts to be most effective, school staff members have to screen students at the outset of the year. These screening tools are typically quick checks to identify students who may need additional intervention.
- Screening time may range from five minutes to twenty minutes.
- Number sense is critical at the elementary level. Assess various aspects of knowledge of whole numbers—properties, basic arithmetic operations, understanding of magnitude, and application of mathematical knowledge to word problems.
- Upper elementary and middle grades screening measures (usually ten minutes) should cover a proportional sampling of grade-level objectives.
Screening tools can focus on basic (e.g., sums to 12, subtraction 0–20, fact families) or advanced (e.g., multiplying multidigit numbers with regrouping, converting numbers to percentages, solving equations) computation skills. Both have empirical evidence for their ability to screen for students who may need supplemental or intensive intervention (VanDerHeyden & Witt, 2005). A more comprehensive list of screening tools can be found at http://www.rti4success.org/resources/tools-charts/screening-tools-chart.
Recommendation 2: Instructional materials for students receiving interventions should focus intensely on in-depth treatment of whole numbers in kindergarten through Grade 5 and on rational numbers in Grades 4 through 8.
With the adoption of recent standards, conceptual understanding of whole number operations should be a focus in Grades K through 5. While other topics are important parts of the curriculum, we know that if students progress through the grades without appropriate surface and deep learning, they run the risk of failing upper-level courses. The same is true for the topics of rational numbers (fractions and decimals) in Grades 4 through 8. Again, focusing on conceptual understanding through the use of concrete and pictorial representations and explicitly making connections to procedural skills and applications is critical here. Just focusing on drill and kill will not provide the support these students need.
Recommendation 3: Instruction during the intervention should be explicit and systematic. This includes providing models of proficient problem solving, verbalizing thought processes, guided practice, corrective feedback, and frequent cumulative review.
The final report of the National Mathematics Advisory Panel (2008) describes characteristics of explicit instruction:
- Clear models provided by teachers for solving a problem using an array of examples
- Extensive student practice of newly learned strategies and skills
- Think-aloud opportunities for students to verbalize decisions and steps
- Extensive feedback for students
Notice how these strategies are those we have been discussing throughout this book. Let’s look in on an intense intervention session. Mrs. Jensen is working with a group of fifth graders who are working with addition of fractions. While the standards call for adding and subtracting fractions with unlike denominators in Grade 5, Mrs. Jensen knows from screening data that these students are still struggling with equivalent fractions and addition of fractions with like denominators. Since these two concepts are essential for working with unlike denominators, she decides to begin her session focusing on building sets of equivalent fractions. She gathers a set of fraction bars for each student. (Fraction bars are physical models of shaded bars to represent various fractions. Additionally, the bars are color coded according to the denominator. Halves are green, thirds are yellow, fourths are blue, etc.) Mrs. Jensen also decides that she will limit the student work to related fractions, so she pulls the halves, fourths, eighths, and twelfths from the deck for the first activity, which is a memory game. As the students enter, she has the fraction bars set out in a rectangular array face down on the table. She explains and models the rules of the game to the students. They take turns turning over two bars. If the shaded amounts are the same, they keep the bars, and if not, they turn them back over and the next student takes a turn.
When the game is over, students place their pairs of matching bars face up. Mrs. Jensen reviews how to write fractions for each bar—the number of shaded parts is the numerator, and the total number of parts is the denominator. She works together with the students to practice writing several fractions. The last part of the lesson is for the students to record the fractional numbers for each matching pair they found. As students are recording their pairs, Mrs. Jensen is writing some of their equations on the board. She also invites students to add other pairs they may have found.
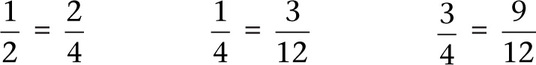
Mrs. Jensen works with the students to review the vocabulary (numerator, denominator, equivalent fractions, equation) for this concept. She also has these words on her word wall. This gives the students the language they need to have a discussion about what they notice.
Mrs. Jensen guides the discussion with questions that will focus students on looking for patterns. Her learning intention for this lesson is for students to see the relationships among equivalent fractions. By the time students leave, they have demonstrated a conceptual understanding that equivalent fractions are built on multiplying the numerator and the denominator by the same factor. Even more deeply, they are beginning to see that in doing so, they have actually multiplied the fraction by a name for one. She has taken forty-five minutes to develop this concept, and when students return in a few days, she will increase the set of fractions to include thirds, fifths, sixths, and tenths. Students will continue to work on recognizing equivalent fractions using concrete and pictorial representations and making explicit connections to symbolic representations.
Notice that Mrs. Jensen has a very clear understanding of the progression of topics that is necessary before students can even begin to reach the final goal of adding fractions with unlike denominators. She carefully plans the sequence of her lessons, making certain that she is spending enough time to ensure that students have a conceptual understanding of the topic before moving to procedural rules and skills. While this takes more time than what might be spent in the regular class’s mathematics instruction, students are getting the support they need through lessons that are more explicit and systematic.
Recommendation 4: Interventions should include instruction on solving word problems that is based on common underlying structures.
Word problems provide a context for understanding what happens when I am operating on numbers. How do I know what operation to perform in a given situation? Did you know there are fifteen different situations that call for addition or subtraction (National Governors Association Center for Best Practices & Council of Chief State School Officers, 2010)? Too often, teachers give students a variety of addition or subtraction word problems with a mix of these contexts before students have had the chance to explore, model, and understand each one. Research shows that the use of key words, a strategy often used by teachers, is ineffective (van de Walle, Karp, & Bay-Williams, 2013). Another strategy may be to have students come up with their own strategies for solving problems. A group of fourth graders was asked how they determined what operation to use when solving a problem. The overall response was, “When the problem has more than two numbers in it, you add because that is the only operation that you can do with more than two numbers. If it has two numbers and they are close together, you subtract. If they are far apart, you divide, but if you get a remainder, then that is wrong so you multiply the numbers instead.” Many of us have seen similarly strange approaches to solving word problems! Providing students with explicit instruction on problem-solving situations such as those in Figures 7.4 and 7.5 will provide experience through modeling and making connections that help them not only to solve problems but also to see the underlying structure and meaning for each operation.
Recommendation 5: Intervention materials should include opportunities for students to work with visual representations of mathematical ideas, and interventionists should be proficient in the use of visual representations of mathematical ideas.
Students need many opportunities to work with physical and then pictorial representations of mathematical ideas. Early learning of number and place value and operation concepts should incorporate the use of linking cubes or bundling straws. Fraction work should include fraction bars, rectangles, or circles. It is important for students to be able to physically manipulate materials to help them see the structure of what is happening when they do a particular mathematics operation. After ample time to work with concrete materials, explicit connections should be made to pictorial representations. Too often, we give students some time to work with materials and we expect them to make the transfer to pictures with little instruction. Following many opportunities to work with visual representations, explicit connections to the symbolic (numerals) representation should be made. In making that transition to mathematical notation, it is helpful for the teacher to model how to write an expression or equation using numbers while students are working with physical or pictorial representations. When students are ready, they can begin to make the connection to symbolic notation.
Recommendation 6: Interventions at all grade levels should devote about ten minutes in each session to building fluent retrieval of basic arithmetic facts.
Expecting students to become fluent is more than “go home and memorize the plus sixes tonight.” Fluency means that students think about facts flexibly, efficiently, and accurately (Bay-Williams & Kling, 2014). Young children need carefully planned and sequenced instruction to develop strategies that support all of the components of fluency. This is built on using models, finding patterns, and making connections.
Figure 7.4 Addition and Subtraction Situations

Source: National Governors Association Center for Best Practices & Council of Chief State School Officers (2010). Adapted from Box 2-4 of Mathematics Learning in Early Childhood, National Research Council (2009), pp. 32, 33.
1 These take apart situations can be used to show all the decompositions of a given number. The associated equations, which have the total on the left of the equal sign, help children understand that the equal sign does not always mean “makes” or “results in” but always does mean “is the same amount as.”
2 Either addend can be unknown, so there are three variations of these problem situations. Both Addends Unknown is a productive extension of this basic situation, especially for numbers less than or equal to ten.
3 For the Bigger Unknown or Smaller Unknown situations, one version directs the correct operation (the version using more for the bigger unknown and using fewer for the smaller unknown). The other versions are more difficult.
Figure 7.5 Multiplication and Division Situations
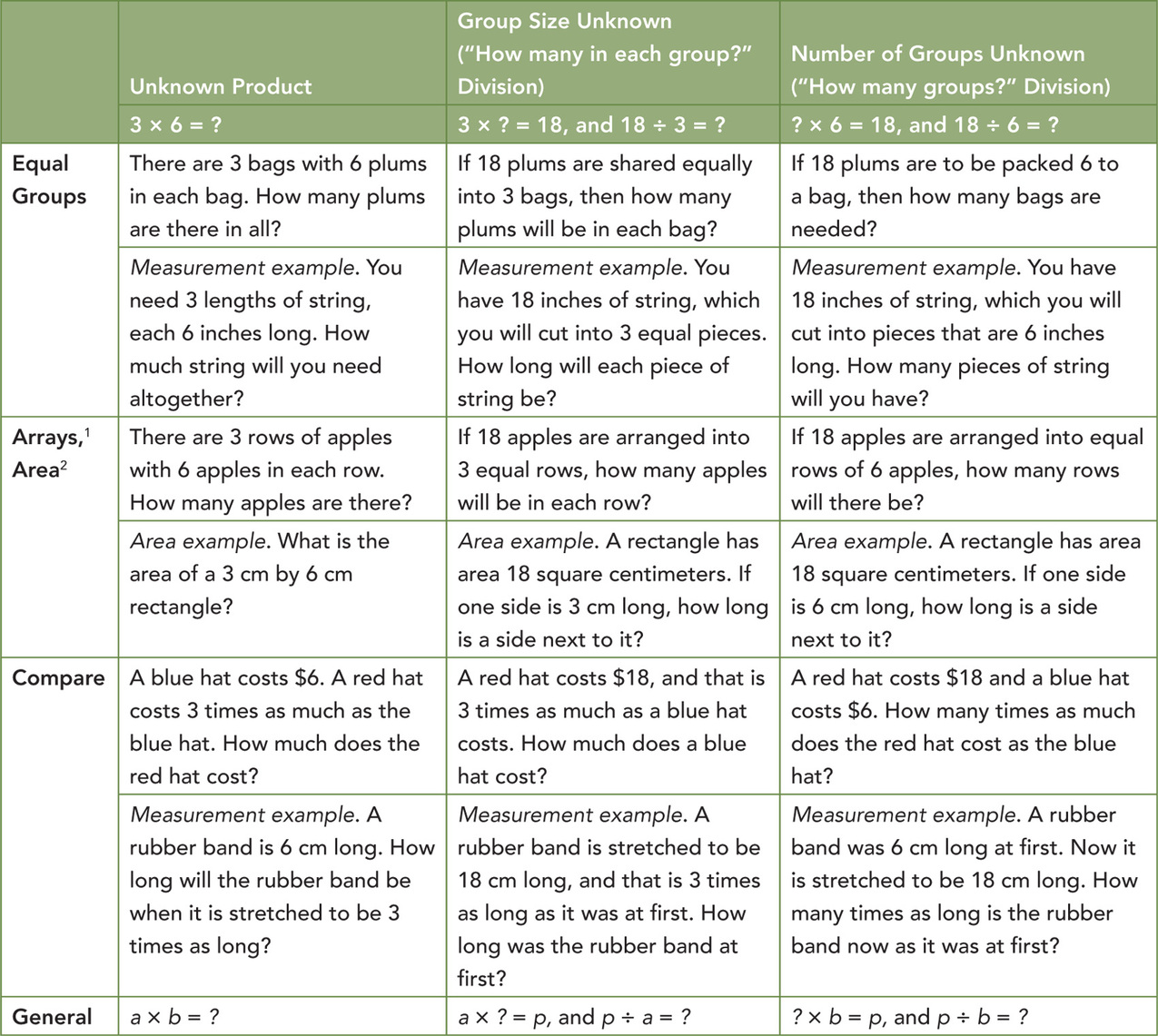
Source: National Governors Association Center for Best Practices & Council of Chief State School Officers (2010).
Note: The first examples in each cell are examples of discrete things. These are easier for students and should be given before the measurement examples.
1 The language in the array examples shows the easiest form of array problems. A harder form is to use the terms rows and columns: The apples in the grocery window are in 3 rows and 6 columns. How many apples are in there? Both forms are valuable.
2 Area involves arrays of squares that have been pushed together so that there are no gaps or overlaps, so array problems include these especially important measurement situations.
Recommendation 7: Monitor the progress of students receiving supplemental instruction and other students who are at risk.
Progress monitoring is a scientifically based practice that is used to assess students’ academic performance and evaluate the effectiveness of instruction. Progress monitoring can be implemented with individual students or an entire class.
Both formative and summative evaluations can be used to monitor progress. What is important is that there is a specific plan for tracking and following the data that show student growth and progress so that further instruction can be based on individual student needs.
- Assessment tools for monitoring progress are available from multiple sources (such as the National Center on Student Progress Monitoring, www.studentprogress.org). It is essential that assessments are capable of identifying growth.
- Curriculum-embedded assessments might be commercially, researcher, or district/school developed. Unit tests, mastery tests, daily probes, and other assessments can be used to base decisions on which concepts need to be reviewed, which need to be retaught, and which have been mastered.
Recommendation 8: Include motivational strategies in Tier 2 and Tier 3 interventions.
Let’s face it, mathematics taught poorly can be boring. On the other hand, when taught well using a variety of teaching techniques (group work, rich tasks, games), it can be one of the most exciting subjects in the school curriculum! Constant drill and kill, use of worksheets, and textbook pages with nothing but computational exercises can be lethal to motivating all students, but especially those who struggle with mathematics. Thinking about how to make a topic interesting and tapping into the curiosity of students can make all the difference in student success but also in encouraging students to develop a growth mindset. Who doesn’t like a good mystery or a game? Think of the mathematical tasks you provide for your students as potentially a good mystery to solve or a game that is fun to play but also provides opportunity to learn or practice a particular concept or skill.
There are many good resources available on the Internet, but beware—for every good website with great activities, rich problems, or games, there are likely ten times as many websites with poor examples or resources that do little to inspire, support, or motivate students.
In summary, RTI efforts are based on the expectation that students receive quality core instruction as part of their ongoing participation in school. Also known as good first teaching, quality core instruction comprises Tier 1 of the RTI efforts. It’s unreasonable to expect that all students receive supplemental and intensive interventions—there isn’t time or money for that. If the vast majority of students are not being impacted by the regular classroom environment, we would suggest that the tenets in this book are not in place. In school systems that implement high-quality instruction, based on the influences on achievement outlined in this book, and then monitor the impact of those actions, fewer and fewer students need the extensive support offered through RTI (Gersten et al., 2009). To our thinking, quality core instruction includes at least the following:
- Teacher clarity on, and communication about, the learning intentions and success criteria
- Student ownership of the expectations for learning
- Positive, humane, growth-producing teacher-student relationships
- Modeling and direct instruction of content
- Collaborative learning opportunities on a daily basis
- Small group learning based on instructional needs rather than perceived ability
- Spaced (rather than mass) independent practice and application of content
These are easy to write, and obvious to many, but not yet common in classrooms around the world. When these actions become the norm in classrooms, the need for additional interventions declines and students learn more and better mathematics.
Intervention for Advanced Students
While much of the research on intervention has a focus on struggling students, highly advanced students will benefit from intervention as well. These are students who need more than a differentiated classroom provides. They are students who can consistently find the correct answer but may struggle to explain why their answer is correct because “they just know it.” These are students who begin the school year having already mastered many of the grade-level standards. Overall, they likely represent the top 3 to 5 percent of students at a given grade level.
Assessment is critical for these students because spending time with content they already know leads to boredom and misbehavior. These students can benefit from serving as peer tutors if they have the social/emotional development to do this successfully, as described in Chapter 6. It is also important, however, that these students continue to learn new mathematics and explore the mathematics they know in a variety of contexts and in increasingly rigorous settings. Researchers such as Sheffield (1999) and Lubinski and Benbow (2006) have a long history of work with these students and strategies that work effectively for them. These students can benefit from curriculum compacting (National Association for Gifted Children, n.d.), a strategy in which teachers replace content students have already mastered with new content, enrichment options, or other activities.
New content might mean that students explore mathematics beyond their grade-level standards. For example, the ideas and problems in Mathematics, A Human Endeavor (Jacobs, 1994) are an excellent beginning for extending student thinking (deeper understanding and transfer learning) in the upper elementary grades. In these tasks, students are looking at the uses of mathematics in everyday life and see how mathematics relates to reasoning. The tasks are rich and complex while remaining accessible without a great deal of formal mathematical instruction. Enrichment options could include more highly differentiated tasks such as projects with a larger scope. In order to work on these specialized assignments, students should be grouped with others who have similar learning needs.
From time to time, student success with this new content or more highly differentiated tasks may indicate that students are ready to move on to the next grade level’s mathematics content. It is essential that this decision is made based on good evidence of visible learning—surface, deep, and transfer—of all grade-level standards. Too often, the decision to accelerate students, particularly to have students placed in Algebra 1 early, is made as a status marker for parents rather than a decision that is driven by evidence of student mastery and learning needs. As we have said throughout this book, visible evidence of learning should guide instruction and help keep every student challenged.
Learning From What Doesn’t Work
Thus far, we have focused our attention on influences that can positively impact students’ learning. We explored surface, deep, and transfer levels of learning and noted that there are some instructional protocols that work better at each level. We also shared ways in which teachers could determine their impact on student learning and then respond when the impact was not as expected. Now, it’s time to focus on some things that we know from John’s research really don’t work to build students’ mathematical thinking. We don’t want teachers to undo all of their hard work by engaging in practices that waste valuable learning time or may even be harmful to student understanding. Unfortunately, these are too often common in use. Even worse, many of these practices are the result of not focusing on the potential impact of effective teaching strategies, and instead spending time cataloging a student’s shortcomings.
Grade-Level Retention
Students are often retained in a grade level based on their achievement. The meta-analyses of this indicate that the practice is actually having the reverse effect, with an effect size of –0.13. As Frey (2005) and others have noted, grade-level retention is not a defensible practice. But schools and districts still hold on to the hope that another year of schooling will ensure that students learn to read and write at higher levels. Why would another year of the same curriculum, often the same type of teaching, and the same assessment tasks make a difference? What most students who struggle need is not more of the same, but demonstrably different and better instruction. Instead, they would be wise to consider Response to Intervention. In most RTI efforts, students receive supplemental and intensive interventions throughout the year, delivered by knowledgeable adults who can monitor and adjust as needed to reach a desired level of achievement.
Ability Grouping
We have lost count of the number of times we have talked with well-meaning educators who hope that the solution to their students’ achievement lies in grouping students by their perceived ability. Taking a grade level of students and giving one teacher the lowest performing students, another teacher average performing students, and yet another the highest performing students may be popular, but the evidence is clear that it is not the answer. The two most common forms of ability grouping are
- Within-class grouping—putting students into collaborative groups based on the results of an assessment
- Between-class grouping—separating students into different classes, courses, or course sequences (curricular tracks) based on their previous academic achievement
The risk in writing this is that some readers will overgeneralize. Within-class and between-class ability grouping should be avoided. These sorts of rigid, long-term grouping are sometimes known as tracking and typically assume student learning needs and potential remain constant over time. This practice is not supported by research. But needs-based instruction, with flexible groups, should not be eliminated. Student-centered teaching, basing instructional actions on students’ understanding, and then engaging students in small group learning can be very effective provided the grouping is flexible rather than fixed. The key to this approach is the condition that the groups change and the instruction must match the needs of the learner, including those needs based on ability. Let’s look at the difference, occurring at the same school. In one sixth-grade classroom, the teacher administered a preassessment to determine student knowledge of measuring volume. She grouped her students based on their scores. The students with the lowest scores were in one group, slightly better performers formed a second group, and so on. She then met with groups over several weeks, providing instruction to each group. Sounds familiar and logical, right? It just didn’t work. The postassessments were not much different from the original samples. The lowest performing students were still the lowest, but their scores inched up a barely perceptible amount. That was a lot of work for very little benefit.
Down the hall, another sixth-grade teacher administered the same assessment. She then analyzed the patterns of errors and misconceptions found in her students’ work and continually regrouped students based on the original assessment but also on daily exit tickets to determine who was still having difficulty. On one day, she met with a group of students who needed more support generalizing the formula for finding the volume of a rectangular solid, and later with another group of students who needed the right questions to connect their understanding of volume of rectangular solids to the volume of cylinders. While she was working with small groups, she used many of the differentiation protocols mentioned earlier to reinforce and extend concepts for those students who were ready to move on.
In the same amount of time as was available to her colleague, she was able to address many of the instructional needs of her students using small groups. And the results speak for themselves. The average score increased a full performance level, and there wasn’t a single student remaining who did not understand the concept and procedure of finding the volume of cylinders and applying this to a variety of applications. These may seem like subtle differences, but they are important. Small group instruction is effective, but not when the intervention for the students is solely the ability of the group. The groups have to be flexible so that the instruction each group receives aligns with its current performance and understanding.
Simply said, there is no evidence to suggest that rigid ability grouping over long periods of time will yield breakthrough results. The effect size of ability grouping is negligible in terms of impact, yet it remains common in many schools. As typically implemented, the greatest effects of ability grouping are to disrupt the learning community, socially ostracize some learners, and compromise social skills, to name a few (Sapon-Shevin, 1994). And the effects on minority groups is much more serious, with more minority students likely to be in lower ability classes destined to low performance based on low expectations, and often with the least effective teachers (Butler, 2008).
Matching Learning Styles With Instruction
Another practice that has become widespread, but for which there is no supporting evidence, is rigidly matching learning styles with instruction. It may very well be that there are differences in how we prefer to access and share information, and that preference may change in different situations with different groups of people, but teaching students in a way that is limited to our perception of their particular type of intelligence is of very little value. Let’s take for example a student named Musab. He loves music. He has earbuds in any time they’re allowed. He quotes rap songs in response to questions and essay prompts. He sings quietly in the halls and performs in every talent show the school offers. He can listen to a tune and immediately replicate it on a piano. Some might say that he is gifted in the area of music. Others might say that his preferred learning style is musical. Does that mean he is excused from developing interpersonal skills? Should we excuse his errors in computation? Should his teachers be encouraged to sing their lessons and rap their instructions? And if he’s in class with students who have other preferences, should we separate him? NO. Matching instruction with a perception of a learning style is not going to radically raise achievement in mathematics. Why condemn Musab to one form of learning (via music), when indeed he needs to be taught other ways to learn? Let’s acknowledge that there are differences in learners, but let’s not label students. Instead, let’s focus on instructional routines and habits that will ensure all students learn at high levels. Teachers may need to use a variety of methods to capitalize on multiple ways of learning, but the mistake is to categorize students into one or more learning styles and consider that enough.
Test Prep
Test prep, including teaching test-taking skills, is another area for which there is insufficient evidence to warrant continued use. We’ve all done it because there is an appeal to one’s surface logic to teaching students generic test-taking skills. It just wastes a lot of precious time. The small effect we have noted is mainly related to short-term gains, but there is little long-term gain, the learning does not transfer, and more often than not, the material learned via test prep is forgotten soon after the test! Instead, teach learning and study skills as an integral part of every lesson (not as a separate subject). Focus on teaching students the content and how to learn this content, as this has been shown to be much more effective in increasing student achievement on external measures of success. That’s not to say that students shouldn’t understand the format of a test, but that only takes a short time. They should be taught about how to best prioritize time doing any task, as this can be a critical test-prep skill—but again, do this within the context of the regular lessons, not as a stand-alone skill. Test prep and teaching test-taking skills are consuming significant numbers of instructional minutes, despite the fact that we know there is no evidence that these measures are going to inherently improve instruction or learning (Hattie, 2015; Hattie & Donoghue, 2016).
Another aspect of test preparation to be considered is stopping all teaching before a high-stakes test. We have all been there, and in many states, teachers’ performance is based on our students’ results on these tests. We know that distributed practice over time has a much higher impact than stopping all new instruction several weeks before the test for the sake of doing a massive review. As one of our colleagues so accurately describes it, “The best test prep is ongoing, high-quality instruction.”
Homework
The final lesson we offer with respect to learning from what doesn’t work focuses on homework. Overall, homework has little impact on students’ learning. In this case, it’s worth it to examine the value of homework at different grade levels. At the elementary level, homework has a limited impact on student learning, with an effect size of 0.10. At the middle school level, the effect size is 0.30, whereas at the high school level, the effect size is 0.55. The major reason for these differences comes from the nature of homework. Homework that provides another chance to practice something already taught and the student has begun to master can be effective (and much high school homework is of this nature), but homework that involves new materials, projects, or work a student may struggle with when alone is least effective (and too much elementary homework is of this nature). Importantly, homework may not be the answer to increasing students’ achievement, and efforts to raise the rigor of schooling by assigning more independent learning that students must complete at home is misguided and potentially harmful. Students can succeed just as much from what they do in school, so we should not ask them to create a school at home where many students need adult expertise. While nearly all parents want to help their students, some do not know how. Many parents can be poor teachers of school work!
This section has been focused on teacher actions that do not work. We could have also focused on the finger pointing common in some schools. Yes, mobility has a negative impact on students’ learning, as does summer vacation. John (Hattie, 2012) noted that about 50 percent of the achievement variation found in schools is attributed to student characteristics and demographics. Unfortunately, in many schools, that 50 percent gets all the play. After the students themselves, teachers have the biggest impact on student achievement, followed by school effects, the principal, parents, and the home. This is really, really important: a significant amount of the variance in student achievement is attributed to teachers. What teachers do matters. How teachers think really matters. Making informed decisions about what actions to take, based on evidence, should be the focus of professional learning sessions and grade-level or department conversations rather than admiring problems and blaming students for the conditions in which they live.
Visible Mathematics Teaching and Visible Mathematics Learning
Students need to witness their own learning. To do so, they need a teacher who is clear in communicating the learning intentions and success criteria. They need lots of formative evaluation paired with feedback to measure their progress as they move toward transfer. In turn, teachers need a clear sense of their own impact on student learning. Only then do teaching and learning become visible to everyone in the room. Figure 7.6 summarizes the relationship between what we do as teachers and how those teaching behaviors create the conditions for transferring learning.
As we’ve said many times, teachers should focus on learning. It’s a mindset that we all need if we are going to ensure that students develop. A major theme throughout this book is about how teachers think (and also how we want students to think). John (Hattie, 2012) suggests ten mind frames that can be used to guide decisions, from curriculum adoptions to lesson planning (Figure 7.7). Taken together, these mind frames summarize a great deal of the “what works” literature.
Conclusion
Measuring one’s impact on student learning means that assessment is a prominent feature of the classroom. The purpose is not to grade students’ work, but to measure progress and compare it with the teaching that has occurred. Daily assessment is a chief way for teachers to make instructional decisions about what will occur next. Ways to check for understanding include asking questions, using exit tickets, and giving students lots of opportunities to self-assess. But these remain moment-in-time snapshots if not further contextualized through the administration and analysis of pre- and postassessments and regularly paced progress monitoring. The assessments discussed in this book are a reminder of the many ways we have of tracking student progress. But it’s what we do with them that counts. If assessment is used for nothing more than sorting students, we will continue to achieve the results we have always gotten. These assessments are measures of our progress, too, but only if we choose to look closely at our impact.
The risk to our students in failing to examine our impact is significant and damaging. The reliance on ineffective practices such as in-grade retention and ability grouping is the result of decisions by well-meaning but misguided adults who have focused their attention on the characteristics of students at the exclusion of the effectiveness of the instruction they have received. We should know our students well and teach to their strengths while closely monitoring learning gaps. But the evidence is clear. Although what the student brings to school in terms of his or her learning background is important, a significant percentage of achievement variance lies within the teacher’s influence (Hattie, 2009). Yet too often, the vigor with which teachers locate explanations that lie with the student have far outstripped their efforts to examine their impact on student learning and adjust accordingly.
“I am a change agent.”
This isn’t a platitude. In the hands of an effective teacher, visible teaching and learning center our practices. It’s an essential mind frame, and one that is vital if one is going to foster transfer of learning. It’s true that some students will engage in transfer learning without any of us paying much attention to it, but that signals a lost opportunity as well. The key word in the first sentence is agent. As teachers, we have the potential for tremendous agency—to make learning happen—if we’d only seize the chance to do so. Being a change agent means bearing witness to student learning, reflecting on it, and recognizing that student progress tells us something about ourselves. How will we ever know what students are truly capable of if we don’t get deeply involved in their learning lives?
This book has been about empowering educators to do exactly that. The profession is filled with dedicated people who have devoted their professional careers to improving the lives of children and youth. Prowess in mathematics matters. And the good news is that teachers matter. We mean this not as coffee-cup sentimentality, but rather as an empowering sentiment. What teachers do matters when they scale learning to move from surface, to deep, to transfer learning, and match approaches to their students’ conceptual levels of knowledge. What teachers do matters when they monitor their impact and use that information to inform instruction and intervention. What teachers do matters when they reject institutional practices that harm learning. And best of all, what teachers do matters when they make mathematics learning visible to their students so students can become their own teachers.
Reflection and Discussion Questions
- In what ways is the formative evaluation process a part of your classroom routine? In particular, think about the situations in which you provide feedback without grades. How can you do this more effectively and/or more often as part of your instructional practice?
- Consider the framework for differentiated instruction discussed in this chapter. Thinking back over the recent units of study you have taught, what forms of differentiation do you use most often? Which forms would your students benefit from your using more often? How can you accomplish this?
- This chapter discussed intervention as a tool for supporting learners where differentiation does not provide enough support or challenge. What does intervention look like in your school or classroom? How can you use what you’ve learned in this chapter (and this book) to strengthen your intervention program for both advanced and struggling learners?
- What mind frames (Figure 7.7) resonate most for you? How does this impact your practice?