Preface
We believe that everyone can and should learn mathematics. We believe that numbers and the mathematics we use to make sense of them are amazing and beautiful. Some of the ways people have experienced mathematics instruction didn’t invite them into that beautiful space. If you love numbers and the way you were taught mathematics, this book is for you. It will help you extend and validate your teaching repertoire. But if you dislike mathematics because of how you were taught, this book is also for you because it will provide you with ideas for improving students’ learning and perhaps improve your own understanding along the way. This book is about teaching ideas in ways that propel students into the beauty, logic, usefulness, and joy of mathematics.
Why Learn Mathematics?
Mathematics knowledge is one of the significant gatekeepers in modern society. Demonstrating understanding of mathematics in high school opens doors to college. Passing college mathematics classes increases the likelihood that a student will actually earn a degree. Most of us know that people who do better in school, and who attend school for a longer portion of their lives, go on to live longer, healthier, happier lives. Unfortunately, those who don’t do well in mathematics often get locked out of these benefits (Stinson, 2004). It may be stating the obvious, but we will say it anyway: People who understand mathematics have a higher quality of life.
According to Forbes magazine, the top ten highest earning college degrees are computer engineering, economics, electrical engineering, computer science, mechanical engineering, finance, mathematics, civil engineering, political science, and marketing. These degrees have one thing in common—mathematics. Another service aimed at helping young people choose a college major, www.payscale.com, found that the top forty-eight highest paying college majors are mathematics related. The lack of adults with high levels of mathematical understanding consistently makes mathematics teaching positions among the most difficult to staff (Ingersoll, 2011).
The recognition of mathematics as a gatekeeper dates at least as far back as Plato’s Republic. Plato (1996) argued that, although mathematics was important for all people who take part in everyday transactions, the study of math would take some from “Hades to the halls of the gods” (p. 215). But Plato, like many of his contemporaries, believed that mathematics education should be reserved for those that were “naturally skilled in calculation.”
Plato’s analysis of mathematics as a determinant of one’s future success is still very much true. We now know that his assertion that mathematics should be reserved for those “naturally skilled in calculation” is absolutely false. This argument has been used for centuries to keep traditionally underrepresented groups, including females and students who live in poverty, out of high-level mathematics classes (Stinson, 2004) and, in turn, out of the top and middle of our economic structure. But neurological and brain studies have contributed to educational research, showing that all but a small group of students with significant cognitive disabilities are capable of success in high-level mathematics courses given the right instruction and resources (Boaler, 2015). Suggesting that groups of students won’t be good at mathematics isn’t only harmful, it’s inaccurate. But, as Boaler notes, to be successful, students must receive high-quality instruction.
A major problem among many math teachers and students is that they believe they have to be talented or smart to successfully undertake mathematics. But if you review the biographies of great mathematicians, the common denominator is that they knew how to struggle. They knew that it was not exceptional talent that enabled success but the ability to persist; to enjoy the struggle; to see the growth of their learning as a function of seeking help and listening to others solve problems; and to try, try again (Lin-Siegler, Ahn, Chen, Fang, & Luna-Lucero, 2016).
Aspects of Mathematics Instruction That Works
There is an ongoing debate about what makes for good mathematics instruction, and how similar or different good mathematics instruction is to instruction in other disciplines such as English language arts, science, or history. The traditional approach to mathematics teaching has been one of explicitly teaching procedures and algorithms first, and then allowing students to build fluency through a lot of repeated practice. This is often thought of as “show-and-tell” or “drill-and-kill” mathematics, and is sometimes (wrongly) labeled as “direct instruction.” Our definition of direct instruction includes much more than showing and telling students how to perform the computational skills they are learning. In Chapter 4, you will see an argument that there is a role for this expanded definition of direct instruction. In that chapter, we’ll discuss when and how direct instruction might show up appropriately in a lesson, and the type of learning for which it is most effective.
Some researchers have argued that most children perform better in mathematics and can apply it more successfully to real-life situations when they first wrestle with a rich problem, make meaning of an idea and build conceptual understanding through a problem-solving process, consolidate that understanding by learning the associated procedures and skills, and then apply that understanding to real-life situations. Some people might label this as “inquiry-based” or “problem-based” instruction.
We believe that the story is not so black-and-white. Depending on the learning goals, and where students are in their learning progression, there is a balance of methods that makes for high-impact instruction and effective learning. In fact, in the United States, one of the three instructional shifts called for by the Common Core and other state standards for mathematics is a focus on rigor, which is defined as a balance among conceptual understanding, procedural skills and fluency, and application with equal intensity (National Governors Association Center for Best Practices & Council of Chief State School Officers, 2010).
While researchers and experts work to achieve consensus about quality instruction, teachers have to design and deliver instructional experiences for students. That’s why we wrote this book. We know that there is “no ‘one way’ to teach mathematics” (National Council of Teachers of Mathematics [NCTM], 2000, p. 18). There are common threads and research-based principles that define high-quality mathematics instruction, as well as common thinking about what defines poor mathematics instruction. To our thinking, mathematics instruction—like any good instruction—must be intentionally designed and carefully orchestrated in the classroom, and should always focus on impacting student learning. We believe that mathematics teaching is most powerful when it starts with appropriately challenging learning intentions and success criteria. Teachers need to be clear on where their students are, where they need to go, and what the achievement of learning milestones looks like. We also believe that good mathematics learning is rooted in discourse and collaboration—both with teachers and among peers—and is orchestrated around appropriately challenging tasks. We think students should be doing more of the thinking and talking than the teacher. Finally, we believe that students deserve to own their learning. They must be partners in understanding with metacognition (thinking about their own thinking) and evaluating where they are going, how they are doing, and where to go next. These beliefs are reinforced by what the National Council of Teachers of Mathematics (2014, p. 10) has defined as the eight effective Mathematics Teaching Practices:
- Establishing mathematics goals to focus learning
- Implementing tasks that promote reasoning and problem solving
- Using and connecting mathematical representations
- Facilitating meaningful mathematical discourse
- Posing purposeful questions
- Building procedural fluency from conceptual understanding
- Supporting productive struggle in learning mathematics
- Eliciting and using evidence of student learning
Mobilizing the Visible Learning Evidence
Our hope is that this book will help to guide you as you plan your mathematics instruction. We outline specific actions that, when used in concert, strategically, and at the appropriate times based on learners’ needs, will help students build their mathematical confidence and competence. The difference between this book and others is that we draw on the extensive research base John Hattie first developed and published in Visible Learning (2009) and has extended since then (e.g., 2012). The recommendations we make in this book are those that we believe hold the most power, because they stem from the research analysis that John has done, representing more than 300 million students. These recommendations are also supported by specific studies that mathematics education researchers have done over the past fifteen years, which will be referenced throughout this book.
For teachers unfamiliar with Visible Learning, we’d like to take a moment to explain. The Visible Learning database is composed of more than 1200 meta-analyses, with more than 70,000 studies and 300 million students. That’s big data when it comes to education. In fact, some have claimed it’s the largest educational research database amassed to date. To make sense of so much data, John focused his work on synthesizing meta-analyses. A meta-analysis is a statistical tool for combining findings from different studies with the goal of identifying patterns that can inform practice. In other words, they are studies of studies. The tool that is used to aggregate the information is an effect size. An effect size is the magnitude, or size, of a given effect. Effect size information helps readers understand the impact in more measurable terms. For example, imagine a study in which teaching students mathematics while having them chew gum resulted in statistically significant findings (p < 0.01, for example). People might buy stock in gum companies, and a new teaching fad would be born.
But then suppose, upon deeper reading, you learned that the gum-chewing students had a 0.03-month gain over the control group, an effect size pretty close to zero. You also learn that the sample size was very large, and the results were statistically significant because of that even though the impact was not very valuable. Would you still buy gum and have students chew away? Probably not (and we made this example up, anyway).
Understanding the effect size lets us know how powerful a given influence is in changing achievement, or how much bang you get for your buck. Some things are hard to implement and have very little impact. Other things are easy to implement and still have limited impact. We search for things that have a greater impact, some of which will be harder to implement and some of which will be easier to implement. When you’re deciding what to implement to impact students’ mathematical learning, wouldn’t you like to know what the effect size is? Then you can decide if it’s worth the effort. John was able to demonstrate that influences, strategies, actions, and so on with an effect size greater than 0.40 allow students to learn at an appropriate rate, meaning a year of growth for a year in school. Before this level was established, teachers and researchers did not have a way to determine an acceptable threshold, and thus weak practices, often with studies that were statistically significant, continued.
Figure P.1 The Barometer for the Influence of Teaching Test-Taking
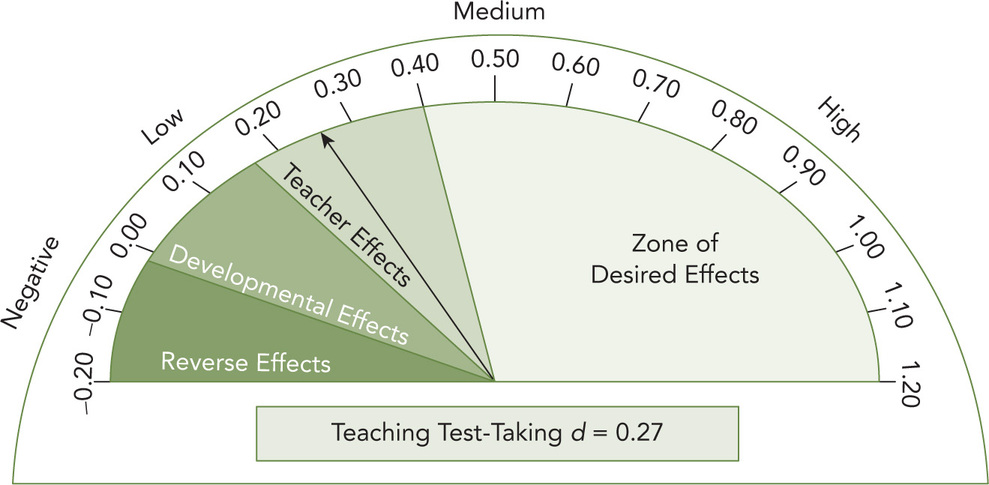
Source: Adapted from Hattie (2012).
Let’s take two real examples.
First, let’s consider teaching test-taking. There have been many efforts to review or reteach or coach students to do better on tests, such as the SAT or state accountability assessments. To help people understand effect sizes, John created a barometer so that information could be presented visually. The barometer for teaching test-taking can be found in Figure P.1. As you can see, the effect size is 0.27, well below the zone of desired effects of 0.40. This is based on 10 meta-analyses, with 267 studies, and a total population of 15,772. Although it’s appealing to want to teach students the test before they take it, the evidence suggests that there are more effective ways for impacting students’ learning.
Figure P.2 The Barometer for the Influence of Classroom Discussion
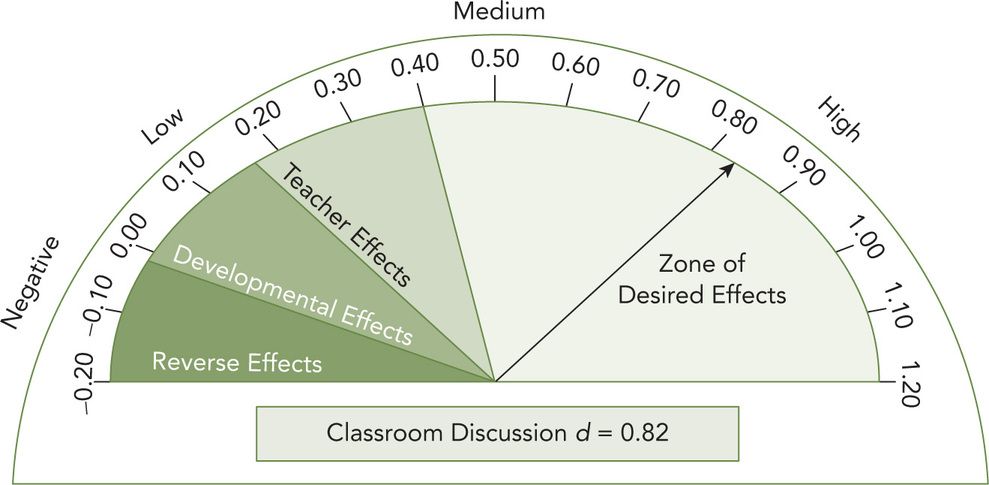
Source: Adapted from Hattie (2012).
Second, let’s consider increasing classroom discourse (synonymous with classroom discussion or dialogue). Students would be invited to talk with their peers in collaborative groups, working to solve complex and rich tasks. The students would not be ability grouped, but rather grouped by the teacher intentionally to ensure that there is academic diversity in each group as well as language support and varying degrees of interest and motivation. As can be seen in the barometer in Figure P.2, the effect size of classroom dialogue, or what we prefer to call discourse, is 0.82, well above our threshold, and likely to result in two years of learning gains for a year of schooling. Note that instructional practice aligns with the NCTM effective mathematics teaching practice of facilitating meaningful mathematical discourse as well as the Common Core Standards for Mathematical Practice (MP) of expecting students to construct viable arguments and critique the reasoning of others (MP 3). Other state and national standards list this practice as mathematical communication or communication and interpretation (see Appendix C). As a teacher, you would be wise to focus your energy on building classroom discourse rather than attempting to teach test-taking.
The Structure of Visible Learning for Mathematics
In the first chapter of this book, we focus on the methods John used to create Visible Learning. We explore in greater depth the concepts of meta-analysis and effect sizes. We also define and begin to discuss the importance of surface, deep, and transfer learning, including the impact of various instructional moves on each type of learning. The claim is that in all subjects, students have to develop surface-level understanding if they are ever going to go deep. In this book, it’s important to note that we do not define surface-level learning as superficial learning of procedures and algorithms. Rather, we define it as the initial development of conceptual understanding, procedural skills, and vocabulary of a new topic. Deep learning is when students begin to make connections among conceptual ideas, and practice and apply procedural skills with greater fluency. It’s when they plan, investigate, elaborate on their conceptual understandings, and begin to make generalizations based on their experiences. And we know that deep learning can facilitate transfer—the ability to more independently apply deeply understood concepts and skills to new and novel situations—which has been our goal all along. For mathematics especially, this is a framing device we have found useful for making decisions about how and when as a teacher you engage in certain tasks, questioning techniques, and teaching strategies to facilitate each level of learning. We will continue to refer to these phases of learning throughout the rest of the book.
In the second chapter, we explore the importance of teacher clarity, which has a strong effect size. In this chapter, we focus on learning intentions and success criteria because that is where teachers start, asking themselves, “What do my students need to learn today, and how will I know if they learned it?” Without a clear path, learning is left to chance. We want to be sure that teachers and students know what they are learning and what success looks like.
In Chapter 3, we will share our thinking about mathematical tasks that require different levels of cognitive demand and discuss what kinds of tasks are appropriate to use within different learning phases, depending on the learning intentions and success criteria defined. This chapter will offer some examples of the kinds of questions that teachers should ask to encourage rich mathematical discourse.
Chapters 4 through 6 discuss three phases of learning—surface, deep, and transfer—and discuss how the learning intentions (i.e., the instructional goals) of any lesson need to be a combination or balance of these phases of learning (Hattie, 2012). Chapter 4 will address the surface phase of learning in detail. Note that surface learning does not mean superficial learning. Rather, surface learning is a time when students initially are exposed to concepts, skills, and strategies. Surface learning is critical, because it provides a foundation on which to build as students are asked to think more deeply. Also, sometimes—but not always—there tends to be more teacher input during surface learning.
In Chapter 5, we define deep learning as a period when students consolidate their understanding and apply and extend some surface learning knowledge to support deeper conceptual understanding. Strategies for helping students to develop deep learning are included in this chapter with examples of how both small group and whole class discourse support deep learning. We think of this as a “sweet spot” that will often take up more instructional time, but can be accomplished only when students have the requisite knowledge to go deeper.
In Chapter 6, you will read about transfer learning as the point at which students take their consolidated knowledge and skills and apply what they know to new scenarios and different contexts. It is also a time when students are able to think more metacognitively, reflecting on their own learning and understanding.
A key point that we will make repeatedly is that teachers must know their students well and understand the impact that they have on their students. In planning lessons, teachers need to be empowered to choose the tasks and approaches that will maximize that impact. Mismatching a task or a pedagogical approach with the nature of learning expected will not create the desired impact. What and when are equally important when it comes to instruction that has an impact on learning. Approaches that facilitate students’ surface-level learning do not work equally well for deep learning, and vice versa. Matching the right approach with the appropriate phase of learning is the critical lesson to be learned.
In Chapters 4 through 6, we also explore more deeply the what, when, and how to give you a clearer picture of how to orchestrate your class based on your learners’ needs and your explicit learning intentions, in order to achieve maximum impact. In these chapters, we will dive more deeply into the kinds of tasks, discussion and questioning techniques, and pedagogical strategies that are appropriate to each phase of learning.
It’s important to point out, too, that learning is not linear. It is recursive. You should feel empowered to understand where in the cycle of learning your students are so that you can strategically select and employ the right tasks and strategies at the right time, based on where individual learners are in the surface-deep-transfer cycle on any given topic of study.
In the final chapter of this book, we focus more deeply on the role of continual assessment to help your learners answer the questions “Where am I?” “How am I doing?” and “Where to next?” We discuss some of the needs around differentiating instruction and response to intervention to help teachers ensure that they’re meeting the needs of all learners, and point you toward resources where you can explore those topics in more depth. You’ll also find several appendixes at the end of this book that cover (a) Hattie’s full list of interventions with their effect sizes; (b) a list of Common Core Standards for Mathematical Practice (MPs) and what they mean in terms of what teachers do and what students do; (c) a non-exhaustive, side-by-side list of other state and international mathematical practice or process standards; (d) a list of NCTM’s eight effective Mathematics Teaching Practices and what they mean in terms of what teachers do and what students do; and (e) a list of resources and websites we recommend to help you make mathematics learning visible.
This book includes a number of features that we hope will help you adopt and implement the practices outlined. For example, we include QR codes and links to videos. In these videos, you’ll meet teachers and hear their perspectives about teaching mathematics. You’ll also visit their classrooms. In addition, we include effect sizes in the margins for easy reference. We also include a number of teaching tips and definitions of terminology in the margins as well as a number of reproducible forms and tools that you can use in your classroom. These forms will be downloadable from our companion website at http://resources.corwin.com/VL-mathematics.
Why This Book Now?
There is a reason there are six authors on this book. No one person can be the expert on learning, and we, as authors, come from a variety of teaching backgrounds across disciplines. We bring together a depth of experience, research, and perspectives that have helped us stretch our own thinking and challenge assumptions. We have worked to pool our knowledge and understanding about excellent instruction, recognize that there are subtle differences about what works when, and offer our best guidance as supported by research from both Hattie’s meta-analyses and some of the excellent research that comes directly from the mathematics education community. Rather than being confined to labels of “researchers” or “literacy people” or “math people,” we like to think of ourselves as “education people.” We have worked together to share with you the what, when, and how of teaching practices that evidence shows work best for student learning in mathematics.
Finally, we feel that teaching begins with a promise. Robyn Jackson, an expert teacher and leader, suggests that teachers make promises to students. Her promises are included in Figure P.3. on the following page. Are these promises that you hope to make to your students? If so, this book will help.
