7
The Role of Information Patterns in Designing Crowdsourcing Contests
Gireeja V. Ranade and Lav R. Varshney
Abstracts
Crowdsourcing contests are used widely by organizations as a means of accomplishing tasks. These organizations would like to maximize the utility obtained through worker submissions to the contest. If this utility is greater than that obtained through alternative means of completing the task (e.g. hiring someone), the task should be crowdsourced. We analyze the utility generated for different types of tasks and provide a rule of thumb for crowdsourcing contest design. Knowledge about the relative strengths of the workers participating in the contest is an important factor in contest design. When the contest organizer is unsure about the strength of the workers, crowdsourcing contests deliver higher utility than would hiring or assignment. Disseminating worker strength information acts as a lever to influence participation and increase utility in the contest. Finally, while crowdsourcing is a good option for generic tasks, it might perform poorly for highly specialized tasks.
Introduction
Information technologies that provide lightning-speed communication at low cost have changed the nature of work. Organizations can now leverage networks, communities, and ecosystems of people to perform tasks. Workforces are globally distributed and diverse. Large projects are broken up into smaller encapsulated pieces. In fact, the millennial generation shows a cultural preference for project-based rather than jobs-based work (Bollier, 2011). Within this environment, methods of collective intelligence have emerged as key business tools (Malone et al., 2010), and are now used by all major companies (Cuenin, 2015). A fundamental understanding of this evolution of work is essential to shape its future form.
A notable example of the decentralized organization of work is crowdsourcing. Crowdpower has been harnessed to design everything from T-shirts to software to artificial intelligence algorithms, by soliciting contributions via open calls (Tapscott & Williams, 2006; Boudreau et al., 2011). The ability to reach a large crowd of skilled workers quickly and inexpensively gives firms an alternative means for accomplishing tasks. As such, it is important to understand the pros and cons of a fluid, crowd-based labor force. To quote the management scientist Thomas Malone, “There is this misconception that you can sprinkle crowd wisdom on something and things will turn out for the best. That’s not true. It’s not magic” (Lohr, 2009). Similarly, Viscusi & Tucci (2018) raise the question of the “right time” for crowdsourcing, and the role that information can play in crowdsourcing. Afuah (2018) also discusses how the makeup of the crowd, and the goals of the seeker (manager) can affect crowdsourcing outcomes. We delve into these questions in this chapter, and focus on the design of crowdsourcing contests based on:
First, we provide a mathematically oriented taxonomy for tasks based on the optimal solution method. This ties in closely with the various forms of crowdsourcing discussed by West & Sims (2017). Our classification gives specific conditions for whether crowdsourcing can generate revenue for the employer for a particular task. A challenge in digital crowdsourcing markets is how to incentivize workers and improve the quality of the work done (Afuah & Tucci, 2012). We take an informational perspective on answering this question with regard to the skill levels of workers. Of course, task formulation is another important aspect for incentivizing workers as well as identifying the appropriate workers for a given task, as discussed by Wallin et al. (2017). We do not consider this aspect here.
In particular, crowdsourcing has been thought of as a good tool for skills identification (Malone et al., 2010). There are two important considerations in choosing a person for a task. The first is the skill-level/strength and ability of the person to perform the task. However, a second and important consideration is the amount of effort the person will put into the task, since this will affect the final utility to the organization. Our theoretical framework provides a heuristic for an organization to find the best person for a job and further incentivize him or her to attain peak performance through crowdsourcing or otherwise. After all, it is human motivation modulating cognitive energy that makes crowd systems go (Varshney, 2012; Chandler & Kapelner, 2013; Ghosh, 2013; West & Sims, 2017).
Our theoretical framework takes a first step towards determining the optimal work structure for a given task: labor-based, division into microtasks, a crowdsourcing contest (internal or external), or something else entirely, as depicted in Figure 7.1. Knowing how to organize work with minimum friction (Varshney, 2012) is critical for the efficient design of the knowledge economy.

Figure 7.1. With the zoo of organizational design possibilities for knowledge work, it is important to know when each is most effective.
The chapter focuses on crowdsourcing contests, where monetary or otherwise tangible rewards are provided to the winners of competitive events. These are also referred to as crowdsourcing tournaments in the remainder of this book. We focus on the case where there is only one winner for each task. This is different from other forms of crowdsourcing where crowd workers do not receive direct extrinsic rewards, such as in social production (e.g. Wikipedia or citizen science initiatives (Benkler, 2006; Howe, 2008)), and is also different from paid microtask forums (e.g. Amazon Mechanical Turk or freelance markets like Upwork) (Chatterjee et al., forthcoming) where there is no contest. Contests may be internal, with competition only among the employees of the organization, or external and open to the public (e.g. Kaggle or TopCoder). Our results apply to both of these types of crowdsourcing.
Previous Work
There has been extensive previous work on the design of crowdsourcing contests. This work has spanned the theoretical space using game-theoretic and statistical models and has also involved experiments and data collection. For example, Archak & Sundararajan (2009) provide a rule of thumb for the prize structure for optimal participation in crowdsourcing contests using a game-theoretic model, whereas Cavallo & Jain (2012) use a model to examine the design of payment mechanisms to workers from the perspective of achieving a socially optimal outcome. Different types of judging in contests, whether cardinal or ordinal, have also been discussed in the context of contest design by Ghosh & Hummel (2015). A recent survey gives a detailed overview of the factors influencing the decision to crowdsource (Thuan et al., 2016).
Certain prior works have focused on the impact of the skill level of workers on contest outcomes. Experiments conducted on Taskcn showed that highly skilled (experienced) players have the most influence on the contest designer’s revenue and drive aggregate reward and reserve-price effects, effectively setting a baseline on submission quality (Liu et al., 2011); an early high-quality submission deters other high-quality players from competing. An all-pay auction model of how players with different skills choose different contests to enter, and a comparison with experiments on Taskcn, demonstrate that as the players get more experienced, the model predictions are close to the empirical data (DiPalantino & Vojnović, 2009).
More broadly, previous work has found that game-theoretic models can serve as good predictors of the outcome in real games. For instance, Boudreau et al. (2016) examined the response of players to increased participation in contests using data from 755 different contests. They found that the response to added participants conformed precisely with the theoretical predictions from Moldovanu & Sela (2001, 2006): while most participants responded negatively, the highest-skilled participants responded positively to the increased participation.
Our work takes an informational perspective on many of these aspects that arise in the design of crowdsourcing contests. Work in decentralized control, game theory, and team theory has traditionally focused on the information pattern or information structure that is available to agents in the game and/or control problem (Ho et al., 1978; Ho et al., 1981). This information pattern essentially captures the notion of “who knows what” in the given setup. For instance, it might capture different parameters regarding a game that various players are aware of—players with more information can be in an advantageous position.
It is well known that these information structures and player reputations affect player participation and game outcomes (Kreps & Wilson, 1982; Rasmusen, 1994). We bring this informational perspective to the story of crowdsourcing and discuss how the “informational lever” of player skills can be used in crowdsourcing contest design. Previous experimental work that studied reputation systems in crowdsourcing has shown that “cheap talk” might indeed influence player behavior and this can have a positive impact on organizer revenues (Archak, 2010).
There has also been empirical work exploring the impact of information in crowdsourcing contests. An examination of event structure empirically found that dyadic contests do not improve performance compared with a single piece rate for simple and short tasks (Straub et al., 2015). Further, empirical investigation of the informational aspect of contest design led to the conclusion that giving feedback on the competitive position in contests tends to be negatively related to workers’ performance: if workers are playing against strong competitors, feedback on their competitive position is associated with workers quitting the task. If the competitors are weak, workers tend to compete with lower effort. Results presented in this chapter provide a theoretical counterpoint to the empirical results from Straub et al. (2015).
Our theoretical development relies heavily on game-theoretic analysis of all-pay auctions (Hillman & Riley, 1989; Amann & Leininger, 1996).
Contributions and Main Results
The main contributions of the chapter are as follows. First, this work compares the efficacy of crowdsourcing contests to task assignment by a manager. Task assignment is meant to capture the situation where a manager chooses a particular worker for the task. This worker then chooses an effort level with which to complete the task and then completes it. The quality of the result depends on the effort the player puts in, and the manager must accept this outcome regardless of the quality. This is roughly the model used in freelance markets (Chatterjee et al., forthcoming), though reputation systems are used there to ensure high-quality performance.
Clearly, the specific map of skill level to players is very important for targeted assignment of tasks—the manager (or task assigner) must have an estimate of the skills for each worker. Highly skilled players can provide high quality outcomes while putting in a lower effort.
Uncertainty regarding skill. The first set of results focuses on modeling the uncertainty a manager has about worker skills. How does this limit the manager’s ability to accurately assign tasks and incentivize people? When and how can crowdsourcing help?
We find that if the manager is uncertain about the skills of the workers involved, crowdsourcing contests are better for single tasks if:
Previous work by Malone et al. (2010) had claimed that the first condition is sufficient, but we see here that it need not be.
Information pattern of worker skills. The second set of results focuses on the information pattern of skill levels among workers. The theoretical results here complement empirical results of Straub et al. (2015) and highlight the impact of varying information sets between workers. Workers may have information about other workers participating in the contest through participation lists and reputation based on statistics or leaderboards (commonly employed by crowdsourcing platforms such as TopCoder and Kaggle). These digital reputations and public rankings provide players with good estimates of the strengths of other players in a contest. This information affects participation and effort levels from the workers.
We find that a weak player is incentivized to put in a very low effort (i.e. quit) if he or she finds out that the other player in the game is very strong. On the other hand, when all the workers in the pool are weak, disseminating this information can increase utility to the organizer. In a pool with strong workers, it is advantageous to keep this information hidden, since this incentivizes the strong players to put in more effort. An obvious informational lever to control the crowd will emerge via participant lists.
Multiple Tasks and Multiple Workers
When organizations may have multiple different tasks and diverse workers, as in crowdsourcing platforms like TopCoder or Kaggle, we find that:
This is a much more complicated set of conditions than described by Malone et al. (2010).
Taxonomy
Another question that is often raised is should we invoke collective intelligence to perform a task? Should this be via collection, contest (tournament), or collaboration (Malone et al., 2010; Afuah et al., 2018)? Within this framework, contests can be thought of as a subtype of collection, where certain contributions are awarded prizes. For collection (e.g. microtasks or contests) to be the appropriate choice, it is claimed that it must be possible to divide the overall activity into small pieces that can be done independently by different members of the crowd. Malone et al. (2010) assert that contests are a useful way of doing collection when only one or a few good solutions are needed. In contrast to this claim, our final multiple-task model demonstrates that under certain conditions, tasks where many solutions are useful to the contest designer are more suitable to be solved using crowdsourcing contests than tasks where only a few good solutions are needed. This turns out to be true because when a large number of qualified players are available, multiple tasks will most effectively mobilize them.
Crowdsourcing Contests as All-Pay Auctions
Our work builds on previous ideas to model crowdsourcing contests as all-pay auctions (DiPalantino & Vojnović, 2009; Archak & Sundararajan, 2009; Liu et al., 2011). Here, we use the terms workers, contestants, players, and bidders interchangeably.
Our goal is to identify the best worker for a given task and incentivize him/her to do his/her best. Crowdsourcing forums such as TopCoder and Kaggle make heavy use of leader boards and public participation records, and we will see herein that such mechanisms for changing information patterns will be critical. The models used here build on these ideas where all players have distinct, public costs. We show that weaker players are deterred from entering when they know strong players are already participating.
We limit attention to auction models with complete information to distill the salient aspects of this comparison. We assume that all players know the skill levels of all other players. High skills implies low costs per unit effort.
Economists have studied first-price all-pay auctions extensively (Hillman & Riley, 1989; Baye et al., 1996). The parallel with crowdsourcing is as follows. A contest designer proposes a task to a pool of players. The players then choose whether to enter the contest. Entering the contest involves submitting a solution (bid) for the task. The contest designer chooses the best solution as the winner and awards the announced prize. A player only gets paid if they are selected as the winner of the contest. However, they forfeit their bid (effort, opportunity cost, etc.) regardless of whether they win, just as in an all-pay auction.
The Model
Consider a crowdsourcing contest with n players (denoted P1 to Pn) and prize value A > 0. To capture the idea that players may have different skill sets and abilities
to perform the given task, we introduce costs per unit effort 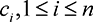 , for each player. For instance, an expert may only need a few hours to complete a
task and would have a low cost per unit effort, whereas a novice might have a much
higher cost. Each player submits a bid
, for each player. For instance, an expert may only need a few hours to complete a
task and would have a low cost per unit effort, whereas a novice might have a much
higher cost. Each player submits a bid 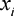 that represents the quality of their submission, at cost
that represents the quality of their submission, at cost  . The prize is awarded to the best submission, i.e. the highest bid
. The prize is awarded to the best submission, i.e. the highest bid  . The valuation of a player,
. The valuation of a player,  is the ratio of the prize value to the cost per unit effort for the player.
is the ratio of the prize value to the cost per unit effort for the player.
Consider a two-player contest with players P1 and P2. Then the expected utilities of the players, E[U1] and E[U1], for their respective bids, are given by
 (7.1)
(7.1)
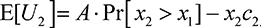 (7.2)
(7.2)
Complete Information Case
First, we consider the complete information setting, where the prize value and players costs, ci, are publicly known. Player bidding strategies depend on the other player costs, but only as a multiset. The specific mapping of costs to players is irrelevant in determining bidding strategies.
Consider the case where 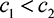 , i.e. P1 is the stronger player. In this case, the all-pay auction has been studied previously
and we restate the results below, adapted to our setting.
, i.e. P1 is the stronger player. In this case, the all-pay auction has been studied previously
and we restate the results below, adapted to our setting.
Theorem 1 (Hillman & Riley (1989)). The two-player contest described above admits a unique Nash equilibrium. At equilibrium,
P1 bids uniformly at random on [0,  ]. P2 bids 0 with probability
]. P2 bids 0 with probability 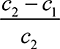 , and with the remaining probability,
, and with the remaining probability, 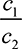 , bids uniformly on [0,
, bids uniformly on [0, ].
].
Theorem 2 (Hillman & Riley (1989)). if  players are involved with strictly increasing costs for P1, P2, P3, i.e. (
players are involved with strictly increasing costs for P1, P2, P3, i.e. ( , and they act as if there were no other agents, then P3 to Pn do not enter the contest at all and submit bids 0 with probability 1.
, and they act as if there were no other agents, then P3 to Pn do not enter the contest at all and submit bids 0 with probability 1.
From Theorem 2, we can see that our model is inaccurate in that it is well known that
more than just two players tend to participate in crowdsourcing contests. This might
be because the assumption of rational players breaks down, or because players underestimate
the competition, or player skill levels are sufficiently similar that it is in fact
rational for many to enter. When one considers an all-pay auction with  players, where there is a set of
players, where there is a set of  players of identical skill levels, there are many asymmetric Nash equilibria, with
more than two players entering the competition (Baye et al., 1996).
players of identical skill levels, there are many asymmetric Nash equilibria, with
more than two players entering the competition (Baye et al., 1996).
We know from empirical studies (Liu et al., 2011) that the strong players in a contest are the most influential for contest outcomes. Hence, we focus on the two-player case here for simplicity, since this allows us to focus on the player skill levels and information pattern of the game very clearly. Building on this, next we consider a model with incomplete information, where players are unaware of the strengths of the competition.
For simplicity, we consider the model with a unique Nash equilibrium, with distinct player costs. Ideas and insights from this model can be extended to the model of Baye et al. (1996).
Asymmetric Information Case
In the asymmetric information case, the prize A is publicly known, but the player costs  are private and known only to the individuals. Players have a prior belief about
other players’ valuations. In the two-player case P1 knows their own cost
are private and known only to the individuals. Players have a prior belief about
other players’ valuations. In the two-player case P1 knows their own cost 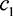 , and also knows that the second player’s valuation,
, and also knows that the second player’s valuation,  , is distributed according to v2 = Uniform[0, 1]. The same is true for P2. This is the setting considered by Amann & Leininger (1996), and the following theorem follows for the symmetric case that we consider.
, is distributed according to v2 = Uniform[0, 1]. The same is true for P2. This is the setting considered by Amann & Leininger (1996), and the following theorem follows for the symmetric case that we consider.
Theorem 3 (Amann & Leininger (1996)). The two-player contest with incomplete information admits a unique Nash equilibrium.
At equilibrium, player Pi, who observes his private valuation  , bids
, bids  · fW(
· fW( )d
)d , where W represents the player Pi’s belief about the other player, and fW(
, where W represents the player Pi’s belief about the other player, and fW(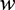 ) is the probability density function of a uniform random variable on [0, 1].
) is the probability density function of a uniform random variable on [0, 1].
Note here that the equilibrium bid of a player 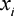 is a deterministic function of their valuation
is a deterministic function of their valuation 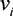 . This is unlike the case with complete public information about player costs, where
players randomize their strategies.
. This is unlike the case with complete public information about player costs, where
players randomize their strategies.
The next section builds on the all-pay auction formalism and game-theoretic characterization we have developed here and categorizes tasks that can be completed on a crowdsourcing contest platform.
A Taxonomy of Tasks
An all-pay auction traditionally assumes that all submitted bids serve as revenue
to the auctioneer. However, in a crowdsourcing contest, this might not be the case.
Some events may have synergy while others have redundancy across entries (Bettencourt,
2009). The utility that the contest designer derives from a task depends on its nature:
we denote contest returns by the function f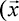 ), where
), where  is the vector of the worker bids. Depending on f, the designer may want to change the parameters of the contest or decide whether
it is even worthwhile to hold an event. The utility derived by the contest designer
is:
is the vector of the worker bids. Depending on f, the designer may want to change the parameters of the contest or decide whether
it is even worthwhile to hold an event. The utility derived by the contest designer
is:
 (7.3)
(7.3)
where  represents the vector of
represents the vector of  bids
bids 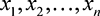 .
.
The function f can provide a mathematically oriented classification of potential crowdsourcing tasks. Tasks may be:
We carry the terms selective and integrative from Schenk & Guittard (2011), which is one among many recent taxonomies for crowdsourcing. Contests that derive
utility from the top- entries interpolate between the extremes of selective and integrative tasks (Archak
& Sundararajan, 2009).
entries interpolate between the extremes of selective and integrative tasks (Archak
& Sundararajan, 2009).
In a selective task, only one working solution is useful to the designer. In this case, the designer typically derives utility from the maximum, and the utility function would be
 (7.4)
(7.4)
On the other hand, an integrative idea generation contest might provide an additive
or even super-additive utility to the designer, but might be subject to a coordination
cost per player ( > 0) and have
> 0) and have
 (7.5)
(7.5)
However, these tasks might also be subject to coordination costs per player, as in
 (7.6)
(7.6)
Modeling market creation though a function is more challenging. The XPRIZE Foundation notes that their goal is “about launching new industries that attract capital, that get the public excited, that create new markets” (Tapscott & Williams, 2010: 131). Thus, independent of the quality of bids, the sheer number of entries provides utility. We model this as
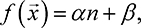 (7.7)
(7.7)
where  is the number of players.
is the number of players.
One may further desire the f function to be upper-bounded by some maximum value. Here, we use f to characterize which tasks are best suited to crowdsourcing contests. As a minimum
requirement, we would like to ensure that the contest designer’s utility 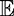 [Utask] is positive, so that no losses are incurred by running a contest. This idea extends
to ensuring against some minimum profit.
[Utask] is positive, so that no losses are incurred by running a contest. This idea extends
to ensuring against some minimum profit.
We consider four examples below. More than just mathematical derivation within the model, our point is to show that the parameters of the player pool influence how a particular task should be solved.
Example 1. In a two-player selective winner-take-all contest, (7.4), the expected utility under equilibrium can be calculated using Theorem 1. Drawing on the theory of order statistics, we take the expected value of the maximum of the bids to get:
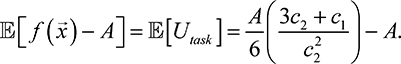 (7.8)
(7.8)
Thus,  [Utask] is positive if and only if
[Utask] is positive if and only if 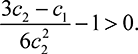 The player strengths
The player strengths 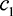 and
and  determine whether the contest designer’s utility is positive. If
determine whether the contest designer’s utility is positive. If  , i.e. the second player is much weaker than the first, then the condition reduces to
, i.e. the second player is much weaker than the first, then the condition reduces to  . On the other hand, if
. On the other hand, if 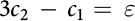 is small, then
is small, then  is a strong enough condition to ensure positive utility.
is a strong enough condition to ensure positive utility.
Example 2. For an integrative task with super-additive f as in (7.5), even a weak player pool can provide positive utility, as below.
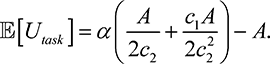 (7.9)
(7.9)
Therefore,  [Utask] > 0 if and only if
[Utask] > 0 if and only if 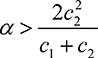 . If
. If 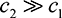 , this reduces to
, this reduces to 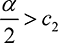 , while if
, while if 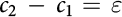 is small, then a sufficient condition for positive
is small, then a sufficient condition for positive  [Utask] is given by
[Utask] is given by 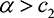 , since
, since  . In the case where
. In the case where 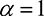 , we see that the positive utility conditions for integrative tasks are weaker than
those for selective tasks.
, we see that the positive utility conditions for integrative tasks are weaker than
those for selective tasks.
Example 3. Consider (7.4) with n players who have strictly decreasing valuations. We noted earlier that in this
case,  almost surely, and hence,
almost surely, and hence,  [Utask] for the contest designer is exactly as (7.8). Clearly, with added coordination costs, as in (7.6), a winner-take-all contest would be exactly the wrong structure.
[Utask] for the contest designer is exactly as (7.8). Clearly, with added coordination costs, as in (7.6), a winner-take-all contest would be exactly the wrong structure.
Example 4. In the case of an event where the objective is market creation, the designer’s utility does not even depend on the effort of the players.
In closing, we observe that if  for all
for all 
 implies that
implies that  , since player bidding strategies are independent of the designer’s valuation function
f. Even with approximate functions, this provides contest designers with a simple rule
of thumb to order potential f functions.
, since player bidding strategies are independent of the designer’s valuation function
f. Even with approximate functions, this provides contest designers with a simple rule
of thumb to order potential f functions.
Crowdsourcing Versus Assignment
Crowdsourcing can be a powerful way of reaching a large pool of workers inexpensively. Further, workers can self-select tasks they want to work on and fluidly move from one task of their choosing to another. The fluidity of the crowdsourcing model allows a player to self-select tasks and the right model might increase the labor force of the future (Bollier, 2011). With this agency, workers will likely choose tasks that they are good at and enjoy. However, it is important not to think of crowdsourcing as a catch-all solution and we should note that sometimes players may not know themselves perfectly.
On the other hand, the assignment of tasks by a manager to a worker requires detailed information about player skill sets. Since different tasks require different skills, it is important that a manager assigns to each worker a task that he or she will be good at. For instance, one software development project may require knowledge of Java, whereas another might require use of DB2. How useful is crowdsourcing for skills identification?
The winner-take-all format provides natural performance incentives without the cost of organizational frameworks. Quite clearly, such a model comes with the benefits and pitfalls of an outcome-based reward structure which have been extensively studied in the literature (e.g. Dixit, 2002). How important are these competitive incentive factors?
Our model addresses the tradeoff between endogenous incentives offered by a contest-based solution versus externally provided incentives, and the effect of observation noise when a manager assigns a task to a player for a selective task with two players. Similar models can easily be developed for integrative or market creation tasks. A second model looks at a multi-task, multi-player setting and captures the potential of crowdsourcing contests in solving hard matching problems and yielding higher utility for both designers and players.
Of course, completion of the task at hand with maximum utility may be only one among many objectives desired by the contest designer. A longer-term perspective may necessitate consideration of completion of many (similar or dissimilar) tasks over time, which may require workforce evolution and retention. Further, it has been observed empirically that crowdsourcing contests may be inefficient, since they are prone to over-effort; in aggregate, players may exert more than fifteen times the effort required to complete the task (Varshney et al., 2011). Direct assignment of tasks to players minimizes such over-effort and can offer training benefits. These issues are not addressed in the models here but are discussed elsewhere (Varshney et al., 2011; Singla et al., 2014).
Crowdsourcing a Single Task
The key model we use in this chapter involves modeling the skills of players, the
skills required to complete a certain task. Let each task be represented by a  -bit binary number. This binary representation of the task corresponds to the skills
required to complete that task. Thus if two tasks have exactly the same
-bit binary number. This binary representation of the task corresponds to the skills
required to complete that task. Thus if two tasks have exactly the same 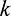 -bit binary representation, they require exactly the same skills. Tasks that require
very different skills have binary representations that are very far away from each
other.
-bit binary representation, they require exactly the same skills. Tasks that require
very different skills have binary representations that are very far away from each
other.
Similarly, we think of each player being represented by a  -bit string that represents his or her skill level. This model is similar to the model
used by Hong & Page (2001). The objective of a manager is then to assign to each task a person who is “closest”
in the skill space to the task.
-bit string that represents his or her skill level. This model is similar to the model
used by Hong & Page (2001). The objective of a manager is then to assign to each task a person who is “closest”
in the skill space to the task.
To model this, we examine the Hamming distance between tasks and worker. If this distance is low, then the worker has a good skill set for the task and if the Hamming distance is large, the worker has a poor skill set for the task. Thus the Hamming distance serves as a proxy for the overall skill level of a worker with respect to a task.
The key point of this model is that we can now quantitatively model the imperfect worker information of a manager, as a noisy observation on the binary skill vector of the work. Say the manager observes each skill vector with a bit flip probability, σ. Using only this observation, the manager is now required to assign a player to a task. Naturally, the manager chooses that player that appears to be closest to the task in Hamming distance.
Complete information case. Now consider a two-player setup with complete information. Thus all the player/worker
strengths/skill levels are known to all the other players entering the contest, though
the manager may have a noisy observation. Let player 1 be the stronger player for
the task, i.e. let P1 be the Player who is closest in Hamming distance to the task. Let  represent the distances of Players 1 and 2 from the task, which serve as a proxy
for the costs incurred for the players. As per our assumption,
represent the distances of Players 1 and 2 from the task, which serve as a proxy
for the costs incurred for the players. As per our assumption,  .
.
Let  and
and  represent the length-
represent the length- skill vectors of the two players, and
skill vectors of the two players, and  be the two independent noise vectors ~Bernoulli(σ). The manager observes
be the two independent noise vectors ~Bernoulli(σ). The manager observes  and
and 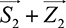 , which are at distances
, which are at distances  and
and  from the task.
from the task.
First, let us calculate the utility achieved with noiseless perfect assignment. The
stronger player, player 1, will at best exert  effort to complete the task, since any extra effort would lead to a negative expected utility for the
player. Let
effort to complete the task, since any extra effort would lead to a negative expected utility for the
player. Let  be the base fraction of effort exerted by players through external (non-competition-based)
incentives. If
be the base fraction of effort exerted by players through external (non-competition-based)
incentives. If  is the base utility obtained by the contest-designer, then with optimal assignment
the expected utility is given by
is the base utility obtained by the contest-designer, then with optimal assignment
the expected utility is given by
 (7.10)
(7.10)
Theorem 4. The expected utility achieved by targeted assignment, 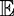 [Uman], and crowdsourcing contest mechanisms with public valuations,
[Uman], and crowdsourcing contest mechanisms with public valuations,  and,
and,  , are given as
, are given as
 (7.11)
(7.11)
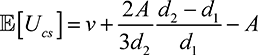 (7.12)
(7.12)
respectively, where Pr(r) is the probability that the task is assigned to the correct player, and can be calculated as below.
Proof. It is a straightforward expectation that gives  [Uman] as (7.11), once we have Pr(r). To calculate Pr(r), we note that an error will be made by the manager if they observe that P2 is closer to the task than P1, i.e.
[Uman] as (7.11), once we have Pr(r). To calculate Pr(r), we note that an error will be made by the manager if they observe that P2 is closer to the task than P1, i.e.  even though
even though 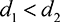 . Hence,
. Hence, 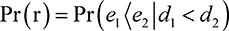 . Hence, we are interested in the change in
. Hence, we are interested in the change in  compared to
compared to 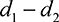 . This probability is the same as that if
. This probability is the same as that if 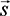 1 were perturbed by noise
1 were perturbed by noise  ~ Bernoulli(
~ Bernoulli( ), where
), where 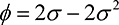 , with
, with  2 unchanged. Let dch be the change in
2 unchanged. Let dch be the change in 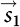 1 due to the noise
1 due to the noise  . Then,
. Then,
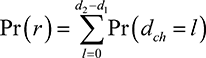 (7.13)
(7.13)
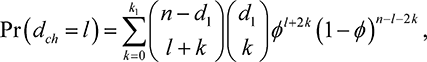 (7.14)
(7.14)
where  . The remaining calculations are omitted for brevity.
. The remaining calculations are omitted for brevity.
Since a crowdsourcing mechanism picks out the maximum bidder, we can calculate the
distribution of the expected utility under equilibrium as the 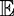 [max(
[max( ,
,  )], where bids
)], where bids  and
and  have distributions as specified by Theorem 1. This gives (7.12).
have distributions as specified by Theorem 1. This gives (7.12).
Asymmetric information case. Now, consider the case of asymmetric information, where players do not know each
other’s distances 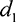 and
and  . At most they might have some distributional information about their competitors.
We assume each player knows his or her own distance from the task perfectly.
. At most they might have some distributional information about their competitors.
We assume each player knows his or her own distance from the task perfectly.
Theorem 5. Consider the two-player game with private valuations 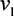 and
and  . Let a player’s belief about their opponent’s strategy (i.e. the bid they expect
the opponent to play) be Uniform[0, 1]. Then, the expected utility achieved with crowdsourcing contest mechanisms,
. Let a player’s belief about their opponent’s strategy (i.e. the bid they expect
the opponent to play) be Uniform[0, 1]. Then, the expected utility achieved with crowdsourcing contest mechanisms,  [Ucsa], is given as
[Ucsa], is given as
 (7.15)
(7.15)
Proof. From Theorem 3, we know that if the player valuation is  , then at equilibrium a player will submit the bid where fW(w) = 1 if wɛ[0, 1] and fW(w)=0 otherwise. Then, xi(vi)is given by
, then at equilibrium a player will submit the bid where fW(w) = 1 if wɛ[0, 1] and fW(w)=0 otherwise. Then, xi(vi)is given by
 (7.16)
(7.16)
Since the higher bid will come from the stronger player, Player 1, we use v1 in the expression above to give the result.
Discussion. To gain more insight into the theorems, Figures 7.2, 7.3, and 7.4 show the relative utility obtained by the task designer with different values of the managerial noise and base level of effort. Since empirical productivity estimates show that θ might be about 0.5, we vary θ between 0.3 and 0.6. The relative strengths of the two players can affect whether crowdsourcing or managerial assignment provides higher returns. Note these figures serve as examples and changes to θ,ϕ,d1, and d2 may affect the plots.

Figure 7.2. One strong one weak player. Since the strong player does not know that the other player is weak, they exert more effort and the asymmetric information setup has higher revenue than the complete information setup.
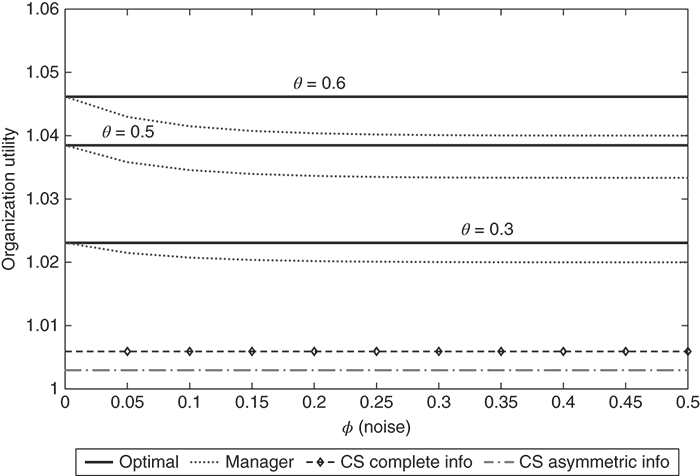
Figure 7.3. Two weak players. Player 1, who is weak, does not know that Player 2 is also weak and vice versa, and so neither exerts much effort (since their own valuation is low they have reason to believe the other player is stronger). They do not even exert the level of effort that would be exerted in the complete information case and the manager utility obtained with asymmetric information is lower than that with complete information.

Figure 7.4. Two strong players. With two strong players, both bid strongly based on their own valuation since each has reason to believe they are the stronger player, and asymmetric information does better than complete information.
As Figure 7.2 shows, crowdsourcing offers the greatest advantage over assignment when the skill levels in the pool of players are diverse, regardless of the information workers have about each other. We see that with a weak pool of players, targeted assignment performs better than crowdsourcing (Figure 7.3). With two strong players, noise does not matter much, and crowdsourcing does not offer significant advantages in identifying skill (Figure 7.4) when players are aware of who else is entering the contest.
Now let us consider the information pattern between the workers. Consider first Figure 7.2. Here, since the strong player does not know whether the second player is stronger or weaker than thems. Hence, they are incentivized to exert more effort than they would in a setting with complete information, and the utility to the manager is higher in the case of asymmetric information. On the other hand, when both players are weak, as in Figure 7.3, the asymmetric information setup extracts less utility than does the complete information setup. This is because both players believe they are the weaker of the two players. Neither person thinks they have a significant chance of winning and neither exert much effort. Finally, in the case where the whole pool is made of strong players, as in Figure 7.4, each assumes they have a high chance of winning and places a relatively high bid. Unlike the complete information case, the effort levels are not bottlenecked by the strength of the weaker player, and the effective utility to the manager is much higher than in the case of complete information.
These observations suggest that dissemination of information regarding player skills can be used as an “informational lever” by a contest designer to elicit higher effort from the players. If the manager has a rough idea about the multiset of skills in the player pool, they can use this to tune the release of this information through leader boards or participant lists. Releasing information might be useful to get weaker and mid-level players to participate in the game. Hiding information might be useful to get stronger players to put in greater effort.
Crowdsourcing Multiple Tasks
Now we consider multiple tasks, to be completed by multiple players. Here, we restrict our attention to the complete information case only. Matching multiple tasks and multiple potential solvers is a complex assignment problem (Chatterjee et al., forthcoming). It is tempting to believe that crowdsourcing mechanisms could provide a natural scheme through which players will self-select appropriate tasks. Not only would players choose suitable tasks, but the competition could provide performance incentives. This section explores a simple multi-player, multi-task model.
We would like to explore a setting with 2n tasks of two types each. One set of n tasks might be dependent on Java programming skill and, say, the other set of skills is dependent on graphic design. The players are also categorized into these two types and there are n players for each type. Players of a given type are better at tasks of the same type. A Java programmer (or graphic artist) can complete a Java task (or graphic design task) at a low cost (cl), whereas hey have a high cost (ch) for a graphic design task (or Java task).
We find that:
We introduce some new notation to set up the framework. Consider a setting with 2n tasks denoted by (EJ(1),…, EJ(n)) and (EJ(1),…, EG(n)) and 2m players denoted by (PJ(1),…, PJ(m)) and (PG(1),…, PG(m)), with m≥n. There are n tasks of each of two types: Java-based (type J) or graphic design-based (type G), and similarly, m players of each type.
Players of a given type are better at tasks of the same type. A Java programmer (or
graphic artist) can complete a Java task (or graphic design task) at a low cost (cl), whereas they have a high cost (ch) for a graphic design task (or Java task). PJ(i) has cost 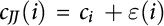 =
=  for tasks EJ(1) to EJ(n), and cost
for tasks EJ(1) to EJ(n), and cost 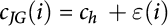 =
=  for EG(1) to EG(n). Costs for PG(i), i.e. cGG(i) and cGJ(i), are defined similarly. The ɛ(i) are to be thought of as error terms:
for EG(1) to EG(n). Costs for PG(i), i.e. cGG(i) and cGJ(i), are defined similarly. The ɛ(i) are to be thought of as error terms: 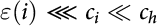 . Base effort
. Base effort  is as defined earlier. Without loss of generality, assume that the player costs are
ordered:
is as defined earlier. Without loss of generality, assume that the player costs are
ordered:

The optimal utility, Uopt, is achieved when each player is matched to a task of his or her type. This total utility is the sum of utilities of the events less the reward paid out, and acts as our baseline. This is given by
 (7.17)
(7.17)
However, doing this matching manually is difficult, which motivates the use of crowdsourcing.
Theorem 6. In the framework described above, if the manager observes an incorrect player type
with probability  , then the expected contest designer utility,
, then the expected contest designer utility, , is
, is
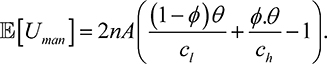 (7.18)
(7.18)
Proof. An expectation calculation gives
 (7.19)
(7.19)
Substituting values of the costs gives the desired (7.18).
Now consider the crowdsourcing scenario. Each player can submit entries for any task,
however, finally only one player will be picked per task and each player can only
win one contest. Note that with enough skilled competitors, crowdsourcing can yield
higher utility than even optimal assignment (7.17), since  , and is often close to 0.5.
, and is often close to 0.5.
Theorem 7. In a crowdsourcing contest, as described above, when 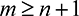 , the expected utility from crowdsourcing is
, the expected utility from crowdsourcing is
 (7.20)
(7.20)
as  .
.
Proof. First, consider all tasks of the type. For notational ease, let 
This problem essentially boils down to an all-pay auction, with n identical goods 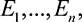 and
and 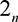 , and players. The n highest bidders will be assigned the n tasks. Such auctions with multiple goods and players have been extensively studied
(Barut & Kovenock, 1998; Clark & Riis, 1998), and we build on this work here.
, and players. The n highest bidders will be assigned the n tasks. Such auctions with multiple goods and players have been extensively studied
(Barut & Kovenock, 1998; Clark & Riis, 1998), and we build on this work here.
When all the players have unequal valuations, this game has a unique Nash equilibrium,
in which only the strongest 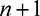 players actively bid, while the rest almost surely bid 0. Thus, only players
players actively bid, while the rest almost surely bid 0. Thus, only players  to
to 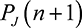 with values
with values  to
to  will actively submit entries for tasks of type J.
will actively submit entries for tasks of type J.
From Clark & Riis (1998), we know that  to
to  will randomize over the interval [
will randomize over the interval [ , where
, where
 (7.21)
(7.21)
 randomizes uniformly over
randomizes uniformly over 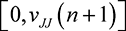 .
.
Let 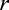 be a parameter such that
be a parameter such that  if
if  , else
, else  if
if  . Then, the distribution of the bidding strategy (Clark & Riis, 1998)
. Then, the distribution of the bidding strategy (Clark & Riis, 1998)  , for
, for  is given by
is given by
 (7.22)
(7.22)
Player  submits 0 with probability
submits 0 with probability  , and otherwise randomizes according to eq. (7.22) with
, and otherwise randomizes according to eq. (7.22) with 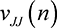 in place of
in place of 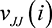 .
.
The expected utility of each player in this case is given by  . The expected payoff to the contest designer would be the sum of the
. The expected payoff to the contest designer would be the sum of the  highest bids of the players.
highest bids of the players.
As n becomes large, players submit entries close to the upper bound 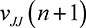 . Similar to the two-player all-pay auction where no players bid higher than the weaker
player’s valuation, the weakest player’s valuation
. Similar to the two-player all-pay auction where no players bid higher than the weaker
player’s valuation, the weakest player’s valuation 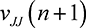 is an upper bound on the bids of all players. Note that if
is an upper bound on the bids of all players. Note that if  for all
for all  , the lower bound for the support of the mixed strategies of all players is close
to 0.
, the lower bound for the support of the mixed strategies of all players is close
to 0. 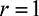 for most
for most  in this interval, and
in this interval, and
 (7.23)
(7.23)
Since all players adopt the same strategy, the probability of any one player winning
is  . Thus, the expected bid is the difference of the expected gross surplus and the expected
utility,
. Thus, the expected bid is the difference of the expected gross surplus and the expected
utility,
 (7.24)
(7.24)
 (7.25)
(7.25)
With the assumption  for all
for all  , we have that the expected bid for player
, we have that the expected bid for player  is
is  .
.
Now consider the tasks of type G. The 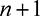 strongest players for this task are the players of type G. Since these players were strictly weaker than the players of type J for the tasks of type J, none actively participated in any of those tasks. However, they will actively bid
on the tasks of type G, following exactly the same patterns as the players of type J in bidding on the tasks of type J. Hence, the total expected utility to the contest designer, using crowdsourcing in
the case of approximately identical costs (or values) for all players of a type, is
given by
strongest players for this task are the players of type G. Since these players were strictly weaker than the players of type J for the tasks of type J, none actively participated in any of those tasks. However, they will actively bid
on the tasks of type G, following exactly the same patterns as the players of type J in bidding on the tasks of type J. Hence, the total expected utility to the contest designer, using crowdsourcing in
the case of approximately identical costs (or values) for all players of a type, is
given by
 (7.26)
(7.26)
 (7.27)
(7.27)
Theorem 8. If 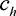 is high enough that
is high enough that  , then the expected utility from crowdsourcing
, then the expected utility from crowdsourcing 
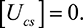
Proof. This result follows just as Theorem 7. Intuitively, since there are only enough players to complete the task, each player is assured of winning a task and thus has no incentive to put in a non-zero bid.
Note that lack of competition leads to low performance by all players. Instead, in this case if tasks were assigned by a manager, albeit noisily, significant utility could be derived for at least some of the tasks. The natural thought process might lead us to believe that crowdsourcing contests are good for skill discovery—it is easy to think that expert players will clearly become obvious in a competitive setting. This setting gives a clear example where this would not be the case. Crowdsourcing may not be a good solution when the contest designer has many tasks of a specialized nature that require highly skilled players who are in short supply. This model easily extends to more than two types of events and players.
When it is possible to divide a large project into smaller tasks, the best way to harness multiple players is through multiple tasks. A first-price auction with multiple players only incentivizes the two strongest players to enter the contest. However, if contest designers are able to divide a large task into many smaller tasks of different types that are matched to the different types of players in the crowd, both the designers and the players could receive higher utilities. Our guidelines for crowdsourcing tasks both support and complement those from Malone et al. (2010).
Conclusions and Future Research
Complementing empirical work in the area of crowdsourcing contest design, we have developed a theoretical framework that may guide organizations considering crowdsourcing contests to do work. The basic idea is to find the best workers for jobs, and incentivize them to do their best, with various informational levers for crowd control. More broadly, we have tried to understand the implications, strengths, and weaknesses of more fluid task-focused labor markets.
The simple models presented here are only a first step. Models involving multiple prizes, and also those which take into account repeated game effects such as player learning and retention costs, are necessary future work. Our larger goal is to understand the best ways in which to organize work when there are many design possibilities for different types of tasks and information patterns.
Acknowledgments
We thank Eric Bokelberg, Ankur Mani, Anshul Sheopuri, and Lada Adamic for helpful discussions.