The effort to understand the universe is one of the very few things which lifts human life a little above the level of farce and gives it some of the grace of tragedy.

—Steven Weinberg1

THE QUARKS

Considerable theoretical effort went into attempting to classify the new particles that were turning up at the accelerator labs. In 1961, something akin to the periodic table of the chemical elements was independently developed by a Caltech physics professor Murray Gell-Mann and Israeli physicist (and high-ranking military officer and government official) Yuval Ne'eman. It was called the Eightfold Way, after the Buddha's path to enlightenment. More technically, the theory was based on a mathematical symmetry group called SU(3). Symmetry groups are mathematical classifications of various types of symmetry transformations. For example, the group of rotations in three dimensions is O(3).

In 1964, Gell-Mann and Caltech graduate student George Zweig independently proposed a natural explanation for the Eightfold Way in which hadrons, including the proton and neutron, were composed of more elementary constituents that Gell-Mann dubbed quarks. Until this time, all known particles had either zero, positive, or negative electric charge that was an integer multiple of the unit electric charge, e. The electron has charge –e; the proton has charge +e. Gell-Mann and Zweig made the crucial assumption that quarks had fractional charge. Using current terminology, the proton is composed of two u (“up”) quarks, each with charge +2/3e, and a d (“down”) quark with charge –1/3e, for a net charge of e: uud. The neutron is udd for a net charge of zero. Note there is no negative nucleon that can be formed with a triad of u and d quarks.

Antiprotons and antineutrons, which had been confirmed at the Berkeley Bevatron in 1955 and 1956, are made of antiquarks. The antiproton, 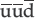, has charge –e. The antineutron is electrically neutral.

Baryons in general are composed of three quarks. Their antiparticles are composed of three antiquarks. Mesons, on the other hand, are composed of quark-antiquark pairs.

Gell-Mann and Zweig also proposed a third quark, now called s (“strange”), which has charge –1/3e and a strangeness S = –1. Its antiparticle 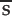has charge +1/3e and a strangeness S = +1.

The same year, a particle called the omega-minus baryon (Ω^–), which had previously been predicted by Gell-Mann and others, was found after a surprisingly short search at Brookhaven National Laboratory.2 It had exactly the properties expected if it was composed of three s quarks (sss). That is, it is a singlet of charge –e and strangeness –3. The discovery bubble-chamber picture and its interpretation is given in figure 11.1. No Ω⁰ or Ω⁺ was ever seen, consistent with the fact that sss is the only combination of three s quarks. An antimatter version 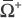with charge +e and strangeness +3 was detected shortly thereafter. With the discovery of the omega baryons, the quark model of matter was convincingly established. It was further reinforced by the failure to discover any hadrons that could not be composed of quarks.

Experiments in the 1970s in which electrons and neutrinos were scattered from protons and neutrons (I worked on several of the neutrino experiments at Fermilab and CERN) revealed point-like structures inside the nucleons with fractional charge, fitting all the hypothesized properties of quarks. These experiments provided direct evidence for point-like constituents inside the proton and neutron, just as the Rutherford-Geiger-Marsden experiment provided direct evidence for the point-like nucleus inside the chemical atom.

The three-quark model successfully described all the hadrons up until 1974, when evidence was found for a fourth quark with a property analogous to strangeness, dubbed charm, that was also conserved in strong interactions but not in weak interactions. The quark was labeled c (“charmed”). Soon hadrons containing c quarks were discovered. In 1977 evidence was found for yet another quark, b (“bottom” or, sometimes, “beauty”).

PARTICLES OF THE STANDARD MODEL

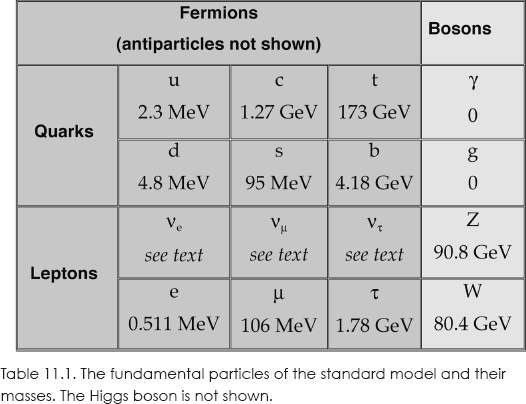
By 1980, the particles shown in table 11.1 were established as the elementary ingredients of the standard model that remains in effect today, pending results from the Large Hadron Collider (LHC).³ We have three generations, or families, each having two quarks and two leptons, accompanied by their antiparticles (not shown). In the table, the top row of quarks has charge +2/3e and the second row has charge –1/3e. All the hadrons that had been discovered by the end of the 1980s were built from combinations of these quarks. The t (“top” or sometimes, “truth”) quark that joins with the b quark in the third generation is so much heavier than the other quarks (174 GeV, where 1 GeV = 1 billion electron volts, and a proton mass is 0.938 GeV) that it was not confirmed until 1995, when Fermilab reached sufficiently high energy to produce it.

The top row of leptons in table 11.1 contains the three different types of neutrinos, each having zero charge. The second row has the electron, muon, and tauon, with charge –e. The antiparticles have opposite charge. The masses of the particles are also shown in the table.

The story of neutrino mass is a profound one. For years, it appeared that the masses of the neutrinos were all zero. However, there was no theoretical reason for this to be the case. If they had masses, however, experiments already established that these masses were far smaller than the lightest known particle with mass, the electron.

The first evidence for a nonzero mass for neutrinos came in 1998 in an experiment called Super-Kamiokande, in a mine in Japan.4 I played a minor role in this experiment; however, in 1980 I proposed the technique that was used at a neutrino conference in Wisconsin in the context of another planned experiment that was never constructed.⁵

The neutrinos listed in the table, ν_e, ν_μ, ν_τ, do not have definite mass states, which means they are not stable. Rather they are mixtures of three stable neutrino mass states ν₁, ν₂, ν₃ that have the following mass (square) limits,

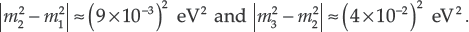
Neutrinos have a remarkable, purely quantum mechanical property called neutrino oscillation. If you start out with a pure beam of muon neutrinos, for example, it will eventually transmogrify into a beam containing all three types. This was the property my collaborators and I at Super-Kamiokande observed in 1998, which determined that neutrinos have mass. If they were massless, they wouldn't oscillate.

The evidence that neutrinos have mass came from the observations of the flux of muon neutrinos produced in the upper atmosphere as they passed through Earth to the detector. Those traveling a greater distance had the greatest chance of changing type and, sure enough, we saw fewer muon neutrinos coming straight up through the center of Earth than just below the horizon.

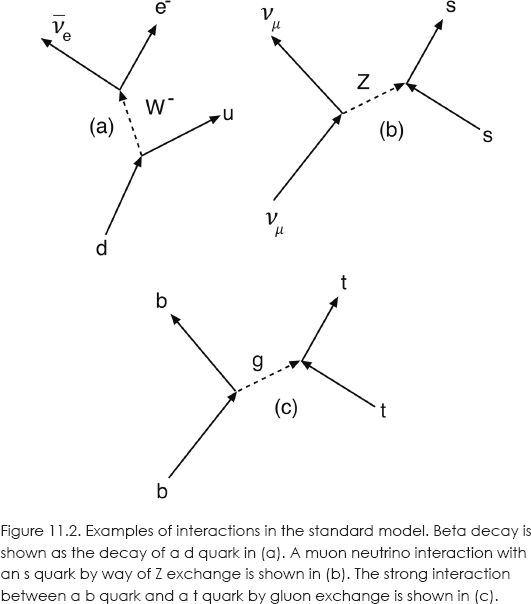
The quarks and leptons are all fermions with spin ½. In addition, the standard model contains twelve “gauge bosons,” spin 1 particles that mediate the various interactions between the quarks and leptons. These include the photon, which mediates the electromagnetic interaction as described previously. Three bosons, W⁺, W^–, and Z, mediate the weak interaction. Eight gluons, g, mediate the strong interaction. Some examples of elementary particle reactions are given in figure 11.2.

While this may seem complicated, remember that these elementary particles are all we have needed for the last three decades to account for every observation without a single anomaly. This contrasts with the anomalies with the phenomenon of light that we have seen existed at the close of the nineteenth century. Only now, with the LHC, are new elementary particles to be anticipated.

Indeed, most of these elementary particles are of interest only to particle physicists and cosmologists. When considering the ingredients of matter that most people deal with—not only in everyday life, but also in almost all scientific laboratories everywhere—the number of elementary particles needed now is the same as was needed in 1932. Recall that in 1932 all of matter was seen to be composed of protons, neutrons, and electrons. Along with the photon to provide light, all we needed was four particles. Today, while the LHC data are being accumulated, most of us can still get by with four particles: the u and d quarks, the electron, and the photon.

GAUGE SYMMETRY

Early in the twentieth century, another symmetry was discovered that played a role of increasing importance and eventually provided the foundation of the standard model of elementary particles and forces. This was gauge symmetry. The easiest way I can think to describe gauge symmetry is to view it as rotational symmetry inside the abstract, multidimensional space that physicists use to provide additional degrees of freedom beyond those provided by four-dimensional space-time. These degrees of freedom include electric charge along with the various quantities that appear in the standard model, such as baryon number, lepton number, strangeness, and charm. In string theory, the additional degrees of freedom appear as curled-up extra-spatial dimensions, but my discussion does not require this assumption. Indeed, I am deliberately avoiding covering string theory in this book because I want to stick to only well-established, empirically based knowledge.

Gauge symmetry first appeared in classical electrodynamics. Besides the conservation principles already discussed, another conservation principle has been a part of physics since the first experiments on electricity by Benjamin Franklin and others. Although not immediately recognized as such, this is the principle of charge conservation that I introduced in chapter 8.

If charge is conserved, then there must be a corresponding symmetry principle.⁶ This principle is gauge symmetry.

Classical electrodynamics contains a four-dimensional vector field called the vector potential from which the electric and magnetic fields can be calculated. It was discovered long ago that it was possible to change this field by what was called a gauge transformation without changing the electric and magnetic fields.⁷ It was proved that invariance under a gauge transformation leads to charge conservation.

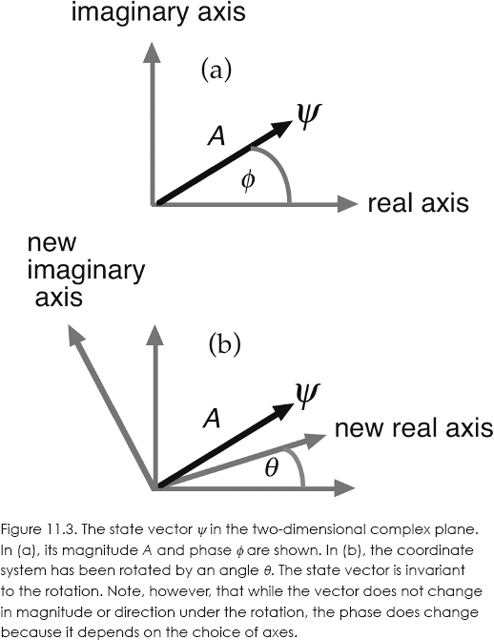
Earlier, I likened a gauge transformation to a rotation of a coordinate system in an abstract space. In the case of quantum mechanics, the state of a system is specified by a state vector in such a space. In the simplest case, the space is the two-dimensional complex plane and the state vector is represented by the wave function, which is a complex number having a magnitude and a phase.⁸ A rotation in the complex plane changes the phase but not the magnitude of the wave function, so the probability of the state, given by the square of the magnitude, is unchanged. That is, the probability calculated in quantum mechanics is invariant to the rotation of the complex plane, as illustrated in figure 11.3. The invariance of probability under gauge transformations is called unitarity.

When you make a global gauge transformation, where the phase change is the same at every place in space and time, the equation of motion for the wave function of a particle is invariant to the change in phase, which leads to charge conservation. However, if you make a local transformation, where the phase change depends on place and time, the equation of motion for the wave function of a particle is not invariant. Now comes a big surprise. You can make the equation of motion locally gauge invariant by adding a field to the equation. And what is that field? It is exactly the vector potential field that gives Maxwell's equations!

In other words, the electromagnetic field is simply an artifact that is added to the equations of physics in order to make them locally gauge invariant. Thus, the electromagnetic field is what is called a gauge field, and when it is quantized, we get a “gauge boson” called the photon.

When the number of dimensions of abstract space is increased, additional fields appear. These are precisely the fields associated with the weak and strong interactions. When they are quantized, we get the other gauge bosons of the standard model.

FORCES IN THE STANDARD MODEL

As we have seen, the remarkable success of relativistic quantum field theory in describing the electromagnetic force was not followed immediately by a successful application to the weak and strong nuclear forces. However, once the quark-lepton scheme of elementary particles was established and the power of gauge transformations recognized, theoretical physicists were able, in a few short years in the 1970s, to produce a relativistic quantum field theory that unified the electromagnetic and weak forces into a single entity called the electroweak force. Abdus Salam, Sheldon Glashow, and Steven Weinberg shared the 1979 Nobel Prize in Physics for this work.

Electroweak unification was also a theory of the breaking of electroweak unification. That is, it showed how it itself is violated. The electromagnetic and weak forces are unified at very high energies, above about 1 TeV (1 TeV = 1 trillion electron volts). At these energies, the masses of the W and Z bosons are zero, like the mass of the photon. But this leads to the weak force having the same unlimited range as the electromagnetic force. This grossly contradicted the data from the sub-TeV experiments of the time, which indicated a range of the weak force a thousand times smaller than the radius of a proton.

Weinberg and Salam independently discovered a process by which electroweak symmetry is broken. This is called the Higgs mechanism and will be described in the next section. Associated with the Higgs mechanism is a particle called the Higgs boson. As we will see later in this chapter, a particle of mass in the range 125 to 126 GeV that looks very much like the Higgs boson was reported by two independent experiments at the LHC on July 4, 2012.

The theory of electroweak symmetry breaking predicted that the mass of the charged W bosons would be 80 GeV and the mass of the neutral Z boson would be 91 GeV, where in these units the proton mass is 0.938 GeV. The W and Z bosons at exactly these masses were detected months apart in 1983 by two independent experiments at CERN. This discovery was considered so important that the experimental leaders, Carlo Rubbia and Simon van der Meer, were awarded the Nobel Prize in Physics with unprecedented speed, just a few months after the announcement. For a very nice, up-to-date history of particle physics that covers all these events up until the end of 2011, just as the Higgs data were coming out, see Massive: The Missing Particle That Sparked the Greatest Hunt in Science by science journalist Ian Sample of the Guardian.9

During the same time that the electroweak theory was being developed, physicists working on the strong interaction were able to develop a relativistic quantum field theory of the strong interaction. Dubbed quantum chromodynamics (QCD), it became part of the standard model. QCD was based on the idea that quarks carry what is called color charge. Quarks are proposed to come in three “colors,” red, green, and blue, where these properties are analogous to those of the familiar primary colors of visible light, although there is no direct connection between the two phenomena.10

All observed hadrons are color neutral, that is, “white.” Baryons, such as the proton and omega-minus, are composed of one red, one green, and one blue quark. By being different colors, the Pauli exclusion principle, which prevents identical fermions from being in the same quantum state, is avoided.

Antiquarks have the corresponding complementary colors: cyan, magenta, and yellow. Mesons, such as the pion and kaon, are composed of one quark and an antiquark of complementary color, so they are also white.

In QCD, the strong force is mediated by gluons. The basic interaction vertex is seen in figure 11.4.

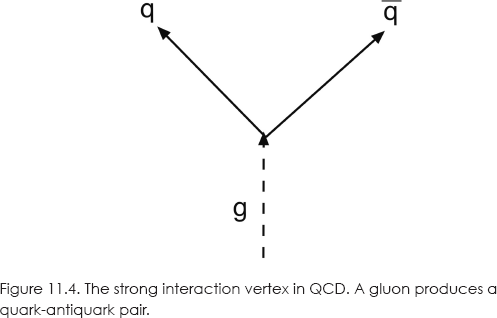
There are eight different gluons: two white (colorless) and six with all the colorful combinations that can be made from red, green, and blue quarks and their cyan, magenta, and yellow antiquarks. For example, red plus cyan is white, while red plus magenta is something nonwhite.

Tests of QCD have been difficult because no one has ever produced free quarks in the laboratory. Indeed, if one did, that would constitute a violation of one of the prime tenets of QCD: free quarks cannot exist. The reason is that the color force increases with the separation between two quarks. When that separation exceeds a few femtometers, the color charge is discharged. This is analogous to the discharge that takes place between two electrically charged bodies in a conducting medium that we see as a spark or a bolt of lightning. While a vacuum is nonconducting for electric charge, it is conducting for color charge.

Recall that the single pion exchange diagram failed as a mechanism for the interaction of nucleons because of the high value of the strength factor α_s. So why should we expect it to work here? Good fortune. Recall that the electromagnetic strength factor a varied very slowly with energy, but too slowly to worry about for most applications. In the case of α_s, the energy dependence is rapid, and at high energies α_S becomes small enough to weaken the force. This is called asymptotic freedom, since quarks become increasingly free as they collide at higher and higher energies.

But you still can't kick them out of a nucleus (at least according to QCD) because of color charge breakdown. When you bang quarks together at increasingly high energies, as in a proton-proton or proton-antiproton collider, you just produce more and more quark-antiquark pairs that form mesons and quark-quark-quark trios that form baryons. And that's what you see when you look at the pictures taken at today's colliding beam detectors: E = mc² in all its glory. The more energy, the more new particles are made from that energy.

All the aspects of the standard model have been subject to numerous tests, and no experiment has, as of this writing, uncovered any violation. However, the real crucial tests are coming up as the LHC moves into full-scale operation.

THE HIGGS BOSON

The unification of the electromagnetic and weak forces just described was strongly counterintuitive. If the two forces are just two different manifestations of the same basic electroweak force, how can their ranges of influence be so vastly different? The electromagnetic force has unlimited range, reaching us from galaxies 13 billion light-years away, while the weak nuclear force can reach only 10^–18 meter, a thousand times less than the radius of a proton. And these are the same force?

As we have seen, the bosons that act as the carriers of forces have masses inversely proportional to their ranges. The photon has zero mass, while the weak bosons, W and Z, have masses of 80 GeV and 91 GeV, respectively. The strong force is an exception. The gluon has zero mass and the small range of the strong force results from other factors. As described in the preceding section, the vacuum conducts color charge, which prevents gluons from traveling more than about a proton radius.

Clearly, electroweak unification is broken at our current level of experimentation. This is an example of spontaneous broken symmetry.

The standard model is based on gauge symmetry. That symmetry is believed to hold at very high temperatures, such as those in the early universe. At that time, the W and Z bosons and all other particles had zero mass. So a fundamental question is, how did these particles and others get their masses?

In 1964, a decade before the development of the standard model, six physicists published three independent papers in the same issue of Physical Review Letters suggesting a way by which particles gain mass.11 To his expressed embarrassment, the process was named the Higgs mechanism after just one of the authors, a British professor named Peter Higgs. The other authors deserve mention. They are: Robert Brout (now deceased), François Englert, Gerry Guralnik, Dick Hagen, and Tom Kibble.

I referred earlier to the very informative and entertaining history of particle physics published in 1993 by Nobel laureate and then Fermilab director Leon Lederman, with help from Dick Teresi, called The God Particle.12 Lederman had used that expression to describe the Higgs particle in a lecture, partly as a joke. As we have seen, he is a great comedian. However, Lederman was also partly serious in emphasizing the fundamental role of the Higgs particle, existing everywhere in space, sort of like a god, and providing for the masses of particles. Most physicists hated the name. Higgs winced at it, calling it aggrandizing and offensive. Lederman said he offended two groups of people: those who believe in God and those who don't. But his publisher liked it and the media loved it.¹³

Higgs and the other authors had shown mathematically how the weak bosons are able to gain mass by a phase transition, the spontaneous breaking of the underlying gauge symmetry. The process left behind a field of scalar (spin-zero) particles called Higgs bosons that exist throughout space.¹⁴

Let me try to explain the concept in simple terms, although, as always, one can never do justice to a theory when words have to be substituted for mathematics.

In chapter 12, I will discuss the cosmology of the early universe. For our purposes here, let us assume it was originally in a state of perfect symmetry. As an analogy not to be taken too literally, think of a spherical ball of magnetite, a naturally magnetic form of iron oxide, heated to a very high temperature. Because of thermal motion, the iron atoms in the ball, which are like little bar magnets, point in random directions so, as a whole, the system is spherically symmetric. As the magnetite cools, it drops below a certain critical temperature and the random motions of the atoms slow down, allowing the little magnets to line up with each other because of their mutual interaction. The result is that the ball of magnetite becomes a magnet. Spherical symmetry is broken as a particular north–south axis is singled out. Note that this direction is random. This is an example of spontaneous symmetry breaking. The breaking of the symmetry results in the appearance of a field—the magnetic field.

Now, in the case of the Higgs mechanism, the symmetry that is broken is not in space-time but abstract state-vector space. Fields that are generated in this way are called gauge fields. The Higgs field is a gauge field. And the Higgs boson is the quantum of the Higgs field.

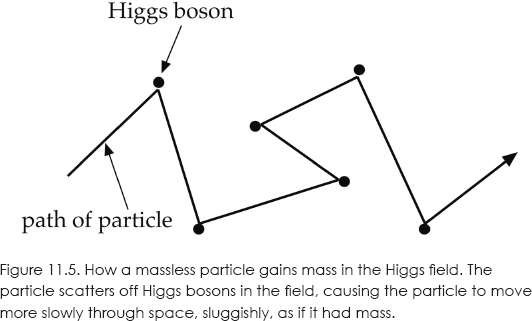
So how does the Higgs boson generate the masses of elementary particles? A crude, intuitive explanation is given in figure 11.5.

As a particle passes through the medium of the Higgs field, it collides with the Higgs bosons that manifest the field. Although the particle is moving at the speed of light along each leg, it scatters off the Higgs bosons and effectively slows down its progress through the medium. That is, it behaves more sluggishly—as if it had more inertia or mass. The photon does not interact directly with the Higgs and so remains massless.

Although, as we have seen, the Higgs mechanism was suggested several years earlier; it was built into the standard model in the 1970s. For over a decade, the Higgs boson remained the only particle in the model whose existence was not empirically confirmed—that is, until July 2012. Note it is the only spin-zero particle in the standard model, although there may be additional Higgs bosons in extensions of that model that might come about as new data come in.

The Higgs boson turned out to be the key to electroweak unification. As mentioned, Weinberg and Salam discovered that the Higgs field was responsible for the symmetry breaking that separates electromagnetism from the weak nuclear force leaving the photons massless while the W and Z bosons gain mass. And that wasn't all the Higgs did for the theory. In 1971, Dutch physicists Gerhardus ‘t Hooft and Martinus Veltman proved that the Higgs mechanism provides for the renormalization of all theories of the type called Yang-Mills theories, of which the electroweak force and other forces of the standard model are specific examples.

MAKING AND DETECTING THE HIGGS

Let me give an idea of how the Higgs boson might be produced and detected at the Large Hadron Collider. The LHC collides protons again protons.

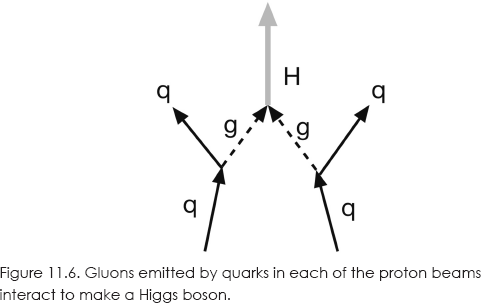
In figure 11.6, one way of many that this can produce Higgs bosons is illustrated. Gluons emitted by quarks in the protons interact to make a Higgs boson.

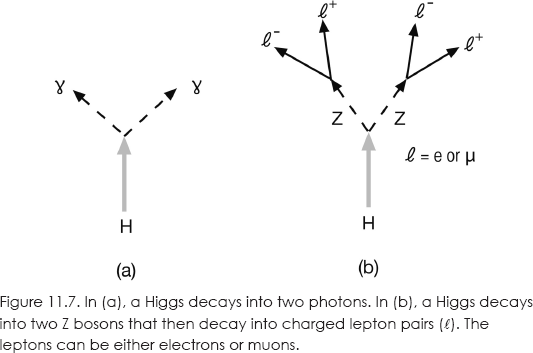
Now what about detection? Again many possibilities exist, but I will look at the two that have provided the best current evidence. In figure 11.7 (a), we have the Higgs decaying into two photons (γ-rays). In (b), the Higgs decays into two charged lepton pairs (l) that can be either muons or electrons.

In either case, the energy and momentum of the outgoing particle assumed to be from the Higgs decay are measured. From these, the mass of whatever produced the observed particles can be calculated. If that object is a particle, this should show up as a peak in the statistical distribution of as many such events as can be accumulated. The greater the number of events, the greater the statistical significance of the peak. When the chances of the peak being a statistical fluctuation are less than about one in ten thousand (in particle physics convention; some other fields have embarrassingly lower standards), a tentative discovery can be claimed. Only after independent replication, however, will the scientific consensus express confidence in the claim.

HUNTING THE HIGGS

Despite being proposed almost fifty years ago at this writing, and despite its crucial role in the highly successful standard model, the Higgs boson remained until now the only unconfirmed ingredient of that model. This has been presumably because its mass was too high to be produced with the particle accelerators available prior to the LHC. Ian Sample provides a detailed survey of the various experiments that unsuccessfully sought evidence for the Higgs until the first hints seen at the LHC in December 2011.15 I will provide only a sketch.

In the 1980s, US physicists set out to go full speed ahead and build the largest colliding beam accelerator the world had ever seen: the Superconducting Super Collider (SSC). Although at the time I was working on very high-energy gamma-ray and neutrino astronomy, I attended a couple of the summer workshops that Fermilab organized in Snowmass, Colorado. I was still an accelerator physicist at heart and supported the SSC enthusiastically.

President Ronald Reagan gave his approval, and in 1988 the site was selected to be Waxahachie, Texas. It may have been no coincidence that the new president elected that year, George H. W. Bush, was (nominally) a Texan. However, geologically it was a good site and the state of Texas also put up $1 billion to help pay costs. Construction began in 1991. The collider was to be a ring 87.1 kilometers (54.1 miles) around and would collide beams of protons together, each with energy 20 TeV.

Lederman's book, The God Particle, along with another excellent popular book by Steven Weinberg, Dreams of a Final Theory,¹⁶ both published about the same time, were intended to generate public support for the project, which would cost billions. When, in 1993, the estimated cost jumped from $4.4 billion to $12 billion, Congress took another look. By that time, $2 billion had already been spent and the tunnel for the ring was almost 30 percent complete.

However, the project had strong opposition from influential physicists in other fields, notably Nobel laureate Phillip Anderson, who deeply resented the way particle physicists were always saying their work was more fundamental than his field of condensed matter physics.17 Yet the Higgs mechanism was first suggested by Anderson in his work on superconductors a year before the Higgs et al. publications. Furthermore, the accelerator would involve the most massive use of superconductivity, for which Anderson won his award, the world had ever seen.

Also voicing strong opposition was the incoming president of the American Physical Society, materials scientist James Krumhansl. With this high-level opposition within the physics community, and with a Congress unconvinced of its value, the SSC didn't stand a chance.¹⁸

Weinberg, who teaches at the University of Texas, feels that the SSC might have had better luck if the originally favored site, Lederman's Fermilab, had been chosen.¹⁹ Much of the infrastructure and expert staff would have already been in place rather than having to be built up from scratch. With the scientifically unjustified $25 billion International Space Station also earmarked for Texas, the two giant Texas projects had little support in the rest of the country. The SSC was canceled by a vote of 2 to 1 in Congress, while the space station passed by one vote. Although President Bill Clinton had voiced mild support for the SSC, he signed the bill canceling the project on October 31, 1993.

This event marked a sharp decline in support for elementary particle physics in the United States that has continued to this day. Physics graduate students (including my own son) looked elsewhere for opportunities. (He found a good one in functional magnetic resonance imaging, fMRI.)

The United States was beaten in the hunt for the weak bosons, and now it would be beaten in the hunt for the Higgs. Although Fermilab made a valiant effort with its Tevatron collider, the focus shifted to Europe, first with the Large Electron-Positron Collider (LEP), and then with the Large Hadron Collider at the CERN laboratory in Geneva. Perhaps American physicists might have been smarter to follow the CERN model, where many countries play major roles and contribute money. Why does the United States have to lead in everything, anyway? In any case, American physicists have participated significantly in the latest CERN experiments.

After a huge effort, LEP failed to find the Higgs and was shut down in 2000 so its tunnel could be used for the LHC. The Tevatron was terminated in 2011. While the LHC is huge and still costs billions, it is smaller and cheaper than the SSC would have been, using an already-existing tunnel “only” 27 kilometers long compared to 87.1 kilometers and “only” 14 TeV total collision energy compared to 40 TeV for the SSC. In his book, Lederman had predicted that the Higgs would be seen at the SSC by 2005. It certainly would have settled the matter one way or the other and would have probed far deeper than the LHC will be able to.

This is to not to take any credit away from the LHC and the thousands of dedicated and talented scientists and engineers who have brought it into being. The LHC first began circulating beams of protons in opposite directions on September 10, 2008. It is currently operating at 4 TeV per proton beam and is scheduled to run at 7 TeV per beam in 2014, after a shutdown of twenty months for the upgrade.

Of the six detectors assembled at the LHC, two—ATLAS (A Toroidal LHC Apparatus) and CMS (Compact Muon Solenoid)—are general-purpose detectors that are involved in the hunt for the Higgs and other new phenomena. As of the Higgs announcement, the ATLAS collaboration consisted of 3,000 scientific authors from 174 institutions in 38 countries. CMS consisted of 3,275 physicists (of which 1,535 are students), and 790 engineers and technicians, from 179 institutes in 41 counties.

HIGGS CONFIRMED!

On July 4, 2012, CERN announced that both ATLAS and CMS have seen a signal in the mass range of 125 to 126 GeV that is very likely the long-sought-after Higgs boson, or a reasonable facsimile. The statistical significance in each case was reported as “5-sigma,” which implies that the probability it was a statistical fluctuation is one in 3.5 million. That is, each experiment taken alone was highly significant statistically. Even more important was the independent replication. Both the two-photon and four-lepton decay modes were seen.

It still remains to be demonstrated conclusively that this is indeed the Higgs boson and not some composite object made of already-known particles. So far it looks as expected for the Higgs of the standard model, but that may change as more data come in.

In late July 2012, ATLAS20 and CMS²¹ submitted papers to Physics Letters that provided more details and improved statistical significance.

MASS

I need to correct a common misunderstanding about the role that the Higgs boson, if indeed it exists, plays in the universe. Media reports, and even some public statements by physicists, have left the impression that the Higgs is responsible for the mass of the universe. This is not true. It is actually responsible for only a small fraction of the total mass of the universe.

This is not to say that the Higgs boson is not important. The main role of the Higgs in the standard model of elementary particles is to provide for the symmetry breaking of the unified electroweak force by giving mass to the weak bosons and splitting the electromagnetic and weak nuclear forces. It also gives mass to the other elementary particles, except for the massless photon and gluon. If elementary particles did not have mass, they would all be moving at the speed of light and would never stick together to form stuff like stars, cats, and you and me.

The mass of the universe is not simply the sum of the masses of the elementary particles that constitute matter. As we have seen, Einstein showed that the mass of a body is equal to its rest energy. If that body is not elementary but composed of parts, then its rest energy as a whole will be the sum of the energies of its parts. This sum will include the kinetic and potential energies of the parts in addition to their individual rest energies.

Now, for the bodies of normal experience, such as your neighbor's cat, the kinetic and potential energies of their parts are small compared to their rest energies. So, for all practical purposes, the total mass of a cat is equal to the sum of the masses of its parts.

This is even true at the microscopic scale. The masses of chemical elements are, typically, thousands of MeV, while the kinetic and binding energies are a few tens of eV. Only when you get down to the nuclei of the chemical elements do you get kinetic and potential energies that are measurable fractions of rest energies.

Inside nuclei, we have nucleons—protons and neutrons—that are themselves composed of quarks. Since quarks do not appear as free particles outside nucleons, we have to estimate their masses from studying the effects of their mutual interactions on the properties of nucleons and other particles that are composed of quarks. Fortunately, there are only six quarks but hundreds of particles (hadrons) made from these quarks to provide data to pin down quark properties. By using supercomputers to make numerical calculations referred to as Lattice QCD,22 physicists have obtained reliable estimates of quark masses, which are given in table 11.1. The result: the masses of the quarks inside a proton or neutron constitute only 1 percent of its mass. The other 99 percent is due to the potential energy of the strong force.

The objects familiar to most humans, including most scientists, have masses that are essentially given by the number of protons and neutrons they contain. So we can say that only 1 percent of that mass arises from the masses of quarks. Furthermore, this normal stuff is itself only 5 percent of the total mass of the universe. So the Higgs contribution to the mass of the universe, unless it has something to do with dark matter or dark energy (see chapter 12), is at most one part in two thousand.

GRAND UNIFICATION

In the decades since the development of the standard model, numerous attempts have been made to figure out what might come next as we explore to ever higher energies and smaller distances. The first step was to build on the successes of the past. When we look at the history of physics, one grand principle especially stands out, that is, unification.

When Newton realized that the same force was responsible for an apple falling to the ground as was responsible for the moon falling around Earth, he unified terrestrial and celestial gravity. When Faraday and Maxwell showed that electricity and magnetism were the same phenomenon, they unified electromagnetism. When Salam, Glashow, and Weinberg developed the electroweak model, they unified the electromagnetic and weak nuclear forces.²³

In the standard model, the strong nuclear force exists independently of the electroweak force, yet both are gauge theories. So it was obvious to attempt to unify these forces in what became known as GUTs for Grand Unified Theories.²⁴ As we have seen, symmetry groups play an important role in the standard model. In a unification scheme, some higher-order group, that is, one with many degrees of freedom, is assumed to describe the underlying symmetry, which then breaks down to give the structure we observe at lower energies. This is precisely the situation we described for the electroweak force. At high energies, the electromagnetic and weak forces are unified and their gauge bosons are all massless. The symmetry group is SU(2) × U(1). At lower energies, the electroweak force breaks down into electromagnetism, whose symmetry group is U(1), and the weak force, whose symmetry group is SU(2).

The problem with grand unification is that there are many groups to choose from, and without data, you can only speculate. In 1974, Sheldon Glashow and Howard Georgi made the reasonable proposal to start with the simplest symmetry group that could break down to the standard model, what is called minimal SU(5). Of all the other proposed GUTs, only minimal SU(5) made predictions that were testable with existing technology. But this prediction was an important one. Most theories that push beyond the standard model anticipate that the proton must be ultimately unstable. Otherwise, we cannot account for the fact that there exists a billion times as much matter as antimatter in the universe. The standard model makes no distinction between the two.

Minimal SU(5) made the specific prediction that the proton would decay into a positron and neutral pion,

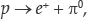
at a rate of one every 10^30±1 years. Many other decay modes are possible, but this one has the shortest lifetime as well as detectable decay products. The π⁰ decays almost immediately into two gamma-ray photons.

Now, we can't watch a single proton for 10^30±1 years, but ten tons of water contain 6 × 10³⁰ protons, so if we watch this much water for a year, we might see six protons decay. In the early 1980s, several experiments were mounted to search for proton decay. They were all installed deep underground, where the background from cosmic-ray muons was greatly reduced. The most sensitive of these, located deep in mines in Cleveland, Ohio, and Kamioka, Japan, contained 3,300 tons and 1,040 tons of purified water, respectively. However, none of these experiments, or any of several others I have not mentioned, witnessed proton decay. Thus, they effectively falsified minimal SU(5).

Incidentally, some philosophers of science argue that theories in physics are never falsified because their authors always fiddle things around to make them still consistent with the data. That claim is falsified by this example. While other GUTs were not ruled out, minimal SU(5) definitely was. There was no fiddling to be done. Note that a negative result can often be just as important as a positive one, as was the case here. These experiments were far from failures.

In 1996, the Kamioka detector was expanded to 50,000 tons of purified water and dubbed “Super-Kamiokande” (Kamiokande = Kamioka Nucleon Decay Experiment). I mentioned this experiment, in which I collaborated, earlier in this chapter where I discussed how it found evidence for neutrino mass in 1998. Super-K is still in operation and continues to search for proton decay. I left the project in 1999 shortly before retiring from the University of Hawaii. Results published in 2009 place a lower limit on the proton lifetime for the above reaction of 8.2 × 10³³ years.25 A number of other decay channels have been explored with similar negative but still extremely useful results.

SUPERSYMMETRY

As we have seen, all particles, elementary or not, divide up into two categories: bosons, such as the photon, Higgs boson, and helium atom, that have zero or integral spin; and fermions, such as the electron and lithium nucleus, that have half-integral spin. The principle of supersymmetry (SUSY) proposes that the basic laws of physics do not distinguish between bosons and fermions.

SUSY therefore predicts that every known boson has a “spartner” fermion and every known fermion has a “spartner” boson. The fermion electron is spartnered with a boson selectron. The boson photon is spartnered with a fermion photino. The fermion quark is spartnered with a boson squark. You get the idea. (Don't physicists have fun with the names they give things?) Supersymmetry implies that we can take, for example, the equations of QED that allow us to calculate the interaction of photons and electrons to high precision and apply them to the interaction of photinos and electrons, photons and selectrons, and photinos and selectrons.

Now it is clear that, like electroweak symmetry, supersymmetry is broken in our current universe; otherwise, the spartners of known particles would be just as common as the particles themselves because they would have the same masses, low enough to be detected long ago. A selectron would have the same mass as an electron. Since no one has detected any of these particles yet, they must be very massive (or nonexistent).

Indeed, theoretical estimates indicate that SUSY should show up at the LHC. As of this writing, when the collider has already been in operation for two years and has already seen what looks like the Higgs boson, no sign of SUSY has been found. In fact, when this book was in press, unpublished results were trickling in that, for all practical purposes, suggest SUSY is being ruled out by the failure to detect any sparticles in the expected mass range. If the LHC fails to detect SUSY, much of the theoretical effort over the past two or three decades will have been largely wasted. In particular, string theory will have to be abandoned as the ultimate “theory of everything” (TOE). I wouldn't be disappointed, though, because it would mean that we are finally learning something new.