CHAPTER 5
Celestial Lighthouses for Testing Relativity
It is unlikely that Joe Taylor and Russell Hulse will ever forget the summer of 1974. It started uneventfully enough. Taylor, a young professor at the University of Massachusetts at Amherst, had arranged for his graduate student Hulse to spend the summer at the Arecibo Radio Telescope in Puerto Rico looking for pulsars. They had put together a sophisticated observational technique that would allow them to scan a large portion of the sky using the radio telescope in such a way that it would be especially sensitive to signals from pulsars. At that time around a hundred pulsars were known, so their main goal was to add new ones to that list, in the hope that, by sheer weight of numbers, they could learn more about this class of astronomical objects. But apart from the possible payoff at the end of the observations, the bulk of the summer would be spent in rather routine, repetitive observing runs and compilation of data that, as in many such astronomical search programs, would border on tedium. But on 2 July, good fortune struck.
On that day, almost by accident, Hulse discovered something that would catapult both Hulse and Taylor into the astronomical headlines, excite the astrophysics and relativity communities, and ultimately yield the first confirmation of one of the most important predictions of general relativity.
At least as far as relativists are concerned, the discovery ranks up there with the discovery of pulsars themselves. That discovery was equally serendipitous. In late 1967, radio astronomer Antony Hewish and his graduate student Jocelyn Bell at Cambridge University were attempting to study quasars by exploiting the phenomenon of scintillation, the rapid variation or “twinkling” of the radio signal that is caused by clouds of electrons in the solar wind out in interplanetary space. These variations are typically random in nature and are weaker at night when the telescope is directed away from the Sun, but in the middle of the night of 28 November 1967 Bell recorded a sequence of unusually strong, surprisingly regular pulses in the signal. After a month of further observation, she and Hewish established that the source of this signal was outside the solar system, and that the signal was a rapid set of pulses with a period of 1.3372795 seconds.
As a standard of time measurement, these pulses were as good as any atomic clock that existed at the time. It was so unexpected to have a naturally occurring astrophysical source with such a regular period that, for a while, they entertained the thought that the signals were a beacon from an extraterrestrial civilization. They even denoted their source LGM, for little green men. The Cambridge astronomers soon discovered three more of these sources, with periods ranging from a quarter to one and a quarter seconds, and other observatories followed with their own discoveries. The little green men theory was quickly dropped, because if the signal was truly from an alien civilization then it should have shown a Doppler shift as the alien planet orbited around its alien star. The only Doppler shift they saw was due to the Earth’s motion around our Sun. The sources of these signals were renamed “pulsars” because of the pulsed radio emission.
This discovery had an enormous impact on the world of astronomy. The discovery paper for the first pulsar was published on 24 February 1968 in the British science journal Nature, and in the remaining ten months of that year over one hundred scientific papers were published reporting either observations of pulsars or theories of the pulsar phenomenon. In 1974, Hewish was rewarded for the discovery with the Nobel Prize in Physics, along with Martin Ryle, one of the pioneers of the British radio astronomy program. In some circles controversy still lingers over the decision of the Swedish Academy not to include Bell in the award. Now a renowned astronomer, academic leader and proponent of women in science, Dame Bell-Burnell (“Dame” being the female title that accompanies knighthood) has consistently expressed agreement with the Nobel decision.
Within a few years of the discovery, there was a general consensus about the overall nature of pulsars. Pulsars are simply cosmic lighthouses: rotating beacons of radio waves (and in some cases of optical light, X-rays and gamma rays) whose signals intersect our line of sight once every rotation period. The underlying object that is doing the rotating is a neutron star, a highly condensed body, typically a bit more massive than the Sun, but compressed into a sphere of around 20 kilometers in diameter, 500 times smaller than a white dwarf of a comparable mass, or 100,000 times smaller than a normal star of that mass. Its density is therefore about 500 million metric tons per cubic centimeter, comparable to the density inside the atomic nucleus. Neutron stars are so dense that a single teaspoon of neutron star matter on Earth would weigh the same as about 1,000 Great Pyramids of Giza in Egypt. As their name would indicate, neutron stars are made mostly of neutrons, with a contamination of protons and an equal number of electrons. Because a neutron star is so dense, it behaves as the ultimate flywheel, its rotation rate kept constant by the inability of frictional forces to overcome its enormous rotational inertia. Actually, there are some residual braking forces that do tend to slow it down, but an example of how small this effect can be is given by the original Bell–Hewish pulsar: its period of 1.3373 seconds is observed to increase by only 43 nanoseconds per year. Of the one hundred or so pulsars known by 1974, every one obeyed the general rule that it emits radio pulses of short period (between fractions of a second and a few seconds), and with a period that is extremely stable, except for a very, very slow increase. We will see that this rule almost proved to be the downfall of Hulse and Taylor.
Why a neutron star? Was this just a figment of the theorist’s imagination, or was there some natural reason to believe in such a thing? In fact, neutron stars did begin as a figment of the imagination of the astronomers Walter Baade and Fritz Zwicky in the mid 1930s, as a possible state of matter one step in compression more extreme than the white dwarf state. This remarkable suggestion was made only a few years after the discovery of the neutron! Such highly compressed stars, they suggested, could be formed in the course of a supernova, a cataclysmic explosion of a star in its death throes, that occurs in galaxies throughout the universe, including our own. While the outer shell of such a star explodes, producing a flash of light that can momentarily exceed the light output of the entire galaxy and ejecting a fireball of hot gas, the interior of the star implodes until it has been squeezed to nuclear densities, whereupon the implosion is halted, leaving a neutron star as the cinder of the supernova. The neutron star should also be spinning very rapidly, for the following reason. All stars for which decent data exist are known to rotate, the Sun being the nearest example. Therefore, just as the figure skater spins more quickly when she pulls in her arms, exploiting the conservation of angular momentum, so too the collapsing, rotating core of the supernova should speed up.
Of the five supernovae in our galaxy of which we have historical records during the past thousand years, one occurred in the constellation Taurus in 1054. It was recorded by Chinese astronomers as a “guest star” that was so bright that it could be seen during the day. The remnant of that supernova is an expanding shell of hot gas known as the Crab Nebula. The observed velocity of expansion of the gas is such that, if traced backward in time for about 950 years, it would have originated in a single point in space. Several months after the discovery of the first pulsars, radio astronomers at the National Radio Astronomy Observatory trained the telescope on the central region of the Crab Nebula and detected radio pulses. The discovery was confirmed at the Arecibo observatory, and the pulse period was measured to be 0.033 seconds, the shortest period for a pulsar known at the time. Moreover, compared to other pulsars, the Crab pulsar was slowing down at an appreciable rate, around 10 microseconds in period per year. Put another way, the time required for the period to change by an amount comparable to the period itself is around 1,000 years, which is just the approximate age of the pulsar if it was formed in the 1054 supernova. Finally, if the pulsar is a rotating neutron star, the loss of rotational energy implied by its slowing spin turned out to be enough to keep the nebula of gas sufficiently hot to glow with the observed intensity.
The fact that all these observations were so consistent with one another provided a beautiful confirmation of the rotating neutron star model for pulsars. The most recent nearby supernova occurred in 1987 in the Large Magellanic Cloud, a small satellite galaxy to the Milky Way.
Other aspects of pulsars are not so clean cut or so simple, however, and one of these is the actual mechanism for the “lighthouse beacon,” if indeed that is how the radio pulses are produced. In the conventional model, a pulsar is thought to have one important feature in common with Earth: its magnetic northern and southern poles do not point in the same direction as its rotation axis. On Earth, for instance, the geomagnetic northern pole is near Ellesmere Island, in the far north of Canada, not in the middle of the Arctic Ocean, as is the north pole of the rotation axis. There is one key difference, however. The magnetic field of a generic pulsar is a trillion times stronger than that of Earth. Such enormous magnetic fields produce forces that can strip electrons and ions from the surface of the neutron star and accelerate them to nearly the speed of light. This causes the particles to radiate copiously in radio waves and other parts of the electromagnetic spectrum, and because the magnetic field is strongest at the poles, the resulting radiation is beamed outward along the northern and southern magnetic poles. Because these poles are not aligned with the rotation axis, the two beams sweep the sky, and if one of them hits us, we record a pulse and call the source a pulsar. The precise details of this mechanism are still not fully worked out, partly because we have absolutely no laboratory experience with magnetic fields of such strength and with bulk matter at such monstrous densities. However, using massive computer simulations, researchers have recently been making progress in comprehending how the beams originate.
Nevertheless, by the summer of 1974 there was agreement on the broad features of pulsars. They were rapidly rotating neutron stars whose periods were very stable except for a very slow increase with time. It was also clear that the more pulsars we knew about and the more detailed observations we had, the better the chances of unraveling the details.
This is what motivated and guided Hulse and Taylor in their pulsar search. The receiver of the 1,000 foot radio telescope at the Arecibo observatory was driven so that as the Earth rotated, in one hour the instrument could observe a strip of sky a sixth of a degree wide by three degrees long. At the end of each day’s observations the recorded data were fed into a computer, which looked for pulsed signals with a well-defined period. If a candidate set of pulses was found, it had to be distinguished from terrestrial sources of spurious pulsed radio signals, such as radar transmitters and automobile ignition systems. The way to do this was to return later to the portion of the sky to which the telescope was pointing when the candidate signals were received and see if pulses of almost exactly the same period were present. If so, they had a good pulsar candidate that they could then study further, such as by measuring its pulse period to the microsecond accuracy characteristic of other pulsars. If not, forget it and move on to another strip of the sky.
The day-to-day operation of the program was done by Hulse, while Taylor made periodic trips down from Amherst throughout the summer to see how things were going. On 2 July, Hulse was by himself when the instruments recorded a very weak pulsed signal. If the signal had been more than 4 percent weaker, it would have fallen below the automatic cutoff that had been built into the search routine and would not even have been recorded. Despite its weakness, it was interesting because it had a surprisingly short period, only 0.059 seconds. At the time, only the Crab pulsar had a shorter period. This made it worth a second look, but it was 25 August before Hulse got around to it.
The goal of the 25 August observing session was to try to refine the period of the pulses. If this were a pulsar, its period should be the same to at least six decimal places, or to better than a microsecond, over several days, because even if it were slowing down as quickly as the Crab was, the result would be a change only in the seventh decimal place. That is where the troubles began. Between the beginning and the end of the two-hour observing run, the computer analyzing the data produced two different periods for the pulses, differing by almost 30 microseconds. Two days later, Hulse tried again, with even worse results. As a result, he had to keep going back to the original discovery page in his lab notebook and cross out and re-enter new values for the period. His reaction was natural: annoyance. Because the signal was so weak, the pulses were not clean and sharp like those from other pulsars, and the computer must have had problems getting a fix on the pulses. Perhaps this source was not worth the hassle. If Hulse had actually adopted this attitude and dumped the candidate, he and Taylor would have been the astronomical goats of the decade. As it turned out, the suspicious Hulse decided to take an even closer look.
During the next several days, Hulse wrote a special computer program designed to get around any problems that the standard program might be having in resolving the pulses. But even with the new program, data taken on 1 and 2 September also showed a steady decrease of about 5 microseconds during the two-hour runs. This was much smaller than before, but still larger than it should be, and it was a decrease instead of the expected increase. To continue to blame this on the instruments or the computer was tempting, but not very satisfying.
But then Hulse spotted something. There was a pattern in the changes of the pulse period! The sequence of decreasing pulse periods on 2 September appeared to be almost a repetition of the sequence of 1 September, except it occurred 45 minutes earlier. Hulse was now convinced that the period change was real and not an artifact. But what was it? Had he discovered some new class of object: a manic depressive or bipolar pulsar with periodic highs and lows? Or was there a more natural explanation for this bizarre behavior?
The fact that the periods nearly repeated themselves gave Hulse a clue to an explanation. The source was indeed a well-adjusted pulsar, but it wasn’t alone! The pulsar, Hulse postulated, was in orbit about a companion object, and the variation in the observed pulse period was simply a consequence of the Doppler shift (see Figure 5.1). When the pulsar is approaching us, the observed pulse period is decreased (the pulses are jammed together a bit), and when it is receding from us the pulse period is increased (the pulses are stretched out a bit). Actually, optical astronomers are very familiar with this phenomenon in ordinary stars. As many as half the stars in our galaxy are in binary systems (systems with two stars in orbit about each other), and because it is rarely possible to resolve the two stars telescopically, they are identified by the up-and-down Doppler shifts in the frequencies of the spectral lines of the atoms in the atmospheres of the stars. In most ordinary stellar binary systems, the Doppler shifts of the spectra of both stars are observed; however, occasionally one of the stars is too faint to be seen, so astronomers can detect the motion of only one of the stars. And in recent years many exoplanets have been deduced by observing only the Doppler shifted spectra of the parent star. Such appeared to be the case here, where the pulse period was playing the same role as the spectral line in an ordinary star. One of Hulse’s problems with this hypothesis was a practical one: he couldn’t find any decent books on optical stellar binary systems in the Arecibo library because radio astronomers don’t usually concern themselves with such things.
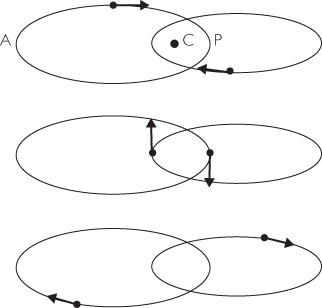
Figure 5.1 Orbit of a binary system such as the one containing the binary pulsar. The orbit of each body is an ellipse, and their velocities are shown here with arrows. The center of mass C of the system is the focus of each ellipse, while the periastron of one body is denoted P, and the apastron is A.
Now, because the dish of the Arecibo telescope is built into a natural bowl-shaped valley in the mountains of Puerto Rico, it could only look at the source when it was within 1 hour on either side of the zenith or overhead direction (hence the two-hour runs), and so Hulse couldn’t just track the source for hours on end; he could only observe it during the same two-hour period each day. But the shifting of the sequence of periods in the 1 and 2 September data meant that the orbital period of the system must not be commensurate with 24 hours, and so each day he could examine a different part of the orbit, if indeed his postulate was right. On Thursday 12 September he began a series of observations that he hoped would unravel the mystery (see Figure 5.2).
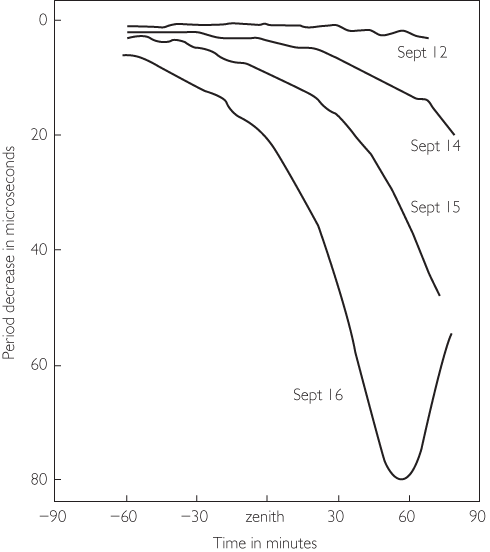
Figure 5.2 Pulse period changes of the binary pulsar over a five-day period in September 1974. Adapted from a page of Russell Hulse’s notebook.
On 12 September the pulse period stayed almost constant during the entire run. On 14 September, the period started from the previous value and decreased by 20 microseconds over the 2 hours. The next day, 15 September, the period started out a little lower and dropped 60 microseconds, and near the end of the run it was falling at the rate of 1 microsecond per minute. The speed of the pulsar along the line of sight must be varying, first slowly, then rapidly. The binary hypothesis was looking better and better, but Hulse wanted to wait for the smoking gun, the clinching piece of evidence. So far the periods had only decreased. But if the pulsar is in orbit, its motion must repeat itself, and therefore he would eventually be able to see a phase of the orbit when the pulse period increased, ultimately returning to its starting value to continue the cycle.
He didn’t have long to wait. The very next day, 16 September, the period dropped rapidly by 70 microseconds, and with only about 25 minutes left in the observing run it suddenly stopped decreasing, and within 20 minutes it had climbed back up by 25 microseconds. This was all Hulse needed, and he called Taylor in Amherst to break the news. Taylor flew immediately down to Arecibo, and together they tried to complete the solution of this mystery. However, the real excitement was still to come.
The first thing they determined was the orbital period, by finding the shortest interval over which the pattern of pulse readings repeated. The answer was 7.75 hours, so the 45-minute daily shift that Hulse had seen was just the difference between three complete orbits and one Earth day.
The next obvious step was to track the pulse period variations throughout the orbit to try to determine the velocity of the pulsar as a function of time. This is a standard approach in the study of ordinary binary systems, and a great deal of information can be obtained from it. If we adopt Newtonian gravitation theory for a moment, then we know that the orbit of the pulsar about the center of mass of the binary system (a point somewhere between the two, depending upon their relative masses) is an ellipse with the center of mass at one focus (see Figure 5.1). The orbit of the companion is also an ellipse about this point, but because the companion is unseen, we don’t need to consider its orbit directly. The orbit of the pulsar lies in a plane that can have any orientation in the sky. It could lie on the plane of the sky, in other words perpendicular to our line of sight, or we could be looking at the orbit edge on, or its orientation could be somewhere between these extremes. We can eliminate the first case, because if it were true, then the pulsar would never approach us or recede from us and we would not detect any Doppler shifts of its period. We can also forget the second case, because if it were true, then at some point the companion would pass in front of the pulsar (an eclipse) and we would lose its signal for a moment. No such loss of the signal was seen anywhere during the eight-hour orbit. So the orbit must be tilted at some angle relative to the plane of the sky.
That is not all that can be learned from the behavior of the pulsar period. Remember that the Doppler shift tells us only the component of the pulsar velocity along our line of sight; it is unaffected by the component of the velocity transverse to our line of sight. Suppose for the sake of argument that the orbit were a pure circle. Then the observed sequence of Doppler shifts would go something like this: starting when the pulsar is moving transverse to the line of sight, we see no shift; one-quarter period later it is moving away from us, and we see a negative shift in the period; one-quarter cycle after that it is again moving transverse, and we see no shift; one-quarter cycle later it is moving toward us with the same velocity, so there is an equal positive shift in the period; after a complete orbital period of seven and three-quarter hours, the pattern repeats itself. The pattern of Doppler shifts in this case is a nice symmetrical one, and totally unlike the actual pattern observed.
The observed pattern tells us that the orbit is actually highly elliptical or eccentric. In an elliptical orbit, the pulsar does not move on a fixed circle at a constant distance from the companion; instead it approaches the companion to a minimum separation at a point called periastron (the analogue of perihelion for the planets) and separates from the companion one-half of an orbit later to a maximum distance at a point called apastron. At periastron, the velocity of the pulsar increases to a maximum, and following periastron it decreases again, all over a short period of time, while at apastron, the velocity slowly decreases to a minimum value and afterward it slowly increases again.
The observed behavior of the Doppler shift with time indicated a large eccentricity (see Figure 5.3). Over a very short period of time (only two hours out of the eight) the Doppler shift went quickly from zero to a large value and back, while over the remaining six hours, it changed slowly from zero to a smaller value in the opposite sense and back. In fact, the 16 September smoking gun observation saw the pulsar pass through periastron, while the 12 September observations saw the pulsar moving slowly through apastron. Detailed study of this curve showed that the separation between the two bodies at apastron was four times larger than their separation at periastron. It also showed that the direction of the periastron was almost perpendicular to the line of sight, because the periastron (the point of most rapid variation in velocity) coincided with the largest Doppler shift (the point where the pulsar has the smallest amount of transverse motion).
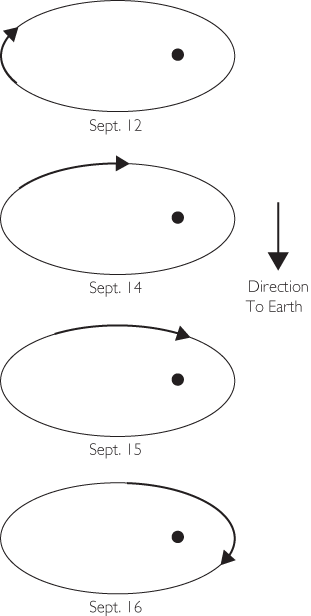
Figure 5.3 Location of the pulsar in its orbit. On 12 September, the pulsar is moving through apastron; its speed is low and slowly varying, so there is little change in the observed period (see Figure 5.2). The pulsar is moving away from us, so the period is longer than the “rest” period. On 14 September the pulsar is moving almost transversely, so there is little Doppler shift, and the period is shorter than before. On 15 September, the pulsar is starting to move toward us and is speeding up as it nears periastron; the pulse period decreases markedly toward the end of the run. On 16 September the pulsar starts out moving almost transversely, then quickly passes through periastron, so its velocity toward us quickly reaches a maximum, then decreases; the pulse period rapidly reaches a minimum and then increases. The portion of the orbit seen during the same two-hour interval each day varies because the orbital period is 7.75 hours, so the portion seen is 45 minutes further advanced each day.
At this point, things began to get very interesting. The actual value of the velocity with which the pulsar was approaching us, as inferred from the decrease in its pulse period, was about 300 kilometers per second, or about one-thousandth of the speed of light! The velocity of recession was about 75 kilometers per second. These are high velocities! The speed of the Earth in its orbit about the Sun is only 30 kilometers per second. Combining the speed information with the orbital period, one could estimate that the average separation between the pulsar and its companion was only about as large as the radius of the Sun.
When news of this discovery began to spread in late September 1974 it caused a sensation, especially among general relativists. The reason is that the high orbital speeds and close proximity between the two bodies made this a system where effects of general relativity could be measurable.
In fact, even before Hulse and Taylor’s discovery paper on the binary pulsar appeared in print (but too late to stop the presses), Taylor and his colleagues had detected one of the most iconic effects of general relativity, known as the “periastron advance” of the orbit.
According to Newton’s gravitational theory, the orbit of a planet about its star is generally an ellipse, with the long axis of the ellipse always pointing in the same direction. For a binary star system, each body moves on an ellipse with the center of mass of the system as a focus (see Figure 5.1), but both ellipses are fixed in orientation. Any deviation from a pure Newtonian gravitational force between the two bodies, such as the gravitational tug of a third nearby body, or a modification of Newton’s laws provided by a theory like general relativity, can cause the ellipse to rotate or “precess,” as illustrated in Figure 5.4. As a result, the periastron, or point of closest approach, will not always be in a fixed direction, but will advance slowly with time.
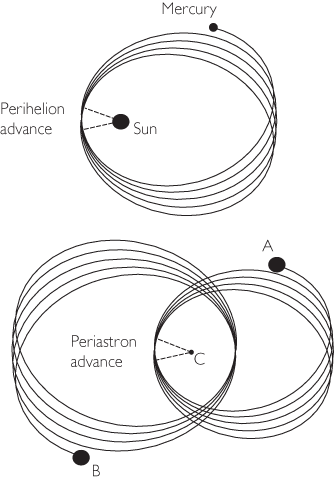
Figure 5.4 Top panel: Advance of the perihelion of Mercury’s orbit around the Sun. Because the Sun is so massive, it barely moves. The rate of advance has been greatly exaggerated. Bottom panel: Advance of the periastron of two stars A and B of comparable mass orbiting around their center of mass C.
In the case of Mercury orbiting the Sun, astronomers had already established by the middle of the nineteenth century that its point of closest approach, called the perihelion, was advancing at a rate of 575 arcseconds per century. It was reasonable to assume that this was the result of the perturbing effects of the other planets in the solar system (Jupiter, Venus, Earth, etc.), and French astronomer Urbain Jean Joseph Le Verrier, who was the director of the Observatory of Paris, set out to calculate these effects. In 1859 he announced that there was a problem. The sum total of the effects of the planetary perturbations fell short of the observed advance of the perihelion by about 43 arcseconds per century (here we are quoting the modern value of the discrepancy). Le Verrier had recently become famous by predicting that some anomalies in the orbit of Uranus were being caused by a more distant planet, a prediction confirmed months later when German astronomers, using his calculations as a guide, discovered Neptune. It was therefore natural for Le Verrier and his contemporaries to postulate that the anomaly in Mercury’s orbit was due to a planet between Mercury and the Sun. They even gave the planet the name Vulcan, after the Roman god of fire. Despite numerous claimed sightings of Vulcan over the next 60 years, no credible evidence for the planet was ever found.
Einstein was well aware of the problem of Mercury’s anomalous perihelion advance, and in fact he used it as a way to test and ultimately reject earlier versions of his theory, notably a “draft” theory he had devised in 1913 with mathematician Marcel Grossmann. In November 1915, when everything seemed to be falling into place theoretically for his latest attempt, the tipping point occurred when his calculations showed that the theory gave the correct value for the missing perihelion advance. He later wrote that this discovery gave him “palpitations of the heart.”
In 1915, the agreement that Einstein found was fairly crude, because the observations of Mercury’s orbit were not very accurate. But since the 1970s Mercury’s perihelion advance has become another high-precision confirmation of general relativity, made possible by high-precision radar tracking of planets and spacecraft. The most recent test was made using Mercury MESSENGER. In 2011, MESSENGER became the first spacecraft to orbit Mercury, and radar measurements of the orbiter were made until the spacecraft ended its mission in 2015 with a controlled crash on the surface of Mercury. The data from that mission yielded a measurement of Mercury’s perihelion advance in agreement with general relativity to a few parts in 100,000. Improved measurements down to the level of parts per million may be possible with data from the joint European-Japanese BepiColombo mission to place two orbiters around Mercury, launched in late 2018.
If Einstein’s theory indeed played a role in Hulse and Taylor’s system, then measuring the binary analogue of Mercury’s advance was of high priority, and during a two and a half month observing program that ended on 3 December 1974, Taylor and his colleagues tried to pin it down. Coming up was the seventh installment of the Texas Symposium on Relativistic Astrophysics that had begun in Dallas in 1963. After cycling twice through a trio of cities that included Austin and New York, it was back in Dallas. The data analysis was completed just in time for Taylor to reveal to the audience on 20 December that the rate of periastron advance for the binary pulsar was 4 degrees per year. This advance rate is about 36,000 times larger than the rate for Mercury, but that’s not a surprise. Because of the higher orbital speed and smaller separation in the binary system, the raw effects of general relativity are roughly 100 times larger than for Mercury, and the binary system completes 250 times more orbits per year, so the cumulative effect on the periastron builds up faster. Taylor would return to the Texas symposium four years later with an even more impressive announcement.
While it was great to see Einstein’s theory in action in a new and exotic arena outside the solar system, Taylor’s measurement didn’t actually provide a real test of the theory. The problem is that the prediction of general relativity for the periastron advance for a binary system depends on the total mass of the two bodies; the larger the mass, the larger the effect. It also depends on other variables, such as the orbital period and the ellipticity of the orbit, but these are known from the observations. Unfortunately, we do not know the masses of the two bodies with any degree of accuracy. All we know is that they are probably comparable to that of the Sun in order to produce the observed orbital velocity, but there is enough ambiguity, particularly in the tilt of the orbit with respect to the plane of the sky, to make it impossible to pin the masses down any better from the Doppler shift measurements alone. Well, if we can’t test general relativity using the periastron advance measurement, what good is it?
It is actually of tremendous good, because we can turn the tables and use general relativity to weigh the system! If we assume that general relativity is correct, then the predicted periastron advance depends on only one unmeasured variable, the total mass of the two bodies. Therefore, the measured periastron advance tells us what the total mass must be in order for the predicted and measured values to agree. From the fall 1974 observations, the inferred total mass was about 2.6 solar masses. Eventually, the periastron advance could be measured so accurately, 4.226585 degrees per year, that the total mass of the system was pinned down to 2.8284 solar masses. This was a triumph for general relativity. Here, for the first time, the theory was used as an active tool in making an astrophysical measurement, in this case the determination of the total mass of a distant system to high precision.
The relativists’ intuition that this system would be a new laboratory for Einstein’s theory was confirmed. But there was more to come.
During the first few months of observations of the pulsar, it was realized that this was a very unusual pulsar, over and above it being in a binary system. Once the strange variations in its observed pulse period were seen to be due to Doppler shifts resulting from its orbital motion, these variations could be removed from the data, allowing the observers to examine the intrinsic pulsing of the object, as if it were at rest in space. Its intrinsic pulse period was 0.05903 seconds, but if it was slowing down, as do other pulsars, it was doing so at an unbelievably low rate. It took almost an entire year of observation to detect any change whatsoever in the pulse period, and when the data were finally good enough to measure a change, it turned out to be only a quarter of a nanosecond per year. This was 50,000 times smaller than the rate at which the Crab pulsar’s period changed. Clearly, any friction that the spinning neutron star was experiencing was very, very small, a fact that was consistent with the observation that its radio signal is so feeble that Hulse almost missed it. At this rate, the pulsar would change its period by only half a percent in a million years. The steadiness and constancy of this pulsar made it one of the best timepieces the universe had ever seen! In later years, many rapidly spinning but very steady pulsars would be detected; we will return to them in Chapter 9.
This remarkable steadiness made it possible for the observers to change how they made the measurements. Instead of measuring pulse periods (the difference in time between adjacent pulses) and the changes induced in the periods by the Doppler shift and various relativistic effects, they were able to measure the arrival times of individual pulses. The pulsar was so steady that Taylor and his colleagues could keep track of the radio pulses as they came into the telescope, and even when they had to interrupt the observations for long periods of time, while they returned to their home universities for such “mundane” duties as teaching, or while the telescope was used for other observing programs, they could return to the telescope after such breaks and pick up the incoming train of pulses without losing track of a single beep. To see why this leads to a big improvement in accuracy, consider a simple example. Suppose you can measure arrival times to a basic accuracy of a hundredth of a second. If the pulse period is 1 second, that implies that you can measure the period to 1 percent. But now if you measure the arrival time of pulse number 1 to a hundredth of a second, and then wait 50 seconds and measure the arrival time of pulse number 51 to the same precision, you will have measured the combined period of 50 pulses to a hundredth of a second, or that of a single pulse to one part in 5,000. How do you know that it was pulse 51 and not pulse 39 or 78? Because knowing the period to one part in 100, you know that the error in arrival time after 50 seconds is less than a whole pulse period, and so the pulse that arrives can’t be anything but number 51.
Eventually, this arrival-time technique allowed them to determine the characteristics of the pulsar and the orbit with accuracies that began to boggle the mind: for the intrinsic pulsar period, 0.059030003217813 seconds; for the rate at which the intrinsic pulse period was increasing, 0.272 nanoseconds per year; for the rate of periastron advance, 4.226585 degrees per year; for the orbital period, 27906.9795865 seconds. Because the pulsar period changes by the quoted amount in the last three digits each year, when scientists refer to a measured pulsar period they must also refer to a specific date when that value would be true; in this case, the conventional date is 11 December 2003.
There was more to this accuracy than just an impressive string of significant digits. It also yielded two further relativistic dividends. The first of these was another example of applied relativity, or relativity as the astrophysicist’s friend. Beside the ordinary shift of the pulses’ arrival times caused by the varying orbital position of the pulsar, there are two other phenomena that can affect it, both relativistic in nature. The first is the time dilation of special relativity: because the pulsar is moving around the companion with a high velocity, the pulse period measured by an observer foolish enough to sit on its surface (he would, of course, be crushed to nuclear density) is shorter than the period observed by us. In other words, from our point of view the pulsar clock slows down because of its velocity. Because the orbital velocity varies during the orbit, from a maximum at periastron to a minimum at apastron, the amount of slowing down will be variable, but will repeat itself each orbit. The second relativistic effect is the gravitational redshift, a consequence of the principle of equivalence, as we have already seen in Chapter 2. The pulsar moves in the gravitational field of its companion, while we the observers are at a very great distance; thus, the period of the pulsar is redshifted, or lengthened, just as the period (or the inverse of the frequency) of a spectral line from the Sun is lengthened. This lengthening of the period is also variable because the distance between the pulsar and the companion varies from periastron to apastron, and it also repeats itself each orbit.
The combined effect of these two phenomena is a periodic up and down variation in the observed arrival times, over and above that produced by the orbital position. But whereas the orbital motion changed the pulse period in the fifth decimal place, these effects, being relativistic, are much smaller, changing the pulse period only beginning at the eighth decimal place. It is extremely difficult to measure such a small periodic variation, given the inevitable noise and fluctuations in such sensitive data, but within four years of continual observation and improvement in the methods, the effect was found, and the size of the maximum variation was 184 nanoseconds in the pulse period. Again, as with the periastron, this observation does not test anything, because the predicted effect turns out to contain another unknown parameter, namely the relative masses of the two bodies in the system. The periastron advance gives us the total mass, but not the mass of each body. Therefore we can once again be “applied relativists” and use the measured value of this new effect to determine the relative masses. The result was 1.438 solar masses for the pulsar, and 1.390 solar masses for the companion, good to about 0.07 percent. The understanding and application of relativistic effects here played a central role in the first precise determination of the mass of a neutron star.
These results for the masses of the two bodies were also interesting because they were consistent with what astrophysicists thought about the companion to the pulsar. Because it has never been seen directly, either in optical, radio or X-ray emission, we must use some detective work to guess what the companion might be. It certainly cannot be an ordinary star like the Sun, because the orbital separation between the pulsar and the companion is only about a solar radius. If the companion were Sun-like, the pulsar would be plowing its way through the companion’s outer atmosphere of hot gas, and this would cause severe distortions in the radio pulses that must propagate out of this gas. Such distortions are not seen. Therefore, the companion must be much smaller, yet still have 1.4 times the mass of the Sun. Such astronomical objects are called “compact” objects, and astrophysicists know of only three kinds: white dwarfs, neutron stars and black holes.
The currently favored candidate for the companion is another neutron star, based on computer simulations of how this system might have formed from an earlier binary system of two massive stars that then undergo a series of supernova explosions to leave two neutron-star cinders. The fact that both masses turn out to be almost the same is consistent with the observation that in these computer models, the central core of the pre-supernova star tends to have a mass close to 1.4 solar masses. After the outer shell of each star is blown away, the leftover neutron stars each have about this mass. This mass is called the Chandrasekhar mass, after the astrophysicist Subrahmanyan Chandrasekhar, who determined in 1930 that this value was the maximum mass possible for a white dwarf (this discovery earned “Chandra” a share of the Nobel Prize in Physics in 1983). Because a pre-supernova core is similar in many respects to a white dwarf, it is not surprising that this special mass crops up here as well.
According to these models, the pulsar that Hulse detected was formed in the first supernova explosion, which left a spinning pulsar with a strong magnetic field but without really affecting the companion star. But the fate of such a pulsar in isolation is to spin down, causing its magnetic field to weaken to such a degree that it no longer generates a detectable pulsar beam. This pulsar followed this track. Meanwhile, the massive companion star evolved toward its own inevitable supernova explosion, but first it underwent an expansion of its gaseous atmosphere, a common occurrence in the evolution of massive stars. The pulsar skimmed across this atmosphere, getting spun up to a rapid rotational speed, just as a beach ball spins up as it skims across water. It ended up as a weakly magnetized, rapidly spinning pulsar with a weak pulsar beam, pretty much as Hulse detected. The companion star finally exploded, leaving a second pulsar, again without affecting the first pulsar, and eventually the companion pulsar spun down enough that its beam was too weak to detect. The final system, then, is an old neutron star “recycled” as a fast pulsar (the one Hulse detected), and a young neutron star but “dead” pulsar (the one Hulse did not detect).
But the biggest payoff of the binary pulsar was yet to come.
General relativity predicts that binary star systems emit gravitational radiation. We will devote most of Chapter 7 to a discussion of the history and nature of gravitational waves. For our purposes here, the main thing we need to know is that by 1974, gravitational radiation was an active subject, and relativists were dying to find some. Even though Joseph Weber of the University of Maryland had claimed detection of waves as early as 1968, later experiments by other workers had failed to confirm his results, and the general feeling was that gravitational waves had not yet been found. Therefore, when the binary pulsar was discovered, and it was seen to be a new laboratory for relativistic effects, it seemed like a godsend. The binary pulsar could be used in the search for gravitational waves.
But not in the obvious sense. Because the binary pulsar is 29,000 light years away, the gravitational radiation that it emits is so weak by the time it reaches the Earth, and is of such low frequency (about 6 cycles per day), that it is undetectable by any detectors of today or the foreseeable future. On the other hand, general relativity predicts that gravitational waves carry energy away from the system, and therefore the system must be losing energy. How will that loss manifest itself? The most important way is in the orbital motion of the two bodies, because after all, it is the orbital motion that is responsible for the emission of the waves. A loss of orbital energy produces a speed-up of the two bodies and a decrease in their orbital separation. This seemingly contradictory statement can be understood when you realize that the total orbital energy of a binary system has two parts: a kinetic energy associated with the motion of the bodies, and a gravitational potential energy associated with the gravitational force of attraction between them. So although a speed-up of the bodies causes their kinetic energy to increase, a decrease in separation causes their potential energy to decrease by about twice as much, so the net effect is a decrease in energy. The same phenomenon happens, for example, when an Earth satellite loses energy because of friction against the residual air in the upper atmosphere; as it falls toward Earth it goes faster and faster, yet its total energy is declining, being lost in this case to heat. In the case of the binary pulsar, the speeding up combined with the decreasing separation will cause the time required for a complete orbit, the orbital period, to decrease.
Here was a way to detect gravitational radiation, albeit somewhat indirectly, and a number of relativists pointed out this new possibility in the fall of 1974, soon after the discovery of the binary pulsar. As we will see in Chapter 7, the effects of gravitational radiation are exceedingly weak, and this was no exception. The predicted rate at which the 27,000 second orbital period should decrease was only on the order of some tens of microseconds per year. Although this was an exciting possibility, the small size of the effect was daunting, and some thought it would take ten to fifteen years of continual observation to detect it.
Now flash forward just four years, to December 1978: the Ninth Texas Symposium on Relativistic Astrophysics, this time in Munich, Germany (Munich is in the state of Bavaria, sometimes considered the Texas of Germany). Joe Taylor was scheduled to give a talk on the binary pulsar. Rumor had it that he had a big announcement, and only a few insiders knew what it was. Cliff knew because he was scheduled to follow Taylor to present the theoretical interpretation of his results. A press conference had been set up for later in the day. In a succinct, fifteen-minute talk (a longer, more detailed lecture was scheduled for the following day), Taylor presented the bottom line: after only four years of data taking and analysis they had succeeded in detecting a decrease in the orbital period of the binary system, and the amount agreed with the prediction of general relativity, within the observational errors. This beautiful confirmation of an important prediction of the theory was a fitting way to open 1979, the centenary year of Einstein’s birth.
It turned out that the incredible stability of the pulsar clock, together with some elegant and sophisticated techniques for taking and analyzing the data from the Arecibo telescope that Taylor and his team had developed, resulted in such improvements in accuracy that they were able to beat by a wide margin the projected timetable of ten years to see the effect. These improvements at the same time allowed them to measure the effects of the gravitational redshift and time dilation, and thereby measure the mass of the pulsar and of the companion separately. This was important because the prediction that general relativity makes for the energy loss rate depends on these masses, as well as on other known parameters of the system, so they needed to be known before a definite prediction could be made. With the values of about 1.4 solar masses for both stars, general relativity makes a prediction of 75 microseconds per year for the orbital period decrease. The most recent analysis of the data shows agreement with the prediction to better than 0.2 percent. The 1993 Nobel Prize in Physics was awarded to Hulse and Taylor for the discovery of the system and for the confirmation of the existence of gravitational radiation.
These results triggered intensive searches for more binary pulsars at the world’s largest radio telescopes, resulting in an explosion in the number of known pulsars. More than 2,600 pulsars are currently known. What was once “the” binary pulsar has now joined around 290 other pulsars in binary systems. Most are utterly uninteresting for general relativity because they are so widely separated that the effects of the theory are unimportant or undetectable. A few pulsars are known to have planets, presumably not particularly habitable. Only about a hundred of the binaries have orbital periods shorter than a day, which makes them potential fodder for relativity. Some have white dwarf companions, while others appear quite similar to the original Hulse–Taylor binary pulsar. Two systems stand out, however.
The first was discovered in 2003 by Marta Burgay and collaborators using the Parkes 64 meter radio telescope in Australia. This system turned out to be full of surprises. The pulsar’s orbital period was a factor of three shorter than that of the Hulse–Taylor binary, making it even more compact and relativistically interesting. The measured periastron advance was a remarkable 17 degrees per year, indicating a total mass of about 2.6 solar masses. A few months after the discovery, followup observations detected weak pulses from the companion! This was the first (and so far the only) double pulsar detected. In fact the two pulsars fit the same theoretical profile as the Hulse–Taylor system: pulsar A was evidently an old recycled pulsar, spun up to a spin period of only 23 milliseconds, while pulsar B, with a longer spin period of 2.8 seconds and a very feeble pulsed signal, was an almost dead, younger pulsar.
Because the variations of the pulses of both pulsars could be tracked, the two orbits could be fixed with more certainty than was the case for the Hulse–Taylor system. From these observations, along with the periastron advance, it was possible to determine the two masses directly: 1.338 and 1.249 solar masses for the main pulsar and the companion pulsar respectively. This in turn could be shown to imply that the orbit was almost perfectly edge-on relative to the line of sight. As a consequence, once per orbit, the signal from the main pulsar would pass close to the companion neutron star, and would therefore experience the Shapiro time delay in its propagation. This delay was measured, and the results agreed completely with the predicted delay, based on the measured mass of the companion. The same effect presumably occurred for the signal from the companion passing by the primary, but the companion’s pulsed signal was too weak and ragged to be useful for measuring such tiny effects. The effect of time dilation and the gravitational redshift on the primary’s observed pulse period was measured, and agreed with the prediction of general relativity. The decreasing orbit period was also measured, and it too agreed with the theory’s prediction for gravitational radiation energy loss, with a precision today even better than that for the Hulse–Taylor pulsar.
There was one more surprise. The radio pulses from the primary pulsar A were known to be partially eclipsed by the passage of the secondary pulsar B across the line of sight, and the on-off flickering of the signal during the eclipse occurred on a roughly 3 second timescale, the same as the rotation period of pulsar B. This was not because the signal hit the actual neutron star, but because it passed through the highly charged “magnetosphere” of the companion. This is a region of strong magnetic fields and charged particles that wraps around the magnetic equator of the neutron star, and is much larger in diameter than the star itself. It is shaped more like a donut or bagel, with the neutron star residing in the middle of the hole (see Figure 5.5). The pulsar beam from B propagates along the magnetic poles in a direction perpendicular to the plane of the donut. It is essentially the same as the magnetosphere of the Earth, except that the Earth’s magnetosphere is strongly distorted by the solar wind. The dense cloud of charged particles that are trapped within the magnetosphere can absorb and scatter radio waves as effectively as the solid material of the neutron star itself. So, as pulsar A passes behind pulsar B during the orbital motion, its signal can be absorbed or not by the magnetosphere of pulsar B, depending on the orientation of the pulsar at that moment. This model beautifully explained the pattern of eclipses, except for one thing. Over many orbits of the system, the detailed shape of the eclipse pattern drifted with time, contrary to what the model predicted.
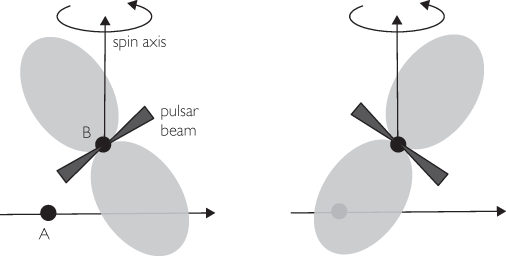
Figure 5.5 Pulsar B rotates about its spin axis with a period of 2.8 seconds, with its magnetic axis (which produces the pulsar beam) and donut-shaped magnetosphere (in gray) not aligned with the spin axis. Left: Pulsar A passes behind pulsar B, but the signal directed out of the page misses the magnetosphere. Right: After half a rotation of pulsar B, the magnetosphere now blocks the signal from pulsar A, causing an “eclipse.”
General relativity gave the solution. As we saw in Chapter 4, the spin of an object should change direction slowly with time as the object moves through the curved spacetime of another body. This effect, known as the “geodetic precession,” was one of the two effects verified by the Gravity Probe-B experiment. If the spin direction of the pulsar changes slowly with time, then, as can be seen in Figure 5.5, the signals from pulsar A might encounter a fatter or thinner part of the magnetosphere as time goes on. Incorporating this effect into the model gave complete agreement with the eclipse data, including the long-term changes, and the amount of geodetic precession of the spin needed to fit the data agreed with the prediction of general relativity. Sadly, general relativity also killed the “double” pulsar, because by 2008, the spin had precessed so much that the beam of pulsar B no longer passed across the Earth, and the system became a “single” binary pulsar. Pulsar B may reappear in 2035 when the wobbling spin brings its beam back into alignment with the Earth.
The second stand-out pulsar was discovered in 2014 by Scott Ransom and collaborators, using the Green Bank radio telescope in West Virginia. But instead of being in a binary system, this pulsar was in a triple star system, with two white dwarf companions. This is not as unlikely as it may seem. While the numbers are uncertain, as many as a fifth of the stars in the Milky Way could be in triple star systems. Alpha Centauri, our nearest neighbor, and Polaris, the North Star, are actually in triple systems, with two stars in a fairly close binary orbit and a more distant third star orbiting the pair. This new system is similar in that it consists of a close inner binary and a distant third star. The pulsar has a spin period of 2.73 milliseconds, and a mass of 1.44 solar masses. It is orbited once every 1.6 days by a white dwarf of only one fifth of a solar mass. This pair is orbited by a 0.4 solar mass white dwarf, with an orbital period of 327 days. Both orbits are almost perfect circles, and lie on the same plane (see Figure 5.6).
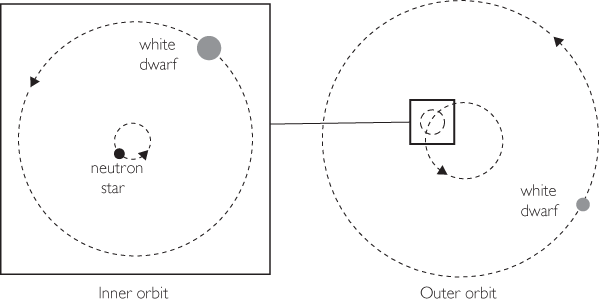
Figure 5.6 Pulsar in a triple system. Left: The neutron star is in a 1.6 day orbit with a low-mass white dwarf. Right: This inner binary is in a 327 day orbit with the other white dwarf.
Everything about this system made it pretty useless for testing general relativity in the same manner as either the Hulse–Taylor binary or the double pulsar. The motions were too slow and the orbital separations too large for relativistic effects on the orbits to be very interesting. The orbits were too circular for the periastrons to be even located, let alone for their advances to be measured. The mass of the inner white dwarf was too small for the gravitational redshift of the pulsar signal to be measurable. The inclination of the orbits relative to the plane of the sky was found to be about 40 degrees, so the radio signal from the pulsar would pass nowhere near either white dwarf, making the Shapiro delay negligible. And finally, the emission of gravitational radiation would be far too feeble for the decrease in the orbital periods to be detectable.
So why was this discovery so fantastic for general relativity? The answer goes back to the founding idea of general relativity, the principle of equivalence. In Chapter 2 we discussed how Einstein’s insight about the equivalence between gravity and acceleration led him to a curved spacetime picture for gravitation. This was based upon the observational fact that bodies fall with the same acceleration, independently of their internal structure or composition. This idea is usually called the “weak equivalence principle,” and was already appreciated in the ancient world. In 400 ce, Ioannes Philiponus wrote “… let fall from the same height two weights, of which one is many times as heavy as the other … the difference in time is a very small one.” Even before Galileo, this principle had been expounded and tested in the 1500s by Giambattista Benedetti and Simon Stevin, and if Galileo actually did drop things from the Leaning Tower of Pisa during his time there between 1589 and 1592, he was probably just demonstrating to his students what was by then a well-known concept. Even Isaac Newton carried out experiments using pendula to test this equality. As we noted in Chapter 2, the challenge of testing the weak equivalence principle to high precision was taken up by Eötvös at the turn of the twentieth century. Because this principle is so crucial for the foundation of Einstein’s theory, the effort to test it to higher and higher precision has continued to the present day. The current state of the art comes from two sources. One is a series of experiments carried out by a group headed by Eric Adelberger at the University of Washington in Seattle, called the “Eöt-Wash” experiments, that show that different materials fall with the same acceleration to a few parts in ten trillion. The other is a space experiment called MICROSCOPE, launched in 2016 by the French Space Agency, that yielded a limit of parts in a hundred trillion.
One interesting and important conclusion can be drawn from these results. Recall that the mass of an atomic nucleus is made up of the masses of the individual neutrons and protons, but that’s not all. These neutrons and protons are held together by the strong forces that bind the nucleus. Einstein has taught us through special relativity that energy and mass are different manifestations of the same thing. Therefore, the mass of the atomic nucleus is made up of the sum of the masses of the individual neutrons and protons, and the “mass” associated with the binding energy. Now, since different elements have different amounts of nuclear internal energy per unit mass, and since experiments tell us that the different kinds of nuclei fall with the same acceleration, then the energy of the nuclear forces must “fall” with the same acceleration as do the nuclear particles themselves. A similar conclusion applies to the electromagnetic energy associated with the forces between the charged protons and electrons. So it would seem that not only do the fundamental building blocks of matter, such as protons, neutrons and electrons, fall with the same acceleration, but so do the various forms of energy associated with their interactions with each other, such as nuclear, electromagnetic and weak interactions.
But the standard model of fundamental particles tells us that there is a fourth interaction: gravitation. What about the energy associated with it? Does gravitational energy fall with the same acceleration as matter and the other forms of energy? The experiments we have just described don’t provide an answer, because the internal gravitational energy of the laboratory-scale bodies employed in those experiments is utterly negligible. To get a meaningful amount of gravity, you need a large amount of mass, and therefore to test the equivalence principle including gravitational energy you need objects like planets or stars.
The first person to contemplate this possibility was Kenneth Nordtvedt. Born in Chicago, he received an undergraduate degree from MIT, took a Ph.D. degree at Stanford University, and had post-doctoral research positions back in the Boston area at Harvard and at MIT. But by 1965 he had developed a dislike for the lifestyle and politics of big cities, especially on either of the coasts, and had resolved to head for the heartland of America. When offered an assistant professorship at the then small Montana State University in tranquil and beautiful Bozeman, he accepted readily and headed west to begin his academic career in earnest.
Although his Ph.D. thesis was in solid-state physics, around 1967 he turned his attention to gravity and asked whether a massive body with its own internal gravity, such as the Earth, would fall in an external gravitational field with the same acceleration as, say, a ball of lead. To try to answer this question, Nordtvedt devised a way of treating the motion of planetary-size bodies that would be valid in any curved spacetime theory of gravity, or at least in a broad class of such theories. The equations he developed could encompass general relativity, the Brans-Dicke theory, then the leading alternative theory to Einstein’s, and many others, in one fell swoop. To find the actual prediction of a chosen theory, such as general relativity, all one had to do was to specialize the equations by fixing the numerical values of certain coefficients that appeared in them. The calculations were complicated, with many, many terms in the final equation describing the acceleration of a massive body, but when all was said and done, two remarkable results emerged.
First, when the equations were specialized to general relativity there was a tremendous cancelation of terms, and the result was that different massive bodies would have exactly the same acceleration, regardless of how much internal gravity they possessed. Therefore, in general relativity the acceleration of gravitationally bound bodies was predicted to be the same as that of laboratory-size bodies. This beautiful prediction of general relativity, the equivalence of acceleration of bodies from the smallest to the largest sizes, is sometimes called the strong equivalence principle. Later research would show that this equivalence also applies to neutron stars and even black holes.
There was another remarkable result of Nordtvedt’s calculations. In most other theories of gravity, including that of Brans and Dicke, the complete cancelation did not occur and a small difference in acceleration remained, depending on how strongly bound by internal gravity the bodies were. Therefore, even though these theories guaranteed that laboratory-size bodies fall with the same acceleration, satisfying the weak equivalence principle, as soon as one considered bodies with significant amounts of self-gravitational binding, the bodies would fall differently. In other words, in such theories, gravitational energy falls at a slightly different rate than mass and other forms of energy, such as nuclear energy, electromagnetic energy and so on. Thus, theories such as the Brans–Dicke theory were compatible with the weak equivalence principle, but not compatible with the strong equivalence principle. Today this is called the Nordtvedt effect.
Nordtvedt then proposed to search for this effect in the motion of the Moon. Consider the acceleration of the Earth and the Moon in the field of the Sun (see Figure 5.7). The gravitational energy per unit mass of the Moon is about one twenty-fifth that of the Earth, so they could in principle fall with different accelerations because the Earth is more tightly bound by its own gravity than is the Moon. Suppose, for the sake of argument, that the Moon falls with a slightly larger acceleration than the Earth (whether it is larger or smaller depends on the theory of gravity). The Moon orbits the Earth, but is being accelerated toward the Sun slightly more strongly than the Earth is; therefore, on each succeeding orbit the Moon is pulled a little closer to the Sun. What started out as a nearly circular orbit becomes elliptical, and on each orbit the ellipse becomes more and more elongated toward the Sun, until the Moon is pulled catastrophically from the hold of the Earth and plunges with a great splash into the Sun. Is the Nordtvedt effect a lunar calamity? Actually not, because we have forgotten an important fact: the Sun is in orbit about the Earth (as seen from the Earth’s frame, of course). Thus, just as the Moon’s orbit is elongated toward the Sun on one revolution of the Moon, by the next lunar revolution, 27 days later, the Sun has moved by about 27 degrees in its orbit (the Sun’s rate of revolution about the Earth is 360 degrees in 365 days, or about 1 degree per day), so on the next revolution, the elongation must occur in a direction toward the new position of the Sun. On the following revolution of the Moon, the elongation must be directed toward a still newer position, and so on. Therefore, instead of building up to a disastrous size, the elongation of the Moon’s orbit that would be caused by the Nordtvedt effect maintains a fixed size, but is always oriented with its long axis toward the Sun. If the Moon were predicted to fall with a slightly smaller acceleration than the Earth, then the elongation would be in the opposite direction, with its long axis directed away from the Sun. If, as in general relativity, the two fall with the same acceleration, there would be no predicted elongation of this sort.
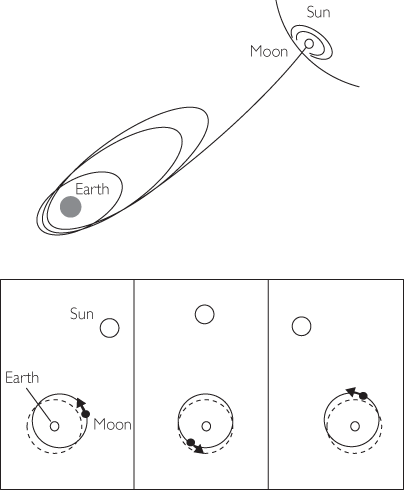
Figure 5.7 Lunar catastrophe or orbit perturbation? If the Moon fell with larger acceleration than the Earth toward the Sun, its orbit would become progressively more elongated until it was pulled into the Sun. But because the Earth–Sun orientation is changing because of the Earth’s orbital motion, the elongation never builds up and instead merely produces a shifted orbit that always points toward the Sun (solid curves). In general relativity, the elongation does not occur at all (dashed curves).
The crucial question is how large this effect might be. When Nordtvedt put in all the numbers, he found that the size of the elongation in the Brans–Dicke theory, for instance, could be as large as 1.3 meters, or about 4 feet. In general relativity, of course, the effect was zero. While this may seem like a ridiculously small effect, it would soon become eminently measurable.
After Apollo 11 astronaut Neil Armstrong took his first step on the Moon on 21 July 1969, he had a number of tasks to perform, one of which was to walk a few hundred meters from the lander and place on the lunar surface a device called a “retroreflector,” an early version of the retroreflectors used on the LAGEOS satellites (page 75). This was a flat surface embedded with cube corner reflectors that could take a laser beam sent from Earth and reflect it back in the same direction from which it came. One could then send a short laser pulse from Earth, have it bounce off the retroreflector and return to Earth. Measuring the round-trip travel time of the pulse would give a measure of the Earth–Moon distance, with a precision that was expected to be of the order of 100 centimeters, easily sufficient to look for a possible Nordtvedt effect. Within a week and a half of deployment of the Apollo 11 retroreflector, astronomers at Lick Observatory in California had succeeded in bouncing laser pulses off it, and measuring the round-trip travel time to a precision corresponding to several meters. Subsequently, four other retroreflectors were placed on the Moon, two US devices, deployed by astronauts during Apollo 14 and 15, and two French-built reflectors, deposited during the Soviet unmanned missions Luna 17 and 21. By 1975, analyses of the laser ranging data showed absolutely no evidence of the Nordtvedt effect, to a precision of 30 centimeters, to the delight of Nordtvedt and anybody who feels that general relativity is correct. As Nordtvedt was fond of saying, “scientifically, zero can be just as important a number as any other.”
Today, lunar laser ranging is carried out at over forty observatories worldwide, with ranging precisions in the millimeter regime, yielding important science about the Earth–Moon orbit, the rotation of the Moon, continental drift on Earth, and even whether Newton’s constant of gravitation is constant in time (it is, to the uncertainty in the measurement, which is a few parts in ten trillion per year). And recent analyses have continued to show no evidence of the Nordtvedt effect. One way to summarize the results is to state that the Earth and Moon fall toward the Sun with the same acceleration to a few parts in ten trillion, comparable to the limits achieved by tests of the weak equivalence principle, such as the Eöt-Wash and MICROSOPE measurements.
The pulsar in a triple system carried this test of the Nordtvedt effect into a new realm of extreme gravity. The system is a variant of the Earth–Moon–Sun system, with the inner neutron star / white dwarf binary substituting for the Earth and Moon, and the outer white dwarf substituting for the Sun. The mass relationships are different, with the Sun dominating the masses in the solar system case, and the neutron star dominating in the pulsar case. But the question is the same: do the neutron star and its white dwarf companion fall with the same acceleration toward the distant white dwarf?
The crucial difference is this. Whereas the internal gravitational binding energy of the Earth and the Moon represent only about a billionth of their total mass, the gravitational energy of a neutron star represents as much as 15 percent of its total mass. In other words, if you could somehow go into the neutron star and count up all the protons, neutrons, electrons and any other exotic particles that you might find, multiply each by its mass and add it all up, you would get something like 1.6 solar masses. The actual measured mass is 1.4 solar masses. The difference of about 0.2 solar masses, multiplied by the square of the speed of light, is the gravitational binding energy, and is in fact a negative number.1 This is analogous to the phenomenon by which the mass of a helium nucleus is slightly smaller than the mass of four hydrogen nuclei (protons), so that when four protons fuse to form helium in the Sun, that mass difference becomes the energy on which we rely (in this example, the binding energy comes from the strong nuclear interactions). The binding energy of a typical white dwarf is parts in ten thousand of its mass, much larger than that of the Earth or Moon, but much smaller than that of a neutron star.
Soon after the pulsar in a triple was discovered, the team set about looking for the Nordtvedt effect. If, for example, the neutron star were to fall with larger acceleration than its companion, then its orbit would be displaced slightly toward the distant white dwarf, while the orbit of the inner white dwarf would be displaced slightly in the opposite direction, and the displacement would rotate in time to track the distant companion (as in Figure 5.7). In July 2018, Anne Archibald, who led the data analysis, announced that they had found no evidence in the pulsar signal for such orbital dispacement of the pulsar. The data showed that the neutron star and the white dwarf fall with the same acceleration to about three parts in a million, showing no Nordtvedt effect, and in complete agreement with general relativity.
Because the strong internal gravity of the neutron star could have produced an anomalous effect (and does, in many alternative theories), this constitutes a beautiful test of general relativity in the strong-field regime. Even more extreme tests of Einstein’s theory are possible, but for these, we must first discuss black holes, as we do in the next Chapter.