CHAPTER 7
Gravitational Waves Detected At Last!
The room is small and windowless. At the front of the room stand five chairs, two large video panels and a podium displaying the logo of the NSF, the US National Science Foundation. The audience comes from around the world and includes scientists, government officials and reporters. They whisper in anticipation of a major announcement that the scientific rumor mill has been mongering for a couple of months. At 10:30 a.m. on Thursday 11 February 2016, NSF Director France Cordova welcomes the audience to the National Press Club in Washington DC.
Two thousand miles away, in the small town of Bozeman, Montana, Nico and twenty people sit at a table in a small room of the eXtreme Gravity Institute at Montana State University. This room has windows with a beautiful view of the mountains, but nobody is paying attention to the scenery. All eyes are focused on the television in the front of the room. The screen has a live internet stream from the National Press Club. Nobody pays attention to the celebratory cake waiting on the center of the table.
Five hundred miles to the south, in Aspen, Colorado, Cliff and eighty physicists and astronomers watch the same feed in an auditorium of the Aspen Center for Physics. They are participating in a workshop on stars and gas at the centers of galaxies, but the day’s schedule has been pushed back by two hours so that everybody can watch this event.
After briefly extolling the NSF’s commitment to funding cutting-edge research in fundamental science, Cordova sits down and the man sitting next to her approaches the podium. He is tall, middle aged, with graying hair, wearing a blue suit, with a blue shirt and a paisley tie. His tired eyes reveal that the past few months have seen very, very long hours. He places some notes on the podium.
“Ladies and gentlemen,” he says. “We have detected gravitational waves. We did it!” he exclaims, and the audience bursts into applause. The twenty people in the room in Bozeman applaud; the audience in Aspen applauds. At institutes and universities around the world, scientists of all stripes break out in applause. David Reitze, the Director of the Laser Interferometer Gravitational-Wave Observatory, or LIGO for short, has just announced the most important scientific discovery of the twenty-first century (at least so far).
Around 1.2 billion years ago, in a very distant galaxy, two black holes crashed against each other. Each black hole was roughly thirty times more massive than our Sun, but in actual size was only about as big as Albania or Haiti. They were circling around each other at roughly half the speed of light, locked by gravity in a fatal dance, when they merged to form a single black hole. The event created ripples in the fabric of space and time that traveled outward in all directions at the speed of light. On 14 September 2015, those same spacetime waves finally arrived at the Earth, passed through the LIGO instruments and produced an unmistakable gravitational wave reading. This was the event that David Reitze had just announced to the world.
Within hours, congratulations poured in, from Stephen Hawking, from President Barack Obama, from leaders of the CERN accelerator center in Geneva. Twenty months later, a remarkably short time for the normally glacial Swedish Academies, the 2017 Nobel Prize in Physics was awarded to three of the founders of LIGO: Rainer Weiss, Kip Thorne and Barry Barish. “Gravitational wave astronomy” became an “official” field, hailed even by some of the astronomers who once lobbied against LIGO.
Gravitational waves were not always so in vogue.
At one point, Einstein himself thought he had proven that gravitational waves were not real! The definitive proof by theorists that they are real would not be achieved until the late 1950s, and the first experimental evidence that they exist would come in 1979, as we saw in Chapter 5. A 1969 claim by physicist Joseph Weber to have actually detected the elusive waves would soon be undone by the failure of other scientists to replicate his results. The story of gravitational waves is rich in science, of course, but is also a story of human personalities and foibles, of debates and controversies, and of big science, politics and money. It is a hundred-year-long saga that starts with a botched paper by Einstein himself.
In May 1916, Einstein published a major review article on his general theory of relativity that pulled together all the bits and pieces of the short papers that he had presented at the Prussian Academy of Sciences the previous November into a coherent exposition. He then immediately began to work on gravitational waves.
Einstein was a devotee of James Clerk Maxwell (1831–1879), the Scottish physicist who in 1867 united the seemingly disparate phenomena of electricity and magnetism into a single framework, known as electromagnetism. Maxwell’s equations are still a central ingredient of modern physical science, from electrical engineering to high-energy particle physics. A deep understanding of Maxwell’s theory underlies the technology in our most beloved devices, such as televisions, cellphones and laptops. Maxwell’s equations are at the core of physics and engineering education today, and that was also the case in the late nineteenth century when Einstein was a student.
Maxwell’s key insight was that electricity and magnetism could be understood through the idea of an electromagnetic field, a physical quantity that encodes information about the force exerted on a charged object anywhere in space. Even if you don’t realize it, you have probably been exposed to the concept of a field before. You may have observed the way iron filings on a sheet of paper array themselves to display the field of the magnet under the paper. You know that Earth’s magnetic field helps to protect us from the harmful energetic particles streaming from the Sun and creates the aurora borealis and the aurora australis. And you have heard of the gravitational field of the Earth, which is responsible for the force that allegedly caused the famous apple to fall on Newton’s head, and that also holds the Moon in its orbit.
In addition, Maxwell showed that his equations had solutions in which the electric and magnetic fields oscillate, feeding off each other to produce a wave that travels at the same speed as light. He suggested that these waves were light, an idea that was confirmed experimentally by Heinrich Hertz in Germany in 1887.
Several scientists, including Hendrik Lorentz in the Netherlands and Henri Poincaré in France, began to wonder well before Einstein whether there could also be waves of gravity itself, simply by analogy with Maxwell’s electromagnetic waves. Furthermore, because Einstein’s special theory of relativity said that nothing could travel faster than light, it seemed logical that gravity should not be instantaneous. The effects of gravity should travel with a finite speed, and this speed should not be greater than that of light. But speculate was the best they could do, because they didn’t have an actual theory of gravity to work with.
But in 1916 Einstein had an actual theory, and he set out, in the spirit of his hero Maxwell, to see if his equations had solutions that would resemble waves. He completed the calculations and published the result in June 1916. Unfortunately, the paper was full of what could charitably be called “bone-headed” mathematical and conceptual errors. Einstein’s colleague, Norwegian physicist Gunnar Nordström, helped Einstein find and correct the mistakes, and Einstein published a second gravitational wave paper in 1918.
Einstein showed that a varying system, such as a dumbbell spinning about an axis perpendicular to its handle (Figure 7.1), will emit gravitational waves that travel at the speed of light. He also found that the waves carry energy away from the rotating dumbbell, just as light waves carry energy away from a light source. As we saw in Chapter 5, this loss of energy in a binary pulsar system is what Hulse and Taylor measured, thereby verifying, albeit indirectly, that gravitational waves exist. It’s the same loss of energy that brought the two black holes to their final embrace, emitting the burst of gravitational waves that LIGO detected.
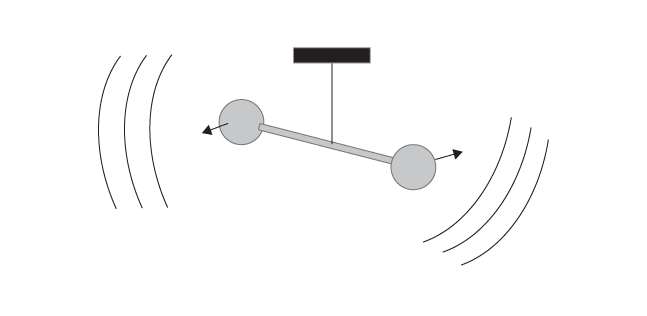
Figure 7.1 Einstein’s spinning dumbbell generating gravitational waves.
But there were aspects of his gravitational wave solution that Einstein didn’t fully understand. In Maxwell’s theory there are two solutions for electromagnetic waves. For example, if you have a wave propagating horizontally in the laboratory, one solution could have the oscillating electric field pointing vertically (it is always perpendicular to the direction of propagation); the other solution would then have it pointing horizontally but still perpendicular to the direction of propagation. These two cases are called the “modes of polarization” of the electromagnetic wave, and a general light wave consists of a combination of the two modes. A charged particle encountering the electric field of the first mode would move up and down, just as a ball moves up and down on a water wave at the beach. This is in contrast to sound waves, where the motion of the molecules of the medium which carries the sound is always along the direction of propagation of the waves. The concept of polarization is exploited for example in polarized sunglasses, which are designed to block one mode of polarization preferentially. They are most useful at protecting your eyes when the mode that is blocked is the one that is dominant when light scatters off the pavement in front of your car or off the water at the beach.
In the case of gravity, Einstein also found two modes of polarization of the gravitational waves (we’ll get to what those modes look like shortly), and those modes traveled with the same speed as light. But there were additional solutions to the equations whose meaning was not so clear, and to make matters worse, the speed of these modes was not fixed by the equations. In a 1922 paper, Eddington analyzed Einstein’s gravitational waves carefully. He pointed out that Einstein had made a small calculational error in his 1918 paper, making his formula for the energy lost off by a factor of two. He also observed that the additional modes of Einstein were probably not physically real, but instead might be waves in the coordinates used to describe the problem. He made the dismissive remark that “the only speed of propagation relevant to them is the speed of thought.”
What does the statement “waves of the coordinate system” mean? It is a tenet of general relativity that you can label points in space and time in essentially any way you like and measurements made of the physical phenomena using devices such as clocks or telescopes or laser beams will be the same. Let us describe a simple example, not in spacetime but on a two-dimensional surface in a suitable city like Manhattan in New York City, where a very nice Starbucks store is located. There are a number of ways to tell your friend where the Starbucks is. The city itself has a grid of numbered avenues, say First, Second, Third Avenues pointing in one direction, and of numbered streets, say 65th, 66th, 67th Streets, pointing in the perpendicular direction. Many US cities are laid out in this regular way. This grid provides a “coordinate system” for the city, and let’s say the nice Starbucks is located at the corner of Third Avenue and East 66th Street. However, you could use a very different coordinate system to direct your friend. You could give her the GPS coordinates of the store, and she could get there using her smartphone. The GPS coordinates are based on a grid of lines of longitude and latitude, which are not in general aligned with the avenue–street grid. Starbucks is there with your latte waiting no matter what coordinate system you use.
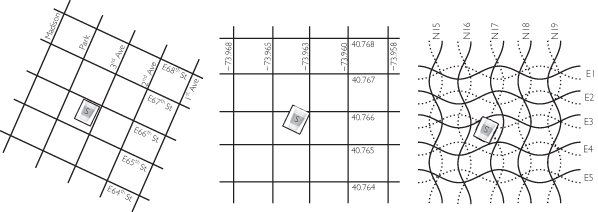
Figure 7.2 Coordinate systems for finding Starbucks in upper east side Manhattan. Left: System based on the grid of streets. Middle: System based on GPS coordinates. Right: System based on grid of numbered ropes being jiggled crazily by giants.
Now consider a third coordinate system, defined by a grid of parallel ropes held taut by giants standing at the edge of the neighborhood where Starbucks is located. There are two sets of parallel ropes, one set perpendicular to the other, with the ropes in each direction labeled E1, E2, E3, etc., and N15, N16, N17, etc. In this system, Starbucks might be located at E3–N17, i.e. at the intersection of rope #E3 in one direction and rope #N17 in the other direction. Your friend could just as easily get to Starbucks using this system. Now suppose that the giants start jiggling the ropes so that they all oscillate in some complicated manner in the horizontal plane. In this coordinate system, the Starbucks store seems to be going crazy, now at E3–N17, now at E2.9–N16.8, then back to E3–N17, then E3.1–N17.2, and so on. Using this coordinate system to get your friend to Starbucks would be complicated (in fact the values of the coordinates would depend on her time of arrival), but it could be done. Yet the customers at Starbucks feel nothing, since after all, the store is not actually moving. They have no idea that the location of the store is sloshing back and forth when described using the giants’ wavy coordinates.
This is the bottom line: coordinates are merely convenient labels of points and have no physical significance. In general relativity there are four coordinates, three for space and one for time, but the basic idea is the same. We can label points in spacetime using any convenient coordinates, but they will have no consequences for the physics that goes on, including the experiments we do using physical apparatus to measure the physical phenomena. Today, students in our general relativity courses learn this up front and eventually become comfortable with it.
But Einstein was not totally comfortable with it, even though he used the concept as the central guidepost for developing his theory. After all, he called it the “general” theory (as opposed to his 1905 “special” theory of relativity) because the theory was valid in “general” coordinate systems. Even Eddington, who understood general relativity at least as well as Einstein did, and probably better than any one else at that time, seemed slightly unsure what to make of these wavy coordinates. Today we think of their ruminations on the meaning of these modes as rather quaint, but we have the benefit of hindsight based on a century of research and teaching in the subject.
Still, Eddington’s comment about some gravitational waves traveling at the “speed of thought” served to make the whole topic seem rather dubious, and it would be almost thirty-five years before the issue was fully settled.
The case for gravitational waves was not helped when, in 1936, Einstein tried to claim that they do not exist.
In 1933 Einstein moved to the United States to escape Nazi Germany, taking a job at the Institute for Advanced Studies, near Princeton University in New Jersey. This institute had been founded three years earlier to serve as a center for knowledge and discovery, and also became a refuge for intellectuals escaping Nazi oppression. In 1934 Einstein hired Nathan Rosen as his assistant, a physicist from Brooklyn, New York who had studied physics at MIT. An “assistant” in those days played the role of what today we would call a “postdoc,” someone typically with a physics Ph.D. who acts as a research assistant to a senior scientist in a hands-on apprenticeship for a few years.
Einstein and Rosen set out to revisit Einstein’s 1918 calculation to determine whether gravitational waves were truly real. Einstein’s 1918 paper had used an approximate version of his theory to predict the existence of such waves, but they now wanted to determine whether the exact theory led to the same prediction. To their surprise, the exact theory seemed to predict the opposite! The solution they found was singular, or infinite, in certain parts of spacetime, just as Schwarzschild’s “Massenpunkt” solution was singular at the Schwarzschild radius. Reasoning that singularities are unphysical, they concluded the entire solution also had to be unphysical. In 1936, Einstein and Rosen submitted their disproof of gravitational waves for publication in the Physical Review scientific journal.
Following a policy that had only recently been instituted, the editor of Physical Review, John Tate, sent the Einstein–Rosen paper to an external scientist to be reviewed. Given that one of the authors was Einstein, Tate had some misgivings about this, but saw no reason to make an exception, especially considering the surprising claim made in the paper. The anonymous referee recommended that the paper not be accepted for publication without major corrections.
Today, peer review is the norm for publication in serious scientific journals, and it is an essential tool to ensure the validity of new results. Typically, a journal’s editor will send a new submission to one or more experts for comments and critiques, and it is only once these experts reach a consensus for publication that the submission is accepted. But in 1936 this practice was not common at all and was almost unheard of in Europe, where Einstein was used to publishing papers. So when Einstein received Tate’s reply with the anonymous referee’s criticism, he was offended and withdrew his submission. He wrote to Tate that he had “sent the manuscript for publication,” not to be disclosed to an anonymous expert. Einstein never submitted another paper to Physical Review.
If Einstein had actually read the report of the referee, our story would be quite different, since the referee had spotted a serious mistake in their paper. Instead, Einstein submitted the original paper, without any modifications, to the Journal of the Franklin Institute, a small journal published in Philadelphia, which accepted it without refereeing in 1937. By this point, Rosen had moved to the University of Kiev in present-day Ukraine, so Einstein had hired a new assistant, Leopold Infeld, a Polish physicist. Infeld arrived at the Institute for Advanced Studies around the time that the Einstein–Rosen paper was being accepted by the Franklin Institute journal, and Einstein was excited to talk with him about his new paper and the discovery that gravitational waves did not exist after all.
Infeld was initially skeptical. It was hard to believe that Einstein’s theory, which resembled Maxwell’s theory of electricity and magnetism in so many respects, did not have gravitational waves similar to Maxwell’s waves. But Einstein was an eminence in physics, and he soon convinced Infeld that his argument was correct. Around this time, however, Howard Percy Robertson, a Princeton professor who had done work that would lay the foundations of general relativistic cosmology, was returning from a sabbatical at Caltech. When Infeld met Robertson, he told him about the Einstein–Rosen result, but Robertson dismissed it and, a few days later, showed Infeld exactly what the problem was. Once again it was the coordinates!
Robertson explained to Infeld that if one were to transform the solution that Einstein and Rosen had found to coordinates adapted to a cylinder, then the infinities that so troubled them would all be pushed to the axis of the cylinder, where the source of the gravitational waves should reside, and where their solution would not be applicable. Infeld was impressed that Robertson appeared to have solved the problem just based on their brief discussion.
The singularities found by Einstein and Rosen are called “coordinate singularities” and are today understood to be artifacts of the choice of coordinates and therefore have no effect on the physics. Even as mundane a place as the South Pole on the surface of the Earth is the location of a coordinate singularity. There, the latitude is − 90 degrees, but there are an infinite number of possibilities for the longitude, since all the lines of longitude converge there. But standing at the scientific research station at the South Pole you would never know this, and in fact you could lay down a nice grid of streets on the ice and find Starbucks (if there were one there) just as easily as you could in Manhattan. As we discussed before, physics cannot depend on the coordinate choices one makes. Infeld rushed to tell Einstein about this, only to be told by Einstein that he had just reached the same conclusion on his own.
With input and advice from Infeld and Robertson, Einstein heavily revised the paper, already in galley proofs from the journal. He changed the title, added a new section on cylindrical gravitational waves, and altered the main conclusion: his exact theory of general relativity did predict the existence of (at least cylindrical) gravitational waves. In 2005, through some inventive detective work, our colleague Daniel Kennefick was given permission by the current editors of Physical Review to examine Tate’s log book of submitted papers and confirmed that the anonymous referee of the Einstein–Rosen paper had been none other than Robertson himself!
Once again, sorting out what was real about gravitational waves proved to be a problem, and would not really be resolved for another twenty years. Recall that this period was the “low water mark” for the field of general relativity, when few scientists were interested in it or worked on it. But in the mid 1950s the beginnings of a rebirth in the subject began to take hold, leading to the great renaissance for general relativity during the 1960s described in Chapter 1. Science historians who study our field point to two conferences on general relativity as being particularly influential. The first was in Bern, Switzerland in 1955. The meeting was convened to celebrate the fiftieth anniversary of Einstein’s “miracle year” when, while working as a patent clerk in that city, he developed special relativity and made groundbreaking discoveries in quantum mechanics and atomic physics. It also turned out to memorialize Einstein, who had died three months before the meeting. The second conference was in Chapel Hill, North Carolina in 1957.
In fact, these two meetings became so legendary that when the International Committee on General Relativity and Gravitation was formed a few years later and decided to organize a big “GR” conference every three years, they retroactively renamed these two meetings “GR0” and “GR1.” In 2019, GR22 was held in Valencia, Spain.
Although gravitational radiation was not a major topic in either meeting, it was discussed. In Bern, Nathan Rosen reviewed cylindrical gravitational waves. In Chapel Hill, John Wheeler and Joseph Weber argued that, despite the rather unrealistic physical setup, cylindrical waves were physically measurable. And a 27-year-old British graduate student named Felix Pirani discussed his recent paper showing precisely how the waves would affect material particles and how you would measure the effects.
Imagine a ring of eight disks (hockey pucks, for example) arrayed in a circle on a table, free to slide across the table without any kind of friction (see the snapshot on the far left of the top panel of Figure 7.3). A gravitational wave passes vertically through the table (into the page of the figure). The strength or amplitude of the wave is a sine wave, starting at zero, growing to a maximum, returning to zero, then to a minimum and then returning to zero. According to Einstein’s theory, the disks on opposite sides of the center of the circle are pushed apart in one direction while being pushed together in the perpendicular directions, as in the second snapshot in the top panel of Figure 7.3. As the wave amplitude passes through zero, the disks then return to the circular shape (third snapshot). As the amplitude goes negative, the disks are pushed together and apart in the opposite sense (fourth snapshot). Finally, after one complete cycle of the wave, the disks return to the circular shape (fifth snapshot). As we have already discussed, a general gravitational wave can contain two modes of polarization. The action of the second mode is shown in the bottom panel of Figure 7.3. It is the same as the first mode, except that the pushing together and apart is along the diagonals, at 45 degrees compared to the first mode. The two modes are conventionally called the “plus (+)” and “cross (×)” modes, because if you overlay the five snapshots in each case, the pattern reminds you of a plus sign or of a multiplication or cross-out sign.
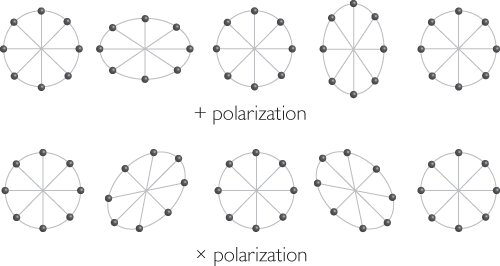
Figure 7.3 Two modes of polarization of a gravitational wave propagating perpendicularly into the page. Snapshots show a set of eight disks on a frictionless surface. From left to right, the snapshots show the disks every quarter of a cycle. The top row displays the plus polarization; the bottom row shows the cross polarization.
Now, we have mentioned many times already that gravity is really due to the warping or distortion of spacetime, and you may have read many newspaper articles or internet stories describing gravitational waves as stretching and squeezing spacetime in order to produce the patterns shown in Figure 7.3. So it is fair to ask, doesn’t the wave also stretch and squeeze the table so that the disks don’t actually slide? The answer is that the response of an object to warping spacetime depends on what other forces are acting on it. Our disks have no forces acting on them in the horizontal direction (assuming zero friction) and so they respond “fully” to the spacetime distortions induced by the wave. On the other hand, the atoms that make up the table are being acted upon by the interatomic electric forces produced by all the surrounding atoms, and these forces are enormous compared to the force of gravity. So the distortion of the table is much, much, much smaller than the displacement of the disks. Thus, the disks will actually slide.
In fact, this was the basis of an ingenious argument made at the Chapel Hill conference by a “Mr. Smith” to underscore the reality of gravitational waves. Mr. Smith was actually the famous American physicist Richard Feynman, who had registered for the meeting under the pseudonym in part to indicate his low opinion about the status of general relativity research at the time. Drawing on Pirani’s description of how objects would move, he pointed out that if you introduced a bit of friction onto the surface of the table, then as the disks slide back and forth, the table would heat up a bit. Therefore some energy would have been transferred from the gravitational waves to the tabletop, a clear and unambiguous sign of a physical effect. He actually used a pair of beads sliding on a rod in his discussion, and so his argument has gone down in physics history as Feynman’s “sticky beads” proof of the reality of gravitational waves.
Pirani received his Ph.D. in 1958 under Hermann Bondi at King’s College, London, and over the next few years he, Bondi and others would show in clear and unambiguous terms that gravitational waves are real, can be measured and carry energy away from their sources. The long period of uncertainty inspired by Eddington’s jibe was over.
So we have answered one question: gravitational waves are physically real and measurable.
But an equally important question is: are there any waves to measure? Any decent physicist would say, let’s generate the waves and then detect them. In 1887, Hertz had created electromagnetic waves using an electrical discharge, and then detected the effects of the waves at the other end of his lab. Could one take one of the dumbbells that Einstein imagined in his 1916 calculations and generate gravitational waves to be detected somewhere else? Unfortunately, it was not too hard to show that the waves produced by such a setup would be hopelessly weak, utterly undetectable by even the most far-fetched scheme. However, gravity depends on how much mass you have, and so perhaps one needs astronomical bodies to generate gravitational waves. But in the late 1950s, this did not seem very promising either. According to the astronomers, the universe was a very quiet place, where almost nothing happened. Planets revolved sedately around the Sun, stars hardly ever changed, and galaxies just sat there, moving slowly away from each other as the universe gradually expanded. To be fair, there were supernovae, stellar explosions seen, for example, in 1054, 1572 and 1604, but these were rare events, and it was not known how much if any gravitational radiation they emitted.
A third question is: if there were gravitational waves passing through the Earth, could one build a practical detector sensitive enough to sense them? The person who took on this challenge was Joseph P. Weber. To his many detractors Weber was a tragic figure, whose work was flawed and whose claims were roundly refuted. To others, he was the father of gravitational wave detection whose insights established many of the principles that enabled the successful detections using laser interferometers. His story illustrates the sometimes fitful and complex ways in which science advances, and is also a case study in how science works.
Weber was the son of Lithuanian Jews who settled in New Jersey and New York in the early 1900s. Born in 1919, he graduated from the US Naval Academy in 1940, served in World War II, and after the war led the Navy’s electronic countermeasures section, retiring from the Navy as lieutenant commander.
In 1948, the University of Maryland appointed him as an engineering professor under the stipulation that he quickly earn a Ph.D. degree. Weber asked George Gamow, a physics professor at George Washington University in Washington DC, famous for his explanation of radioactivity through quantum physics, if he would be his Ph.D. advisor. Ironically, this was the same year that Gamow and his student Ralph Alpher had theoretically predicted the existence of the first light after the big bang, today called the cosmic microwave background (CMB) radiation. But instead of suggesting to Weber that he should work on the experimental detection of this first light, Gamow turned Weber away. In 1965 this radiation was detected, almost by accident, by Arno Penzias and Robert Wilson, two Bell Telephone Laboratory scientists.
After Gamow’s rejection, Weber decided to work on the physics of atoms with Keith Laidler, earning a Ph.D. in 1951 from The Catholic University of America. His thesis led to a paper that he submitted for presentation at an international conference in Canada on “coherent microwave emission.” This paper had many of the key ideas and concepts that would lead to the maser (microwave amplification by stimulated emission of radiation) and ultimately to the laser (where “microwave” is replaced by “light”). Charles Townes was also working on this problem and asked Weber for a copy of his paper, while Nikolay Basov and Aleksandr Prokhorov in the Soviet Union were independently working along the same lines. In 1964, Townes, Basov and Prokhorov were awarded the Nobel Prize in Physics for their construction of the first masers and lasers. Although Weber was also nominated for the Nobel Prize at the same time, he never received it.
According to Kip Thorne, Weber’s interest in general relativity began to grow after the maser discovery, because Weber wished to move into a field of study with less Nobel drama. In 1955 he took a sabbatical at the Institute for Advanced Studies to study gravitational radiation with Wheeler (their presentation at the 1957 Chapel Hill meeting was a result of that work), and then continued his studies at the Lorentz Institute for Theoretical Physics in the Netherlands.
And after these preliminary studies, he set out to do the unthinkable: to detect gravitational waves. Around 1958, he began the project in earnest, first doing the required theoretical calculations to determine just what the physical effects of a passing wave would be on a solid mass, in contrast to a set of disks sliding on a table, and then building an apparatus. By 1965 he had put a simple detector into operation. It consisted of a solid cylinder of aluminum (the reason for aluminum was a mundane one: it was cheap), about a meter in diameter by two meters in length. It weighed about 1.5 tons.
When a gravitational wave passes through the cylinder in a direction perpendicular to its axis, the spacetime distortion in the wave tries to stretch and squeeze the bar end-to-end (see Figure 7.4). There is also stretching and squeezing in the perpendicular directions, but this turns out to be less easy to measure so we will ignore it. As we remarked before, because of the solid material in the bar between the ends, they do not move freely the way two sliding disks would with the same separation, and so the response to the wave can be tiny by comparison.
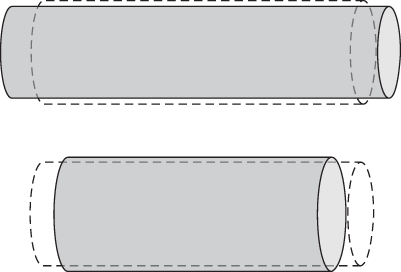
Figure 7.4 Distortions of a “Weber bar” induced by a gravitational wave traveling perpendicularly into the page that you are reading (vastly exaggerating the scale of the effect). Dashed lines indicate the undistorted cylinder. Top panel: The bar is stretched horizontally, while being squeezed in the other directions. Bottom panel: One half cycle later the bar is squeezed horizontally while being stretched in the other directions.
However, the bar has a property that the sliding disks do not. If you were to hit the bar on the end with a hammer, it would vibrate for a considerable time at a single frequency, called its “resonant frequency.” Every child learns about the phenomenon of resonance at an early age. A playground swing moves back and forth with a characteristic frequency that depends on its length. If you push the swing with exactly the same frequency, achieved most easily by pushing once every cycle right when the swing returns to you (or if you are alone, by kicking your legs once each cycle at an optimal time), you can achieve thrilling amplitudes of swing. What’s more, you continue to swing for a while even after the pushing has stopped, until friction from air or from the ropes brings the swing to a halt.
Weber had very good reasons for choosing a resonant bar as opposed to sliding disks. As a possible source of gravitational waves, he was thinking about supernovae, the only kind of “extreme” event known at the time. He imagined that the gravitational signal from such an event would be a short-lived “burst,” possibly no longer than a small fraction of a second, and that it would be “broad-band,” namely that it would contain waves with a broad range of frequencies as opposed to a single frequency, like a pure sound tone. If some part of the signal was at the resonant frequency of his bar, then the bar would be excited strongly, and in addition it would continue to oscillate at its resonant frequency after the burst had passed, giving more time for his sensors to measure the oscillations. The resonant frequency of his bar happened to be around a thousand cycles per second, or in the kilohertz band, in the same ball park as what one would estimate for the frequency of waves from a supernova. To measure the compression and extension of the bar, Weber bonded devices called “piezoelectric transducers” around the bar at the middle to convert the strains into electrical signals that could be recorded and analyzed. Nevertheless, it was still a daunting prospect: even the crudest estimate of the signal from a supernova in the Milky Way galaxy implied a change in length of his bar of about the diameter of a proton!
Weber devoted a great deal of effort to ensure that his bar was isolated from external disturbances, such as seismic vibrations or the effects of nearby traffic that could set the bar into oscillations and mimic the effect of gravitational waves. This required suspending the bars using the thinnest wires that would support the weight and attaching those wires to supports made of alternating layers of rubber and steel. He also shielded his bars from external electric and magnetic fields.
In June 1969, Weber made the stunning announcement that he was detecting signals simultaneously in two detectors spaced 1,000 kilometers apart, one in Maryland, and the other at Argonne National Accelerator Laboratory near Chicago. The reason for using two detectors is simply that any one detector is often in oscillation because of disturbances from the environment that leak in despite his best attempts to isolate the bar from such noise, and because of the inevitable random internal motions by the atoms inside the bar produced by heat energy. Therefore, in a single bar it is difficult if not impossible to distinguish a disturbance from a gravitational wave from a disturbance of an environmental or thermal origin. As early as 1967, Weber had reported disturbances in a single bar, but he could not reliably claim that they were from gravitational waves. However, with two detectors separated by such a large distance, a disturbance that appears simultaneously in both detectors would be unlikely to be environmental or thermal because the probability of such a random coincidence is very small. Coincident events would therefore be good candidates for gravitational waves. Even more remarkable than the 1969 report of coincident events was his announcement in 1970 that the rate of such events was highest when the detectors were oriented perpendicular to the direction of the center of the galaxy, implying that the sources were indeed extraterrestrial, perhaps concentrated near the Galactic Center. These reports caused a sensation both in scientific circles and in the popular press.
There were two problems, however. The observed events occurred with a disturbance size and at a rate (around three times per day) that shocked theorists, for it implied a rate of gravitational wave bursts at least a thousand times what they predicted. This in itself was not necessarily bad, for often the mark of an important experimental discovery in physics is the degree to which it upsets theoretical sacred cows.
The second problem was more devastating, however. The main body of Weber’s coincidence results were reported between 1969 and 1975. But by 1970, independent groups worldwide had built their own detectors with claimed sensitivities equal to or better than Weber’s, yet between 1970 and 1975, none of these groups saw any unusual disturbances over and above the inevitable noise. By 1980 there was a general consensus that gravitational waves had not been detected by Weber. Weber never accepted any of this and he continued to work on the detection of gravitational waves with resonant bars until his death in 2000.
So, is this a story of a tragic failure or of a great success? It is certainly a good example of the self-correcting nature of science. The acceptance of new results always requires their external confirmation, typically done by carrying out the experiment again in a different setting and perhaps with more sophisticated instruments. In Weber’s case, his results could not be replicated, so his claim was not accepted.
But as John Wheeler put it in 1998: “No one else had the courage to look for gravitational waves until Weber showed that it was within the realm of the possible.”
Over time, a more nuanced view of Weber’s legacy has emerged. Prior to Weber, the field of general relativity was almost completely dominated by theorists. The field was often called a “theorist’s paradise and an experimentalist’s purgatory.” During the Chapel Hill conference, Feynman complained that the problem with general relativity is the lack of experiments. Weber’s announcement induced experimentalists from other branches of physics to get involved in general relativity, such as William Fairbank from low-temperature physics, Ronald Drever from magnetic resonance work, Vladimir Braginsky from precision measurements, Heinz Billing from computer science, Edoardo Amaldi from elementary particle physics, J. Anthony Tyson from astronomy, and others. It also piqued the interest of a young MIT professor named Rainer Weiss, who would soon lay the foundations of the LIGO instrument. These experimentalists helped to transform the landscape of the field into one with a healthy synergy between theorists and experimentalists.
Weber’s work also helped transform theory. As we have seen, when Weber started building his detectors, the main concern of theorists with regard to gravitational waves was their physical reality. After his announcement, the direction shifted dramatically as theory groups around the world starting thinking about plausible (and also implausible) astrophysical sources for the enormous signals he was claiming. Although no scenario was ever found that could explain Weber’s signals, the insights gained and the techniques developed during this period helped to advance the growing interactions between general relativists and astrophysicists that had begun with the discoveries of quasars, pulsars and the cosmic background radiation during the 1960s.
Weber’s work also had a personal impact on one of us. At the time of Weber’s first announcement, Cliff had completed his first year as a Caltech graduate student and was thinking about doing a summer project in Kip Thorne’s research group. Thorne told him:
I am worried that if Weber is correct, then general relativity itself might be wrong. I want you to spend the summer finding out all there is to know about the current experimental support for the theory and to think about what might be done in the future to prove the theory right or wrong.
That launched Cliff’s fifty-year-long career in general relativity!
The consensus that Weber had not found waves did not end the effort to detect them, of course. Many groups continued to develop advanced bar detectors. One strategy involved cooling the entire bar and associated sensing devices to one or two degrees above absolute zero, in order to reduce the size of the disturbances due to the thermal motions of the atoms inside the bar. Some groups replaced the piezoelectric crystals used by Weber with sophisticated sensors attached to the ends of the bars, leading to greatly improved performance. Some fabricated their bars out of different materials such as sapphire that might have an improved response to the gravitational wave excitations.
None of these groups reported credible detections, but instead established increasingly stringent upper limits on the strength of gravitational waves bathing the Earth. Although by 1979, as we saw in Chapter 5, the measurements of the binary pulsar had verified the existence of gravitational waves, the actual waves emitted by that system were far too weak and of too low a frequency to be detectable by resonant bars. Work continued on bars for another 25 years, but gradually declined for lack of funding until the last “Weber bars” ceased operations for gravitational wave detection around 2008. But important advances were made in the course of this research, in new techniques for isolating the bars from things like seismic noise, in the control of thermal noise and in data analysis techniques. Many of these lessons would be used in helping to develop an alternative detector concept that began to emerge during the 1970s, the laser interferometer.
The laser interferometer is based on an apparatus devised by US scientist Albert A. Michelson originally to measure the speed of light very accurately, but then famously used by him and Edward W. Morley in 1887 to try to detect the motion of the Earth through the “aether,” the hypothetical medium through which light supposedly propagated. Schematically, Michelson’s interferometer consists of two straight arms set at right angles to each other (Figure 7.5). Each arm has a mirror at one end. At the intersection where the arms are joined, a half-silvered mirror splits a light beam into two, each traveling down one arm, each reflected back by the mirror at the end of each arm. When the two beams recombine, they interfere to produce a characteristic pattern of fringes that depends on the difference in time required for the two beams to make the round trip. Michelson and Morley failed to detect any effect of motion through the aether, and the conundrum inspired by that failure ultimately led to Einstein’s special theory of relativity.
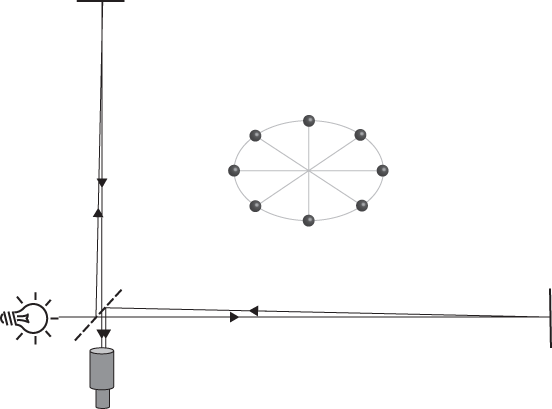
Figure 7.5 Schematic version of a laser interferometer. Light from a laser is split by a half-reflecting mirror and travels along two perpendicular arms. Mirrors at each end reflect each beam back. The beams are brought together at a sensor. If the waves interfere constructively, a bright spot is seen; if they interfere destructively, a dark spot is seen. A “plus”-polarized gravitational wave that travels perpendicularly into the page you are reading will stretch one arm while compressing the other, thus altering the interference between the two light beams.
Michelson’s interferometer is an excellent tool for measuring distance precisely, because a change in the length of an arm of a quarter of the wavelength of light will turn a bright spot at the output into a dark spot. Since the wavelength of light is measured in millionths of a meter, it is easy to see the potential, at least in principle, of measuring the tiny changes in separation between objects induced by a gravitational wave. The reader might again ask: the gravitational wave changes the distance between the mirrors and the beam splitter, but doesn’t it also affect the propagation of the light ray? The answer is yes, but just as in the example of the disks sliding on the table, the two effects do not cancel each other out, and there is a true, measurable change in the brightness of the output beam.
The first to think about such a scheme were the Russian physicists M. Gerstenshtein and V. Pustovoit in 1963, but their work was not recognized until many years later. Weber and his student Robert Forward independently considered this possibility, and Forward actually built the first prototype for an interferometric detector in 1972. But the person generally credited with showing how to turn this idealized concept into a large-scale device that might actually detect gravitational waves is Rainer Weiss, or Rai, as he is known to all his colleagues.
Rai’s family escaped Nazi Germany and relocated to New York City in 1939. A brilliant tinkerer in anything electronic, he started his studies in electrical engineering at MIT, but left Boston in his junior year to pursue a romantic relationship in Chicago that would eventually fizzle out. Upon his return to MIT, he discovered he had been expelled because he had gone AWOL. Undaunted, he managed to convince MIT physicist Jerrold Zacharias to give him a job as a technician in his lab. Around that same time, Zacharias was working on the first practical version of an atomic clock, based on cesium atoms. With the help of Zacharias, Rai was readmitted to MIT, finished his undergraduate degree in 1955 and finally obtained a Ph.D. under Zacharias in 1962.
After a two-year stint as a postdoc with physicist Robert Dicke at Princeton University, where he began to develop experiments to test general relativity, he returned to MIT in 1964 as an assistant professor. At the urging of radio astronomer Bernard Burke, he took an interest in the cosmic microwave background radiation, recently detected by Penzias and Wilson. This radiation is the remains of the hot electromagnetic radiation that would have dominated the universe in its earlier phase, now cooled to a few degrees above absolute zero by the subsequent expansion of the universe. Cosmological theory suggested that the strength of this radiation should have a very specific dependence on the wavelength of the radiation, known as a “black-body spectrum,” but measurements made using sensors on rockets threatened to discredit this prediction. Rai and his graduate student flew a device on a high-altitude weather balloon that showed convincingly in 1973 that the spectrum was that of a black body, and also measured its temperature to be 3 degrees above absolute zero (the modern measured value is 2.725°). Rai would later be a leader on NASA’s Cosmic Background Explorer satellite, which would make even more precise measurements of the properties of this radiation between 1989 and 1993.
But he had never truly forgotten about his first love, gravity experiments. Around 1968, MIT asked him to teach a class on general relativity, but not being an expert on the theoretical side of the subject, he chose to focus on the experimental side, using a small 1961 primer on general relativity and gravitational waves that had been written by Weber. But when he studied Weber’s discussion of using resonant bars, he could not understand how Weber could achieve the sensitivity needed to detect the waves. So he assigned a homework problem in his course: find a way to measure gravitational waves by sending light beams between things. The students were stumped, so not much came out of that homework set. Soon Weber was claiming detections, to Rai’s skepticism, and so he decided to think more seriously about the interferometer idea. He analyzed in detail every source of noise or disturbance he could think of and concluded that, with a large enough interferometer, it might be possible to beat Weber’s sensitivity by a factor of a thousand. He also recognized a key difference between Weber’s resonant bars and an interferometer. The bars respond strongly only to the part of the gravitational wave whose frequency is close to the resonant frequency of the bar, whereas if one suspended the mirrors in the interferometer on long pendula, they would respond fully to the gravitational wave, no matter what its frequency was, just like our frictionless hockey pucks.
Thinking that this analysis was not worth publishing as a scientific paper, he wrote it up in a twenty-three page report printed in one of MIT’s quarterly newsletters in 1972. The concepts laid out in his report would become the foundation of LIGO’s design.
While preparing his MIT report, he requested and obtained funding from MIT to build a small prototype with arms 1.5 meters long, and around 1975 he wrote a proposal to the NSF to continue this work. Despite positive reviews, the proposal was turned down. The proposal came to the attention of Heinz Billing at the Max Planck Institute in Munich. One of the pioneers of computer science, Billing had recently returned to physics, and his group was engaged in using resonant bars to check Weber’s claims. Turned on by Rai’s description of the potential of interferometry for detecting waves, he and his colleagues started to build a prototype. Soon his laboratory was paid a visit by Ron Drever, who also had been working on bar detectors, and now became intrigued by this new approach. Drever (1931–2017) was a brilliant and inventive physicist at the University of Glasgow, who at the age of twenty-nine performed an exquisite experiment using nuclear magnetic resonance techniques to show that the mass of an atom does not depend on its orientation relative to the Galaxy or relative to the Earth’s velocity through the universe. Drever’s group began to build a prototype interferometric detector.
Kip Thorne at Caltech also began to think about interferometers, spurred by a late-into-the-night discussion with Rai Weiss at a hotel in Washington during a NASA committee meeting. His group had been at the forefront of the theory of gravitational wave sources, but he felt that Caltech should also have a presence in the experimental side, and so he recruited Drever to move to Caltech in 1979, where he began to build a 40 meter prototype.
It had become clear that tabletop or laboratory-scale prototype interferometers were fine for technology development, but that they would not be sufficiently sensitive to ever detect the kinds of gravitational waves that might reasonably be expected from astrophysical sources. Instead, devices with arms as long as many kilometers would be needed. The reason is that the change in distance between two objects that a gravitational wave induces is proportional to the distance. If you double the distance between the beam splitter and the mirror, you double the displacement, and therefore you double the difference between the light beams when they recombine. Go from a 40 meter prototype to a 4 kilometer system and you increase the effect by 100. Unfortunately, you also increase the cost by a similar factor. One reason is that the light must propagate through an ultra-high vacuum, otherwise the fluctuations in the light speed caused by its interactions with the atoms in the residual gas or air would have a larger effect than the displacements of the mirrors caused by a gravitational wave. There was also general agreement that, just as with Weber’s bars, two widely separated interferometers would be needed in order to claim a credible detection. It was thus also becoming clear that gravitational wave detection would be very costly.
As a result, at the urging of the NSF, Caltech and MIT agreed in 1984 to cooperate on the design and construction of LIGO, with joint leadership by Weiss, Thorne and Drever. This leadership arrangement proved unworkable, however, and in 1987, astrophysicist and former Caltech Provost Rochus E. Vogt was appointed LIGO director. By 1992, initial funding for construction had been provided by the US Congress, and sites in Hanford, Washington and Livingston, Louisiana had been selected. Barry Barish, a high-energy particle physicist, replaced Vogt as LIGO director in 1994 and oversaw the construction and commissioning of the detectors and the initial gravitational wave searches. The plan for LIGO involved two stages: building and operating the interferometers with proven technology, with a sensitivity where gravitational waves might be detected, and then to upgrade them with advanced technology to a level where waves would be detected, if general relativity and our understanding of astrophysics were correct. Searches for gravitational waves with the initial LIGO were carried out between 2002 and 2010. To nobody’s surprise, no waves were detected. On the other hand, the interferometers reached the sensitivities they were designed to achieve and much experience was gained in operations and data analysis. Between 2010 and 2014, the interferometers were shut down in order to install advanced technology that had been under development, such as more powerful lasers, improved mirrors and better isolation from seismic disturbances. By September 2015, the instruments were as much as ten times more sensitive than in the initial LIGO.
But the Americans were not the only ones who wanted to detect gravitational waves. Alain Brillet was a French physicist at the National Research Center in Orsay near Paris who had worked with Jon Hall at the University of Colorado in 1979 to do a twentieth-century version of the famous Michelson–Morley experiment, but using a laser as the light source in the interferometer. Adalberto Giazotto was an elementary particle physicist at the National Institute of Nuclear Physics in Pisa, Italy who had taken an interest in gravitational wave detection, and particularly in the problem of seismic isolation of the mirrors. Together they proposed a large European interferometer, which was ultimately built near the town of Cascina, about 15 kilometers south-east of Pisa, and named Virgo after the Virgo cluster of galaxies. Drever’s group in Glasgow and Billing’s group in Munich combined forces to propose a large interferometer. Because of funding limitations, caused in part by the cost of the reunification of Germany, they had to settle for 600 meter arms, compared to the 4 kilometers of LIGO and 3 kilometers for Virgo. That instrument, called GEO-600, was built near Hannover, Germany. Researchers in Australia initially built advanced resonant bar detectors, and then moved into interferometers, but could never convince their government to go beyond an 80 meter prototype called AIGO, sited near Perth in Western Australia. Japanese teams also became very active, and have recently completed an ambitious interferometer, the Kamioka Gravitational Wave Detector (KAGRA), a 3 kilometer instrument built deep inside Mount Ikeno near Hida, Japan, where numerous underground physics experiments studying neutrinos, dark matter and proton decay have been run using inactive shafts and tunnels from the Kamioka mine (see Chapter 9).
You might be picturing an intense international race and competition to be the first to detect gravitational waves, but in fact quite the opposite happened. Recall Weber’s dictum that you had to have more than one detector to be sure that you have detected gravitational waves. In addition, since the mirrors in the interferometers respond immediately and freely to a passing gravitational wave, by recording the difference in time of arrival of the same signal in two widely separated interferometers, you can get some idea of the direction of the source. The principle is the same as the one we discussed in Chapter 3 (see Figure 3.5), whereby the difference in arrival time of a radio wave at two separated radio telescopes can be used to determine the source direction. Two interferometers give only limited information about the location of the source on the sky; the more interferometers you have, the more accurately you can pinpoint the source. For this to work, different teams have to cooperate, regardless of the desire of any individual or national agency to garner the glory of being “first.” So while LIGO and Virgo were still under construction, the leadership of the two projects began the delicate negotiations that would ultimately lead in 2007 to the LIGO–Virgo Collaboration, a rather remarkable structure that views the two LIGO instruments and Virgo as a single network of three interferometers, with full data sharing and transparency, coordination of schedules, and so on. (For colleagues of ours who are members of the collaboration, it also means an unbelievable number of teleconferences across many continents, resulting often in highly inconvenient work hours!) The GEO-600 and AIGO teams joined the collaboration to work on technology development. Despite its lower sensitivity, GEO-600 also made observations when the LIGO and Virgo instruments were offline, just in case a strong event, such as a nearby supernova, might occur. Virgo also adopted a two-stage development strategy, similar to the initial-to-advanced LIGO track. When the first detection was made on 14 September 2015, advanced-Virgo was still about a year away from being up and running, so the signal was only seen by the LIGO interferometers, yet the discovery paper published in 2016 included all the members of Virgo as co-authors. The paper had over a thousand authors. In the next chapter we will see how important this cooperation proved to be, when we discuss what signals were actually detected and what they implied.
By early 2015 both LIGO interferometers were working, and entered what is called an “engineering run,” during which the operators of the instruments poke and prod them, tweak the dials and alter various settings, all in an effort to get the maximum performance. That run was scheduled to end on 18 September, when all tweaking would cease and an “observing run” would begin. But the engineers completed their work about a week ahead of schedule, and both interferometers were performing quietly, awaiting official kick-off of the observing run. On 14 September at 5:51 a.m., Eastern Daylight Time, the Livingston instrument recorded a signal, and 7 milliseconds later the Hanford detector recorded the same signal. The signal, known thereafter by the name GW150914 (GW for gravitational wave, followed by the date in yymmdd format), arrived close to a hundred years after Einstein published his theory. In the next chapter we will describe the detection and what we learned from it.
Before we do that, there is one final aspect of gravitational waves that we need to discuss. In various newspaper reports about gravitational waves, you may have encountered the phrase “listening to gravitational waves.” Many popular books on this subject use musical motifs, such as Marcia Bartusiak’s Einstein’s Unfinished Symphony or Janna Levin’s Black Hole Blues; Chapter 9 of this book talks about a “loud” future instead of a bright future. What is that all about? Normally you think about astronomers “gazing” at the heavens, “seeing” a supernova explosion, or “watching” a planet transit in front of the Sun. Why do we “listen” to the universe with gravitational waves?
The reason has to do with the fundamental difference between electromagnetic waves and gravitational waves. When electromagnetic waves, a.k.a. light, impinge upon some material, such as the retina of your eye, the electric and magnetic fields of the light waves push on the charged electrons in the material and generate an electrical current. If you prefer the quantum mechanical picture in which light consists of “photons,” then the photons knock the electrons loose from their host atoms. The current is then sent from the retina of your eye to the optic nerve and then to your brain. The current could be produced in the CCD device in your camera or smartphone. Or it could be in the conducting antenna of a radio telescope. The act of “seeing” in all its manifestations basically amounts to using light to move electrons and thereby to produce electrical currents.
Gravitational waves act very differently, causing bits of mass (not charge) to move back and forth relative to each other via the stretching and compressing of spacetime (recall the hockey pucks in Figure 7.3). So when a gravitational wave passes through your head, it causes the eardrum and bones in one ear to move relative to those in the other ear. It also tries to stretch and compress your skull in the same manner, but since your skull is rather rigid, it can resist that effect to a large degree. The elements of your inner ear, on the other hand, are more free to move, and in doing so, they strike the membrane of the cochlea, forcing the fluid inside to move back and forth, triggering a set of hairs that convert the oscillations into electrical impulses that travel through nerves to your brain. The only difference between sound waves and gravitational waves in this regard is that sound waves use the expansion and compression of air to move the eardrum, while gravitational waves use the expansion and contraction of spacetime itself to produce the same effect.
But we cannot sense all possible vibrations of our eardrums. This is because the conversion of the oscillations into electrical impulses is not efficient enough for frequencies below about 20 hertz (for the lowest-pitched sounds) or above about 20,000 hertz (for the highest-pitched sounds). Other mammals, such as dogs, can hear up to 45,000 hertz, while the greater wax moth can hear sounds up to 300,000 hertz! Dog whistles, in fact, leverage this physics principle: they produce vibrations in the air that are too high a frequency for the human ear to pick up, but that can be easily heard by dogs.
As we will learn in the next chapter, the waves from GW150914 had a frequency in the region between 40 and 300 hertz, well within the human audible band. So why didn’t people around the world hear the signal? The answer is the incredible weakness of gravitational waves. The minimum eardrum motion that we can detect is about a nanometer, or a millionth of a millimeter. The gravitational waves detected by LIGO moved our eardrums by about a trillionth of a nanometer! Alternatively, we could have heard those waves if the source had been extremely close, about twice as far from the Sun as Neptune, instead of over a billion light years away. We should be happy that this was not the case. Since the source was two black holes each about thirty times the mass of the Sun in a close orbit around each other, their normal gravitational tug on the Sun and planets would have disrupted the Solar System (or prevented its formation in the first place) long before we came along.
Instead of eardrums, we have the mirrors of LIGO and Virgo. Instead of the tiny bones of the inner ear and the cochlea, we have laser beams bouncing off the mirrors, capable of detecting their motions to better than a thousandth of the diameter of a proton. The laser interferometers of LIGO and Virgo are our tools for listening to gravitational waves. And what have we learned from these sounds?