Appendix A

A.1 Fundamentals of Linear Algebra

This section presents some of the most common concepts from linear algebra that have direct application to robotics and autonomous systems. The interested reader is referred to the numerous excellent texts on this topic, such as [18], for a detailed discussion. This book will restrict its attention to linear algebra over thevector space of images ‐tuples of real numbers images . The operations ofvector addition andmultiplication of vectors by scalars are defined intuitively in terms of component‐wise operations. If images , images , and images , for addition,

Multiplication of a vector images by a scalar images is likewise defined component‐wise as

One of the implications of this definition is that for a subset images to be a vector subspace of images , thezero vector must be contained in images . Since the scalar images can always be chosen, the requirement that images be closed with respect to multiplication of vectors by a scalar means that images for any vector images . The most common way to define vector subspaces is by considering thespan of a a fixed finite set of vectors.

The definition above asserts that the span of a set of vectors is in fact a vector subspace. This is not difficult to see. A vector subspace must be closed with respect to the operations of vector addition and multiplication of a vector by a scalar. Suppose that images are two arbitrary vectors in the span of the vectors images . By definition there must be two sets of coefficients images and images such that the finite linear combinations of these vectors may be defined as

and

However, if this is the case, the sum can be written as

and it follows that the vector images lies in the span of this set of vectors. Similarly, if images lies in the span of the set of vectors images and images is any real number, it can be written that

Thus, the vector images also lies in the span of these vectors. The span of the set of vectors is therefore closed with respect to vector addition and multiplication of vectors by scalars, so it is a vector subspace of images .

The reader should carefully note that the above definition states that the range and nullspace of a matrix images are vector subspaces of images and images , respectively. Since the range of a matrix images is defined to be the span of its column vectors, it is closed under the operations of vector addition and multiplication of vectors by scalars, following the reasoning after Definition A.2.

The definitions of the range and nullspace of a matrix images have been introduced because they are immediately useful in the analysis of numerous problems in robotics. The following theorem shows that the range of a matrix images and the nullspace of the transposed matrix images induces anorthogonal decomposition. This decomposition is useful in applications where a matrix equation must be solved; it enables a geometric interpretation.

This theorem is interpreted as follows. For any vector images in images , images can be written in the form

where images lies in the range of images , images lies in the nullspace of images , and images .

A.1.1 Solution of Matrix Equations

Now consider the matrix equation

(A.2)

where images is an images matrix, images is an images vector, and images is an images vector. With the fundamental definition of the range of a matrix given in the previous section, an alternative way to express the fact that matrix Equation (A.2) has at least one solution may be defined.

Theorem A.2 summarized the fact that the existence of a solution to the matrix Equation (A.2) can be interpreted as a requirement that vector images lies in the range of the matrix images . The next theorem shows that multiple solutions to the matrix equation exist if and only if the nullspace of the matrix images contains some non‐zero vector.

A.1.2 Linear Independence and Rank

It has been shown that the existence of a solution of the matrix Equation (A.2) can be couched in terms of the range of the matrix images in Theorem A.2. The characterization of multiple solutions of this equation is given in terms of the nullspace of the matrix images in Theorem A.3. While these two theorems provide a geometric interpretation of the solution of the matrix Equation (A.2), it is also common to discuss solutions of this equation in terms ofrank conditions on the matrix images . The definition of the rank of a matrix images is prepared for by introducing the notion oflinear independence of a set of vectors and abasis for a vector subspace of images .

If a set of vectors images is linearly dependent it is possible to express at least one of the vectors in terms of the remaining vectors in the set. To see why this is the case, suppose that the set of vectors is not linearly independent. This means that there is some set of coefficients, not all equal to zero, such that

Suppose, without loss of generality, that the coefficient images in this summation. In this case images can be solved for in the form

Collections of vectors that are linearly independent play a critical role in determining bases for vector subspaces.

The definition of a basis for a vector subspace, as well as its dimension, will make it possible to give a precise description the existence and multiplicity of solutions to the matrix Equation (A.2). This description will be given in terms of the rank of a matrix images .

The column rank of a matrix images is the dimension of the range of images . The following theorem notes that these two values are equal for a given matrix.

One implication of the above theorem is that the largest possible dimension of any subspace images contained in images is the dimension images of the ambient space.

A.1.3 Invertibility and Rank

It has been shown that the existence and uniqueness of solutions to the linear matrix equations images can be described in terms of the range and nullspace of the matrix images when images . When images is a square matrix, the existence and uniqueness of the solutions to this equation can be discussed in terms of theinvertibility of images .

The following theorem summarizes several well known facts relating the inverse, rank, range, nullspace, and determinant of the matrix images to the existence and uniqueness of solutions to the linear matrix equation images .

The proof of all of these properties can be carried out using the definitions and theorems developed thus far, but in some cases they can be lengthy. With the use of thesingular value decomposition, introduced in Section A.1.4, it is straightforward to show the equivalence of these properties. Therefore, the proof of this theorem is deferred until the next section.

A.1.4 Least Squares Approximation

Some of the common, fundamental theorems that describe the matrix Equation (A.2) have been discussed in Sections A.1.1 and A.1.2. It is often the case that the matrix equation images cannot be solved exactly. It may be that the information given isinconsistent with the form of the matrix equation. This often occurs if the data in the coefficient matrix images or the right hand side images is obtained via experiment. Even if the data is known precisely or analytically, it can also happen that the solution images to this equation is desired if it exists, but it is sufficient if it is merely “close to satisfying” the equation. This occurs often in the synthesis of control laws, for example.

No matter the motivation, vectors images that only approximately solve the matrix Equation (A.2) can be found by replacing Equation (A.2) with an optimization problem. A vector images should minimize the norm of theresidual ordefect images

(A.3)

The norm images is greater than or equal to zero for all possible choices of images , and it can only equal zero when images equals zero. Thus, if the matrix Equation (A.2) has an exact solution, then it exactly solves the optimization problem in Equation (A.3). However, it is always possible to solve Equation (A.3), even if Equation (A.2) does not have an exact solution. This fact enables us to define approximate solutions of the matrix Equation (A.2).

The solution of the alternative optimization problem in Equation (A.3) uses a property of orthogonal matrices derived in Chapter . The norm of a vector does not change when acted upon by arotation matrix. For the problem at hand, consider the norm of the residual images when this vector is premultiplied by some orthogonal matrix images ,

The minimization in Equation (A.3) is equivalent then to the minimization problem

(A.4)

The orthogonal matrix images can be chosen to simplify the computational task.

In practice there are many reasonable choices for the construction of the matrix images . Methods based on Givens transformations, Householder transformations, and Jacobi rotations are just a few of the orthogonal matrices that can be used in this approach. The interested reader should consult [18] for a complete summary. This book will only discuss one such method based on the singular value decomposition of a matrix.

Suppose that images , so that the problem isoverdetermined orexactly determined. Partition the matrix images so that images corresponds to the first images columns of the matrix images and images corresponds to the next images columns of images in

and conformally partition the matrix images into the images diagonal matrix images and the images zero matrix

This decomposition is appled to theoptimization problem in Equation (A.4) by choosing images to be equal to images .

(A.6)

(A.7)

(A.8)

(A.9)

The term images is independent of the choice of vector images . The first term, however, can be solved using the following theorem.

Next, the proof of Theorem A.7 will be reconsidered using the singular value decomposition of the matrix images .

First, it is clear that property (i) is equivalent to property (ii) by the definition of the matrix inverse. Next, it will be shown that property (i) is equivalent to property (iii). The singular value decomposition of the square matrix images is given by

where images , images , and images are all images matrices. Suppose that images is invertible. We will show that images is invertible. Since it can be written that

and images is assumed to be invertible, the inverse of the term on the right is equal to

Therefore, images is a diagonal, non‐negative matrix for which the inverse exists. The inverse of a diagonal matrix images is obtained by inverting the diagonal elements of images , and because of this there are no zeros on the diagonal of images . Therefore, images , as the determinant of a diagonal matrix is equal to the product of the terms on the diagonal. Therefore, if images is invertible, then images since

In addition, this sequence of steps can be reversed, starting with the assumption that images , next deducing that images , proceeding to argue that images is invertible, and finally concluding that images is invertible. Therefore, property (i) holds if and only if property (iii) holds.

Next, the matrix images will be partitioned according to the number of non‐zero singular values in images for which

In this equation it is assumed that there are images non‐zero singular values, so that images is a images matrix, images and images are images matrices, and images and images are images matrices. By inspection, images and images . From the proof that properties (i) and (iii) are equivalent, it is known that images exists if and only if images has no zeros on the diagonal. This is equivalent to saying that images . It follows that

which states that property (i), (iv), and (v) are equivalent.

Finally, it is known that images is equal to the number of linearly independent columns of images , which is the same as the dimension of images . Since images , and all of the columns of images are orthogonal and therefore linearly independent, images . This shows that property (vi) is equivalent to property (i).

Example A.2

Consider again the matrix Equation (A.10) in Example (1). That example stated that the matrix Equation (A.10) has at least one solution if images lies in the range of the matrix images . Derive a simple condition that can be used to check theconsistency of the matrix equation for a given right hand side images .

Solution

First, there are many computational tools that can be used to construct a basis for the range of a matrix images , such as the QR decomposition or the singular value decomposition [18]. However, a simple test is desired that can be used for the problem at hand. Theorem A.1 provides one relatively easy way to check the consistency of the matrix equation for a specific right hand side. Theorem A.1 states that any vector images in images can be decomposed into the sum of a vector images that lies in the range of a matrix images and a vector images that lies in the nullspace of the transposed matrix images . Moreover, the vectors images and images are orthogonal. It is not difficult to calculate the nullspace of the matrix images in this problem. As before, partition the matrix images into its columns images . This partitioning of images into columns also partitions images into rows via

(A.11)

The nullspace of images is defined to be the vector subspace

The set of vectors that are perpendicular to images and images can be defined as any multiple of the cross product images . This shows that

Suppose Theorem A.1 is used to decompose the vector images into two such perpendicular components images . The matrix equation has a solution if and only if images lies in the range of the matrix images , which holds only if images . In other words, a solution exists if and only if images . Because images is perpendicular to the nullspace of images , it must be true that

Given the right hand side vector images , this equation is simple to check.

A.1.5 Rank Conditions and the Interaction Matrix

The derivation of theimage based visual servo control law required a solution to the matrix equation

for the velocity of the origin and angular velocity of thecamera frame in theinertial frame. The matrix images was shown to have dimension images where images is the number ofsystem feature points. This matrix is not square in general, which complicates the discussion of the solution of the associated matrix equation. Rewrite the equation above in the form

where images is an images matrix, images is an images vector of unknowns, and images is a images vector of given right hand side values.

A.2 The Algebraic Eigenvalue Problem

Thealgebraic eigenvalue problem appears in many contexts in the study of dynamics and control of robotic systems. It is used to definespectral decompositions that are important in understanding the stability of linear systems, and it is used to construct diagonalizations of real symmetric matrices. This latter construction is important in the definition ofprincipal axes for theinertia matrix of a rigid body.

It is essential to note that the definition of the eigenvector requires that images is a non‐trivial vector. In other words, images cannot identically equal zero. This definition also shows that an eigenvector is a direction that is invariant under the application of the matrix images . It is also evident that if images is an eigenvector of the matrix images , then so is images for any scalar images . The eigenvectors of images are said to be determined only up to a scalar multiple.

One of the most common descriptions of solutions to the algebraic eigenvalue problem can be inferred by applying the theory from the last few sections about the solvability of linear systems.

The definition of the eigenvectors images and eigenvalues images in Definition A.7 requires that

(A.12)

for some scalar images and a vector images that is not identically equal to the zero vector. It is known from the discussion in Section A.1.2 that if the matrix images is invertible, there is a unique solution to the system of equations

for any choice of the right hand side images . Therefore, if the matrix images is invertible, there is a unique solution to Equation (A.12), and it must be that images . However, this case is not of interest for the solution of the algebraic eigenvalue problem. Therefore, the matrix images must not be invertible to allow for multiple solutions, and to permit a non‐trivial images that satisfies Equation (A.12). Section A.1.2 showed that the matrix images is invertible if and only if images . Thus images is an eigenvalue of the matrix images if and only if

If images is an images matrix, the equation images yields an images th order polynomial in images that must be equal to zero. This polynomial equation is called thecharacteristic equation of the algebraic eigenvalue problem. Every images th order polynomial has images (complex) roots, and it is concluded that every images matrix has images eigenvalues.

This theorem shows that the eigenvalues of the images matrix images are defined from the roots of the characteristic polynomial images . Even if images is a real matrix, so that the coefficients in the characteristic polynomial are real, the roots of the characteristic polynomial can still be complex. Also, while every images matrix has images eigenvalues, it is not always the case that there are images distinct eigenvectors. This phenomenon is studied in more detail in Section A.2.2.

A.2.1 Self‐adjoint Matrices

For an important class of matrices, those matrices that areself‐adjoint, a full set of images eigenvectors can be found. A matrix images is self‐adjoint whenever

where images is the complex conjugate of the matrix images . In the applications under consideration, only real matrices will be considered, and a real matrix is self‐adjoint when it issymmetric. The following theorem shows that it is possible to construct an orthonormal basis for images in terms of the eigenvectors of images in this case. This result is a special case of thespectral theory associated with self‐adjoint matrices.

First, (i) will be shown to hold. Suppose that images is an eigenvalue and images is an eigenvector of images with

(A.13)

If images is an eigenvalue of images , it is also an eigenvalue of images . Let images be the eigenvector of images corresponding to images ,

(A.14)

Premultiply Equation (A.13) by images and Equation (A.14) by images to attain

The conjugate transpose of the second equation is taken and subtracted from the first to obtain

In general images is not equal to zero, which implies that images . Therefore, the eigenvalue images must be real.

Next, (ii) will be shown to hold. Suppose that images and images are distincteigenpairs of the matrix images . That is, assume that images . The following two equations are satisfied for theseeigenpairs,

Similar to the discussion of (i), premultiply the first equation above by images , premultiply the second equation above by images , and subtract the transpose of the resulting second equation from the first to obtain

Since the eigenvalues are distinct, images . Therefore, images , or images is orthogonal to images .

For the proof of (iii), it is known that

which shows directly that images and images are images orthogonal.

For the proof of (iv), if the eigenvalues are distinct and the eigenvectors are assumed to each have magnitudes equal to 1 (a common choice for systematically defining eigenvectors), the two properties of the modal matrix images may be directly evaluated as

and

using the analysis already presented. If the eignevalues are not distinct, it is possible to show that the dimension of any eigenspace is finite and has a basis of mutually perpendicular eigenvectors.

A.2.2 Jordan Canonical Form

The spectral theory for self‐adjoint matrices in the last section provides a way to diagonalize a self‐adjoint matrix in terms of its eigenvectors. As already noted, not all images matrices have a full set of images linearly independent eigenvectors. A nearly diagonal factorization that is qualitatively similar to the spectral factorization can be achieved by employing theJordan canonical rorm of a general images matrix. This factorization is particularly useful for the study of the stability of linear systems, as studied in Chapter utilizing feedback linearization to compensate for nonlinear terms.

Note that the columns of the matrix images , in contrast to the matrix images for the self‐adjoint case, is not necessarily constructed from the eigenvectors of the matrix images . The columns of images are sometimes denoted the generalized eigenvectors of the matrix images . The interested reader is referred to [18] for a discussion.

A.3 Gauss Transformations and Factorizations

It is often the case in the study of the dynamics of robotic systems that a matrix system of equations that have the form

(A.15)

must be solved, where images is an images matrix, images is an images vector of unknowns, and images is a known images vector. In some cases, these equations must be solved symbolically, while in other cases a numerical solution suffices. Several conditions in Sections A.1.3, and A.1.4 guarantee the existence and uniqueness of solutions to systems of equations having the form shown in Equation (A.15). In particular, it has been shown that if there is a unique solution images to Equation (A.18), the solution of these equations is equivalent to the calculation of the inverse images of the matrix images . The proof of Theorem A.7 following Theorem A.9 shows that the singular value decomposition can be used to calculate the inverse of a matrix when it exists. Unfortunately, the singular value decomposition is computationally expensive compared to several alternative numerical algorithms; thus, other methods are often preferred in robotic system applications. This section will discuss one such choice that uses sequences of Gauss transformations to derive the inverse of a matrix images , or equivalently, to solve equations having the form shown in Equation (A.15).

The strategy underlying the use of Gauss transformations to solve Equation (A.15) is easy to describe. Suppose two sequences can be found such that

and

of images invertible matrices such that premultiplication of images by the product of the images and postmultiplication of images by the product of the images is equal to the identity matrix, as in the equation

(A.16)

If this is the case, the inverse if the matrix images can be written as

(A.17)

Note that it is critical in this construction that each of the matrices images or images in the sequence is invertible for each images and images . The principle conclusion discussed in this section is that such a product can be constructed provided certainpivot elements of the matrix images are not equal to zero. The construction is carried out usingGauss transformations.

A Gauss transformation is a matrix that is equal to the identity matrix except for a single off‐diagonal entry. Such a matrix has either the lower triangular form shown in Figure (A.1) where images is the off‐diagonal entry located at row images and column images , or it has the upper triangular form shown in Figure (A.2) where images is the off‐diagonal entry located at row images and column images .

bapp01f001 — Figure A.1 Gauss transformation, lower triangular form.

bapp01f002 — Figure A.2 Gauss transformation, upper triangular form.

It is clear that each of these matrices has an inverse, and it is simple to calculate the inverse as

A Gauss transformation has several properties that can be attributed to its highly structured form that are crucial in applications. Lower triangular matrices images will be discussed first and several properties of these matrices will be derived. It will be shown how to select such a matrix so that premultiplication of images by the matrix will zero out a specific entry in images below the main diagonal. If a matrix images is premultiplied by a judiciously selected sequence of such matrices, it is possible to make all of the entries below the main diagonal of the resulting matrix equal to zero. In other words, the product

can be made upper triangular.

Then, it will be argued that similar constructions based on the upper triangular matrices images can be achieved. Postmultiplication of the matrix images by a carefully constructed images can be made to zero out a specific entry above the main diagonal. Postmultiplication of images by a suitably crafted collection of these matrices will result in all entries above the main diagonal set equal to zero. In other words, the product

can be made lower triangular.

Finally, both types of matrices will be used together to achieve the images decomposition of a matrix images into the product of a lower triangular and an upper triangular matrix. Consider first the Gauss transformation images . It is crucial to the understanding of Gauss transforms to observe that premultiplication of a matrix images by images only changes row images and leaves the rest of the matrix images unchanged. In fact, it is straightforward to observe that the only terms that are modified by premultiplication by images are denoted by images for images in the product below

(A.18)

(A.19)

Each newly modified term in row images denoted images in Equation (A.18) is given by

(A.20)

for images . Consider this equation for the choice of images ,

If the diagonal term images , it is possible to choose images so that the Guass transformation images introduces a zero at the entry images of the matrix images . The condition images can be inforced by choosing images since

The diagonal entry images is known as thepivot term, and the success of this strategy relies on the fact that images is not equal to zero. The observations that premultiplication by images affects only row images , and that images can be chosen so that images , leads to a general procedure for constructing a sequence of matrices images that drives the matrix images to a lower triangular form. The matrices images can be successively chosen to zero out entries while progressing down each column below the main diagonal. That is, entries are zeroed out, as depicted in Figure (A.3). It is left as an exercise to show that this algorithm is guaranteed to zero out all the sub‐diagonal entries of the matrix images , provided that the pivot elements images for images are non‐zero. These steps are summarized in Figure (A.4).

bapp01f003 — Figure A.3 Progression of zeros below diagonal.

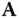All of the observations made thus far regarding the lower triangular Gauss transformations images can be extended to the upper triangular Gauss transformations images with some minor modifications. Postmultiplication of images by images modifies only the entries of the column images . Equation (A.21) depicts the elements images for rows images in column images that are modified when we compute the product images

(A.21)

(A.22)

As in the case of images , it is possible to introduce a zero at location images provided the pivot term images on the diagonal is not zero. Each term images for rows images in column images satisfies the equation

For the specific choice of images ,

(A.23)

If images is defined as images ,

(A.24)

Analogous to the strategy summarized in Figure (A.4), the sequence of upper triangular Gauss transformations can be used to make the product

(A.25)

lower triangular. Figures (A.5) and (A.6) summarize the sequence of entries that are successively set to zero in this strategy.

bapp01f005 — Figure A.5 Progression of zeros above diagonal.