Chapter 6
Control of Robotic Systems

Chapters (2), (3), (4) and (5) have described a large collection of tools that can be used to study the kinematics and derive the equations of motion of robotic systems. This chapter poses and solves several classical problems that arise in the control of robotic systems. This is a vast topic, and one with a long history. An overview of some of the most commonly encountered robotic control problems is presented. This chapter derives joint space, full state feedback control strategies, while Chapter discusses task space feedback control methods. The latter class is well suited to applications in vision based control of robots. Upon completion of this chapter, the student should be able to:

Define the essential ingredients of a control problem for a robotic system.

State various definitions of stability and apply them to robotic systems.

State Lyapunov's direct method and apply it to study the stability of robots.

Formulate computed torque or inverse dynamics controllers for robotic systems.

Discuss the structure of inner and outer loop controllers for robotic systems.

Formulate controllers based on passivity principles for robotic systems.

6.1 The Structure of Control Problems

Many of the common robotic systems encountered in this book have been shown to be governed by equations that have the form

(6.1)

where is an ‐vector of generalized coordinates, is the generalized mass or inertia matrix, is the ‐vector of nonlinear functions of the generalized coordinates and their derivatives, and is an ‐vector of actuation torques or forces. If is invertible, it always possible to rewrite these second order governing equations as a system of first order ordinary differential equations. First define

The resultant governing equations can then be written as

(6.2)

This system is the desired set of first order nonlinear ordinary differential equations subject to the initial condition at the time .

Control methods for robotic systems will be studied using both the second order form in Equation (6.1) and the first order form in Equation (6.2). The first order form is particularly useful in the analysis ofstability, a topic covered in Section 6.2. The expression of the equations of motion in second order form is convenient in deriving some specific control laws. The discussions ofcomputed torque controllers in Section 6.6 or controllers based onpassivity principles in Section 6.8 are based on Equation (6.1).

The ultimate goal in Chapters and was to derive the governing equations of motion in the general form shown in Equations (6.1) or (6.2). In applications numerical or analytical methods are used to solve for the trajectory of the generalized coordinates images for images , given a prescribed set of input functions images for images . Completion of this task solves the classicalforward dynamics problem of robotics. Problems of control theory seek the solution to a different problem: given some desired goal, can the input images be chosen for images so that the system achieves that goal? Many different control problems have been studied over the years. Control strategies are usually categorized depending on (1) the goal the control strategy seeks to attain, and (2) the method used to reach that goal. Common goals include disturbance rejection, error minimization, trajectory tracking, or system stabilization.

6.1.1 Setpoint and Tracking Feedback Control Problems

Two types of goals will be considered in this chapter. The first type isposition control orsetpoint control which seeks to drive the robotic system to a desired state. The goal in setpoint control is to find the actuation input images for images such that the state approaches some fixed, desired state

(6.3)

as images . A typical problem in setpoint control might seek to find the controls images that position and orient the end effector of a robotic arm in some prescribed configuration in the workspace. The second type of control problem studied in this chapter is that oftracking control. The goal of a trajectory tracking controller is to find a control input images such that

as images . The mapping images is a vector of desired, time varying trajectories. As the name suggests, a problem in tracking control might seek to find the control inputs that steer a radar antenna or camera so that it always points at some moving target. It is possible to view a setpoint control law as a special case of a tracking control law. However, it can be easier to state conditions that guarantee that the setpoint control objective is achieved, and for this reason these two problems are studied independently.

6.1.2 Open Loop and Closed Loop Control

In addition to the goal that defines a particular control strategy, the means for achieving that goal differentiates control techniques. One of the most fundamental differences among control strategies distinguishes betweenopen loop control andclosed loop control methods. This distinction is based on the structure of the control input images . An open loop control method is one that chooses the control input images to be some explicit function of the time images alone. If, on the other hand, the actuation input images is given as some function of the states images and perhaps time images ,

the vector images defines a (full state) closed loop control or feedback control strategy. Feedback controllers have many desirable properties. Two important reasons that they are are attractive include the fact that they are amenable to real time implementations using measurements of output, and they reduce the sensitivity of systems to disturbances. This book will only study full state feedback controllers. Sections 6.6, 6.7, and 6.8 discuss several approaches for deriving setpoint or tracking feedback controllers.

6.1.3 Linear and Nonlinear Control

It has been emphasized in this book that the governing equations for most robotic systems are nonlinear: it is an unusual case when they happen to be linear. Chapter showed that Newton–Euler formulations can yield systems of nonlinear ordinary differential equations (ODEs) or differential‐algebraic equations (DAEs). Chapter demonstrated that Hamilton's principle or Lagrange's equations also yield systems of nonlinear ODEs or DAEs. In most undergraduate curricula, the first, and often only, discussion of control theory is restricted tolinear systems. A powerful and comprehensive theory of linear control theory has been developed over the past several decades. The focus onlinear control theory during undergraduate program is justified: it enables the study of linear ODEs that arise in numerous problems from applications in mechanical design, heat transfer, electrical circuits, and fluid flow.

The development of control strategies fornonlinear systems, such as those studied in robotics, is significantly more difficult than that for linear systems. One source of trouble is the fact that the study of the stability is much more complicated for nonlinear systems than linear systems. In addition, the underlying structure of linear control systems is easier to describe than that for nonlinear systems. Each of these issues will be discussed briefly.

The concepts of stability andasymptotic stability (introduced in Definitions 6.2 and 6.3) for general nonlinear systems are local definitions. This means that the assurances that trajectories that start close to an equilibrium remain nearby for all time are guaranteed to be true only when the initial conditions reside in some neighborhood of the equilibrium under consideration. It can be the case that the neighborhood in which the stability guarantees hold is a very small set. If the initial conditions are too far from the equilibrium, and are outside this neighborhood, the guarantee of stability does not hold. In contrast, for linear systems, the neighborhood of the equilibrium is always the whole space. This fact means that for linear systems, local stability impliesglobal stability. It can be a formidable task to prove that a nonlinear system satisfies conditions of global stability. When designing controllers, assurances of global stability and convergence are most desired.

Discussions of stability, including the considerations above, are central in the synthesis of control strategies. The question of whether a system can be rendered stable through the introduction of feedback control is made rigorous via the definition ofstabilizability of dynamic systems. In addition to stabilizability, there are other qualitative properties of dynamic systems that have been defined that are essential to understanding the feasibility of certain control design tasks. For example, the definition ofcontrollability makes clear when it is possible to drive or steer a system to certain configurations. The definition ofobservability describes the ability to reconstruct the state from a specific set of system observations or measurements. There is a rich theory that has been developed for linear systems that provides practical means for determining stabilizability, controllability, and observability. These techniques can be applied to many realistic problems and are now standard tools available in control synthesis software. For certain smooth nonlinear systems the corresponding notions of stabilizability, controllability, and observability have been defined, but the application of these principles to a specific nonlinear system can be exceptionally difficult. The interested student can consult [21] for a detailed discussion.

For the reasons above, the derivation of a control strategy for a nonlinear system, such as a typical robotic system, can be significantly more challenging than that for a linear system.

Fortunately, the structure of the governing equations for many robotic systems is such that it is often possible to define a feedback control law that transforms the set ofnonlinear ODEs into a system oflinear ODEs. This is possible, as will be shown, for robotic manipulators that constitute a kinematic or serial chain that is ground based. It is important to realize that this transformation, which chooses a feedback control to change or modify a set of governing nonlinear ODEs into a system of linear ODEs, cannot be carried out for an arbitrary nonlinear system. It is the special form of certain robotic systems that makes this approach feasible. The question of when this strategy is possible for general systems is studied systematically in the control theory community as the problem offeedback linearization. A good treatment of the problem can be found in [21]. This approach is also known as themethod of dynamic inversion or as computed torque control in the robotics literature. Overviews of these approaches for robotic systems are found in [15] and [30]. Most descriptions of feedback linearization cast the theory in terms of systems of first order ODEs, while descriptions of computed torque control or dynamic inversion retain the structure of second order ODEs that appear directly in either Newton–Euler or analytical mechanic formulations of dynamics. This observation makes it possible to view the approaches derived within the context of dynamic inversion or computed torque control as special cases of the theory of feedback linearization.

6.2 Fundamentals of Stability Theory

This chapter discusses the fundamentals of how to construct and analyze methods of feedback control for robotic systems. The single most important requirement of any control strategy is that the dynamic system that results from the use of the control law is stable. While the relative merit of different control strategies can be quantified via different measures of performance, any viable control technique must yield a stable system.

Stability theory can be framed using different levels of abstraction, as well as under various operating hypotheses. Stability in metric spaces is studied in [40], for example, whereas a stochastic framework is employed in [32]. The stability of infinite dimensional systems is considered in [13], and finite dimensional systems are studied in [19]. Popular treatments that develop stability theory as it is applied to the control of systems of ordinary differential equations can be found in [28, 42], or [44]. These last three references provide a good background for the material in this section, as well as additional advanced material of general interest to robotics control. Finally, the textbooks [3,30] discuss how the general techniques in stability theory can be tailored to specific classes of robotic systems. The discussion of stability here begins by introducing a few background definitions.

It is important to note in this definition that a motion or trajectory associated with thenon‐autonomous system in Equation 6.2 depends parametrically on the initial time images and initial condition images . Sometimes this dependency is emphasized by writing

An equilibrium images of the system, being a constant trajectory that does not depend on time, must satisfy the equations images and images . That is, the trajectory associated with an equilibrium starts at images and remains at images for all time images . The following theorem makes precise the notion of stability for an equilibrium: it takes the form of a standard images proof.

Definition 6.2 imposes requirements only in some neighborhood of the equilibrium under consideration, and for this reason it is sometimes said to define thelocal stability of an equilibrium. If the radius images in the definition can be selected to be arbitrarily large, the equilibrium is said to beglobally stable. In this book, any discussion of stability may be assumed to be a discussion of local stability, and any discussion of global stability will be explicitly labeled as such.

Figure 6.1 illustrates a graphical interpretation of the definition of stability. As shown in the figure, the equilibrium images can be visualized as a trajectory that starts at the fixed point images in the space of initial conditions and is extended as a constant function for all time images . The parameter images defines a tube of radius images centered about the constant trajectory images that is extruded along the time axis. The system is stable if for any images it is possible to find a disk of radius images about the initial condition images such that any trajectory starting in the disk remains inside the tube of radius images for all time. It follows that if the neighborhood of the equilibrium is chosen to be small enough, all trajectories starting in the neighborhood remain bounded for all time.

Figure 6.1 Graphic representation of stability.

The application of this definition becomes more clear in the following example.

Example 6.1

Consider the two link robot depicted in Figure 5.24 and studied in Problem 5.17 of Chapter . Suppose that the second link is locked in position where

Discuss the stability of this system when the control torque .

Solution

The governing equation of motion for the revolute joint may be extracted from Problem 5.17 as

under the assumptions of this example. It can be further simplified to emphasize the essential features of the stability analysis. The location of the mass center along the arm may be defined as

and the total mass and the inertia about the point 0 may be defined via the equations

Using these parameters, the governing Equation can be rewritten as shown in Equation (6.1)

(6.4)

Next, this Equation can be cast in the form of a first order ODE as in Equation (6.2). Define images and choose the definition of the state variables to be

Therefore,

The equilibria for the system satisfy

where images is the set of integers. The stability of the equilibria may be studied by multiplying the governing Equation (6.4) by images and employing the identity

Integrating this identity in time shows that the total mechanical energy images in the system is a constant,

(6.5)

Figure 6.2 depicts the constant value contours of this integral of motion projected onto the images – images plane as a function of the trajectories images . The equilibria in this figure are located on the images axis where images for images . This figure shows that the equilibria for odd values of images are unstable. To visualize this, imagine a tube of radius images centered about any of these equilibria and extruded out of the page along the time axis. Any disk, having any radius images , centered about the equilibrium images associated with an odd value of images will contain some trajectories that leave the images ‐tube for images large enough. For example, one such disk is depicted that has radius images and is centered at the initial condition for the equilibrium at images . No matter how small of a value of images is chosen in the figure, some of the initial conditions inside the disk generate trajectories that depart the images ‐tube. Analogous reasoning also shows that the equilibria associated with even values of images are stable.

No alt text required — Figure 6.2 Plot of for , stable equilibrium marked with , unstable equilibrium marked with . Disc of radius around shown with dashed line.

The solution of this example using MATLAB can be found in Example 6.1 of the MATLAB workbook for DCRS.

The analysis carried out in Example 6.1 is typical of the reasoning employed in studying the stability of a nonlinear system. In particular, the example shows that the concept of stability is associated with a specific trajectory or equilibrium. The ODE representing the robot in Example 6.1 has an infinite number of stable equilibria, as well as an infinite number of unstable equilibria. If the state space of the dynamical system representing the robot is selected to be a manifold, then there are a finite number of equilibria. See 10. The following definition introduces two stronger forms of stability,asymptotic stability andexponential stability. These notions of stability are used in the design of both setpoint and tracking controllers and play an important role in this discussion.

Note that the definitions of asymptotic and exponential stability of equilibria require that they be stable. Figure 6.3 depicts the trajectories of a system that satisfies images for any initial condition. That is, all trajectories are attracted to the equilibrium at the origin. However, the equilibrium at the origin is not stable, hence it is not asymptotically stable. It should be emphasized that Definition 6.3 requires that an asymptotically equilibrium must be stable and attractive: attractivity alone is not enough.

A dynamical system that attracts to the origin, but is not stable at the origin. — Figure 6.3 A dynamical system is attracted to the origin, but is not stable at the origin.

A stable equilibrium is asymptotically stable if a disk of radius images can be found for which trajectories that start at any initial condition in that disk converge to the equilibrium as images . An equilibrium is exponentially stable if it is asymptotically stable and converges to the equilibrium at an exponential rate. Again, it is emphasized that Definition 6.2 imposes conditions only in neighborhood of radius images about the equilibrium, and for this it is sometimes said that the equilibrium islocally asymptotically stable. If the radius images can be chosen to be arbitrarily large, the equilibrium is said to beglobally asymptotically stable. In this book an asymptotically stable equilibrium is understood to mean a locally asymptotically stable, and globally asymptotically stable equilibria are explicitly labeled as such.

The next example shows that these two types of stability appear naturally in typical control problems.

Example 6.2

The equations of motion for the control problem in Example 6.1 may be written in the form

(6.6)

where images is the control input.

Suppose now in this example that the control input torque in Example 6.1 is selected to be

where images are constants. Discuss the stability of the system.

Solution

For this choice of feedback control law, the system equations of motion are equivalent to the second order ODE

Note that this choice of feedback control exactly cancels the nonlinear term from the governing equation, and yields a linear ordinary differential equation as a result. This is a common strategy in many control synthesis problems for robotic systems. We will study this approach in general terms in Section 6.6 where it is known as the method ofdynamic inversion or computed torque control. This equation may be rewritten in terms of the natural frequency images and damping ratio images by introducing the identities images and images so that

(6.7)

The equilibrium of this system is given by

since

Assuming that images , the solution of Equation (6.7) can be written as

with images the damped natural frequency. It is therefore evident that

for some constant images that depends on the initial condition. From the solution for images above, the following bound exists

Similarly,

and it follows that

Let images be the open ball centered at the origin of radius images , images . The bound (6.2) guarantees that if images , then images as images . The equilibrium at the origin of the closed loop system is therefore exponentially stable. In fact, the origin is globally exponentially stable since the constant images can be chosen to be arbitrarily large.

Example 6.2 in the MATLAB workbook for DCRS creates a phase portrait plot of a neighborhood of the equilibrium of the origin. The phase portrait provides a graphical illustration of stability; it illustrates which trajectories converge to the origin.

6.3 Advanced Techniques of Stability Theory

The previous section introduced the definitions of stability, asymptotic stability, and exponential stability. These definitions were applied directly in Examples 6.1 and 6.2 to study a simple robotic system. In Example 6.2, the stability of the equilibrium at the origin was studied by explicitly solving for the solution of the closed loop governing equations. In Example 6.1, the equation of motion was multiplied by images and integrated in time to find a conserved quantity. The critical step wrote the time derivative of the the total mechanical energy images in the form

which was integrated in time to yield

(6.8)

The study of the stability of different equilibria is straightforward using this conserved or invariant quantity.

The study of the stability of control methods for realistic robotic systems can be sufficiently difficult that it is not feasible to solve analytically the closed loop governing equations. It therefore is not practical, or seldom even possible, to use the explicit analytical solution to design and study a feedback control law.

Fortunately, the strategy in which conserved quantities such as energy are identified to study stability can be generalized and applied to many practical robotic systems. These generalizations of energy principles are applied by invoking Lyapunov's direct method. It is now a standard practice in the study of robotic systems to use variants of Lyapunov's direct method to analyze their stability. The study of the finer points of this approach to stability theory extends beyond the scope of this book. This book will introduce only those definitions and theorems that find the most frequent use in applications; no proofs of the underlying theorems are given. The texts [44] or [28] can be consulted for the proofs and for an expanded discussion of Lyapunov theory as it is applied to systems of ODEs. It is also worth observing that this framework has been extended to broader classes of abstract dynamic systems. A good overview can be found in [40].

6.4 Lyapunov's Direct Method

The theorems of Lyapunov's direct method introduceLyapunov functions, which constitute the principal tools for the study of stability. The discussion begins by defining useful ways of describing the growth, or decay, of functions.

Examples of class images functions are readily available. They are positive functions that pass through the origin and are non‐decreasing. The functions images or images are class images functions, as are images for images . Some of these functions are depicted in Figure 6.4.

Examples of class K functions, f(x)=xp for 0ltltltpltltlt∞. — Figure 6.4 Examples of class 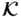functions, 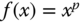for .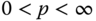

The collection of class images functions are used to define notions of positivity and negativity that are suitable for the study of stability. It will be shown that stability and asymptotic stability are guaranteed if a Lyapunov function images can be identified that is(locally) positive definite and whose time derivative images is(locally) negative definite. The definitions below establish what is meant when a Lyapunov function is said to be positive and its derivative negative.

With this definition, one of the most common forms of Lyapunov stability theorems may be stated. This theorem will be the principal tool used in this book for the study of stability of robotic systems.

It should be noted the above theorem is stated for an equilibrium located at the origin. This is not a restriction in practice. Analysis of non‐zero equilibria begins with a change of variable to shift the equilibrium and define a new set of equations as required in Theorem 6.1.

In order to enforceglobal asymptotic stability (i.e. images ), an additional condition on the Lyapunov function of radial unboundedness must be enforced. As the norm of the state approaches infinity, the Lyapunov function must also approach infinity. Additional details may be found in [28].

A function images that has the properties noted in Theorem 6.1 is aLyapunov function. The most difficult task in using Lyapunov's direct method can be in determining a candidate Lyapunov function. Fortunately, for many robotic systems, there are often good candidates. Researchers have derived, categorized and documented examples of Lyapunov functions for many classes of robotic systems. The reader can see [15] or [30] for examples. Many Lyapunov functions can be derived from, or related to, conserved or energy‐like quantities. The following example is typical in that the Lyapunov function is chosen to be the total mechanical energy.

Example 6.3

Use Theorem 6.1 to show that the equilibrium at images for the robotic system studied in Example 6.1 is stable.

Solution

The governing equation in Example 6.1 is the nonlinear second order ODE

which has an equilibrium of interest at images . Theorem 6.1 is stated in terms of a system of first order nonlinear ODEs that have an equilibrium at the origin. Thus, the analysis begins by shifting the coordinates so that the equilibrium under investigation occurs at the origin. Defining the state to be

allows for the governing equation to be written as

with images . The equilibrium images at the origin corresponds to the equilibrium images , as desired. The total mechanical energy of the system is chosen as the Lyapunov function with

The constant images , which corresponds to a choice of the zero potential energy datum, has been added to ensure that

Graphic representation of shifted sine function used in the Lyapunov function — Figure 6.5 Shifted sine function used in the Lyapunov function.

It is also clear from the plot shown in Figure 6.5 that images is a locally positive definite function on the neighborhood of the origin defined by

The derivative of images along the trajectories of the system is

Since images for all images and images , the equilibrium at the origin is stable. Note that the analysis yields only a local stability guarantee: the neighborhood images is a proper subset of images .

Example 6.1 of the MATLAB workbook for DCRS depicts the Lyapunov function images over a neighborhood of the origin. A trajectory whose initial condition resides in this neighborhood of the equilibrium at the origin is depicted, and it is illustrated that the the Lyapunov function evaluated over this trajectory, images , is non‐increasing.

6.5 The Invariance Principle

The definitions and theorems introduced in the last section that constitute Lyapunov's direct method can be applied to many robotic systems. Several examples throughout this chapter will show that they can be employed directly for the derivation and study of control methods. For example, when seeking to design a controller for a robotic system, it is often desirable to establish some form of asymptotic stability. In the example of setpoint control, a controller is desired such that the joint variables and their derivatives approach some desired constant value as images ,

This condition might correspond to the task of positioning the end effector of a kinematic chain at a prescribed location and orientation. The problem of tracking control seeks a feedback function that causes the joint variables or their derivatives to track some desired trajectories as images ,

In both of these problems, the goal of the control strategy can be cast as a requirement in terms of the asymptotic stability of the error images and its derivative images ; namely, that

as images in both cases.

The technique for establishing asymptotic stability via Lyapunov's direct method requires that the Lyapunov function images is positive, and that the derivative images is negative, for all states in some neighborhood of the equilibrium under consideration. Moreover, the most useful control designs would reach such conclusions for all states, and not just in some neighborhood of the equilibrium. It is always preferable to obtain global, as opposed to local, guarantees of stability in control design. It is usually not difficult to guarantee that images is locally positive definite. Energy or energy‐like quantities often exist for robotic systems that are positive and non‐decreasing, and these are often used in constructing Lyapunov functions for the system. However, it is frequently the case that images isnegative semi‐definite, with

for all images , but not locally negative definite. In such cases Lyapunov's direct method only guarantees stability of an equilibrium and makes no claim regarding asymptotic stability. The following example is typical of this situation and is a common occurrence in realistic applications.

Example 6.4

Show that

is a Lyapunov function for the closed loop system studied in Example 6.2 that is positive definite. Show that the derivative images along the system trajectories is negative semi‐definitive and use Lyapunov's direct method to conclude that the equilibrium at the origin is stable.

Can this Lyapunov function and Theorem 6.1 be used to conclude that the equilibrium at the origin is asymptotically stable?

Solution

First, it can be seen that

for the constant images . The function images is positive definite since the neighborhood can be chosen as images in the inequality above. The derivative of images along the trajectories is calculated as

Substituting the equation of motion results in images . Therefore,

and the equilibrium at the origin is globally stable by Theorem 6.1. However, Theorem 6.1 cannot be applied to conclude that the equilibrium at the origin is asymptotically stable since the function images is not locally negative definite for all images in an open neighborhood images of the origin images . For example, for any state images with images , it is evident that images . But images , so images is not locally negative definite in any neighborhood of the origin. Example 6.2 already established that the origin is globally asymptotically stable by explicitly solving the governing equations. In this case it is clear that the application of Lyapunov's direct method, in the form of Theorem 6.1, does not yield the strongest conclusions possible regarding the stability of the equilibrium at the origin.

There are various techniques to overcome the difficulties associated with a Lyapunov function that has a derivative that is negative semi‐definite but not negative definite. The most popular method is based on LaSalle's invariance principle, which requires the definitions of apositive invariant set, aweakly invariant set, and aninvariant set.

Definition 6.6 stipulates that a set images is positive invariant if every trajectory that starts in images stays in images for all time images . The set images where images is an equilibrium is one example of an positive invariant set. A set images is weakly invariant if for each images there is a trajectory images (defined over all time images ) that passes through images . 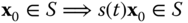A set images is invariant with respect to the system in Equation (6.9) if both images and the complement of images are positive invariant. See Figure 6.6 for a graphic interpretation of positive invariance, weak invariance, and invariance.

It is important to observe that LaSalle's theorem holds for systems of autonomous ODEs; ones that do not depend explicitly on time. The conclusion of LaSalle's principle is that trajectories are attracted to the largest weakly invariant subset contained in

Suppose that images is the largest weakly invariant subset contained in images . A trajectory is attracted to images provided

as images where images is the distance from images to the set images

While the conclusions of LaSalle's principle is of interest in its own right, it is usually employed in control applications by showing that the largest invariant subset images contains a single element images . Then the invariance principle implies that

The conclusion is precisely what is required to show that a stable equilibrium is in fact asymptotically stable. Example 6.5 applies this strategy in a typical robotics problem.

Example 6.5

Show that LaSalle's invariance principle can be used to conclude that the equilibrium at the origin is asymptotically stable in Example 6.4.

Solution

It has already been established that the derivative satisfies images when the Lyapunov function is selected to be images . These identities hold over any open ball images of radius images that contains the origin. In fact, if the closed and bounded set images such that it is contained in images , then all the trajectories that start in images stay in images . This fact follows since images , and therefore images is non‐increasing as a function of time images . It is always true that images , and therefore images implies images . Hence, all the hypotheses of LaSalle's principle hold. It is known therefore that trajectories are attracted to the largest weakly invariant subset images . A set images is weakly invariant provided it is positive invariant and there is a full trajectory images for images that passes through each element images . So images if and only if images for images and images . It is known that

if and only if images for images . The equation of motion

shows that

The equilibrium at the origin is the only element in the largest positive invariant subset images . Therefore,

as images , and asymptotic stability of the equilibrium at the origin is proved.

6.6 Dynamic Inversion or Computed Torque Control

Chapters and showed that the governing equations for a natural system can be written in the form

(6.11)

where images is an images ‐vector of generalized coordinates, images is an images generalized mass or inertia matrix, images is an images ‐vector of nonlinear contributions to the equations of motion, and images is an images ‐vector of actuation torques or forces. The vector images contains contributions from the potential energy images of the system as well as the Coriolis and centripetal terms. The vector images has been shown in Chapter to have the specific structure

(6.12)

where is an generalized damping matrix. Since the generalized inertia matrix is symmetric and positive definite, it is always invertible. Therefore, it is possible to solve for the vector of second derivatives

Thecomputed torque control law selects the actuation torques to be

(6.13)

where is a new, as of yet undetermined, control input vector. With this choice of the actuation torques, the governing equations become

(6.14)

Equation (6.14) is a linear system that has been obtained from the nonlinear Equations (6.11). A nonlinear control law is defined in Equation (6.13) that transforms the system of governing nonlinear ODEs in Equation (6.11) into a system of linear ODEs in Equation (6.14). All of the rich theory that has been developed in linear control theory can now be brought to bear on the system in Equation (6.14). There is a wide collection of control functions images that can be selected in Equation (6.14) that yield specific desirable behavior in the unknown generalized coordinates images . The next theorem discusses one popular feedback strategy that achieves tracking control. The control images is selected so that the generalized coordinates and their derivatives asymptotically track some desired variables images and their derivatives images .

The requirement that images is images ‐uniformly elliptic means that there exist two constants images such that for any vector images , then

for all images . Among other things, this condition ensures that the inverse of images exists and is not singular for any configuration images . Likewise, the assumption that images is a continuous, bounded function on images precludes the possibility that there exist “singular” states of velocities for which images is unbounded.

First note that the feedback law above is exactly the computed torque control in Equation (6.13) for which

(6.16)

(6.17)

The control images is said to contain thefeedforward control images , theposition feedback images and thederivative feedback images . When the feedback is substituted into the governing equation, a new set of equations is obtained for the tracking error,

(6.18)

Define the Lyapunov function

for the closed loop error in Equations (6.18). The function images is positive everywhere except at the origin, where it is equal to zero. If the derivative of the Lyapunov function is computed along the trajectories of the closed loop system, it is found that

Thus, images is negative semi‐definite on any neighborhood of the origin. Therefore, the origin is stable. To show that the origin is asymptotically stable, LaSalle's principle can be used. It states that the trajectories of the system are attracted to the largest invariant subset images of the set

However, images is identically equal to zero if and only if images is identically equal to zero since images is positive definite. That is,

It can be concluded from the equation of motion that the only states in the set images are those (that have a trajectory) images for which

for all images . Since images is symmetric positive definite, the tracking error is identically equal to zero, so that

for all images . In other words, this shows that images if and only if images . It follows that the only invariant subset of images is images . Hence, the origin of the closed loop error equations is a globally, asymptotically stable equilibrium.□

If the physical system is instrumented so that images and images can be measured, it is possible to calculate the actuator forces and moments in images via Equation (6.13) in the implementation of the closed loop feedback control law. It is for this reason that this feedback equation is called the computed torque control law. The choice of control in Equation (6.13) is also said to be derived fromdynamic inversion since the control input images can be interpreted as the solution of a classical inverse dynamics problem. This description will be explained.

Illustration of spherical robot center of mass offsets. — Figure 6.9 Spherical robot center of mass offsets.

The forward dynamics problem associated with the governing equations in Equation (6.11) is the same problem studied in Chapters and . In this problem the actuation forces images are given, and Equation (6.11) is solved for the second derivatives of the generalized coordinates images . In other words, the problem of forward dynamics uses Equation (6.11) to define a mapping from inputs to outputs

If the control in Equation (6.13) is chosen, images is obtained. When the result is substituted into Equation (6.11),

(6.19)

Now Equation (6.19) is solved for the actuation torques from the vector images . The inverse mapping is defined consequently as

The computed torque control is also known as the control determined by dynamic inversion.

This methodology admits an implementation of the control strategy in terms of a well known architecture. The architecture combines a nonlinear compensator and outer loop controller in a natural way. The structure of the overall system is depicted in Figure 6.7. In this figure the governing equations of the robot are embodied in the block labeled “Robotics EOM”. The input to this block is the actuation inputs images and the outputs of the block are the generalized coordinates images and their derivatives images . The nonlinear compensator in the block labeled “dynamic inversion” calculates actuator inputs given the input images using Equation (6.19). This nonlinear transformation is achieved via the solution of the inverse dynamics problem. Finally, the outer loop controller takes as feedback the desired trajectories images and their derivatives images and the generalized coordinates images and their derivatives images , and from these calculates the control input images . In Theorem 6.4 the outer loop controller calculates images from Equation (6.15). This calculation is carried out in terms of a linear gain matrix acting on the tracking and tracking rate error, images . In general, this matrix multiplication can be replaced by a suitable transfer function to implement more general classes of outer loop control.

Figure 6.7 Architecture of computed torque control.

Example 6.6

Consider the spherical robotic manipulator shown in Figures 6.8 and 6.9. Derive a controller for this robot that uses the exact computed torque in Theorem 6.3 with proportional‐derivative feedback in the outer loop to achieve setpoint control. Select the system parameters to be images kg, images m and images m. Choose the gain matrices images and images in Theorem 6.3 to have the form images and images , where the gains are selected to be images , or images , and suppose the desired state is

The initial and final configurations of the robotic manipulator in this example are shown in Figures 6.10(a) and (b). Evaluate the performance of this controller by plotting the state trajectories, set point error, and control inputs as a function of time.

Illustration of spherical robot frames. — Figure 6.8 Spherical robot frames.

Illustration of (left) initial configurations and (right) final configurations. — Figure 6.10 (a) Initial configurations and (b) final configurations.

Solution

The computed torque control low in Theorem 6.3 has the form in Equation (6.13) images , where

and the outer loop control signal images is given by

When this feedback law is substituted into the equations of motion, the closed loop system is governed by the equations

(6.20)

(6.21)

(6.22)

This last set of equations has been obtained using the fact that images and images . Each of these ODEs has the exact same form since the gain matrices are chosen to be diagonal matrices with the same value on the diagonal. The Equations (6.20), (6.21), and (6.22) can be written as

where images and images is the error in degree of freedom images for images The solutions of the error equation have identical structure and differ only in their initial conditions. Figures 6.11(a), (b), and (c) depict the trajectories of images and images when the initial condition has been selected as

Time histories of generalized coordinates and actuation inputs. (a) Trajectory θ1(t). (b) Trajectory θ2(t). (c) Trajectory dqr(t). (d) Actuation torque m1(t). (e) Actuation torque m2(t). (f) Actuation force f(t) — Figure 6.11 Time histories of generalized coordinates and actuation inputs. (a) Trajectory . (b) Trajectory . (c) Trajectory . (d) Actuation torque . (e) Actuation torque . (f) Actuation force .

and the target is given by

Since the initial conditions for images and images are equal in this simulation, the solutions for images and images are identical functions of time, as shown in Figures 6.11(a) and (b). The trajectories do approach the desired target values, as guaranteed in Theorem 6.3; however, some choices of the feedback gains images and images result in rather slow convergence. The convergence of the end effector to the desired terminal location when images requires roughly 50 s. Since the initial condition images matches the desired values images , the trajectory for images is the constant trajectory as depicted in Figure 6.11(c). This response is expected because the solution of Equation (6.20) for the tracking error, when the initial condition of the tracking error and its derivative are equal to zero, is just the function images . Whenever the performance of a setpoint controller is studied, the convergence of the states and the actuation forces required to achieve convergence must also be analyzed. It would serve no purpose to design a controller that requires an actuation authority that exceeds the capabilities of the available actuators. Figure 6.12(a) depicts the actuation torque that is required to drive revolute joint 1 in this simulation over the time period images s, and Figure 6.12(b) depicts the actuation torque for joint 2 over the same period. These two plots illustrate a common feature of feedback linearization techniques: the exactly canceling feedback often induces large transient actuation forces and torques. The figures show that these transient, or startup, input actuation histories can be quite large when the gains are large.

Graphical representation of input torque transients. (Left) Input torque m1(t) and (right) input torque m2(t) — Figure 6.12 Input Torque Transients. (a) Input torque and (b) input torque .

The steady state behavior of the actuation torques acting at the 1 and 2 joints is depicted in Figures 6.11(d) and (e). Note that the steady state responses are at least an order of magnitude less than the peak transient, for large values of the gain. It should also be noted that actuation torque 1, since it does not need to counter the force of gravity, approaches zero as time increases. The torque images must counteract the torque generated by gravity and approaches a finite static value as time increases. The actuation force for the prismatic joint is shown in Figure 6.11(f). Again, this force approaches a non‐zero value since it must counter the force due to gravity on link 3. A key observation from these results that is true across many control problems is that “high gain” controllers that achieve improved convergence induce larger actuation inputs. Finding the optimal balance between performance in error, required actuation authority, actuation bandwidth, and system stability makes control synthesis a challenging task.

Example 6.7

Consider the spherical robotic manipulator studied in Example 6.6. Derive a controller that uses the exact computed torque in Theorem 6.3 with proportional‐derivative feedback in the outer loop to achieve tracking control. Select the system parameters to be images and images , identical to those in Example 6.6. Choose the gain matrices images and images in Theorem 6.3 again to have the form images and images , where the gains are selected to be images , or images . Suppose that the desired trajectory is now

where images and images . Evaluate the performance of this controller by plotting the state trajectories, tracking errors and control inputs as a function of time for the closed loop system.

Solution

This example has been included to emphasize the fact that the setpoint control law is essentially identical to the exactly canceling computed torque tracking controller. Just as in Example 6.6, the closed loop equations that govern the error in tracking are

which may be consolidated into

The tracking error in each degree of freedom satisfies the same linear ODE, subject to perhaps different initial conditions in the tracking error and its derivative. Figures 6.13(a), (b), and (c) depict the state trajectories for images , and images , respectively, for the different choices of the gains images and images .

All approach their desired trajectories at an exponential rate as images , as predicted in theory. The actuation inputs images , and images are depicted in Figures 6.13(d), (e), and (f), respectively. The required actuation moments and torques vary periodically with the frequency of the desired trajectories. As in Example 6.6, the exactly canceling control laws result in transient peaks that far exceed the steady state input values. Figures 6.14(a) and (b) show that the highest gain, which corresponds to the best tracking performance, yields peak actuation torques that occur over a very brief period. The oscillatory steady state trajectories of the torque and force inputs in Figures 6.13(d), (e), and (f) have magnitudes that are only a small fraction of the startup transient values.

Graphical representation of actuation input transient response. (Left) Actuation torque m1(t) and (right) actuation torque m2(t) — Figure 6.14 Actuation input transient response. (a) Actuation torque and (b) actuation torque .

6.7 Approximate Dynamic Inversion and Uncertainty

Section 6.6 presented the fundamentals of dynamic inversion or computed torque control. This approach to the control of robotic systems is one of the most popular starting points for control design. The methodology is applicable to a reasonably large collection of systems, and can also be used to motivate and understand alternative control schemes. Still, one notable drawback of this approach is that the exact cancellation of unwanted terms requires knowledge of the explicit form of the nonlinearities that appear in the governing equations. Since these nonlinear terms depend parametrically on the link mass, moments of inertia, and products of inertia, the approach also requires exact knowledge of these constants. In practice, the exact values for these constants are not known and the introduction of acomputed control torque never achieves the desired exact cancellation. Just as importantly, some applied forces to which the robotic system is subject are very difficult to determine in principle or in practice. Friction, dissipative forces and moments, and nonlinear effects like backlash and hysteresis fall into this category.

The lack of knowledge of the exact form of the nonlinearities is one reason that the analysis described in Section 6.6 for the computed control torques is at best an idealization. There is always some mismatch in practice among the terms to be canceled using a computed torque control law. This section will extend the analysis and allow for the possibility that the actuation vector in Equation (6.13) is only approximately equal to the computed torque control. Suppose now that the control input is given by

(6.23)

where images and images are approximations to the generalized mass or inertia matrix images and nonlinear term images , respectively, in Equation (6.13). The form of the governing equations will also be generalized; suppose that the equations of motion for the robot are

(6.24)

and that images denotes an unknown disturbance torque. The governing equations can be rewritten using the controller (6.23) derived from approximate dynamic inversion as

(6.25)

Equation (6.25) can be written in the compact form images , where images is a measure of the mismatch in exact cancellation

and images and images measure the approximation error for the generalized inertia matrix and nonlinear vector images and images . Equations (6.25) reduce to the form achieved via exact cancellation in Equation (6.14) when images , images and images , as expected.

Many controllers can be derived using the framework described above. One frequently used controller cancels the gravity terms only, approximates the generalized inertia matrix as the identity, and uses proportional‐derivative (PD) control for the outer loop. This controller is able to drive the robot so that it approaches a desired final constant pose as images . This is another simple example of setpoint control.

Theorem 6.3 shows that the method of approximate dynamic inversion can be used to achieve setpoint control when only the nonlinear term due to images is canceled and a PD controller is employed in the outer loop. Many other controllers based on approximate dynamic inversion appear in the literature. The next example provides one technique for achieving a stabilizing controller in the presence of disturbances and uncertainty using a discontinuous control law. This control law is written in a simple form, one that emphasizes that an asymptotically stable response is achieved if the unknown uncertainty images is small enough. Practical versions of the theorem, that establish a priori bounds on the uncertainty images , can be found in the literature. See for example [15].

Theorem 6.5

Let the equations of motion of a robotic system have the form in Equation (6.24). Suppose images is an images ‐vector of desired trajectories, define the tracking error to be images , and define images . Suppose that the following three conditions hold:

(1) The matrix is a symmetric positive definite solution of the Lyapunov equation
(6.27)

where

is an symmetric positive definite matrix, and are symmetric positive definite gain matrices.
(2) The control input is defined to be
(6.28)

where is a positive constant and .
(3) The input in Equation (6.24) is selected to be the approximate dynamic inversion control in Equation (6.23) where
(6.29)

If the uncertainty satisfies for all , then the equilibrium at the origin of the tracking error dynamics is asymptotically stable

Strictly speaking, the introduction of a discontinuous control input as in Equation (6.28) requires the introduction ofchattering solutions ormeasure valued solutions of the governing equations. An interested reader can consult [13] for the details. It turns out that the analysis via Lyapunov's direct method can be extended to this case. Substitution of Equation (6.29) into Equation (6.24) results in the closed loop equations of motion

with

These equations can be written in state space form by introducing the states

Define the Lyapunov function images for the images defined in Equation (6.27). When the Lyapunov function is differentiated along the system trajectories,

The derivative of the Lyapunov function equals images when images . If images , the derivative becomes

The last two terms on the right in this case can be bounded such that

Therefore, the derivative along the system trajectories satisfies images . It has been shown that images is apositive definite function and images is a negative definite function on any open neighborhood of the origin. Therefore, the origin of the tracking error dynamics images is asymptotically stable.□

Theorem 6.5 shows that one means of constructing a tracking controller that accommodates uncertainty in the system dynamics is to introduce the switching feedback signal images defined in Equation (6.28). Such a controller achieves good performance, in principle. If the disturbance or unknown dynamics that gives rise to the mismatch images satisfies images for all images , then the tracking error and its derivative converge to zero asymptotically. Still, there are a couple of troublesome issues with such a “hard” switching controller. One difficulty is theoretical in nature. As mentioned earlier, when the right hand side of the governing system of ordinary differential equations is discontinuous, the rigorous justification for the Lyapunov stability argument must be expressed in terms of generalized solutions. Such an analysis is beyond the scope of this text. See [3,13,30] for a discussion of the details in this case. In addition to such theoretical considerations, there are practical reasons why the “hard” switching controller can be problematic in applications. It is common that this controller exhibits high frequency oscillation as the actuation varies. Moreover, it is not simple to predict when a particular system will exhibit such a pathological response regime because the closed loop system is nonlinear.

The following theorem illustrates that it is possible to address some of these problems by using a “smoothed” switching control. The smoothed switching controller introduces another parameter images that defines a region over which the control input varies in a smooth way between the large output amplitudes of the “hard” switching controller. The right hand side of the resulting closed loop system is continuous, and the system can be described by a conventional, continuous Lyapunov function. As a result, more esoteric notions of generalized solutions are not required for the analysis or interpretation of this control law. In practical terms, the introduction of the parameter images gives an explicit bound on the size of the set over which the switching control varies in amplitude. It is possible as a consequence to eliminate the high frequency oscillation associated with chattering control input signals.

Figure 6.15 Visualization of uniform ultimate boundedness.

The next two examples study controllers based on approximate dynamic inversion for typical robotic systems.

Example 6.8

Consider once again the spherical robotic manipulator studied in Examples 6.6 and 6.7. Derive the controller that uses the PD feedback and gravity compensation as described in Theorem 6.4 to achieve setpoint control for the spherical robot. Select the system parameters to be images kg, images m, and images m. Choose the gain matrices images and images in Theorem 6.4 to have the form images and images , where the gains are selected to be images , or images , and the desired state is

Evaluate the performance of this controller by plotting the state trajectories, set point error and control inputs as a function of time.

Solution

The controller for the spherical robot based on PD feedback and gravity compensation chooses the control torque images in Equation (6.23) to be

Figures 6.16(a), (b), and (c) depict state trajectories for the specified choices of gains, and Figures 6.16(d), (e), and (f) depict actuation inputs images , and images as function of time for these gains. As expected, all state trajectories approach their respective desired values as images . A comparison of the qualitative behavior of these trajectories in comparison to those trajectories obtained using the exactly canceling computed torque yields some important observations. The trajectories for images and images in this example are indeed different functions of time, even though the initial conditions for these two variables are identical. The closed loop governing equations for images and images are different coupled nonlinear equations when the approximate dynamic inversion in Theorem 6.4 is used. In contrast, when the exact computed torque in Example 6.6 is used, the closed loop equations for images and images are identical. In that case the feedback linearization yields the same function of time, images in Example 6.6 whenever the initial conditions for images and images are the same.

The differences in the axial displacement images in Example 6.6 and the current case shown in Figure 6.16(c) are also striking. In Example 6.6 the initial condition for the axial displacement matches the target state, and the closed loop governing equation is a linear ODE. The solution in Example 6.6 for the error dynamics is just the function that is equal to zero for all time. In contrast, the error dynamic associated with images in Figure 6.16(c) is not identically equal to zero in the current example, even though the initial conditions and target states are identical. The closed loop equations for all of the unknowns are coupled when using the PD and gravity compensation controller. Even though the tracking error in the variable images starts at zero for the controller in this example, it quickly becomes non‐zero due to its coupling to the images and images states. With regards to the actuation loading, the controller exhibits large transient variations at startup, particularly for large gains as shown in Figure 6.17. This is a typical problem of many controllers when abrupt or instantaneous changes in the system states are required, as is the case for the setpoint controller in this example. The states are initially images , and it is desired to have images as images increases.

Graphical representation of actuator inputs transients response. (Left) Input torque m1(t) and (right) input torque m2(t) — Figure 6.17 Actuator inputs transients response. (a) Input torque and (b) input torque .

Example 6.9

Construct a set point controller based on approximate feedback linearization with a sliding mode term to drive the spherical robotic manipulator studied in Examples 6.6, 7, and 6.8 to the desired final configuration where images and images . Suppose that the true values of the physical parameters are identical to those in Example 6.8. Let images denote the common, true value of the mass links images Suppose that the physical parameters images and images are known exactly, but that the mass images of the links is approximated by images . Design a controller to drive the robotic arm to the desired state when the approximate mass estimate images may be in error up to images of the true mass images .

Solution

By inspection, the generalized mass matrix images and nonlinear vector images can be factored into the expressions

where images and images are known functions. The approximations images and images of images and images , respectively, are chosen to be

where images is the ratio of the exact mass images to the approximate mass images . With these definitions of the approximate generalized mass matrix images and the approximate nonlinear vector images , the errors images and images that appoximate the nonlinear terms and the resulting disturbance images can be written as

where images and images is the sliding mode control term. Note that the feedback control term images can be implemented without explicit knowledge of the true mass images .

The control law is first implemented with a discontinuous sliding mode controller for images . In this case,

(6.31)

Figure 6.18 depicts the trajectories in time of the generalized coordinates, input forces and torques, Lyapunov function images , and disturbance images when the gains images and images , the sliding mode control gain images , the value of images , and the matrix images are the solution of Lyapunov's equation images with images ,

(6.32)

Time histories generated by discontinuous sliding mode controller. (a) State trajectories, steady state. (b) State trajectories, transients. (c) Input forces and torques. (d) Lyapunov function V(x(t)). (e) Disturbance d(t) and gain k. (f) Contributions to dVdt — Figure 6.18 Time histories generated by discontinuous sliding mode controller. (a) State trajectories, steady state. (b) State trajectories, transients. (c) Input forces and torques. (d) Lyapunov function . (e) Disturbance and gain . (f) Contributions to .

The trajectories depicted in Figure 6.18 are typical in several respects of results obtained with discontinuous sliding mode controllers. In Figures 6.18(a) and (b), the generalized coordinates quickly converge to the sliding surface at approximately images s, but thereafter converge rather slowly towards their desired values. Figure 6.18(c) illustrates the input forces and torques. The control inputs exhibit chattering as the controls drive the system response repeatedly across the sliding surface after images s. The controller also requires a linear actuator that can deliver up to 150 N of force and motors that generate over 150 N m of torque. Even if the actuators have the authority to deliver the input forces and torques shown in the figure, the bandwidth is prohibitively high during the chattering regime.

Figures 6.18(d) and (e) show the value of the Lyapunov function images and the disturbance images evaluated along the system trajectory. The gain images has been selected appropriately in that it is always true that images during this simulation, and it is expected that the theoretical guarantees of stability convergence should hold. Finally, Figure 6.18(f) illustrates several contributions to the derivative of the Lyapunov function. This graph is based on the fact that the derivative images can be computed from the equation

(6.33)

The figure shows that the black line representing images is always negative, as required in the proof of stability. The contribution due to the uncertainty is equal to images and may be positive, but it is always dominated by the negative sliding mode term images .

Next, consider the regularized sliding mode controller which is given by

(6.34)

Figure 6.19 depicts the corresponding system trajectories when all the controller gains are identical, except that the boundary layer variable is chosen to be images . Qualitatively, the trajectories of the generalized coordinates depicted in Figures 6.19(a) and (b) are similar to those shown in Figures 6.18(a) and (b) that are obtained with the discontinuous sliding mode controller. However, while the trajectories obtained with the discontinuous controller are guaranteed to converge to their desired values, the trajectories generated by the continuous controller are only guaranteed to converge to some neighborhood of the desired values. The size of this neighborhood is guaranteed to be images in size and can be made smaller by reducing the size of the boundary layer images .

The most drastic difference between the two controllers is illustrated by contrasting Figures 6.18(c) and 6.19(c). While the discontinuous controller exhibits a significant chattering regime, the control inputs generated by the regularized sliding mode controller do not. As a result, the continuous controller is physically realizable, whereas the discontinuous controller is not. However, as the boundary layer images is decreased further and further, the control inputs will become increasingly similar to those of the discontinuous system and will exhibit increasing degrees of chattering.

Time histories generated by regularized sliding mode controller. (a) State trajectories, steady state. (b) State trajectories, transients. (c) Input forces and torques. (d) Lyapunov function. (e) Disturbance d(t) and gain k. (f) Contributions to d — Figure 6.19 Time histories generated by regularized sliding mode controller. (a) State trajectories, steady state. (b) State trajectories, transients. (c) Input forces and torques. (d) Lyapunov function . (e) Disturbance and gain . (f) Contributions to .

6.8 Controllers Based on Passivity

The derivation of controllers based on approximate dynamic inversion leads to a family of practical control strategies, ones that are designed for a number of different performance metrics. Another class of popular controllers have been derived that rely on theskew symmetry of the matrix images and associatedpassivity properties of the governing equations. It has been shown in Chapter that the governing equations for anatural system can be written in the form

(6.35)

For this equation of motion the matrix is skew symmetric. That is, the identity

holds for any vector . As before, define the tracking error to be .

The construction of controllers based on passivity can be carried out by introducing the filtered tracking error and the auxiliary variables and as

(6.36)

(6.37)

(6.38)

where is a positive diagonal matrix. The controller based on passivity chooses the control input

(6.39)

where is a positive, diagonal gain matrix. With this choice of control input , the closed loop system dynamics are governed by the equations

Example 6.10

Consider the spherical robotic manipulator studied in Examples 6.6, 7, and 6.8. Derive a controller based on passivity as described in Theorem 6.7 to achieve tracking control. Select the system parameters to be images kg, images m, and images m. Choose the gain matrices images and images in Theorem 6.7 to have the form images and images , where the gains are selected to be images , or images . Assume that the desired trajectory is

with images and images . Write a program to simulate the performance of the controller for the control gains and desired trajectories. Plot the state trajectories, the tracking error and the control inputs as a function of time.

Solution

The controller for the spherical robotic manipulator based on passivity principles in Theorem 6.7 has the form in Equation (6.39)

where images and images are defined in Equations (6.36), (6.37), (6.38), and

In contrast to the case when exact cancellation of nonlinearities is achieved using the ideal computed torque control, the resulting equations that govern the closed loop system are neither decoupled nor linear. It is not possible to obtain a simple closed form solution of the governing closed loop equations as in Examples 6.6 or 6.7. Figures 6.20(a) through (f) depict the state trajectories and control input time histories for the closed loop system when the initial condition has been selected to be

Figures 6.20(a), (b), and (c) depict the state trajectories images , and images , respectively, for the various choices of feedback gains images and images . Good tracking performance is evident for images and images , while the asymptotic convergence of images to its desired trajectory is rather slow. Figures 6.20(d), (e), and (f) depict the control input time histories. The input authority required for this controller is similar in magnitude to that encountered in Example 6.6 or 6.7. The steady state magnitude of the input torque images oscillates between images N m, and the actuation force varies from images N and images N as images . The magnitudes of the startup transient actuation forces and moments are several times their steady state magnitudes.

6.9 Actuator Models

Modern robotic systems, including the diverse array described in Chapter , utilize a wide array of actuators. The actuators may include conventional electric motors, hydraulic cylinders, or pneumatic pistons. These common actuation systems have numerous variants and individual designs, each having specific advantages and drawbacks. They may require models with tailored governing equations to represent the physics of their operation. Each may exhibit its own characteristic nonlinearities, which must be accounted for in modeling and control synthesis. Moreover, ever increasing numbers of novel and unconventional actuators appear in robotics applications each year. These include actuators based on shape memory alloys, biomaterials, electrochemicals, electrostructural materials, and magnetostructural materials. The research into alternative systems is driven by the need for more compact, lightweight, high authority, and high bandwidth actuation systems.

6.9.1 Electric Motors

Of all the possible actuation devices, the electric motor is the most common in robotic systems. Nearly all electric motors operate based on the principles ofelectromagnetic induction whereby a current carrying wire immersed in a magnetic field undergoes a force. Electric motors operate by passing a current through loops of wire that are aligned relative to an external magnetic field so that the force turns the rotor. Electric motors are popular owing to their relative simplicity, fast response, and large startup torque output. There are many different types of electric motors including direct current (DC), induction, synchronous, brushless, and stepper motors. This section focuses on the fundamentals of electric motors and stresses those aspects of electric motor architecture that are common to many electric motors.

This section presents the physical foundations and derives the governing equations for apermanent magnet DC motor shown schematically in Figure 6.21. A DC motor works by virtue of the Lorentz force law. This law can be used to show that the force images acting on a conductor of length images that carries current images in the magnetic field having magnetic flux images is given by images , where images is a unit vector along the length of the wire. Consider a loop of wire that rotates in the magnetic field having magnetic flux images along the unit vector images as shown in Figure 6.22. In this case the force on the wire from images to images is given by

A similar calculation shows that the force acting on the wire from images to images is images . The net torque applied on the wire loop in the configuration shown is therefore

This torque will cause the loop to rotate counterclockwise about the images axis until the loop passes the images – images plane.

Structure of permanent magnet DC motor. — Figure 6.21 Permanent magnet DC motor.

Illustration of loop of wire carrying a current in the magnetic field having flux B. — Figure 6.22 Loop of wire carrying a current in the magnetic field having flux .

If the loop rotates and passes the vertical plane in Figure 6.22, the sign of the moment about the images axis changes. A DC motor as depicted in Figure 6.21 utilizes acommutator to avoid the reversal in sign of the torque generated in this example of a rotating loop of wire. The primary components of the DC motor depicted in Figure 6.21 include astator that contains the north and south magnetic poles, thearmature that rotates relative to the stator, and the commutator that is fixed to the armature. Thebrushes maintain a sliding contact between the commutator and the power source that drives the motor. The commutator is made of segments that are electrically isolated from each other and are fixed to the rotating armature. The ends of the wire loops are connected to the commutator segments. The commutator segments rotate relative to the stator and maintain contact to the external power supply through the brushes. Practical motors have windings that contain many loops, instead of the single loop shown in Figure 6.21. The resultant torque generated by a winding having images loops is

This expression may be recast in terms of a single torque constant images that collects the electromechanical properties of the motor into a single term, such that

(6.40)

Equation (6.40) provides a characterization of how the applied torque varies with the input current, but it does not describe how the current varies as a function of time. Whenever a conductor moves in a magnetic field, a voltage develops across that conductor. This induced potential difference is theback electromotive force (EMF) voltage. Faraday's law states that the back EMF voltage is equal to the time derivative of themagnetic flux linkage images in the winding

The magnetic flux linkage images in the winding that contains images turns is

where the magnetic flux linkage images in a single loop is defined as

In this equation images is the magnetic flux, images is a unit vector perpendicular to the loop of wire, and the integral is carried out over the area enclosed by the wire. The linkage images is computed to be

where images is the angle between the images axis and the loop of wire ( images for the example under consideration). The voltage that develops across the ends of the winding is consequently

The constant images is the back EMF constant of the electric motor. Kirchoff's voltage law can now be applied around the circuit formed by the power supply, brushes, commutator and armature windings to show that

where images is the armature inductance and images is the armature resistance. These results in the following theorem.

Example 6.11

Suppose that the images constraint that drives link 1 of the spherical robotic manipulator is actuated by a DC motor. What are the changes to the resulting equations of motion for the system?

Solution

As shown in Problem 5.25, the equations of motion for the spherical robotic manipulator can be written in the form

(6.41)

where images is the vector of generalized coordinates, images is the actuator input, and the generalized mass matrix and nonlinear right hand side are

This example determines the torque images when the joint 1 is driven by a DC motor. Figure 6.23 provides a free body diagram of link 1. The torque images is applied on the link by the motor shaft, the torque images is the torque applied to the armature that is connected to the rotating shaft, and the torque images is the reaction torque applied on the stator by the ground. Applying Euler's second law about the images axis for the armature results in

(6.42)

Illustration of free body diagram of link 1 — Figure 6.23 Free body diagram of link .

where images is the inertia of the armature about the images axis. From Theorem 6.8 it is known that the circuit through the armature satisfies

(6.43)

(6.44)

The following observations are made regarding the full system of governing equations.

The most general form of the governing equations, when , and are non‐negligible, is obtained by solving Equation (6.42) for the torque and substituting the result into Equation (6.41). When Equation (6.43) is appended to the resulting system of equations, four differential equations are obtained:

These equations can be cast as a system of seven nonlinear, first order equations where the state and the input is the voltage .
If the inductance is negligible, it is possible to solve for the current in Equation (6.43). In this case the system of governing equations can be reduced to the form
If the inertia of the armature is negligible, the torque applied by the magnetic field on the armature is equal to the torque applied on the link 1 by the motor. That is,

In this case the governing equations are

The analysis in Example 6.11 is based on the application of the Newton–Euler equations for individual bodies that make up the robotic system and the application of Kirchoff's voltage law for the electrical circuit. This approach can be used to study any robotic system. Often it can be advantageous to deduce the form of the equations of motion that include actuator physics for the robotic system using principles of analytic mechanics. This strategy simply adds the appropriate additional terms to the kinetic and potential energy that are introduced by the physics of the actuator. In such a strategy it is often possible to derive the equations of motion without an actuator model, and then to add terms subsequently that account for actuator physics. The following example illustrates the utility of this method.

Example 6.12

Suppose that link 2 of the spherical robotic manipulator is actuated by a DC motor. What are the changes to the resulting equations of motion?

Solution

The governing equations for the spherical robotic manipulator have been derived as

where

The calculation of the generalized force images has been carried out assuming that the actuator torque images is applied to link 2 and the equal and opposite torque images is applied to link 1 about the horizontal revolute joint. A DC motor is introduced that actuates joint 2 by fixing the stator and motor casing to link 1 and by fixing the armature and drive shaft to link 2. Because of these additions, the mass and inertia matrices for both links should be updated to include the additional contributions to each rigid body,

Illustration of free body diagrams. (a) Link 1, (b) link 2 — Figure 6.24 Free body diagrams. (a) Link 1, (b) link 2.

The forces and moments that act between the two links, which now include the rigidly attached stator and rotor, are depicted in Figure 6.24. The reaction forces images , and images , and moments images and images enforce the constraints associated with the revolute joint and perform no virtual work. They do not contribute to the equations of motion obtained via Lagrange's equations. The actuation moment images is precisely the torque applied to the armature about the revolute joint axis. Therefore,

where images and images are the armature resistance and inductance in the motor. The governing equations, including the model for the electric motor that drives joint 1 studied in Example 6.11, can be written in the form

It is important to note that the generalized mass matrix images in the above equation is the new mass matrix obtained with the addition of the motor components to each of the links. Just as in Example 6.11, it is possible to derive special forms of these equations if it happens that armature inertia or motor inductance are negligible.

6.9.2 Linear Actuators

This book focuses on constructing robotic systems primarily through the introduction of either revolute or prismatic joints, or a superposition of these joints. The previous section introduced the fundamental underlying principles by which a DC motor converts electrical energy into rotational motion. These systems can be applied directly to drive revolute joints in robotic systems. Actuators that are used commonly to drive prismatic joints include hydraulic cylinders, pneumatic pistons, and electromechanical linear motors. Hydraulic and pneumatic actuation can be attractive in applications that require large loads and stroke. Earth moving machinery, such as an excavator or bulldozer, makes use of hydraulic cylinders. Electrical linear motors are used in applications that require rapid response and portability, and they are common components used for actuation of robotic systems. This section focuses on the class ofelectromechanical linear motors.

An electromechanical linear motor is an actuator that combines a conventional electric motor and a mechanical subsystem to convert the rotational motion of the motor into translational motion. The mechanical subsystem may consist of a screw mechanism or gears, for example. Figure 6.25 illustrates the primary components of a typical electromechanical linear motor. The electric motor rotates the lead screw which translates the linear stage along the guide rails. The drive nut embedded in the linear stage is prevented from rotating by the guide rails of the drive casing as it travels along the lead screw.

Figure 6.25 Schematic of an electromechanical linear motor.

Example 6.13

Derive the equations of motion for the electromechanical linear motor shown in Figure 6.25 when the motor is fixed in the inertial frame and a force images is applied to the linear stage.

Solution

The kinetic energy of the system can be written

where images is the mass of the linear stage, images is the moment of inertia of the armature and drive shaft, images is the displacement of the linear stage, and images is the rotation of the armature. The displacement images and rotation images satisfy the kinematic equation

where images is the pitch constant of the lead screw that has units of m images . The virtual work performed by the applied external force images acting on the linear stage and by the torque images applied to the armature is

Lagrange's equations yield

The combined set of electrical and mechanical domain equations for the linear motor are

where images is the armature inductance, images is the armature resistance, images is the back EMF constant, images is the motor torque constant, and images is the input voltage. The mechanical subsystem equation can be written in terms of the displacement of the motor as

Example 6.14

Suppose that link 3 of the spherical robot manipulator is actuated using an electromechanical linear motor as depicted in Figure 6.25. Assume that the inertia matrix of the armature and drive shaft assembly is negligible and that the links can be modeled as lumped masses located at their mass centers. Find the complete set of governing equations when actuator dynamics discussed in Examples 6.11 and 6.12 are included in the model of the robotic system.

Solution

Suppose that the linear actuator in Figure 6.25 is mounted in the robotic arm such that the electric motor housing and stator are fixed to the link 2 and the linear stage is rigidly attached to link 3, the telescoping arm. In this case the mass and inertia matrix of link 2 are modified so that they include the additional terms due to the actuator. Let images and images be the mass and inertia matrix of all of the components of the linear actuator that are rigidly attached to link 2.

Likwise, the mass and inertia matrices for link 3 are modified to include contributions of additional terms for the attached actuator. Let images be the mass and inertia matrix of the components of the electromechanical actuator that are rigidly attached to link 3,

The distance images that has been used to locate the center of mass of link 3 as a function of time is related to the displacement images in the actuator via

where images is a constant. The addition of mass to link 2 and link 3 will alter the locations of the mass centers of the links, and it is assumed that images and images reflect these updated center of mass positions. The rotation images of the armature relative to the motor casing is related to the displacement of the linear actuator images , where images is the screw pitch having units of meters per radian. The kinetic energy of the armature and drive shaft can be written as

where images is the velocity of the mass center of the armature and drive shaft assembly, and images is the angular velocity of the armature

With all of these changes, the kinetic energy of the robot can be written as

The kinetic energy has been written explicitly in this form to emphasize that the armature and drive shaft make contributions to the total kinetic energy. It has been assumed that these terms are negligible in the remainder of this example. The final form of the kinetic energy, using a lumped mass approximation, assuming the armature mass and inertia are negligible, and observing that the link 1 center of mass does not translate, becomes

The potential energy has the form images , where the mass images and definition of images account for the actuator mass contributions. The virtual work performed by the electromagnetic torque images acting on the armature is equal to images .

Kirchoff's voltage law for the armature circuit is

where images and images are the armature inductance and resistance, respectively, images is the motor back EMF constant, images is the armature current, and images is the input voltage. The final system of governing equations is therefore

The generalized mass matrix images and nonlinear right hand side images have the same form as derived in previous problems for this robotic structure, but with the coefficients images and images modified for the addition of mass of the linear actuator.

If the equations are collected from Examples 6.11 and 6.12 for the joint 1 and 2 actuators, along with these equations for the linear actuator, the following equations can be constructed to represent the robotic system with actuator dynamics

In this equation, images and images are modified from their nominal values without actuators to account for the mass and inertia of the two rotational and one linear actuator. The next section will show that these equations are one example of a general form for the equations of motion of robotic systems that include actuator dynamics.

6.10 Backstepping Control and Actuator Dynamics

This chapter has discussed several methods for deriving feedback controllers having the structure images for robotic systems that take the form

(6.45)

Stability and convergence of the controlled system is based on analysis of a Lyapunov function that is tailored to the form of the governing Equation (6.45) and the specific feedback input images . As noted in the previous section, it is rare for actuation torques or forces to be directly controlled in practice. It is much more common that commanded inputs take the form of voltages or currents that drive motors, which in turn generate forces or moments that act on the robot. It has been shown that one of the general models that includes actuator dynamics arising from DC motors or electromechanical linear actuators consists of a set of coupled and mechanical and electrical subsystems

(6.46)

(6.47)

where images is the diagonal images inductance matrix, images is the diagonal images resistance matrix, images is the diagonal images back EMF constant matrix, and images is the diagonal images torque constant matrix. Equations (6.46) and (6.47) can also be rewritten in first order form as a pair of equations

(6.48)

(6.49)

Suppose that an ideal feedback law images could be imposed directly in Equation (6.48). Also suppose that the stability of the motion of images that would result when this ideal feedback is substituted into Equation (6.48) is guaranteed by a Lyapunov function that satisfies

(6.50)

However, when the coupled pair of Equations (6.48) and (6.49) are considered together, it is the input images for images that is imposed, and it cannot be guaranteed that the desired control law images holds for each images . Define a new state images as

that measures how closely the evolution of the coupled system comes to satisfying the ideal control law. With the introduction of the new state images , the governing equations in first order form can now be expressed as

By using the assumption that the control law images corresponds to the Lyapunov function images that satisfies the conditions in Equation (6.50), it is possible to define a feedback controller for the coupled pair of equations. Choose the Lyapunov function

When the derivative of the Lyapunov function images is calculated along the trajectories of the coupled pair of equations,

Now suppose images is chosen to be

(6.51)

For this case, it follows that

Therefore, the equilibrium at the origin of the coupled dynamics governing images is asymptotically stable. The use ofbackstepping control is shown in the following example.

Example 6.15

Design a setpoint controller for the robotic system studied in Example 6.14 using a backstepping controller by using the Lyapunov function and feedback controller based on ideal dynamic inversion.

Solution

Define the state

where images . The “ideal feedback law” that consists of a feedforward component that achieves dynamic inversion and a PD outer loop is defined as

When the state images that measures how well the state images follows that ideal dynamic inversion control law is defined, the mechanical equations of motion can be written as

Define the Lyapunov function associated with the state images to be images where images is a symmetric, positive definite solution of Lyapunov's equation

for some symmetric, positive matrix images . Such a matrix images is guaranteed to exist since images is Hurwitz. images may be verified as a Lyapunov function for the uncoupled equation in images that is obtained when images , or images , for all images .

The electrical domain equations, expressed in terms of the new state, become

Next, the derivative images of the feedback is expanded as

The electrical subsystem governing equation can therefore be written as

As derived in Equation (6.51), images . This requires that

This identity holds when the input voltages images to the actuators are prescribed as

(6.52)

Now, the ability of the control input voltages images to generate the desired asymptotic behavior will be verified. With the actuator voltages images in Equation (6.52), the vector images becomes

Calculating the derivative of the Lyapunov function images along the trajectories of the coupled mechanical–electrical system results in

This shows that images and images for images . Therefore, the origin of the coupled dynamics is asymptotically stable.

6.11 Problems for Chapter 6, control of Robotic Systems

6.11.1 Problems on Gravity Compensation and PD Setpoint Control

Problem 6.1 A two degree of freedom PUMA model was derived in Problem 5.21 for the robot depicted in Figures 5.25 and 5.26. The generalized coordinates for this robot are selected to be

where and are the angles for revolute joints 1 and 2, respectively. The generalized forces are

where and are the actuation torques that act about the revolute joints 1 and 2, respectively. Let the system parameters for this robot be kg and m. Derive the controller that uses PD feedback with gravity compensation as described in Theorem 6.4 for this robot to achieve setpoint control. Write a program to simulate the performance of the controller. Plot the state trajectories, setpoint error, and control inputs as a function of time for various choices of the initial conditions, the target state and the choice of feedback gains.
Problem 6.2 A three degree of freedom model was derived in Problem 5.22 for the PUMA robot depicted in Figures 5.25 and 5.26. The generalized coordinates for this robot are selected to be

where and are the angles for revolute joints and 3, respectively. The generalized forces are

where , and are the actuation torques that act at revolute joints , and 3, respectively. Let the system parameters for this robot be m, m, m, m, and kg. Derive the controller that uses PD feedback with gravity composition as described in Theorem 6.4 for this robot to achieve setpoint control. Write a program to simulate the performance of the controller. Plot the state trajectories, setpoint error, and control inputs as a function of time for various choices of the initial conditions, the target state and the choice of feedback gains.
Problem 6.3 A two degree of freedom model was derived in Problem 5.23 for the PUMA robot depicted in Figures 5.25 and 5.26. The generalized coordinates for this robot are selected to be

where and are the angles for revolute joints 1 and 2, respectively. The generalized forces are

where and are the actuation torques that act at the revolute joints 1 and 2, respectively. Let the system parameters for this robot be kg, kg , kg , kg , m, and m. Derive the controller that uses PD feedback with gravity composition as described in Theorem 6.4 for this robot to achieve setpoint control. Write a program to simulate the performance of the controller. Plot the state trajectories, setpoint error, and control inputs as a function of time for various choices of the initial conditions, the target state and the choice of feedback gains.
Problem 6.4 A three degree of freedom model was derived in Problem 5.24 for the Cartesian robot depicted in Figure 5.27. The generalized coordinates for this robot are selected to be

where , and are the translations in the inertial directions, respectively. The generalized forces are

where , and are the actuation forces acting along the prismatic joints along the inertial , and directions, respectively. Let the system parameters for this robot be kg, kg, and kg. Derive the controller that uses PD feedback with gravity compensation as described in Theorem 6.4 for this robot to achieve setpoint control. Write a program to simulate the performance of the controller. Plot the state trajectories, setpoint error, and control inputs as a function of time for various choices of the initial conditions, the target state and the choice of feedback gains.
Problem 6.5 A three degree of freedom model was derived in Problem 5.25 for the spherical wrist depicted in Figures 5.28 and 5.29. The generalized coordinate for this robot are selected to be

where and are the angles for joints , and 3, respectively. The generalized forces are

where , and are the actuation torques that act at joints , and 3, respectively. Let the system parameters for this robot be kg, kg, kg, kg , kg , kg , kg , kg , m, and m. Derive the controller that uses PD feedback with gravity composition as described in Theorem 6.4 for this robot to achieve setpoint control. Write a program to simulate the performance of the controller. Plot the state trajectories, setpoint error, and control inputs as a function of time for various choices of the initial conditions, the target state and the choice of feedback gains.
Problem 6.6 A three degree of freedom model was derived in Problem 5.26 for the SCARA robot depicted in Figures 5.30 and 5.31. The generalized coordinates for this robot are selected to be

where and are the joint variables for revolute joints 1 and 2, respectively, and is the joint variable for prismatic joint 3. The generalized forces are

where and are the actuation moments that drive revolute joints 1 and 2, respectively, and is the actuation force that drives prismatic joint 3. Let the system parameters for this robot be kg, kg, kg, m, m, m, and m. Derive the controller that uses PD feedback with gravity composition as described in Theorem 6.4 for this robot to achieve setpoint control. Write a program to simulate the performance of the controller. Plot the state trajectories, setpoint error, and control inputs as a function of time for various choices of the initial conditions, the target state and the choice of feedback gains.
Problem 6.7 A three degree of freedom model was derived in Problem 5.27 for the robot depicted in Figures 5.30 and 5.31. The generalized coordinates for this robot are selected to be

where and are the joint variables for revolute joints 1 and 2, respectively, and is the displacement along prismatic joint 3. The generalized forces are

where and are the joint torques for revolute joints 1 and 2, respectively, and is the joint force for prismatic joint 3. Let the system parameters for this robot be kg, kg, kg, m, m, kg , kg , kg . Derive the controller that uses PD feedback with gravity composition as described in Theorem 6.4 for this robot to achieve setpoint control. Write a program to simulate the performance of the controller. Plot the state trajectories, setpoint error, and control inputs as a function of time for various choices of the initial conditions, the target state and the choice of feedback gains.
Problem 6.8 A three degree of freedom model was derived in Problem 5.28 for the robot depicted in Figures 5.32 and 5.33. The generalized coordinates for this robot are selected to be

where is the joint angle for revolute joint 1, and and are the displacements for prismatic joints 2 and 3, respectively. The generalized forces are

where is the actuation torque that acts as revolute joint 1, and and are the actuation forces that act along prismatic joints 2 and 3, respectively. Let the system parameters for this robot be kg, kg, kg, m, m, m, m and m. Derive the controller that uses PD feedback with gravity composition as described in Theorem 6.4 for this robot to achieve setpoint control. Write a program to simulate the performance of the controller. Plot the state trajectories, setpoint error, and control inputs as a function of time for various choices of the initial conditions, the target state and the choice of feedback gains.
Problem 6.9 A three degree of freedom model was derived in Problem 5.29 for the robot depicted in Figures 5.32 and 5.33. The generalized coordinates for this robot are selected to be

where is the angle revolute joint 1, and and are the displacements for prismatic joints 2 and 3, respectively. The generalized forces are

where is the actuation torque for revolute joint 1, and and are the actuation forces that act at along the prismatic joints 2 and 3, respectively. Let the system parameters for this robot be kg, kg, kg, kg , kg , m, m, m, m, and m. Derive the controller that uses PD feedback with gravity composition as described in Theorem 6.4 for this robot to achieve setpoint control. Write a program to simulate the performance of the controller. Plot the state trajectories, setpoint error, and control inputs as a function of time for various choices of the initial conditions, the target state and the choice of feedback gains.

6.11.2 Problems on Computed Torque Tracking Control

Problem 6.10 Consider the robot studied in Problem 6.1. Derive a tracking controller that uses the exact computed torque control with the outer loop selected to be PD feedback as in Theorem 6.3. Write a program to simulate the performance of the controller. Plot the state trajectories, tracking error, and control inputs as a function of time for various choices of the initial conditions, desired trajectories, and the choice of feedback gains.
Problem 6.11 Consider the robot studied in Problem 6.2. Derive a tracking controller that uses the exact computed torque control with the outer loop selected to be PD feedback as in Theorem 6.3. Write a program to simulate the performance of the controller. Plot the state trajectories, tracking error, and control inputs as a function of time for various choices of the initial conditions, desired trajectories, and the choice of feedback gains.
Problem 6.12 Consider the robot studied in Problem 6.3. Derive a tracking controller that uses the exact computed torque control with the outer loop selected to be PD feedback as in Theorem 6.3. Write a program to simulate the performance of the controller. Plot the state trajectories, tracking error, and control inputs as a function of time for various choices of the initial conditions, desired trajectories, and the choice of feedback gains.
Problem 6.13 Consider the robot studied in Problem 6.4. Derive a tracking controller that uses the exact computed torque control with the outer loop selected to be PD feedback as in Theorem 6.3. Write a program to simulate the performance of the controller. Plot the state trajectories, tracking error, and control inputs as a function of time for various choices of the initial conditions, desired trajectories, and the choice of feedback gains.
Problem 6.14 Consider the robot studied in Problem 6.5. Derive a tracking controller that uses the exact computed torque control with the outer loop selected to be PD feedback as in Theorem 6.3. Write a program to simulate the performance of the controller. Plot the state trajectories, tracking error, and control inputs as a function of time for various choices of the initial conditions, desired trajectories, and the choice of feedback gains.
Problem 6.15 Consider the robot studied in Problem 6.6. Derive a tracking controller that uses the exact computed torque control with the outer loop selected to be PD feedback as in Theorem 6.3. Write a program to simulate the performance of the controller. Plot the state trajectories, tracking error, and control inputs as a function of time for various choices of the initial conditions, desired trajectories, and the choice of feedback gains.
Problem 6.16 Consider the robot studied in Problem 6.7. Derive a tracking controller that uses the exact computed torque control with the outer loop selected to be PD feedback as in Theorem 6.3. Write a program to simulate the performance of the controller. Plot the state trajectories, tracking error, and control inputs as a function of time for various choices of the initial conditions, desired trajectories, and the choice of feedback gains.
Problem 6.17 Consider the robot studied in Problem 6.8. Derive a tracking controller that uses the exact computed torque control with the outer loop selected to be PD feedback as in Theorem 6.3. Write a program to simulate the performance of the controller. Plot the state trajectories, tracking error, and control inputs as a function of time for various choices of the initial conditions, desired trajectories, and the choice of feedback gains.
Problem 6.18 Consider the robot studied in Problem 6.9. Derive a tracking controller that uses the exact computed torque control with the outer loop selected to be PD feedback as in Theorem 6.3. Write a program to simulate the performance of the controller. Plot the state trajectories, tracking error, and control inputs as a function of time for various choices of the initial conditions, desired trajectories, and the choice of feedback gains.

6.11.3 Problems on Dissipativity Based Tracking Control

Problem 6.19 Consider the robot studied in Problem 6.1. Derive a tracking controller that uses the controller based on dissipativity principles in Theorem 6.7. Write a program to simulate the performance of the controller. Plot the state trajectories, tracking error, and control inputs as a function of time for various choices of the initial conditions, desired trajectories, and the choice of feedback gains.
Problem 6.20 Consider the robot studied in Problem 6.2. Derive a tracking controller that uses the controller based on dissipativity principles in Theorem 6.7. Write a program to simulate the performance of the controller. Plot the state trajectories, tracking error, and control inputs as a function of time for various choices of the initial conditions, desired trajectories, and the choice of feedback gains.
Problem 6.21 Consider the robot studied in Problem 6.3. Derive a tracking controller that uses the controller based on dissipativity principles in Theorem 6.7. Write a program to simulate the performance of the controller. Plot the state trajectories, tracking error, and control inputs as a function of time for various choices of the initial conditions, desired trajectories, and the choice of feedback gains.
Problem 6.22 Consider the robot studied in Problem 6.4. Derive a tracking controller that uses the controller based on dissipativity principles in Theorem 6.7. Write a program to simulate the performance of the controller. Plot the state trajectories, tracking error, and control inputs as a function of time for various choices of the initial conditions, desired trajectories, and the choice of feedback gains.
Problem 6.23 Consider the robot studied in Problem 6.5. Derive a tracking controller that uses the controller based on dissipativity principles in Theorem 6.7. Write a program to simulate the performance of the controller. Plot the state trajectories, tracking error, and control inputs as a function of time for various choices of the initial conditions, desired trajectories, and the choice of feedback gains.
Problem 6.24 Consider the robot studied in Problem 6.6. Derive a tracking controller that uses the controller based on dissipativity principles in Theorem 6.7. Write a program to simulate the performance of the controller. Plot the state trajectories, tracking error, and control inputs as a function of time for various choices of the initial conditions, desired trajectories, and the choice of feedback gains.
Problem 6.25 Consider the robot studied in Problem 6.7. Derive a tracking controller that uses the controller based on dissipativity principles in Theorem 6.7. Write a program to simulate the performance of the controller. Plot the state trajectories, tracking error, and control inputs as a function of time for various choices of the initial conditions, desired trajectories, and the choice of feedback gains.
Problem 6.26 Consider the robot studied in Problem 6.8. Derive a tracking controller that uses the controller based on dissipativity principles in Theorem 6.7. Write a program to simulate the performance of the controller. Plot the state trajectories, tracking error, and control inputs as a function of time for various choices of the initial conditions, desired trajectories, and the choice of feedback gains.
Problem 6.27 Consider the robot studied in Problem 6.9. Derive a tracking controller that uses the controller based on dissipativity principles in Theorem 6.7. Write a program to simulate the performance of the controller. Plot the state trajectories, tracking error, and control inputs as a function of time for various choices of the initial conditions, desired trajectories, and the choice of feedback gains.