Chapter 4
Newton–Euler Formulations
The field of dynamics consists of the study of kinematics and kinetics. Chapter 2 of this book discusses the foundations of kinematics, and Chapter 3 presents specific formulations for kinematics of spatial robotic systems. The study of kinematics provides the language used to describe the geometry of motion. The field of kinetics studies the connection between the forces and moments that act on a mechanical system and its resulting motion. Two general approaches to the study of kinetics are covered in this chapter and the next. This chapter discusses the collection of methods known as Newton–Euler formulations of the dynamics of robotic systems. Chapter 5 presents an alternative approach, those methods based on techniques of analytical mechanics. Upon the completion of this chapter, the student should be able to
- Define and calculate the linear momentum of a rigid body.
- Define and calculate the angular momentum of a rigid body.
- Define and calculate the center of mass and inertia matrix of a rigid body.
- State and employ Euler's laws for the motion of rigid bodies in a robotic system.
- Employ recursive order
formulations to study robotic system dynamics.
4.1 Linear Momentum of Rigid Bodies
Elementary principles that describe the dynamics of a point mass or particle define thelinear momentum as the product of the mass of the particle and its velocity. The linear momentum of a system of particles is the sum of the linear momenta of the individual particles in the system. As highlighted in the following definition, the linear momentum of a rigid body can be viewed as a limiting case of the definition for a system of particles. The linear momentum of a rigid body is the integral of the velocity over all the differential mass elements that make up the rigid body.
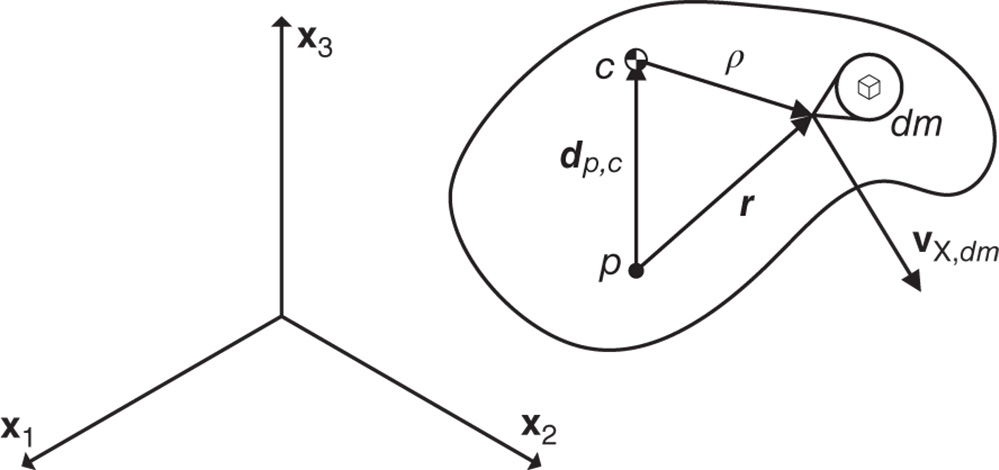
Figure 4.1 Rigid body with differential mass element.
Definition 4.1 is given in terms of the velocity of each of the infinite collection of points that make up the rigid body under consideration. Thecenter of mass is introduced to obtain an expression for linear momentum that depends on the velocity of a single point. As a result, the center of mass is used to describe the motion of a mechanical system in terms of a finite set of variables.
The above definition of the center of mass can be used to derive an expression for the linear momentum of a rigid body in terms of the center of mass velocity. The linear momentum of a rigid body is the product of the rigid body center of mass velocity and the total rigid body mass.
Applications to robotic systems often introduce numerous frames of reference to formulate the equations of motion. The next example uses the definition of the center of mass to calculate its location for a link in a typical robotic system.
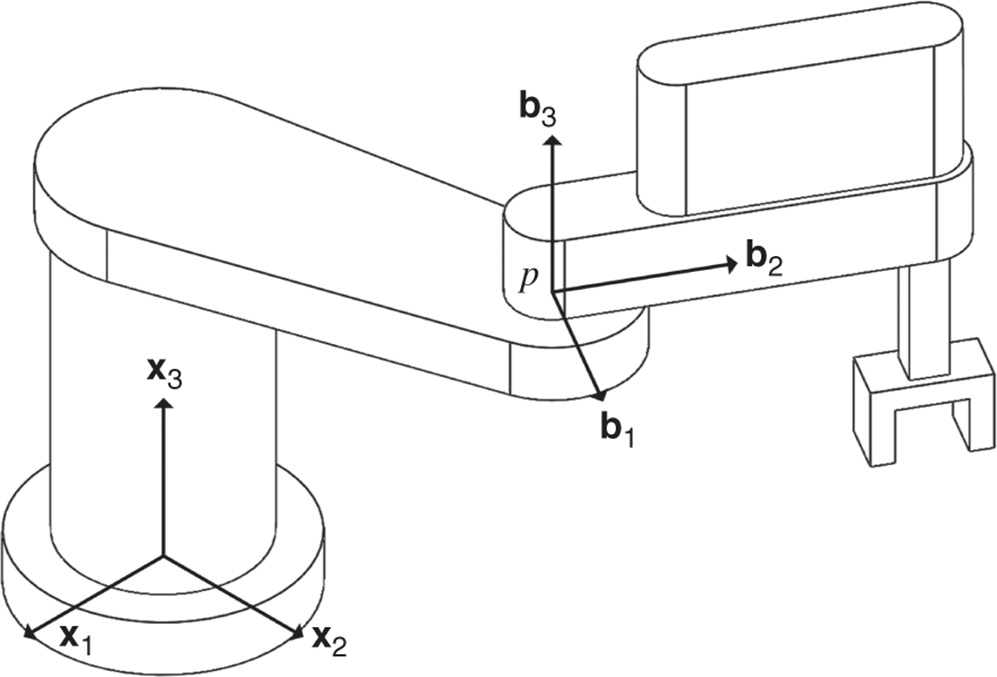
Figure 4.2 SCARA robot.

Figure 4.3 SCARA robot link 2 inertia estimation.
It will be shown later in this chapter that the initial step in deriving the equations of motion for a robot often requires the evaluation of the linear momentum of its links. The next examples illustrate how the calculation of the linear momentum for realistic three dimensional solids, such as the links of robotic systems, is simplified when the location and velocity of themass center are known.
4.2 Angular Momentum of Rigid Bodies
4.2.1 First Principles
Theangular momentum about a point 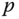 of a single particle in motion is equal to the “moment of momentum.” That is, the angular momentum is the cross product of the position vector that connects the point
of a single particle in motion is equal to the “moment of momentum.” That is, the angular momentum is the cross product of the position vector that connects the point 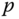 to the particle and the linear momentum of the particle. The angular momentum of a system of particles is the sum of the angular momenta of the individual particles. As with the linear momentum of a rigid body, the definition of the angular momentum of a rigid body can be interpreted as a limiting case as the number of particles increases. The summation over all the particles in the system is replaced by an integral over all the differential mass elements that make up the rigid body.
to the particle and the linear momentum of the particle. The angular momentum of a system of particles is the sum of the angular momenta of the individual particles. As with the linear momentum of a rigid body, the definition of the angular momentum of a rigid body can be interpreted as a limiting case as the number of particles increases. The summation over all the particles in the system is replaced by an integral over all the differential mass elements that make up the rigid body.
There is no restriction on the point 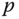 about which the angular momentum may be calculated in Definition 4.3. In practice, it is often convenient to calculate the angular momentum about an arbitrary point
about which the angular momentum may be calculated in Definition 4.3. In practice, it is often convenient to calculate the angular momentum about an arbitrary point 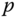 by relating it to the angular momentum about the center of mass. Theorem 4.2 describes this relationship.
by relating it to the angular momentum about the center of mass. Theorem 4.2 describes this relationship.
The next two examples show that the angular momentum of realistic three dimensional bodies, such as the rigid links of a robotic system, can be calculated directly from their definition. As when calculating linear momentum, the task of calculating the angular momentum can be facilitated by utilizing the knowledge of the position and velocity of the center of mass.
An important qualitative observation will also be made in these examples: the calculation of angular momentum for rigid bodies often introduces some common integrals over the body, namely thecross products of inertia and themoments of inertia. These integrals appear so frequently that they are discussed in detail in Sections 4.2.2 and 4.2.3 of this chapter. The cross products of inertia and moments of inertia also appear frequently in calculations of the kinetic energy of a robotic system; hence their important role in theanalytical mechanics formulations that are presented in Chapter 5.
Theorem 4.2 states a general relationship between the angular momentum about an arbitrary point 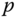 and about the center of mass
and about the center of mass 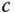 of a rigid body. The theorem was derived by decomposing the position vector into the sum
of a rigid body. The theorem was derived by decomposing the position vector into the sum  . Another useful form for the angular momentum can be achieved by decomposing the velocity vector instead of the position vector. The next theorem makes use of this strategy. The resulting form for the angular momentum will be critical in the discussions of the inertia matrix in the following sections.
. Another useful form for the angular momentum can be achieved by decomposing the velocity vector instead of the position vector. The next theorem makes use of this strategy. The resulting form for the angular momentum will be critical in the discussions of the inertia matrix in the following sections.
4.2.2 Angular Momentum and Inertia
The last section introduced the definition of angular momentum for rigid bodies and derived theorems that can be used for its calculation. As shown in Examples 4.4 and 4.5, the calculation of angular momentum can require the evaluation of integrals over the body that have the form 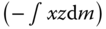 ,
, 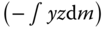 and
and  . The integrals
. The integrals  and
and  are examples of the cross products of inertia, and the integral
are examples of the cross products of inertia, and the integral  is an example of a moment of inertia of a rigid body. The cross products and moments of inertia are used to construct theinertia matrix for a rigid body. These definitions are important because most commonly encountered expressions for angular momentum in applications are cast in terms of theinertia matrix.
is an example of a moment of inertia of a rigid body. The cross products and moments of inertia are used to construct theinertia matrix for a rigid body. These definitions are important because most commonly encountered expressions for angular momentum in applications are cast in terms of theinertia matrix.
The inertia matrix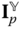 about the point
about the point 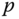 relative to the frame
relative to the frame 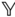 utilizes the
utilizes the  superscript to denote the basis vectors for which the matrix is defined. As in earlier chapters, the convention that a superscript denotes the coordinates of a vector relative to a specific choice of frame is used. For example, if
superscript to denote the basis vectors for which the matrix is defined. As in earlier chapters, the convention that a superscript denotes the coordinates of a vector relative to a specific choice of frame is used. For example, if 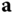 is an arbitrary vector,
is an arbitrary vector, 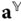 denotes the components of the vector
denotes the components of the vector 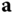 as expressed in terms of the
as expressed in terms of the  basis. The inertia matrix about a point
basis. The inertia matrix about a point 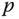 relative to a frame
relative to a frame  contains the components of theinertia tensor expressed in terms of thetensor basis
contains the components of theinertia tensor expressed in terms of thetensor basis
 . A vector is a first order tensor, and the inertia tensor is a second order tensor. Appendix A contains a detailed discussion of tensors for the interested reader.
. A vector is a first order tensor, and the inertia tensor is a second order tensor. Appendix A contains a detailed discussion of tensors for the interested reader.
The point  used to define the angular momentum
used to define the angular momentum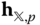 in Definition 4.3 can be any point in the mechanical system. The most general form for the angular momentum in terms of the inertia matrix that will be used is derived in the following theorem.
in Definition 4.3 can be any point in the mechanical system. The most general form for the angular momentum in terms of the inertia matrix that will be used is derived in the following theorem.
This theorem will be proven while carrying out the proof of Theorem 4.5. Equation 4.6 is useful in many applications because of its generality. For example, this theorem will constitute the technical foundation for the most general variant ofEuler's second law of motion for rigid bodies presented in Section 4.3 of this chapter. This form of Euler's second law serves as the foundation for the numerically efficientrecursive order
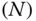 formulations of kinematics and dynamics of robotic systems.
formulations of kinematics and dynamics of robotic systems.
Still, despite its generality, Theorem 4.4 is frequently modified so that it is easier to use in direct application to individual problems. It is most common to select the point 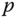 in applications so that the term
in applications so that the term 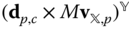 is identically equal to zero. This is most easily accomplished by choosing the point
is identically equal to zero. This is most easily accomplished by choosing the point  to be either fixed in the frame
to be either fixed in the frame 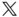 , or by selecting the point
, or by selecting the point 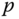 to be the center of mass of the rigid body.
to be the center of mass of the rigid body.
Theorem 4.5 will be used in numerous applications, and it is vital to note the different roles of the frames 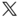 ,
, 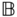 and
and 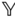 in the theorem. The body fixed frame is
in the theorem. The body fixed frame is 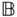 , which is assumed to move relative to the frame
, which is assumed to move relative to the frame  . In the next section Euler's laws will be stated, which hold in aninertial frame. The inertial frame will be chosen to be
. In the next section Euler's laws will be stated, which hold in aninertial frame. The inertial frame will be chosen to be  . In other words, the frames
. In other words, the frames 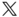 and
and 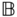 are connected to the physics of the problem at hand. The frame
are connected to the physics of the problem at hand. The frame  can be any frame whatsoever, and is used to provide a basis to conveniently express the components of the physical vectors
can be any frame whatsoever, and is used to provide a basis to conveniently express the components of the physical vectors 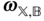 and
and  .
.
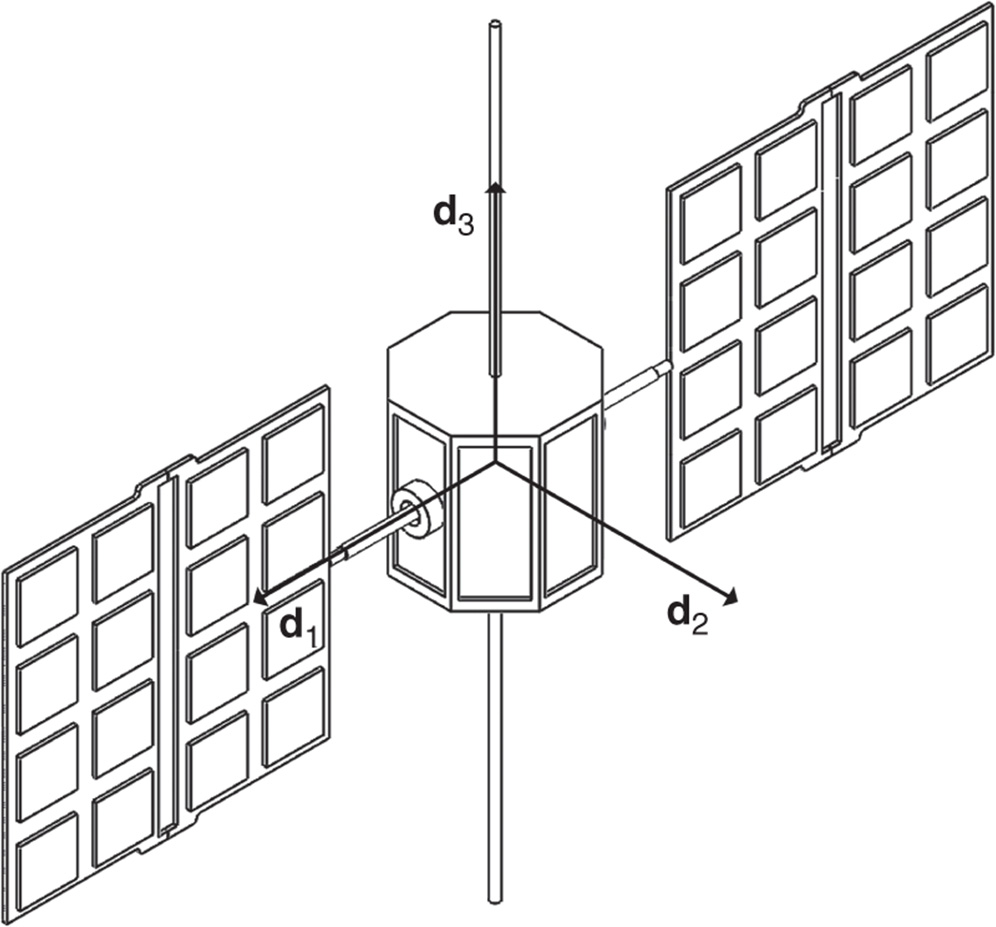
Figure 4.7 Satellite with body fixed frame.
4.2.3 Calculation of the Inertia Matrix
The integrals that appear in the Definition 4.4 depend on the choice of the frame 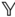 . With all the possible choices available for the frame
. With all the possible choices available for the frame  in Theorem 4.5, it is important that efficient techniques are available for calculating inertia matrices relative to different coordinate frames. This section describes several theorems and techniques that facilitate the calculation of the inertia matrix in typical applications.
in Theorem 4.5, it is important that efficient techniques are available for calculating inertia matrices relative to different coordinate frames. This section describes several theorems and techniques that facilitate the calculation of the inertia matrix in typical applications.
Sections 4.2.3.1 and 4.2.3.3 discuss theinertia rotation transformation law and theparallel axis theorem. The inertia rotation transformation law describes how to relate inertia matrices calculated with respect to two frames with the same origin but different orientations. The parallel axis theorem describes how to relate inertia matrices calculated with respect to two frames having parallel orientations, but with origins at the center of mass and an arbitrary point 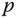 . By combining these two results, the inertia matrix relative to any arbitrary frame can be calculated if the inertia matrix relative to a given frame is known.
. By combining these two results, the inertia matrix relative to any arbitrary frame can be calculated if the inertia matrix relative to a given frame is known.
Section 4.2.3.2 summarizes the construction ofprincipal axes with respect to which the inertia matrix assumes a diagonal form. When possible, it is convenient to cast problems in terms of the principal axes, as it reduces the number of parameters in the equations of motion.
Section 4.2.3.4 details the role of symmetry in the calculation of the inertia matrix. It will be shown that by identifying coordinate planes of symmetry it is often possible to conclude that certainproducts of inertia in the inertia matrix are zero, without having to calculate them explicitly.
4.2.3.1 The Inertia Rotation Transformation Law
This section derives the equation used to relate rotation matrices that are defined from frames that have a common origin, but are rotated relative to one another. The equations derived in Theorem 4.6 are a special case of thetensor transformation laws familiar intensor analysis. A comprehensive treatment can be found in [7]. The theorem below summarizes the transformation laws that relate the inertia matrices associated with frames that are rotated relative to one another.
These expressions should be compared and contrasted to the trnasformation laws for the components of a vector  ,
,

The coordinate change for a vector, which is a first order tensor, premultiplies the components by a rotation matrix. The coordinate transformation for the inertia matrix, which is a second order tensor, premultiplies and postmultiplies the components by a rotation matrix and its transpose, respectively. See Appendix A for a detailed discussion.
4.2.3.2 Principal Axes of Inertia
Theorem 4.6 provides a direct way to calculate the inertia matrix relative to some rotated frame from the inertia matrix associated with a given frame, provided the two frames have a common origin. In general, the inertia matrix is a full  matrix. There are certain choices of the frame that simplify the form of the inertia matrix. The definition of the principal axes, given below, describes a choice of coordinates that yields a diagonal inertia matrix.
matrix. There are certain choices of the frame that simplify the form of the inertia matrix. The definition of the principal axes, given below, describes a choice of coordinates that yields a diagonal inertia matrix.
For rigid bodies with complex geometry, it may not be evident that there is any special structure of the inertia matrix. However, for any point in a rigid body there is always a set of axes at the point relative to which the inertia matrix is diagonal. That is, there exists a set of principal axes at every point in the rigid body. The following theorem summarizes this fact.
4.2.3.3 The Parallel Axis Theorem
Theorem 4.6 summarizes how the inertia relative to one set of axes may be used to calculate the inertia relative to a rotated basis. The two frames must have the same origin when applying Theorem 4.6. The parallel axis theorem, in contrast, relates the inertia matrix about a point 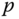 in terms of the inertia matrix about the center of mass. In this case the frames are not rotated relative to each other; they are parallel.
in terms of the inertia matrix about the center of mass. In this case the frames are not rotated relative to each other; they are parallel.
The parallel axis theorem is lengthy, as written in Theorem 4.8. The following theorem expresses the parallel axis theorem in matrix form and can be useful in programming implementations.
4.2.3.4 Symmetry and Inertia
The explicit calculation of the integrals that appear in the inertia matrix can be difficult to calculate analytically. In cases of complex geometry, the calculation of closed form expressions can be intractable. Numerical techniques to estimate the inertia matrix are now a standard feature of solid modeling and computer aided design software. The algorithms involved in such calculations are not complex, and require implementation of numerical quadrature formulae to estimate the integrals as a weighted sum of functional evaluations. The most difficult task in implementing this approximation procedure is the characterization of the geometry of the rigid body, but this is precisely the job at which solid modeling and computer aided design programs excel.
Still, even for the most complex geometric models, it is often possible to reduce the work required to evaluate the inertia matrix by utilizing the body's symmetry. The identification of a specific coordinate plane of symmetry implies that cross products of inertia involving the coordinate perpendicular to the plane of symmetry are equal to zero. Before stating this theorem, the mathematical definition of acoordinate plane of symmetry will be presented.
This definition specifies that a plane of symmetry splits the body into two pieces that are reflections of each other across the plane of symmetry. The importance of identifying a plane of symmetry in applications is demonstrated in the following theorem.
Building on this definition for a single variable function, a multivariable function  is anodd function in the
is anodd function in the  argument if the function
argument if the function  is a anodd function when the other variables are held fixed. In addition, there is a special property of odd functions related to integration.
is a anodd function when the other variables are held fixed. In addition, there is a special property of odd functions related to integration.
The proof of Theorem 4.10 has the same structure. Suppose that the 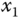 –
–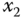 plane of the frame
plane of the frame 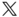 is a plane of symmetry of the rigid body. By definition,
is a plane of symmetry of the rigid body. By definition,

By using the fact that the density  outside of the body, this integral can be written as
outside of the body, this integral can be written as

The integrand in 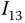 is an odd function of
is an odd function of  that is integrated over a symmetric domain, and is equal to zero.□
that is integrated over a symmetric domain, and is equal to zero.□
4.3 The Newton–Euler Equations
A first course in dynamics introduces Newton's laws of motion, which are applicable to bodies that are idealized as point masses.Newton's first law holds that in the absence of applied external forces, a mass at rest remains at rest, or if it is in motion it travels along a straight line with constant velocity.Newton's second law maintains that the sum of forces acting on a point mass is equal to the time rate of change of the linear momentum of the point mass. A critical feature of the Newton's laws of motion is that they are stated with respect to observations made in aninertial reference frame.
Robotic systems are most often comprised of collections of rigid bodies whose mass is distributed spatially. While it is sometimes possible to create reasonable approximations of robotic systems using lumped mass or point mass approximations, this is frequently not the case. The required generalization of Newton's laws of motion for rigid bodies having distributed mass are given byEuler's laws of motion.
Theorems 4.11 and 4.12 can be used in applications, but it is often the case that alternative forms are sought. Euler's first law can also be stated as the fact that the resultant force acting on a rigid body is equal to the mass of the rigid body multiplied by the acceleration of the center of mass of the body in an inertial frame.
The form of Euler's second law stated in Theorem 4.12 requires that the point  is fixed in the inertial frame
is fixed in the inertial frame . This restriction can be a serious drawback in many applications. For example, in space robotics it is not convenient to impose this condition. However, a suitable alternative form may be derived. Euler's second law can also be stated for the case when the point
. This restriction can be a serious drawback in many applications. For example, in space robotics it is not convenient to impose this condition. However, a suitable alternative form may be derived. Euler's second law can also be stated for the case when the point 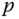 is selected to be the center of mass of the rigid body.
is selected to be the center of mass of the rigid body.
The above proof illustrates that Theorems 4.12 and 4.14 are equivalent; either form could be selected as Euler's second law. As a final topic in this section, alternative laws are presented that are derived from Euler's second law that relate angular momentum and moments about an arbitrary point 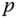 that is fixed on a rigid body.
that is fixed on a rigid body.
4.4 Euler's Equation for a Rigid Body
Euler's first and second laws as stated in Theorems 4.11 and 4.12 can be used to derive the equations of motion for mechanical systems comprised of rigid bodies. When treating complex mechanical systems that consist of rigid bodies connected by ideal joints, the choice of kinematic variables and frames of reference can be quite complicated. The choice of kinematic variables is often tailored to the problem at hand to simplify calculations. The following theorem discusses one of the most common such applications of Euler's first and second laws,Euler's equations of rotational motion for a single rigid body. It is assumed in these equations that the body fixed frame defines a set of principal axes that have their origin at the center of mass.
4.5 Equations of Motion for Mechanical Systems
Euler's first law in Theorem 4.11 and Euler's second law in Theorem 4.12 give a complete description of the dynamics of mechanical systems that consist of rigid bodies. This section discusses the use of these principles in realistic problems that arise when studying robotic systems.
4.5.1 The General Strategy
A general outline of the steps used to derive the equations of motion from Euler's laws for mechanical systems is given in Figure 4.14. The set of steps that appear in Figure 4.14 can be difficult to apply in practice, and experience is required to become adept at deriving the equations of motion for complex systems. The complexity of the resulting equations can vary dramatically based on the selection of the kinematic variables, or, depending on the choice of frames, in a particular problem.
- 1. Derive the equations of motion for each body,

- 1.1 Create afree body diagram for body
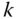 .
. - 1.2 Formulate Euler's first law for body
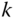 .
.
- 1.2.1 Calculate the acceleration of the center of mass of body
 .
. - 1.2.2 Sum forces equal to the derivative of the linear momentum.
- 1.2.1 Calculate the acceleration of the center of mass of body
- 1.3 Formulate Euler's second law for body
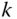 .
.
- 1.3.1 Calculate the derivative of the angular momentum.
- 1.3.2 Sum moments equal to derivative of the angular momentum.
- 1.1 Create afree body diagram for body
- 2. Assemble the collection of equations above into a governing set ofdifferential‐algebraic equations, orDAE's, having the form

- 3. Eliminate algebraic unknowns
 and write the governing equations as a system ofordinary differential equations, or ODE's, having the form
and write the governing equations as a system ofordinary differential equations, or ODE's, having the form
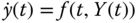
Figure 4.14 Methodology to derive the equations of motion.
The successful application of the steps in Figure 4.14 requires numerous theorems and principles that have been introduced in Chapters 2, 3, and 4. The calculation of the acceleration of the center of mass builds on the foundations developed in Chapter 2 and on the specific formulations of kinematics for robotics summarized in Chapter 3. The determination of the derivative of the angular momentum in Steps 2.2.1 or 2.3.1 of Figure 4.14 requires a working knowledge of the use ofangular velocities introduced in Chapter 2 in Section 2.5.1 and the derivative theorem in Theorem 2.12. Even with a strong understanding of these definitions and underlying principles, practice will guide the careful selection of the kinematic variables and frames in a particular problem.
4.5.2 Free Body Diagrams
The creation of an accuratefree body diagram is essential in the sequence of steps in Figure 4.14. The free body diagram releases a rigid body from all external constraints on the body and represents the effect of these constraints by unknown reaction forces and moments that act between the bodies. The representation of constraint forces and moments that act between bodies in a mechanical system connected byideal joints can be treated systematically. The sum of thenumber of degrees of freedom of an ideal joint and the number of constraint reaction forces and moments that act between the bodies connected by that joint is always equal to six. In fact, much more can be said about the complementary nature of the kinematic constraints introduced by an ideal joint and the associated reaction forces and moments. This complementarity is the subject of the next theorem.
Before applying this theorem in a number of examples, it must be emphasized that the statement of the theorem concludes that there are in general
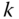 reaction forces or moments. It can occur that the value of some of the components of these reaction forces or moments are equal to zero. Strictly speaking, it is perhaps more accurate to say that the joint in question can support
reaction forces or moments. It can occur that the value of some of the components of these reaction forces or moments are equal to zero. Strictly speaking, it is perhaps more accurate to say that the joint in question can support 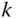 reaction forces or moments, but that some of these reactions may be equal to zero. The next few examples will show how to create free body diagrams for some typical mechanical systems. Each example has been selected to emphasize the practical implications of Theorem 4.17 and the methodology outlined in Figure 4.14
reaction forces or moments, but that some of these reactions may be equal to zero. The next few examples will show how to create free body diagrams for some typical mechanical systems. Each example has been selected to emphasize the practical implications of Theorem 4.17 and the methodology outlined in Figure 4.14
The free body diagrams developed in Examples 4.12 and 4.13 are prototypical of those derived in a host of mechanical systems encountered in applications. Additional examples are considered in the problems at the end of this chapter. The goal in creating free body diagrams is to enable the determination of the equations of motion from Euler's first and second laws. The following examples use the free body diagram to cast the equations of motion in simple case studies. In Example 4.14, the mass and inertia matrix that appear in Euler's laws are assumed to be negligible, and the force and moment summations take a particularly simple form. We use this analysis to confirm that the composite joint satisfies Theorem 4.17.
The last few examples have derived the appropriate free body diagrams that are associated with rigid bodies connected by ideal joints. Euler's first and second laws have been applied in the case where the mass and inertia matrix of one of the bodies are negligible; the resulting equations of motion resemble those obtained in elementary statics problems of engineering. The next two examples study robotic systems in three spatial dimensions. First, a single degree of freedom of motion is considered, followed by the generalization to the two degree of freedom case. The resulting equations of motion significantly increase in complexity as the number of degrees of freedom increase.
The equations of motion for mechanical systems in realistic problems with three dimensional kinematics can be quite complicated in form. The next example studies another two link robotic system. Because of the symmetry of the bodies with respect to the selected frames of reference, and the restriction of motion so that only 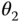 varies, the equations of motion take a familiar form in Example 4.18.
varies, the equations of motion take a familiar form in Example 4.18.
The equations of motion derived in Example 4.18 assumed a particularly simple form due to symmetry and the fact that there is but a single degree of freedom. In general, however, the equations of motion can be quite complex. In this next example it is shown that by allowing the joint variable  in Example 4.18 to vary in time as an unknown, the resulting equations of motion for the system again become increasingly more complicated.
in Example 4.18 to vary in time as an unknown, the resulting equations of motion for the system again become increasingly more complicated.
4.6 Structure of Governing Equations: Newton–Euler Formulations
Examples 4.16, 4.17, 4.18, and 4.19 demonstrate that the system of equations obtained via the application of Euler's first and second law to robotics applications is unavoidably complicated. An essential step in the study of Newton–Euler formulations casts the derived equations into one of a few possible canonical mathematical forms. This step is important from a theoretical standpoint since in many cases analysts have developed a theory that can be consulted to study existence, uniqueness, or stability of solutions for general classes of problems. From a practical viewpoint, once the equations are written in a standard from, it is possible to employ common and well understood numerical techniques for their study. While there are many possible structural forms in which the governing equations can be cast, two standard forms will be considered in this book. The equations of motion will be written as a system ofdifferential algebraic equations or DAEs, or as a set ofordinary differential equations or ODEs.
4.6.1 Differential Algebraic Equations (DAEs)
There are two types of variables that appear in the governing equations in Newton–Euler formulations of dynamics, as shown in Examples 4.16, 4.17, 4.18, and 4.19. One set of variables are explicitly differentiated with respect to time, while others are not. The subset of variables that are differentiated with respect to time are referred to as differential unknowns, while those that are not differentiated are known as algebraic unknowns. A collection of equations that couples both types of variables constitutes a system of DAEs. The form of DAEs that will be used in this text have the structure

where 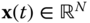 is the collections of differential variables,
is the collections of differential variables, 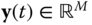 is the collection of algebraic variables, the function
is the collection of algebraic variables, the function  and
and 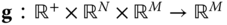 . There are a total of
. There are a total of  variables in the above
variables in the above  equations. It is straightforward to express the equations derived via Newton–Euler methods in this form, as shown in the next examples.
equations. It is straightforward to express the equations derived via Newton–Euler methods in this form, as shown in the next examples.
4.6.2 Ordinary Differential Equations (ODEs)
In most applications of Newton–Euler formulations to realistic robotic systems, the resulting equations contain both differential and algebraic variables. As discussed in the last section, it is natural to study these systems as a collection of DAEs. Still, it is most common in the literature to eliminate the algebraic unknowns via algebraic manipulation. There are technical conditions, expressed in terms of the Jacobian of the algebraic constraint equations in Equation 4.41, that guarantee that it is possible to solve the last 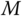 equations in 4.41 for the algebraic unknowns
equations in 4.41 for the algebraic unknowns 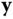 in terms of
in terms of 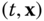 . The expressions for
. The expressions for 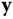 in terms of
in terms of  can then be substituted into the first line of Equation 4.41, thereby eliminating the algebraic unknowns. The interested reader should consult [27] or [2] for the complete description. When this procedure is feasible, the resulting form of the governing equations is a collection of ODEs of the form
can then be substituted into the first line of Equation 4.41, thereby eliminating the algebraic unknowns. The interested reader should consult [27] or [2] for the complete description. When this procedure is feasible, the resulting form of the governing equations is a collection of ODEs of the form

where 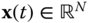 and
and  . It must be emphasized that although the procedure discussed above to reformulate a set of DAEs in the form of Equation 4.41 into Equation 4.44 is easy to describe in principle, it can be difficult to achieve in practice. This is certainly the case for complex robotic systems. Despite the difficulty of the task, there are several reasons that motivate the attempt.
. It must be emphasized that although the procedure discussed above to reformulate a set of DAEs in the form of Equation 4.41 into Equation 4.44 is easy to describe in principle, it can be difficult to achieve in practice. This is certainly the case for complex robotic systems. Despite the difficulty of the task, there are several reasons that motivate the attempt.
(1) Order reduction. For any system, the number of 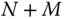 DAEs is always larger than the reduced number of
DAEs is always larger than the reduced number of  ODEs. The difference in complexity can be substantial for robotic systems. In fact, most of the unknowns in a kinematic chain are associated with the algebraic variables. If it is desired to construct a feedback law that must be updated in real time, the cost in estimation of the solution of a set of DAEs can be prohibitive. For example, for an
ODEs. The difference in complexity can be substantial for robotic systems. In fact, most of the unknowns in a kinematic chain are associated with the algebraic variables. If it is desired to construct a feedback law that must be updated in real time, the cost in estimation of the solution of a set of DAEs can be prohibitive. For example, for an 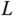 link kinematic chain having one degree of freedom at each joint,
link kinematic chain having one degree of freedom at each joint, 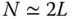 and
and  .
.
(2) Theoretical foundations. The study of ODEs and their numerical approximation is much more mature than the corresponding state of affairs for DAEs. The study of DAEs is continuously evolving. Furthermore, the current theoretical framework for DAEs is more difficult to state and has more restrictions on its applicability. Broad statements about the existence, stability, convergence and stability of DAEs are less common. Again, references [2] and [27] can be consulted for advanced presentations.
(3) Control theoretic issues. It has already been noted in (1) above that the computational cost associated with the numerical solution of DAEs can be prohibitive in control applications. Just as importantly, nearly all of the supporting theory and algorithms for the control of robotic systems has been derived for systems of ordinary differential or discrete difference equations. This body of research is impressive and represents decades of research and development. The study of the control of DAEs does not have as mature a theoretical and computational infrastructure.
The next two examples illustrate how the algebraic unknowns can be eliminated for relatively simple problems.
4.7 Recursive Newton–Euler Formulations
4.7.1 Recursive Calculation of Forces and Moments
In Chapter 3 recursive algorithms for determining velocities and derivatives of velocities have been derived for the kinematic chain depicted in Figure 3.20 or Figure 3.21. The joints are numbered from 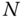 to 1 starting at the joint nearest the base body and decreasing toward the tip. The recursive algorithms developed in Sections 3.4.1 and 3.4.3 start with the joint connected to the base body, and then solve for velocities or derivatives of velocities as we move from inboard to outboard joints.
to 1 starting at the joint nearest the base body and decreasing toward the tip. The recursive algorithms developed in Sections 3.4.1 and 3.4.3 start with the joint connected to the base body, and then solve for velocities or derivatives of velocities as we move from inboard to outboard joints.
This section will show that the calculation of joint forces and torques can be carried out starting at joint 1 toward the tip of the kinematic chain and proceeding inward toward the base. As in the study of velocities and accelerations, a recursive method is possible because of the special structures of the matrices that relates joint forces and torques, acceleration, and angular acceleration. The reason that the recursion in this section progresses from tip to base is because the coefficient matrix in Theorem 4.18 is exactly equal to the transpose of the coefficient matrix that appears in either Theorem 3.4 or Theorem 3.5. The following theorem summarizes this matrix equation.
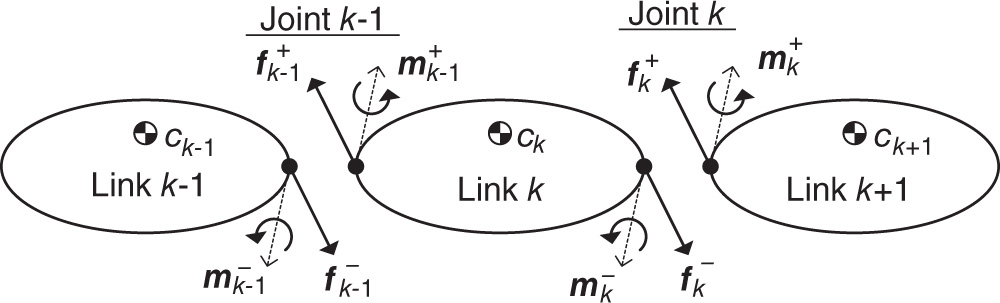
Figure 4.31 Joint loading convention.
The coefficient matrix that appears in Equation 4.46
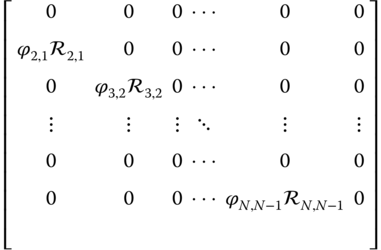
is the transpose of the coefficient matrix that appears in the recursive calculation of the velocity and acceleration in Equations (3.13) in Theorem 3.4 and (3.30) in Theorem 3.5. In both of those cases, the structure of the coefficient matrix enables a recursive procedure that starts with the last row, which corresponds to the root of the kinematic chain. In the current case, for solving the forces and moments, the structure of the lead coefficient matrix makes it possible to solve the first equation for the forces and moments in 
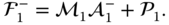
Suppose that all of the velocities and angular velocities have been solved for using the recursive algorithm described in Section 3.4.1, and that all of the derivatives of velocities and angular velocities have been solved for using the recursive algorithm summarized in Section 3.4.3. When this is the case, it is possible to evaluate all of the terms on the right side of the above equation immediately and obtain 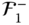 . With this, the solution can proceed to the second row in Equation 4.46 and solve for
. With this, the solution can proceed to the second row in Equation 4.46 and solve for 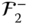 as
as

Since all the terms required to evaluate the right side of this equation are known, 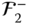 may be calculated. This process is continued until all the joints
may be calculated. This process is continued until all the joints  have been processed. The following table summarizes this recursive algorithm for the calculation of the reaction forces and moments.
have been processed. The following table summarizes this recursive algorithm for the calculation of the reaction forces and moments.
- 1. Solve for the velocities and angular velocities using the recursive algorithm in Section 3.4.1.
- 2. Solve for the derivatives of the velocities and angular velocities using the recursive algorithm in Section 3.4.3.
- 3. Iterate from outboard joints to inboard joints.
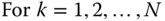
- 3.1 Form the bias inertial force
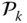 .
.

- 3.2 Form the transition operator
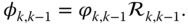
- 3.3 Form the generalized inertia and mass matrix

- 3.4 Calculate the forces and moments
(4.59)

- 3.1 Form the bias inertial force
Figure 4.32 Recursive algorithm for calculating forces and moments.
4.8 Recursive Derivation of the Equations of Motion
Sections , and 4.7.1 have shown that the forward kinematics problem for either velocities or accelerations, as well as the calculation of joint forces or torques, can be solved efficiently via recursive order  algorithms. This section will show that the equations of motion for robotic systems that form a kinematic chain as depicted in Figure 3.20 and 3.21 can be written in terms of constituent matrices that were introduced in Sections , and 4.7.1. Reference [24] gives a comprehensive account of this formulation, or see [14] for a similar discussion. The velocities and angular velocities for the kinematic chain are collected in the
algorithms. This section will show that the equations of motion for robotic systems that form a kinematic chain as depicted in Figure 3.20 and 3.21 can be written in terms of constituent matrices that were introduced in Sections , and 4.7.1. Reference [24] gives a comprehensive account of this formulation, or see [14] for a similar discussion. The velocities and angular velocities for the kinematic chain are collected in the  vector
vector

where point  is attached to body
is attached to body 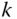 on the outward side of joint
on the outward side of joint  . The terms
. The terms 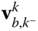 are the components relative to the basis for the frame
are the components relative to the basis for the frame 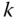 of the velocity vector
of the velocity vector 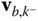 . The terms
. The terms 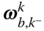 are the components relative to the basis for the frame
are the components relative to the basis for the frame  of the angular velocity vector
of the angular velocity vector  . Equation (3.13) can be written in terms ofsystem vectors of unknowns as
. Equation (3.13) can be written in terms ofsystem vectors of unknowns as
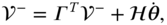
where the assembled system vectors  and
and 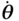 are defined as
are defined as
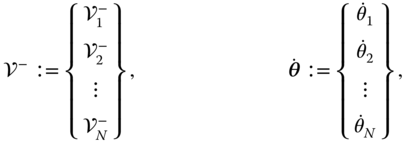
and the system matrices 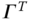 and
and 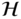 are defined as
are defined as
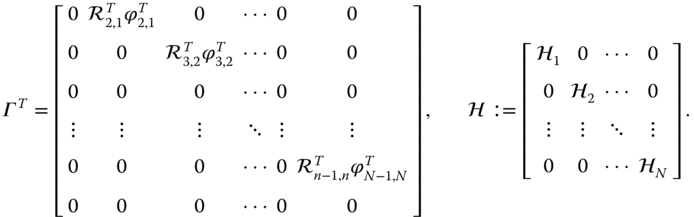
The matrix  and its transpose
and its transpose 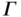 will appear repeatedly in the derivatives that follow. A similar equation can be obtained from Theorem 3.5 for the derivatives of the velocities and angular velocities. The vectors
will appear repeatedly in the derivatives that follow. A similar equation can be obtained from Theorem 3.5 for the derivatives of the velocities and angular velocities. The vectors 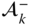 that are used to formulate the kinematic problem for the accelerations are defined to be
that are used to formulate the kinematic problem for the accelerations are defined to be

The primary result in Section 3.4.3 as made explicit in Theorem 3.5 is that the derivatives of the velocity and angular velocities satisfy the system equation

where the system vectors  and
and 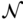 are defined as
are defined as
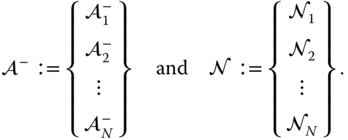
Finally, recall the definition of the  vector
vector

which contains the components relative to frame 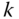 of the force vectors
of the force vectors 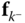 and moments
and moments 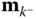 that are applied at point
that are applied at point  on body
on body 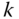 at the joint
at the joint  . Equation 4.48 in Theorem 4.18 holds that the joint forces and moments satisfy the system equation
. Equation 4.48 in Theorem 4.18 holds that the joint forces and moments satisfy the system equation
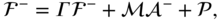
where the system vectors 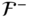 and
and 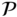 , and system matrix
, and system matrix 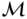 , are defined to be
, are defined to be

The determination of the equations of motion for the kinematic chain depicted in Figures 3.20 and 3.21 is straightforward once Equations 4.71, 4.72, and 4.73 are derived. Equations 4.72 and 4.73 may be solved for 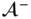 and
and 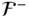 , respectively, to obtain
, respectively, to obtain


Equation 4.74 is then substituted into 4.75 to obtain an expression for the joint forces and torques
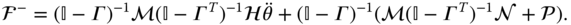
In this equation, the vector 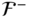 contains the joint forces and moments acting on each body in the kinematic chain.
contains the joint forces and moments acting on each body in the kinematic chain.
The final equations of motion for the kinematic chain are obtained by noting that all of the forces and moments that act on the individual joints of the body can be decomposed into constraint forces and moments  and actuation torques as
and actuation torques as

where  is the actuation torque generated about the axis
is the actuation torque generated about the axis 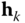 for
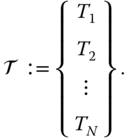
for 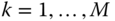 . The system vector of actuation torques has been introduced into this equation as
. The system vector of actuation torques has been introduced into this equation as
By definition, the constraint forces and moments  are orthogonal to the actuation torques. Since the direction of the
are orthogonal to the actuation torques. Since the direction of the  actuation torque is given by
actuation torque is given by 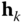 , the condition that the constraint forces are perpendicular to the actuation forces and moments can be written as
, the condition that the constraint forces are perpendicular to the actuation forces and moments can be written as
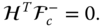
Equation 4.77 can be premultiplied by 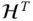 to utilize this orthogonality condition and obtain the equation
to utilize this orthogonality condition and obtain the equation
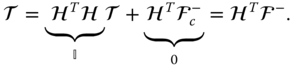
This equation calculates the projection of all of the joint forces and moments along the direction of the actuation torques. Recall that each 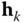 is a unit vector by definition, which guarantees that
is a unit vector by definition, which guarantees that
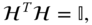
with 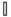 an appropriately dimensioned identity matrix. The final equations of motion for the robotic system can be obtained by combining Equations 4.76 and 4.78 to attain
an appropriately dimensioned identity matrix. The final equations of motion for the robotic system can be obtained by combining Equations 4.76 and 4.78 to attain

4.9 Problems for Chapter 4, Newton–Euler Equations
4.9.1 Problems on Linear Momentum
Problems 4.1,4.2, and 4.3 refer to the robotic manipulator shown in Figures 4.35 and 4.36. This robot has revolute joints about the  ,
,  , and
, and 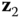 axes. The joint variables
axes. The joint variables 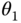 ,
, 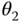 , and
, and 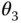 are measured about the
are measured about the  ,
,  , and
, and  axes, respectively. In each case the angle
axes, respectively. In each case the angle  is measured from the positive
is measured from the positive 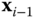 axis to the positive
axis to the positive  axis, for
axis, for  .
.
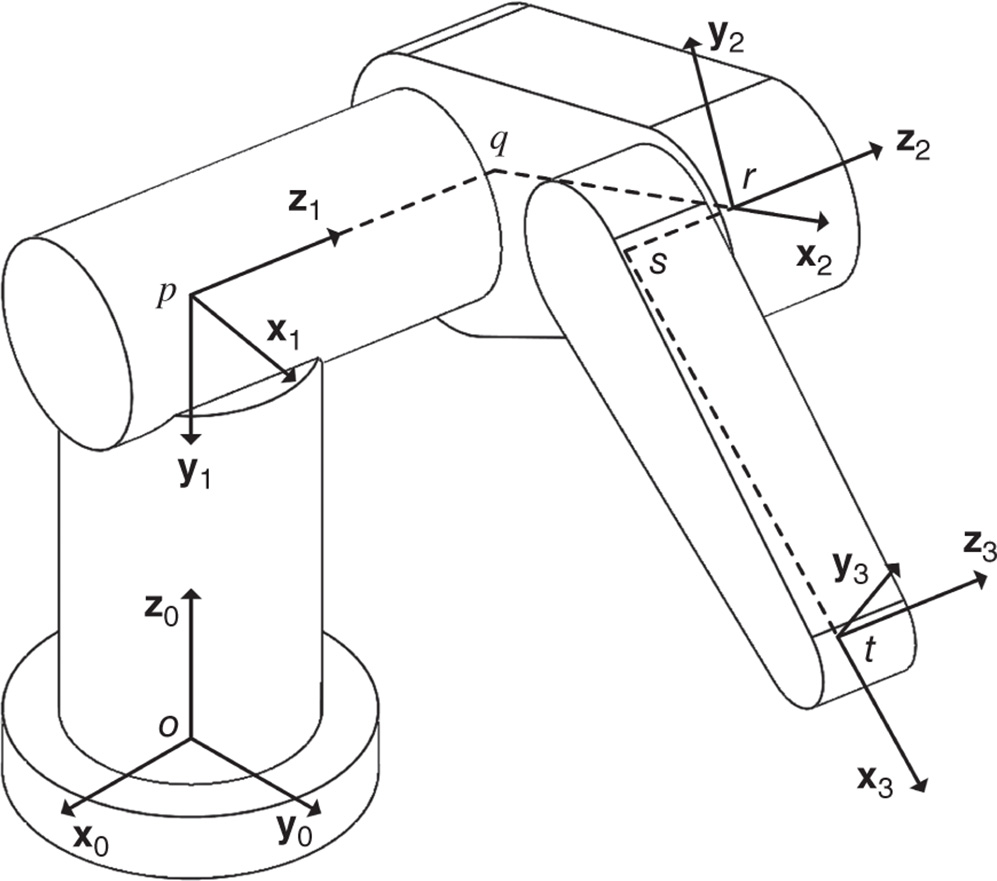
Figure 4.35 PUMA robot frame definitions.
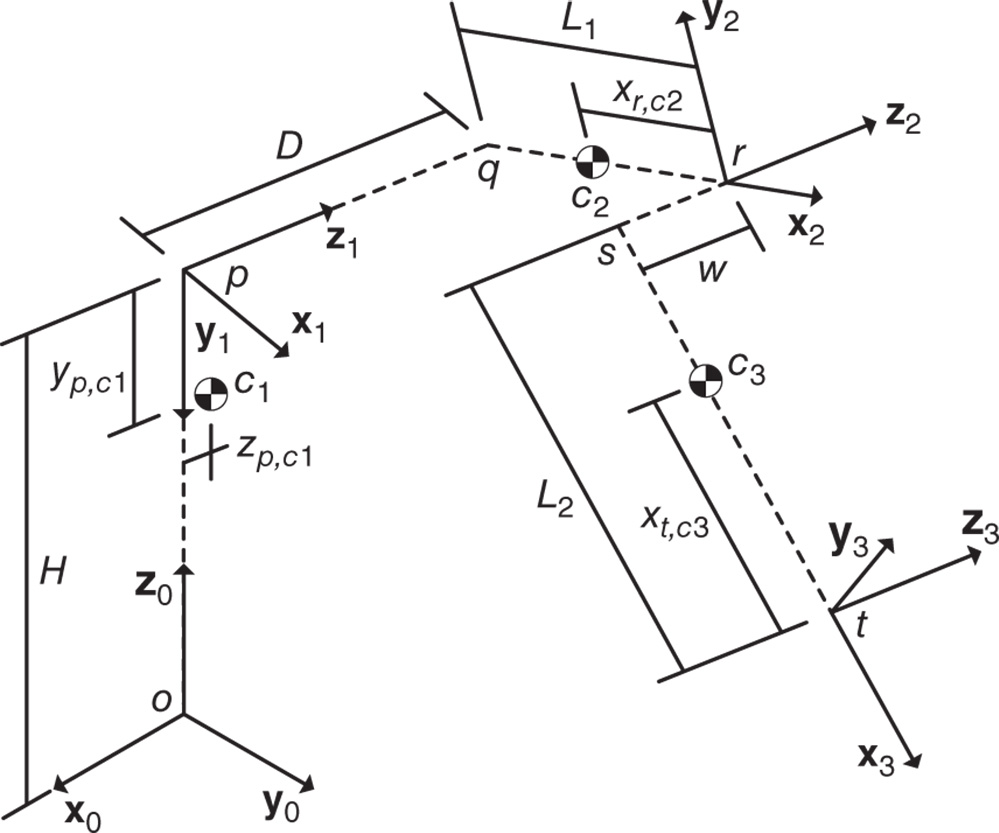
Figure 4.36 PUMA robot joint and mass center offsets.
- Problem 4.1 Compute the linear momentum in the 0 frame of link 1, the shoulder, for the robot shown in Figures 4.35 and 4.36. Express your answer in terms of the basis for the 1 frame and 0 frame.
- Problem 4.2 Compute the linear momentum in the 0 frame of link 2, the inner arm, for the robot shown in Figures 4.35 and 4.36. Express your answer in terms of the basis for the 2, 1 and 0 frames.
- Problem 4.3 Compute the linear momentum in the 0 frame of link 3, the outer arm, for the robot shown in Figures 4.35 and 4.36. Express your answer in terms of the basis for the 3, 2, 1 and the 0 frames.
Problems 4.4,4.5, and 4.6 refer to the SCARA robot shown in Figures 4.37 and 4.38. This robotic manipulator has two revolute joints about the
 and
and  directions and a prismatic joint along the
directions and a prismatic joint along the  direction. The joint variables
direction. The joint variables  and
and  are measured about the
are measured about the  and
and  axes, respectively. In each case the angle
axes, respectively. In each case the angle 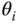 is measured from the positive
is measured from the positive  axis to the positive
axis to the positive 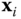 axis, for
axis, for 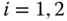 .
.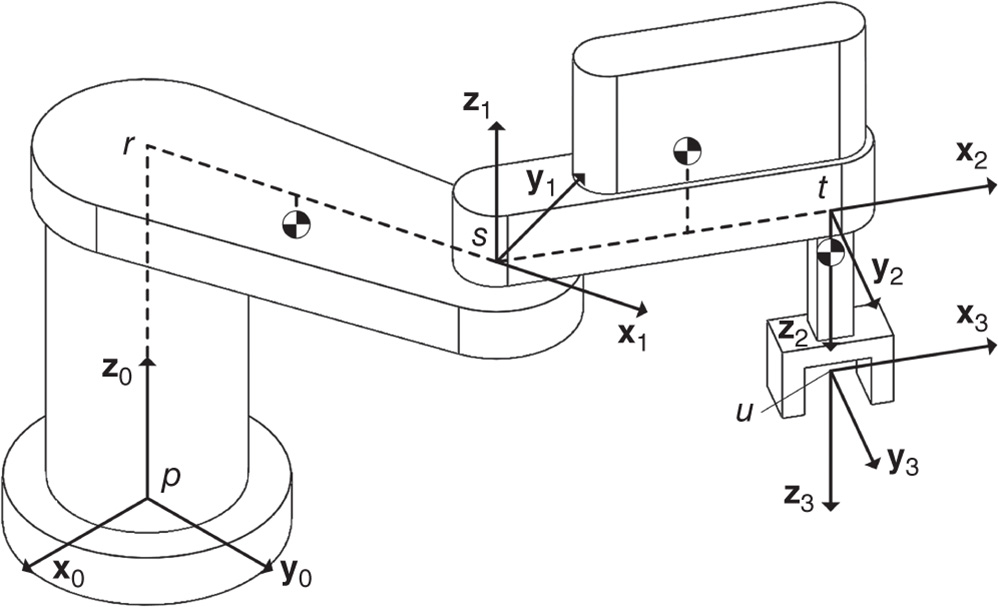
Figure 4.37 SCARA robot frame definitions.
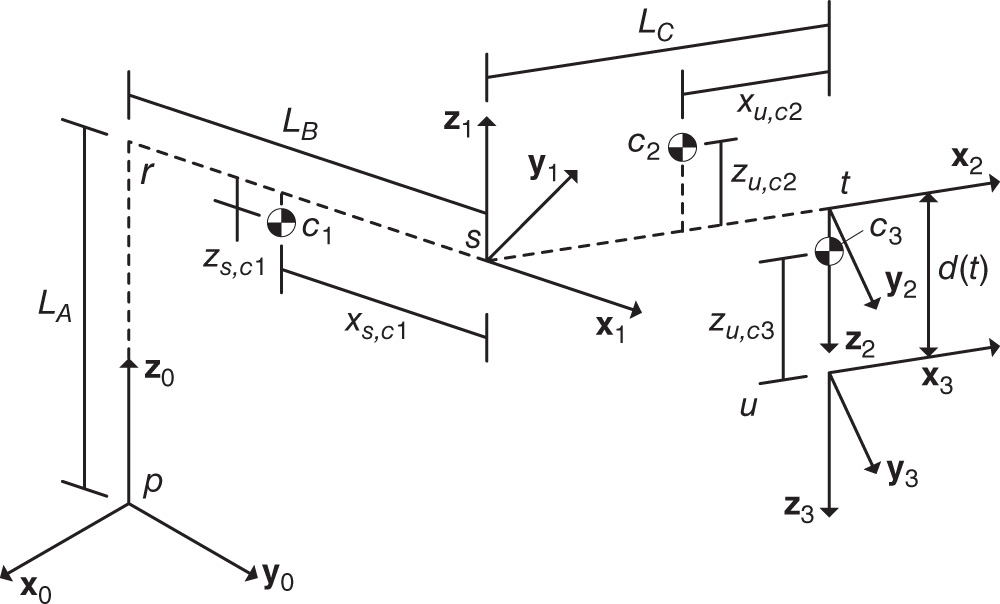
Figure 4.38 SCARA robot joint and mass center offsets.
- Problem 4.4 Compute the linear momentum in the 0 frame of link 1, the inner arm, for the robot shown in Figures 4.37 and 4.38. Express your answer in terms of the basis for the 1 frame and 0 frame.
- Problem 4.5 Compute the linear momentum in the 0 frame of link 2, the outer arm, for the robot shown in Figures 4.37 and 4.38. Express your answer in terms of the basis for the 2, 1, and 0 frames.
- Problem 4.6 Compute the linear momentum in the 0 frame of link 3, the tool carriage, for the robot shown in Figures 4.37 and 4.38. Express your answer in terms of the basis for the 3, 2, 1, and 0 frames.
Problems 4.7,4.8, and 4.9 refer to the robotic manipulator shown in Figures 4.39 and 4.40. This robotic manipulator has a revolute joint along the
 direction, and it has a prismatic joints along the
direction, and it has a prismatic joints along the  ,
, 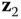 , and
, and  directions. The tool carriage, which is not shown, has its center of mass located at point
directions. The tool carriage, which is not shown, has its center of mass located at point 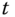 . The joint variable
. The joint variable 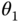 is measured about the
is measured about the 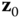 axis. The angle
axis. The angle 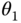 is measured from the positive
is measured from the positive  axis to the positive
axis to the positive 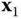 axis. The height
axis. The height  from the point
from the point 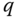 to the point
to the point 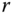 is the joint variable measuring displacement along the
is the joint variable measuring displacement along the  axis, the length
axis, the length 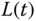 from the point
from the point 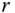 to the point
to the point 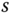 is the joint variable measuring displacement along the
is the joint variable measuring displacement along the 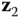 direction, and the distance
direction, and the distance 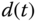 from the point
from the point 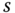 to the point
to the point 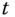 is the joint variable along the
is the joint variable along the 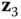 axis.
axis.
Figure 4.39 Cylindrical robot frame definitions.
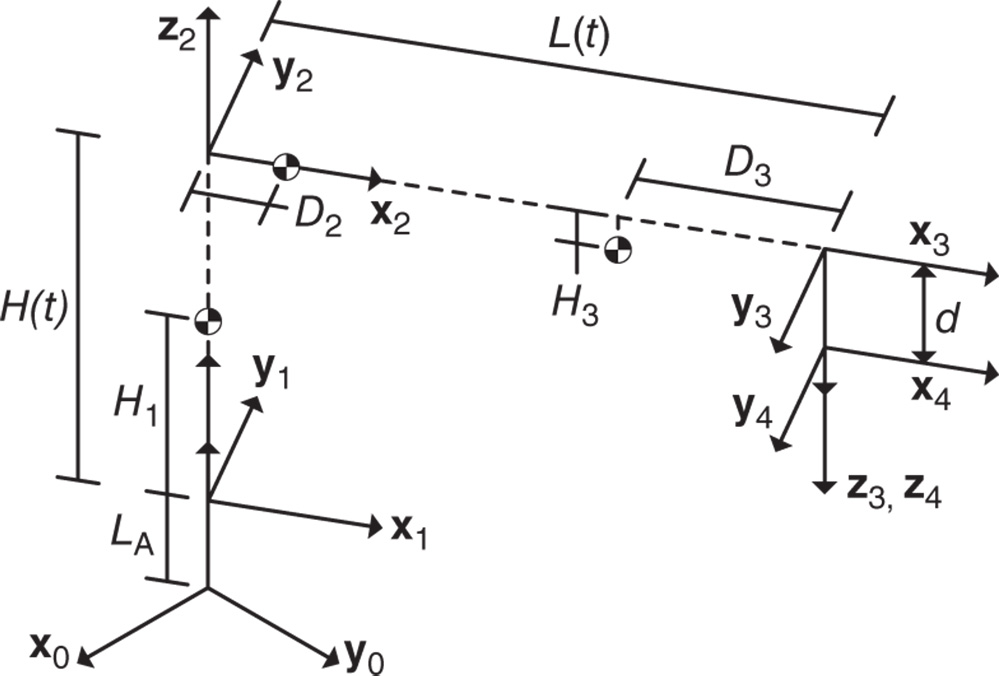
Figure 4.40 Cylindrical robot joint and mass center offsets.
- Problem 4.7 Compute the linear momentum in the 0 frame of link 1, the vertical arm, for the robot shown in Figures 4.39 and 4.40. Express your answer in terms of the basis for the 1 and 0 frames.
- Problem 4.8 Compute the linear momentum in the 0 frame of link 2, the horizontal arm, for the robot shown in Figures 4.39 and 4.40. Express your answer in terms of the basis for the 2, 1, and 0 frames.
- Problem 4.9 Compute the linear momentum in the 0 frame of link 3, the tool carriage, for the robot shown in Figures 4.39 and 4.40. Express your answer in terms of the basis for the
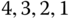 , and 0 frames.
, and 0 frames.
4.9.2 Problems on the Center of Mass
- Problem 4.10 Figure 4.41a depicts the terminal component in an industrial robot. Assume that the mass density is uniform and that the body can be approximated as the union of two cylinders having radii and lengths
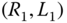 and
and 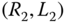 . The location of the center of mass of each cylinder is shown in the figure. Find the mass center of this composite rigid body.
. The location of the center of mass of each cylinder is shown in the figure. Find the mass center of this composite rigid body. 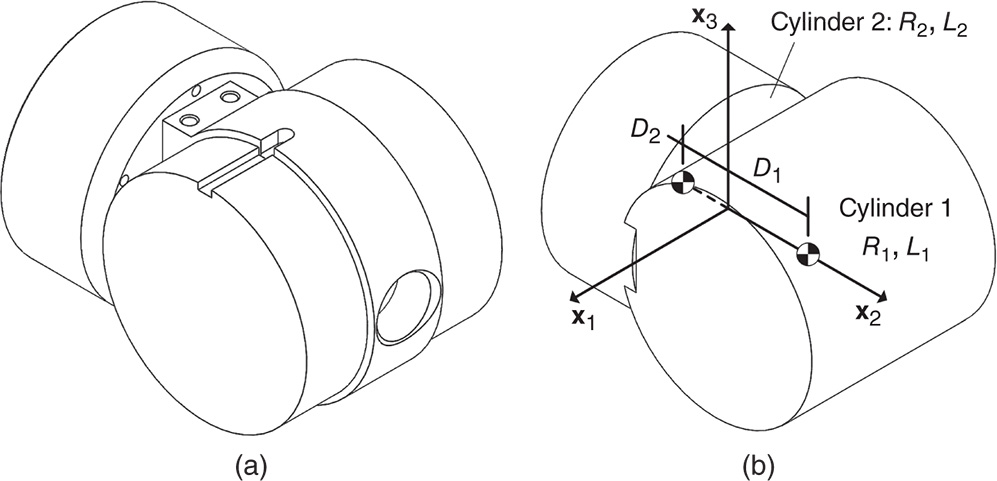
Figure 4.41 Industrial robot end effector component. (a) Detailed design. (b) Geometric primative. - Problem 4.11 Figure 4.42a depicts the fixed base of a robotic assembly. Assume that the mass density is uniform and can be approximated as the union of a cylinder with radius and length
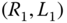 and a rectangular prism of dimensions
and a rectangular prism of dimensions  , as shown in 4.42b. The location of the center of mass of each cylinder is also shown in Figure 4.42b. Find the mass center of this composite rigid body relative to the
, as shown in 4.42b. The location of the center of mass of each cylinder is also shown in Figure 4.42b. Find the mass center of this composite rigid body relative to the  frame.
frame. 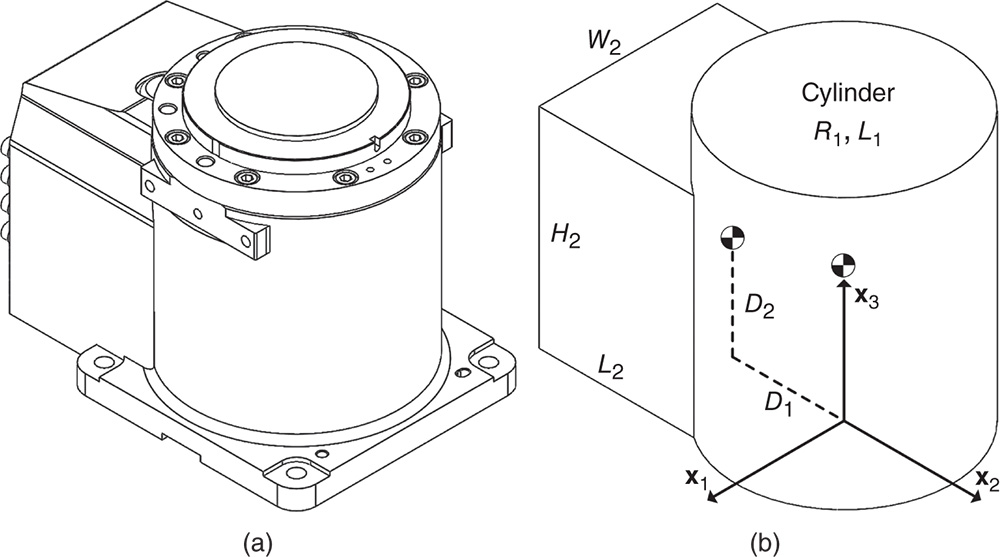
Figure 4.42 Industrial robot fixed base component. (a) Detailed design. (b) Geometric primative. - Problem 4.12 Figure 4.43a depicts the mounting bracket for an industrial robot. Assume that the mass density is uniform and can be approximated as the union of three rectangular prisms. The location of the center of mass of each is shown in Figures 4.43a and 4.43b. Find the mass center of this composite rigid body.
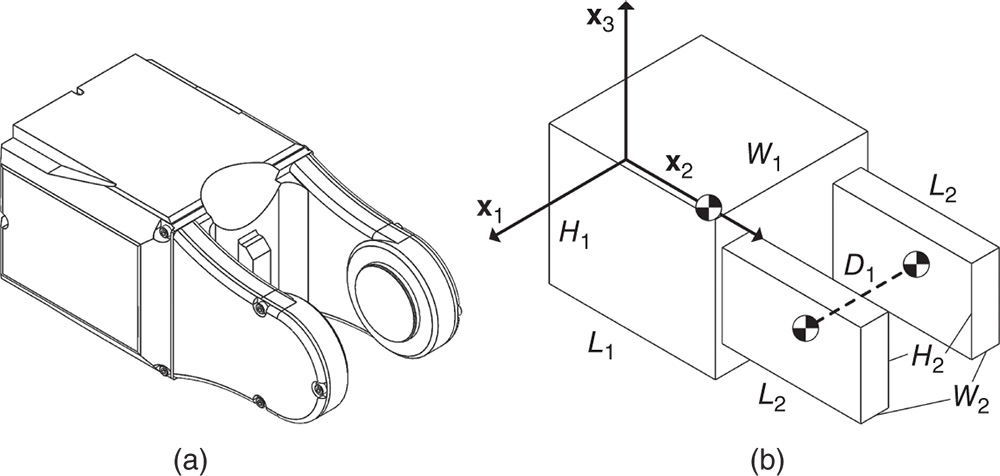
Figure 4.43 Industrial robot mounting bracket component. (a) Detailed design. (b) Geometric primative.
Problems 4.13 and 4.14 study a two link robot that consists of link 1 and 2, as shown in Figures 4.44a and 4.44b. The center of mass coordinates of link 1 with respect to frame 1 are
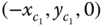 , and the center of mass coordinates of link 2 with respect to frame 2 are
, and the center of mass coordinates of link 2 with respect to frame 2 are 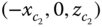 .
.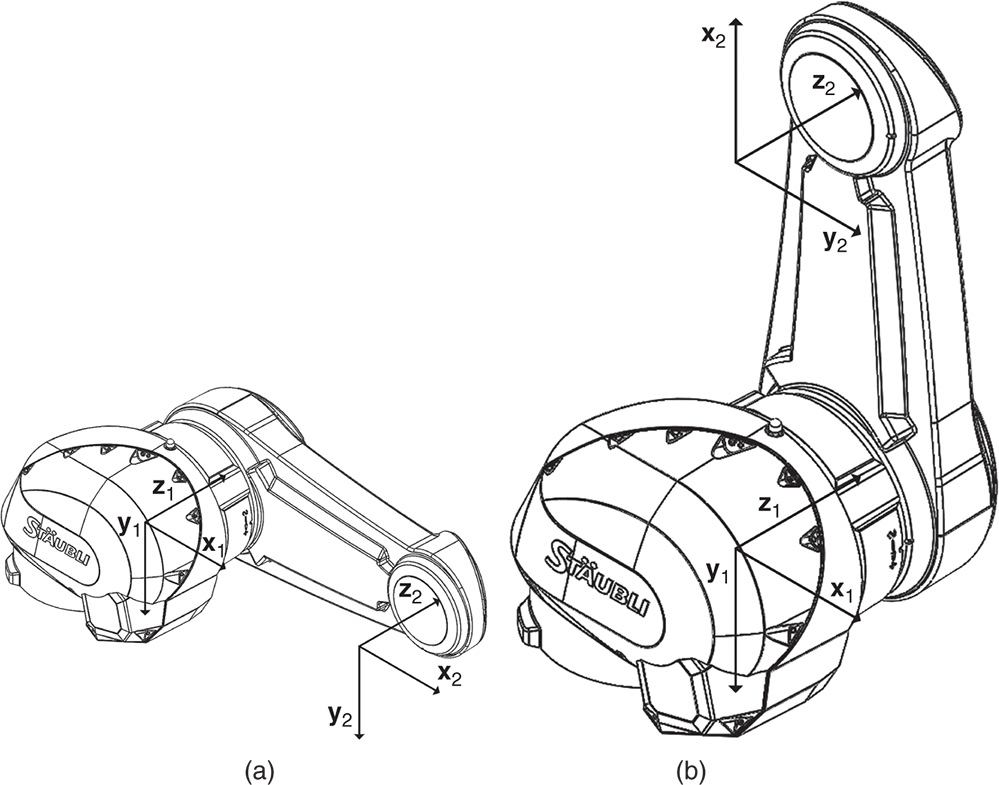
Figure 4.44 Links
 and
and  of an industrial robot. (a) Horizontal configuration. (b) Vertical configuration.
of an industrial robot. (a) Horizontal configuration. (b) Vertical configuration. - Problem 4.13 The two link robot in Figure 4.44a is locked in the horizontal configuration shown. At the instant shown, assume that
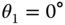 , or
, or 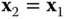 . Calculate the location of the center of mass of the robot in this configuration in terms of the frame 1.
. Calculate the location of the center of mass of the robot in this configuration in terms of the frame 1. - Problem 4.14 The two link robot in Figure 4.44b is locked in the vertical configuration shown. As the instant shown, assume that
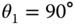 , or
, or  at the instant shown. Calculate the location of the center of mass of the robot in this configuration in terms of frame 1.
at the instant shown. Calculate the location of the center of mass of the robot in this configuration in terms of frame 1.
4.9.3 Problems on the Inertia Matrix
- Problem 4.15 Consider the rigid body studied in Problem 4.10. Assume the origin of frame
 (point
(point 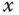 ) is located along the axis of cylinder 2 and
) is located along the axis of cylinder 2 and  is parallel to the axis of cylinder 1. Use symmetry arguments to show that the form of the inertia matrix about the point
is parallel to the axis of cylinder 1. Use symmetry arguments to show that the form of the inertia matrix about the point  relative to the
relative to the  frame is given by
frame is given by
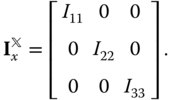
In other words, use symmetry arguments to show that the
 frame defines a set of principal axes for the composite body. Derive the entries of this matrix by using the parallel axis theorem for each of the components of this composite body.
frame defines a set of principal axes for the composite body. Derive the entries of this matrix by using the parallel axis theorem for each of the components of this composite body. - Problem 4.16 Consider the rigid body studied in Problems 4.10 and 4.15. Calculate the inertia matrix relative to axes parallel to the
 frame but whose origin is at the center of mass of the composite body.
frame but whose origin is at the center of mass of the composite body. - Problem 4.17 Consider the rigid body studied in Problem 4.12. Use symmetry arguments to show that the form of the inertia matrix about the point
 (the origin of frame
(the origin of frame  ) relative to frame
) relative to frame  is given by
is given by

In other words, use symmetry arguments to show that the
 frame defines a set of principal axes for the composite body. Derive the entries of this matrix by using the parallel axis theorem for each of the components of this composite body.
frame defines a set of principal axes for the composite body. Derive the entries of this matrix by using the parallel axis theorem for each of the components of this composite body. - Problem 4.18 Consider the rigid body studied in Problems 4.12 and 4.17. Calculate the inertia matrix relative to axes parallel to the
 frame but whose origin is at the center of mass of the composite body.
frame but whose origin is at the center of mass of the composite body. - Problem 4.19 Consider the rigid body studied in Problem 4.11. Use the parallel axis theorem to calculate the inertia matrix relative to frame
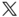 at its origin.
at its origin. - Problem 4.20 Consider the rigid body studied in Problems 4.10,4.15, and 4.16. Calculate the inertia matrix about the point
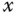 relative to the frame that is is obtained by rotating the
relative to the frame that is is obtained by rotating the 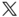 frame by
frame by 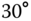 about the
about the 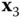 axis.
axis. - Problem 4.21 Consider the yoke studied in Problems 4.12,4.17, and 4.18. Calculate the inertia matrix about the point
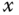 relative to the frame that is obtained by rotating the
relative to the frame that is obtained by rotating the 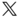 frame by
frame by 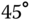 about the
about the 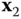 axis.
axis. - Problem 4.22 Consider the two link robot shown in Figure 4.44a and studied in Problem 4.13. Calculate the inertia matrix with respect to frame 1 at its origin for the system in this configuration.
- Problem 4.23 Consider the two link robot shown in Figure 4.44b and studied in Problem 4.14. Calculate the inertia matrix with respect to frame 1 at its origin for the system in this configuration.
- Problem 4.24 Consider the satellite studied in Example 4.13 and shown in Figure 4.17. Let
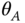 and
and  be the joint variables that measure the rotation of solar arrays
be the joint variables that measure the rotation of solar arrays  and
and 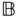 about the
about the 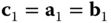 axis. Suppose the principal moments of inertia of the satellite body about its own center of mass relative to the
axis. Suppose the principal moments of inertia of the satellite body about its own center of mass relative to the 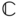 frame are given in the form
frame are given in the form
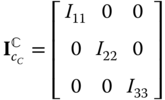
and the principal moments of inertia of each solar array about their own centers of mass
 and
and 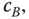 respectively) relative to their own body fixed frame are given in the form
respectively) relative to their own body fixed frame are given in the form
Find an expression for the inertia matrix of the satellite relative to the
 frame for any joint angle
frame for any joint angle  and
and 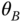 .
.
4.9.4 Problems on Angular Momentum
Problems 4.25,4.26, and 4.27 refer to the PUMA robot shown in Figures 4.35 and 4.36.
- Problem 4.25 Compute the angular momentum in the 0 frame of link 1, the shoulder, shown in Figures 4.35 and 4.36 about its own center of mass. Express your answer in terms of a frame whose origin is at the center of mass and that is parallel to the 1 frame.
- Problem 4.26 Compute the angular momentum in the 0 frame of link 2, the inner arm, depicted in Figures 4.35 and 4.36 about its own center of mass. Express your answer in terms of a frame whose origin is at the center of mass and that is parallel to the 2 frame.
- Problem 4.27 Compute the angular momentum in the 0 frame of link 3, the outer arm, depicted in Figures 4.35 and 4.36 about its own center of mass. Express your answer in terms of a frame whose origin is at the center of mass and that is parallel to the 3 frame.
Problems 4.28 and 4.29 refer to the robotic manipulator depicted in Figures 4.37 and 4.38.
- Problem 4.28 Calculate the angular momentum of the 0 frame of link 1, the inner arm, shown in Figures 4.37 and 4.38 about its own center of mass. Express your answer in terms of a frame that has its origin at the center of mass and that is parallel to the 1 frame.
- Problem 4.29 Calculate the angular momentum in the 0 frame of link 2, the outer arm, shown in Figures 4.37 and 4.38 about its own center of mass. Express your answer in terms of a frame that has its origin at the center of mass and that is parallel to the 2 frame.
Problems 4.30,4.31, and 4.32 refer to the robotic manipulator depicted in Figures 4.39 and 4.40.
- Problem 4.30 Compute the angular momentum in the 0 frame of link 1, the vertical arm, shown in Figures 4.39 and 4.40 about its own center of mass. Express your answer in terms of the basis for frames 1 and 0.
- Problem 4.31 Compute theangular momentum in the 0 frame of link 2, the horizontal arm, shown in Figures 4.39 and 4.40 about its own center of mass. Express your answer in terms of the basis for frames 2, 1 and 0.
- Problem 4.32 Compute theangular momentum in the 0 frame of link 3, the tool carriage, shown in Figures 4.39 and 4.40 about its own center of mass. Express your answer in terms of the basis for frames 4, 3, 2, 1 and 0.
4.9.5 Problems on the Newton–Euler Equations
- Problem 4.33 Frame
 is fixed in the outer link and frame
is fixed in the outer link and frame  is fixed in the inner link of thespherical joint shown in Figure 4.45. What are the constraints on the displacement and rotation imposed by the spherical joint on the bodies having fixed frames
is fixed in the inner link of thespherical joint shown in Figure 4.45. What are the constraints on the displacement and rotation imposed by the spherical joint on the bodies having fixed frames  and
and  ? How many degrees of freedom does the spherical joint have? Draw consistent free body diagrams for the spherical joint.
? How many degrees of freedom does the spherical joint have? Draw consistent free body diagrams for the spherical joint. 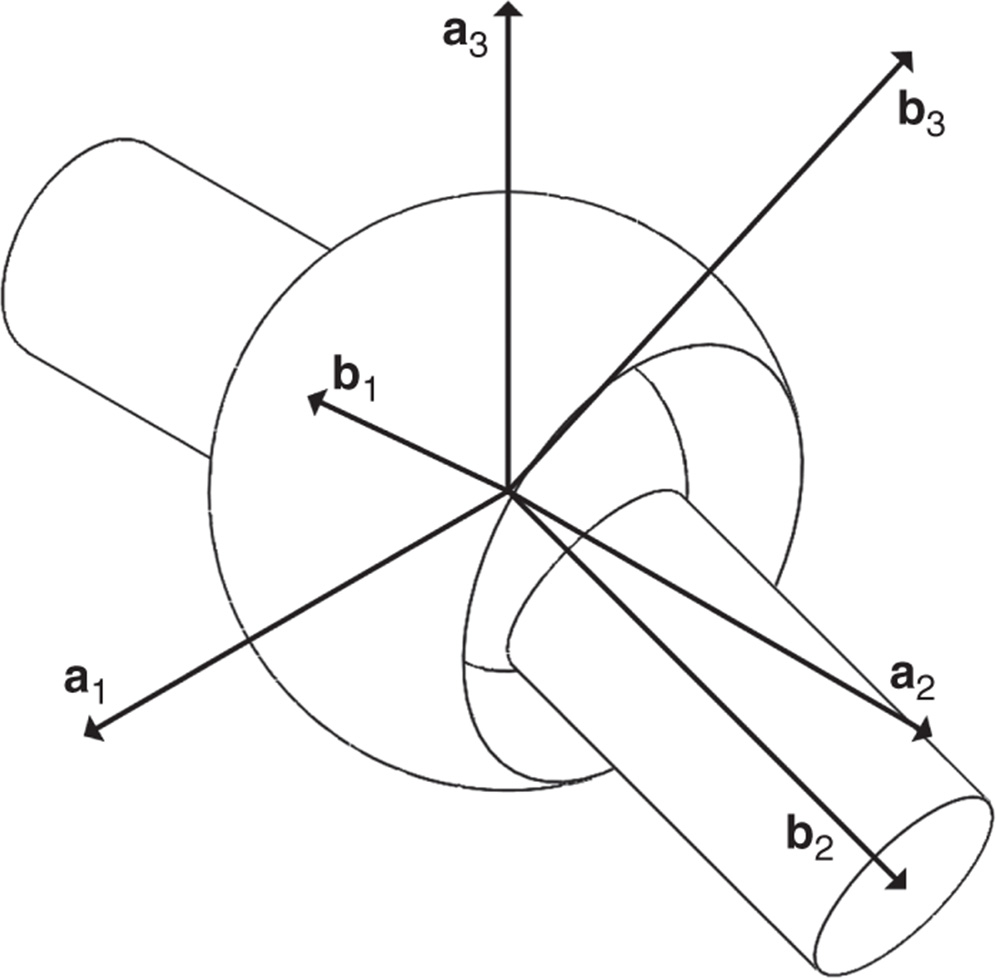
Figure 4.45 Spherical joint frames. - Problem 4.34 Theuniversal joint shown in
Figure 4.46 is comprised of a yoke with body fixed frame
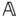 , a yoke with body fixed frame
, a yoke with body fixed frame 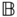 , and the crossbar with body fixed frame
, and the crossbar with body fixed frame 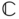 . Draw a set of complete free body diagrams for three components that make up the universal joint. Then, assume the mass and inertia matrix of the cross bar are negligible and derive an equivalent set of free body diagrams that eliminate the crossbar. How many degrees of freedom does the universal joint have?
. Draw a set of complete free body diagrams for three components that make up the universal joint. Then, assume the mass and inertia matrix of the cross bar are negligible and derive an equivalent set of free body diagrams that eliminate the crossbar. How many degrees of freedom does the universal joint have? 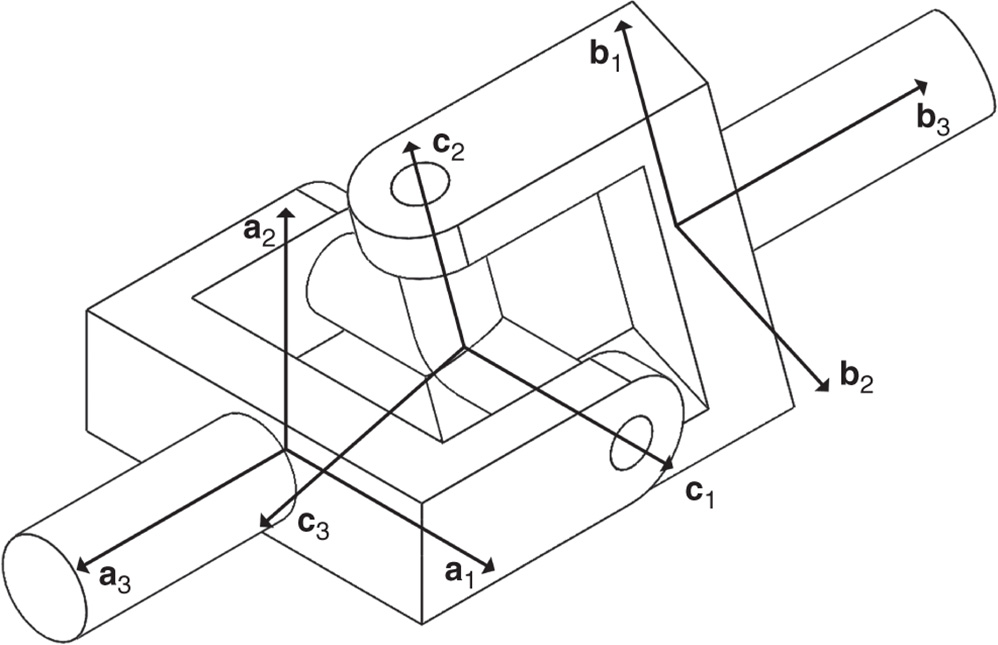
Figure 4.46 Universal joint frames. - Problem 4.35 Use the results of Problem 4.3 to write Euler's first law for link 3, the outer arm, of the PUMA robot in Figure 4.35.
- Problem 4.36 Use the results of Problem 4.6 to write Euler's first law for link 3, the tool carriage, for the SCARA robot in Figure 4.37.
- Problem 4.37 Use the results of Problem 4.7 to write Euler's first law for link 1, the vertical arm, of the cylindrical robot in Figure 4.39.
- Problem 4.38 Use the results of Problem 4.8 to write Euler's first law for link 2, the horizontal arm, of the cylindrical robot in Figure 4.39.
- Problem 4.39 Use the results of Problem 4.9 to write Euler's first law for link 3, the tool carriage, of the cylindrical robot in Figure 4.39.
- Problem 4.40 Use the results of Problem 4.27 to write Euler's second law for link 3, the outer arm, of the PUMA robot shown in Figure 4.35.
- Problem 4.41 Use the results of Problem 4.30 to write Euler's second law for link 1, the vertical arm, of the cylindrical robot in Figure 4.39.
- Problem 4.42 Use the results of Problem 4.31 to write Euler's second law for link 2, the horizontal arm, of the cylindrical robot in Figure 4.39.
- Problem 4.43 Use the results of Problem (4.32) to write Euler's second law for link 3, the tool carriage, of the cylindrical robot in Figure 4.39.
- Problem 4.44 Write Euler's second law for link 2, the inner arm, of the robot in Example 4.17, taking moments about point
 instead of the mass center of the arm. Note that the point
instead of the mass center of the arm. Note that the point  is not fixed in the inertial frame in this problem.
is not fixed in the inertial frame in this problem. - Problem 4.45 Write Euler's second law for link 1, the shoulder, of the robot in Example 4.17, taking moments about the point
 . Note that the point
. Note that the point  is fixed in the inertial frame.
is fixed in the inertial frame.