Chapter 1
Introduction

In this chapter the collection ofrobotic systems that are studied in this book are introduced. The field of robotics embraces topics requiring expertise in a number of technical disciplines including mechanical engineering, electrical engineering, computer science, applied mathematics, industrial engineering, cognitive science, psychology, biology, bio‐inspired design, and software engineering. Moreover, the family of robotic systems that can be designed and fabricated today is growing rapidly. Reasons for this trend are based in economics and the maturity of the technological infrastructure supporting robotics. A wide variety of sensing and actuation technologies that are portable, compact, and inexpensive are now readily available. These building blocks can be used to construct a plethora of robotic systems using commercial off‐the‐shelf technology. The broad scope of the robotics field precludes a comprehensive theoretical summary of the disciplines relevant to all of these diverse systems being given. Instead, this text specifically deals with the construction of models of the kinematics and dynamics of typical robotic systems, and the derivation of control strategies for these systems. Upon completion of this chapter, the student should be able to:

1.1 Motivation

Over the past few decades, the robotic systems that undergraduate and graduate students are expected to be able to design and analyze has expanded dramatically. It is now commonplace in varying engineering disciplines to ask relatively inexperienced engineers and researchers to design, analyze, and construct prototypical robotic systems. Students may encounter such challenges in either undergraduate or graduate design projects, or immediately upon taking a job in industry or at a national laboratory. Projects may be as varied as the development of a computer controlled, multi‐axis stage for positioning of laser Doppler vibration measurements, the development of a flapping wing autonomous flight vehicle, the modification of a commercial vehicle for autonomous operation, or the development of a humanoid robot. The diversity and complexity of this list continues to grow every year.

While the study of robotics has been popular for several decades, the recent rapid expansion of robotic systems in commercial markets can be attributed in part to the fact that sensors and actuators have become increasingly cost effective, modular, and portable. This trend has lead to the emergence of the field ofmechatronics, which has played a key role in the spread of robotics technologies. Mechatronics is a multidisciplinary field of study that integrates aspects of mechanisms, electronics, computer hardware/software, systems theory, and information technologies into a unified practical design methodology. The fusion of these topical areas that define the study of mechatronics is depicted in Figure 1.1. A key feature of mechatronic systems is that they often feature built‐in intelligence that is applied to the task for which they are designed.

Depiction of fields of expertise associated with mechatronics.

Figure 1.1 Fields of expertise associated with mechatronics.

Although the range of mechatronic systems is vast, there are features common to most, if not all, such systems. Figure 1.2 illustrates a schematic drawing of signal flow for a typical mechatronic system. Computer systems connect the mechatronic system to sources of intelligence, be it user inputs/outputs to include humans in the operation and/or algorithms to interpret sensor data and make decisions for the mechatronic systems. The electrical system conditions signals passing between the computer and mechanical systems, along with regulating the electrical power provided to the mechatronic system. The mechanical systems consist of the physical system(s) that interact with their environment. Commands from the digital computer systems to the analog electrical systems pass through adigital‐to‐analog converter, and these commands are implemented on actuators connecting the electrical and mechanical systems. Sensors integrated into the mechanical systems generate signals passed to the electrical systems, and these signals (after conditioning) are communicated to the computer systems through ananalog‐to‐digital converter.

Mechatronics is elevated to a field distinct from its contributing fields by the need to balance consideration of mechanical, electrical and information technology factors when designing an overall system. Assessing the signal processing and algorithmic requirements for operating a physical system, and meeting these requirements intelligently and efficiently, distinguishes mechatronics as a unique discipline and not simply an exercise in hardware connectivity. While some systems may require complex multi‐core processors to operate in real time, others may simply require a simple embedded controller. Interested readers can refer to the following textbooks for a more in‐depth study of mechatronics as an integrating approach to engineering design [1,8,11].

Illustration of structure of a typical mechatronic system.

Figure 1.2 Structure of a typical mechatronic system.

As the robotics infrastructure has matured, expectations of students in the field of robotics has correspondingly increased. A decade ago a beginning student might have been asked to create a simple two‐dimensional model of a robotic system. Older textbooks are filled with such introductory problems that serve to familiarize students with the fundamentals. However, technical tools and analytical skills are now required that facilitate modeling of robot kinematics and dynamics in three spatial dimensions.

Fortunately, the tools that are applicable throughout the design and analysis process have also evolved and matured. A few years ago, the computational tools available for the systematic design, analysis, and study of complex robotic systems were limited in number. At that time a student faced with the creation of a detailed model of a realistic robotic system was confronted with a daunting task. The determination of the kinematics and dynamics of robotic systems via hand calculation was a lengthy and tedious job for all but the simplest cases. Once the heroic effort of deriving a formulation was complete, the student was faced with coding the governing equations in a low level programming language such as C or Fortran. It is no exaggeration that the time involved in this task could be measured in months, or worse, years, of effort.

Now, two separate and complementary collections of commercial software packages make this problem much more manageable. First, there is an ever expanding list of specialized three dimensional modeling programs such as

  • Autodesk Inventor
  • SolidWorks
  • Pro Engineer
  • MSC Adams
  • LabView

that are available for building highly detailed and general models of the kinematics, dynamics, and control of robotic systems. These packages vary in the generality of their simulation capabilities, but all allow numerical approximation of the solutions of the forward kinematics and dynamics problems. Some also incorporate programming interfaces for the introduction of user‐defined controls. These software packages can be expensive to purchase. However, most universities have software contracts with the vendors of these packages. Most large engineering firms or government laboratories also have licenses for a portfolio of these analysis programs. Many of the more complex examples in this book have been modeled by students under an academic license for Autodesk Inventor.

As useful as the programs above can be, sometimes greater flexibility is needed in formulating the governing equations of dynamics or in deriving a control architecture for a robotic system. As an example, when a model is created for the purpose of constructing a controller for a specific robot system, a symbolic set of equations for hardware implementation is often required. Some programs have the option of explicitly generating symbolic code that is suitable for hardware implementation. It should be noted that the packages listed above vary dramatically in the ways that they handle code generation. There is currently a highly competitive market of software tools to download controller equations to specific hardware platforms. Still, it is often the case that a standard commercially available software simulation tool, such as those listed above, does not allow the flexibility that a practicing control engineer requires. It can also be the case that an analyst wants to implement a controller in terms of a highly efficient algorithm, like the recursive formulations discussed in Chapters or . These algorithms may not be supported by a specific commercial software package. It should come as no surprise that no matter how well a commercial package is designed, a user will often desire some functionality that is not available.

In such cases, the software packages that support symbolic computation can be used to great advantage. These are general purpose, object‐oriented, high level programs that define their own computing languages. Examples include:

  • MATLAB
  • Mathematica
  • Mathcad
  • Maple

Each of these software programs has developed its own object oriented, high level language that performs calculations on a large number of different types of mathematical objects. For example, they usually have a large library of operators based on linear algebra, signal processing, and calculus. The mathematical objects may be matrices and vectors, or they can be discrete dynamical systems, or they might take the form of systems of ordinary differential equations. A few lines of code in the language of these packages can replace thousands of lines of code in a low level programming language like C, C++ or Fortran. Perhaps most importantly for this text, each of these programs has a syntax that enables symbolic computation. This is a computing engine that incorporates most well known operations defined in differential or integral calculus. For the most part, tedious operations can be performed using these symbolic variables with minimal input from the analyst. Both public domain and commercial packages designed expressly for the study of robotic systems have been written in several of these computing languages. This text makes extensive use of some of these packages in solving the examples in the text and the problems at the end of each chapter. In many cases the solutions of the problems are carried out by writing general purpose programs that address fundamental robotics problems; a family of high level functions that solve core robotics problems are provided with the solutions for this text.

1.2 Origins of Robotic Systems

Robotic systems have been traced historically to efforts by early artists, artisans, craftsmen, engineers, and scientists to create machines that mimic humans in action or reasoning. The modern notion of a robotic system emerged as society sought to create surrogates that can replace human labor in jobs that are menial, tiresome or even dangerous. Even before industrial robots became commonplace, the potentially transformative role of automatons in the workplace was imagined. The role of robots as factory workers has been noted repeatedly over the years. The word “robot” was coined by the Czech writer Karel Capek in the playRossum's Universal Robots published in 1920. Capek wanted to describe the repetitive and boring nature of robotic tasks. The word “robot” originates from the Czech word “robota” which means “work” or “forced labor”. The play studied moral questions arising in the creation and use of digitally programmed slaves. This has been a recurring theme in novels, plays, and movies. For example, the novelist Kurt Vonnegut explores the angst and disillusionment of a society with the displacement of human workers by automation in the more recent novelPlayer Piano.

Despite these cautionary tales, robots have proliferated as a means of replacing human labor in adverse environments. The first reprogrammable digitally controlled robot was created in 1954 by George Devol. This robot,Unimate, was an industrial manipulator having a spherical workspace and was used to lift and move heavy production parts in a factory setting. It was purchased by General Motors in 1960 and was the forerunner of the large collection of industrial robots that are now commonplace along modern factory assembly lines. Demands on performance have been a driving force in the use of robotics in industry. The load capacity, repeatability, precision, and speed afforded by modern robotic systems far exceed the capabilities of man.

Current definitions of what constitutes a robotic system vary dramatically, but all definitions convey the idea that robots perform menial or repetitive tasks. Merriam‐Webster's Dictionary defines a robot as

  • a machine that looks like a human being and performs various complex tasks, or
  • a device that automatically performs complicated often repetitive tasks.

The first definition above requires that robots appear to be humanoid, and while some robotic systems do indeed have a humanoid appearance, this definition would exclude many of the robotic systems in this book. A critical attribute of robotic systems that this definition omits, one that is important to engineers and scientists who actually build robotic systems, is that robots are controlled by computers. This fact is made explicit in the Cambridge Dictionary which defines a robot as

  • a machine used to perform jobs automatically, which is controlled by a computer.

Some definitions of robots have arisen in view of the historical concentration of robots in factories and along assembly lines. The Robotics Institute of America defines a robot as

  • a reprogrammable, multi‐functional manipulator designed to move material, parts, tools, or specialized devices through various programmed motions for the performance of a variety of tasks.

This definition focuses on the robot as amultifunctional manipulator orrobotic arm, but neglects a wide range of mobile robots designed to explore and map environments without the need for a manipulator to interact with these environments.

All of the definitions of robots above are accurate in some contexts, but do not describe the breadth of systems that will be considered in this book. The definition of a robotic system that will be used in this book is given below.

This definition expands those previously introduced and is broad enough to encompass the examples encountered in this book. A robot need not have humanoid form, and it does not necessarily have the form of a multi‐functional manipulator. The above definition emphasizes that robotic systems exhibit some level of autonomy. They operate, to varying degrees, independent of human intervention. They have sensors such as cameras, laser ranging sensors, acoustic proximity sensors, or force transducers that allow them to sense their environment via measurements. This data is subsequently used by the robot to react to its environment. For example, an autonomous ground, air, marine, or space vehicle may change course to avoid obstructions or debris; a dexterous manipulator may change the pressure with which a tool is gripped based on force transducer measurements; a robotic manipulator may use camera measurements to position a tool in the workspace. Finally, the definition makes explicit that a robot is a mechanical system, one that is built from the interconnection of components.

In summary, a robotic system is made possible through the synthesis of theory and techniques from many fields, perhaps most notably mechanical engineering, electrical engineering, and information technology. The field of mechatronics facilitates and enables the development of complex robotic systems from standard sub‐systems and has accelerated the maturation of the robotics field in recent years. This relationship among some of the primary fields contributing to robotics is depicted in Figure 1.3.

Illustration of fields contributing to robotics.

Figure 1.3 Fields contributing to robotics.

1.3 General Structure of Robotic Systems

As will be discussed in the following sections, there are a diverse population of robots that have been developed over the years, ranging from robotic manipulators to mobile robots that traverse the air, land, or sea. These robots may emulate humans or animals, or have novel topologies to accomplish desired tasks. However, despite these differences, there are some common features that many robots share that are discussed in this section.

Figure 1.4 depicts several components of a typical robotic system. Nearly all robotic systems featureactuators. The actuators serve as the muscles of the system and produce motion. Their power is usually supplied electrically, pneumatically, or by hydraulics. Since many robots are either controlled remotely or make provision for interruptions to their autonomous operation from outside agents, many robots include acommunicator of some sort. The communicator is a unit that transmits information to a host and/or receives instructions from a remote operator. As noted earlier, an essential feature of any robot is that it exhibit some level of autonomy or intelligence. Acontrol unit is a vital component of nearly all robotic systems. It may consist of a single processor, or may be a central computer that integrates the activities of several microprocessors. Many robotic manipulator systems, underwater autonomous vehicles, or space robots must directly mechanically manipulate their environment. Anend effector that consists of agripping device at the end of a manipulator arm can therefore be essential to the operation of the robot. The end effector can be used to make intentional contact with an object or to produce the robot's final effect on its surroundings. In some cases there may be several manipulator arms or gripping mechanisms. Since a robot must interact with its environment, and usually lacks much information about its surroundings, many robots also includesensor suites that include a variety of sensing modalities. Eachsensor is usually a transducer of some kind whose inputs are physical phenomena and whose outputs consist of electronic signals. Finally, since mobility, sensing and actuation require energy expenditure, a robot must have apower supply of some type. Most frequently this is an energy storage device such as a battery. In some instances the robot may be tethered to a fixed power supply. For example, a military or industrial exoskeleton may require so much power that it is only feasible to connect to a remote local power supply while the suit is worn in a warehouse to move heavy payloads.

Picture of typical mobile robotic system components

Figure 1.4 Typical mobile robotic system components [4–6].

Any particular robotic system may include many of these components, or simply a few in each category. An autonomous military ground vehicle will usually host a wide variety of vision sensors, motion sensors including a ground positioning system (GPS) and compass, thermal sensors, and chemical sensors. A simple table top robotic manipulator in a laboratory might only have joint encoders to sense motion. Figure 1.5 illustrates a typical robotic manipulator that might be suitable for a laboratory benchtop. The figure emphasizes the data flow within the robotic system. In this system, the robot is usually equipped with rotary encoders that return measurements of angular motion at the joints to the controller and computer. In this particular system, a vision or laser tracking sensor is also configured to provide measurements of the end effector position and velocity. This measurement is returned to the computer to assist controlling the position tracking of the end effector along a desired trajectory. It should also be noted that this figure, while giving a general picture of the topology and connectivity of a robotic system, lacks many details that are necessary for a real robotic system. For example, the motor controllers are not shown in the figure, nor are the amplifiers or signal conditioners that may be required between the primary components.

Illustration of typical robotic manipulator system components.

Figure 1.5 Typical robotic manipulator system components.

1.4 Robotic Manipulators

An important type of robotic system that is studied often in this text is therobotic manipulator orrobotic arm. Robotic systems of this kind were some of the first to achieve widespread use in industry. As noted in the previous section, robotic manipulators have become a standard feature of modern assembly lines. They perform a host of tasks including welding, spraying, pick and place operations, drilling, cutting, and lifting. Many of the analytical techniques, modeling methodologies, and control strategies introduced in this text are demonstrated on examples that treat robotic manipulators. The reasons for this choice are numerous. Robotic manipulators are some of the simplest examples of practical robotic systems. Their study helps clarify the underlying principles and problems encountered when studying more complex systems. Although an autonomous marine vehicle may not resemble a robot on an assembly line, the general form of the mathematical problem that must be solved to control these two types of systems can be surprisingly similar. The same is true for modeling and control of autonomous ground or air vehicles. General methodologies applicable to one system can often be a starting point for the development of models and controllers for others. Moreover, it is often the case that a sub‐system of an autonomous robotic system can be modeled or controlled using techniques developed for robotic manipulators. For example, the arms or legs of a humanoid robot or an imaging payload that actively controls the line of sight of a camera on an autonomous air vehicle may be modeled using techniques from robotic manipulators.

1.4.1 Typical Structure of Robotic Manipulators

Many robots consist of a number of individual bodies orlinks that are connected byjoints. The individual bodies that make up the robot are often treated as rigid bodies, and that is the assumption throughout this text. However, for high speed or highly loaded mechanisms, elastic effects of the material body become significant and should be taken into consideration. The joints that connect the links in the robot can be quite complex and may themselves exhibit highly non‐trivial mechanics including flexibility, hysteresis, backlash, or friction. An ideal joint is an interconnection between rigid bodies of a robotic system that allows only specific, predefined relative motions such as translation or rotation. Mathematically, an ideal joint imposes a kinematic constraint on the motion between rigid bodies that is based on the joint geometry. Common types of ideal joints include revolute, prismatic, universal, spherical or screw joints. Figure 1.6 depicts a few of these ideal joints and summarizes some of their properties.

Illustration of ideal joints and their properties.

Figure 1.6 Ideal joints and their properties.

The two simplest types are the prismatic joint or revolute joint. Nearly all of the robotic systems studied in this text consist of these two types. Many of the other types of ideal joints can be modeled by combining these two. For example, a universal joint consists of a pair of revolute joints with their joint axes orthogonal to one another. A prismatic joint allows only relative translation between two links along a prescribed axis, while the revolute joint permits only relative rotation about a prescribed axis.

An independent variable that is used to describe the motion of a robot, or the relative motion allowed by an ideal joint, is often called adegree of freedom. The number of degrees of freedom of an ideal joint is the number of independent variables required to model the relative motion that the joint permits. A robot has images degrees of freedom if it requires images independent variables to describe all of its possible configurations. The revolute and prismatic joints are consequentlysingle degree of freedom joints. If the joint constraints are independent of one another, the number of degrees of freedom images for a general mechanism can be calculated as

(1.1) equation

where images is then number of links, images is the number of joints, and images is the number of degrees of freedom for joint images . For planar mechanisms images and for spatial mechanisms images .

More details on the properties of the ideal joints are presented in Chapters and . Precise mathematical definitions of the degrees of freedom for mechanical systems, and robots in particular, are discussed in Chapter .

1.4.2 Classification of Robotic Manipulators

Now that the basic definitions of links, joints, and degrees of freedom for typical robotic manipulators have been defined, a summary of different ways in which robots are classified is provided. Again, although this discussion focuses on robotic manipulators, some of the classifications are pertinent to other classes of robots. For example, classification of robots by driver technology and drive power applies equally well to all types of mobile robots whether they operate in the air, on land, under water, or on the water's surface.

1.4.2.1 Classification by Motion Characteristics

One of the most common means of differentiating among different robot architectures considers motion characteristics. Aplanar manipulator is one in which all the moving links in the mechanism perform planar motions that are parallel to one another. In contrast, aspatial manipulator is one in which at least one of the moving links demonstrates a general spatial motion. In other words images in Equation (1.1). In some cases the manipulator is constructed so that only very specific kinds of motion are possible. Aspherical manipulator is constructed so that the moving links perform spherical motions about a common stationary point. Acylindrical manipulator is constructed so that the end effector travels on the surface of a cylinder. More details of these two types of manipulators are discussed in Sections 1.4.3.2 and 1.4.3.4.

1.4.2.2 Classification by Degrees of Freedom

Another means of classifying robots is based on the number and type of degrees of freedom. Ageneral purpose robot possesses images degrees of freedom if it is a planar robot or images degrees of freedom if it is spatial robot. A robot isredundant if it posses more than images degrees of freedom. A redundant robot can be used to move around obstacles and operate in tightly confined spaces. A robot isdeficient if it has less than images degrees of freedom.

1.4.2.3 Classification by Driver Technology and Drive Power

Robots are often characterized by the nature and type of their drive technology. Anelectric robot employs DC servo motors or stepper motors. These robots have the advantage that they are clean and relatively easy to control. Ahydraulic robot is preferred for tasks that require a large load carrying capacity. Care and maintenance is required to handle leaks and fluid compressibility problems. For high speed applications, apneumatic robot is often preferred. These robots are generally clean, but can be hard to control due to challenges associated with air compressibility.

Adirect drive manipulator is one in which each joint is driven directly by an actuator without any torque transmission mechanism. These drives can be bulky and heavy but do not exhibit backlash or drive flexibility, which can render robotic control more difficult. Finally, aconventional manipulator generates a driver torque that is magnified by a transmission mechanism. Usually this is achieved via gear reduction or by a harmonic drive unit. This design allows the use of smaller actuators. However, the gear mechanisms suffer from backlash, and the harmonic drives inherently exhibit flexibility effects.

1.4.2.4 Classification by Kinematic Structure

Kinematic structure is a topic of great importance to robotics and is yet another means that can be used to classify different types of robots. The kinematic structure of a robot results from itssystem connectivity. This topic has been studied extensively in multibody dynamics and has had a profound impact on robotics. The study ofmultibody dynamics is closely related to robotics, and strong references for the basic theory can be found in [14,46,24]. Many of the results discussed in this book can be considered as special cases within the general study of multibody dynamics. Generally speaking, the field of robotics is usually more concerned with problems of forward kinematics, inverse kinematics, or control synthesis, and the field of multibody dynamics tends to focus more on the study of numerical methods for approximations of the solution of the forward dynamics problem. It has been known for some time in the field of multibody dynamics that theconnectivity topology of a system can have a dramatic influence on the complexity of simulating or deriving a control strategy for a system.

A robotic system is said to have the connectivity of akinematic chain if there is one and only one connected path that traverses a system from the first to the last link. Such a robot is also often referred to as aserial manipulator or as aopen loop manipulator in the robotics literature. A single arm or leg of a humanoid robot is a good example of a kinematic chain. Multibody systems that form a kinematic chain have the simplest connectivity topology. It is this class of robotic systems for which the richest collection of formulations and control strategies have been derived. The kinematics of chains is studied carefully in Chapter , their dynamics is studied in Chapters and , and their control is the topic of Chapters and .

A multibody system is said to havetree topology connectivity when it is built from an assembly of kinematic chains and no closed loops are formed by their interconnection. A full body humanoid robot or a space station in orbit are two familiar examples of systems having a tree topology connectivity. It is relatively straightforward to extend the techniques for modeling and control of kinematic chains to treat systems that have tree topology connectivity, although such methods must often be extended to account for the rigid body motion of the robotic system as a whole.

Finally, a robotic system is said to haveclosed loop connectivity whenever it is possible to construct a continuous path that starts at one link, traverses several other links, and finally connects to the original link. The multibody model of an autonomous ground vehicle is an example of a system that has closed loop topology if its suspension system has closed loops. Two robotic manipulators that cooperate in the task of lifting a large payload also form a system that has closed loop topology. The Stewart platform depicted in Figure 1.8 is a common robotic platform that has closed loop connectivity.

Robotic manipulator systems with closed loop connectivity are commonly referred to asparallel manipulators in the field of robotics. General robotic systems that have closed loop topology are not addressed in this introductory book.

Of course, some systems are constructed from sub‐systems that constitute both open and closed loop chains. In some industrial manipulators, such as the Fanuc S‐900W, a four‐bar push‐rod linkage is used to drive the intermediate joints, which in turn are mounted on the robot base or waist. This design reduces the inertia of the manipulator. Such a system, which contains both open and closed loop chains as sub‐systems, is known as ahybrid manipulator.

Picture of industrial Stewart platforms.

Figure 1.8 Industrial Stewart platforms.

In summary, robotic systems that have the form of a kinematic chain are the most basic; other more complicated robotic systems can be assembled from them. Methods for analyzing, simulating, or synthesizing a controller for kinematic chains can be applied to sub‐systems having more complex connectivity. Robotic manipulators serve as prototypical examples of robots that form kinematic chains.

1.4.2.5 Classification by Workspace Geometry

The last method for classifying the robots discussed looks at theirworkspace geometry. Themanipulator workspace is the volume of space that the end effector can reach. The set of points where every point can be reached by the end effector in at least one orientation or pose is thereachable workspace. The set of points where every point can be reached by the end effector in all possible orientations or poses is called thedextrous workspace. By definition, it follows that the dexterous workspace is a subset of the reachable workspace. It should be noted that most industrial serial manipulators are designed with their first three moving links longer than the remaining links. These inner links are used primarily for controlling the end effector position. The remaining outboard links are used typically for controlling the end effector pose or orientation. Often, the sub‐assembly associated with the first three links is denoted the arm, and the remaining outboard links constitute the wrist. Figure 1.9 shows four common types of workspaces.

Illustration of various workspace geometries.

Figure 1.9 Various workspace geometries.

1.4.3 Examples of Robotic Manipulators

In the next few sections a few of the most common robotic manipulators are described. All of these examples consist of a few links joined by either prismatic joints or revolute joints. These joints can be either driven or passive.

A driven joint is one in which an actuator directly generates motion, either translation (prismatic joint) or rotation (revolute joint). In a driven joint, a linear or rotational motor is connected to each link constrained by the joint. If a joint is not driven by an actuator, it is said to be a passive joint. For example, in the pantograph shown in Figure 1.7, assume the two prismatic joints (J1 and J2) are controlled by linear actuators. These are thus driven joints. The remaining revolute joints (J3–J8) are now passive joints, as the motion between the bodies at these joints is prescribed by the motion of the two active joints.

Usually, the manipulators are designated by a sequence such as PPP or RPP that indicate the type and ordering of the prismatic (P) and revolute (R) joints that make up the robot. For example, a PPP robotic manipulator is constructed from three prismatic joints, while an RPP robot is built from a revolute joint that is followed by two successive prismatic joints. This designation is often a good indicator, in broad terms, of the general geometry and functionality of a robotic manipulator.

1.4.3.1 Cartesian Robotic Manipulator

ACartesian robot is aPPP manipulator defined by three mutually orthogonal prismatic joints. Figure 1.10 depicts a typical example. The PPP arm is one of the simplest robotic manipulators. This type of multi‐functional arm is sometimes called a gantry or a traverse, depending on the context in which it is used. A gantry is usually a suspended version of a Cartesian robot used for positioning large industrial payloads. A traverse is often used for positioning optical experiments or surgical tools. A PPP manipulator has several advantages owing to its simple geometry. Models for PPP robots are easy to derive, as are the control laws that are used to position and move these robots. The simplest models for PPP manipulators have equations of translational motion along three perpendicular directions that are decoupled. Since no rotational degrees of freedom are included in a Cartesian robot, these systems tend to be rigid or structurally stiff. They can sustain and deliver large loads and achieve high precision in positioning. One drawback of this robot is that it requires a large area in which to operate, and the workspace is smaller than the robot itself (Figure 1.9). Another drawback is that the guides for the prismatic joints must be sealed from foreign substances, which can complicate maintenance.

Picture of Cartesian robot by the Sepro Group.

Figure 1.10 Cartesian robot by the Sepro Group. http://www.sepro-group.com.

1.4.3.2 Cylindrical Robotic Manipulator

Suppose the first prismatic joint in the Cartesian robot is replaced with a revolute joint. By making a judicious choice of the direction of the axis of rotation, the resulting RPP robot is an example of a cylindrical robot. One example of a cylindrical robot that is analyzed in this text is depicted in Figure 1.11. It is easy to see that the location of the end of the horizontal arm in the cylindrical robot can be expressed in terms of cylindrical coordinates, which gives this robot its name. Its workspace takes the form of a hollow cylinder. Again, this manipulator has several advantages owing to its structural simplicity. While the kinematic and dynamic models of a cylindrical manipulator are more complex than that of a Cartesian robot, they are still simple to derive. The associated control laws are likewise quite straightforward to determine. The topology of the RPP manipulator makes it well suited for reaching into work pieces that have cavities or other similar complex geometries. It can achieve high precision and is used for pick and place operations on an assembly line. One disadvantage of this type of robot is that the back of the robot can protrude into the workspace in some configurations. This can cause interference with the workspace and complicates path planning and control. As in any robot that uses prismatic joints with external guides, the guide surfaces must be clean and free of debris. This can make upkeep and maintenance more difficult.

Picture of cylindrical robot by ST Robotics.

Figure 1.11 Cylindrical robot by ST Robotics. http://www.strobotics.com/index.htm.

1.4.3.3 SCARA Robotic Manipulator

The SCARA (selective compliance articulated robot arm) RRP robot was introduced as a compromise between highly rigid robots such as the Cartesian robotic manipulator and robots that can access geometrically complex workspace s such as the spherical manipulator. One example of this robot is shown in Figure 1.12. Since the axes of the two revolute joints are parallel in a SCARA robot, this robot is relatively compliant in motion that occurs in the horizontal plane and relatively stiff in motion normal to this plane. The variation in compliance between these two modes of motion gives this robot its name. The workspace of this robot is highly structured. The SCARA manipulator can be an attractive robot for precision pick and place operations, for example.

Picture of Epson SynthisTM T3 all-in-one SCARA robot.

Figure 1.12 Epson SynthisTM T3 all‐in‐one SCARA robot. http://www.epsonrobots.com.

1.4.3.4 Spherical Robotic Manipulator

The RRP spherical robotic manipulator is formed from two perpendicular revolute joints and a prismatic joint. For some choices of the fixed offset dimensions between the joints, the motion of the tool or tip of the manipulator arm can be expressed in terms of spherical coordinates, which gives this robot its name. Some of the most famous robotic manipulators that have appeared over the years have been of this type. The Unimate robot discussed in Section 1.2 and shown in Figure 1.13 is an example of a spherical manipulator.

Picture of unimate spherical robot.

Figure 1.13 Unimate spherical robot.

The primary advantage of this robot architecture is its suitability to a wide range of tasks that must be carried out over complex geometries. The spherical workspace accessible by this robot is large compared to the robot size. Unfortunately, this flexibility comes at a cost. The kinematic and dynamic models of the spherical robot are more complicated than those for Cartesian or cylindrical manipulators, which leads to control laws that are likewise more complex. The introduction of an additional perpendicular axis of rotation yields a robot that is less rigid and more compliant than the Cartesian manipulator. The result is that the spherical robot can be less precise in positioning. Generally speaking, a spherical robot can be more appropriate for tasks such as welding or painting that require somewhat less precision than pick and place operations, but require accessibility over a large and complex workspace.

1.4.3.5 PUMA Robotic Manipulator

Historically, one of the most widely used robotic manipulators on assembly lines is the PUMA (Programmable Universal Machine for Assembly) RRR robot. An example of a PUMA robot is depicted in Figure 1.14. The first revolute joint of this robot is about the vertical axis, and the next two parallel revolute joints are perpendicular to the vertical axis. The widespread use of the PUMA robot can be attributed to the fact that it has a rich kinematics and can access a large hemispherical workspace. With the introduction of three rotational axes along two perpendicular directions, however, the PUMA is less rigid than the Cartesian robot. It is well suited to applications that require a large and highly reconfigurable workspace.

Picture of PUMA Robot.

Figure 1.14 PUMA Robot.

1.4.4 Spherical Wrist

The previous section presented variants of the PPP, RPP, RRP, and RRR robotic arms and gave an overview of some of their advantages. The spherical wrist is an RRR robotic component that often appears as a sub‐system that is attached to these more complex manipulators. Figure 1.15 illustrates the spherical wrist in detail. The wrist is built from three revolute joints whose axes of rotation intersect at a common point, the wrist center. The anthropomorphic arm in Figure 1.16 is similar: a spherical wrist sub‐system is connected to the end of the arm. Not only does this design resemble human anatomy, it has an important pragmatic implication for control design. This common geometry is attractive in that it makes it possible to decouple the task of positioning the wrist center and orienting the tool at the end of the spherical wrist. This topic is discussed in Chapter when inverse kinematics is covered.

Illustration of spherical wrist.

Figure 1.15 Spherical wrist.

1.4.5 Articulated Robot

The articulated robot arm or anthropomorphic robot arm is a manipulator that is able to achieve motions that resemble those of the human arm. All anthropomorphic robot arms have at least three revolute joints, and it is common that they have five, six, or more, revolute joints. A typical configuration is depicted in Figure 1.16 where a spherical wrist has been attached to an RRR robotic arm. Note that the first three degrees of freedom resemble that of the PUMA robot studied in Section 1.4.3.5. The first, vertical revolute joint permits the motion that is sometimes known as the arm sweep. The next two joints are referred to as the shoulder and elbow joints, respectively. The result is an arm that can access a large workspace, and it can pose the tool located at its tip at an arbitrary orientation. The anthropomorphic arm finds widespread use in welding and spraying on assembly lines. In comparison to the other robotic manipulators discussed, this arm does have a complicated geometry. The corresponding equations that describe the kinematics and dynamics of this robotic system are complicated in form, as are the control laws derived from these models.

Picture of articulated robotic arm.

Figure 1.16 Articulated robotic arm. http://www.kuka-robotics.com.

1.5 Mobile Robotics

In the last section several of the most common multi‐functional robotic arms were described. It was noted that they can can vary dramatically in form, operation, and application. This section summarizes another major subset of robotics: mobile robots, including humanoid or full‐body anthropomorphic robot, and autonomous air/ground/marine vehicles.

1.5.1 Humanoid Robots

It was shown in Section 1.4.5 that anthropomorphic or humanoid arms have reached a point of maturity in the robotics field: they are ubiquitous in factories throughout the world. The creation of full‐body humanoid robots, in comparison, remains an area of active research. From the earliest stages in the emergence of the robotics field, designers have dreamed of creating robots that resemble humans in both appearance and function. Early craftsmen and artisans, as well as artists and inventors, sought to create mechanical systems that would emulate human actions. These early researchers included such notables as Leonardo Da Vinci. His early efforts, and those of others, while visionary, met with limited success due to the lack of technological infrastructure. Today, the infrastructure has evolved to the point where current anthropomorphic robots are evaluated in the performance of sometimes surprisingly complex tasks. A good example is the RoboCup international autonomous soccer competition. Since the inception of the humanoid league in 2002, teams that create humanoid robots have come from all over the world to this annual event. Figure 1.17 illustrates one such robot created by student researchers at Virginia Tech under the direction of Professor Dennis Hong, who is now a professor at the University of California, Los Angeles (UCLA).

Picture of humanoid robot for RoboCup soccer competition.

Figure 1.17 Humanoid robot for RoboCup soccer competition. Created by students at Virginia Tech under the direction of Professor Dennis Hong, currently of UCLA.

The complexity of these humanoid soccer players is impressive. Each robotic player must be able to run, walk, kick, and block shots, which are difficult mobility challenges for two legged robots. Each robot must also be capable of image based perception and feature recognition during the course of a match. Finally, the robots must have the onboard processing hardware and software that enables them to predict and react to the play of the game in a strategic and coordinated fashion. Full scale humanoid robots are also currently under development by researchers around the world. While the potential applications are diverse, it is hoped that these full scale robots will have roles in the care of the elderly or in the design and testing of prosthetics. Figure 1.18 shows CHARLI, a full scale humanoid robot also created by students under the supervision of Professor Dennis Hong.

Picture of humanoid robot CHARLI.

Figure 1.18 Humanoid robot CHARLI. Created by students at Virginia Tech under the direction of Professor Dennis Hong, currently of UCLA.

The full complexity of humanoid robot design, analysis, and fabrication far exceeds the scope of this text. This text does, however, show how to develop kinematic models, dynamic models, and control schemes that are applicable to typical subsystems that make up such a humanoid robot. Examples and problems related to the arm or leg assemblies of humanoid robots can be found in Chapters , , , and . Typical research topics for this class of robot that continues to fascinate researchers include the study of the dynamics and control of bipedal locomotion, perception, vision based control, vision based perception, dexterous manipulation, and human–machine interaction.

1.5.2 Autonomous Ground Vehicles

The design, analysis, and fabrication of robotic ground vehicles, or autonomous ground vehicles (AGV) has been carried out in this country and around the world for several years. Most of the autonomous ground vehicles that have appeared over the years fall within the class of research vehicles that have been designed to establish the feasibility of a solution for some specific technical problem in the field of mobile robotics.

Only recently has it become clear that the field of AGV robotics has matured to the point where it is reasonable to expect the appearance of reliable, high performance commercial and military robots in the near future. One reason for optimism is the spectacular success of the DARPA (Defense Advanced Research Projects Agency) Grand Challenge and Urban Challenge competitions that were held between 2004 and 2008. The DARPA Grand Challenge was first held in 2004. After a series of qualification events, robot developers from across the country met at a 142 mile test track in the California desert. While no team completed the entire course in the first year that the event was held, four teams finished the race in 2005. In 2007 the DARPA Urban Challenge was held. This contest required that entry vehicles operate autonomously in an urban environment, reacting to other vehicles in traffic. Figure 1.19 illustrates the AGV Odin. This vehicle was created by students under the direction of Dr. Al Wicks of Virginia Tech and full time researchers at TORC, a company specializing in the creation of autonomous ground vehicles. The vehicle Odin was one of three robotic cars that successfully completed the DARPA Urban Challenge.

Picture of autonomous ground vehicle Odin.

Figure 1.19 Autonomous ground vehicle Odin. Created by students directed by Dr. Alfred Wicks of Virginia Tech and researchers from TORC, www.torctech.com.

Figure 1.20 depicts examples of military ground vehicles, also created by Dr. Al Wicks and TORC, that evolved from the technology derived from the vehicle Odin. The use of autonomous ground vehicles by the military reduces the risk to troops. Contemporary research topics pertinent to AGVs can include autonomous guidance, navigation and control, autonomous exploration and mapping, sensor fusion, estimation and filtering techniques, hybrid AGV design, and active energy management for increased endurance.

Picture of the autonomous remote controlled HMMWV, ARCH.

Figure 1.20 The autonomous remote controlled HMMWV, ARCH. Created by students directed by Dr. Alfred Wicks of Virginia Tech and researchers from TORC, www.torctech.com.

1.5.3 Autonomous Air Vehicles

Over the past five years, it has become commonplace to encounter news on the radio, television, or internet that describes military operations that feature the use of autonomous air vehicles (AAVs). Since, as noted earlier, robots have proliferated historically in jobs that are dirty, dull, or dangerous, it should come as no surprise that they have become a critical part of the military air vehicle inventory.

While present generation drones are remotely piloted and do not make decisions to engage targets autonomously, the do exhibit some autonomy. They react to their environment, for example, as they sense their orientation, heading and position, and as they correct for navigational errors via an autopilot. In this sense, every commercial or military aircraft with an autopilot can be considered a robotic system. By convention, however, AAVs are usually classified as those air vehicles that do not contain a pilot and exhibit some level of mission‐level autonomy. The degree of autonomy exhibited by AAVs increases with each passing year. Current strategic plans make provision for AAVs that engage targets autonomously in the next few decades.

By their nature, AAVs are necessarily more complex than their ground based counterparts. With this complexity comes an increased cost that limits the routine use of autonomous flight vehicles, at least presently. Most examples of AAVs have been fielded by the military of governments all over the world. Despite their expense, applications of robotic air vehicles continue to expand in the commercial sector. Many applications have been identified by government agencies other than the military. Autonomous flight vehicles have been proposed for applications in agriculture, disaster relief, police surveillance, and border security. Figure 1.21 depicts an autonomous helicopter that is being used to conduct geophysical mapping of radioactive sources. This research effort is under the direction of Dr. Kevin Kochersberger of the Unmanned System Laboratory at Virginia Tech.

Picture of autonomous rotorcraft for radiation sensing.

Figure 1.21 Autonomous rotorcraft for radiation sensing. Created by students under the direction of Professor Kevin Kochersberger of Virginia Tech.

One noteworthy trend in this segment of the robotic industry is the increasing number of small air vehicles, or even micro air vehicles, that have been introduced over the past few years. It is now common to find examples of small, fixed wing robotic air vehicles that have a wing span measuring from a few inches to a few feet in length. Figure 1.22 shows the fleet of SPAARO autonomous aircraft that Professor Craig Woolsey at Virginia Tech uses in a variety of research activities. These vehicles support research in applications ranging from automation of commercial agriculture and remote sensing of airborne pathogens to coordinated control of autonomous vehicle teams.

Picture of fleet of SPAARO AAVs.

Figure 1.22 Fleet of SPAARO AAVs. Used in the research program of Professor Craig Woolsey of Virginia Tech.

1.5.4 Autonomous Marine Vehicles

Just as there are significant differences in the design and fabrication of AGVs and AAVs, the development of an autonomous marine vehicle poses its own special challenges. The nature of these obstacles is illustrated in a number of the autonomous surface vehicles (ASVs) and autonomous underwater vehicles (AUVs) that have been developed over the past few years. Consider the task of operating a robotic surface marine vehicle along a river or a coastal region.

Often, some notion of the overall path to be taken is known, but littoral waters can have numerous unforeseen hazards. They must be sensed and avoided during any mission. Obstacles and hazards can be on the surface, at the waterline, or under the surface. For military vehicles, the ability to attack or flee at high speeds is an important capability to have. The task of navigating a vehicle along a partially unknown course, at high speed, defines a control problem of exceptional difficulty. As difficult as is the control of an AAV such as the Predator, it does not have to operate routinely in close proximity to collision hazards. The reaction time and computational time for deciding contingent actions is very short when obstacles loom immediately ahead or below a marine vehicle. Figure 1.23 depicts one example of an ASV that was created by student researchers under the direction of Dr. Dan Stilwell of Virginia Tech. These researchers have concentrated on the creation of robotic marine vehicles that operate autonomously, potentially at high speeds, in riverine environments. Of course, the deployment of autonomous marine vehicles is further complicated by the fact that the vehicles may be limited to travel on the surface of a body of water, or they can be designed for undersea travel. Figure 1.24 depicts an AUV created at Virginia Tech by Professor Dan Stilwell.

Picture of ASV. Created by students under the direction of Dr. Dan Stilwell of Virginia Tech.

Figure 1.23 ASV. Created by students under the direction of Dr. Dan Stilwell of Virginia Tech.

Picture of AUV Javelin. Created by students under the direction of Professor Dan Stilwell of Virginia Tech.

Figure 1.24 AUV Javelin. Created by students under the direction of Professor Dan Stilwell of Virginia Tech.

1.6 An Overview of Robotics Dynamics and Control Problems

The overview in Sections 1.2, 1.4, and 1.5 mentions some of the disciplines that influence the study of robotic systems. This book studies several classical problems that arise in the dynamics and control of nearly all robotic systems. These are the problems of forward kinematics, inverse kinematics, forward dynamics, and inverse dynamics/feedback control of robotic systems. The essential features of these problems will be described in Sections , 1.6.3, and 1.6.4 and these sections discuss how they arise for typical robotic systems. The presentation uses the flapping wing robot depicted in Figure 1.25 as a case study to illustrate the underlying principles. Section 1.6.5 discusses how, despite their apparent dissimilarity, these same problems arise in the control of mobile robots.

Picture of flapping wing robot.

Figure 1.25 Flapping wing robot.

1.6.1 Forward Kinematics

Just as researchers have sought to design and build robots that mimic humans in form and action, so too have designers striven to build robots that resemble animals. Efforts to create bio‐inspired flapping wing robots are one particularly challenging example. These designs represent a significant departure from that of most existing commercial flying vehicles. A successful design of a flapping wing robot is difficult in part due to a lack of understanding of the inherently complex nonlinear and unsteady aerodynamics surrounding the vehicle. This area continues to be an active topic of research. In this section we discuss various robotic analysis problems for a robot that drives a flapping wing for wind tunnel testing. The task of building a flapping wing vehicle, while exceptionally difficult, provides an excellent example of how the classical problems of forward kinematics, inverse kinematics, forward dynamics, and feedback control can arise in applications.

One of the first considerations in building a model of a robot of the type depicted in Figure 1.25 is the choice of the variables that will be used in its representation. This topic is discussed in general terms in Chapter , and a summary of the more common representations for articulated robotic systems is presented in Chapter . While there are exceptions, the most popular choice of variables for articulated mechanical systems is joint variables that define how the bodies of a robotic system move relative to one another. If the entire robotic system also undergoes rigid body motion with respect to a defined ground reference (instead of being fixed to that reference), as seen in the study of the space robotics or full body humanoids, the joint variables must be supplemented with additional variables to represent the net motion.

In Figure 1.26, the robot is fixed rigidly to the ground. Therefore, the use of joint variables alone suffices to represent the dynamics. The joint variables in this example are the joint anglesimages , and images that determine the relative rotations of the bodies at individual revolute joints. It is also frequently the case that joint variables are selected to be the relative displacements between the bodies when a robot includes prismatic joints that permit translation. In general, a generic set of joint variables is denoted by by images for images where images is the number of degrees of freedom. The problem of forward kinematics studies how the configuration of the robot changes as the joint variables are varied. For example, for the flapping wing robot, it is desired to design a system such that the wings trace out motions that resemble as closely as possible the motion of actual birds. The problem of forward kinematics seeks to find the position, velocity, and acceleration of typical points like images on the robot in Figure 1.25 given the time histories images of the joint variables for images .

Picture of robotic flapping using robot and joint variables θ1,θ2,θ3, and θ4.

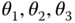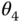Figure 1.26 Robotic flapping using robot and joint variables images , and images .

This problem can be stated succinctly: let images and images be the position, velocity and acceleration of the point images relative to the ground, or 0, frame; find the mapping from the joint variables and their derivatives to the position, velocity and acceleration of point images on the robot.

equation

It is important to realize that this problem must be solved as part of nearly all modeling or control tasks. The specific choice of joint angles used in Figure 1.26 are defined using the Denavit–Hartenberg convention, one of the most commonly used general strategies for describing articulated robots that form kinematic chains. This topic is covered in detail in Chapter .

1.6.2 Inverse Kinematics

While solving the problem of forward kinematics is an important first step in many modeling and control problems, it does not answer all the important questions regarding the motion of a given robot. In the case at hand of the flapping wing robot, the wings should be able to trace out trajectories that mimic those of real birds, or as close as possible given the robot geometry. By taking video recordings of birds in flight, it is possible to generate estimates of the trajectories that certain points on the wings trace out as a function of time. Suppose these experimentally collected trajectories of point images on the wings are treated as input data. That is, suppose the position, velocity and acceleration of the point images as a function of time are given. The problem of inverse kinematics seeks to find the joint variables and their derivatives given the position, velocity, and acceleration of a point images on the robotic system. In other words the mapping from the positions, velocities, and accelerations of point images on the robot to the joint variables and their derivatives should be found.

equation

It is evident that this problem seeks to find the inverse of the mapping studied in the forward kinematics problem. It is well known that the inverse kinematics problem can be much more difficult to solve than the forward kinematics problem. The inverse kinematics problem can have no solutions or multiple solutions, depending on the robot geometry and design objectives. Chapter discusses some of the difficulties encountered in the solution of inverse kinematic problems.

1.6.3 Forward Dynamics

The problems of forward kinematics and inverse kinematics are purely geometric in nature. There is no provision for or consideration of the forces or moments that must be applied to achieve a specific motion. For many of the robotic systems studied in this book, the governing equations can be written in the form

equation

where images is an images nonlinear generalized mass or inertia matrix, images is an images vector of nonlinear functions including Coriolis and centripetal terms, and images is an images vector of forces or torques applied to the robot by actuators. This is a nonlinear, second‐order system of coupled ordinary differential equations (ODEs). A common general strategy for studying these equations introduces the state variables images that stacks the generalized coordinates images and their derivatives images in the form

equation

and rewrites the governing system of equations as

(1.2) equation

where images is the set of control inputs.

The problem of forward dynamics seeks to solve these equations for the state images , thereby obtaining the joint variables images and their derivatives images , given the input forces and torques in images . The solution procedure may be analytic or numerical, but the models of most practical robots are so complex that analytic solutions are not usually feasible. The numerical approximate solution of these equations utilizes the rich and well developed collection of time stepping numerical algorithms for nonlinear ordinary differential equations. Specific algorithms that are commonly used to generate numerical approximations of the solutions include the popular family of Runge–Kutta techniques, linear multi‐step methods, and specialized schemes that are tailored to stiff systems. The solution of the forward dynamics problem can be used in many facets of robotic design and analysis.

1.6.4 Inverse Dynamics and Feedback Control

The problem of forward dynamics can be solved to understand how a specific set of input forces and torques in images induce a corresponding time history of the joint variables images for images . The solution of the forward dynamics problem can be described as finding the dynamic behavior of the system given an input actuation time history images , images . Similar to the relationship between forward and inverse kinematics, the problem of inverse dynamics of a robotic system can be thought of as asking a converse question: what must the control input history images , images , be as a function of the generalized coordinates images to yield a specific dynamic behavior?

However, when considering practical systems, there is often a disconnect between the prescribed desired state vector images and the estimated state vector images from sensors associated with the robotic system, internal (e.g., joint encoders) or external (e.g., workspace cameras. By incorporating techniques from control theory alongside inverse dynamic analysis, feedback control laws may be designed to calculate appropriate actuation inputs trajectories images as a function of the desired and estimated states images and images .

While there are numerous specific control problems that make sense for a robotic system, a tracking control problem is easy to pose for the flapping wing robot. Suppose again that video post‐processing methods have been used to identify the trajectories of points on the wings of actual birds in flight. One example of a trajectory tracking problem seeks to find the input torques and forces images as a function of time that will drive the robot so that the points on the wing approach the experimentally collected trajectories as time images increases. Many variants of this problem can be defined depending on the type of measurements and the metric used to define how closely the robot follows the desired trajectories. Mathematically, many of these control problems can be interpreted as a constrained optimization problem where some cost or performance functional images is minimized. The optimization problem is solved for the best input images in the set of admissible controls images in the sense that

(1.3) equation

subject to the constraint that the state images satisfies the equations of motion in Equation (1.2).

1.6.5 Dynamics and Control of Robotic Vehicles

The fundamental dynamics and control problems for robotics, and their role in the study of a typical flapping wing robot, were discussed in Sections 1.6.1, 1.6.2, 1.6.3, and 1.6.4. The example used for illustration in these sections could just as well have been selected to be any of the robotic manipulators. The structural similarity among these systems is striking. Perhaps surprisingly, each of the fundamental problems of robotics and dynamics – forward kinematics, inverse kinematics, forward dynamics, and feedback control synthesis – can also be stated when robotic systems that are autonomous vehicles are considered. In many cases the language used to describe the variants of these problems is different depending on the type of vehicle, even though the underlying problems are structurally similar in form. For example, the trajectory tracking or path following problem that seeks to position a tool mounted on a robotic arm is mathematically similar to that of guidance and navigation of autonomous vehicles. In addition, it is also common that robotic manipulators are mounted on autonomous vehicles, as shown in Figure 1.27. Another example of this latter type includes the combined space shuttle and remote manipulator system. It is possible to speak of the guidance and navigation of the vehicle and the control of the robotic manipulator. These problems are in fact coupled, and the solution of dynamics and control problems for the coupled system can be substantially more difficult than that associated with only the base vehicle or only the manipulator.

Picture of AGV, iRobot PackBot, with manipulator arm.

Figure 1.27 AGV, iRobot PackBot, with manipulator arm.

While the study of robotic manipulators provides a foundation that can be used to help formulate and solve dynamics and control problems for autonomous systems, there remain many substantial differences between methodologies for autonomous vehicles. One of the principal differences between formulations of the dynamics of AGVs, AAVs, ASVs, or AUVs is that the set of variables used to describe motion must be capable of representing rigid body motion. While the general study of kinematics in Chapter covers many of the topics needed to study this problem, the specific methodologies for robots having the form of kinematic chains in Chapter are not sufficient to represent the rigid body motion of an autonomous vehicle. Fortunately, for many of the different types of autonomous vehicles, it is the case that governing equations have the form shown in Equation (1.2). Many problems of vehicle control are solved by casting the control problem as one of optimization, as summarized in Equation (1.3).

1.7 Organization of the Book

The study of robotic systems begins with an exposition of the fundamental principles of kinematics in Chapter . The chapter constitutes a self‐contained introduction to the field of kinematics in three spatial dimensions and establishes notation and conventions for common mathematical expressions used throughout the book. Particular emphasis is placed on the foundations of kinematics in three spatial dimensions, including the study of vectors, coordinate systems, and rotation matrices. General definitions of linear position, velocity, and acceleration with respect to different frames of reference are introduced, as well as angular velocity and angular acceleration. The chapter concludes with a collection of some of the most commonly used theorems of kinematics. These include the theorems that introduce relative velocity (Theorem 2.16) and relative acceleration (Theorem 2.17), the derivative theorem (Theorem 2.12) and the addition theorem (Theorem 2.15) for angular velocity.

Chapter introduces refinements of the principles of kinematics that are tailored to specific types of robotic systems. The chapter introduces homogeneous transformations that are used to relate rigid body motions of links in a robotic system. Mathematical models of ideal joints between the links that comprise the system are discussed. In addition to these general topics in kinematics of robotic systems, the chapter discusses two popular methods (Denavit–Hartenberg and recursive) for the representation of robotic systems that form kinematic chains. In the presentation of the Denavit–Hartenberg convention, explicit constructions of the homogeneous transforms associated with the bodies in a kinematic chain are derived. A general procedure is detailed for defining the link parameters that determine the kinematics of a serial chain. The recursive formulation of the forward kinematics problem, in contrast to the Denavit–Hartenberg formulation, has been specifically based on efficiency in calculation. This formulation notes the highly structured nature of the kinematic relationship between successive bodies in a kinematic chain, and it exploits this structure to derive algorithms for recursive calculation of the kinematics. The chapter closes with a discussion of inverse kinematics.

Chapter discusses the strategy for deriving the equations of motion of robotic systems using Newton–Euler formulations. General definitions of linear and angular momentum of rigid bodies are introduced. The inertia matrix of a rigid body is introduced to facilitate the calculation of the angular momentum of components in a robotic system. The Newton–Euler equations are introduced as a means for deriving the equations of motion of general robotic systems. This chapter further extends the recursive formulation first studied in Chapter , and the resulting approach is used for the derivation of the equations of motion of robotic systems. It is demonstrated that the equations of motion of kinematic chains can be derived recursively by exploiting the structure of the same matrices that arise in the kinematics formulation. The equations of motion derived via the Newton–Euler formulation have the form of nonlinear differential‐algebraic equations, or DAEs. It is demonstrated in the chapter that these equations can be re‐cast as a set of nonlinear ordinary differential equations, or ODEs.

Methods of analytical mechanics, as they are used to derive the equations of motion of robotic systems, are introduced in Chapter . The chapter begins with the statement of Hamilton's principle and explains how it can be interpreted as a problem of variational calculus. Its solution yields the equations of motion for the robotic system. Since the kinetic energy and potential energy of many robotic systems have the same functional form, it is possible to derive Lagrange's equations from the variational calculus problem generated by Hamilton's principle. Hamilton's extended principle is presented as a means of incorporating contributions due to the presence of non‐conservative forces in the equations of motion. A standard form for the governing equations for a large class of robotic systems is derived using Lagrange's equations. Finally, the chapter presents the method of Lagrange's equations with Lagrange multipliers that is appropriate for deriving governing equations in terms of redundant collections of variables. This approach results in a system of nonlinear DAEs, in general.

Methods of feedback control of robotic systems are presented in Chapter . The general form and structure of control problems are discussed, and an overview of stability theory is given. The fundamental principles of stability theory are presented, and the use of the Lyapunov functions to establish stability for practical robotic systems is discussed. These techniques are critical to modern approaches of control synthesis for robotic systems. Lyapunov's direct method and LaSalle's invariance principle are applied to establish stability and convergence of typical set point and tracking controllers. Feedback controllers based on exact feedback linearization or computed torque control, approximate dynamic inversion, and passivity principles are derived. The chapter finishes with an introduction to actuator models, emphasizing electric motors and electromechanical linear actuators.

The final chapter of this book, Chapter , discusses techniques of image‐based control for robotic systems. The ideal pinhole camera model is discussed in detail, which enables a succinct presentation of image based visual servo (IBVS) control strategies. Stability and asymptotic stability of IBVS control methods is established, as well as the role of singular configurations in the performance of these methods. The general approach of task space control formulations, in contrast to the joint space methods described in Chapter , is presented. Task space formulations of visual control objectives is the final topic in Chapter .

1.8 Problems for Chapter 1

  1. Problem 1.1 Briefly summarize the origins of the word “robot”.
  2. Problem 1.2 Define what is meant by a robotic system in this book. How does this definition differ from other common definitions?
  3. Problem 1.3 Define the following terms that commonly appear in the study of robotics:
    • Actuator
    • Sensor
    • Workspace
    • Ideal joint
    • Joint variable
    • Passive joint
    • Driven joint
    • Precision, accuracy, and resolution
    • Repeatability
    • Tool frame
    • End effector.
  4. Problem 1.4 Define the following robotic manipulators, describe their general features, and find commercially available examples of each.
    • Cartesian robot
    • Cylindrical robot
    • Spherical robot
    • SCARA robot
    • PUMA robot
    • Anthropomorphic arm.
  5. Problem 1.5 Define the fundamental problems of
    • Forward kinematics
    • Inverse kinematics
    • Forward dynamics
    • Feedback control

    for robotic systems. Find and describe an explicit example of each problem for a commercially available robotic system.

  6. Problem 1.6 Discuss examples of how the fundamental problems of the dynamics and control of robots (forward kinematics, inverse kinematics, forward dynamics, and feedback control) may arise in the development of humanoid robots. Describe specific sub‐problems for each of the fundamental problems in this application area.
  7. Problem 1.7 Discuss examples of how the fundamental problems of the dynamics and control of robots (forward kinematics, inverse kinematics, forward dynamics, and feedback control) may arise in the development of autonomous ground vehicles. Describe specific sub‐problems for each of the fundamental problems in this application area.
  8. Problem 1.8 Discuss examples of how the fundamental problems of the dynamics and control of robots (forward kinematics, inverse kinematics, forward dynamics, and feedback control) may arise in the development of autonomous air vehicles. Describe specific sub‐problems for each of the fundamental problems in this application area.