Chapter 15
Getting Back to Basics: Numbers and Operations
IN THIS CHAPTER
 Refreshing your memory on types of numbers and basic operations
Refreshing your memory on types of numbers and basic operations
 Getting the skinny on bases, exponents, and radicals
Getting the skinny on bases, exponents, and radicals
 Keeping order of operations in mind
Keeping order of operations in mind
 Grabbing your share of fractions, decimals, and percentages
Grabbing your share of fractions, decimals, and percentages
 Making comparisons by using ratios and proportions
Making comparisons by using ratios and proportions
 Bringing numbers down to size with scientific notation
Bringing numbers down to size with scientific notation
Those of you who majored in math in college probably look at the math section of the GMAT like an old friend. Those of you who haven’t stepped into a math class since high school are more likely dreading it. You know who you are! Don’t worry, this chapter takes you back to the beginning with a review of the concepts you’ve learned through the years but may have temporarily forgotten. In this chapter, you see problems that test your knowledge of the math building blocks, such as number types, basic operations, exponents and radicals, fractions, and ratios. These concepts form the foundation of more complicated math problems, so this stuff is important to know. For example, you could end up with a completely wrong answer if you solve for real numbers when the question asks for integers. Some GMAT-takers may end up kicking themselves (and that looks just plain odd) for missing relatively simple problems because they were unfamiliar with some basic terminology. To avoid this unfortunate (and awkward) position, make sure you’re well-heeled in math basics.
Just Your Type: Kinds of Numbers
Since the Stone Age, humans have found it necessary to rely on numbers to get through daily living. In hunter-gatherer cultures, the people made notches in bones to count, for example, the number of days in a lunar cycle or perhaps to indicate how long the nomadic tribe spent in a particular location until it found food. But through the millennia, humankind soon realized that numbers could become large and unwieldy. Hence, the advent of number classifications and operations!
Although understanding modern mathematical operations may have burst prehistoric man’s cerebral cortex, it’ll surely be easier for you after you complete this review. For the GMAT, you need to know the more common types of numbers, such as integers, rational numbers, real numbers, and prime numbers. And you should at least be aware of some of the less common types, such as irrational and imaginary numbers.
-
Integers: Numbers that belong to the set of all positive and negative whole numbers with 0 included. Integers can’t be fractions or decimals or portions of a number. Integers include –5, –4, –3, –2, –1, 0, 1, 2, 3, 4, and 5 and continue infinitely on either side of 0. Integers greater than 0 are called natural numbers or positive integers. Integers less than 0 are called negative integers.
 Take care when working with 0. It’s neither positive nor negative.
Take care when working with 0. It’s neither positive nor negative. - Rational numbers: Numbers that are expressed as the ratio of one integer to another; that is, numbers that can be expressed as fractions. Rational numbers include all positive and negative integers, zero, fractions, and decimal numbers that either end or repeat. For example, the fraction
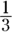 can be expressed as
can be expressed as 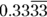 . Rational numbers don’t include numbers like
. Rational numbers don’t include numbers like 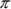 or radicals like
or radicals like  because the decimal equivalents of these numbers don’t end or repeat. They’re called irrational numbers.
because the decimal equivalents of these numbers don’t end or repeat. They’re called irrational numbers. - Real numbers: All numbers that you normally think of as numbers. Real numbers belong to the set that includes all integers, rational numbers, and irrational numbers. Think of real numbers as those numbers represented by all the points on a number line, either positive or negative or zero. Real numbers are also those numbers you use to measure length, volume, or weight. So when the GMAT asks you to give an answer expressed in terms of real numbers, just solve the problem as you normally would.
- Imaginary numbers: Any number that isn’t a real number. So an imaginary number is a number like
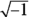 . Think about it: You know that when you square any positive or negative real number, the result is a positive number. This means you can’t find the square root of a negative number unless the root is simply not a real number. So imaginary numbers include square roots of negative numbers or any number containing i, which represents the square root of –1. Won’t you be a fascinating conversationalist at your next soiree!
. Think about it: You know that when you square any positive or negative real number, the result is a positive number. This means you can’t find the square root of a negative number unless the root is simply not a real number. So imaginary numbers include square roots of negative numbers or any number containing i, which represents the square root of –1. Won’t you be a fascinating conversationalist at your next soiree! - Prime numbers: All the positive integers that can be divided by only themselves and 1; 1 isn’t a prime number. The smallest prime number is 2, and it’s also the only even prime number. This doesn’t mean that all odd numbers are prime numbers, though. Also, 0 can never be a prime number because you can divide 0 by every natural number there is. To determine prime numbers, consider this series: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, and so on. What makes these numbers unique is that the only two factors for these numbers are 1 and the number itself.
You probably won’t encounter this term on the GMAT, but in case it comes up at cocktail parties, you should know that 0 and positive numbers other than 1 that aren’t prime numbers are called composite numbers. A composite number has more than two factors, so it’s the product of more than simply itself and the number 1. Questions regarding prime numbers appear fairly frequently in GMAT math sections. Here’s a sample of one you may see.
 Which of the following expresses 60 as a product of prime numbers?
Which of the following expresses 60 as a product of prime numbers?
(A) 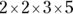
(B) 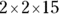
(C) 
(D) 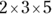
(E) 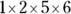
This question tests your knowledge of prime numbers. Because the correct answer has to be a series of prime numbers, eliminate any choice that contains a composite (or non-prime) number. So Choices (B) and (E) are out (even though the product of both is 60) because 15, 1, and 6 aren’t prime numbers. Then, eliminate any answers that don’t equal 60 when you multiply them. Choice (C) is 90, and Choice (D) is 30, so the answer must be Choice (A). It’s the correct answer because it contains only prime numbers whose product equals 60.
It’s Not Brain Surgery: Basic Operations
Now that you’re a bit more comfortable with some terms, it’s time to take a stab at manipulating numbers. Figuring out how to do operations, which we discuss in the following sections, is pretty simple, almost as simple as 1-2-3. It doesn’t take a brain surgeon to open your mind to endless possibilities.
Adding, subtracting, multiplying, and dividing
You’re probably pretty familiar with the standard operations of addition, subtraction, multiplication, and division. But even these math basics have some tricky elements that you may need to refresh your memory on.
Putting two and two together: Addition
Adding is pretty simple. Addition is just the operation of combining two or more numbers to get an end result called the sum. For example, here’s a simple addition problem:
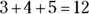
Addition also has two important properties that you may remember from elementary school: the associative property and the commutative property. Understanding these simple concepts for the GMAT math questions is important:
- Associative property: The associative property states that the order in which you choose to add three or more numbers doesn’t change the result. It shows how numbers can group differently with one another and still produce the same answer. So regardless of whether you add 3 and 4 together first and then add 5 or add 4 and 5 together followed by 3, you still get an answer of 12.
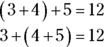
- Commutative property: The commutative property states that it doesn’t matter what order you use to add the same numbers. Regardless of what number you list first in a set of numbers, they always produce the same sum. So
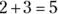 is the same as
is the same as 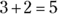 .
.
Depleting the supply: Subtraction
Subtraction, as you probably know, is the opposite of addition. You take away a value from another value and end up with the difference. So if 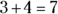 , then
, then 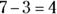 .
.
In subtraction, order does matter, so neither the associative property nor the commutative property applies. You get completely different answers for 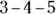 , depending on what method you use to associate the values. Here’s what we mean:
, depending on what method you use to associate the values. Here’s what we mean:

but
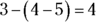
The order of the values counts in subtraction, too. For example, 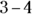 isn’t the same as
isn’t the same as 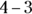 (
(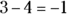 , but
, but 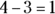 ).
).
Increasing by leaps and bounds: Multiplication
Think of multiplication as repeated addition with an end result called the product: 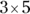 is the same as 5 + 5 + 5. They both equal 15.
is the same as 5 + 5 + 5. They both equal 15.
On the GMAT, you may see several signs that represent the multiplication operation. A multiplication sign can be designated by  or simply with a dot, like ∙. And in many instances, especially when variables are involved (for more about variables, see Chapter 16), multiplication can be indicated by just putting the factors right next to each other. So ab means the same thing as
or simply with a dot, like ∙. And in many instances, especially when variables are involved (for more about variables, see Chapter 16), multiplication can be indicated by just putting the factors right next to each other. So ab means the same thing as 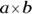 , and 2a is the same as
, and 2a is the same as 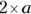 . One of these back-to-back factors may appear in parentheses: 2(3) means
. One of these back-to-back factors may appear in parentheses: 2(3) means 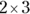 .
.
Multiplication is like addition, in that the order of the values doesn’t matter. So it obeys the commutative property:
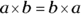
And the associative property:

Another property associated with multiplication is the distributive property. So you may encounter this multiplication problem:
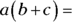
You solve it by distributing the a to b and c, which means that you multiply a and b to get ab and then a and c to get ac, and then you add the results together like this: 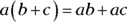 .
.
Sharing the wealth: Division
Finally, there’s division, which you can consider to be the opposite of multiplication. With division, you split one value into smaller values. The end result is called the quotient. So whereas 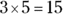 ,
, 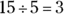 , and
, and 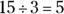 .
.
As in subtraction, order matters, so division doesn’t follow either the commutative or associative properties. Also, just so you’re familiar with any terms you may encounter on the GMAT, the number at the beginning of any equation using division (15 in the last expression) is called the dividend and the number that goes into the dividend is the divisor (3 in the last expression).
The division sign may be represented by a fraction bar. For more info on fractions, see “Splitting Up: Fractions, Decimals, and Percentages,” later in this chapter.
Checking out the real estate: Properties of real numbers
In addition to basic operations, the GMAT expects you to know the fundamental properties of the numbers you’re working with. These include absolute values, evens and odds, and positives and negatives.
Absolutes do exist: Absolute value
To simplify things, just think of the absolute value of any real number as that same number without a negative sign. It’s the value of the distance a particular number is from 0 on a number line. The symbol for absolute value is | |, so the absolute value of 3 is written mathematically as |3|. And because the number 3 sits three spaces from 0 on the number line, 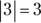 . Likewise, because –3 sits three spaces from 0 on the number line, its absolute value is also 3:
. Likewise, because –3 sits three spaces from 0 on the number line, its absolute value is also 3:  .
.
 Which of the following is the complete set of solutions for x when
Which of the following is the complete set of solutions for x when 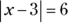 ?
?
(A) 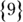
(B) 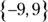
(C) 
(D) 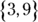
(E) 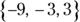
To find one solution for x, remove the absolute-value sign and solve:
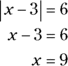
You know 9 is a solution for x, so you can eliminate Choice (E) because it doesn’t contain 9. You can’t end with Choice (A), though; you have to consider that the value within the absolute value signs could be negative. To accomplish this feat, multiply the terms between the bars by –1 and then solve for x:
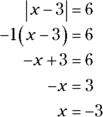
Because the value in the absolute-value signs may be either negative or positive, x may be either –3 or 9. Choice (C) is the complete set of solutions.
A balancing act: Even and odd numbers
We’re pretty sure you know that even numbers are integers divisible by 2: 2, 4, 6, 8, 10, and so on. And odd numbers are those integers that aren’t divisible by 2: 1, 3, 5, 7, 9, 11, and so on.
You’re probably with us so far, but what’s important to remember for the GMAT is what happens to even or odd numbers when you add, subtract, or multiply them by one another.
Here are the rules regarding evens and odds for addition and subtraction:
- When you add or subtract two even integers, your result is an even integer.
- When you add or subtract two odd integers, your result is also even.
- If you add or subtract an even integer and an odd integer, your result is an odd integer.
Here’s what you should know about multiplying even and odd integers:
- When you multiply an even number by an even number, you get an even number.
- When you multiply an odd number by an even number, you also get an even number.
- The only time you get an odd number is when you multiply an odd number by another odd number.
Division rules are a little more complex because the quotients aren’t always integers; sometimes they’re fractions. Here are a few rules to know:
- When you divide an even integer by an odd integer, you get an even integer or a fraction.
- An odd integer divided by another odd integer results in an odd integer or a fraction.
- An even integer divided by another even integer can result in either an odd or even quotient, so that’s not very helpful.
- When you divide an odd integer by an even one, you always get a fraction; because fractions aren’t integers, the quotient for this scenario is neither odd nor even.
 If a and b are different prime numbers, which of the following numbers must be odd?
If a and b are different prime numbers, which of the following numbers must be odd?
(A) ab
(B) 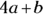
(C) 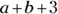
(D) 
(E) 
To solve this number theory question, think of numbers for a and b that represent their possible values. Then substitute these values into the answer choices to eliminate all that can be even. When considering values for a and b, make sure to include 2 because it’s the only even prime number. Neither 1 nor 0 is an option because neither is prime.
Substitute 2 for a or b in Choice (A), and you see that it can be even because the rules tell you that any time you multiply an even number by another number, you get an even number. You also know that Choice (B) can be even because 4 (an even number) times any number is an even number. If 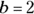 and you added that to 4a, you’d be adding two even numbers, which always gives you an even sum. Again, if
and you added that to 4a, you’d be adding two even numbers, which always gives you an even sum. Again, if  in Choice (C), then a would have to be an odd prime number. You add a (odd) to b (even) to get an odd sum. Then you add that odd number to the odd number 3, which results in an even number. Choice (D) can be even if both a and b are odd. An odd number times an odd number is an odd number. When you subtract an odd number, like 3, from another odd number, you get an even number.
in Choice (C), then a would have to be an odd prime number. You add a (odd) to b (even) to get an odd sum. Then you add that odd number to the odd number 3, which results in an even number. Choice (D) can be even if both a and b are odd. An odd number times an odd number is an odd number. When you subtract an odd number, like 3, from another odd number, you get an even number.
By process of elimination, the answer must be Choice (E). It doesn’t matter whether a or b in Choice (E) is even or odd; 4a and 4b will always be even, because anytime you multiply an even number by another number, you get an even number. When you add two evens, you get an even number, so 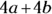 is an even number. And because an even number plus an odd number is always odd, when you add that even result to 3, you get an odd number, always. The correct answer is Choice (E).
is an even number. And because an even number plus an odd number is always odd, when you add that even result to 3, you get an odd number, always. The correct answer is Choice (E).
Half empty or half full: Positive and negative numbers
Positive and negative numbers have their own set of rules regarding operations, and they’re even more important to remember than those for even and odd integers. Here’s what you need to know for multiplying and dividing:
- When you multiply or divide two positive numbers, the result is positive.
- When you multiply or divide two negative numbers, the result is also positive.
- Multiplying or dividing a negative number by a positive number gives you a negative result (as does multiplying or dividing a positive number by a negative number).
As you may expect, you need to know some things about adding and subtracting positives and negatives:
- When you add two positive numbers, your result is a positive number.
- When you add two negative numbers, the resulting sum is negative.
- When you add a positive number to a negative number, the result is positive when the number with the largest absolute value is positive and negative when the number with the largest absolute value is negative.
- If you subtract a negative number from another number, you end up adding the positive version of the negative number to the other number. For example,
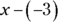 is the same thing as
is the same thing as 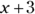 .
.
Using Little Numbers for Big Values: Bases and Exponents
Because multiplication can be thought of as repeated addition, you can think of exponents as repeated multiplication. This means that  is the same as
is the same as 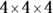 or 64. In the example, you refer to 4 as the base and the superscript 3 as the exponent. If you add a variable into this mix, such as
or 64. In the example, you refer to 4 as the base and the superscript 3 as the exponent. If you add a variable into this mix, such as 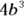 , the base becomes b and the 4 becomes what’s known as the coefficient. In our example, the coefficient 4 is simply multiplied by
, the base becomes b and the 4 becomes what’s known as the coefficient. In our example, the coefficient 4 is simply multiplied by 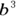 .
.
As a high school algebra teacher used to scream (usually when he caught his students napping): “The power governs only the number immediately below it!” (that is, the base). So the exponent doesn’t affect the coefficient. Only the base gets squared or cubed or whatever the exponent says to do.
This rule brings up some fascinating properties regarding positive and negative bases and even and odd exponents:
- A positive number taken to an even or odd power remains positive.
- A negative number taken to an odd power remains negative.
- A negative number taken to an even power becomes positive.
On the other hand, anytime you have an exponent of 2, you have two potential roots, one positive and one negative, for the expression. For example, if 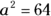 , then
, then 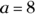 or –8. So 64 has two possible square roots: either 8 or –8.
or –8. So 64 has two possible square roots: either 8 or –8.
In the following sections, we outline a few rules for adding, subtracting, multiplying, and dividing exponents. We also clue you in on how to figure out the powers of 0 and 1 and what to do with fractional and negative exponents.
Adding and subtracting with exponents
The only catch to adding or subtracting with exponents is that the base and exponent of each term must be the same. So you can add and subtract like terms such as 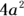 and
and 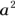 like this:
like this: 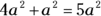 and
and 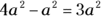 . Notice that the base and exponent remain the same and that the coefficient is the only number that changes in the equation.
. Notice that the base and exponent remain the same and that the coefficient is the only number that changes in the equation.
Multiplying and dividing with exponents
The rules regarding multiplying and dividing exponents are pretty numerous, so to keep them straight, we’ve set up Table 15-1 for you. The table describes each rule and gives you an example or two.
TABLE 15-1 Rules for Multiplying and Dividing with Exponents
|
Rule |
Examples |
|---|---|
|
To multiply terms with exponents and the same bases, add the exponents. |
|
|
If the expression contains coefficients, multiply the coefficients as you normally would. |
|
|
When you divide terms with exponents and the same bases, just subtract the exponents. |
|
|
Any coefficients are also divided as usual. |
|
|
To multiply exponential terms with different bases, first make sure the exponents are the same. If they are, multiply the bases and maintain the same exponent. |
|
|
Follow the same procedure when you divide terms with different bases but the same exponents. |
|
|
When you raise a power to another power, multiply the exponents. |
|
|
If your expression includes a coefficient, take it to the same power. |
|
Figuring out the powers of 0 and 1
Exponents of 0 and 1 have special properties that you’ll have to commit to memory:
- The value of a base with an exponent of 0 (such as
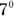 ) is always 1.
) is always 1. - The value of a base with an exponent of 1 is the same value as the base (
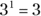 ).
).
Dealing with fractional exponents
If you see a problem with an exponent in fraction form, consider the top number of the fraction (the numerator) as your actual exponent and the bottom number (the denominator) as the root. So to solve 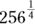 , simply take 256 to the first power (because the numerator of the fraction is 1), which is 256. Then take the fourth root of 256 (because the denominator of the fraction is 4), which is 4, and that’s your answer. (Find out more about roots in the “Checking Out the Ancestry: Roots” section later in this chapter.) Here’s what it looks like mathematically:
, simply take 256 to the first power (because the numerator of the fraction is 1), which is 256. Then take the fourth root of 256 (because the denominator of the fraction is 4), which is 4, and that’s your answer. (Find out more about roots in the “Checking Out the Ancestry: Roots” section later in this chapter.) Here’s what it looks like mathematically:
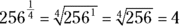
The GMAT may also present you with a variable base and a fractional exponent. You handle those the same way, like this:
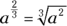
This is what you get when you take a to the second power and then find its cube root.
Working with negative exponents
A negative exponent works like a positive exponent with a twist. A negative exponent takes the positive exponent and then flips the base and exponent around so that together they become the reciprocal (see the section, “Defining numerators, denominators, and other stuff you need to know about fractions,” later in this chapter), like this:
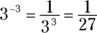
To see how the GMAT may test exponents, check out a sample problem.
 If
If 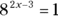 , what is the value of x?
, what is the value of x?
(A) 0
(B) 1.5
(C) 2
(D) 8
(E) 10.5
The trick to mastering this problem is to remember that a number to the power of 0 is equal to 1. So, for the expression to equal 1, 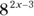 must equal
must equal 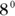 . When you know that
. When you know that 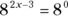 , you know
, you know 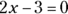 . Solve for x.
. Solve for x.
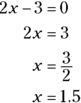
The simple answer to this perhaps initially confusing problem is Choice (B). If you picked Choice (C), you may have thought the exponent was equal to 1 instead of 0.
Checking Out the Ancestry: Roots
If you like exponents, you’ll love roots, which are also known as radicals. Roots are sort of the opposite of exponents. The square root of a number is the number that you square to get that number. So because you square 3 to get 9, the square root of 9 is 3. What could be simpler?
There are as many roots as there are powers. Most of the time, the GMAT has you work with square roots, but you may also see other roots. That won’t intimidate you, though. If you come upon a cube root or fourth root, you’ll recognize it by the radical sign, 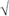 .
.
For example, the cube root of 27 is expressed as 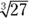 . This expression asks what number, when raised to the third power, equals 27. Of course, the answer is 3 because
. This expression asks what number, when raised to the third power, equals 27. Of course, the answer is 3 because 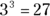 .
.
 If
If 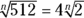 , then n = ?
, then n = ?
(A) 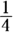
(B) 
(C) 1
(D) 4
(E) 8
You can solve this equation most easily by simplifying the radical. The nth root of 512 is equal to 4 times the nth root of 2. Consider the factors of 512: 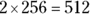 , so
, so 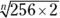 , which also equals
, which also equals 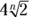 .
. 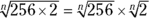 , so you know that
, so you know that 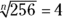 , which is the same as saying
, which is the same as saying 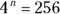 . Because
. Because 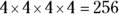 ,
, 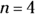 , and Choice (D) is the correct answer.
, and Choice (D) is the correct answer.
Roots obey the same rules as exponents when it comes to performing operations. You can add and subtract roots as long as the roots are of the same order (that is, square root, cube root, and so on) and the same number. Here are a couple of examples:
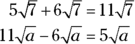
When you need to multiply or divide radicals, make sure the roots are of the same order (such as all square or all cube roots) and you’re good to go! For multiplication, just multiply what’s under the radical signs, like this:
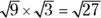
Divide what’s under the radical signs like this:
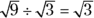
And here’s how a question about operations with radicals may appear on the GMAT.

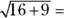 ?
?
(A) 5
(B) 7
(C) 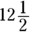
(D) 25
(E) 625
 Pay attention to the values underneath the radical. In this question, the line of the square root symbol extends over the entire expression, so you’re supposed to find the square root of 16 + 9, not
Pay attention to the values underneath the radical. In this question, the line of the square root symbol extends over the entire expression, so you’re supposed to find the square root of 16 + 9, not 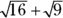 . It’s a subtle but major difference!
. It’s a subtle but major difference!
First, add the values under the radical sign: 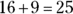 . The square root of 25 is 5, so Choice (A) is the correct answer. If you chose 7, you determined the square root of each of the values before you added them together. For 7 to be the correct answer, your problem should have been written with two separate square root signs,
. The square root of 25 is 5, so Choice (A) is the correct answer. If you chose 7, you determined the square root of each of the values before you added them together. For 7 to be the correct answer, your problem should have been written with two separate square root signs, 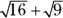 .
.
Order of Operations: Please Excuse My Dear Aunt Sally
Basic arithmetic requires that you perform the operations in a certain order from left to right. Okay, so maybe you don’t have an aunt named Sally, but this section’s title is a helpful mnemonic for the order you use when you have to perform several operations in one problem. What that means is that if you have an expression that contains addition, subtraction, multiplication, division, exponents (and roots), and parentheses to boot, it helps to know which operation you perform first, second, third, and so on.
The acronym PEMDAS (Please Excuse My Dear Aunt Sally) can help you remember to perform operations in the following order:
- Parentheses
- Exponents (and roots)
- Multiplication and Division
- Addition and Subtraction
Here’s an example:
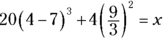
First, evaluate what’s inside the parentheses:
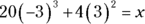
Then evaluate the exponents:
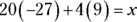
Then multiply:
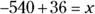
Finally, do the addition and subtraction from left to right:
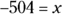
Splitting Up: Fractions, Decimals, and Percentages
Fractions, decimals, and percentages are interrelated concepts; they all represent parts of a whole. You’ll likely need to convert from one form to the other to solve several problems on the GMAT math.
Fractions are really division problems. If you divide the value of a by the value of b, you get the fraction 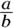 . So
. So  .
.
To convert the fraction to a decimal, you simply perform the division indicated by the fraction bar: 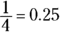 .
.
To convert a decimal back to a fraction, you first count the digits to the right of the decimal point; then divide the original number over a 1 followed by the same number of zeroes as there were digits to the right of the decimal. Then you simplify. So 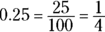 ;
;  .
.
Changing a decimal to a percent is really pretty easy. Percent simply means out of one hundred, or times 100. To perform the conversion, you move the decimal two places to the right. Then you write the resulting number as a percent. For example, 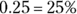 , and
, and 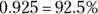 .
.
To turn a percent back into a decimal, you follow the procedure in reverse. You move the decimal point two spaces to the left and lose the percent sign, like this:  .
.
You may encounter a GMAT problem that asks you to find something like the portion of garbage that’s paper when you know that out of 215 million tons of garbage, about 86 million tons of the total garbage are paper products. You should be able to express the answer as a fraction, decimal, and percent.
As a fraction: 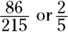
As a decimal: 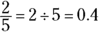
As a percent: 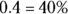
Don’t worry: We provide all the details you need to know about dealing with fractions and percentages in the following sections.
Defining numerators, denominators, and other stuff you need to know about fractions
GMAT questions may refer to the numerator or the denominator of a fraction. The numerator is the number on top and represents the part of the whole. The denominator is the number on the bottom and represents the whole.
To better understand these terms, picture a cherry pie sliced into eight equal pieces (see Figure 15-1) and a hungry family of seven, each of whom has a slice after dinner (or before dinner if they’re sneaky).
The shaded pieces of pie show how much of the dessert was gobbled up by the family; the unshaded piece shows what’s left of the pie when the family is finished.
To put this pie into terms of a fraction, the total number of pieces in the pie to begin with (the whole) represents the denominator, and the number of pieces that were eaten (the part of the whole) is represented by the numerator. In this case, the number of pieces that were eaten made up 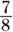 of the total pie, so 7 is the numerator and 8 is the denominator. To look at the scenario another way, you can say that the fraction of pie that was left is
of the total pie, so 7 is the numerator and 8 is the denominator. To look at the scenario another way, you can say that the fraction of pie that was left is 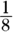 of what you started with.
of what you started with.

© John Wiley & Sons, Inc.
FIGURE 15-1: Fraction of a pie.
Here are a few other fraction definitions you should be familiar with:
- Proper fractions: Fractions where the numerator is less than the denominator. Examples of proper fractions are
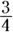 and
and 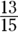 .
. - Improper fractions: Fractions where the numerator is either greater than or equal to the denominator. An example is
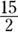 .
. - Mixed fractions: Another way of formatting improper fractions is with a whole number and a proper fraction, such as
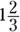 .
. - Reciprocal: The flip-flop of a fraction. The numerator and denominator switch places. So the reciprocal of
 is
is  . To get the reciprocal of a whole number, you simply divide 1 by your number. So the reciprocal of 5 is
. To get the reciprocal of a whole number, you simply divide 1 by your number. So the reciprocal of 5 is  . The reciprocal of a variable a is
. The reciprocal of a variable a is 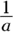 , just as long as
, just as long as 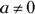 .
.

You multiply the whole number (2) by the denominator (3) to get 6; add the numerator (2) to 6, which gives you 8; and place that value over the original denominator of 3.
To convert an improper fraction to a mixed number, you divide the numerator by the denominator and put the remainder over the denominator, like this:
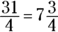
First, you divide 31 by 4: 4 goes into 31 seven times with a remainder of 3 ( and
and 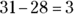 ). Put the remainder over the original denominator, and place that fraction next to the whole number, 7.
). Put the remainder over the original denominator, and place that fraction next to the whole number, 7.
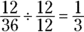
The largest common factor of 12 and 36 is 12. When you divide the fraction by  , it’s the same as dividing by 1. And any number divided by 1 equals the original number. You know that
, it’s the same as dividing by 1. And any number divided by 1 equals the original number. You know that  has the same value as
has the same value as 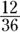 . It’s just in simpler terms.
. It’s just in simpler terms.
Adding and subtracting fractions
Because fractions are parts of whole numbers, they’re not as easy to add together as 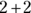 . To add or subtract fractions, you must give them the same denominator. Then all you do is either add or subtract the numerators and put that value over the original denominator, like this:
. To add or subtract fractions, you must give them the same denominator. Then all you do is either add or subtract the numerators and put that value over the original denominator, like this: 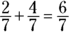 ;
; 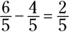 .
.
To determine the least common denominator, consider values that are divisible by both 3 and 9. When you multiply 3 by 9, you get 27. So both 3 and 9 go into 27, but that’s not the smallest number that both 3 and 9 go into evenly. Both 3 and 9 are factors of 9, so the least common denominator is 9 rather than 27.
Convert  to
to 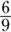 by multiplying the numerator and denominator by 3. The second fraction already has a denominator of 9, so you’re ready to add:
by multiplying the numerator and denominator by 3. The second fraction already has a denominator of 9, so you’re ready to add:
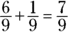
Multiplying and dividing fractions
Multiplying fractions is easy. Just multiply the numerators and the denominators. Reduce if you have to:
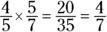
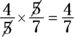
Dividing fractions is pretty much the same as multiplying them except for one very important additional step. Here’s what you do to divide two fractions:
- Find the reciprocal of the second fraction in the equation (that is, turn the second fraction upside down).
- Multiply (yes, multiply) the numerators and denominators of the resulting fractions.
Here’s an example:

To test your knowledge of how to perform operations with fractions, the GMAT may present you with a straightforward equation, such as the following.

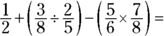
(A) 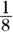
(B) 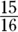
(C) 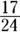
(D) 
(E) 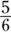
To solve this problem, you need to know how to perform all four operations with fractions. Be sure to follow the order of operations. (See the earlier section, “Order of Operations: Please Excuse My Dear Aunt Sally,” for details.)
First, compute the operations inside the first set of parentheses:

Then, figure out the value of the second set of parentheses:
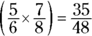
Now the equation looks like this:
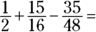
The least common denominator of 2, 16, and 48 is 48. To convert the denominator in the first fraction to 48, you multiply the fraction by 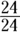 :
:
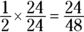
To convert the denominator in the second fraction to 48, you need to multiply by 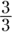 :
:

Now you can compute the expression:
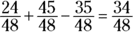
That’s not one of your answer options, so you need to simplify the fraction. Divide the numerator and denominator by 2 to get 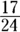 , which is Choice (C).
, which is Choice (C).
Knowing how to perform operations with fractions comes in handy for percent problems, too.
 What is 75% of
What is 75% of 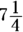 ?
?
(A) 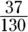
(B) 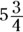
(C) 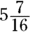
(D) 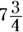
(E) 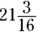
This question asks you to determine a percent of a fraction. Note that the answers are in fraction form rather than decimal form, which means you need to work out the problem so it ends up as a fraction rather than a decimal.
Whenever you see the word of in a word problem, you know it means multiply. Therefore, you’re multiplying 75 percent by 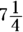 . Converted to a fraction, 75 percent is
. Converted to a fraction, 75 percent is 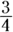 , so you’re trying to find the answer to
, so you’re trying to find the answer to 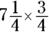 . Converting
. Converting 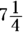 from a mixed fraction gives you
from a mixed fraction gives you 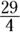 , so the answer is
, so the answer is 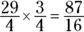 .
.
Convert to a mixed fraction: 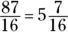 . The answer is Choice (C).
. The answer is Choice (C).
 You can easily eliminate Choices (D) and (E). Obviously, 75 percent of
You can easily eliminate Choices (D) and (E). Obviously, 75 percent of 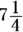 has to be less than
has to be less than 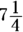 .
.
Calculating percent change
Percent change is the amount a number increases or decreases expressed as a percentage of the original number. For example, if a store normally sells tennis shoes for $72 and has them on sale for $60, what is the percent change of the markdown? To get the percent decrease, simply take the difference in price, which is $12, and divide that number by the original price:
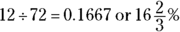
How can that be? The reason the numbers don’t seem to add up is because when you drop the price the first time, you take 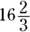 percent of $72, which is a bigger number to take a percent from than the lower sale price.
percent of $72, which is a bigger number to take a percent from than the lower sale price.
So what percent of the marked-down price of $60 must you increase the price by in order to get the original price of $72? To find out, take the difference in price, $12, and determine what percent that is of the sale price of $60:

So it’s a 20 percent increase from 60 to 72.
- To find the result of a percent increase, multiply the original number by 1 plus the rate as a decimal.
- To find the result of a percent decrease, multiply the original number by 1 minus the rate as a decimal.
So if you increase 100 by 5 percent, you multiply 100 by  :
:
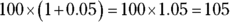
If you decrease 100 by 5 percent, you multiply 100 by 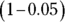 .
.
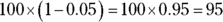
Try a sample percent change problem.
 A file cabinet that originally cost $52 is on sale for 15% off. If the sales tax on office furniture is 5% of the purchase price, how much is the total cost of the file cabinet at its sale price?
A file cabinet that originally cost $52 is on sale for 15% off. If the sales tax on office furniture is 5% of the purchase price, how much is the total cost of the file cabinet at its sale price?
(A) $7.80
(B) $40.00
(C) $44.20
(D) $46.41
(E) $48.23
This word problem asks you how to deal with two percentages, the subtraction of the percentage discount and the addition of the percentage sales tax. First, calculate the discount.
You can figure 15 percent in your head by knowing that 10 percent of 52 is 5.20 and half of that (5 percent) is 2.60, so the discount is $7.80. Now subtract the discount from the original price: $52.00 – $7.80 = $44.20. The discount price for the cabinet is $44.20.
You still need to calculate the sales tax, so don’t choose Choice (C)! You know that 5 percent of 44.20 is half of 4.42 (10 percent), or 2.21. You add $2.21 to $44.20. The only answer that ends in 1 is Choice (D). You can do the math to verify your guess, but Choice (D) is the correct answer: $44.20 + $2.21 = $46.41. Not a bad price for some much-needed organization!
Taking it further: Repeated percent change
Now suppose you want to show a percent change repeated over a period of time, such as when you need to figure out how much interest accrues on a bank account after several years. To do so, you take the formula for percent change a step further.
Suppose you have $100 in a bank account at the end of 2012, and you want to know how much money will be in that same account at the end of 2022 at an annual interest rate of 5 percent. No fair pulling it out when the stock market is making a bull run! One way to figure this out is by using the percentage increase formula. The first step looks something like this:
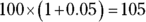
So you have $105 at the end of the first year.
To get the correct answer, tweak the formula a bit by adding an exponent. The exponent will be the number of times the original number changes. The formula looks like this, where n is the number of changes:
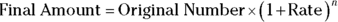
Plug the numbers into the formula and solve:
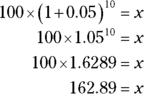
So after 10 years, you’d have $162.89 in the bank.
To show a repeated percent decrease over time, you’d use this similar formula:
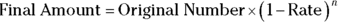
Making Comparisons: Ratios and Proportions
A ratio is the relation between two like numbers or two like values. A ratio may be written as a fraction (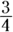 ), as a division expression (
), as a division expression (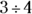 ), or with a colon (3:4), or it can be stated as “3 to 4.”
), or with a colon (3:4), or it can be stated as “3 to 4.”
Because a ratio can be regarded as a fraction, multiplying or dividing both terms of a ratio by the same number doesn’t change the value of the ratio. So 1:4 = 2:8 = 4:16. To reduce a ratio to its lowest terms, simplify the ratio as you would a fraction. (See the earlier section, “Defining numerators, denominators, and other stuff you need to know about fractions.”)
Ratios often crop up in word problems. Suppose an auto manufacturer ships a total of 160 cars to two dealerships at a ratio of 3 to 5. This means that for every three cars that go to Dealer 1, five cars ship to Dealer 2. To determine how many cars each dealership receives, add the terms of the ratio, or 3 + 5, to get the total number of fractional parts each dealership will get: 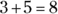 . The first dealership will receive
. The first dealership will receive 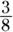 of 160 cars, or
of 160 cars, or 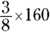 , which equals 60. The second dealership receives
, which equals 60. The second dealership receives  of 160 cars, or 100.
of 160 cars, or 100.
A proportion is a relationship between two equal ratios. It may be written as the proportion sign :: or with an equal sign. So you can read 1:4 :: 2:8 as “1 is to 4 as 2 is to 8.”
The first and last terms in a proportion are called the extremes, and the second and third terms are called the means. If you multiply the means together and multiply the extremes together and then compare the products, you find that the products are the same:
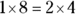
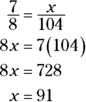
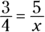
rather than this:
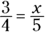
Here’s what a GMAT ratio problem may look like.
 If the ratio of 4a to 9b is 1 to 9, what is the ratio of 8a to 9b?
If the ratio of 4a to 9b is 1 to 9, what is the ratio of 8a to 9b?
(A) 1 to 18
(B) 1 to 39
(C) 2 to 9
(D) 2 to 36
(E) 3 to 9
At first, this problem may appear to be more difficult than it actually is. If 4a to 9b is a 1 to 9 ratio, then 8a to 9b must be a 2 to 9 ratio, because 8a is 2 times 4a. If 4a equals 1, then 8a must equal 2. The answer, therefore, has to be Choice (C).
Playing the Numbers: Scientific Notation
Scientific notation is a simple way to write out humongous (technical term) or teensy weensy (another technical term) numbers so they’re more manageable. You express a number in scientific notation by writing it as the product of a number and a power of 10. Simply move the decimal point so all digits except one are to the right of the decimal point; then multiply that decimal number times 10 raised to an exponent that equals the number of places you moved the decimal point. If you’re working with a large number and you moved the decimal point to the left, the exponent is positive:
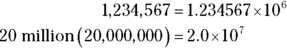
To display very small numbers in scientific notation, you move the decimal point to the right so one value is to the left of the decimal point. When you move the decimal point to the right, the exponent is negative. In this example, the decimal point moved six places to the right:
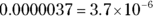
Here’s how the GMAT may test you on scientific notation.
 The number of organisms in a liter of water is approximately
The number of organisms in a liter of water is approximately 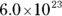 . Assuming this number is correct, about how many organisms exist in a covered Petri dish that contains
. Assuming this number is correct, about how many organisms exist in a covered Petri dish that contains 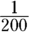 liters of water?
liters of water?
(A) 6.9
(B) 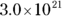
(C) 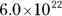
(D) 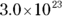
(E) 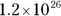
This question uses many words to ask you to the find the answer to  . If a liter of water contains a certain number of organisms,
. If a liter of water contains a certain number of organisms,  liter of water would contain the same number of organisms divided by 200. Try not to let the wording of the question confuse you.
liter of water would contain the same number of organisms divided by 200. Try not to let the wording of the question confuse you.
So if 6.0 divided by 200 equals 0.03, the answer is 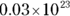 , but that’s not scientific notation because the decimal point is in the wrong place. Move the decimal point two places to the right and decrease the power by two (remember that when you move the decimal point to the right, the exponent is negative, so you subtract). The answer is Choice (B),
, but that’s not scientific notation because the decimal point is in the wrong place. Move the decimal point two places to the right and decrease the power by two (remember that when you move the decimal point to the right, the exponent is negative, so you subtract). The answer is Choice (B), 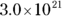 .
.
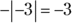 because although the absolute value of –3 is 3, the negative sign outside the bars makes the end result a negative.
because although the absolute value of –3 is 3, the negative sign outside the bars makes the end result a negative. , then
, then 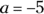 . That is, the cube root of –125 is –5.
. That is, the cube root of –125 is –5.
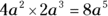
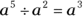
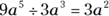
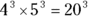 ;
; 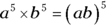
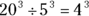 ;
; 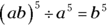
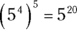 ;
; 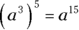
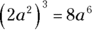
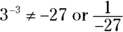 .
.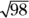 , you’re not done yet. Just think of the factors of 98 that are perfect squares. You know that
, you’re not done yet. Just think of the factors of 98 that are perfect squares. You know that  , and 49 is a perfect square:
, and 49 is a perfect square:  . Put these factors under the radical sign:
. Put these factors under the radical sign: 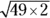 . Now you can extract the 49 from the square root sign because its square root is 7. The result is
. Now you can extract the 49 from the square root sign because its square root is 7. The result is  . Here’s how you may see this situation on the GMAT.
. Here’s how you may see this situation on the GMAT.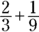 , you know you have to change the denominators before you add.
, you know you have to change the denominators before you add.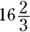 percent, you may think the price returns to its original value. But that’s not right. If you increase the lower price of $60 by 0.1667, you get just about a $10 increase. The price goes from $60 to just about $70:
percent, you may think the price returns to its original value. But that’s not right. If you increase the lower price of $60 by 0.1667, you get just about a $10 increase. The price goes from $60 to just about $70: 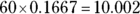 ;
; 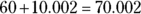 .
.