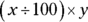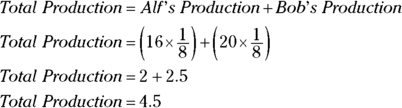Chapter 16
Considering All the Variables: Algebra
IN THIS CHAPTER
 Defining variables and other fundamental algebra terms
Defining variables and other fundamental algebra terms
 Solving your problems with algebraic operations
Solving your problems with algebraic operations
 Simplifying your life with factoring
Simplifying your life with factoring
 Getting functions to function
Getting functions to function
 Cracking the mysteries of solving algebraic equations and inequalities
Cracking the mysteries of solving algebraic equations and inequalities
Algebra is the study of properties of operations carried out on sets of numbers. That may sound like mumbo-jumbo, but the idea is that algebra is really just a form of arithmetic in which symbols (usually letters) stand for numbers. You use algebra to solve equations and to find the value of a variable. For example, how often have you heard the command, “Solve the equation for x”?
The algebra concepts tested on the GMAT are limited to the ones you’d use in a first-year algebra course, so you’re at no disadvantage if you’ve never taken Algebra II. But many GMAT math problems involve basic algebra, and this chapter provides what you need to know to excel on all of them.
Defining the Elements: Algebraic Terms
Before we jump into solving algebra problems, we define some terms you need to know in the following sections. Although the GMAT doesn’t specifically test you on the definitions of variable, constant, and coefficient, it does expect you to know these concepts when they crop up in the questions.
Braving the unknowns: Variables and constants
You’ll see a lot of variables in algebra problems. They’re the symbols that stand for numbers. Usually the symbols take the form of letters and represent specific numeric values. True to their name, variables’ values can change depending on the equation they’re in.
Think of variables as abbreviations for discrete things. For example, if a store charges different prices for apples and oranges and you buy two apples and four oranges, the clerk can’t ring them up together by simply adding  to get 6. That would be incorrectly comparing apples and oranges! So, to express the transaction in algebraic terms, you use variables to stand in for the price of apples and oranges, something like 2a and 4o.
to get 6. That would be incorrectly comparing apples and oranges! So, to express the transaction in algebraic terms, you use variables to stand in for the price of apples and oranges, something like 2a and 4o.
In contrast, constants, as their name implies, are numbers with values that don’t change in a specific problem. Letters may also be used to refer to constants, but they don’t change their value in an equation as variables do (for example, a, b, and c stand for fixed numbers in the formula 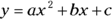 ).
).
Coming together: Terms and expressions
Single constants and variables or constants and variables grouped together form terms; terms are any set of variables or constants you can multiply or divide to form a single unit in an equation. You can combine these single parts in an equation that applies addition or subtraction. For example, the following algebraic expression has three terms: 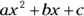 . The first term is
. The first term is 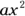 , the second term is bx, and the third term is c.
, the second term is bx, and the third term is c.
Terms often form expressions. An algebraic expression is a collection of terms that are combined by addition or subtraction and are often grouped by parentheses, such as 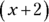 ,
,  , and
, and 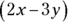 . Although an expression can contain just one term, it’s more common to think of expressions as combinations of two or more terms. So, in the apples and oranges scenario we presented earlier, you can make an expression for combining two apples and four oranges, which may look something like this:
. Although an expression can contain just one term, it’s more common to think of expressions as combinations of two or more terms. So, in the apples and oranges scenario we presented earlier, you can make an expression for combining two apples and four oranges, which may look something like this: 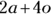 .
.
A coefficient is a number or symbol that serves as a measure of a property or characteristic. In 2a + 4o, the variables are a and o, and the numbers 2 and 4 are the coefficients of the variables. This means that the coefficient of the variable a is 2 and the coefficient of the variable o is 4.
In an algebraic expression, terms involving the same variable, even if they have different coefficients, are called like terms. For example, in the expression 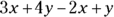 , 3x and –2x are like terms because they both contain the single x variable; 4y and y are also like terms because they both contain the y variable and only the y variable.
, 3x and –2x are like terms because they both contain the single x variable; 4y and y are also like terms because they both contain the y variable and only the y variable.
You can combine (add/subtract) like terms together, but you can’t combine unlike terms. So, in the expression 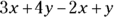 , you can subtract the terms with the common x variable:
, you can subtract the terms with the common x variable: 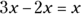 . And you can add the like terms with the common y variable:
. And you can add the like terms with the common y variable: 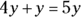 (if a variable has no visible numerical coefficient, it’s understood that its coefficient is 1; therefore, y is understood to be 1y). All this combining results in the final expression of
(if a variable has no visible numerical coefficient, it’s understood that its coefficient is 1; therefore, y is understood to be 1y). All this combining results in the final expression of 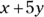 , which is a much simpler expression to work with. We work with many more algebraic expressions in the section, “Maintaining an Orderly Fashion: Algebraic Operations,” later in this chapter.
, which is a much simpler expression to work with. We work with many more algebraic expressions in the section, “Maintaining an Orderly Fashion: Algebraic Operations,” later in this chapter.
Knowing the nomials: Kinds of expressions
Expressions carry particular names depending on how many terms they contain. On the GMAT, you’ll work with monomials and polynomials.
A monomial is an expression that contains only one term, such as 4x or 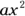 . A monomial is, therefore, also referred to as a term in an algebraic expression.
. A monomial is, therefore, also referred to as a term in an algebraic expression.
Poly means many, so we bet you’ve already figured out that a polynomial is an expression that has more than one term. These multiple terms can be added together or subtracted from one another. Here are a couple of examples of polynomials:
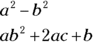
Polynomials can have more specific designations, depending on how many terms they contain. For example, a binomial is a specific kind of polynomial, one that contains two terms, such as 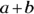 or
or 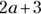 . And a trinomial is a polynomial with three terms, like
. And a trinomial is a polynomial with three terms, like 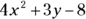 .
.
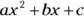
We discuss this very important expression in the “Solving quadratic equations” section, later in this chapter.
Maintaining an Orderly Fashion: Algebraic Operations
Symbols like +, –,  , and
, and  are common to arithmetic and algebra. They symbolize the operations you perform on numbers. Arithmetic uses numbers with known values, such as
are common to arithmetic and algebra. They symbolize the operations you perform on numbers. Arithmetic uses numbers with known values, such as 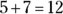 , in its operations (visit Chapter 15 for more on basic arithmetic operations), but algebraic operations deal with unknowns, like
, in its operations (visit Chapter 15 for more on basic arithmetic operations), but algebraic operations deal with unknowns, like 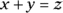 . This algebraic equation can’t produce an exact numerical value because you don’t know what x and y represent, let alone z. But that doesn’t stop you from solving algebra problems as best you can with the given information. In the following sections, we show you how to add, subtract, multiply, and divide expressions with unknowns.
. This algebraic equation can’t produce an exact numerical value because you don’t know what x and y represent, let alone z. But that doesn’t stop you from solving algebra problems as best you can with the given information. In the following sections, we show you how to add, subtract, multiply, and divide expressions with unknowns.
Adding to and taking away
From arithmetic, you know that 3 dozen plus 6 dozen is 9 dozen, or
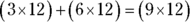
In algebra, you can write a somewhat similar equation by using a variable to stand in for the dozen: 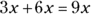 . And you can subtract to get the opposite result:
. And you can subtract to get the opposite result: 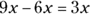 .
.
For example, to tackle the expression 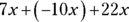 , you find the sum of the two positive numbers (7x and 22x) and then subtract the value of the negative number (because adding a negative is the same as subtracting a positive), like this:
, you find the sum of the two positive numbers (7x and 22x) and then subtract the value of the negative number (because adding a negative is the same as subtracting a positive), like this:
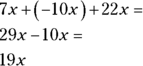
That’s fine for adding and subtracting like terms, you may say, but what about working with unlike terms? You can’t combine terms with different symbols or variables the same way you can when the symbols are the same. For instance, take a look at this example:
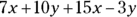
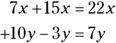
which gives you this final expression:
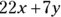

Here’s how an algebra problem may look on the GMAT.
 For all x and y,
For all x and y, 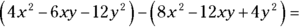 ?
?
(A) 
(B) 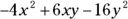
(C) 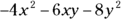
(D) 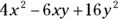
(E) 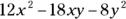
The easiest way to approach this problem is to distribute the negative sign to the second expression (see the later section, “Distributing terms”) and combine the two expressions with like terms by following these steps:
-
Distribute the negative sign (multiply each term in the second expression by –1).
Remember that subtracting is the same as adding a negative number. So your problem is really
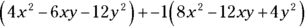 . Distributing the negative sign changes the second expression to
. Distributing the negative sign changes the second expression to 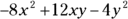 , because a negative times a positive makes a negative and two negatives make a positive.
, because a negative times a positive makes a negative and two negatives make a positive. - Combine the expressions with like terms together:
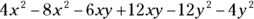
- Add and subtract like terms:
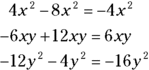
- Put the terms back into the polynomial:
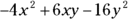
So the answer is  , which is Choice (B). If you chose any of the other answers, you either distributed the negative sign improperly or you added and subtracted the like terms incorrectly.
, which is Choice (B). If you chose any of the other answers, you either distributed the negative sign improperly or you added and subtracted the like terms incorrectly.
 Eliminate wrong answers as you combine terms. For instance, once you determine that the first term is
Eliminate wrong answers as you combine terms. For instance, once you determine that the first term is 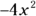 , you can eliminate Choices (D) and (E).
, you can eliminate Choices (D) and (E).
 After you’ve combined like terms, double-check that you’ve used the correct signs, particularly when you change all the signs like you did in the second expression. The other answer choices for the sample problem are very similar to the correct choice. They’re designed to trap you in case you make an addition or subtraction error. Add and subtract carefully, and you won’t fall for these tricks.
After you’ve combined like terms, double-check that you’ve used the correct signs, particularly when you change all the signs like you did in the second expression. The other answer choices for the sample problem are very similar to the correct choice. They’re designed to trap you in case you make an addition or subtraction error. Add and subtract carefully, and you won’t fall for these tricks.
Multiplying and dividing expressions
Multiplying and dividing two or more variables works just as though you were performing these same operations on numbers with known values. So if 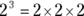 , then
, then 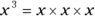 . Likewise, if
. Likewise, if 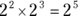 , then
, then 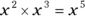 . Similarly, if
. Similarly, if  , then
, then 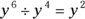 .
.
The process is pretty simple for monomials, but polynomials may be a little more complicated. In the next sections, we explore the different methods for multiplying and dividing polynomials.
Distributing terms
You can distribute terms in algebra just like you do in arithmetic. For example, when you multiply a number by a binomial, you multiply the number by each term in the binomial. In this example, you multiply 4x by each term inside the parentheses:
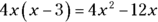
With division, you do the same operation in reverse.
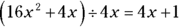
Here’s an example of a GMAT question for which you can use distribution to answer.
 For all x,
For all x, 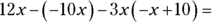 ?
?
(A) 10x
(B) 
(C) 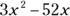
(D) 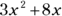
(E) 
This question tests your ability to add, subtract, and multiply terms in an algebraic expression. First, use distribution to multiply –3x by 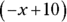 :
:
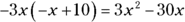
Now the equation looks like this:
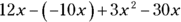
Combine the terms that contain the x variable:
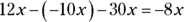
So the answer to the equation is Choice (E): 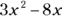 .
.
Stacking terms
One easy way to multiply polynomials is to stack the two numbers to be multiplied on top of one another. Suppose you have this expression: 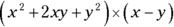 .
.
You can stack this expression just like an old-fashioned multiplication problem. Just remember to multiply each of the terms in the second line by each term in the first line.
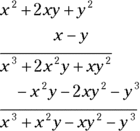
The GMAT may ask you to divide a polynomial by a monomial. Simply divide each term of the polynomial by the monomial. Here’s how you’d divide the expression  :
:
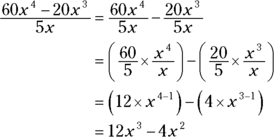
Taking a shine to the FOIL method
You can multiply binomials by using the FOIL method. FOIL is an acronym for first, outer, inner, last, which indicates the order that you multiply the terms from one binomial by the terms of the second binomial before adding their products. Take a look at this example:

Multiply the first terms in each binomial — 4x and 3x.
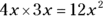
Then multiply the outer terms (4x and 8) to get 32x and the inner terms (3x and –5) to get –15x. You can add the products at this point because they’re like terms.
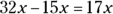
Last, multiply the last terms.
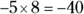
Combine the products to form the resulting expression.
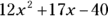
You may recognize this expression as the quadratic polynomial we discussed in the earlier section, “Knowing the nomials: Kinds of expressions.”

So if you’re asked to multiply  , you know without using FOIL that the answer is
, you know without using FOIL that the answer is  or
or 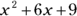 . And
. And 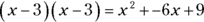 or
or  .
.
If you’re able to keep track of the terms, you can use FOIL to multiply terms in the proper order without taking the time to stack them. The FOIL method comes in handy for solving GMAT problems like the next one.
 When the polynomials
When the polynomials  and
and 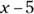 are multiplied together and written in the form
are multiplied together and written in the form 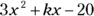 , what is the value of k?
, what is the value of k?
(A) 2
(B) 3
(C) –5
(D) –11
(E) –20
This question asks you for the constant in the middle term of the quadratic expression formed by multiplying 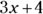 and
and 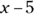 . Remember with FOIL, you multiply the first, outer, inner, and last. The problem gives you the first term: 3x2. The last is also there: –20. Because the problem provides the product of the first terms and last terms, all you have to do to get the middle term is to multiply the outer and inner numbers of the two expressions and then add them together.
. Remember with FOIL, you multiply the first, outer, inner, and last. The problem gives you the first term: 3x2. The last is also there: –20. Because the problem provides the product of the first terms and last terms, all you have to do to get the middle term is to multiply the outer and inner numbers of the two expressions and then add them together.
- Multiply the outer numbers:
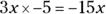
- Multiply the inner numbers:

So the middle term of the quadratic is 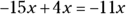 . The constant k must equal –11, which is Choice (D).
. The constant k must equal –11, which is Choice (D).
Extracting Information: Factoring Polynomials
Factors are the numbers you multiply together to get a product. So, factoring a value means you write that value as a product of its factors. For the GMAT, you should know how to pull out the common factors in expressions and the two binomial factors in a quadratic polynomial. We show you how to do both in the following sections.
Something in common: Finding common factors
To simplify polynomials for complex problems, extract their common factors by dividing each term by the factors that are common to every term. You can think of the process as the opposite of distributing terms. For example, to find the common factors of the terms in the expression  , follow these steps:
, follow these steps:
-
Consider the coefficients.
Because –7 is common to both –14 and –35, take this factor out of the expression by dividing both terms by –7. Then put the remaining expression in parentheses next to the common factor:
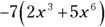 .
. -
Now look at the variables.
Because
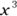 or a multiple of it is common to both terms, divide both terms in parentheses by
or a multiple of it is common to both terms, divide both terms in parentheses by 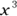 , multiply x3 by the other common factor (–7), and put the remaining expression in parentheses:
, multiply x3 by the other common factor (–7), and put the remaining expression in parentheses: 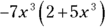 .
.So,
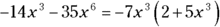 .
.
Two by two: Factoring quadratic polynomials
The GMAT also expects you to know how to factor quadratic polynomials. To accomplish this task, you have to perform the FOIL operations in reverse to come up with a couple of binomial factors that look something like this: 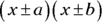 .
.
For example, look at the following quadratic polynomial:
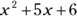
To find its factors, draw two sets of parentheses: ( )( ). The first terms of the two factors have to be x and x because 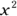 is the product of x and x. So you can add x as the first term for both sets of parentheses. You know that the operation in both terms must be addition because both the middle and last terms of the quadratic expression are positive:
is the product of x and x. So you can add x as the first term for both sets of parentheses. You know that the operation in both terms must be addition because both the middle and last terms of the quadratic expression are positive:
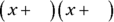
To find the second terms for the two factors, ask yourself which two numbers have a product of 6 (the third term of the quadratic) and add up to the number 5 (the coefficient of the quadratic’s second term). The only two factors that meet these two criteria are 2 and 3. The other factors of 6 (6 and 1, –6 and –1, –2 and –3) don’t add up to 5. So the binomial factors of the quadratic equation are  and
and 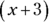 .
.
There’s a timesaving way to factor binomials that are made up of a difference of perfect squares, such as  . Factors for these types of quadratic polynomials (known as the difference of perfect squares) result in the following form:
. Factors for these types of quadratic polynomials (known as the difference of perfect squares) result in the following form:

The variable x is the square root of the first term, and a is the square root of the second term. So the factors of 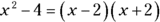 .
.
This factoring technique is very easy to memorize and can help you answer some algebra questions much more quickly than if you were to take the time to carry out long calculations. For example, if you’re asked to multiply factors 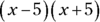 , you can use the FOIL method to figure out the answer, but spotting that the correct answer will be the difference of two perfect squares is much faster. You know the correct answer is
, you can use the FOIL method to figure out the answer, but spotting that the correct answer will be the difference of two perfect squares is much faster. You know the correct answer is 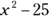 without performing time-consuming calculations.
without performing time-consuming calculations.
Likewise, if you need to factor 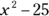 , all you do is figure the square root of
, all you do is figure the square root of 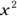 and the square root of 25 and enter those values into the proper factoring form for perfect square quadratics. You know right away that the factors are
and the square root of 25 and enter those values into the proper factoring form for perfect square quadratics. You know right away that the factors are 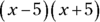 .When you break down the quadratic polynomial, you’ll be able to solve quadratic equations. For more about how to do this, see the section, “Solving quadratic equations,” later in this chapter.
.When you break down the quadratic polynomial, you’ll be able to solve quadratic equations. For more about how to do this, see the section, “Solving quadratic equations,” later in this chapter.
Knowing how to multiply polynomials with variables can help you more efficiently solve similar problems that don’t contain variables, such as this one:
 What is the value of
What is the value of  ?
?
(A) –1
(B) 0
(C) 1
(D) 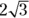
(E) 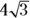
You may look at this question and think “Gee, I wish I had a calculator to help me add and subtract the stuff in the parentheses.” But then you may notice that this problem looks a lot like multiplying binomial expressions. All you need is FOIL!
- Multiply the first terms:
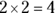
- Notice that the inner and outer terms will cancel each other because you’re adding and subtracting the same terms:

- Multiply the last terms:

- Combine the remaining terms:
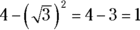
The answer is Choice (C) — no calculator needed.
Minding Your Ps and Qs: Functions
Some of the GMAT math questions involve functions. Simply put, functions are relationships between two sets of numbers; each number you put into the formula gives you only one possible answer. Functions may sound complicated, but they’re really pretty simple. A function problem looks something like this:
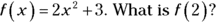
We explore the terminology of functions and how to find the domain and range of functions in the following sections.
Standing in: Understanding function terminology
Before we show you how to solve function problems, you need to know a few definitions. Table 16-1 gives you the terms we use when we discuss functions.
TABLE 16-1 Defining Terms for Functions
|
Term |
Definition |
|---|---|
|
Function |
A rule that turns each member of one set of numbers into a member of another set. |
|
Independent variable (input) |
The number you want to find the function of; the x in f(x). |
|
Dependent variable (output) |
The result of substituting the independent value into the function, f(x). (This is like your y variable.) |
|
Domain |
The set of all possible values of the independent variable. |
|
Range |
The set of all possible values of the dependent variable. |
Functions on the GMAT are usually displayed with the letters f or g. For example, f(x) is used to indicate the function of x, and it simply means “f of x.”
Don’t let this language confuse you. All you really have to do is substitute the indicated value for x in the function.
To see how functions work, consider the earlier example:
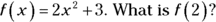
The initial expression means that the function of x is to square x, multiply the result by 2, and then add 3. To calculate the function exercise with the number f(2), you just substitute 2 for x in the expression and solve.

So when x is 2, f(x) is 11. That’s all there is to it! The function notation is really just a fancy way of telling you to perform a substitution.
Here’s another example.
 If
If 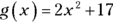 , what is g(12)?
, what is g(12)?
(A) 12
(B) 17
(C) 100
(D) 288
(E) 305
If you quickly consider the situation, you can eliminate Choices (A), (B), and (C) right away. When you substitute 12 for x in the function, you square 12, which is 144. The answer then results from multiplying by and adding to that number, so you know the result will be greater than 100. Furthermore, the answer in Choice (D), 288, is just 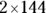 . You still have to add 17, so the answer probably isn’t Choice (D) either. Without much calculation, you can eliminate enough answers to determine that Choice (E) is correct. But to do the calculations, just substitute 12 for x and solve:
. You still have to add 17, so the answer probably isn’t Choice (D) either. Without much calculation, you can eliminate enough answers to determine that Choice (E) is correct. But to do the calculations, just substitute 12 for x and solve:
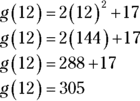
The answer is definitely Choice (E).
That was a pretty simple problem. But functions can get more complicated on the GMAT. Check out this example.
 If
If 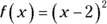 , what is
, what is 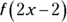 equal to?
equal to?
(A) 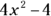
(B) 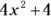
(C) 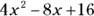
(D) 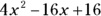
(E) 
Don’t try to do this one in your head. Begin by plugging in 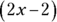 for x. Then solve.
for x. Then solve.
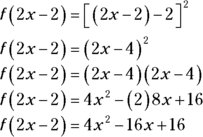
So the correct answer is Choice (D).
Taking it to the limit: Domain and range of functions
The domain of a function is the set of all numbers that can possibly be an input of a function, the x in f(x). The range of a function is the set of all numbers that can possibly be an output of a function, the value for f(x). In other words, if you think of the domain as the set of all possible independent variables values you can put into a function, the range is the set of all possible dependent variables values that can come out of any particular function. Domain and range questions aren’t difficult, but you need to be aware of some basic rules to determine the proper limits of the domain and range. The GMAT also tests you on graphing functions on the coordinate plane, but we discuss that in Chapter 18.
Mastering the territory: Domain
Unless a problem specifies otherwise, the domain of a function includes all real numbers, which means that the only numbers that aren’t included in the domain are numbers that aren’t real (see Chapter 15 for more info on imaginary and real numbers). Here are some properties of numbers that aren’t real and, therefore, can’t be part of the domain of a function:
- A real number can’t be a fraction with a denominator of 0, because then the number would be undefined.
-
A real number can’t be an even-numbered root of a negative number. Even-numbered roots of negatives aren’t real numbers because any number that’s squared or has an even-numbered power can’t result in a negative number.
For example, there’s no such thing as
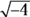 because there’s no one number that you can square that results in a negative 4. So
because there’s no one number that you can square that results in a negative 4. So 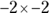 will always equal positive 4.
will always equal positive 4.
To see how the first rule affects domain, look at this function:
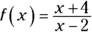
Normally, the domain of x in a function can contain an unlimited number of values. In the preceding example, though, you have a fraction in the function, which puts the variable x in the denominator. Because your denominator can’t add up to 0, the denominator of 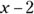 can’t equal 0. This means that x can’t equal 2. In terms of functions, the domain of f(x) is, therefore,
can’t equal 0. This means that x can’t equal 2. In terms of functions, the domain of f(x) is, therefore, 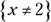 . That’s all there is to it!
. That’s all there is to it!
Here’s a function that relates to the second rule:
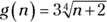
In this function, you have an even-numbered radical sign with the variable n within it. You know that the root of an even-numbered radical, in this case, the 4th root, can’t be a negative number. Otherwise, you wouldn’t have a real number as your final answer. Therefore, the number under the radical sign can’t be less than 0. So 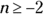 . The result is that the domain of the function g(n) is
. The result is that the domain of the function g(n) is 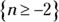 .
.
The GMAT may test your knowledge of domain with a problem such as the following.
 Determine the domain of the function
Determine the domain of the function  .
.
(A) 
(B) 
(C) 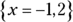
(D) 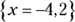
(E) 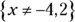
This problem involves simple algebra. You know the denominator can’t equal 0, so set the trinomial in the denominator equal to 0, and solve for x to find out what x can’t be. We show you how to solve trinomials later in the “Solving quadratic equations” section.
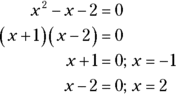
 You’re not finished! If you picked Choice (C) as your answer, your factoring would have been absolutely right, but your answer would be absolutely wrong. Answer Choice (C) gives you only the values for x that make the denominator equal to 0. You’re trying to find the values that make the denominator not equal to 0.
You’re not finished! If you picked Choice (C) as your answer, your factoring would have been absolutely right, but your answer would be absolutely wrong. Answer Choice (C) gives you only the values for x that make the denominator equal to 0. You’re trying to find the values that make the denominator not equal to 0.
So, the correct answer is Choice (A); x can be any real number other than –1 and 2 because if x were equal to –1 or 2, the denominator would be 0, and the value would be undefined. If you chose Choice (B), you switched the signs of the factors. If you chose Choices (D) or (E), you found the correct factors of the denominator but mistakenly divided the numerator by each root of the denominator.
Roaming the land: Range
Just as the domain of a function is limited by certain laws of mathematics, so, too, is the range. Here are the rules to remember when you’re determining the range of a function:
- An absolute value of a real number can’t be a negative number.
- An even exponent or power can’t produce a negative number.
Check out some situations where these rules come into play. Look at the following functions:
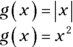
Each of these functions can result only in an output that’s a positive number or 0. So in each case, the range of the function of g is greater than or equal to 0. Here’s a question that puts the range rules to work.
 What is the range of the function
What is the range of the function 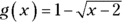 ?
?
(A) 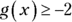
(B) 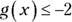
(C) 
(D) 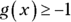
(E) 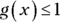
 First, you have to make the radical a real number. The value within the square root sign has to be equal to or greater than 0. So, x has to be equal to or greater than 2, because any value less than 2 would make the radical a negative value. To check the possible outputs, consider several values for x.
First, you have to make the radical a real number. The value within the square root sign has to be equal to or greater than 0. So, x has to be equal to or greater than 2, because any value less than 2 would make the radical a negative value. To check the possible outputs, consider several values for x.
If x is the lowest value, 2, you’d figure the output of the function like this:
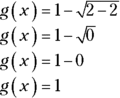
So you know that g(x) can be equal to 1.
If x is a higher value than 2, say 6, then you’d calculate the output like this:
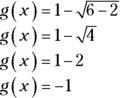
Now you know that any value for x that’s higher than 2 results in a lower value for the output of the function. Therefore, g(x) has to equal 1 or be less than 1, and the correct answer is Choice (E).
 Getting confused and looking for the domain when you should be finding the range is very easy. If you chose Choice (C), you solved for the domain of x. If you chose Choices (A) or (B), you’re hung up trying to make the number under the radical a positive number. If you chose Choice (D), you simply don’t know how to solve for range, so be sure to review this section.
Getting confused and looking for the domain when you should be finding the range is very easy. If you chose Choice (C), you solved for the domain of x. If you chose Choices (A) or (B), you’re hung up trying to make the number under the radical a positive number. If you chose Choice (D), you simply don’t know how to solve for range, so be sure to review this section.
Putting On Your Thinking Cap: Problem Solving
You may be wondering how the GMAT tests your knowledge of algebra concepts. Well, wonder no more. The following sections present you with many of the ways you’ll use algebra to solve GMAT math problems.
Isolating the variable: Linear equations
A linear equation is an algebra equation that contains an unknown variable and no exponent greater than 1. In other words, these equations are fairly easy.
In its simplest form, a linear equation is expressed as 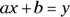 , where x is the variable and a and b are constants. Here are two things to keep in mind when you’re solving linear equations:
, where x is the variable and a and b are constants. Here are two things to keep in mind when you’re solving linear equations:
- Isolate the variable in the equation you’re trying to solve, which means you work to get it all by itself on one side of the equation. In other words, you’re solving for x.
- Whatever operation you perform on one side of the equation, you must do to the other side.
This easy question asks you to solve a linear equation: If 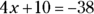 , what is the value of x?
, what is the value of x?
Solve for x by isolating the variable on one side of the equation:
-
Eliminate 10 from the left side of the equation by subtracting it.
(Remember that if you do something to one side of the equation, you need to do the same thing to the other side. Otherwise, your math teacher is liable to rap you on the knuckles with a slide rule.) Here’s what happens when you subtract 10 from both sides:
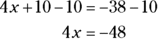
- Divide both sides by 4, and you have your answer.
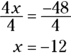
The value of x is –12.
You tackle division problems the same way. So if you’re asked to solve for x in the problem 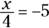 , you know what to do. Isolate x to the left side of the equation by multiplying both sides of the equation by 4:
, you know what to do. Isolate x to the left side of the equation by multiplying both sides of the equation by 4:
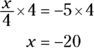

The lowest number that 5, 15, and 10 go into evenly is 30, so that’s your least common denominator. Multiply each fraction by a fraction equivalent to 1 that will give you 30 in the denominators, like this:
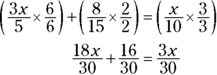
Now you can eliminate the fractions by multiplying both sides of the equation by 30:
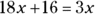
Then just solve for x:
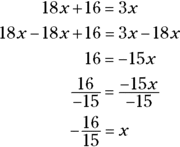
Bringing in the substitution: Simultaneous equations
Solving for x is simple when it’s the only variable, but what if your equation has more than one variable? When you have another equation that contains at least one of the variables, you can solve for either variable. These two equations are called simultaneous equations. You just solve one of the equations for one of the variables and then plug the answer into the other equation and solve. Here’s a simple example.
If 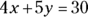 and
and 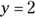 , what is the value of x?
, what is the value of x?
Because the second equation tells you that y is 2, just substitute 2 for the value of y in the first equation and you’re on your way:
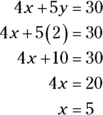
That’s all there is to it!
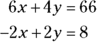
Your goal is to find a way to remove one of the variables. Here’s how:
-
Examine the equations to determine what terms you can eliminate through addition or subtraction.
If you multiply the entire second equation by 3, you can eliminate the x terms in both equations because
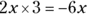 , and
, and 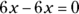 . Just be sure to multiply each term in the equation by the same value. So the second equation becomes
. Just be sure to multiply each term in the equation by the same value. So the second equation becomes  .
. - Stack the equations, combine like terms, and solve for y.
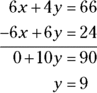
-
Plug the value of one variable into one of the equations and solve for the other value.
You’ve found that y = 9, so substitute 9 for the value of y in one of the equations to solve for x.
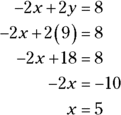
Therefore, the solutions, also referred to as roots, to the simultaneous equations are x = 5 and y = 9.
Knowing that you can find solutions for variables when you have as many separate linear equations as the number of distinct variables they contain can help you answer some data sufficiency questions, such as this example.
 What is the value of x?
What is the value of x?
(A) Statement 1 is sufficient.
(B) Statement 2 is sufficient.
(C) The two statements are sufficient together.
(D) Each of the statements is sufficient alone.
(E) Neither statement nor both together is sufficient.
You can’t solve for x using either of the statements by itself. The best you can do is solve for x in terms of y in either case. So the answer is either Choice (C) or (E). Without lifting a pencil, you know that the answer is Choice (C); the statements are sufficient together. Each of the two distinct equations contains the same two variables, so the conditions are met to reach a clear value for x. You don’t have to take the time to actually solve for x during the exam, but we’ll take you through the process in case you aren’t convinced.
Combine like terms in Statement 2:
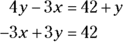
Multiply all terms in the Statement 2 equation by 3 so you can eliminate the y value when you stack the two equations:
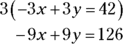
Stack the equations and solve:
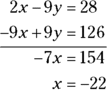
Not playing fair: Inequalities
An inequality is a statement such as “x is less than y” or “x is greater than or equal to y.”
In addition to the symbols for add, subtract, multiply, and divide, mathematics also applies standard symbols to show how the two sides of an equation are related. You’re probably pretty familiar with these symbols, but a little review never hurts. Table 16-2 gives you a rundown of the symbols you’ll deal with on the GMAT.
Performing operations with inequalities
You treat inequalities a lot like equations. Isolate the variable to one side and perform the same operations on both sides of the inequality. The only difference is that if you multiply or divide by a negative number, you need to reverse the direction of the inequality sign. So, here’s how you solve this inequality:
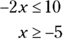
TABLE 16-2 Mathematical Symbols for Equality and Inequality
|
Symbol |
Meaning |
|---|---|
|
= |
Equal to |
|
|
Not equal to |
|
|
Approximately equal to |
|
> |
Greater than |
|
< |
Less than |
|
|
Greater than or equal to |
|
|
Less than or equal to |
Working with ranges of numbers
You can also use inequalities to show a range of numbers. For example, the GMAT may show the range of numbers between –6 and 12 as an algebraic inequality, like this:
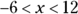
To show the range between –6 and 12 including –6 and 12, you use the 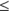 sign:
sign:
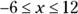
You can add or subtract values within a range. For example, you add 5 to each part of 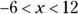 , like this:
, like this:
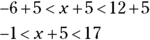
And you can perform operations between different ranges, such as 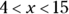 and
and 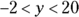 . To find the sum of these two ranges, follow these steps:
. To find the sum of these two ranges, follow these steps:
- Add the smallest values of each range:
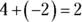
- Add the largest values of each range:

- Create a new range with the sums:
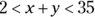
This means that the range of values of 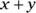 is
is 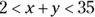 .
.
Here’s an example of how the GMAT may ask you to deal with inequalities.
 If
If 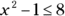 , what is the smallest real value x can have?
, what is the smallest real value x can have?
(A) –9
(B) –6
(C) –3
(D) 0
(E) 3
This problem asks you to determine the smallest real value of x if 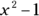 is less than or equal to 8. Solve the inequality for x:
is less than or equal to 8. Solve the inequality for x:

Or 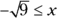 because the product of two negative numbers is also positive.
because the product of two negative numbers is also positive.
So,  . Remember that the square root of a number may be positive or negative. The square root of 9 is either 3 or –3. Because –3 is less than 3, –3 must be the smallest real value of x.
. Remember that the square root of a number may be positive or negative. The square root of 9 is either 3 or –3. Because –3 is less than 3, –3 must be the smallest real value of x.
To make sure you’re right, you can eliminate answer choices by using common sense. For example, –9 in Choice (A) would make 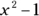 equal 80, and –6 in Choice (B) would make
equal 80, and –6 in Choice (B) would make 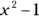 equal 35. So neither Choice (A) nor (B) can be a solution for x. In Choice (D), 0 is a solution for x, but it isn’t the smallest solution, because you know that –3 is a possibility. Choice (E) can’t be right because it’s larger than two other possible solutions, –3 and 0. So Choice (C) is the correct answer.
equal 35. So neither Choice (A) nor (B) can be a solution for x. In Choice (D), 0 is a solution for x, but it isn’t the smallest solution, because you know that –3 is a possibility. Choice (E) can’t be right because it’s larger than two other possible solutions, –3 and 0. So Choice (C) is the correct answer.
Solving quadratic equations
When you set a quadratic polynomial equal to 0, you get what’s called a quadratic equation. An example of the classic quadratic form is 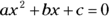 , where a, b, and c are constants and x is a variable that you have to solve for. Notice that 0 is on one side of the equation, and all non-zero terms are on the other side.
, where a, b, and c are constants and x is a variable that you have to solve for. Notice that 0 is on one side of the equation, and all non-zero terms are on the other side.
Quadratic equations may appear in slightly different forms. For example, all the following equations are quadratic equations because they contain a squared variable and equal 0:
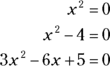
Factoring to find x
The GMAT may give you a quadratic equation and ask you to solve for x. The simplest way to solve a quadratic equation is to try to factor the equation into two binomials, just like you did earlier in the section, “Two by two: Factoring quadratic polynomials.”

To factor this trinomial, consider what numbers multiply together to become 5 that also have a sum of –6.
The two factors of 5 are 5 and 1 or –5 and –1. To get a sum of –6, you need to go with the negative values. Doing so gives these two binomial factors: 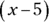 and
and 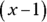 . So the resulting equation is
. So the resulting equation is  .
.
To solve for x, you set each of the binomial factors equal to 0. You can do so because you know that one of the factors must equal 0 if their product is 0.
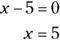
and
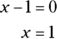
Now the solutions (or roots) to the equation are clear: 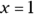 and
and  . Both 1 and 5 are possible solutions for x in this quadratic equation.
. Both 1 and 5 are possible solutions for x in this quadratic equation.
Determining solutions for the difference of perfect squares
Finding the solution set for a quadratic equation made up of the difference of perfect squares (like  ) is simple if you remember that
) is simple if you remember that 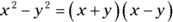 . If the GMAT presents you with the task of solving for x in an equation where the difference of perfect squares is equal to 0, you know that x equals the positive and negative values of the square root of y2 (which is the second term).
. If the GMAT presents you with the task of solving for x in an equation where the difference of perfect squares is equal to 0, you know that x equals the positive and negative values of the square root of y2 (which is the second term).
So, if you were told to find the solution set for 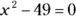 , you’d determine the square root of the second term (49), which is 7. The factors, then, are
, you’d determine the square root of the second term (49), which is 7. The factors, then, are 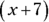 and
and  . Therefore, the solution set for this problem is
. Therefore, the solution set for this problem is  and
and 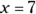 , which are indeed the positive and negative values of the second term’s square root!
, which are indeed the positive and negative values of the second term’s square root!
Using the quadratic formula
Solving quadratic equations is easy when the solutions come out to be nice, round numbers. But what if the ultimate solutions are harsh-looking radicals or perhaps not even real roots? For the rare GMAT occasions when you can’t simply solve a quadratic equation by factoring, you may have to use the quadratic formula, which is a rearrangement of the classic equation: 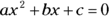 . It looks like this:
. It looks like this:
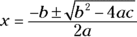
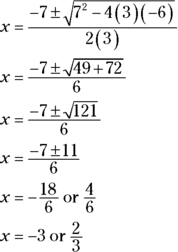
The solutions for x are 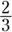 and –3. Whew! Luckily, the GMAT won’t give you many quadratic equations that require you to apply this formula. But you’ll know what to do if you encounter one of the few.
and –3. Whew! Luckily, the GMAT won’t give you many quadratic equations that require you to apply this formula. But you’ll know what to do if you encounter one of the few.
Reading between the lines: Word problems
The GMAT tests algebra and arithmetic concepts in word problems as well as mathematical equations. In fact, word problems are more common on the GMAT than straightforward equation-solving. So you have to know how to translate the English language into mathematical expressions. (You’ll probably see a few geometry word problems, too, but algebra is more common on the GMAT.)
TABLE 16-3 Common Words and Their Math Equivalents
|
Plain English |
Math Equivalent |
|---|---|
|
More than, increased by, added to, combined with, total of, sum of |
Plus (+) |
|
Less than, fewer than, decreased by, diminished by, reduced by, difference between, taken away from |
Minus (–) |
|
Of, times, product of |
Multiply ( |
|
Ratio of, per, out of, quotient |
Divide ( |
|
x percent of y |
|
|
Is, are, was, were, becomes, results in |
Equals (=) |
|
How much, how many, a certain number |
Variable (x, y) |
Here’s an example of how you play foreign language interpreter on GMAT word problems.
 On the first day of an alpine slalom competition, the total combined time of Grace’s two runs was 1 minute and 57 seconds. If twice the number of seconds in her first run was 30 seconds more than the number of seconds in her second run, what was her time in seconds for the first run?
On the first day of an alpine slalom competition, the total combined time of Grace’s two runs was 1 minute and 57 seconds. If twice the number of seconds in her first run was 30 seconds more than the number of seconds in her second run, what was her time in seconds for the first run?
(A) 15
(B) 30
(C) 49
(D) 68
(E) 147
Focus on what you’re supposed to figure out. The question asks for the time of Grace’s first run in seconds. So you know you have to convert her total time to seconds so you’re working in the correct units. A minute has 60 seconds, which means that Grace’s total time was 60 + 57, or 117 seconds.
 You can immediately eliminate Choice (E) because Grace’s first run couldn’t have been longer than the sum of her two runs. Now apply your math translation skills. You have two unknowns: the time of Grace’s first run and the time of her second run. Let x stand for the first unknown and y for the second.
You can immediately eliminate Choice (E) because Grace’s first run couldn’t have been longer than the sum of her two runs. Now apply your math translation skills. You have two unknowns: the time of Grace’s first run and the time of her second run. Let x stand for the first unknown and y for the second.
 You can solve a problem with two variables when you know two equations that involve those two variables. So search the problem for two equations.
You can solve a problem with two variables when you know two equations that involve those two variables. So search the problem for two equations.
For the first equation, the problem tells you that the total time of the two runs is 117 seconds. According to the English-to-math-translation dictionary, that means  . You’ve got one equation!
. You’ve got one equation!
You also know that 2 times (×) the number of seconds in her first run (x) was (=) 30 seconds more (+) than her time for the second run (y). Translation please?  .
.
After you have the two equations, you can use substitution or stacking to solve for x. For this problem, stacking is faster. Notice that 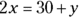 is the same as
is the same as 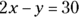 . When you stack and add the two equations, you can eliminate the y variable because
. When you stack and add the two equations, you can eliminate the y variable because  .
.
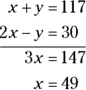
So, Grace ran her first race in 49 seconds, which is Choice (C). If you chose Choice (D), you solved for y instead of x. Grace’s second run was 68 seconds.
Burning the midnight oil: Work problems
Work problems ask you to find out how much work gets done in a certain amount of time. You use this formula for doing algebra work problems:
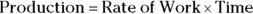
Production means the amount of work that gets done. Because you get that quantity by multiplying two other numbers, you can say that production is the product of the rate times the time.
Here’s how you’d apply the formula on a GMAT work problem.
 There are two dock workers, Alf and Bob. Alf can load 16 tons of steel per day, and Bob can load 20 tons per day. If they each work eight-hour days, how many tons of steel can the two of them load in one hour, assuming they maintain a steady rate?
There are two dock workers, Alf and Bob. Alf can load 16 tons of steel per day, and Bob can load 20 tons per day. If they each work eight-hour days, how many tons of steel can the two of them load in one hour, assuming they maintain a steady rate?
(A) 2.5
(B) 4.5
(C) 36
(D) 160
(E) 320
This question asks you to find the amount of production and gives you the rate and the time. But to calculate the rate properly, you must state the hours in terms of days. Because a workday is eight hours, one hour is  of a day. Figure out how much Alf loads in one hour (
of a day. Figure out how much Alf loads in one hour (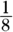 of a day) and add it to what Bob loads in one hour.
of a day) and add it to what Bob loads in one hour.
So, Alf and Bob load 4.5 tons of steel in one hour (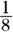 of a day), which is Choice (B). If you chose Choice (C), you figured out the total production for one day rather than one hour.
of a day), which is Choice (B). If you chose Choice (C), you figured out the total production for one day rather than one hour.
Going the distance: Distance problems
Distance problems are a lot like work problems. The formula for computing distance or speed problems is this:
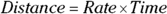
Any problem involving distance, speed, or time spent traveling can be boiled down to this equation. The important thing is that you have your variables and numbers plugged in properly. Here’s an example.
 Abby can run a mile in seven minutes. How long does it take her to run
Abby can run a mile in seven minutes. How long does it take her to run 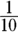 of a mile at the same speed?
of a mile at the same speed?
(A) 30 seconds
(B) 42 seconds
(C) 60 seconds
(D) 360 seconds
(E) 420 seconds
 Before you do any calculating, you can eliminate Choice (E) because 420 seconds is 7 minutes, and you know it takes Abby less time to run
Before you do any calculating, you can eliminate Choice (E) because 420 seconds is 7 minutes, and you know it takes Abby less time to run 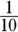 of a mile than it does for her to run a mile.
of a mile than it does for her to run a mile.
The problem tells you that Abby’s distance is 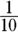 of a mile. You can figure her rate to be
of a mile. You can figure her rate to be 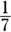 because she runs 1 mile in 7 minutes. The problem is asking how long she runs, so you need to solve for time. Plug the numbers into the distance formula:
because she runs 1 mile in 7 minutes. The problem is asking how long she runs, so you need to solve for time. Plug the numbers into the distance formula:

You need to isolate t on one side of the equation, so multiply both sides by 7:
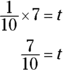
So, Abby runs 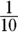 of a mile in
of a mile in 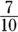 of a minute. Convert minutes to seconds. There are 60 seconds in a minute, and
of a minute. Convert minutes to seconds. There are 60 seconds in a minute, and 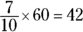 seconds. The correct answer must be Choice (B).
seconds. The correct answer must be Choice (B).
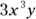 and
and 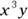 are like terms, but x and
are like terms, but x and 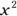 aren’t like terms, and neither are 2x and 2xy.
aren’t like terms, and neither are 2x and 2xy.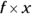 .
.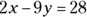




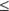
 for x. In this equation,
for x. In this equation, 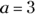 ,
, 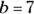 , and
, and 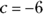 . Plug these numbers into the quadratic formula:
. Plug these numbers into the quadratic formula:  )
) or /)
or /)