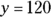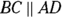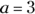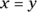Chapter 20
It’s All in the Presentation: GMAT Quantitative Question Types
IN THIS CHAPTER
Diving into data sufficiency questions
Probing problem solving questions
You need more than just math skills to excel on the quantitative section; you also need to know how to approach the questions. This chapter tells you what to expect from the math sections and how to work through the unique ways the GMAT presents the questions.
The kinds of math questions that appear on the GMAT test your ability to reason and think on your feet as you make use of the information you’re given.
Two basic types of questions are intermingled throughout the quantitative section of the GMAT: data sufficiency questions and problem solving questions. Both types of questions require similar skills, but they demand different approaches. In this chapter, we show you how to ace both kinds of questions.
Enough’s Enough: Data Sufficiency Questions
The quantitative section has 31 questions, and about half of them are presented in a unique form called data sufficiency. These questions aren’t particularly hard if you understand how to approach them before you walk into the testing center. However, if you don’t know much about these questions, getting confused and making careless mistakes is easy. Fortunately, you’ve decided to read this book to get a sneak peek. Your knowledge should be more than sufficient for data sufficiency!
You don’t need the solution to find the answer
Unlike the traditional math problems you’ve seen throughout your life, data sufficiency questions don’t actually require you to solve the problem. Instead, you have to evaluate two statements and determine which of those statements provides sufficient information for you to answer the question.
For each data sufficiency problem, you have a question and two statements, labeled (1) and (2). Your job is to decide whether each of the statements gives you enough information to answer the question with general math skills and everyday facts (such as the number of days in a month and the meaning of clockwise). If you need a refresher in the math concepts tested on the GMAT, read Chapters 15 through 19.
Don’t make foolish assumptions when you answer data sufficiency questions. Keep in mind that your job is to determine whether the information given is sufficient, not to try to make up for the lack of data! You’re used to having to come up with an answer to every math problem, so if the statements lack just a little information, you may be tempted to stretch the data to reach a solution. Don’t give in to temptation. For example, if a data sufficiency question provides a four-sided figure, don’t assume that it’s a square unless the data tells you it’s a square — even if knowing that the figure is a square would allow you to solve the problem. Deal only with the information expressly as it’s stated without making unwarranted assumptions.
The answer choices for data sufficiency questions are the same for each question:
(A) Statement (1) alone is sufficient, but Statement (2) alone is not sufficient to answer the question asked.
(B) Statement (2) alone is sufficient, but Statement (1) alone is not sufficient to answer the question asked.
(C) Both Statements (1) and (2) together are sufficient to answer the question asked, but neither statement alone is sufficient.
(D) Each statement alone is sufficient to answer the question asked.
(E) Statements (1) and (2) together are not sufficient to answer the question asked, and additional data are needed.
The computer doesn’t actually designate the answer choices with the letters A through E, but the choices appear in this order (you choose the correct one with your mouse or keyboard), and we refer to them as A, B, C, D, and E to make the discussion simpler.
It’s possible that just one of the statements gives enough data to answer the question, that the two statements taken together solve the problem, that both statements alone provide sufficient data, or that neither statement solves the problem, even with the information provided by the other one. That’s a lot of information to examine and apply in two minutes! Don’t worry. You can eliminate brain freeze by following a step-by-step approach to these questions.
Steps to approaching data sufficiency problems
Take a methodical approach to answering data sufficiency questions, and follow this series of steps:
- Evaluate the question to make sure you know exactly what you’re supposed to solve, and, if you can, decide what kind of information you need to solve the problem.
-
Examine one of the statements and determine whether the data in that one statement is enough to answer the question.
Start with the first statement or whichever one seems easier to evaluate. Record your conclusion on the noteboard.
-
Examine the other statement and determine whether it has enough information to answer the question.
Record your conclusion on the noteboard.
- Evaluate what you’ve written on your noteboard.
- If you recorded yes for both statements, pick the fourth answer, which we designate as Choice (D).
- If you recorded yes for (1) and no for (2), select the first answer, Choice (A) in this book.
- If you recorded no for (1) and yes for (2), choose the second answer, Choice (B) for our purposes.
- If you’ve written no for both statements, go on to the next step.
- Examine the statements together to determine whether the data given in both is enough information to answer the question.
- If the answer is yes, select the third answer, our Choice (C).
- If the answer is no, choose the last answer, the one we’ve designated as Choice (E).
You can boil this method down to a nice, neat chart, like the one shown in Figure 20-1.
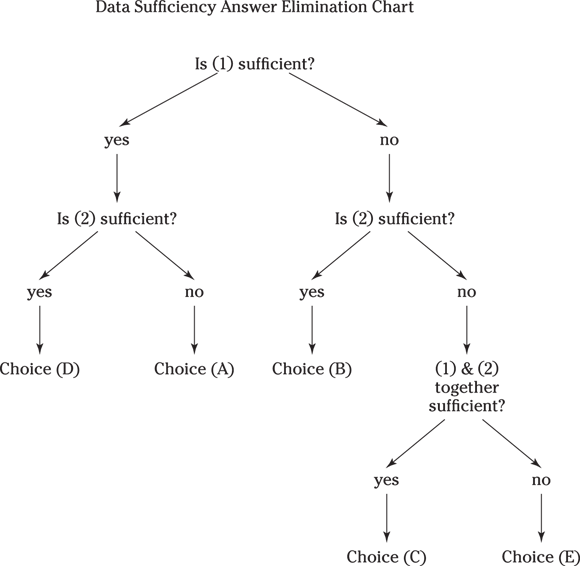
© John Wiley & Sons, Inc.
FIGURE 20-1: Data sufficiency answer elimination chart.
Don’t think too hard about whether an answer provides sufficient information to solve a problem. Data sufficiency questions aren’t necessarily designed to trick you. For example, you deal only with real numbers in these questions, and if a line looks straight, it is.
A statement is sufficient to answer the question if it provides only one possible answer for the question. If the information in a statement allows for two or more answers, the statement isn’t sufficient.
David and Karena were among a group of runners who were raising money for a local charity. If David and Karena together raised $1,000 in the charity race, how much of the money did Karena raise?
- David raised
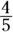as much money as Karena did. - David raised 5 percent of the total money raised at the event.
Use the steps and/or the chart in Figure 20-1 to solve the problem:
-
Know what you have to solve for.
The question asks you to figure out how much money Karena raised for charity. The question gives you the total money raised by David and Karena together
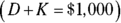but doesn’t specify how much David raised. Check out the statements to see whether either or both of them let you know how much David came up with. If you have David’s figure, you only need to subtract it from $1,000 to get Karena’s figure. -
Consider Statement (1) to determine whether it lets you solve for Karena’s total.
You determined that you needed data that would allow you to separate the money raised by Karena from that raised by David. Knowing that David raised
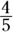as much money as Karena allows you to set up a formula to solve for Karena’s portion. Let K stand for Karena’s contribution and substitute 
for D in the equation 
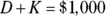. Your new equation is 
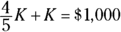. This equation has only one variable, and that variable stands for how much Karena raised. Therefore, you know you can solve the problem by using just the data from Statement (1). You don’t need to actually figure out what K stands for. Just write 
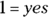on your noteboard. You know that the correct answer is either Choice (A) or Choice (D), but you have to look at Statement (2) to know which. If a question like this one appears at the end of the section and you’re pressed for time, you can guess between Choices (A) and (D), knowing that you have a 50 percent chance of answering correctly without even reading Statement (2). -
Examine Statement (2).
Statement (2) tells you that David raised 5 percent of the total money raised at the event. The question doesn’t tell you how much total money was raised at the event, so you can’t use this information to figure out how much David raised. And if you don’t know how much David raised, you can’t figure out how much Karena raised. Jot down
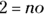on the noteboard. Because (1) is a yes and (2) is a no, the answer has to be Choice (A).
If you’ve read both statements and determined that either Statement (1) or Statement (2) is sufficient alone, two things are true:
- You’re done with the question and can move on the next one.
- The answer can’t be Choice (C) or Choice (E).
Both Choices (C) and (E) apply to the statements when they’re considered together. You don’t need to consider the statements together if either statement is sufficient alone. Your only possible choices if either statement is sufficient are Choice (A) if only Statement (1) is sufficient, Choice (B) if only Statement (2) is sufficient, and Choice (D) if each statement alone is sufficient.
Don’t evaluate whether both statements together answer the problem unless you’ve determined that neither is sufficient alone. The only time you consider (1) and (2) together is when you’ve answered no to both statements. For instance, say the example question replaced Statement (1) with this data: “The event raised a total of $10,000.” Statement (1) wouldn’t be enough to answer the question. But because Statement (2) tells you that David raised 5 percent of the total event money, you can answer the question using the data from both statements. Statement (1) provides the total amount, and Statement (2) allows you to figure out how much David raised based on that amount. If you subtract that amount from $1,000, you’ll have Karena’s total.
Choice (E) would be correct if Statement (1) said, “The event raised more money this year than last year.” In this case, neither statement, nor the two together, could answer the question.
Don’t waste time trying to come up with the actual numeric answer if you don’t have to. When you look at a question like the example, you may be tempted to solve the equation and figure out how much Karena raised. Don’t give in! Finding the number just wastes precious time, and no one gives you extra credit for solving the problem! Instead, use your valuable time to solve other questions in the quantitative section.
Taking a Look at Data Sufficiency Practice Problems
The best way to master the steps for solving data sufficiency questions is to practice on sample problems. Use the set of questions in this section to hone your skills. Make sure you have a piece of scratch paper nearby to simulate the noteboard. You can check your answers by reading through the explanations that follow the questions.
Practice questions
The GMAT gives you about two minutes to answer each quantitative question. So set your timer for ten minutes to get a feel for the time limit you’ll be facing on the actual test. Follow the chart in Figure 20-1 to work your way through the answer choices. If you need to refresh your memory of the answer choices before you begin, see the earlier section, “You don’t need the solution to find the answer.”
1. What’s the value of the two-digit integer x?
- The sum of the two digits is 5.
- x is divisible by 5.
(A) Statement (1) alone is sufficient, but Statement (2) alone is not sufficient to answer the question asked.
(B) Statement (2) alone is sufficient, but Statement (1) alone is not sufficient to answer the question asked.
(C) Both Statements (1) and (2) together are sufficient to answer the question asked, but neither statement alone is sufficient.
(D) Each statement alone is sufficient to answer the question asked.
(E) Statements (1) and (2) together are not sufficient to answer the question asked, and additional data are needed.
2. Office Solutions employs both male and female workers who work either full time or part time. What percentage of its employees work part time?
- Twenty percent of the female employees at Office Solutions work part time.
- Thirty percent of the workforce at Office Solutions is male.
(A) Statement (1) alone is sufficient, but Statement (2) alone is not sufficient to answer the question asked.
(B) Statement (2) alone is sufficient, but Statement (1) alone is not sufficient to answer the question asked.
(C) Both Statements (1) and (2) together are sufficient to answer the question asked, but neither statement alone is sufficient.
(D) Each statement alone is sufficient to answer the question asked.
(E) Statements (1) and (2) together are not sufficient to answer the question asked, and additional data are needed.
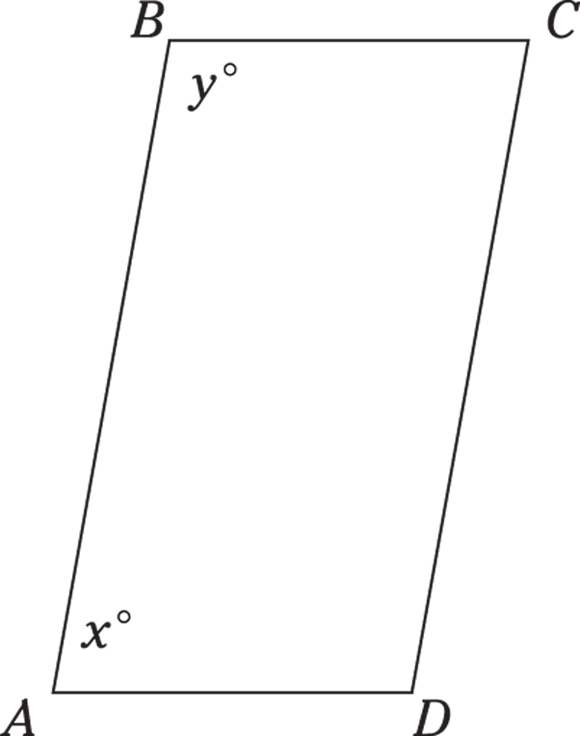
3. What is the value of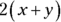 
in the preceding figure?
(A) Statement (1) alone is sufficient, but Statement (2) alone is not sufficient to answer the question asked.
(B) Statement (2) alone is sufficient, but Statement (1) alone is not sufficient to answer the question asked.
(C) Both Statements (1) and (2) together are sufficient to answer the question asked, but neither statement alone is sufficient.
(D) Each statement alone is sufficient to answer the question asked.
(E) Statements (1) and (2) together are not sufficient to answer the question asked, and additional data are needed.
4. Joe uses three different modes of transportation to travel a total of 225 kilometers to visit his aunt. How many kilometers does Joe travel by bus?
- Joe rides his bike 5 kilometers to the bus station where he boards the bus to take him to the train station. He then takes the train 10 times the distance he has traveled by bus.
- The distance Joe travels by bike is
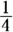the distance he travels by bus, and his train ride is 40 times longer than his bike ride.
(A) Statement (1) alone is sufficient, but Statement (2) alone is not sufficient to answer the question asked.
(B) Statement (2) alone is sufficient, but Statement (1) alone is not sufficient to answer the question asked.
(C) Both Statements (1) and (2) together are sufficient to answer the question asked, but neither statement alone is sufficient.
(D) Each statement alone is sufficient to answer the question asked.
(E) Statements (1) and (2) together are not sufficient to answer the question asked, and additional data are needed.
5. If x and y are real numbers and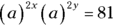 
, what is the value of 
?
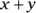(A) Statement (1) alone is sufficient, but Statement (2) alone is not sufficient to answer the question asked.
(B) Statement (2) alone is sufficient, but Statement (1) alone is not sufficient to answer the question asked.
(C) Both Statements (1) and (2) together are sufficient to answer the question asked, but neither statement alone is sufficient.
(D) Each statement alone is sufficient to answer the question asked.
(E) Statements (1) and (2) together are not sufficient to answer the question asked, and additional data are needed.
Answer explanations
The following answer explanations provide not only the correct answer for the data sufficiency practice questions in the preceding section, but also additional insight into how to approach this unique question type. So be sure to read all the info provided here.
-
C. Apply the steps:
-
Find out what to solve for.
This short question gives you little information about x; all you know is that it’s a two-digit integer.
-
Examine Statement (1).
Statement (1) tells you that the sum of the digits is 5. Several two-digit numbers are composed of digits that when added together equal 5: 14, 23, 32, 41, and 50. Statement (1) narrows the field of two-digit numbers down to just these five possibilities, but that’s not good enough. Because you don’t have a single answer, Statement (1) isn’t sufficient. Write down
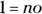. You’ve just eliminated Choices (A) and (D). -
Evaluate Statement (2).
Statement (2) says that x is divisible by 5. You probably realize immediately that every two-digit number ending in 0 or 5 is divisible by 5, so the possibilities are 10, 15, 20, 25, and so on. Clearly, Statement (2) isn’t sufficient, because
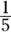of all two-digit numbers are divisible by 5. Write down 
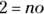. You’ve just eliminated Choice (B). -
Check out what you’ve written.
You have double nos, so you have to consider both statements together.
-
Evaluate the two statements together.
Statement (1) narrows the two-digit numbers down to five possibilities: 14, 23, 32, 41, and 50. Statement (2) narrows the list to those numbers that are divisible by 5. The only possibility from Statement (1) that ends in 0 or 5 is 50. Because 50 is divisible by 5 and the digits add up to 5, it answers the question. The two statements together provide enough information to answer the question. Correct answer: Choice (C).
You’ll notice that, for this question, you had to find the actual answer to the question to determine whether the information was sufficient. Sometimes doing so is the quickest way to determine whether statements provide enough data. An equation may exist that you could’ve set up (and not solved) that would have told you that you had sufficient information. However, on questions like this one, just applying the information to the question is often simpler and quicker. Solving the actual problem is okay if it’s the quickest way to determine that you have enough information. Just remember to stop solving the problem as soon as you determine whether the information is sufficient! -
- E. Here’s an example of how word problems may appear as data sufficiency questions. Apply the steps in the same way you do for solving linear equations:
-
Find out what to solve for.
The question asks you to find the percentage of part-time employees at Office Solutions. You know two facts at this point: (1) Office Solutions employs a certain number of males (m) and a certain number of females (f), and (2) a certain number of employees work either full time (F) or part time (P). That creates four unknown variables. The question doesn’t tell you anything about how many total people (T) Office Solutions employs, so you have another unknown. Here’s what you know in mathematical terms:
and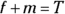 
. -
Examine Statement (1).
The first statement gives you the percentage of female part-time employees but tells you nothing about the percentage of male part-time employees. It takes care of only two of the unknown variables; you’re missing half of what you need to solve the problem. Statement (1) isn’t sufficient. Write down 1 = no, and eliminate Choices (A) and (D).
-
Evaluate Statement (2).
This statement concerns male employees at Office Solutions, but not females, so it’s insufficient by itself. Record your finding as
. The answer can’t be Choice (B). -
Check out what you’ve written.
You have double nos, so consider Statement (2)’s sufficiency when paired with Statement (1).
-
Evaluate the two statements together.
One statement provides a percentage for females and the other offers a percentage for males. You may be on your way to finding the percentage for both.
Read the statements carefully. You may be tempted to think that Statement (2) offers the other half of the solution, but this statement tells you the percentage of all males who work at the company, not just the ones who work part time.You can’t determine the total percentage of part-time workers if you don’t know the ratio of male full-time to male part-time workers. Neither statement is sufficient and the two together don’t cut it. Correct answer: Choice (E).
-
- B. For this problem, you evaluate a four-sided geometric figure:
-
Find out what to solve for.
You know that the sum of the interior angles of four-sided figures is 360 degrees and that x and y are the measures of two of these interior angles, but that’s not enough to determine the value of
. But you knew that. Data sufficiency questions never give you enough information to solve them without considering the statements. So check out what they have to offer. -
Examine Statement (1).
Statement (1) gives you the value of y. You may have examined the figure, assumed that it was a parallelogram, and deduced that x and y are, therefore, angles formed by parallel lines cut by a transversal. That makes them supplementary angles that add to 180 degrees. So if
, 
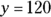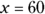, and 
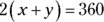. Problem solved! Not so fast. You can’t assume information about a GMAT figure by looking at it. If the figure is supposed to be a parallelogram, the GMAT will give you the information you need to know that. Nothing to this point has indicated that BC and AD are parallel lines, so you have to write no next to Statement (1). -
Evaluate Statement (2).
Well, here you go. Now you know expressly that AB is a transversal that passes through two parallel lines. The two angles x and y are supplementary.
Were you tempted at this point to pick Choice (C)? It’s true that both statements together give you the value of x, but you aren’t looking for the value of x. You’re asked to find the value of 2(x + y). All you need is Statement (2). If the value of x + y is 180, the value of 2(x + y) is 360. Write yes next to Statement (2) on your noteboard and pick Choice (B). You’re done!
You only pick Choice (C) if neither of the two statements by itself solves the problem. After you’ve determined that one of the statements works and the other doesn’t, you know the answer can’t be Choice (C). Follow the line of questions in the chart in Figure 20-1 and you’ll be fine.
-
- D. This data sufficiency question is essentially a simple addition problem.
-
Find out what to solve for.
You know the total distance Joe travels to his aunt’s is 225 kilometers and that he takes different types of transportation, one of which is a bus. Lucky guy! The question asks for the length of Joe’s bus ride. That’s your unknown, so designate the bus ride as x.
-
Examine Statement (1).
From the first statement, you learn that the other modes of transportation are bike (b) and train (t). Great news! It also tells you the exact length of Joe’s bike ride (5 kilometers) and that his train ride is 10 times his bus ride. So
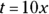. You can set up an equation with this information: 
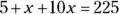. The equation has only one variable, the unknown length of the bus ride. You know you can solve a linear equation with only one variable, so Statement (1) is sufficient. Write yes next to (1) on your noteboard and eliminate Choices (B), (C), and (E). -
Evaluate Statement (2).
Create an equation from the information in the second statement. If Joe’s bike ride (b) is
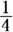as long as his bus ride (x), then 
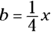. If the train trip (t) is 40 times the length of the bike ride (b), then 
. This gives simultaneous equations. Substitute 
for t in the train ride equation: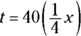 
. So the equation for the bike ride plus the bus ride plus the train trip is this: 
This equation has only one variable, so you know you can solve for x. You don’t have to actually solve for x; you just need to know that you can to know that Statement (2) is also sufficient. Write yes next to (2). Correct answer: Choice (D).
-
- A. The last question in the practice set contains a bunch of unknown variables, so you may think you can’t solve for much. You may be surprised!
-
Find out what to solve for.
Take a few seconds to evaluate the equation. You’re given two factors with exponents, and their product is equal to a perfect square. Both factors have the same base (a), and both contain an exponent with a factor of 2. The problem asks you to find the sum of the other two factors in the exponents of the terms.
-
Examine Statement (1).
From the information in the first statement, you can substitute 3 for a in the equation:
The terms have the same base, so you add the exponents when you multiply the terms:
Now extract the common factor in the exponent:
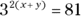
Square 3 to get 9:
Because
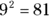, you know that the exponent 
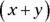must equal 2.You could also find the value of
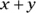by rewriting 81 as a base and exponent: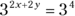 
When the bases are equal, the exponents are equal:
Either way, the information in Statement (1) is sufficient to tell you the value of
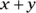. Write yes next to (1) on your noteboard and eliminate Choices (B), (C), and (E). -
Evaluate Statement (2).
This statement tells you that x and y are equal, so you may be tempted to draw from the information in the last statement and assume that x and y each equal 1. Well, that could be true if
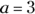. But you no longer know that 
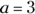. You can’t carry over the information from one statement to evaluate the sufficiency of the other. It’s true that x and y could each equal 1, but they could also each equal 0.5. Start fresh with each statement.If x and y are equal, then you can substitute x for y in the equation, simplify, and solve for a:
Since a is equal to the xth root of 3, the possible values of x, y, a, and, of course,
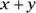, are infinite. For example, if 
, then so does y, and 
. If x and y each equal 3, then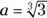 
, and so on. Because Statement (2) results in more than one value for 
, it can’t be sufficient to answer the question. Write no next to (2) on your noteboard. Correct answer: Choice (A).
-
Houston, We Have a Problem: Problem Solving Questions
About half of the 31 math problems on the GMAT quantitative section are data sufficiency questions. The other half are problem solving questions, which (not surprisingly!) require you to apply your mathematical skills to solve a problem. These questions are more like the ones you’ve seen on other standardized tests, like the SAT and ACT. They present you with a question and provide five possible answer choices from which you select the correct answer.
The approach to regular old problem solving questions is less clear-cut than the one for data sufficiency problems, but you should still follow an approach. Arriving at the test center with a practice problem solving plan not only provides you with a groovy little alliteration but also gives you a real edge for answering standard math questions. These techniques apply more directly to some questions than others, but learn all of them so you’re prepared for all types of problem solving questions:
- Examine all the data the question provides to make sure you know exactly what you’re asked to do. Some problems present you with figures, graphs, and scenarios, and some with just an equation with an equal sign. Don’t jump into the answer choices until you’ve given the question a little thought. Isolate exactly what the problem asks you to solve for and what information the problem provides you. Especially for more complex questions and word problems, use your noteboard to keep track of what you know and what you have to find out.
- Eliminate obviously incorrect answer choices if possible. Before you begin solving a more complex math problem, look at the answer choices to root out any clearly illogical options. You can then focus your problem solving, and you won’t pick these answers later through mistaken calculations. You can find more tips for eliminating answer choices in Chapter 2.
- Use the information in the problem. The GMAT rarely presents you with the answer choice that states, “It cannot be determined from the information.” Almost every problem solving question contains enough information for you to figure out the correct answer. But you need to use what you’re given. Pull out the numbers and other terms in a problem and write them on your noteboard in a way that makes the numbers meaningful. Depending on the problem, you may show relationships between quantities, draw simple diagrams, or organize information in a quick table.
- Find the equation. Some GMAT problems provide the equation for you. Others, such as word problems, require you to come up with an equation using the language in the problem. Whenever possible, formulate an equation to solve from the information provided in the problem and write it down on your noteboard.
- Know when to move on. Sometimes you may confront a question that you just can’t solve. Relax for a moment and reread the question to make sure you haven’t missed something. If you still don’t know what to do or if you can’t remember the tested concept, eliminate all the answers you can and record your best guess.
Apply the process to a sample problem.
A survey reveals that the average income of a company’s customers is $45,000 per year. If 50 customers respond to the survey and the average income of the wealthiest 10 of those customers is $75,000, what is the average income of the other 40 customers?
(A) $27,500
(B) $35,000
(C) $37,500
(D) $42,500
(E) $50,000
Scan the question to get an idea of what it’s asking of you. The word problem talks about surveys and averages, so it’s a statistics question. It asks for the average income of 40 out of 50 customers when the average of the other 10 is $75,000 and that the average of all 50 is $45,000.
You can eliminate Choice (E) off the bat because there’s no way that the 40 customers with lower incomes have an average income that’s more than the average income of all 50 customers. Choice (D) is probably wrong, too, because the top ten incomes carry such a high average compared to the total average. You know the answer is either Choice (A), (B), or (C), and you haven’t even gotten down to solving yet!
Quickly eliminating answers before you begin can save you from choosing an answer that comes from making a math error. Sometimes, the test-makers are tricky; they anticipate the kinds of little mistakes you’ll make and offer the resulting wrong answers as distracters in the answer choices. So be sure to eliminate illogical answers before you begin a problem.
You can find the total income of all 50 customers and the total income of the wealthiest 10 customers by using the formula for averages. The average equals the sum of the values in a group divided by the number of values in the group. Apply the formula to find the total income for the group of 50. Then find the total income for the group of 10. Subtract the total income of the 10 from the total income of the 50 to find the total income of the 40. Then you can divide by 40 to get the average income for the group of 40. Here’s how you do it:
Your calculations may be easier if you drop the three zeroes from the salaries. For this problem, shorten $45,000 to $45 and $75,000 to 75. Just remember to add the zeroes back on to your solution when you find it!
-
Find the total income for the group of 50.
The average income is $45 and the number of group members is 50, so use the formula to find the sum of all incomes (x):
-
Find the total income for the group of 10.
The average income is $75 and the number of group members is 10, so use the formula to find the sum (y):
-
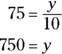
Find the total income for the group of 40.
Subtract the total income of the group of 10 (y) from the total income for the group of 50 (x):
-
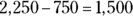
Find the average income of the group of 40.
The sum of the incomes in the group is $1,500, and the number of group members is 40, so apply the average formula:
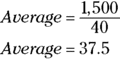
Add three decimal places for the three zeroes you excluded in your calculations, and you have your answer. The average income of the 40 customers is $37,500, which is Choice (C).
Trying Out Some Problem Solving Practice Problems
Here are a few practice questions to help you master the approach to problem solving questions in the quantitative section. When you’re finished answering them, read through the answer explanations to see how you’ve fared.
Practice questions
Try to answer these practice problems in the same amount of time you’ll experience on the actual GMAT (give yourself about ten minutes to answer all five questions). Remember to keep track of the information you know and the information you have to figure out as you work through the problems. Use a piece of scratch paper to simulate the noteboard as you work out the answers.
1. An electronics firm produces 300 units of a particular MP3 player every hour of every day. Each unit costs the manufacturer $60 to produce, and retailers immediately purchase all the produced units. What is the minimum wholesale price (amount the manufacturer receives) per unit that the manufacturer should charge to make an hourly profit of $19,500?
(A) $60
(B) $65
(C) $95
(D) $125
(E) $145
2. If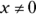 
, what is the value for x in the equation 
?
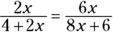(A) –3
(B) 1
(C) 2
(D) 3
(E) 6
3. 
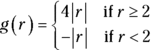
Given the function g defined above, what is the value o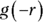f 
if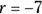 
?
(A) –28
(B) –14
(C) –7
(D) 7
(E) 28
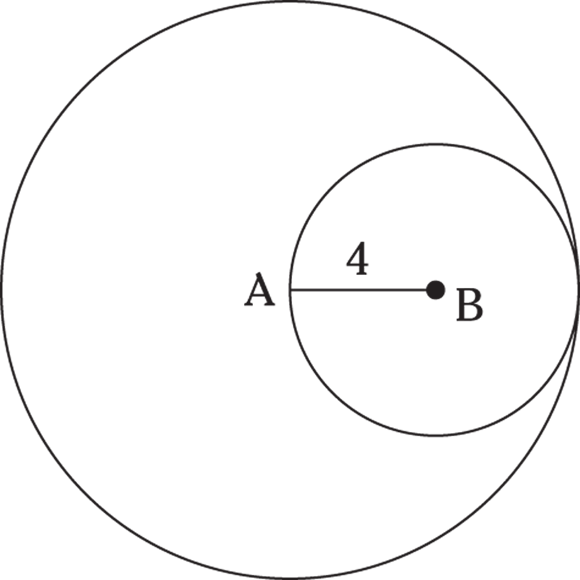
4. In the preceding figure, the circle centered at B is internally tangent to the circle centered at A. The smaller circle passes through the center of the larger circle, and the length of AB is 4 units. If the smaller circle is removed from the larger circle, how many square units of the area of the larger circle will remain?
(A)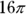 
(B)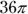 
(C)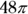 
(D)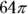 
(E)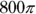 
5. A line with the equation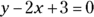 
for all real numbers would pass through which quadrants on the coordinate plane?
(A) I, II, and III only
(B) III and IV only
(C) I, II, III, and IV
(D) I, III, and IV only
(E) II and IV only
Answer explanations
-
D. Note what the question gives and what it’s asking for. It provides units per hour and cost per unit. It also tells you the total desired hourly profit. You’re supposed to find the price per unit.
The first thing to do is eliminate obviously incorrect answer choices. You know that you’re looking for the wholesale price that will yield a profit (which results from price minus cost to produce) of $19,500 per hour. Because the answers given are wholesale prices, you can eliminate Choices (A) and (B). The cost to produce each unit is $60. If the company charged the same amount for the MP3 players as it spent to produce them, it would make no profit, so Choice (A) is obviously incorrect. Choice (B) isn’t much better. At a profit of just $5 per unit and 300 units per hour, the firm would make only $1,500 per hour.
You’ve eliminated two answer choices. Evaluate the data to find the correct answer from the remaining three. You know that 300 units are produced every hour and that those 300 units have to net a profit of $19,500. If you knew the amount of profit per unit, you could add that to the amount each unit costs to produce and get the minimum wholesale price. Set up an equation with x as the profit per unit. Remember that per means to divide:
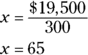
The firm needs to make a profit of $65 per unit.
You can’t stop here and pick Choice (B). You’re not done yet, but you know that because you’ve already eliminated Choice (B).
You have to add profit to the per-unit production cost to get the final wholesale price:
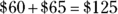
Correct answer: Choice (D).
You could use estimation to solve this problem by rounding $19,500 up to the nearest convenient multiple of 300, which is $21,000, and then dividing 21 by 3 in your head and getting 7. This would tell you that you need a little less than $70 profit from each unit, or a little under $130 as the wholesale price (because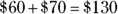 
). -
D. Here’s a relatively simple question that asks you to solve for x. The only element that makes it a little complex is that you’re dealing with variables in fractions. Take a moment to consider the equation. The numerator in the fraction on the right is 3 times the numerator in the fraction on the left. Multiplying the numerator of the left-side fraction would make it equal to the numerator on the right side.
When the numerators of two equivalent fractions are equal, their denominators are also equal, so creating equal numerators allows you to set the denominators equal to each other. Then just solve for x. -
Multiply the left-side fraction by
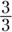.This doesn’t change the value of the fraction, because multiplying by
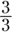is the same as multiplying by 1.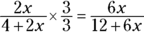 
- Set the denominators equal to each other and solve for x:
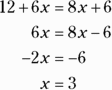
Correct answer: Choice (D).
You can also solve this question by cross-multiplying opposite numerators and denominators:
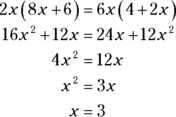
You can solve many GMAT problems by using more than one method. Go with the one that’s easiest for you. -
-
E. This function problem provides you with two outputs depending on the value of the input. If the input is greater than or equal to 2, the output is 4 times the absolute value of the input. If the input is less than 2, the output is the negative of the absolute value of the input.
Don’t let the negative signs mess you up. If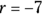 
, then g(–r) is the same as saying g(7), because –(–7) is 7. So the value of the input in this problem is 7.Because 7 is greater than 2, you’ll look to the first rule of the function g(r). The solution to
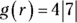is simply 
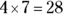. Correct answer: Choice (E).If you confuse the signs, you’ll come up with the negative version of the correct answer, which is Choice (A). You get the other answer choices when you use the incorrect rule.
-
C. This geometry question asks you to find the area of the large circle less the area of the small circle. Apply the formula for finding the area of a circle:
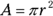.Because the smaller circle passes through the center of the larger one, the radius of the larger circle is two times the radius of the smaller one: The radius of the larger circle equals 8. Apply the area formula to the larger circle:
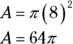
Determine the area of the smaller circle in the same way:
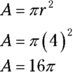
Now subtract the two areas:
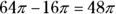
Correct answer: Choice (C).
-
D. This coordinate geometry problem requires you to know the slope-intercept form:
. But before you do any calculations, go ahead and eliminate Choice (C). No way can a straight line pass through all four quadrants of the coordinate plane. When you rearrange the equation into the slope-intercept form by isolating the y variable on the left side, you get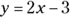 
. The slope-intercept form gives you the y-intercept and slope of the line. The value of b is the y-intercept, and the value of m is the slope. For this kind of question, you may want to draw on your noteboard a coordinate plane graph and label the quadrants I, II, III, and IV. Nothing fancy, mind you, just enough to get your bearings. Now, draw a point below the origin on the y-axis representing –3, the y-intercept. Then draw a line that travels upward from left to right rising two units toward the top of the paper for every one unit to the right. Your figure doesn’t have to be perfect. From a rudimentary drawing, you can immediately see that the line passes through Quadrants I, III, and IV.So Choice (D) is your best choice. Choice (A) would be correct if you had a parallel line with a positive y-intercept. Choice (B) is possible for a line parallel to the x-axis with a negative y-intercept. Choice (E) would require a line with a negative slope passing through the origin.
Any line must travel through at least two quadrants, unless the line runs directly on top of either the x- or y-axis. A line that lies directly on top of an axis doesn’t go through any quadrant. The lines that travel through only two quadrants are those that pass through the origin or are parallel to either the x- or the y-axis. All other lines must eventually travel through three quadrants.Correct answer: Choice (D).