Dos gusanitos
y una urraca voraz
Vadym Paziy1
Dos hermanos gusanitos de seda han discutido sobre quién de los dos llegará antes a casa desde un punto de una colina. La colina tiene forma de cono, con una base circular de 1 m de radio y una ladera (generatriz del cono) de 2 m. La casa se encuentra en un punto diametralmente opuesto al punto de partida. Uno de los gusanitos, de nombre Alegre, escoge el primer camino que encuentra, la base del cono. Sin embargo, su hermano Astuto afirma que conoce el camino más corto para llegar a casa.

Pero ninguno de los dos sabe que en su casa les está esperando una urraca muerta de hambre que se comerá al primero que llegué. En el instante en que Alegre echa a andar, Astuto se pone a calcular la trayectoria que según él es la óptima, lo que le lleva exactamente tres minutos. Una vez la tiene empieza su camino. Suponiendo que los dos gusanos se desplazan con la misma velocidad de 1 mm/s, el desafío consiste en decidir quién será la víctima de la urraca, ¿Alegre o Astuto?
Solución
La base de un cono no es el camino más corto para llegar de un punto de la base al diametralmente opuesto. Existe otro, tal y como se muestra en el siguiente dibujo:

En principio, el desafío está planteado en tres dimensiones. Sin embargo, podemos simplificarlo pasando a un problema en dos dimensiones. Para ello, realizamos un corte recto desde la base hasta el vértice principal del cono y tumbamos lo que queda para obtener una superficie plana.
El resultado se muestra en la siguiente figura.

Observa que el ángulo de apertura α vale 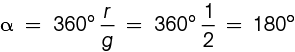 .
.
Además, todas las distancias se conservan (hemos hecho una isometría), con lo que el problema planteado se resuelve con las técnicas básicas de geometría en el plano.
Como en el plano la distancia más corta entre dos puntos es la línea recta, los caminos elegidos por los dos gusanos son los representados en el dibujo.

Esto ya demuestra que el camino de Astuto es el más corto posible.
Calculamos ahora sus longitudes.
Si x es la longitud del camino que elige Astuto, aplicando el teorema de Pitágoras:
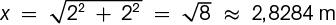 .
.
Llamemos y a la distancia que recorre Alegre. Como va a lo largo de la base del cono, dividiendo entre 2 la longitud de la circunferencia que forma la base obtenemos
 .
.
Como la velocidad de ambos es 1 mm/s el tiempo empleado es:
 .
.
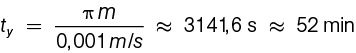 .
.
Por tanto, Astuto tarda unos cinco minutos menos que su hermano. Así que, por desgracia, a pesar de que salió tres minutos después, la urraca se lo come.
1 El desafío ha sido inspirado por un ejemplo propuesto en los cursos de Geometría Diferencial por el profesor Lorenzo Abellanas Rapún, catedrático de Métodos Matemáticos en la Física de la Universidad Complutense de Madrid, a quien estoy muy agradecido.