Construyendo superficies
María Pe Pereira
Supongamos que tenemos una lámina con la forma sombreada en gris de la figura 1 y hecha de un material totalmente deformable que podemos modelar a nuestro antojo, por ejemplo estirándolo cuanto queramos. El desafío consiste en averiguar qué superficie se obtiene pegando adecuadamente los lados con el mismo número (el 1 con el 1, el 2 con el 2, etc.).
Por pegar adecuadamente entendemos que el sentido de las flechas debe coincidir al superponerse. Además, la circunferencia, que tiene el número 1, tiene que pegarse con la arista 1, haciendo coincidir el punto señalado en la circunferencia con los extremos de la arista.

Figura 1
Por ejemplo, con una lámina rectangular podríamos hacer varias superficies:
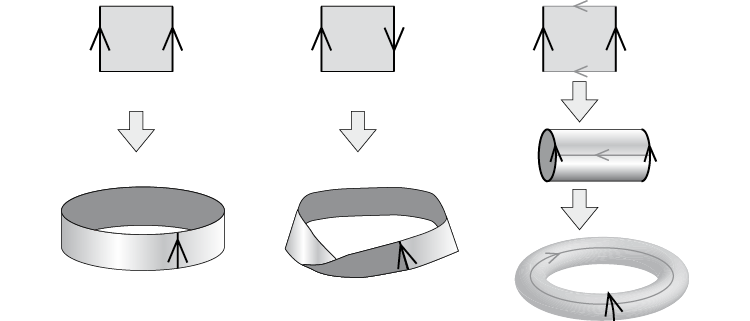
Figura 2. Cilindro, cinta de Möbius y flotador
Puesto que el material del que está hecha la figura es totalmente deformable, podríamos construir muchas superficies distintas, algunas de ellas muy difíciles de describir. Veamos qué posibilidades nos podemos encontrar recordando la clasificación de superficies en el espacio realizada por Möbius en 1870.
En primer lugar las superficies se clasifican en superficies con bordes como el cilindro o la banda de Möbius y en superficies sin bordes como la esfera o un flotador. Lo que Möbius demostró es que cualquier superficie de una sola pieza, sin bordes, sin cruces1, y que podamos construir físicamente2, se puede deformar, sin romperse, hasta convertirla o bien en una esfera o bien en un flotador para un número finito de personas (con un agujero para cada persona).

Figura 3. Esfera, flotador para 1, para 2… y para n personas
En cuanto a las superficies con bordes (sin cruces, etc.), siempre se podrán deformar para dar lugar a la cinta de Möbius o a una de las anteriores (la esfera o algún flotador) a la que se le han recortado una cantidad finita de discos. Por ejemplo, un pantalón se puede deformar (hinchándolo como un balón) a una esfera a la que le recortamos tres discos:

Figura 4. Pantalón
Por tanto, volviendo al enunciado del desafío, pegando los lados del mismo trazo de la figura 1 se puede conseguir exactamente una de las superficies que acabamos de describir. La pregunta es: ¿cuál es esta superficie?
Solución
La solución es un flotador para dos personas. La forma de visualizarlo no es única, en particular no importa el orden en que peguemos los lados.

Figura 5. Posible visualización de la solución
MÁS INFORMACIÓN
Un comentario más sobre el teorema de clasificación citado. En realidad, solo deformando quizá no podamos conseguir siempre una de las superficies descritas, ya que la superficie podría aparecer como hecha un nudo en el espacio. Necesitaríamos entonces cortar la superficie con unas tijeras y volver a pegarla exactamente de la misma manera (si la superficie estuviera dibujada, al volver a pegar el dibujo se recuperaría, luego la superficie sería la misma). Por ejemplo, en la siguiente figura tenemos dos cilindros, aunque el primero de ellos aparece anudado. Cortando por la línea de puntos y volviendo a pegar podemos pasar de uno a otro.

Figura 6. Cilindros
Por último, te invitamos a hacer el pegado del flotador que aparece en la figura 2 (y de la propia figura del enunciado) en órdenes diferentes y comparar el resultado observando cómo quedan las curvas de diferente trazo en los diferentes casos.
Si te has quedado con ganas de saber más, te sugerimos que leas el libro de Vicente Muñoz Velázquez, Formas que se deforman. La topología, RBA, Barcelona, 2011.
En otro estilo, es muy recomendable Planilandia, de Edwin A. Abbot. Esta novelita satírica, publicada en 1884 con el título Flatland: A Romance of Many Dimensions bajo el seudónimo “A Square”,3 explica algunas diferencias entre la geometría de mundos de distintas dimensiones y la aprovecha para criticar las rígidas jerarquías sociales de la Inglaterra victoriana. Existen ediciones recientes en castellano (Laertes, 2008, y José J de Olañeta, 2011), catalán (Laertes, 2011) y gallego (Urco Editora, 2009).
1 Un cruce es el lugar donde dos superficies, o dos trozos de la misma superficie, se cortan en una curva (o en un punto). Por ejemplo, dos planos que se cortan en una recta en el espacio.
2 No podemos realizar físicamente ni superficies infinitas como el plano, ni superficies infinitamente complicadas como superficies con infinitos agujeros (¡porque no tenemos tiempo infinito para hacerlas!)
3 Juego de palabras entre “Cuadrado”, que es el nombre del protagonista, y el término inglés squire, más común en el siglo xix que en nuestros días, que significaba originalmente “escudero” y luego pasó a designar una persona importante en una villa o pueblo, por ejemplo un Juez de Paz.