A Anhang
A.1 Konstruktion einer nicht-messbaren Menge
Es sei λd das Lebesgue-Maß auf 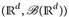 und
und 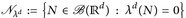 die Familie der Nullmengen. Die Vervollständigung von
die Familie der Nullmengen. Die Vervollständigung von  ist definiert durch
ist definiert durch

eine Menge 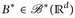 heißt Lebesgue-messbar. Man sieht leicht, dass
heißt Lebesgue-messbar. Man sieht leicht, dass 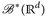 eine σ-Algebra ist,15 und dass
eine σ-Algebra ist,15 und dass 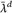 wohldefiniert ist und λd fortsetzt.
wohldefiniert ist und λd fortsetzt.
A.1 Satz. Es gibt Mengen in  , die nicht Lebesgue-messbar sind:
, die nicht Lebesgue-messbar sind: 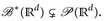
Beweis. Zunächst sei d = 1. Wir nennen x, y ∈ [0, 1) äquivalent, wenn  Mit [x] bezeichnen wir die Äquivalenzklassen
Mit [x] bezeichnen wir die Äquivalenzklassen  . Nach Konstruktion gilt
. Nach Konstruktion gilt 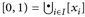 , wobei
, wobei 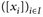 alle Äquivalenzklassen sind.
alle Äquivalenzklassen sind.
Mit Hilfe des Auswahlaxioms finden wir eine Menge L, die aus jeder Klasse [xi] genau ein mi enthält. Insbesondere gilt
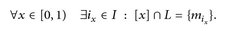
Daher ist 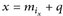 für ein
für ein  , also oder
, also oder
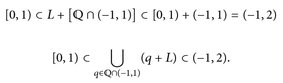
Weiterhin ist 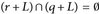 für
für  wäre r + x = q + y für x, y ∈ L mit x ≠ y und damit
wäre r + x = q + y für x, y ∈ L mit x ≠ y und damit 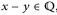 , was nach Konstruktion von L ausgeschlossen ist.
, was nach Konstruktion von L ausgeschlossen ist.
Angenommen, L wäre Lebesgue-messbar, dann sehen wir wegen der σ-Additivität des Lebesgueschen Maßes, dass

Andererseits ist  invariant unter Translationen,
invariant unter Translationen, 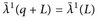 (Satz 4.7), d. h.
(Satz 4.7), d. h.

was offensichtlich nicht möglich ist. Somit ist L nicht Lebesgue-messbar.
Für d > 1 sieht man so, dass [0, 1)d-1 x L nicht Lebesgue-messbar sein kann.
A.2 Berechnung des Spatvolumens
Wir wollen das Volumen eines d-dimensionalen Parallelepipeds (Spat) bestimmen. Es sei  eine invertierbare d x d-Matrix und
eine invertierbare d x d-Matrix und
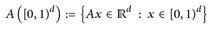
der von A aufgespannte Spat.
A.2 Satz. Für alle A ∈ GL(d,  ) gilt λd [A ([0, 1)d)] = |det A|.
) gilt λd [A ([0, 1)d)] = |det A|.
Für den Beweis von Satz A.2 benötigen wir zwei Hilfssätze.
A.3 Lemma. Es sei D = diag [λ1, ..., λd] , λn > 0, eine d x d Diagonalmatrix. Dann ist λd(D(B)) = det D ⋅ λd(B) für alle Borelmengen  .
.
Beweis. Sowohl D als auch D-1 definieren stetige Abbildungen. Daher ist D(B) für jedes 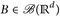 eine Borelmenge. Wegen des Eindeutigkeitssatzes für Maße (Satz 4.5) genügt es, die Aussage für halboffene Rechtecke
eine Borelmenge. Wegen des Eindeutigkeitssatzes für Maße (Satz 4.5) genügt es, die Aussage für halboffene Rechtecke 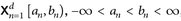 , zu zeigen. Offenbar gilt
, zu zeigen. Offenbar gilt

und

A.4 Lemma. Zu jeder Matrix  gibt es orthogonale Matrizen S, T ∈ O(d) und eine Diagonalmatrix D = diag [λ1, ..., λd] mit strikt positiven Einträgen λn > 0, so dass A = SDT.
gibt es orthogonale Matrizen S, T ∈ O(d) und eine Diagonalmatrix D = diag [λ1, ..., λd] mit strikt positiven Einträgen λn > 0, so dass A = SDT.
Beweis. Die Matrix ATA ist symmetrisch. Daher gibt es eine Matrix U ∈ O(d) mit
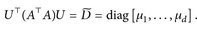
Wir bezeichnen mit 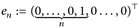 := den n-ten Einheitsvektor und mit |⋅| die Euklidische Norm. Dann ist
:= den n-ten Einheitsvektor und mit |⋅| die Euklidische Norm. Dann ist
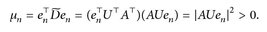
Setze 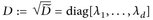 mit
mit  Dann gilt
Dann gilt

und daher ist S:= AUD-1 ∈ O(d). Da T:= UT ∈ O(d), gilt zudem
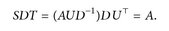
Beweis von Satz A.2. Mit Hilfe von Lemma A.3 und A.4 ergibt sich für 

Wegen S, T ∈ O(d) gilt für die Determinanten |det S| = |det T| = 1. Somit erhält man |det A| = |det (SDT)| = |det S| ⋅ |det D| ⋅ |det T| = det D.
A.3 Messbarkeit der Stetigkeitsstellen beliebiger Funktionen
Es sei (E, d) ein metrischer Raum. Bezüglich der Metrik d bezeichnen wir mit
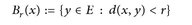
die offene Kugel mit Radius r > 0 und Zentrum x ∈ E. Für eine beliebige Funktion  (Messbarkeit wird nicht vorausgesetzt) setzen wir
(Messbarkeit wird nicht vorausgesetzt) setzen wir

(diam B = supx,y |x – y| ist der Durchmesser der Menge B c  ). Weil r ↦ diam f(Br (x)) eine fallende Funktion von r ist, können wir in der Definition von wf(x) das Infimum infr>0 durch inf0<r<δ ersetzen.
). Weil r ↦ diam f(Br (x)) eine fallende Funktion von r ist, können wir in der Definition von wf(x) das Infimum infr>0 durch inf0<r<δ ersetzen.
A.5 Lemma. Die Funktion f ist im Punkt x genau dann stetig, wenn wf(x) = 0.
Beweis. „⇒“: Es sei f stetig an der Stelle x. Dann gilt
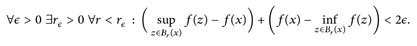
Somit

„⇐“: Für alle r > 0 und x, x′ mit x′ ∈ Br(x) gilt

Indem wir x und x′ vertauschen, erhalten wir
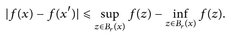
Nun sei wf(x) = 0 angenommen. Dann gibt es für jedes ∊ > 0 ein r∊, so dass für alle r < r∊, und x′ ∈ Br(x)
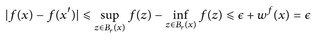
gilt. Das zeigt die Stetigkeit von f an der Stelle x.
A.6 Lemma. wf ist oberhalbstetig, d. h. {wf < α} ist für jedes α > 0 eine offene Menge.
Beweis. Es sei x0 ∈ {wf < α}. Dann gibt es ein r = r(α) > 0 mit
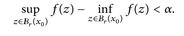
Wähle y ∈ Br/3 (x0). Wegen Br/3 (y) ⊂ Br(x0) gilt

Daher ist y ∈ {wf < α}, also Br/3(x0) ⊂ {wf < α}.
A.7 Satz. Es sei  eine beliebige Funktion. Die Menge der Stetigkeitsstellen Cf:= {x: f ist stetig in x} ist eine Borelmenge.
eine beliebige Funktion. Die Menge der Stetigkeitsstellen Cf:= {x: f ist stetig in x} ist eine Borelmenge.
Beweis. Lemma A.5 zeigt
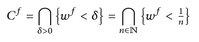
und gemäß Lemma A.6 sind die Mengen  offen, also Borelsch. Daher ist auch deren abzählbarer Schnitt Cf eine Borelmenge.
offen, also Borelsch. Daher ist auch deren abzählbarer Schnitt Cf eine Borelmenge.
A.4 Das Integral komplexwertiger Funktionen
Bisweilen müssen wir das Integral auf komplexwertige Integranden erweitern, z. B. für die Fouriertransformation (Kapitel 22). Da die Abbildung
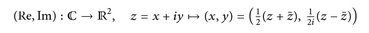
messbar ist und eine messbare Inverse (x, y) = (Re z, Im z) ↦ Re z + i Im z besitzt, können wir  und
und  identifizieren. Damit lässt sich das Integral durch ℂ-Linearität fortsetzen. Es sei
identifizieren. Damit lässt sich das Integral durch ℂ-Linearität fortsetzen. Es sei  eine messbare Funktion und μ ein Maß auf
eine messbare Funktion und μ ein Maß auf  . Wir definieren
. Wir definieren

Das Integral komplexwertiger Funktionen wird dann definiert durch
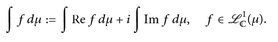
Es ist eine leichte Übung zu zeigen, dass das so fortgesetzte Integral ℂ-linear ist; insbesondere gilt

Die Dreiecksungleichung
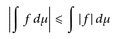
sieht man so: Da ∫ f dμ ∈ ℂ ist, gibt es ein θ ∈ (-π, π], so dass eiθ ∫ f dμ ≥ 0. Daher
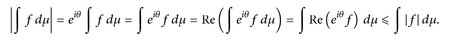
A.5 Regularität von Maßen
Es sei (E, d) ein metrischer Raum,  bezeichne die (bezüglich der Metrik d) offenen,
bezeichne die (bezüglich der Metrik d) offenen,  die abgeschlossenen und
die abgeschlossenen und  die Boreischen Teilmengen von E.
die Boreischen Teilmengen von E.
A.8 Definition. Es sei (E, d) ein metrischer Raum. Ein Maß μ auf  heißt regulär von auβen, wenn
heißt regulär von auβen, wenn

(A.1)
und regulär von innen, wenn μ(K) < ∞ für alle kompakten Mengen K c E und

(A.2)
Ein von außen und innen reguläres Maß heißt regulär.
Regularität hängt wesentlich von der topologischen Ausgangslage ab. Wir beweisen hier nur einige elementare Zusammenhänge, die für Anwendungen wichtig sind. Der Raum E heißt σ-kompakt, wenn es eine aufsteigende Folge kompakter Mengen Kn ↑ E gibt.
Manchmal wird für die innere Regularität die Gültigkeit von (A.2) für alle Borelmengen U gefordert. Allerdings gilt
A.9 Lemma. Es sei (E, d) ein metrischer Raum und μ ein reguläres Maβ. Dann gilt

(A.3)
Ist E σ-kompakt, dann gilt (A.3) für alle 
Beweis. Es sei 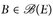 mit μ(B) < ∞.
mit μ(B) < ∞.
1°) Es sei B ⊂ K für ein Kompaktum K und ∊ > 0 fest. Wegen (A.1) existiert eine offene Menge U ⊃ K \ B, so dass μ(U) ≤ μ(K \ B) + ∊. Nun gilt
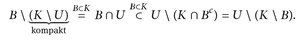
Somit folgt
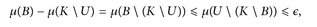
was (A.3) für die hier betrachteten Mengen B impliziert.
2°) Es sei μ(B) < ∞ und ∊ > 0 fest. Wegen (A.1) und (A.2) gilt

Wenden wir 1° auf die Menge B ∩ K ⊂ K an, dann erhalten wir
∃L c B ∩ K, L kompakt: μ(B ∩ K) ≤ μ(L) + ∊.
Nun ist B \ L c (U \ K) ∪ (B ∩ K) \ L und somit

was (A.3) impliziert.
3°) Nun sei E σ-kompakt. Nach Voraussetzung existieren kompakte Mengen Kn ↑E. Da μ(Kn) < ∞ ist, gilt für 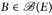 wegen der Maßstetigkeit
wegen der Maßstetigkeit

(beachte: für K c B kompakt gilt L:= K ∩ Kn ⊂ K ∩ B und L ist kompakt). Die umgekehrte Ungleichung ist wegen der Monotonie von μ trivial.
A.10 Satz. Es sei (E, d) ein metrischer Raum. Jedes endliche Maβ μ auf  ist von auβen regulär. Wenn E σ-kompakt ist, dann ist μ auch von innen regulär, also regulär.
ist von auβen regulär. Wenn E σ-kompakt ist, dann ist μ auch von innen regulär, also regulär.
Beweis. Setze
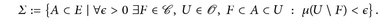
1°) Wir zeigen: ∑ ist eine σ-Algebra.
 ist klar.
ist klar.
(∑2) Sei A ∈ ∑ und ∊ > 0.
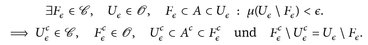
Mithin gilt  und es folgt Ac ∈ ∑.
und es folgt Ac ∈ ∑.
(∑3) Seien  und ∊ > 0.
und ∊ > 0.

Somit
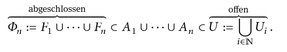
Mit Hilfe der Inklusion
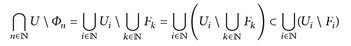
sehen wir mit der Maßstetigkeit und der σ-Subadditivität von μ

Mithin folgt μ(U \ Φn) < 2∊ für alle n > n(e) und daher gilt Un An ∈ ∑.
2°) Wir zeigen: 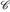 ⊂ ∑ und
⊂ ∑ und 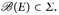 Für abgeschlossene Mengen F ⊂ E ist
Für abgeschlossene Mengen F ⊂ E ist

Wegen der Maßstetigkeit haben wir limn→∞ μ(Un) = μ(F), d. h. F c Un und μ(Un \F) < ∊ für hinreichend große n > N(∊). Das zeigt, dass F ∈ ∑ und
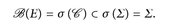
3°) Wir zeigen: μ ist von außen regulär. Wegen 2° gibt es für 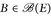 Folgen
Folgen 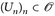 und
und  mit Fn c B c Un und limn→∞ μ(Un) \ Fn) = 0. Somit
mit Fn c B c Un und limn→∞ μ(Un) \ Fn) = 0. Somit
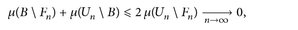
d. h. das Infimum in (A.1) (Regularität von außen) wird angenommen.
4°) Wir zeigen: Wenn E σ-kompakt ist, dann ist μ regulär. Es sei  und Lm ↑ E eine aufsteigende Folge kompakter Mengen und Fn wie in Schritt 3°. Setze
und Lm ↑ E eine aufsteigende Folge kompakter Mengen und Fn wie in Schritt 3°. Setze

Wegen der Maßstetigkeit gilt limm→∞ μ(Fn \ Kn,m) = 0, sowie

Daher gilt auch die Formel (A.2) (sogar für beliebige Mengen 
A.11 Satz. Es sei (E, d) ein metrischer Raum und μ ein Maβ auf  mit μ(K) < ∞ für alle kompakten Mengen K c E.
mit μ(K) < ∞ für alle kompakten Mengen K c E.
- a) Wenn E σ-kompakt ist, dann ist μ von innen regulär.
- b) Wenn es eine Folge
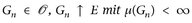 gibt, dann ist μ von außen regulär.
gibt, dann ist μ von außen regulär.
Beweis. a) Es sei Kn ↑ E eine Folge kompakter Mengen. Dann ist μn(B):= μ(B ∩ Kn), B 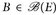 ; für jedes
; für jedes  ein endliches Maß. Wir finden mit der Maßstetigkeit und Satz A.10 für jede Menge
ein endliches Maß. Wir finden mit der Maßstetigkeit und Satz A.10 für jede Menge 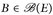
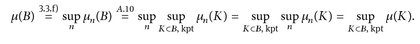
b) Es sei B ∈ ℬ(E) und ∈ > 0. Aus dem Beweis von Satz A.10 (Definition der Familie Σ für die Maße μ{· ∩ Gn)) wissen wir

(A.4)
Für n = 1 ist das der Induktionsanfang für die folgende Aussage

(A.5)
Induktionsschritt n ⇝ n + 1: Wegen der starken Additivität von Maßen gilt

Es ist  . Somit
. Somit
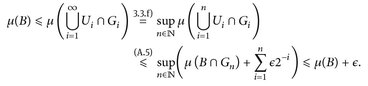
Da ∈ > 0 beliebig ist, folgt die Regularität von außen.

Die σ-Endlichkeit ist im Beweis von Satz A.11 wesentlich: Auf  ist das Zählmaß μ(B):= #B offensichtlich von innen regulär, jedoch gilt die äußere Regularität nicht einmal für einpunktige Mengen.
ist das Zählmaß μ(B):= #B offensichtlich von innen regulär, jedoch gilt die äußere Regularität nicht einmal für einpunktige Mengen.
A.12 Beispiel. a) Das Lebesgue-Maß λd auf  ist regulär. Offensichtlich ist
ist regulär. Offensichtlich ist 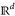 σ-kompakt
σ-kompakt 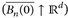 und die offenen Mengen
und die offenen Mengen  . Da λd(Bn(0)) < ∞, folgt die Behauptung aus Satz A.11.
. Da λd(Bn(0)) < ∞, folgt die Behauptung aus Satz A.11.
b) Für jede Borelmenge  gibt es eine Fσ-Menge (= abzählbare Vereinigung abgeschlossener Mengen) F und eine Gδ-Menge (= abzählbarer Durchschnitt offener Mengen) G mit F ⊂ B ⊂ G und λd (G \ F) = 0. Das folgt aus dem Beweis von Satz A.10 (Schritt 3°) und Satz A.11. [✍]
gibt es eine Fσ-Menge (= abzählbare Vereinigung abgeschlossener Mengen) F und eine Gδ-Menge (= abzählbarer Durchschnitt offener Mengen) G mit F ⊂ B ⊂ G und λd (G \ F) = 0. Das folgt aus dem Beweis von Satz A.10 (Schritt 3°) und Satz A.11. [✍]
A.13 Bemerkung. Satz A.11 kann auf verschiedene Arten verallgemeinert werden, wobei stets die Topologie eine besondere Rolle spielt.
- a) Wenn das Maß μ lokal-endlich ist (d. h. jedes x ∈ E besitzt eine offene Umgebung Ux mit μ(Ux) < ∞), dann gilt μ(K) < ∞ für alle Kompakta K ⊂ E.
- b) Ein lokal-endliches Maß auf einem separablen Raum E (d. h. E enthält eine abzählbare dichte Teilmenge) ist σ-endlich.
- c) Ein separabler und lokal-kompakt Raum E ist σ-kompakt.
A.6 Separabilität des Raums Cc(E)
Ein topologischer Raum 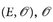 bezeichnet die Topologie oder Familie der offenen Mengen, heißt lokal-kompakt, wenn jeder Punkt x ∈ E eine offene Umgebung U(x) hat, deren Abschluss kompakt ist. Der Raum E hat eine abzählbare Basis, wenn es eine abzählbare Familie
bezeichnet die Topologie oder Familie der offenen Mengen, heißt lokal-kompakt, wenn jeder Punkt x ∈ E eine offene Umgebung U(x) hat, deren Abschluss kompakt ist. Der Raum E hat eine abzählbare Basis, wenn es eine abzählbare Familie 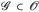 mit
mit  für alle offenen Mengen
für alle offenen Mengen  gibt. Typische Beispiele sind lokal-kompakte metrische Räume (E, d), die eine abzählbare dichte Teilmenge haben.
gibt. Typische Beispiele sind lokal-kompakte metrische Räume (E, d), die eine abzählbare dichte Teilmenge haben.
Wir schreiben Cc(E) für die stetigen Funktionen  mit kompaktem Träger supp
mit kompaktem Träger supp 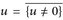 . Wir nennen Cc(E) separabel, wenn es eine bezüglich der gleichmäßigen Konvergenz dichte abzählbare Teilmenge in Cc(E) gibt.
. Wir nennen Cc(E) separabel, wenn es eine bezüglich der gleichmäßigen Konvergenz dichte abzählbare Teilmenge in Cc(E) gibt.
A.14 Satz. Es sei  ein lokal-kompakter topologischer Raum mit abzählbarer Basis. Dann ist der Raum (Cc(E), ∥ · ∥∞) separabel.
ein lokal-kompakter topologischer Raum mit abzählbarer Basis. Dann ist der Raum (Cc(E), ∥ · ∥∞) separabel.
Beweis. Es sei  eine abzählbare Basis von
eine abzählbare Basis von  und
und 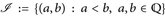 . Es seien
. Es seien 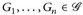 und
und  . Eine Funktion f ∈ Cc(E) mit
. Eine Funktion f ∈ Cc(E) mit

nennen wir an (Gi, Ii)i=1, ...,n adaptiert. Zu jedem solchen Tupel wählen wir eine feste adaptierte Funktion (sofern es eine gibt) und schreiben  für diese Familie. Da die Familie
für diese Familie. Da die Familie  abzählbar ist, ist
abzählbar ist, ist 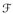 höchstens abzählbar. Für u ∈ Cc(E) gilt
höchstens abzählbar. Für u ∈ Cc(E) gilt

Da supp u kompakt ist, wird supp u durch U(x1) ∪ ··· ∪ U(xn), also für endlich viele x1, ... , xn, überdeckt. Andererseits ist für alle i = 1, ... , n
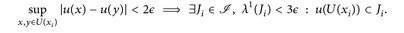
Also ist u an (U(xi), Ji)i=1, ...,n adaptiert. Nun sei 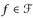 auch an (U(xi), Ji)i=1, ...,n adaptiert. Dann gilt
auch an (U(xi), Ji)i=1, ...,n adaptiert. Dann gilt

Mithin ist ∥ f − ull∞ < 3ε, d. h.  ist eine dichte Teilmenge.
ist eine dichte Teilmenge.
Literatur
- [1] H. W. Alt: Lineare Funktionalanalysis (3. Auflage). Springer, Berlin 1999.
- [2] T. M. Apostol: A proof that Euler missed. Evaluating ζ(2) the easy way. Math. Intelligencer 5 (1983) 59–60.
- [3] S. Bochner: Vorlesungen über Fouriersche Integrale. (3. Auflage). Akademische Verlagsgesellschaft, Leipzig 1932. (Unveränderter Nachdruck: Chelsea, New York (NY) 1948.)
- [4] N. Dunford, J. T. Schwartz: Linear Operators - Part I. Wiley-Interscience, Pure and Applied Mathematics VII, New York 1957.
- [5] G. M. Fichtenholz: Differential- und Integralrechnung I-III. VEB Deutscher Verlag der Wissenschaften, Berlin 1973-74 (6.-8. Auflage).
- [6] F. W. J. Olver et al.: NIST Handbook of Mathematical Functions. Cambridge University Press, Cambridge 2010. (Freier Online-Zugang: http://dlmf.nist.gov/)
- [7] W. Rudin: Analysis (4. Auflage). Oldenbourg, München 2009.
- [8] R. L. Schilling: Measures, Integrals and Martingales. Cambridge University Press, Cambridge 2011 (3rd printing).
- [9] K. Stromberg: The Banach-Tarski Paradox. Am. Math. Mon. 86 (1979) 151–161.
- [10] K. Yosida: Functional Analysis (6th Edition). Springer, Grundlehren der mathematischen Wissenschaften 123, Berlin 1980.