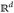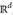Stichwortverzeichnis

Alle Zahlenangaben beziehen sich auf Seitennummern, (Pr. m.n) verweist auf die Aufgabe n(im Kapitel m) auf der jeweils angegebenen Seite.

absolutstetig, 1

äußeres Maß, 1, 2

allgemeiner Transformationssatz, 1, 2

Approximation der Identität, 1 (Pr. 18.7), 2

Atom, 1, 2

Banach-Tarski Paradox, 1

Beppo Levi, 1

– für Reihen, 1, 2 (Pr. 8.2)

Beta-Funktion, 1 (Pr. 20.2)

Bildintegral, 1, 2

Bildmaß, 1

Borel σ-Algebra

– auf , 1

– Spur, 1 (Pr. 2.4), 2

– für Teilmenge, 1 (Pr. 2.4)

Borel-messbar, 1, 2

Borelmenge, 1

– Approximation, 1

Cantor-Menge, 1–2

Cauchy-Schwarz Ungleichung, 1

Cavalieri-Prinzip, 1, 2, 3

Chebyshevsche Ungleichung, 1 (Pr. 10.4)

δ-Funktion, 1

Dichte(funktion), 1, 2

Dichtheit

– C_b ∩ L^p dicht in L^p, 1

– C_c dicht in L^p, 1

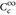– dicht in C_c, 1

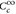– dicht in L^P, 1

– C_Lip n L^p dicht in L^p, 1 (Pr. 23.5)

– A dicht in C_∞, 1

– A dicht in L^p, 1

– ε ∩ L^p dicht in L^p, 1

Diffeomorphismus, 1

– Kriterium, 1

Differenzierbarkeitslemma, 1

Dirac-Maß, 1

Dirichletsches Integral, 1 (Pr. 16.8)

diskretes W-Maß, 1

dominierte Konvergenz (Satz), 1

Dynkin-System, 1, 2 (Pr. 4.4)

– vs. σ-Algebra, 1

– Erzeuger, 1

– minimales Dynkin-System, 1

Eindeutigkeitssatz (Maße), 1

Eindeutigkeitssatz (Produktmaße), 1

einfache Funktion, 1

– dicht in L^p, 1

– Standarddarstellung, 1

Erzeuger

– Borel-σ-Algebra, 1, 2, 3

– Dynkin-System, 1

– Produkt-σ-Algebra, 1

– σ-Algebra, 1

Eulersches Integral, 1 (Pr. 20.2)

Existenzsatz (Produktmaße), 1

Faktorisierungslemma, 1

Faltung, 1

– Eigenschaften, 1–2

– Friedrichsglättung, 1 (Pr. 18.7)

– in ([0,∞), ·),1 (Pr. 18.5)

Faltungssatz, 1

fast überall (f. ü.), 1

Fatous Lemma, 1, 2 (Pr. 8.4), 3 (Pr. 8.5), 4 (Pr. 9.5)

Fortsetzungssatz (Produktmaße), 1

Fouriertransformation, 1

– Differenzierbarkeit, 1 (Pr. 22.4)

– Fortsetzung auf L², 1

– Injektivität, 1

– inverse Fouriertransformation, 1

– Normalverteilung, 1, 2

– positiv semidefinit, 1 (Pr. 22.4), 2

– Rechenregeln, 1–2

– rotationssymmetrische Funktion, 1

– Satz von Bochner, 1

– und schwache Konvergenz, 1, 2 (Pr. 24.3)

– Schwartz-Raum, 1

– Symmetrie, 1

– trivialisiert Faltung, 1

- Umkehrformel für Funktionen, 1

- Umkehrformel von Lévy, 1, 2

– Zusammenhang mit inverser FT, 1

Fresnelsches Integral, 1 (Pr. 13.10)

Friedrichsglättung, 1 (Pr. 18.7)

Frullanisches Integral, 1 (Pr. 13.11)

F_σ-Menge, 1

Fubini (Satz), 1

Gamma-Funktion, 1, 2 (Pr. 20.2)

G_δ-Menge, 1

Höldersche Ungleichung, 1, 2 (Pr. 14.3)

– für 0 < p < 1, 1 (Pr. 14.11)

– für Reihen, 1

Halbring, 1, 2

– kartesisches Produkt, 1

Indikatorfunktion, 1

– Messbarkeit, 1

Integral

– bzgl. Bildmaß, 1, 2

– Eigenschaften, 1

– einfache Funktion, 1

– komplexe Funktion, 1 (Pr. 9.2), 2

– messbare Funktion, 1

– positive Funktion, 1

- rotationssymmetrische Funktion, 1

– bzgl. Zählmaß, 1

Integralsinus, 1,2

integrierbare Funktion, 1

– p-fach integrierbar, 1

– auf einer Menge, 1

– ist f. ü. reell, 1

– Raum ℒ¹, 1

– Raum ℒ^p, 1

– Raum L^p, 1

inverse Fouriertransformation, 1

Jacobi-Determinante, 1

Jacobi-Matrix, 1

Jensensche Ungleichung, 1

Kern/Übergangskern, 1 (Pr. 8.7)

Konvergenz (Maße), 1, 2, 3, 4

– siehe auch schwache Konv., vage Konv.,

Konvergenz in L^p, 1

– f. ü. konvergente Teilfolge, 1

– schwach, 1 (Pr. 24.2)

Konvergenzsatz

– von Lebesgue, 1

– von Riesz, 1

– von Young, 1 (Pr. 11.12)

konvexe Funktion, 1

Kugelkoordinaten, 1–2

ℒ¹-Raum, 1

ℒ^p/L^p-Raum, 1, 2

- Dreiecksungleichung, 1

– ist vollständig, 1

Lebesgue-Maß, 1

- bewegungsinvariant, 1, 2

– Dilatationen, 1 (Pr. 4.9)

– Existenz (auf ), 1, 2

– Existenz (auf ), 1, 2 (Pr. 17.1)

– lineare Transformation, 1

– Nullmenge, 1 (Pr. 4.1), 2 (Pr. 5.3), 3

– orthogonale Transformation, 1

– ist regulär, 1

– translationsinvariant, 1, 2

Lebesgue-Prämaß, 1

Lebesgue-Stieltjes Maß, 1 (Pr. 5.1)

Lebesguescher Konvergenzsatz, 1

Lemma

– von Fatou, 1, 2 (Pr. 8.4), 3 (Pr. 8.5), 4 (Pr. 9.5)

– von Pratt, 1 (Pr. 11.12)

-von Riemann-Lebesgue, 1

– von Urysohn, 1, 2

liminf/limsup von Mengen, 1 (Pr. 2.8), 2 (Pr. 8.5)

Markovsche Ungleichung, 1, 2 (Pr. 10.4)

Maß, 1

– absolutstetig, 1

– additiv, 1

– äußeres Maß, 1

– mit Dichte, 1

– Eindeutigkeit, 1

– endlich, 1

– Fortsetzung, 1

– monoton, 1

– Produkt, 1

– regulär, 1, 2, 3

– σ-endlich, 1, 2 (Pr. 8.8), 3 (Pr. 19.1)

– σ-subadditiv, 1

– signiertes, 1 (Pr. 19.3)

– singulär, 1 (Pr. 19.2)

– stetig, 1, 2, 3

– subadditiv, 1

– unendliches Produkt, 1

– Vervollständigung, 1 (Pr. 3.7), 2 (Pr. 5.4), 3 (Pr. 10.5), 4 (Pr. 15.2), 5

– Vollständigkeit, 1 (Pr. 7.13)

– W-Maß, 1

maßbestimmende Familie, 1

Maßraum, 1, 2

– endlich, 1

– σ-endlich, 1

– W-Raum, 1

messbar

– Borel-messbar, 1

- Lebesgue-messbar, 1

– bzgl. eines Maßes, 1

– Menge, 1

– nicht-messbare Menge, 1

– Stetigkeitsstellen einer Funktion, 1

messbare Abbildung/Funktion, 1, 2

– Eigenschaften, 1

– halbseitig stetig ⇒ messbar, 1 (Pr. 7.10)

– Komposition, 1

– Messbarkeitskriterium, 1, 2

– stetig ⇒ messbar, 1

Messraum, 1, 2

Minkowskische Ungleichung, 1

– für 0 < p < 1, 1 (Pr. 14.11)

– für Doppelintegrale, 1 (Pr. 16.10)

– für Reihen, 1

monotone Klasse, 1, 2 (Pr. 4.5)

monotone Konvergenz (Satz), 1

Negativteil (Funktion), 1

Negativteil (Maß), 1 (Pr. 19.3)

Normalverteilung, 1, 2

Nullmenge, 1 (Pr. 3.7), 2 (Pr. 5.3), 3, 4, 5

offene Menge, 1

p-fach integrierbare Funktion, 1

Parameterintegral

– Differenzierbarkeit, 1

- Stetigkeit, 1

partielle Integration, 1

Partition der Eins, 1

Plancherel (Satz), 1

Polarkoordinaten, 1-2

Portmanteau-Theorem, 1, 2

positives lineares Funktional, 1

– in C_c, 1

– in L^p,

– ist stetig, 1

Positivteil (Funktion), 1

Positivteil (Maß), 1 (Pr. 19.3)

Prämaß, 1, 2 (Pr. 5.6)

– Fortsetzung, 1

– Lebesguesches, 1

Produkt-σ-Algebra, 1, 2, 3

– Erzeuger, 1

Produktmaß, 1

– Eindeutigkeit, 1, 2

– Existenz, 1, 2

– unendliches, 1

Produktmaßraum, 1

Produktmessraum, 1

Radon-Nikodým (Satz), 1, 2, 3

Radon-Nikodým Ableitung, 1

Rechtecke (in ), 1, 2

– sind Halbring, 1

Regularität von Maßen, 1, 2, 3

Reihenvergleichskriterium, 1 (Pr. 9.3)

Riemann-Lebesgue Lemma, 1

Riemann-integrierbar, 1

– Kriterium, 1

– uneigentlich, 1 (Pr. 13.9)

Rieszscher Darstellungssatz

– für C_c, 1

– für L^p, 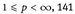, 1

rotationssymmetrische Funktion

- Fouriertransformation, 1

– Integral, 1

Satz

-von Beppo Levi, 1

– von Beppo Levi (Reihen), 1, 2 (Pr. 8.2)

– von Bochner, 1

– von Carathéodory, 1

– von der dominierten Konvergenz, 1

– von der monotonen Klasse, 1 (Pr. 4.5)

-von der monotonen Konvergenz, 1

– von Egorov, 1 (Pr. 9.6)

– von Fubini, 1

– von Kolmogorov, 1

– von Lusin, 1 (Pr. 23.7)

– von Plancherel, 1

– von Radon-Nikodým, 1, 2, 3

– von Riesz-Fischer, 1

– von Tonelli, 1

schwache Konvergenz (Maße), 1, 2

– vs. vage Konvergenz, 1

– Kriterien, 1

Schwartz-Raum, 1

Separabilität von ℒ^p, 1 (Pr. 23.6)

Separabilität von C_c, 167

σ-additiv, 1

σ-Algebra, 1

– Approximation, 1 (Pr. 4.6), 2

– Borelsche, 1

– Erzeuger, 1

– erzeugtvon Abbildung, 1

– erzeugtvon einem (äußeren) Maß, 1

– minimale σ-Algebra, 1

– Produkt, 1

– Spur, 1, 2 (Pr. 2.4)

– topologische, 1

– unendliches Produkt, 1

– Urbild, 1

σ-endlich, 1

σ-subadditiv, 1

signiertes Maß, 1 (Pr. 19.3)

Sombrero-Lemma, 1

Stetigkeit

– impliziert Borel-messbar, 1

Stetigkeit (Maß), 1, 2, 3

Stetigkeitslemma, 1

Stetigkeitssatz von Lévy, 1 (Pr. 24.3)

Straffheit, 1

Tonelli (Satz), 1

Topologie, 1

Transformationssatz für Integrale, 1, 2

– für affin-lineare Transformationen, 1

– für Diffeomorphismen, 1, 2

truncation inequality, 1 (Pr. 22.3)

Ungleichung

– Cauchy-Schwarz, 1

– Chebyshev, 1 (Pr. 10.4)

– L^p-Dreiecksungleichung, 1

– Hölder, 1, 2 (Pr. 14.3)

– Hölder (0 < p < 1), 1 (Pr. 14.11)

– Hölder (Reihen), 1

– Jensen, 1

– Markov, 1

– Minkowski, 1

– Minkowski (0 < p < 1), 1 (Pr. 14.11)

– Minkowski (Doppelintegrale), 1 (Pr. 16.10)

– Minkowski (Reihen), 1

–Young, 1

– Young (Faltung), 1, 2 (Pr. 18.6)

Urysohnsches Lemma, 1, 2

vage Konvergenz (Maße), 1

-vs. schwache Konvergenz, 1

- Kriterien, 1

– vage Beschränktheit, 1

-vage Kompaktheit, 1

Verteilung, 1, 2

Verteilungsfunktion, 1 (Pr. 5.1), 2, 3

Vollständigkeit von L^p, 70

Volumen

– Einheitskugel, 1

– Einheitssphäre, 1

– Spat, 1,2

Wiener-Algebra, 1

Youngsche Ungleichung, 1

– für Faltung, 1, 2 (Pr. 18.6)

Zählmaß, 1

Zuvallsvariable, 1, 2, 3, 4