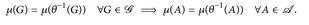4 Eindeutigkeit von Maßen

Ehe wir die Fortsetzbarkeit von und anderen Maßen diskutieren, untersuchen wir, ob es prinzipiell ausreicht, Maße auf einem Erzeuger einer σ-Algebra vorzugeben –z. B. 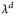auf 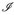. Dabei stoßen wir auf ein grundlegendes Problem: man kann selten 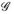konstruktiv zu 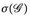erweitern. Einen Ausweg bietet das folgende Hilfsmittel.

 

4.1 Definition. Eine Familie 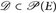heißt Dynkin-System, wenn gilt

(D₁)

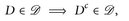
(D₂)

(D₃)

Vergleicht man (D₁)-(D₃) mit (∑₁)—(∑₃), dann folgt sofort, dass jede σ-Algebra auch ein Dynkin-System ist. Wie in § 2.2.a), b) sieht man, dass

und .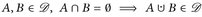

4.2 Satz. a) Für jede Familie existiert ein minimales Dynkin-System mit . 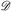heißt das von 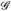erzeugte Dynkin-System. Bezeichnung: .

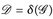b) Stets gilt .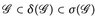

 

Beweis. Teil a) ist analog zu Satz 2.4. Zu b): Da die σ-Algebra 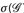ein Dynkin-System ist, für das 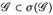gilt, folgt wegen der Minimalität von 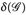, dass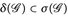

Das folgende Lemma erklärt den Zusammenhang zwischen Dynkin-Systemen und 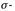Algebren.

 

4.3 Lemma. Es sei 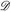ein Dynkin-System.

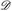ist eine 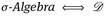ist ∩-stabil (d. h. .

 

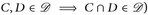Beweis. „⇒“: Ist 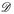eine 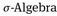dann (∑₁)—(∑₃) ⇒ (D₁)—(D₃), und die ∩-Stabilität folgt aus § 2.2.c).

„⇐“: Wir müssen (∑₃) zeigen: 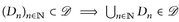. Setze E₁:=D₁ und

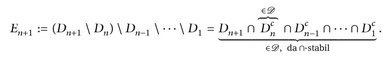
Mithin folgt .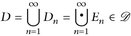

Erzeuger sind i. Allg. kleiner und handlicher als die davon erzeugte σ-Algebra. Daher ist der folgende Satz von großer Bedeutung.

 

4.4 Satz. 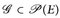∩-stabil .

Beweis. 1°) Offensichtlich gilt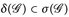

2°) Wäre 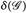eine σ-Algebra dann hätten wir 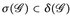, da ja 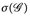die kleinste σ-Algebra ist, für die 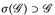gilt; wegen 1° ist 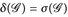. Im Hinblick auf Lemma 4.3 reicht es also zu zeigen, dass 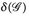∩-stabil ist.

3°) Wir zeigen: 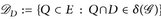ist ein Dynkin-System für jedes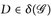

(D₁) Klar.

(D₂) Für 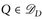gilt auch . Das folgt so:

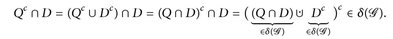
(D₃)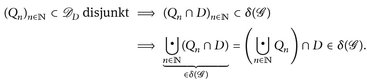

Somit ist .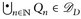

 

4°) Offensichtlich ist 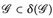; da 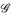∩-stabil ist, gilt

Nun besagt für alle 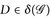gerade, dass ∩-stabil ist.

Einige Autoren verwenden monotone Klassen. Das sind Familien 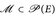mit

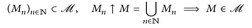
(MC₁)

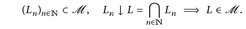
(MC₂)

Für monotone Klassen gilt folgende Aussage, die Satz 4.4 entspricht:

Satz von der monotonen Klasse. Es sei 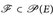eine Familien von Mengen, die stabil unter Schnitten und Komplementbildung ist 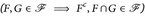. Dann gilt für jede monotone Klasse, dass aus 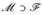sofort 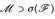folgt. 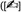Aufgabe 4.5)

Die Aussage und Beweistechnik von Satz 4.4 spielen in der Wahrscheinlichkeitstheorie eine wichtige Rolle. Wir verwenden Dynkin-Systeme zunächst nur im folgenden Satz.

 

4.5 Satz (Eindeutigkeitssatz). Es seien 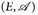ein beliebiger Messraum, 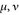zwei Maße und 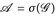mit folgenden Eigenschaften:

a) 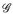ist ∩-stabil,

b)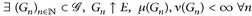

Dann .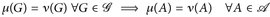

4.6 Bemerkung. a) Die Aussage von Satz 4.5 wird oft auch so geschrieben: 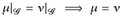. (Dabei ist 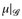die Einschränkung von µ auf die Familie .)

b) Sind µ und v W-Maße, dann kann Bedingung b) in Satz 4.5 weggelassen werden. Denn: µ(E) = ν(E) = 1. Füge o. E. E zu 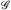hinzu und wähle G_n = E.

 

Beweis von Satz 4.5. Setze 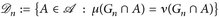, n ∈ .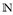

1°) Behauptung: 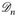ist ein Dynkin-System.

(D₁) Klar.

(D₂) Sei dann ist 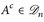weil gilt

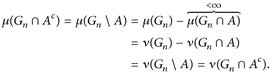
(D₃) Seien paarweise disjunkt. Dann folgt 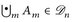aus

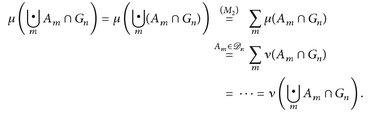
2°) Für alle n gilt

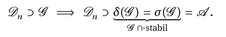
Andererseits:

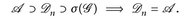
Also:

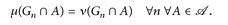
Aufgrund der Stetigkeit von Maßen (Satz 3.3.f) folgt nun

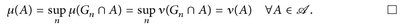
Weitere Anwendungen für Dynkin-Systeme

Die folgenden Resultate zeigen, dass das Lebesgue–Maß 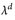– wenn es existiert – ein besonderes Maß ist. Zur Erinnerung

x + B:= {x + b: b ∈ B} ist die um verschobene Menge .

4.7 Satz. a) Das Lebesgue–Maß λ^d ist translationsinvariant, d. h.

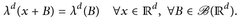
b) Es sei µ ein translationsinvariantes Maβ auf (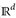, ℬ(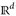)) mit K = µ([0, 1)^d) < ∞. Dann gilt bereits µ = κ · λ^d.

Beweis. Zunächst überlegen wir uns, dass 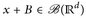für alle 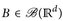— sonst wäre a) sinnlos. Für festes x ∈ 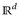setzen wir

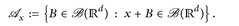
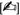Offenbar ist eine σ-Algebra und 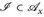. Somit gilt

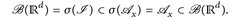
a) Setze ν(B):= λ^d (x + B) für ein festes x ∈ 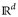und B ∈ ℬ(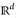)Dann ist ν ein Maß auf ( und

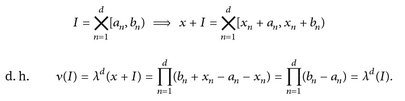
Also gilt , wobei ein ∩-stabiler Erzeuger von ℬ() ist (vgl. Abb. 4.1), für den außerdem [–m, m)^d ∈ , [–, m)^d ↑ 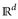,λ^d([-m,m)^d) = (2m)^d < ∞ erfüllt ist. Somit können wir Satz 4.5 anwenden und sehen, dass ν = λ^d gilt.

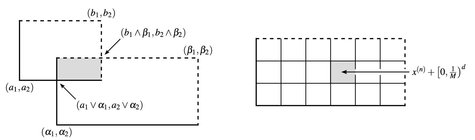
Abb. 4.1. Links: Es gilt 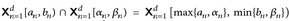. Rechts: Wir parkettieren I mit Rechtecken 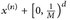der Seitenlänge 1/M und mit linker unterer Ecke x⁽ⁿ⁾. (M ist z. B. das kgV aller Nenner der a_n, b_n ...).

b) Es sei I ∈ 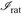. Dann existieren M, k(I) ∈ N und x⁽ⁿ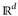⁾ ∈ mit

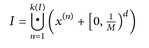
(vgl. Abb. 4.1). Da λ^d und µ translationsinvariante Maße sind, gilt

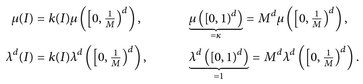
Aus der ersten Zeile erhalten wir und aus der zweiten Zeile ergibt sich 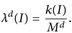Zusammen haben wir µ(I) = κ·λ^d(I) für alle Rechtecke 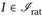. Aus dem Eindeutigkeitssatz 4.5 folgt dann µ = κ · λ^d.

 

Unser nächstes Etappenziel ist der Existenzbeweis für das Lebesgue–Maß (und viele andere Maße!).

Aufgaben

1. Es sei λ^d das d-dimensionale Lebesgue-Maß auf (, ℬ()).
   • (a) Zeigen Sie: 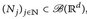, λ^d(N_j) = 0 ∀j ∈ ⇒
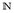   • (b) Für alle r ∈ 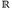gilt {r} ∈ ℬ(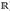) und λ¹ {r} = 0. (Hinweis: Stetigkeit von oben.)
   • (c) Es sei E eine Ebene in 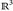. Dann gilt E ∈ ℬ(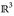)und λ³(E) = 0. (Hinweis: Satz 3.7 und 4.7.)
   • (d) Es sei N eine λ^d-Nullmenge und M ⊂ N. Ist M eine λ^d-Nullmenge?
   • (e) Gegeben sei der Maßraum (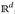, ℬ(), δ_a + δ_b) mit a, b ∈ 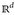. Finde alle δ_a + δ_b-Nullmengen.
2. Es sei k ∈ 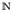und E = {1, 2,… , 2k – 1, 2k}. Ist F = {A ⊂ E: #A ist gerade} ein Dynkin-System bzw. eine σ-Algebra?
3. Bestimmen Sie die Familien (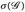) und 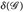auf dem Grundraum E = (0,1) für
   

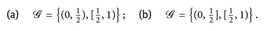
   Hinweis: Beachten Sie die Struktur von σ({A₁, ..., A_n}) für eine Partition A₁, ...,A_n von E (vgl. Aufgabe 2.6), sowie 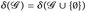und Satz 4.4.

4. (Alternative Charakterisierungvon Dynkin-Systemen) Eine Familie 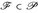(E) ist genau dann ein Dynkin-System, wenn
   

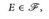
   (D₁)

   

   

   

   

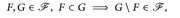
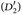
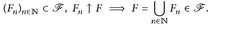
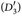
5. (Satz von der monotonen Klasse) Es sei ℳ ⊂ 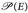eine monotone Klasse (MC), vgl. Seite 15, und ℱ ⊂ 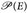eine Familie von Mengen.
   • (a) Es gibt eine minimale MC µ(ℱ) mit ℱ ⊂ µ(ℱ).
   • (b) Es sei ℱ 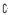-stabil, d. h. F ∈ ℱ ⇒ F^c ∈ ℱ. Dann ist auch µ(ℱ) 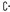-stabil.
   • (c) Es sei ℱ ∩-stabil, d. h. F, G ∈ ℱ ⇒ F ∩ G ∈ ℱ. Dann ist auch µ(ℱ) ∩-stabil.

     Hinweis: Betrachten Sie nacheinander die Systeme

     

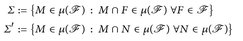
     und zeigen Sie, dass dies auch monotone Klassen mit ℱ ⊂ Σ, Σ′ sind.

   • (d) Beweisen Sie nun mit Hilfe der vorangehenden Teilaufgaben den folgenden

     Satz (monotone Klassen). Es sei ℱ ⊂ eine Familie, die C-stabil und ∩-stabil ist und E ∈ ℱ. Dann gilt für jede monotone Klasse ℳ ⊃ ℱ auch ℳ ⊃ σ(ℱ).

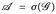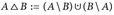6. (Approximation von σ-Algebren) Es sei eine Boolesche Algebra auf E, d. h. E ∈ und ist stabil unter endlichen Schnitten, Vereinigungen und Komplementen. Weiter seien und µ ein endliches Maß auf (E, ). Wir schreiben für die symmetrische Differenz von zwei Mengen A, B ⊂ E. Zeigen Sie:
   • (a) Für jedes ∈ > 0 und A ∈ 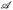gibt es ein G ∈ 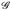mit µ(A∆G) ≤ ∈. Hinweis: Die Familie {A ∈ 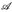: Ve > 0 ∃G ∈ 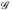: µ (A ∆ G) ≤ ∈} ist ein Dynkin-System.
   • (b) Es seien µ, ν endliche Maße auf (E, 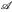). Für jedes ∈ > 0 und A ∈ 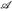gibt es ein G ∈ 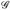mit µ(A ∆ G) ≤ ∈ und ν (A ∆ G) ≤ ∈.
   • (c) Es sei E = 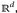, 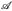= ℬ(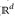) und µ = λ^d. Für eine Menge A ∈ 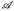gilt µ(A) = 0 genau dann, wenn es für jedes ∈ > 0 eine Folge von Rechtecken gilt, so dass A ⊂ U_nI_n und µ(U_nI_n) ≤ ∈.
7. Es sei (Ω, 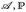,) ein Wahrscheinlichkeitsraum und ℬ, 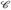⊂ 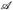seien σ-Algebren. ℬ und 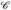heißen (stochastisch) unabhängig, wenn
   

   Seien ℬ = 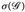und 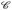= σ(ℋ), wobei und ℋ durchschnittsstabile Mengenfamilien sind. Zeigen Sie:

   

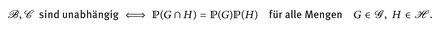
   Hinweis: Beachten Sie die Struktur des Beweises von Satz 4.5.

8. Zeigen Sie, dass Satz 4.5 auch dann gilt, wenn die Folge den Raum E überdeckt, d. h. E = U_n G_n (aber nicht notwendig gegen E aufsteigt), und µ(G_n) = ν(G_n) < ∞ erfüllt.

   Hinweis: Die Mengen G₁ ∪ · · · ∪ G_n erfüllen die Voraussetzungen von Satz 4.5.

9. (Dilatationen) Adaptieren Sie den Beweis von Satz 4.7 und zeigen Sie, dass t · B:= {tb: b ∈ B} für jede Borelmenge B ∈ ℬ.() und t > 0 wiederum Borelsch ist. Weiter gilt
   
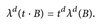
10. (Invariante Maße) Es sei (E, 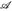, µ) ein endlicher Maßraum und 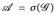für einen ∩-stabilen Erzeuger 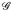. Weiterhin sei θ: E → E eine Abbildung mit θ^-1 (A) ∈ 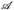für alle A ∈ . Zeigen Sie, dass