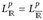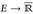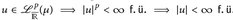14 Die Räume 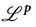 und Lp
und Lp
Es sei (E, 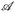 , µ) ein Maßraum. Analog zu den integrierbaren Funktionen
, µ) ein Maßraum. Analog zu den integrierbaren Funktionen 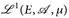 führen wir nun die p-fach integrierbaren Funktionen ein. Diese Räume spielen auch in der Funktionalanalysis eine große Rolle.
führen wir nun die p-fach integrierbaren Funktionen ein. Diese Räume spielen auch in der Funktionalanalysis eine große Rolle.
14.1 Definition. Es sei p ∈ [1, ∞). Dann sind
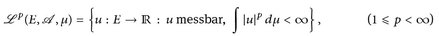

die Räume der p-fach integrierbaren Funktionen. Wir schreiben

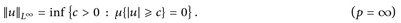
Je nachdem, ob wir das Maß µ, die Grundmenge E oder die Messbarkeit bezüglich  hervorheben möchten, schreiben wir auch
hervorheben möchten, schreiben wir auch  ,
,  ,
, 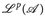 oder nur
oder nur 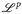 .
.
Die Abbildung 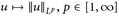 , verhält sich im Wesentlichen wie eine Norm:
, verhält sich im Wesentlichen wie eine Norm:
- a)
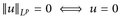 f. ü. (Satz 10.2.a) für p < ∞, trivial für p = ∞).
f. ü. (Satz 10.2.a) für p < ∞, trivial für p = ∞). - b)
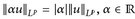 . =
. =
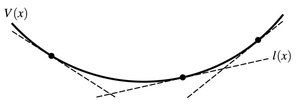
Nur die Dreiecksungleichung für die Norm ist nicht offensichtlich. Dazu benötigen wir eine elementare Ungleichung, die direkt aus Abb. 14.1 abgelesen werden kann.
14.2 Lemma (Youngsche Ungleichung). Die Exponenten p, q ∈ (1, ∞) seien konjugiert, d. h. p–1 + q–1 = 1 (also: q = p/(p – 1)). Dann
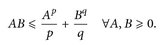
(14.1)
Zusatz: In (14.1) gilt „=“ genau dann, wenn 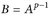 .
.
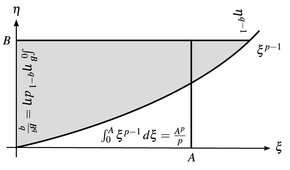
Abb.14.1. Youngsche Ungleichung.
Mit Hilfe der Youngschen Ungleichung können wir die folgende fundamentale Ungleichung für Integrale beweisen.
14.3 Satz (Höldersche Ungleichung). Für 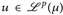 und
und  mit
mit 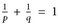 , p, q ∈ [1, ∞], gilt
, p, q ∈ [1, ∞], gilt 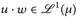 und
und
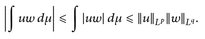
(14.2)
Beweis. Die erste Ungleichung in (14.2) ist klar, die zweite Ungleichung folgt so:
Fall 1: p, q ∈ (1, ∞). Setze
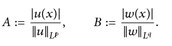
Wegen (14.1) erhalten wir
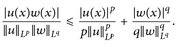
Wir integrieren nun auf beiden Seiten
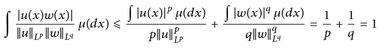
woraus die behauptete Ungleichung durch Multiplikation mit  folgt.
folgt.
Fall 2: p = 1, q = ∞. Definitionsgemäß haben wir 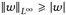 f. ü., also
f. ü., also
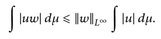
14.4 Korollar (Cauchy–Schwarz Ungleichung). Für u, 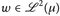 gilt
gilt 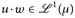 und
und
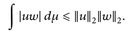
(14.3)
Beweis. Verwende Satz 14.3 mit p = q = 2.
14.5 Korollar (Minkowski-Ungleichung). Für beliebige 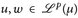 und p ∈ [1, ∞] gilt u + w ∈
und p ∈ [1, ∞] gilt u + w ∈ 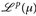 , sowie
, sowie
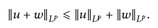
(14.4)
Beweis. Der Fall p = ∞ ist eine Übung. [✍] Sei p ∈ [1, ∞). Zunächst folgt die p-fache Integrierbarkeit aus

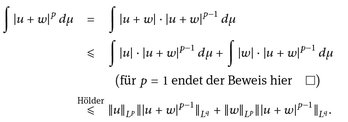
Da q = p/(p – 1) gilt auch
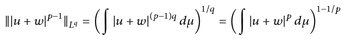
und die Behauptung folgt durch Division mit 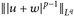 .
.
14.6 Bemerkung. a) Korollar 14.5 besagt insbesondere, dass für u, 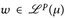 und α,
und α, 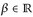 wiederum
wiederum 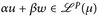 gilt, d. h.
gilt, d. h. 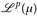 ist ein Vektorraum.
ist ein Vektorraum.
b) 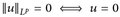 f. ü., d. h.
f. ü., d. h. 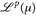 ist nur ein quasi-normierter Raum, da nicht notwendig u ≡ 0 gilt. Es gibt aber ein Standardverfahren, um
ist nur ein quasi-normierter Raum, da nicht notwendig u ≡ 0 gilt. Es gibt aber ein Standardverfahren, um 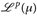 zu einem echten normierten Raum zu machen.
zu einem echten normierten Raum zu machen.
- ▶ u,
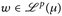 sind äquivalent,
sind äquivalent, 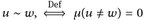 .
. - ▶
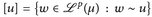 Äquivalenzklasse mit Repräsentant u.
Äquivalenzklasse mit Repräsentant u. - ▶
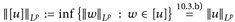 .
. - ▶
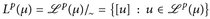 .
. - ▶ Lp(µ) ist ein Vektorraum [✍] und
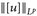 darauf eine Norm.
darauf eine Norm.
Und hier ist die übliche Standardschlamperei (der wir uns aber anschließen werden): Es ist üblich, von Lp-Funktionen zu sprechen und [u] mit einem guten Repräsentanten u0 ∈ [u] zu identifizieren. Beachte
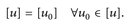

c) u, w ∈ Lp(µ). Dann sind Ausdrücke der Art
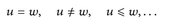
stets bis auf eine Ausnahme-Nullmenge, also „f. ü.“ zu verstehen.
d) 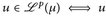 messbar und
messbar und 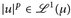 .
.
Wir wollen nun 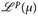 als quasi-normierten Raum studieren.
als quasi-normierten Raum studieren.
14.7 Definition (LP-Konvergenz). Es seien 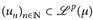 ,
, 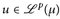 , p ∈ [1, ∞].
, p ∈ [1, ∞].
- a) Die Folge
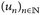 konvergiert in Lp gegen
konvergiert in Lp gegen 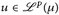 , wenn
, wenn 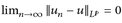 . Wir schreiben
. Wir schreiben 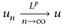 oder LP-limn→∞ un = u.
oder LP-limn→∞ un = u. - b) Die Folge
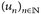 heißt LP-Cauchy-Folge, wenn
heißt LP-Cauchy-Folge, wenn
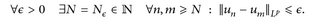
14.8 Bemerkung. a) Jede in Lp konvergente Folge 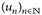 ist auch eine Cauchy-Folge. Wenn u den Lp-Grenzwert bezeichnet, dann sehen wir mit der Minkowski-Ungleichung
ist auch eine Cauchy-Folge. Wenn u den Lp-Grenzwert bezeichnet, dann sehen wir mit der Minkowski-Ungleichung 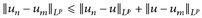 ; die rechte Seite konvergiert für m, n → ∞ gegen Null.
; die rechte Seite konvergiert für m, n → ∞ gegen Null.
b) Es sei 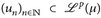 eine Folge, die für alle (oder µ-fast alle) x ∈ E einen punktweisen Grenzwert u(x) = limn→∞ un(x) hat. Dann folgt i. Allg. nicht die Lp-Konvergenz!
eine Folge, die für alle (oder µ-fast alle) x ∈ E einen punktweisen Grenzwert u(x) = limn→∞ un(x) hat. Dann folgt i. Allg. nicht die Lp-Konvergenz!
Hinreichend wäre, wenn zusätzlich 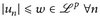 (Satz 11.3 bzw. Satz 14.12).
(Satz 11.3 bzw. Satz 14.12).
Wir zeigen nun die Umkehrung von 14.8.a): Der Raum 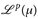 , p ∈ [1, ∞], ist vollständig. Zur Vorbereitung brauchen wir folgendes Hilfsresultat.
, p ∈ [1, ∞], ist vollständig. Zur Vorbereitung brauchen wir folgendes Hilfsresultat.
14.9 Lemma. Es seien 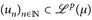 , p ∈ [1, ∞], un ≥ 0. Dann
, p ∈ [1, ∞], un ≥ 0. Dann
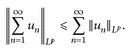
Beweis. Wir verwenden die Minkowski-Ungleichung N mal:
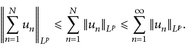
Da 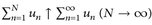 , folgt mit Beppo Levi
, folgt mit Beppo Levi
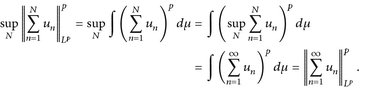
14.10 Satz (Riesz-Fischer). Der Raum 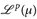 p ∈ [1, ∞], ist vollständig d. h. jede Cauchy-Folge
p ∈ [1, ∞], ist vollständig d. h. jede Cauchy-Folge 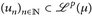 konvergiert gegen ein
konvergiert gegen ein 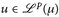 .
.
Beweis. 1°) Hauptproblem: Wie sieht der Grenzwert u aus? Nach Annahme ist 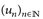 eine Cauchy-Folge, und daher existieren natürliche Zahlen
eine Cauchy-Folge, und daher existieren natürliche Zahlen
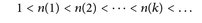
mit
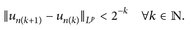
Wir finden u, indem wir un(k+1) als Teleskopsumme schreiben:
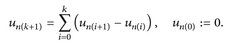
Falls  gilt, dann gilt auch
gilt, dann gilt auch  , d. h.
, d. h.
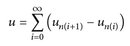
ist ein Kandidat für den Grenzwert.
2°) u ist wohldefiniert. Das folgt aus
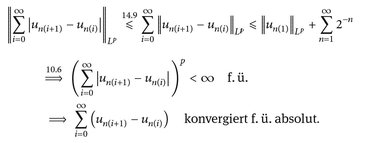
Also ist u f. ü. definiert, und auf der Ausnahmemenge setzen wir u = 0.
3°) Wir zeigen: 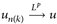 . Es gilt
. Es gilt
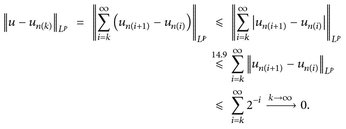
4°) Wir zeigen: 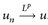 un. Für alle ∈ > 0 und n, n(k) ≥ N∈ gilt
un. Für alle ∈ > 0 und n, n(k) ≥ N∈ gilt
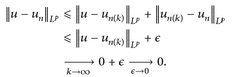
Der Beweis von Satz 14.10 zeigt auch:
14.11 Korollar. Es sei 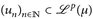 , p ∈ [1, ∞],
, p ∈ [1, ∞], 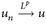 , dann existiert eine Teilfolge
, dann existiert eine Teilfolge 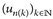 , so dass
, so dass 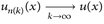 für fast alle x.
für fast alle x.
Wir notieren noch die Lp-Version des Konvergenzsatzes von Lebesgue (Satz 11.3).
14.12 Satz (LP-dominierte Konvergenz). Es sei 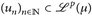 , p ∈ [1, ∞). Wenn
, p ∈ [1, ∞). Wenn
- ▶
 f ü.,
f ü., - ▶► |un| ≤ w f.ü. für alle
 n und ein
n und ein 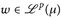 ,
,
dann ist 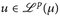 und es gilt
und es gilt
- a)
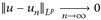 .
. - b)
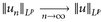 .
.
Beweis. [✍] Hinweis: 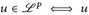 ⇐⇒ messbar &
⇐⇒ messbar & 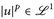 . Beachte wo Nullmengen auftreten und wie sie sich aufbauen. Wende den Satz von der dominierten Konvergenz auf
. Beachte wo Nullmengen auftreten und wie sie sich aufbauen. Wende den Satz von der dominierten Konvergenz auf 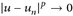 an.
an.

Konvergenz in 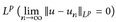 Lp ≠ Konvergenz der LP-Normen
Lp ≠ Konvergenz der LP-Normen 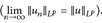
Den genauen Zusammenhang zwischen der „Normkonvergenz“ und „Konvergenz der Normen” gibt der folgende Satz von F. Riesz.
14.13 Satz (Riesz). Es sei 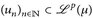 , p ∈ [1, ∞). Wenn
, p ∈ [1, ∞). Wenn 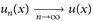 f.ü. und
f.ü. und 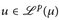 , dann gilt
, dann gilt

Beweis. „⇒“: Es ist 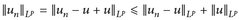 . Indem wir die Rollen von un und u vertauschen, erhalten wir die Dreiecks-Ungleichung „nach unten“
. Indem wir die Rollen von un und u vertauschen, erhalten wir die Dreiecks-Ungleichung „nach unten“
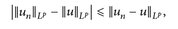
woraus die Behauptung unmittelbar folgt.
„⇐“: Wegen
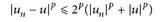
können wir Fatous Lemma auf die Funktionen 2p(|un|p + |u|p) – |un – u|p ≥ 0 anwenden, und erhalten
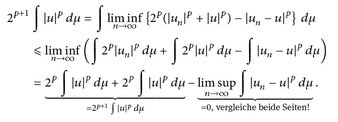
Daher ist 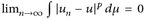 , da für positive Folgen an ≥ 0 aus lim supn an = 0 sofort limn an = 0 folgt.
, da für positive Folgen an ≥ 0 aus lim supn an = 0 sofort limn an = 0 folgt.
14.14 Beispiel. Es sei 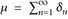 das Zählmaß auf (
das Zählmaß auf (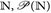 ). Der zugehörige Lp-Raum ist ein Folgenraum, der Raum der p-summierbaren Folgen:
). Der zugehörige Lp-Raum ist ein Folgenraum, der Raum der p-summierbaren Folgen:
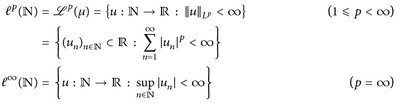
Die Hölder- und Minkowski-Ungleichungen für das Zählmaß werden dann zu den aus der Analysis bekannten Ungleichungen für Reihen.
Hölder-Ungleichung (für Reihen):

Minkowski-Ungleichung (für Reihen):
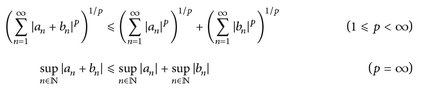
Wir wollen nun noch eine praktische Konvexitätsungleichung herleiten. Dazu benötigen wir ein einleuchtendes - aber unangenehm zu beweisendes - Resultat.
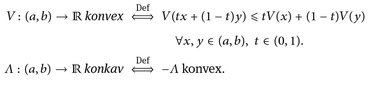
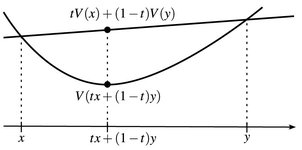
Abb.14.2. Konvexe Funktion.
Lemma. ([8, Lemma 12.13, S. 115 f.]). Es sei 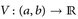 konvex. Dann gilt
konvex. Dann gilt
- a) V(x) = sup {ℓ(x): ℓ affin-linear, ℓ(y) ≤ v(y) ∀y}.
- b) V ist stetig und hat an jeder Stelle x ∈ (a, b) einseitige Ableitungen.
14.15 Satz (Jensen-Ungleichung). Es sei V: [0,∞) → [0,∞) konvex, µ ein W-Maß auf (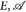 ). Dann gilt
). Dann gilt
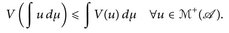
Beweis. 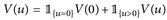 ist messbar, da V|(0,∞) stetig ist. Daher sind alle Integrale definiert. Weiter sei V(∞):= limx→∞ V(x). Ist ∫ V(u) dµ = ∞, dann ist nichts zu zeigen. Sei also ∫ V(u) dµ < ∞.
ist messbar, da V|(0,∞) stetig ist. Daher sind alle Integrale definiert. Weiter sei V(∞):= limx→∞ V(x). Ist ∫ V(u) dµ = ∞, dann ist nichts zu zeigen. Sei also ∫ V(u) dµ < ∞.
Für eine affin-lineare Funktion ℓ(x) = αx β gilt
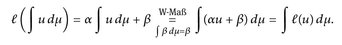
Somit (l bezeichnet stets eine affin-lineare Funktion)
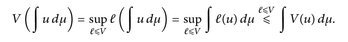
Wir erwähnen noch einige wichtige Spezialfälle.
14.16 Beispiel. Es sei µ ein W-Maß und v, p beliebige Maße.
- a)
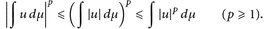
- b)
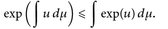
- c) „Jensen konkav“:
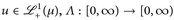 konkav (z. B. √x). Dann gilt
konkav (z. B. √x). Dann gilt

- d) Oft kann man durch geschickte Normierungen die Jensensche Ungleichung auch für allgemeinere Maße anwenden. Für κ:= v(E) < ∞ ist µ:= κ-1ν ein W-Maß. Dann gilt
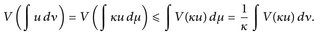
Für ein beliebiges Maß p wählen wir ∫ ∈
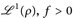 ∫ > 0 und K = ∫ f d p < ∞. Dann ist µ:= k-1 fp ein W-Maß, und
∫ > 0 und K = ∫ f d p < ∞. Dann ist µ:= k-1 fp ein W-Maß, und
Aufgaben
- Es sei (
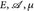 ) ein endlicher Maßraum und 1 ≤ q ≤ p ≤ ∞. Zeigen Sie, dass
und folgern Sie, dass
) ein endlicher Maßraum und 1 ≤ q ≤ p ≤ ∞. Zeigen Sie, dass
und folgern Sie, dass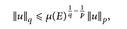
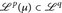 für p ≥ q ≥1.
für p ≥ q ≥1. - Es sei (
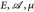 ) ein Maßraum, 1 ≤ p ≤ r ≤ q ≤ ∞ und
) ein Maßraum, 1 ≤ p ≤ r ≤ q ≤ ∞ und 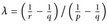 • Zeigen sie:
• Zeigen sie:
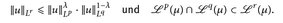
- (Verallgemeinerte Hölder-Ungleichung) Zeigen Sie, dass in einem Maßraum (
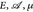 )
für alle messbaren ui ∈ M(
)
für alle messbaren ui ∈ M(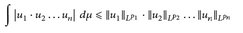
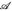 ) und alle pi ∈ (1, ∞) mit
) und alle pi ∈ (1, ∞) mit 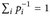 gilt.
gilt. - Es seien (
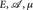 ) ein endlicher Maßraum und u ∈ ℒ1 (µ) mit u > 0 und ∫ u dµ = Zeigen Sie:
) ein endlicher Maßraum und u ∈ ℒ1 (µ) mit u > 0 und ∫ u dµ = Zeigen Sie:

Wie lautet die entsprechende Aussage für ein Wahrscheinlichkeitsmaß?
- Es sei (
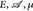 ) ein Maßraum und f, g ℒp(µ). Finden Sie Bedingungen dafür, dass
) ein Maßraum und f, g ℒp(µ). Finden Sie Bedingungen dafür, dass
- (a) fg, f + g und af, a ∈ IR, wieder in ℒp(µ) sind.
- (b) Zeigen Sie, dass ℒ1(µ) und ℒ2(µ) keine Funktionenalgebren sind.
- (c) Zeigen Sie die Dreiecksungleichung nach unten:
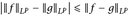
- Es sei
 eine Menge mit mindestens zwei Elementen und
eine Menge mit mindestens zwei Elementen und 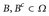 seien nicht leer.
seien nicht leer.
- (a) Bestimmen Sie alle messbaren Abbildungen
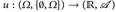 , wenn (i)
, wenn (i) 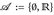 , (ii)
, (ii) 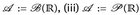 .
. - (b) Charakterisieren Sie für alle p > 0 den Raum
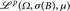 .
.
- (a) Bestimmen Sie alle messbaren Abbildungen
- Für welche p ≥ 1 ist
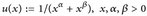 , p-fach Lebesgue-integrierbar?
, p-fach Lebesgue-integrierbar? - Zeigen Sie, dass
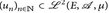 genau dann in ℒ2 konvergiert, wenn limn,m ∫ unum dµ existiert.
genau dann in ℒ2 konvergiert, wenn limn,m ∫ unum dµ existiert. - Es sei (
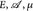 ) ein Maßraum und u ∈ ∩p≥1 ℒp(µ). Zeigen Sie, dass
) ein Maßraum und u ∈ ∩p≥1 ℒp(µ). Zeigen Sie, dass 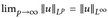 (für unbeschränktes u gilt
(für unbeschränktes u gilt 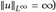 .
. - Es sei (
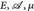 ) ein Wahrscheinlichkeitsraum und ∥u∥lℒq < ∞ für ein q > 0. Zeigen Sie, dass
) ein Wahrscheinlichkeitsraum und ∥u∥lℒq < ∞ für ein q > 0. Zeigen Sie, dass 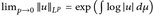 (wir setzen e-∞ = 0).
(wir setzen e-∞ = 0). - Es seien (
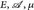 ) ein Maßraum, p ∈ (0,1) und
) ein Maßraum, p ∈ (0,1) und 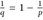 . Zeigen Sie, dass für u, v ∈ ℒP(µ) und
. Zeigen Sie, dass für u, v ∈ ℒP(µ) und 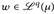 mit u,v,w > 0
mit u,v,w > 0