9 Das Integral messbarer Funktionen
In diesem Kapitel bezeichne (E, 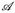 , µ) einen Maßraum. Wir wollen nun das Integral von
, µ) einen Maßraum. Wir wollen nun das Integral von  auf
auf  fortsetzen. Da das Integral linear sein soll, werden wir das Integral durch Linearität fortsetzen. Wie bisher bezeichnen wir mit
fortsetzen. Da das Integral linear sein soll, werden wir das Integral durch Linearität fortsetzen. Wie bisher bezeichnen wir mit  den Positiv- und Negativteil von
den Positiv- und Negativteil von 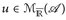 .
.
9.1 Definition.  u: heißt (µ-)integrierbar, wenn
u: heißt (µ-)integrierbar, wenn
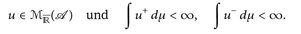
In diesem Fall definieren wir
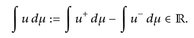
(9.1)
∫ u dµ heißt (µ-)Integral von u. Die Familie der µ-integrierbaren Funktionen ist 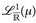 , mit ℒ1(µ) bezeichnen wir die
, mit ℒ1(µ) bezeichnen wir die 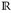 -wertigen integrierbaren Funktionen.
-wertigen integrierbaren Funktionen.

Abb. 9.1. Vom Maß zum Integral - und zurück. Die Abbildung zeigt alle Schritte, wie man vom Maß zum Integral gelangt. Da 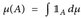 , können wir aus dem Integral das ursprüngliche Maß rekonstruieren.
, können wir aus dem Integral das ursprüngliche Maß rekonstruieren.
9.2 Bemerkung. a) Weitere Schreibweisen: ∫ u dµ = ∫ u(x) µ(dx) = ∫ u(x) dµ(x).
b) Wenn µ = λd, dann nennen wir u Lebesgue-integrierbar und schreiben oft λd (dx) = dx, d. h. ∫ u(x) dx usw.
c) Die Forderung ∫u± dµ < ∞ in Definition 9.1 schließt den Fall „∞ – ∞“ aus. Beachte, dass wir für u ≥ 0 auch ∫ u dµ = ∞ zulassen, dass dann aber nur 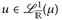 gilt, wenn ∫ u dµ < ∞.
gilt, wenn ∫ u dµ < ∞.
d) Wenn u = f – g eine weitere Darstellung von u als Differenz positiver messbarer Funktionen ist, dann gilt auch ∫ u dµ = ∫ f dµ – ∫ g dµ (sofern die Differenz definiert ist). Das sieht man so: Indem wir u+ – u- = f – g umstellen, erhalten wir 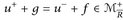 , und damit
, und damit

9.3 Satz (Integrabilitätskriterium). Für eine messbare Funktion 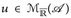 sind folgende Aussagen äquivalent:
sind folgende Aussagen äquivalent:
- a)
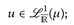
- b)

- c)

- d)

Beweis. a)⇔b) Das ist gerade die Definition des Integrals.
b)⇒c) |u| = u+ + u–⇒ ∫ |u| dµ = ∫ u+ dµ + ∫ u–dµ < ∞.
c)⇔d) Wähle w:= |u|.
d)⇒b) u± ≤ |u| ≤ w ⇒ ∫ u± dµ ≤ ∫ w dµ < ∞.
Die Definition des Integrals ist gerade so gewählt, dass sich die Eigenschaften des Integrals von 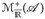 auf
auf  übertragen.
übertragen.
9.4 Satz.  und
und  . Dann
. Dann
a) 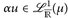 , ∫ αu dµ = α ∫ u dµ; , ∫ αu dµ = α ∫ u dµ; |
(homogen) |
b) 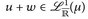 (wenn definiert), ∫ (u + w) dµ = ∫ u dµ + ∫ w dµ; (wenn definiert), ∫ (u + w) dµ = ∫ u dµ + ∫ w dµ; |
(additiv) |
c)  ; ; |
(Verband) |
| d) u ≤ w ⇒ ∫ u dµ ≤ ∫ w dµ; | (monoton) |
| e) |∫ u dµ| ≤ ∫ |u| dµ. | (Dreiecks-Ungl.) |
Beweis. Da u und w messbar sind, sind auch die Funktionen αu, u + w (sofern definiert – „∞ – ∞“-Problematik!), u ∧ w und u ∧ w wiederum messbar. Es reicht daher, die Integrierbarkeit der Beträge zu prüfen.
- a)
 ∈ wegen Satz 9.3 und Lemma 8.8.b). Die Formel für das Integral folgt nun aus (αu)± = αu± (für α ≥ 0) bzw.
∈ wegen Satz 9.3 und Lemma 8.8.b). Die Formel für das Integral folgt nun aus (αu)± = αu± (für α ≥ 0) bzw. 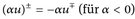 .
. - b)
 wegen Satz 9.3 und Lemma 8.8.c). Die Formel für das Integral folgt nun mit Hilfe von Bemerkung 9.2.d) und der Zerlegung
wegen Satz 9.3 und Lemma 8.8.c). Die Formel für das Integral folgt nun mit Hilfe von Bemerkung 9.2.d) und der Zerlegung

- c)
 .
. - d) Aus u ≤ w folgt u+ ≤ w+ und w–≤ u–. Wegen der Monotonie des Integrals gilt

- e)
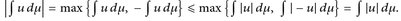
9.5 Bemerkung. Wenn αu + βw in  definiert ist (d. h. „∞ – ∞“ tritt nicht auf), dann besagt Satz 9.4.a), b)
definiert ist (d. h. „∞ – ∞“ tritt nicht auf), dann besagt Satz 9.4.a), b)

Für u, w ∈ ℒ1 (µ) gilt das immer.

- ►
 ist ein Vektorraum.
ist ein Vektorraum.
- ►► Addition: (u + w)(x) = u(x) + w(x), x ∈ E
- ►► skalare Multiplikation: (αu)(x) = αu(x), x ∈ E,

- ► ℒ1 (µ) ∋ u ↦ ∫ u dµ ist positives lineares Funktional.
9.6 Beispiel (Fortsetzung von Beispiel 3.5 und 8.10).
- a) Sei
 ein beliebiger Messraum und γ ∈ E fest. Dann gilt ∫ u(x) δγ(dx) = u(γ) und
ein beliebiger Messraum und γ ∈ E fest. Dann gilt ∫ u(x) δγ(dx) = u(γ) und  und |u(γ)| < ∞.
und |u(γ)| < ∞. - b) Im Maßraum
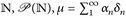 sind alle Funktionen
sind alle Funktionen  messbar. Wegen 8.10.b) gilt
und es folgt
messbar. Wegen 8.10.b) gilt
und es folgt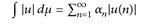
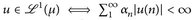 .
.
Für α1 = α2 = ⋯ = 1 ist ℒ1 (µ) der Raum aller absolut-summierbaren Folgen:7
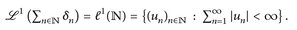
- c) Es sei
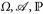 ein W-Raum und
ein W-Raum und 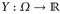 eine Zufallsvariable (d. h. eine messbare Funktion). Dann heißt
der Erwartungswert von Y (wenn
eine Zufallsvariable (d. h. eine messbare Funktion). Dann heißt
der Erwartungswert von Y (wenn
 .
.
Wichtiger Sonderfall: Es sei
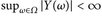 , d. h. Y sei beschränkt. Dann gilt
, d. h. Y sei beschränkt. Dann gilt

Konsequenz: Für jede beschränkte Zufallsvariable
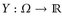 gilt
gilt  und
und  existiert.
existiert.

Die Umkehrung der Aussage c) ist falsch! Betrachte, z. B. in b) die Folge αn = 2-n (damit erhalten wir einen W-Raum) und 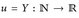 mit Y(n) = n. Dann ist Y nicht beschränkt, aber
mit Y(n) = n. Dann ist Y nicht beschränkt, aber  konvergiert.
konvergiert.
9.7 Definition. Es sei 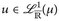 oder
oder 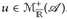 . Dann
. Dann


Beachte: Wir haben  .
.
Definition 9.7 erlaubt es uns insbesondere, das Integral als Funktion des Integrationsbereichs zu verstehen, also A ↦ ∫A…, und dadurch viele neue Maße und Mengenfunktionen zu konstruieren, z. B. wie im folgenden Lemma. [✍]
9.8 Lemma. Es sei  . Dann ist
. Dann ist
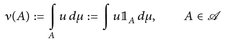
ein Maβ auf (E,  ). ν heißt Maß mit der Dichte(funktion) u (bzgl. µ).
). ν heißt Maß mit der Dichte(funktion) u (bzgl. µ).
9.9 Bemerkung. Folgende Bezeichnungen sind üblich: ν = u · µ oder dν = u · dµ. Oft schreibt man 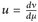 . Diese Bezeichnung kommt vom Hauptsatz der Differential- und Integralrechnung:
. Diese Bezeichnung kommt vom Hauptsatz der Differential- und Integralrechnung:

Mit den Bezeichnungen λ = λ1 und λ(dx) = dx erhalten wir
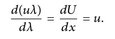
Die positive Dichte u ≥ 0 induziert das Maß ν:

Aufgaben
- Es sei u:
 eine messbare Funktion. Zeigen Sie, dass für ein Maß µ
eine messbare Funktion. Zeigen Sie, dass für ein Maß µ

- (Komplexwertige Integranden) Es sei (E,
 , µ) ein Maßraum und C der Körper der komplexen Zahlen. Wir bezeichnen mit x = Re z und y = Im z den Real- bzw. Imaginärteil von
, µ) ein Maßraum und C der Körper der komplexen Zahlen. Wir bezeichnen mit x = Re z und y = Im z den Real- bzw. Imaginärteil von  und mit
und mit  die Euklidische To pologieauf
die Euklidische To pologieauf 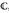 , die die „übliche“ Konvergenz in
, die die „übliche“ Konvergenz in 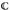 beschreibt. Weiter sei
beschreibt. Weiter sei  . Zeigen Sie:
. Zeigen Sie:
- (a)
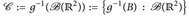 stimmt mit
stimmt mit  überein.
überein.
- (b) Eine Abbildung h: E →ℂ ist genau dann
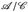 -messbar, wenn Re h und Im h
-messbar, wenn Re h und Im h  - messbar sind.
- messbar sind.
Eine Funktion h: E →ℂ heißt µ-integrierbar, falls Re h und Im h µ-integrierbar sind; wir schreiben
 {µ) für die komplexwertigen µ-integrierbaren Funktionen. Das Integral ist definiert als
{µ) für die komplexwertigen µ-integrierbaren Funktionen. Das Integral ist definiert als  . Dann gilt:
. Dann gilt:
- (c) h → ∫ hdµ definiert auf
 eine C-lineare Abbildung.
eine C-lineare Abbildung. - (d) Re ∫ h dµ = ∫ Reh dµ und Im ∫ hdµ - ∫ Im hdµ.
- (e) ∣∫hdµ∣ ≤ ∫∣h∣dµ.
Hinweis: Da ∫h dµ ∈ ℂ gibt es ein 0 ∈ (-π, π], so dass eiθ ∫ h dµ ≥ 0.
- (f)
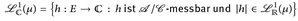 .
.
- (a)
- (Reihenvergleichskriterium)Es sei (E,
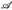 , µ) ein endlicher Maßraum. Zeigen Sie:
, µ) ein endlicher Maßraum. Zeigen Sie:
- (a)
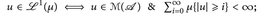
- (b)

- (a)
- Es sei (Ω,
 ) ein Wahrscheinlichkeitsraum. Zeigen Sie, dass eine
) ein Wahrscheinlichkeitsraum. Zeigen Sie, dass eine  -integrierbare Funktion nicht beschränkt sein muss.
-integrierbare Funktion nicht beschränkt sein muss. - (Fatou - verallgemeinert) Es sei (E,
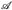 , µ) ein Maßraum und
, µ) ein Maßraum und 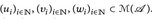 .
.
- (a) Wenn es ein u ∈ ℒ1 (µ) mit ui(x) ≥u(x), i ∈ N, x ∈ E gibt, dann gilt:

- (b) Wenn es ein v ∊ ℒ1 (µ) mit vi(x) ≤v(x), i ∈
 , x ∈ E gibt, dann gilt:
, x ∈ E gibt, dann gilt:
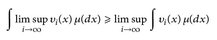
- (c) Wenn w(x) = limi wi (x) für alle x ∈ E existiert und wenn lwi (x) 1 ≤ g(x) für ein g ∈ ℒ1 (µ) und alle x ∈ E gilt, dann ist w ∈ ℒ1 (µ) und
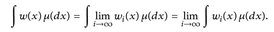
- (d) Zeigen Sie durch ein Gegenbeispiel, dass die halbseitige Beschränktheit durch integrierbare Funktionen eine wesentliche Annahme in (a) und (b) ist.
- (a) Wenn es ein u ∈ ℒ1 (µ) mit ui(x) ≥u(x), i ∈ N, x ∈ E gibt, dann gilt:
- (Satz von Egorov) Es sei (E,
 , µ) ein endlicher Maßraum und
, µ) ein endlicher Maßraum und 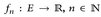 , eine Folge messbarer Funktionen.
, eine Folge messbarer Funktionen.
- (a)

- (b) Wir nehmen an, dass
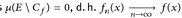 für alle x außerhalb einer Nullmenge. Dann gilt für die Mengen
für alle x außerhalb einer Nullmenge. Dann gilt für die Mengen 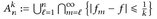

- (c) Satz (Egorov). Auf einem endlichen Maßraum sei
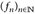 (eine Folge messbarer Funktionen, die punktweise (überall oder außerhalb einer Menge vom Maß Null) gegen eine Funktion f konvergiert. Dann gibt es für jedes ∈ > 0 eine Menge
(eine Folge messbarer Funktionen, die punktweise (überall oder außerhalb einer Menge vom Maß Null) gegen eine Funktion f konvergiert. Dann gibt es für jedes ∈ > 0 eine Menge 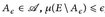 ,so dass fn → f gleichmäßig auf Aε (also:
,so dass fn → f gleichmäßig auf Aε (also:  ).
). - (d) Geben Sie ein Beispiel an, dass die Voraussetzung µ(E) < ∞ für den Satz von Egorov wesentlich ist (betrachten Sie etwa das Zählmaß auf N oder das Lebesgue-Maß auf
 ).
).
- (a)