16 Der Satz von Fubini-Tonelli

Wie im vorangehenden Kapitel seien (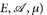) und (F, ℬ, ν) zwei σ-endliche Maßräume. Wir können die Formel für ρ(C) im Satz 15.5 als „Vertauschungssatz für Doppelintegrale“ über eine einstufige Treppenfunktion lesen:

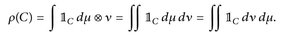
Mit den üblichen Techniken (Sombrero-Lemma, Beppo Levi; vgl. Abbildung 9.1) lässt sich diese Aussage auf positive messbare Funktionen erweitern.

16.1 Satz (Tonelli). Es seien (E, 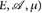, μ) und (F, ℬ, v) zwei σ-endliche Maßräume. Für jede 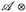ℬ-messbare, positive Funktion u: E x F → [0, ∞] gilt

• a) x → u(x, y), y → u(x, y) (y bzw. x ist fest) sind 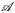- bzw. ℬ-messbar.
• b) y → f u(x, y) u(dx), x → ∫ u(x, y) ν(dy) sind ℬ- bzw. 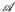-messbar.
• c)

Integrale von positiven messbaren Funktionen darf man immer vertauschen, wenn man +∞ als Wert zulässt. Wenn ein (Doppel-)Integral endlich ist, dann sind alle Integrale endlich.

Beweis. 1°) Zunächst sei 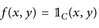für ein C ∈⊗. Für solche f folgt die Behauptung aus Satz 15.5.

 

2°) Nun sei g 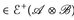). Wir wählen eine Standarddarstellung

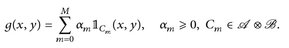
Da 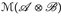⊗ ein Vektorraum ist und da Messbarkeit unter Vektorraum-Operationen erhalten bleibt, folgen a), b) (für u = g) aus den entsprechenden Aussagen für die einzelnen Treppenstufen.

Wegen der Linearität des Integrals gilt das auch für c).

 

3°) Schließlich sei u 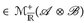∈. Mit dem Sombrero-Lemma (Satz 7.11) finden wir eine Folge einfacher Funktionen g_n 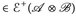∈ mit g_n ↑ u. Der Satz von Beppo Levi (Satz 8.6) zeigt nun, dass die Aussagen a)-c) unter aufsteigenden Limiten bestehen bleiben.

16.2 Korollar (Satz von Fubini). Es seien (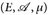), (F,ℬ, ν) zwei σ-endliche Maβräume und u: 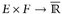sei ⊗ ℬ-messbar. Wenn eines der folgenden drei Integrale endlich ist

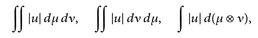
dann sind alle Integrale endlich, und es gilt

• a) ;
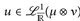• b) 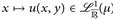für ν-fast alle y;
• c) 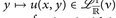für µ-fast alle x;
• d) ;
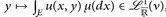• e) ;
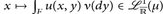• f)

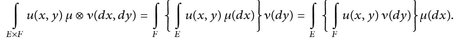
• ▶ „P(x) gilt für μ-fast alle x“ bedeutet: {x: P(x) gilt nicht} ist Teilmenge einer μ-Nullmenge.
• ▶ In Korollar 16.2 ist f) nur wegen a) sinnvoll!

Beweis. Satz 16.1 (Tonelli) zeigt

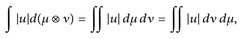
d. h. wenn ein Integralausdruck endlich ist, dann sind alle Integrale endlich. In diesem Fall gilt .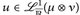

Aus Satz 16.1 folgt auch die Messbarkeit von

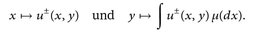
Da u^± ≤ |u|, folgt wegen ∫_F {∫_E, |u(x,y)|μ(dx)} ν(dy) < ∞, das

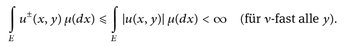
Weiterhin gilt

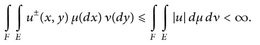
Das zeigt b), d).

c), e) folgen analog.

f) folgt aus u = u⁺ – u^-, aus der Linearität des Integrals

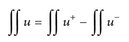
und mit Satz 16.1 angewendet auf .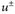

16.3 Beispiel (Partielle Integration (PI)). Der Satz von Fubini kann auch verwendet werden, um klassische Integrationsformeln zu zeigen. Es seien 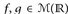Funktionen, die über jeder kompakten Menge von 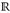integrierbar sind (d. h. lokal-integrierbar, f g ∈ L¹(K, dx) für alle Kompakta 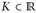). Wir setzen

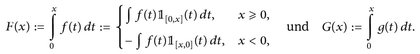
Dann gilt für alle -∞ < a < b < ∞

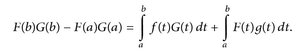
(16.1)

Beweis. Wir haben

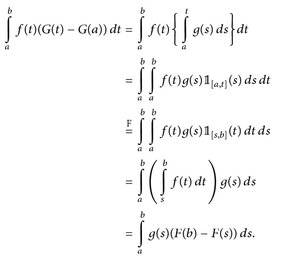
Durch einfaches Umstellen erhalten wir (16.1). Bei der mit „F“ gekennzeichneten Gleichheit haben wir den Satz von Fubini angewendet. Beachte hierbei, dass

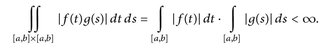
16.4 Beispiel. Mit Hilfe des Satzes von Tonelli können wir ein wichtiges Integral einfach berechnen.

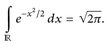
(16.2)

Beweis. Wir setzen 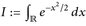. Dann gilt

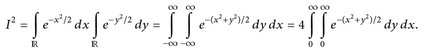
Wir dürfen diese Integrale als (uneigentliche) Riemann-Integrale behandeln. Der Variablenwechsel y = tx, dy = x dt zeigt

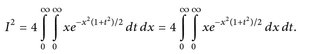
Das innere Integral können wir durch eine Stammfunktion ausdrücken

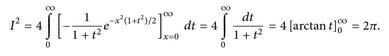
16.5 Beispiel (Integralsinus).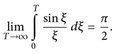

 

Beweis. Beachte, dass 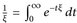sowie Im e^iξ = sin ξ. Der Satz von Fubini zeigt

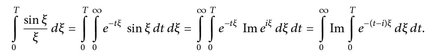
Das innere Integral ergibt

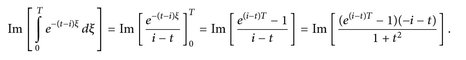
Somit erhalten wir mit dem Satz von der dominierten Konvergenz (Satz 11.3)

Verteilungsfunktionen

Das Cavalierische Prinzip besagt, dass wir das Volumen eines Körpers durch die Summation der Volumina seiner Niveauflächen berechnen können. Das ist auch die Idee, die dem Konzept der Verteilungsfunktion zu Grunde liegt. Die Menge {u ≥ t} beschreibt die Werte des Definitionsbereichs einer messbaren Funktion 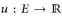wo das Niveau mindestens t erreicht, und die Verteilungsfunktion gibt das zugehörige μ-Maß an.

16.6 Definition. Für u 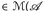∈ heißt 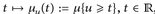, (obere) Verteilungsfunktion oder Verteilungsfunktion (nach oben) von u unter μ.

Vor allem in der Wahrscheinlichkeitstheorie wird t ↦ μ{u ≤ ≥ t} als Verteilungsfunktion bezeichnet. Um die Begriffe sauber zu trennen, sprechen wir daher von einer unteren/oberen Verteilungsfunktion bzw. von einer Verteilungsfunktion nach unten/oben.

Wir könnnen nun das Integral von u (also das „Volumen unter dem Graphen von u“) durch „Aufsummieren“ der Volumina der Niveauflächen berechnen.

16.7 Satz. Für 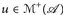gilt

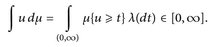
Beweis. Setze U(x, t):= (u(x), t). Dann ist 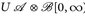-messbar:

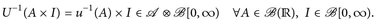
Insbesondere sehen wir 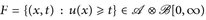. Eine direkte Rechnung ergibt, dass 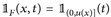ist, da 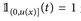genau für u(x) ≥ t gilt. Mit dem Satz von Tonelli folgt nun

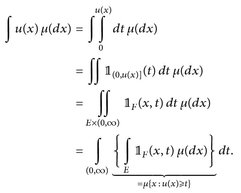
16.8 Korollar. Es sei φ: [0, ∞) → [0, ∞) stetig differenzierbar, 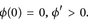. Dann gilt für messbare positive Funktionen u: E → [0, ∞)

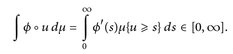
(16.3)

Insbesondere: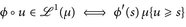 R-integrierbar.

 

Einen der wichtigsten Sonderfälle stellt die konvexe Funktion φ(t) = t^p, t > 0, mit 1 ≤ p < ∞ dar:

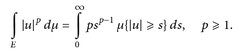
(16.4)

Beweis. Die Funktion φ ∘ u ist messbar, da φ stetig ist.

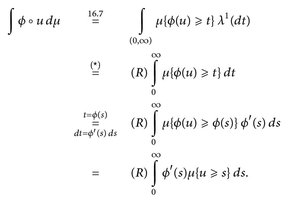
An der Stelle (*), wo wir Riemann – und Lebesgue–Integrale gleichsetzen, gibt es eine Lücke. Hier benötigen wir nämlich, dass t → u{φ(u) ≥ t} f. ü. stetig (siehe a) und beschränkt (siehe b) ist.

• a) Wird mit dem folgenden Lemma erledigt:

  Lemma. Eine monotone Funktion: 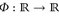hat höchstens abzählbar viele Sprünge und ist somit f ü. stetig.[✍]

• b) Verwendet eine Stutzungstechnik: 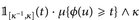ist für alle 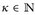beschränkt und nur auf einem kompakten Intervall ≠ 0. Wir führen die obige Rechnung mit dieser Funktion durch, und gehen dann mit Beppo Levi auf beiden Seiten zum Limes κ ↑ ∞ über.

Da alles positiv ist, reicht es für die Integrierbarkeit, wenn ein Integralausdruck endlich ist.

Anmerkungen zur Produkt-σ-Algebra

Wir diskutieren noch eine weitere Charakterisierung der Produkt-σ-Algebra. Dazu seien 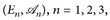Messräume und

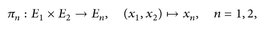
die kanonischen Koordinatenprojektionen. Nach Definition 6.5 ist

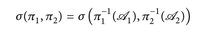
die kleinste σ-Algebra in E₁ × E₂, die π_1, π₂ simultan messbar macht.

 

16.9 Satz. Es seien 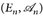und π_n, n = 1, 2, 3, wie oben.

• a)
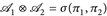
• b) T: 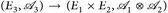, ist genau dann messbar, wenn die Abbildungen 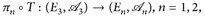messbar sind.
• c) Wenn 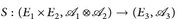messbar ist, dann ist 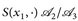-messbar und 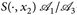-messbar.

Beweis. a) Wegen 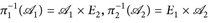, gilt

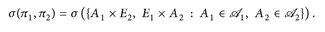
Insbesondere ist 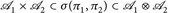und

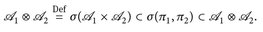
b) Aus 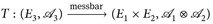, folgt, dass π_n ∘ T messbar ist (n = 1, 2). Umgekehrt seien 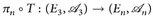messbar (n = 1, 2); dann ist

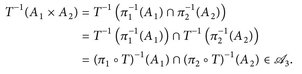
Da 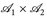die σ-Algebra 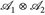erzeugt, folgt die Behauptung.

c) Sei x₁ ∈ E₁, fest. Definiere

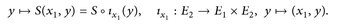
Nun gilt

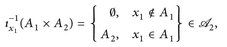
und es folgt, dass 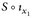messbar ist; 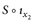behandelt man analog.

Aufgaben

1. Zeigen Sie, dass die folgenden iterierten Integrale existieren und übereinstimmen:
   

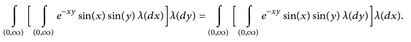
   Zeigen Sie, dass das Doppelintegral bezüglich λ x λ existiert.

2. Zeigen Sie, dass die folgenden iterierten Integrale existieren, aber nicht übereinstimmen. Folgern Sie daraus, dass das Doppelintegral nicht existiert.
   

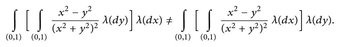
   Hinweis: Der Integrand besitzt eine Stammfunktion und der Wert des linken Integrals ist π/4. Zusatz: Zeigen Sie direkt, dass das zugehörige Doppelintegral nicht existiert.

3. Zeigen Sie, dass die folgenden iterierten Integrale existieren und übereinstimmen:
   

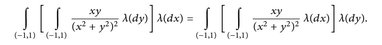
   Zeigen Sie, dass das Doppelintegral dennoch nicht existiert.

4. Berechnen Sie 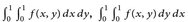und ∫_[0,1]² ∣f(x,y)∣d(x,y) für folgende Funktionen:
   
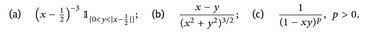
5. Gegeben sei der Messraum 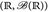. Weiter bezeichne 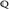die rationalen Zahlen. Für 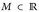definieren wir das Zählmaß auf 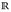durch 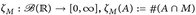. Zeigen Sie:
   • (a) Das Lebesguemaß λ und das Zählmaß 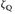sind σ-endlich, das Zählmaß 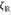ist nicht σ-endlich.
   • (b) .
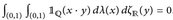   • (c) .
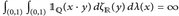   • (d) .
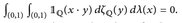   • (e) Warum widersprechen die Befunde in (c),(d) nicht dem Satz von Fubini?
6. • (a) Berechnen Sie das Integral
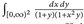
   • (b) Verwenden Sie Teil (a), um das Integral 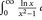dx auszurechnen.
   • (c) Zeigen Sie mit Hilfe einer geeigneten Reihenentwicklung in Teil (b), dass .
7. Es seien 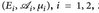zwei σ-endliche Maßräume und 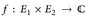eine messbare Funktion. Eine Funktion heißt vernachlässigbar (bezüglich eines Maβes μ), wenn ∫ |f|dμ = 0. Dann sind folgende Aussagen äquivalent:
   • (a) f ist μ₁ ⊗ μ₂ -vernachlässigbar.
   • (b) Für μ₁-fast alle x₁ ist f (x₁,.) u₂-vernachlässigbar.
   • (c) Für μ₂-fastalle x₂ ist f(·, x₂) μ₁ -vernachlässigbar.
8. (Dirichletsches Integral) Zeigen Sie die folgende Integralformel (α_1, a_i p_i x_i > 0):
   

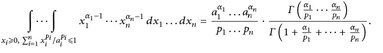
   Hinweis: Integraldarstellung der Eulerschen Beta-Funktion, vgl. Aufgabe 20.2.

9. Es sei 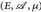ein σ-endlicher Maßraum und f: E → [0, ∞) eine reelle Funktion. Der Subgraph von f ist die Menge 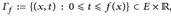, der Graph ist G_f:= {(x, f(x)): x ∈ E}.
   • (a) f ist genau dann Borel-messbar, wenn .
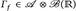   • (b) Wenn f Borel-messbar ist, dann ist G_f eine μ ⊗ λ¹-Nullmenge.

   Hinweis: Satz 16.7 sowie {f > λ} x {t > 0} = U_n {x,λ+ t/n) ∈ Γ_f}.

10. (Minkowskische Ungleichung für Doppelintegrale) Es seien 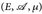und (F, ℬ, ν) zwei σ-endliche Maßräume und 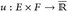eine messbare Funktion. Dann gilt für alle p ∈ [1, ∞)
    

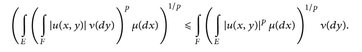
    Hinweis: Wenden Sie Tonelli und Hölder auf 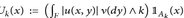:= an, wobei und A_k ↑ E mit μ(A_k) < ∞. Für den Grenzwert k → ∞ verwenden Sie Beppo Levi.