6 Messbare Abbildungen
In diesem Kapitel seien (E,  ) und (E′,
) und (E′,  ) zwei Messräume und T: E → E′ eine Abbildung. Wir interessieren uns dafür, wann T mit den σ-Algebren
) zwei Messräume und T: E → E′ eine Abbildung. Wir interessieren uns dafür, wann T mit den σ-Algebren 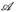 und
und 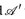 verträglich ist — so wie eine stetige Abbildung mit den Topologien verträglich ist: „Urbilder offener Mengen sind offen.“ Dieser Frage sind wir bereits im Beweis von Satz 4.7 in folgender Form begegnet
verträglich ist — so wie eine stetige Abbildung mit den Topologien verträglich ist: „Urbilder offener Mengen sind offen.“ Dieser Frage sind wir bereits im Beweis von Satz 4.7 in folgender Form begegnet
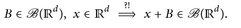
6.1 Definition. Eine Abbildung T: E → E′ heißt  -messbar (kurz: messbar), wenn
-messbar (kurz: messbar), wenn

(6.1)

- ► Alternative Notation für (6.1): (
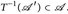 ). Dabei ist
). Dabei ist  ) eine symbolische Kurzschreibweise.
) eine symbolische Kurzschreibweise. - ► T:
 ist eine weitere Bezeichnung für „T ist
ist eine weitere Bezeichnung für „T ist  -messbar.“
-messbar.“
Mit Hilfe von Definition 6.1 können wir das Problem von Satz 3.7 so formulieren: Für die Abbildungen
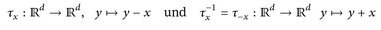
gilt
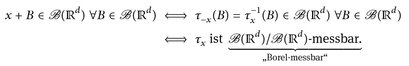
Die Messbarkeit von τx haben wir in Satz 4.7 ad hoc bewiesen, indem wir uns auf den Erzeuger  der σ-Algebra zurückgezogen haben. Das geht jedoch immer.
der σ-Algebra zurückgezogen haben. Das geht jedoch immer.
6.2 Lemma. Es sei  . Dann ist T: E → E′ genau dann
. Dann ist T: E → E′ genau dann  -messbar, wenn
-messbar, wenn

(6.2)
Beweis. Da  gilt (6.1)⇒(6.2). Umgekehrt gelte nun (6.2). Definiere
gilt (6.1)⇒(6.2). Umgekehrt gelte nun (6.2). Definiere

Wegen (6.2) ist  ; außerdem ist Σ′ eine σ-Algebra.
; außerdem ist Σ′ eine σ-Algebra.  Somit findet man
Somit findet man

Der Begriff der messbaren Abbildung ähnelt dem der stetigen Abbildung. Zur Erinnerung:
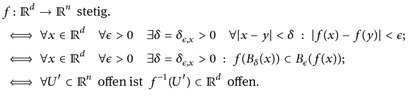
In allgemeinen topologischen Räumen (E,  ), (E′,
), (E′,  ) verwendet man die letzte Äquivalenz als Definition für die (globale) Stetigkeit einer Funktion.
) verwendet man die letzte Äquivalenz als Definition für die (globale) Stetigkeit einer Funktion.

(6.3)
Wiederum ist  symbolisch zu verstehen.
symbolisch zu verstehen.
6.3 Beispiel. Jede stetige Abbildung  ist Borel-
ist Borel- 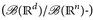 messbar. Denn:
messbar. Denn:  für die offenen Mengen
für die offenen Mengen  des
des  . Dann gilt
. Dann gilt


Achtung: Stetige Funktionen sind Borel-messbar. Umgekehrt folgt aus der Messbarkeit nicht die Stetigkeit. Hier ist ein typisches Gegenbeispiel: Die Funktion  ist messbar aber nicht stetig! Die Messbarkeit folgt aus
ist messbar aber nicht stetig! Die Messbarkeit folgt aus

6.4 Satz. Es seien (En,  ), n = 1, 2, 3, Messräume und S, T messbare Abbildungen
), n = 1, 2, 3, Messräume und S, T messbare Abbildungen
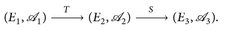
Dann ist auch die Komposition S ∘ T: (E1, 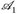 ) → (E3,
) → (E3, 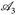 ) messbar.
) messbar.
Beweis. Für alle A ∈  gilt
gilt 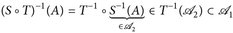 .
.
Oft kennen wir für eine Abbildung T: E → E′ die σ-Algebra  in E′ und suchen eine σ-Algebra
in E′ und suchen eine σ-Algebra 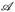 in E, so dass T messbar wird. Derartige Fragestellungen finden wir typischerweise in der Wahrscheinlichkeitstheorie.
in E, so dass T messbar wird. Derartige Fragestellungen finden wir typischerweise in der Wahrscheinlichkeitstheorie.

 entspricht dem (real existierenden) Raum der Beobachtungen mit einer (wenigstens
theoretisch) beobachtbaren Wahrscheinlichkeitsverteilung µ. Der W-Raum (Ω,
entspricht dem (real existierenden) Raum der Beobachtungen mit einer (wenigstens
theoretisch) beobachtbaren Wahrscheinlichkeitsverteilung µ. Der W-Raum (Ω,  ) ist dann ein mathematisches Modell und
) ist dann ein mathematisches Modell und  ist eine Abbildung zwischen Modell und Realität.
ist eine Abbildung zwischen Modell und Realität.
Damit wir mit X und (Ω,  ) arbeiten können, müssen wirfolgende Fragen klären: Mit welchem
) arbeiten können, müssen wirfolgende Fragen klären: Mit welchem 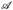 wird X messbar? Wie bildet X die Maße
wird X messbar? Wie bildet X die Maße  und µ ineinander ab?
und µ ineinander ab?
6.5 Lemma (und Definition). Es seien (Ti)i∈I beliebig viele Abbildungen Ti: E → Ei und (Ei, 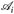 ), i ∈ I, Messräume. Dann ist
), i ∈ I, Messräume. Dann ist

die kleinste σ-Algebra in E, die alle Ti gleichzeitig messbar macht. σ(Ti: i ∈ I) heißt die von den (Ti)i∈I erzeugte σ-Algebra.
Beweis. Für jedes i ∈ I ist Ti: E → Ei genau dann 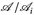 -messbar, wenn
-messbar, wenn  . Also ist
. Also ist

Die Minimalität folgt aus der Definition von σ( ...).
Messbare Abbildungen transportieren insbesondere Maße von (E,  ) nach (E′,
) nach (E′, 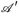 ).
).
6.6 Satz (Bildmaß). Es sei T: (E,  ) → (E′,
) → (E′,  ) messbar und ν ein Maß auf (E,
) messbar und ν ein Maß auf (E,  ). Dann definiert
). Dann definiert
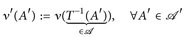
(6.4)
ein Maß auf (E′, ).
).
Beweis. (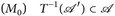 ) ist eine σ-Algebra, d. h. (6.4) wohldefiniert.
) ist eine σ-Algebra, d. h. (6.4) wohldefiniert.
(M1) Wir haben  .
.
(M2) Für  disjunkt sind die
disjunkt sind die  auch disjunkt3. Da ν ein Maß ist, gilt
auch disjunkt3. Da ν ein Maß ist, gilt

6.7 Definition. Das Maß ν′ aus Satz 6.6 heißt Bildmaß (image measure, push-forward) von ν unter T. Übliche Bezeichnungen: T(ν) oder  oder ν ∘ T—1.
oder ν ∘ T—1.
6.8 Beispiel. a) Für alle  gilt
gilt  .
.
b) Es sei (Ω, 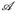 , ℙ) ein W-Raum. Dann heißt
, ℙ) ein W-Raum. Dann heißt
c) Konkretes Beispiel: Zweimaliges Würfeln (z. B. beim Monopoly)

Die Verteilung von ξ (das Bildmaß unter ξ) ist in Tabelle 6.1 angegeben.
Tab. 6.1. Wahrscheinlichkeitsverteilung beim zweimaligen Würfeln


Für  ist jede Abbildung
ist jede Abbildung  messbar, da ξ–1(B) ∈
messbar, da ξ–1(B) ∈ 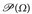 stets gilt.
stets gilt.
6.9 Satz. Es sei T ∈ O(d) eine orthogonale Matrix, d. h. T ∈  . Dann gilt T(λd) = λd.
. Dann gilt T(λd) = λd.
Beweis. Jede Abbildung T ∈ O(d) ist wegen

(Lipschitz-)stetig und somit Borel-messbar. Daher ist das Bildmaß

wohldefiniert und es gilt
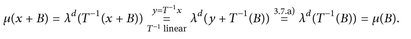
Aus Satz 4.7.b) folgt dann µ(B) = κλd(B) für alle B ∈  . Wir müssen noch die Konstante κ bestimmen. Setze B = B1(0). Da T ∈ O(d), folgt
. Wir müssen noch die Konstante κ bestimmen. Setze B = B1(0). Da T ∈ O(d), folgt
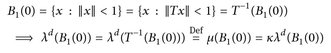
Weil 0 < λd(B1(0)) < ∞ ist, ergibt sich durch Division, dass κ = 1.
6.10 Satz. Für S ∈ GL(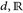 )gilt S(λd) = |det S–1| · λd = |det S|–1λd.
)gilt S(λd) = |det S–1| · λd = |det S|–1λd.
Beweis. Lineare Abbildungen (in endlich-dimensionalen Räumen) sind stetig, also messbar (Beispiel 6.3). Wie im Beweis von Satz 6.9 sieht man für B ∈ 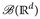

und wegen Satz 4.7 gilt dann schon
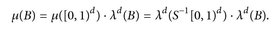
Nun ist S–1 [0,1)d ein Spat (Parallelepiped) mit Kanten

dessen Volumen4 bekanntlich |det S–1 ist.
6.11 Korollar. Das Lebesgue—Maβ λd ist invariant unter Bewegungen.
Beweis. Eine Bewegung ist eine Komposition aus Verschiebungen τx und T ∈ 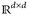 mit det T = ±1. Die Behauptung folgt also aus Satz 6.10.
mit det T = ±1. Die Behauptung folgt also aus Satz 6.10.
Aufgaben
- Es sei (E,
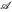 ) ein Messraum, B ⊂ E, A, A1, A2, ... ∈
) ein Messraum, B ⊂ E, A, A1, A2, ... ∈  disjunkt. Welche der folgenden Abbildungen sind messbar? (a)
disjunkt. Welche der folgenden Abbildungen sind messbar? (a)  ; (b)
; (b)  ; (c)
; (c) 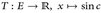 ; (d)
; (d) 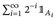 .
. - Es sei E = ℤ = {0, ±1, ±2, ... }. Zeigen Sie:
- (a)
 ist eine σ-Algebra.
ist eine σ-Algebra. - (b) T: ℤ → ℤ, T(n):= n + 2 ist
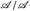 -messbar und bijektiv, aber T–1 ist nicht messbar.
-messbar und bijektiv, aber T–1 ist nicht messbar.
- (a)
- Es sei E eine Menge und (Ei,
 ) Messräume, (I beliebig, i ∈ I) und Ti: E → Ei Abbildungen.
) Messräume, (I beliebig, i ∈ I) und Ti: E → Ei Abbildungen.
- (a) Zeigen Sie: Eine Abbildung f von einem Messraum (F, ℱ) nach (E, σ(Ti: i ∈ I)) ist genau dann messbar, wenn alle Abbildungen Ti ∘ f
 -messbar sind.
-messbar sind. - (b) Es gilt σ(Ti: i ∈ I) = UK⊂I, #K ≤ #ℕ σ(Tk: k ∈ K).
- (c) Folgern Sie aus (a): Eine Funktion f: ℝn → ℝm, x ↦ (f1(x), ..., fm(x)) ist genau dann messbar, wenn alle Koordinatenabbildungen fi:
 , i = 1, 2, ..., m messbar sind.
, i = 1, 2, ..., m messbar sind.
- (a) Zeigen Sie: Eine Abbildung f von einem Messraum (F, ℱ) nach (E, σ(Ti: i ∈ I)) ist genau dann messbar, wenn alle Abbildungen Ti ∘ f
- Es seien (E,
 ) und (E′,
) und (E′,  ) Messräume und T: E → E′ eine Abbildung. Zeigen Sie:
) Messräume und T: E → E′ eine Abbildung. Zeigen Sie:
- (a)
 ;
; - (b) T ist genau dann messbar, wenn σ(T) ⊂
 ;
; - (c) T messbar, ν endliches Maß auf (E,
 ) ⇒ ν ∘ T–1 endliches Maß auf (E′,
) ⇒ ν ∘ T–1 endliches Maß auf (E′,  ). Gilt das auch für σ-endliche Maße?
). Gilt das auch für σ-endliche Maße?
- (a)
- Es sei (E,
 ) ein Messraum. A ∈
) ein Messraum. A ∈  heißtA tom, wenn
heißtA tom, wenn  oder B = A. Zeigen Sie: Messbare Funktionen sind konstant auf Atomen.
oder B = A. Zeigen Sie: Messbare Funktionen sind konstant auf Atomen. - Es sei T: E → Y eine Abbildung und
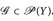 . Zeigen Sie, dass
. Zeigen Sie, dass  .
.

